Oxygen Adsorption on Polar and Non-Polar Zn:ZnO Heterostructures from First Principles
Abstract
:1. Introduction
2. Materials and Methods
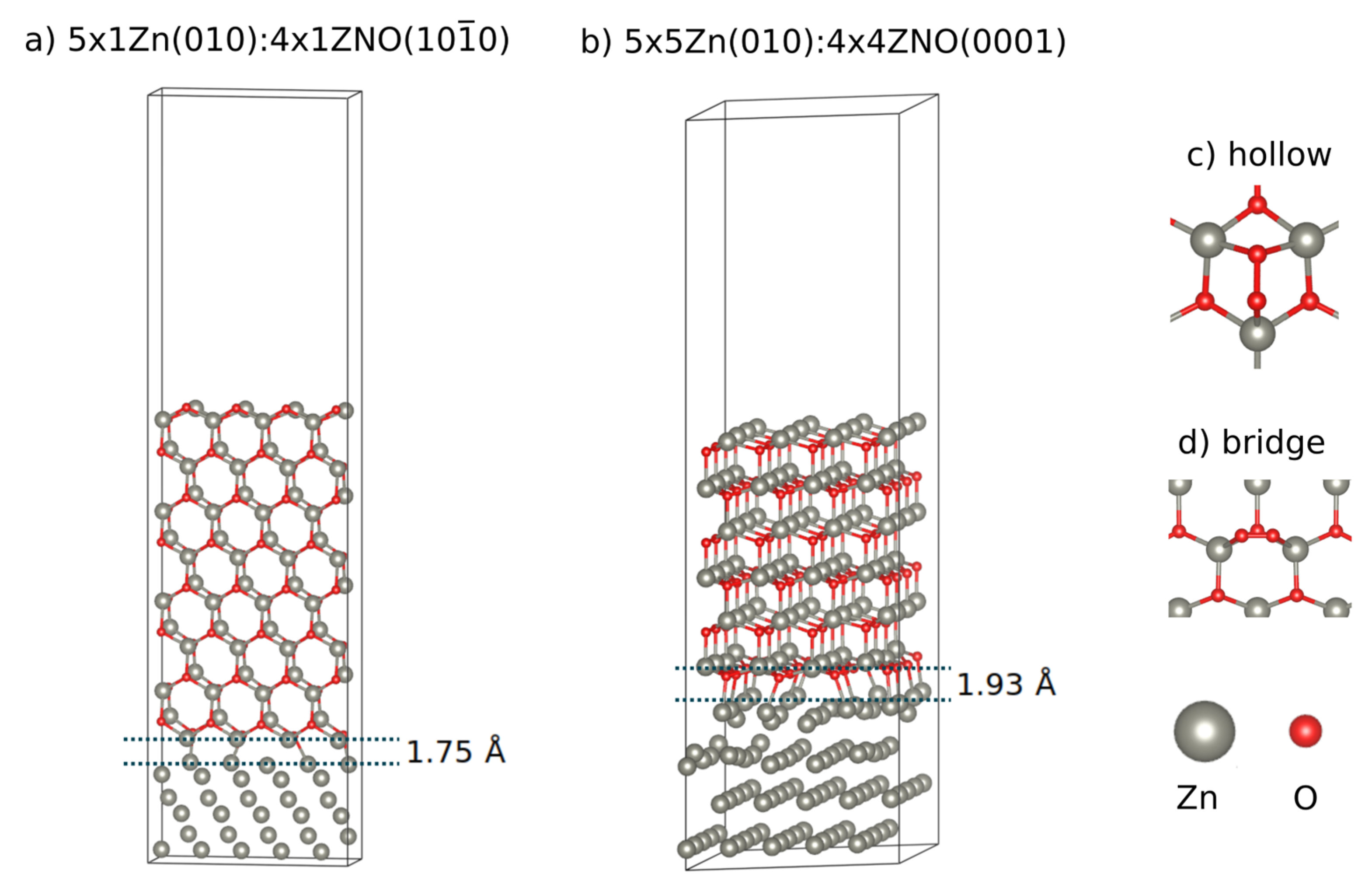
2.1. Models
2.2. DFT Calculations
3. Results and Discussion
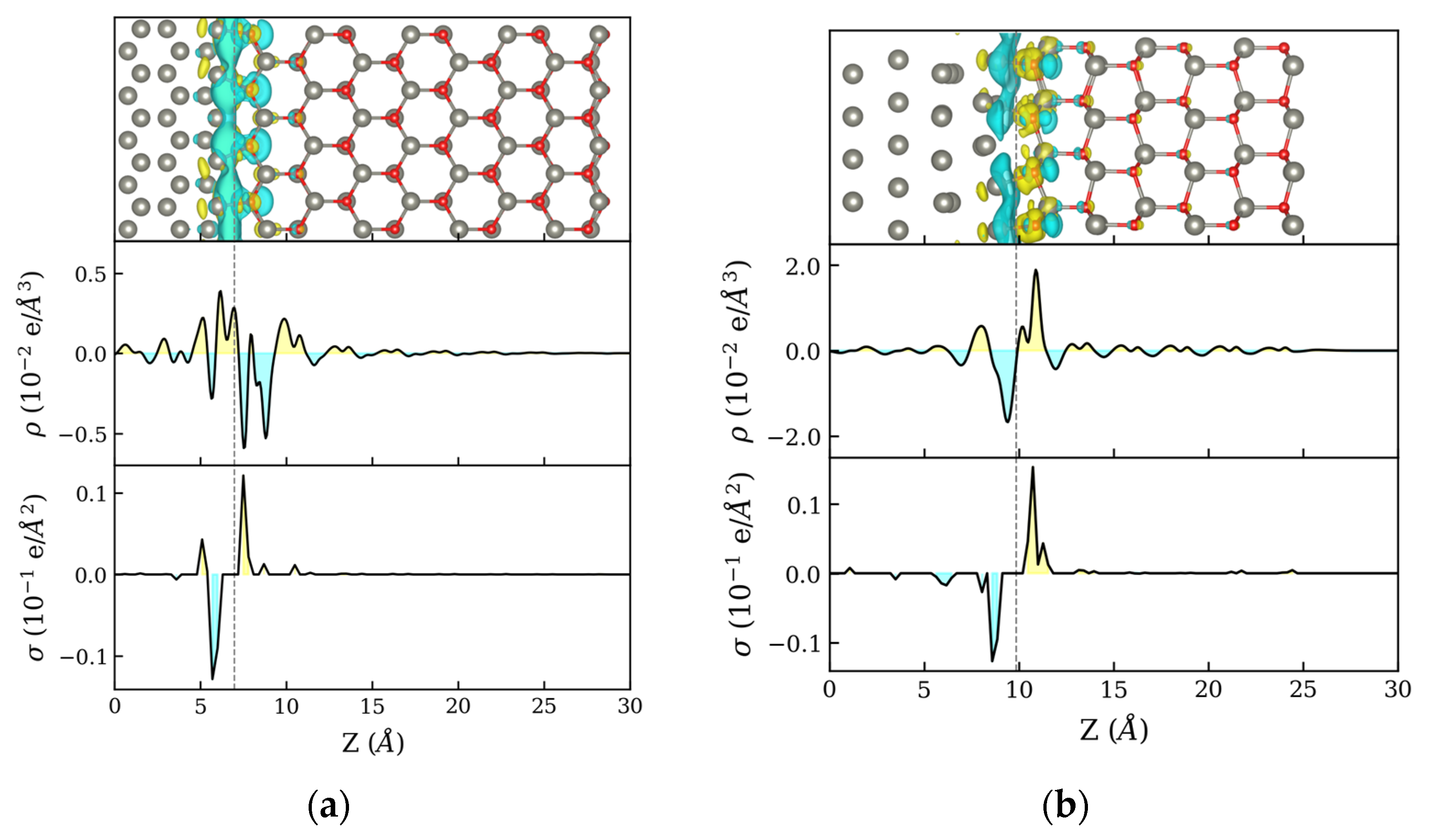
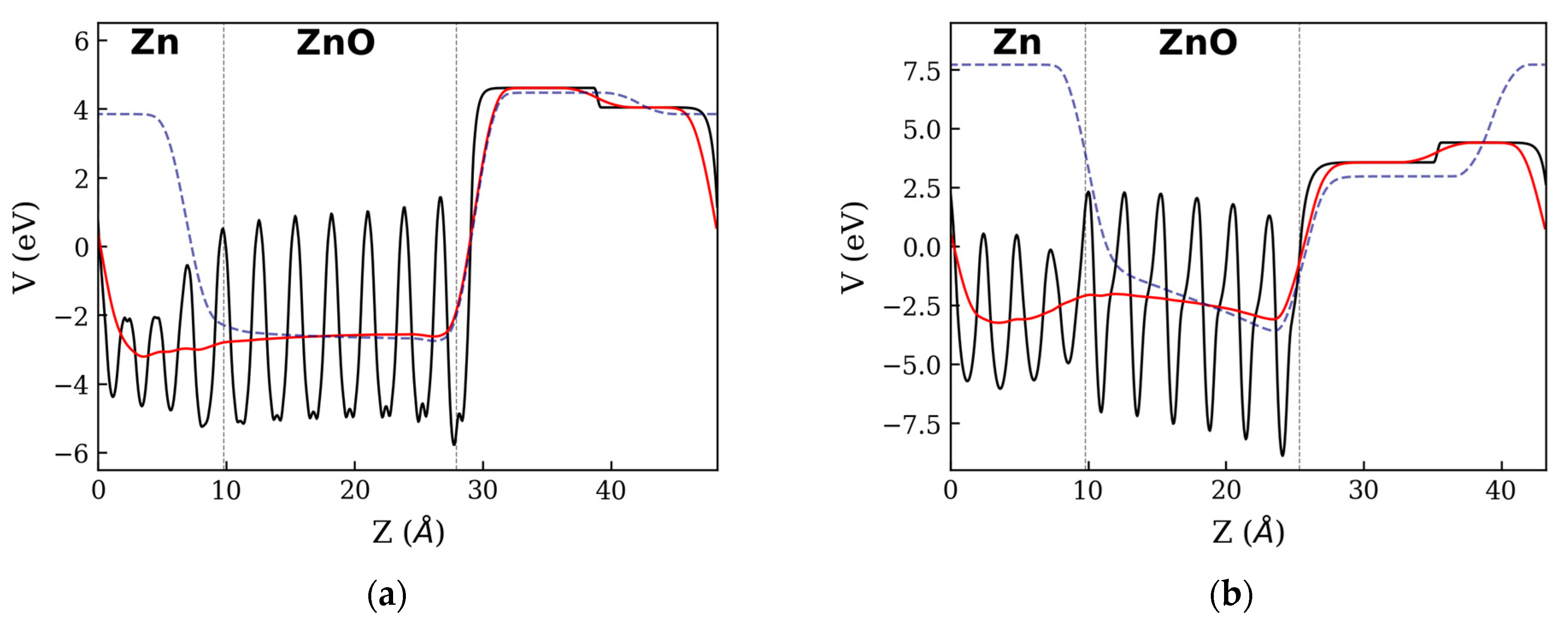
3.1. Zn:ZnO Junctions
3.2. O2 Adsorption on Zn:ZnO
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khan, W.S.; Cao, C.; Chen, Z.; Nabi, G. Synthesis, Growth Mechanism, Photoluminescence and Field Emission Properties of Metal–Semiconductor Zn–ZnO Core–Shell Microcactuses. Mater. Chem. Phys. 2010, 124, 493–498. [Google Scholar] [CrossRef]
- Moezzi, A.; McDonagh, A.M.; Cortie, M.B. Zinc Oxide Particles: Synthesis, Properties and Applications. Chem. Eng. J. 2012, 185–186, 1–22. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, F.; Lu, Y.; Xu, M.; Li, Q. Induction of Zinc Particles on the Morphology and Photoluminescent Property of Globular Zn/ZnO Core/Shell Nanorod Heterojunction Array Architectures. J. Exp. Nanosci. 2016, 11, 383–394. [Google Scholar] [CrossRef]
- Lupan, O.; Chow, L.; Chai, G.; Heinrich, H. Fabrication and Characterization of Zn-ZnO Core-Shell Microspheres from Nanorods. Chem. Phys. Lett. 2008, 465, 249–253. [Google Scholar] [CrossRef]
- Khan, W.S.; Cao, C.; Nabi, G.; Yao, R.; Bhatti, S.H. Catalyst-Free Combined Synthesis of Zn/ZnO Core/Shell Hollow Microspheres and Metallic Zn Microparticles by Thermal Evaporation and Condensation Route. J. Alloys Compd. 2010, 506, 666–672. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Dai, J.Y.; Lam, C.H.; Wang, H.T.; Webley, P.A.; Li, Q.; Ong, H.C. Zinc/ZnO Core-Shell Hexagonal Nanodisk Dendrites and Their Photoluminescence. Acta Mater. 2007, 55, 5039–5044. [Google Scholar] [CrossRef]
- Hu, J.Q.; Li, Q.; Meng, X.M.; Lee, C.S.; Lee, S.T. Thermal Reduction Route to the Fabrication of Coaxial Zn/ZnO Nanocables and ZnO Nanotubes. Chem. Mater. 2003, 15, 305–308. [Google Scholar] [CrossRef]
- Gao, P.X.; Lao, C.S.; Ding, Y.; Wang, Z.L. Metal/Semiconductor Core/Shell Nanodisks and Nanotubes. Adv. Funct. Mater. 2006, 16, 53–62. [Google Scholar] [CrossRef]
- Calderon, V.S.; Gomes, B.; Ferreira, P.J.; Carvalho, S. Zinc Nanostructures for Oxygen Scavenging. Nanoscale 2017, 9, 5254–5262. [Google Scholar] [CrossRef]
- Landolt, D. Corrosion and Surface Chemistry of Metals. Mater. Today 2007, 10, 57. [Google Scholar] [CrossRef]
- Zhdanov, V.P.; Kasemo, B. Cabrera–Mott Kinetics of Oxidation of Nm-Sized Metal Particles. Chem. Phys. Lett. 2008, 452, 285–288. [Google Scholar] [CrossRef]
- Ermoline, A.; Dreizin, E.L. Equations for the Cabrera–Mott Kinetics of Oxidation for Spherical Nanoparticles. Chem. Phys. Lett. 2011, 505, 47–50. [Google Scholar] [CrossRef]
- Zhdanov, V.P.; Kasemo, B. Cabrera-Mott Kinetics of Oxidation of Metal Nanowires. Appl. Phys. Lett. 2012, 100, 243105. [Google Scholar] [CrossRef]
- Mahapatra, A.K.; Bhatta, U.M.; Som, T. Oxidation Mechanism in Metal Nanoclusters: Zn Nanoclusters to ZnO Hollow Nanoclusters. J. Phys. D Appl. Phys. 2012, 45, 415303. [Google Scholar] [CrossRef]
- Mora-Fonz, D.; Lazauskas, T.; Farrow, M.R.; Catlow, C.R.A.; Woodley, S.M.; Sokol, A.A. Why Are Polar Surfaces of ZnO Stable? Chem. Mater. 2017, 29, 5306–5320. [Google Scholar] [CrossRef]
- Ding, Y.; Kong, X.Y.; Wang, Z.L. Interface and Defect Structures of Zn-ZnO Core-Shell Heteronanobelts. J. Appl. Phys. 2004, 95, 306–310. [Google Scholar] [CrossRef]
- Sołtys, J.; Piechota, J.; Łopuszyński, M.; Krukowski, S. Density Functional Theory (DFT) Study of Zn, O2 and O Adsorption on Polar ZnO(0001) and ZnO (0001) Surfaces. J. Cryst. Growth 2013, 374, 53–59. [Google Scholar] [CrossRef]
- Ma, D.; Wang, Z.; Cui, H.; Zeng, J.; He, C.; Lu, Z. First-Principles Study of O2 Adsorption on Al-Doped ZnO(1010) Surface. Sens. Actuators B Chem. 2016, 224, 372–380. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B Condens. Matter Mater. Phys. 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Bashyal, K.; Pyles, C.K.; Afroosheh, S.; Lamichhane, A.; Zayak, A.T. Empirical Optimization of DFT + U and HSE for the Band Structure of ZnO. J. Phys. Condens. Matter 2018, 30, 065501. [Google Scholar] [CrossRef] [PubMed]
- Hinuma, Y.; Grüneis, A.; Kresse, G.; Oba, F. Band Alignment of Semiconductors from Density-Functional Theory and Many-Body Perturbation Theory. Phys. Rev. B 2014, 90, 155405. [Google Scholar] [CrossRef]
- Ma, X.; Wu, Y.; Lv, Y.; Zhu, Y. Correlation Effects on Lattice Relaxation and Electronic Structure of ZnO within the GGA+ U Formalism. J. Phys. Chem. C 2013, 117, 26029–26039. [Google Scholar] [CrossRef]
- Hinuma, Y.; Oba, F.; Kumagai, Y.; Tanaka, I. Band Offsets of CuInSe2/CdS and CuInSe2/ZnS (110) Interfaces: A Hybrid Density Functional Theory Study. Phys. Rev. B Condens. Matter Mater. Phys. 2013, 88, 035305. [Google Scholar] [CrossRef]
- Colombo, L.; Resta, R.; Baroni, S. Valence-Band Offsets at Strained Si/Ge Interfaces. Phys. Rev. B 1991, 44, 5572–5579. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A Fast and Robust Algorithm for Bader Decomposition of Charge Density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- D’Amico, N.R.; Cantele, G.; Perroni, C.A.; Ninno, D. Electronic Properties and Schottky Barriers at ZnO–Metal Interfaces from First Principles. J. Phys. Condens. Matter 2015, 27, 015006. [Google Scholar] [CrossRef]
- Todorova, M.; Neugebauer, J. Identification of Bulk Oxide Defects in an Electrochemical Environment. Faraday Discuss. 2015, 180, 97–112. [Google Scholar] [CrossRef]
- Morkoç, H.; Özgür, Ü. Zinc Oxide; Wiley-VCH: Weinheim, Germany, 2009; ISBN 978-3-52740-813-9. [Google Scholar]
- Gorai, P.; Seebauer, E.G.; Ertekin, E. Mechanism and Energetics of O and O 2 Adsorption on Polar and Non-Polar ZnO Surfaces. J. Chem. Phys. 2016, 144, 184708. [Google Scholar] [CrossRef]



| System | ZnO nº Layers | Eads (eV) | ΔVdW (eV) | Q (e−) | r(O-O) (Å) | r(Zn1-O1) (Å) | r(Zn2-O2) (Å) |
|---|---|---|---|---|---|---|---|
| Zn(010):ZnO() (NPZnOTH) | 4 | −0.315 | −0.138 | 0.318 | 1.278 | 2.264 | 2.268 |
| 8 | −0.213 | −0.145 | 0.165 | 1.253 | 2.489 | 2.491 | |
| Zn(001):ZnO(0001) (PZnOTH) | 4 | −2.432 | −0.136 | 1.133 | 1.474 | 1.931 | 2.041 |
| 6 | −2.556 | −0.157 | 1.134 | 1.473 | 1.935 | 2.044 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castro, A.; Calderon, S.; Marques, L. Oxygen Adsorption on Polar and Non-Polar Zn:ZnO Heterostructures from First Principles. Materials 2023, 16, 1275. https://doi.org/10.3390/ma16031275
Castro A, Calderon S, Marques L. Oxygen Adsorption on Polar and Non-Polar Zn:ZnO Heterostructures from First Principles. Materials. 2023; 16(3):1275. https://doi.org/10.3390/ma16031275
Chicago/Turabian StyleCastro, António, Sebastian Calderon, and Luís Marques. 2023. "Oxygen Adsorption on Polar and Non-Polar Zn:ZnO Heterostructures from First Principles" Materials 16, no. 3: 1275. https://doi.org/10.3390/ma16031275
APA StyleCastro, A., Calderon, S., & Marques, L. (2023). Oxygen Adsorption on Polar and Non-Polar Zn:ZnO Heterostructures from First Principles. Materials, 16(3), 1275. https://doi.org/10.3390/ma16031275






