Towards Highly Efficient, Additively Manufactured Passive Vibration Eliminators for Mechanical Systems
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Samples Preparation
- Acrylonitrile butadiene styrene terpolymer (ABS)—trade name: Z-ABS;
- Natural thermoplastic polyester—polylactic acid (PLA)—trade name: Z-PLA;
- Engineering polymer from the family of nylon/polyamide (PA) filaments—trade name: Z-NYLON;
- Flexible thermoplastic polyurethane (TPU)—trade name: Z-SEMIFLEX.
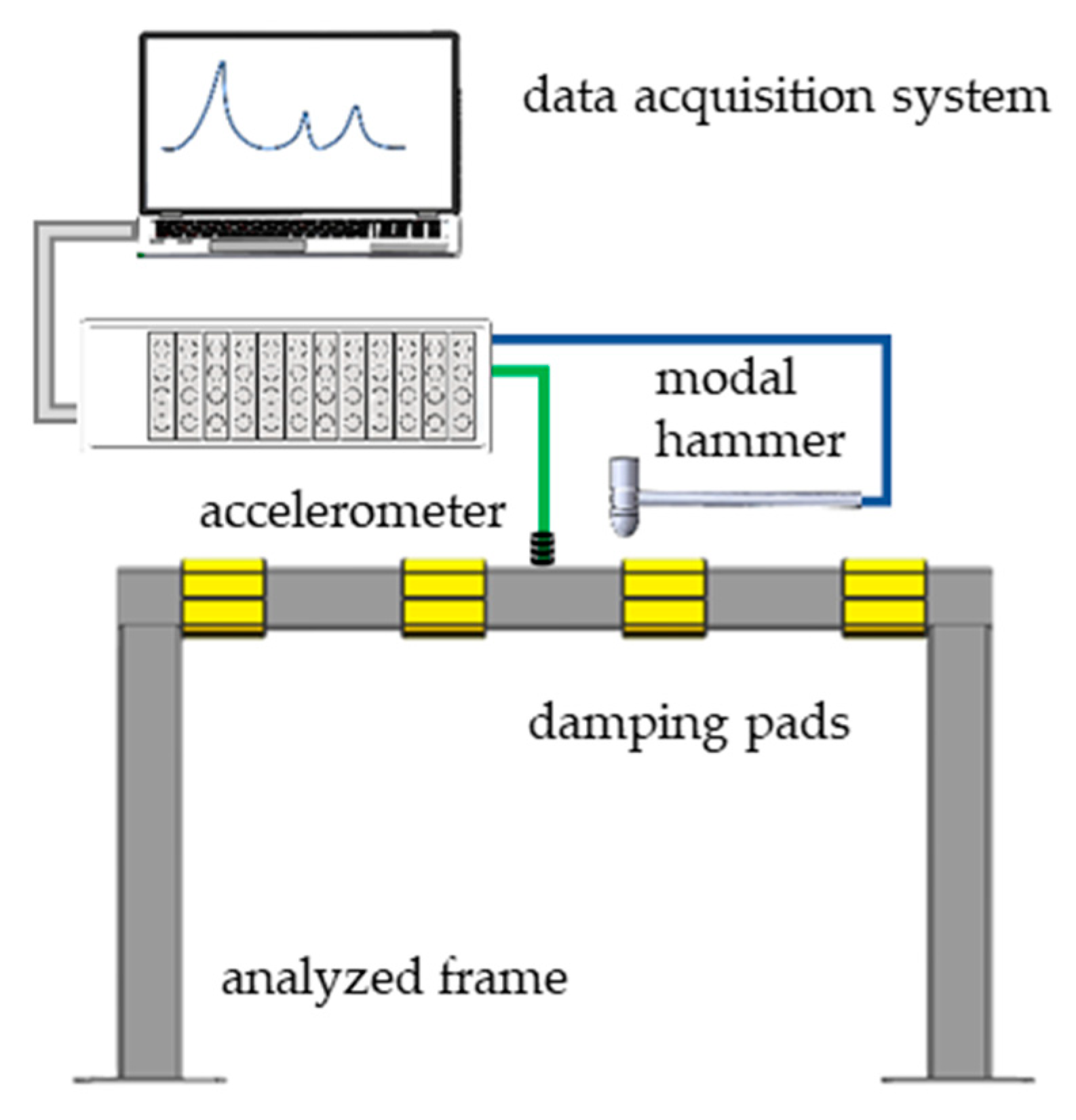
2.2. Characterization Methods
3. Results
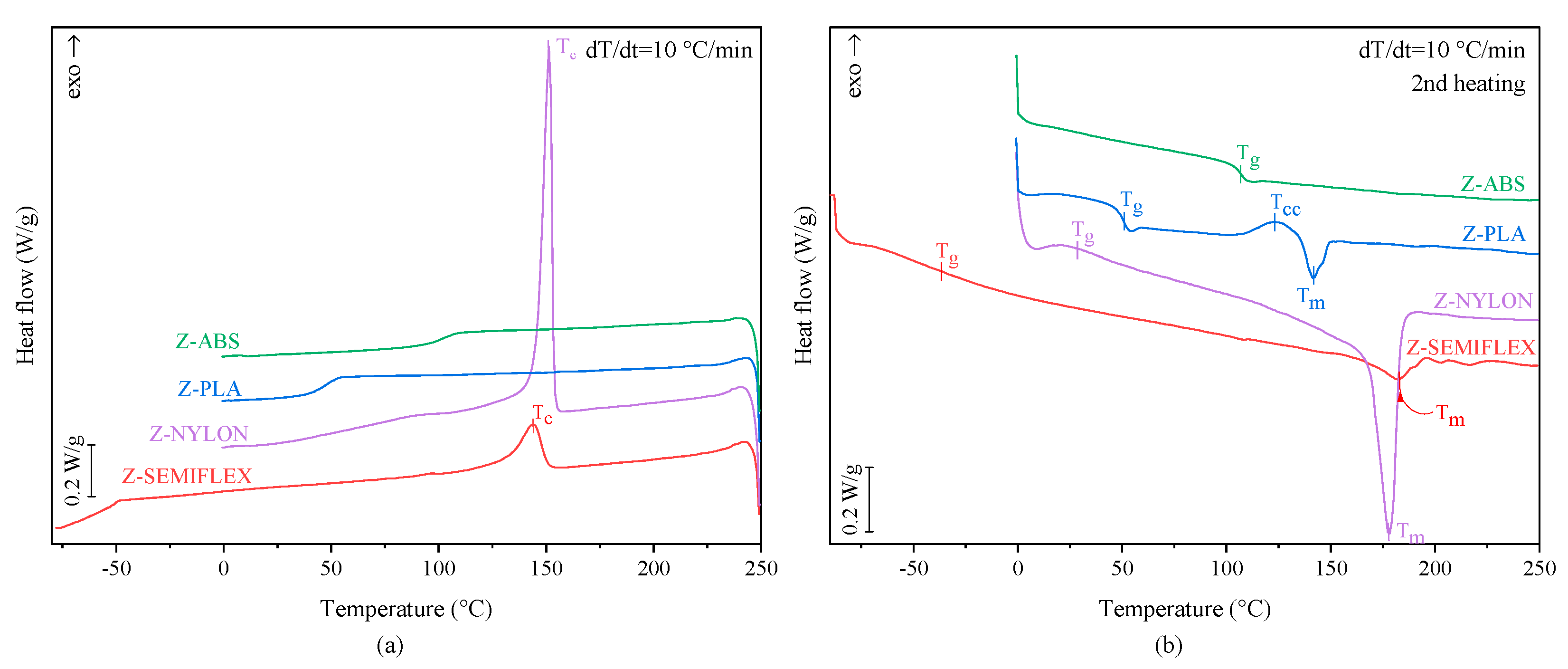
3.1. Crystallization and Glass Transition Behavior
3.2. Dynamic Mechanical Behavior
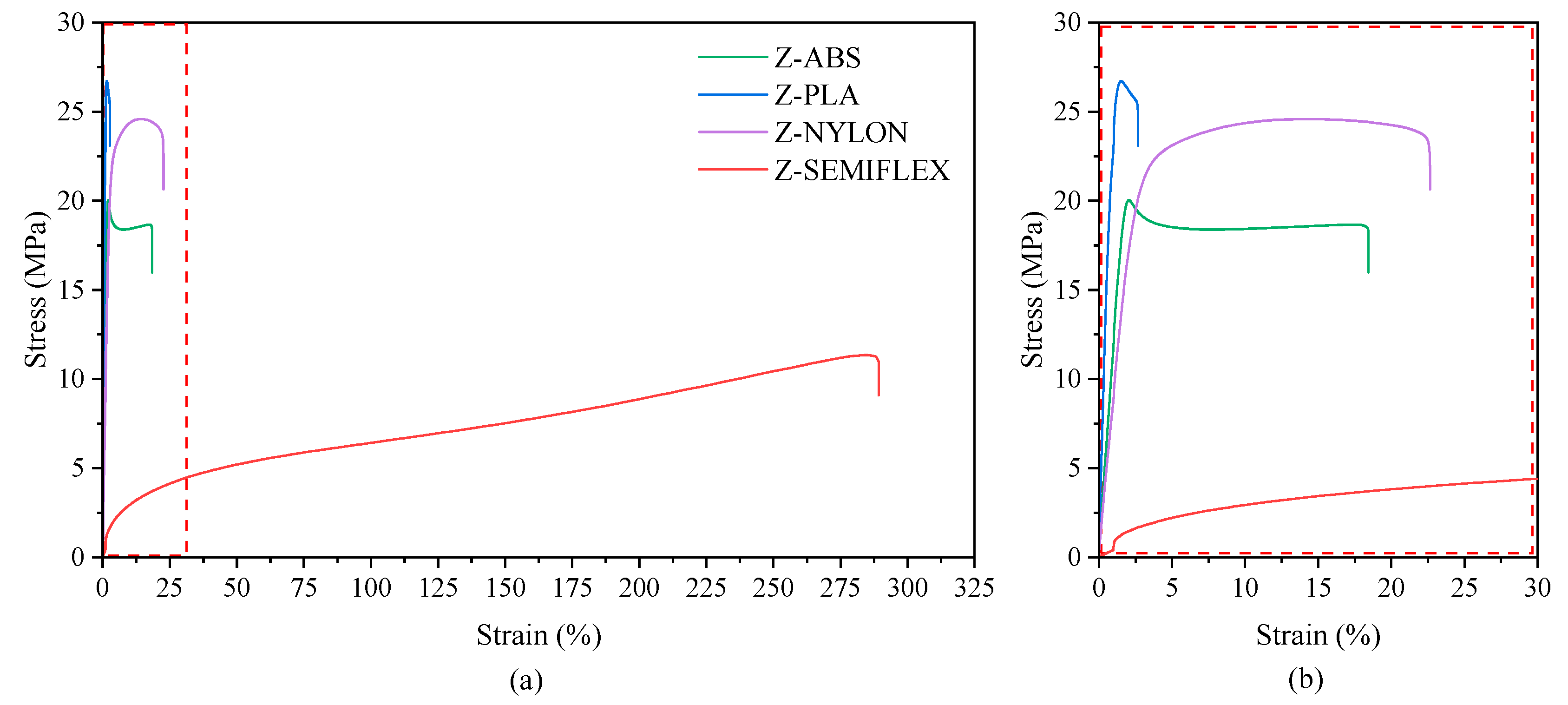
3.3. Mechanical Performance
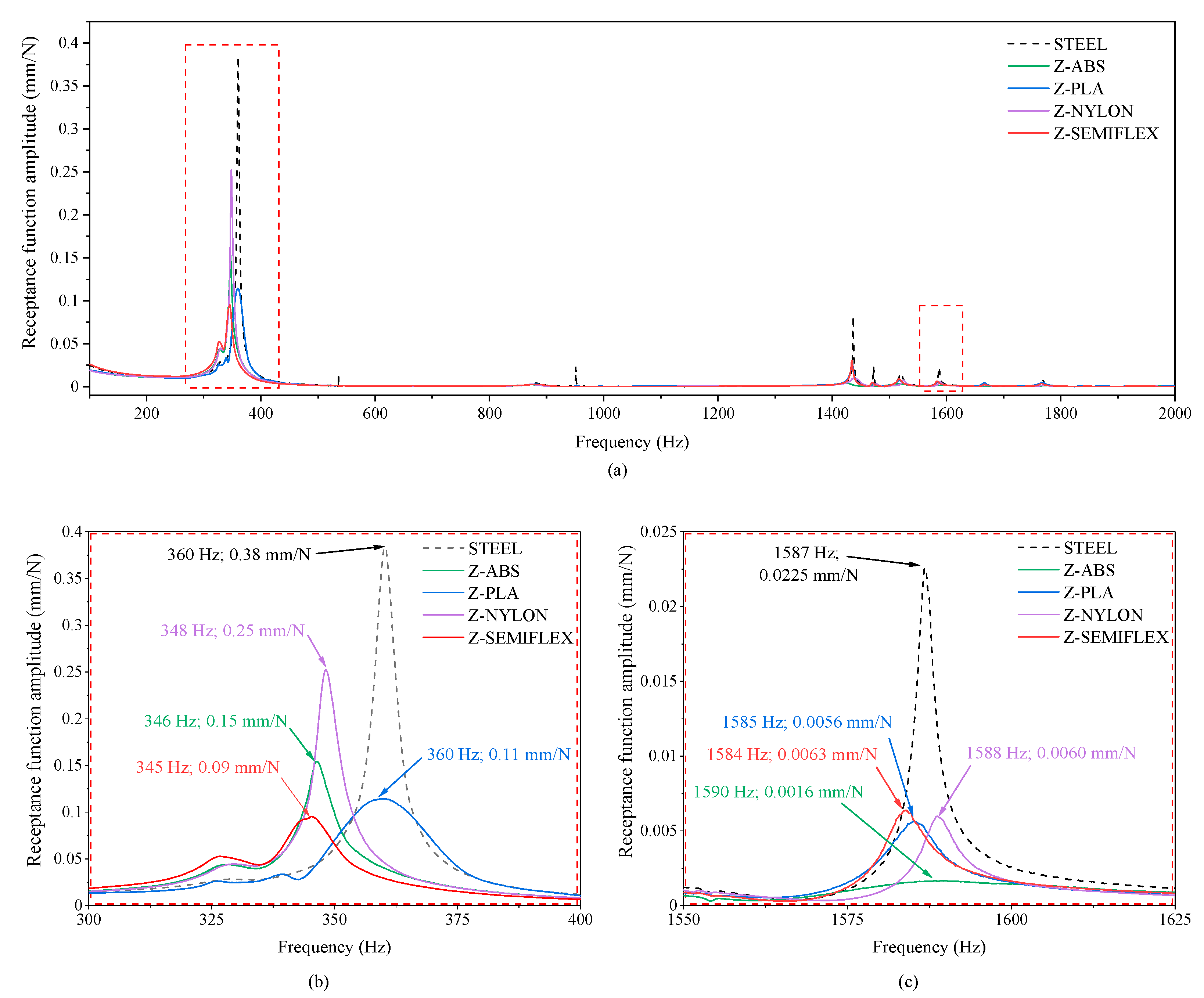
3.4. Impulse Test
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pilch, Z.; Domin, J.; Szlapa, A. The impact of vibration of the 3D printer table on the quality of print. In Proceedings of the 2015 Selected Problems of Electrical Engineering and Electronics (WZEE), Kielce, Poland, 17–19 September 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Grabiec, J.; Pajor, M.; Dunaj, P. Finite Element Modeling of Dynamic Properties of the Delta Robot with Base Frame. Mater. 2022, 15, 6797. [Google Scholar] [CrossRef]
- Okulik, T.; Dunaj, P.; Chodźko, M.; Marchelek, K.; Powałka, B. Determination of dynamic properties of a steel hollow section filled with composite mineral casting. In Lecture Notes in Mechanical Engineering; Pleiades Publishing: Warrensburg, MI, USA, 2019; pp. 561–571. [Google Scholar]
- Dunaj, P.; Berczyński, S.; Chodźko, M. Method of modeling steel-polymer concrete frames for machine tools. Compos. Struct. 2020, 242, 112197. [Google Scholar] [CrossRef]
- Tiboni, M.; Remino, C.; Bussola, R.; Amici, C. A Review on Vibration-Based Condition Monitoring of Rotating Machinery. Appl. Sci. 2022, 12, 972. [Google Scholar] [CrossRef]
- Dunaj, P.; Berczyński, S.; Miadlicki, K.; Irska, I.; Niesterowicz, B. Increasing damping of thin-walled structures using additively manufactured vibration eliminators. Materials 2020, 13, 2125. [Google Scholar] [CrossRef] [PubMed]
- Alujević, N.; Čakmak, D.; Wolf, H.; Jokić, M. Passive and active vibration isolation systems using inerter. J. Sound Vib. 2018, 418, 163–183. [Google Scholar] [CrossRef]
- Baz, A.M. Active and Passive Vibration Damping; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Białas, K. Passive and Active Elements in Reduction of Vibrations of Torsional Systems. Solid State Phenom. 2010, 164, 260–264. [Google Scholar] [CrossRef]
- Marakakis, K.; Tairidis, G.K.; Koutsianitis, P.; Stavroulakis, G.E. Shunt piezoelectric systems for noise and vibration control: A review. Front. Built Environ. 2019, 5, 64. [Google Scholar] [CrossRef]
- Masliyev, V.; Dushchenko, V.; Yepifanov, V.; Nanivskyi, R.; Cherevko, Y.; Masliev, A.; Demydov, A.; Makarenko, Y. Improving The Damping of Vehicle Vibration By Improving Pneumatic Springs. East. Eur. J. Enterp. Technol. 2022, 1, 59–66. [Google Scholar] [CrossRef]
- Wang, W.; Liang, Y.; Zhang, W.; Iwnicki, S. Effect of the nonlinear displacement-dependent characteristics of a hydraulic damper on high-speed rail pantograph dynamics. Nonlinear Dyn. 2019, 95, 3439–3464. [Google Scholar] [CrossRef]
- Novikov, V.V.; Ryabov, I.M.; Pozdeev, A.V.; Chernyshov, K.V.; Chumakov, D.A. Vibrational Protection by Pneumatic Suspension with Hybrid Damping. Russ. Eng. Res. 2022, 42, 661–669. [Google Scholar] [CrossRef]
- Qin, Y.; Tang, X.; Jia, T.; Duan, Z.; Zhang, J.; Li, Y.; Zheng, L. Noise and vibration suppression in hybrid electric vehicles: State of the art and challenges. Renew. Sustain. Energy Rev. 2020, 124, 109782. [Google Scholar] [CrossRef]
- Den Hartog, J.P. Mechanical Vibrations; Courier Corporation: Chelmsford, UK, 1985; ISBN 0486647854. [Google Scholar]
- Casalotti, A.; Lacarbonara, W. Nonlinear Vibration Absorber Optimal Design via Asymptotic Approach. Procedia IUTAM 2016, 19, 65–74. [Google Scholar] [CrossRef]
- Mohamed, A.; Hassan, A.; Omer, A.A. Passive vibration damping of a cantilever plate. IOP Conf. Ser. Mater. Sci. Eng. 2020, 973, 12036. [Google Scholar] [CrossRef]
- Furtmüller, T.; Di Matteo, A.; Adam, C.; Pirrotta, A. Base-isolated structure equipped with tuned liquid column damper: An experimental study. Mech. Syst. Signal Process. 2019, 116, 816–831. [Google Scholar] [CrossRef]
- Nagy-György, P.; Hős, C. Predicting the damping characteristics of vibration dampers employing generalized shear thickening fluids. J. Sound Vib. 2021, 506, 116116. [Google Scholar] [CrossRef]
- Albertelli, P.; Esposito, S.; Mussi, V.; Goletti, M.; Monno, M. Effect of metal foam on vibration damping and its modelling. Int. J. Adv. Manuf. Technol. 2021, 117, 2349–2358. [Google Scholar] [CrossRef]
- Chakraborty, B.C.; Ratna, D. Polymers for Vibration Damping Applications; Elsevier: Amsterdam, The Netherlands, 2020; ISBN 9780128192528. [Google Scholar]
- Chakraborty, B.C.; Srinivasan, P. Vibration Damping by Polymers. In Smart Polymers; CRC Press: Boca Raton, FL, USA, 2022; pp. 262–289. [Google Scholar] [CrossRef]
- Chung, D.D.L. Materials for vibration damping. J. Mater. Sci. 2001, 36, 5733–5737. [Google Scholar] [CrossRef]
- Salahuddin, B.; Mutlu, R.; Baigh, T.A.; Alghamdi, M.N.; Aziz, S. Self-Reinforced Nylon 6 Composite for Smart Vibration Damping. Polymers 2021, 13, 1235. [Google Scholar] [CrossRef]
- Aizat, M.; Karim, A.; Zaman, I. Vibration Control of Structure using Vibration Absorber Made from Polymer Reinforced Natural Fibers. Adv. Res. Nat. Fibers 2019, 1, 1–6. [Google Scholar]
- Praveen, S.; Bahadur, J.; Yadav, R.; Billa, S.; Umasankar Patro, T.; Rath, S.K.; Ratna, D.; Patri, M. Tunable viscoelastic and vibration damping properties of a segmented polyurethane synergistically reinforced with carbon black and anisotropic additives. Appl. Acoust. 2020, 170, 107535. [Google Scholar] [CrossRef]
- Palmieri, M.; Zucca, G.; Morettini, G.; Landi, L.; Cianetti, F. Vibration Fatigue of FDM 3D Printed Structures: The Use of Frequency Domain Approach. Mater. 2022, 15, 854. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Shang, J.; Li, X.; Luo, Z.; Wu, W. Vibration and damping characteristics of 3D printed Kagome lattice with viscoelastic material filling. Sci. Reports 2018, 8, 1–13. [Google Scholar] [CrossRef]
- Hu, H.; Zhang, R.; Shi, L.; Ying, W.B.; Wang, J.; Zhu, J. Modification of poly(butylene 2,5-furandicarboxylate) with lactic acid for biodegradable copolyesters with good mechanical and barrier properties. Ind. Eng. Chem. Res. 2018, 57, 11020–11030. [Google Scholar] [CrossRef]
- Wei, W.; Zhang, Y.; Liu, M.; Zhang, Y.; Yin, Y.; Gutowski, W.S.; Deng, P.; Zheng, C. Improving the damping properties of nanocomposites by monodispersed hybrid POSS nanoparticles: Preparation and mechanisms. Polymers 2019, 11, 647. [Google Scholar] [CrossRef]
- Guidotti, G.; Soccio, M.; Siracusa, V.; Gazzano, M.; Salatelli, E.; Munari, A.; Lotti, N. Novel random PBS-based copolymers containing aliphatic aide chains for sustainable flexible food packaging. Polymers 2017, 9, 724. [Google Scholar] [CrossRef]
- Irska, I.; Paszkiewicz, S.; Gorący, K.; Linares, A.; Ezquerra, T.A.; Jędrzejewski, R. Poly(butylene terephthalate)/polylactic acid based copolyesters and blends: Miscibility-structure-property relationship. Express Polym. Lett. 2020, 14, 26–47. [Google Scholar] [CrossRef]


| Sample | Print Temperature (°C) | Bed Temperature (°C) |
|---|---|---|
| Z-ABS | 270 | 65 |
| Z-PLA | 220 | 60 |
| Z-NYLON | 260 | 80 |
| Z-SEMIFLEX | 225 | 65 |
| Material | Mass, kg |
|---|---|
| Damping pad | |
| Z-ABS | 0.198 |
| Z-PLA | 0.234 |
| Z-NYLON | 0.160 |
| Z-SEMIFLEX | 0.242 |
| Frame | |
| Steel | 12.121 |
| Parameter | Value |
|---|---|
| Sampling rate | 4096 Hz |
| Frequency resolution | 0.5 Hz |
| Signal acquisition time | 2 s |
| Scaling of the frequency response function | global |
| Sample | Glass Transition | Crystallization | Melting | |||||
|---|---|---|---|---|---|---|---|---|
| Tg (°C) | ΔCp (J/g·°C) | Tc (°C) | ΔHc (J/g) | Tcc (°C) | ΔHcc (J/g) | Tm (°C) | ΔHm (J/g) | |
| Z-ABS | 105.9 | 0.30 | - | - | - | - | - | - |
| Z-PLA | 49.3 | 0.39 | - | - | 122.2 | 5.19 | 141.9 | 5.40 |
| Z-NYLON | 30.8 | 0.24 | 151.7 | 77.47 | - | - | 177.7 | 72.95 |
| Z-SEMIFLEX | −36.5 | 0.13 | 143.6 | 15.32 | - | - | 182.0 | 14.95 |
| Sample | E’ at 25 °C (MPa) | Tα (°C) | tanδ at Tα (-) | tanδ at 25 °C (-) |
|---|---|---|---|---|
| Z-ABS | 918 | 119.4 | 1.93 | 0.02 |
| Z-PLA | 1980 | 66.4/107.5 | 1.98/0.53 | 0.01 |
| Z-NYLON | 721 | 61.1 | 0.23 | 0.02 |
| Z-SEMIFLEX | 100 | 34.6 | 0.29 | 0.26 |
| Sample | E (MPa) | σy (MPa) | εy (%) | σb (MPa) | εy (%) | H (°ShD) |
|---|---|---|---|---|---|---|
| Z-ABS | 1110 ± 25 | 20.04 ± 0.24 | 2.04 ± 0.03 | 1830 ± 0.12 | 18.44 ± 2.64 | 67 ± 1 |
| Z-PLA | 2853 ± 65 | 26.72 ± 0.34 | 1.52 ± 0.03 | 24.09 ± 0.57 | 2.69 ± 0.26 | 79 ± 1 |
| Z-NYLON | 950 ± 24 | - | - | 24.59 ± 0.39 | 22.59 ± 2.69 | 62 ± 1 |
| Z-SEMIFLEX | - | - | - | 11.35 ± 0.86 | 289.14 ± 20.72 | 43 ± 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Irska, I.; Kramek, G.; Miądlicki, K.; Dunaj, P.; Berczyński, S.; Piesowicz, E. Towards Highly Efficient, Additively Manufactured Passive Vibration Eliminators for Mechanical Systems. Materials 2023, 16, 1250. https://doi.org/10.3390/ma16031250
Irska I, Kramek G, Miądlicki K, Dunaj P, Berczyński S, Piesowicz E. Towards Highly Efficient, Additively Manufactured Passive Vibration Eliminators for Mechanical Systems. Materials. 2023; 16(3):1250. https://doi.org/10.3390/ma16031250
Chicago/Turabian StyleIrska, Izabela, Grzegorz Kramek, Karol Miądlicki, Paweł Dunaj, Stefan Berczyński, and Elżbieta Piesowicz. 2023. "Towards Highly Efficient, Additively Manufactured Passive Vibration Eliminators for Mechanical Systems" Materials 16, no. 3: 1250. https://doi.org/10.3390/ma16031250
APA StyleIrska, I., Kramek, G., Miądlicki, K., Dunaj, P., Berczyński, S., & Piesowicz, E. (2023). Towards Highly Efficient, Additively Manufactured Passive Vibration Eliminators for Mechanical Systems. Materials, 16(3), 1250. https://doi.org/10.3390/ma16031250







