Uncertain Dynamic Characteristic Analysis for Structures with Spatially Dependent Random System Parameters
Abstract
1. Introduction
2. Representation of the Uncertainty with Random Field
2.1. Gauss Random Field Model
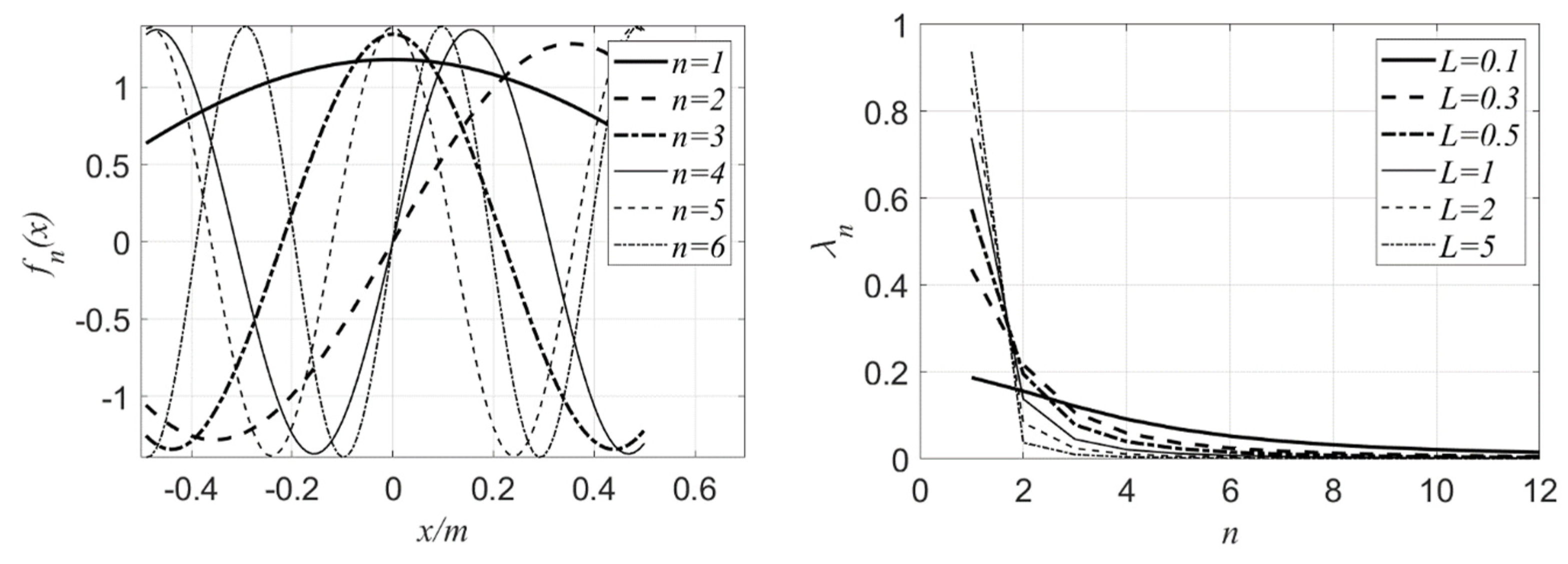
2.2. Karhunen–Loeve Expansion
3. Structural Parameters Uncertainty Characterizing and Quantification
3.1. The Analysis of Structural Dynamic Characteristics with Random Field
- (1)
- Taking any normalized mode shape as the initial solution vector and carrying out the first iteration according to the formula , whereby the first components in both and are normalized to 1.
- (2)
- If , assigning to as the trial solution vector, and repeating step (1) until the k-th iteration meeting , it indicates that the iteration converges if , then and . It should be noted that the ideal results actually cannot be obtained in the actual iteration process due to the existence of errors, but it also means the convergence of iterations when , whereby err is the selected error threshold.
3.2. Multidimensional Kernel Density Estimation
3.3. Maximum Likelihood Estimation
4. Case Study
4.1. I-Beam with One-Dimensional Random Field
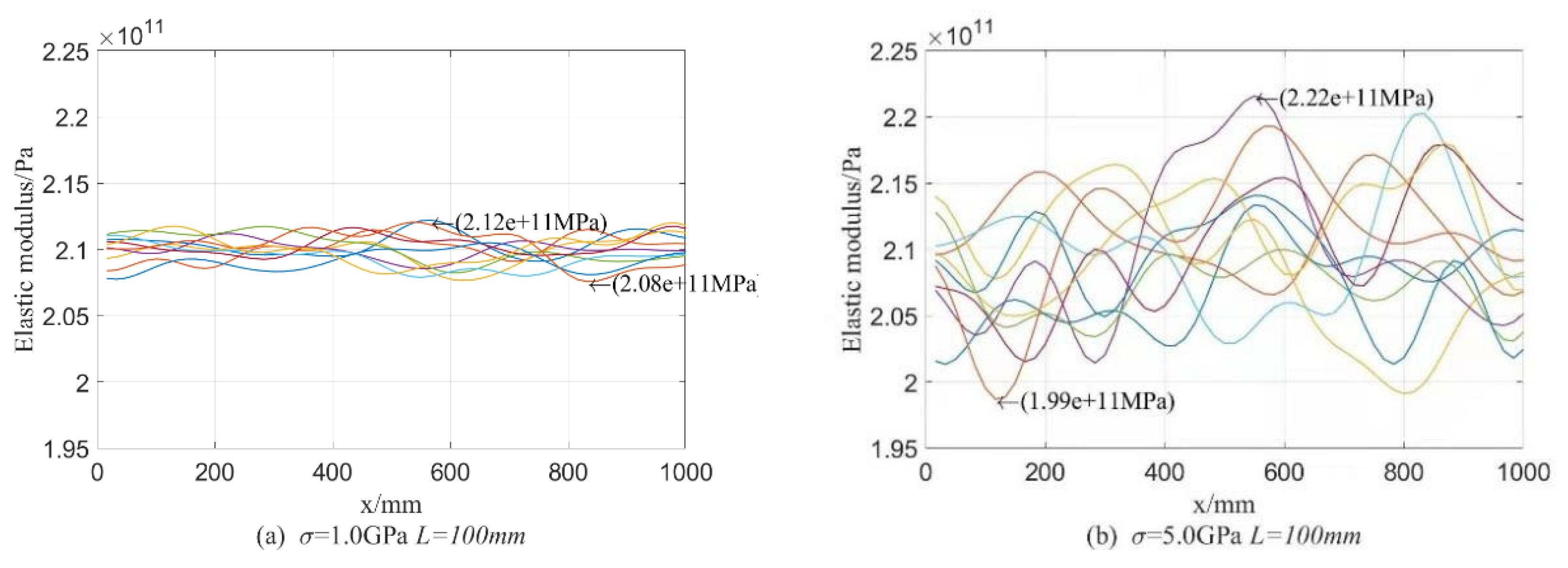
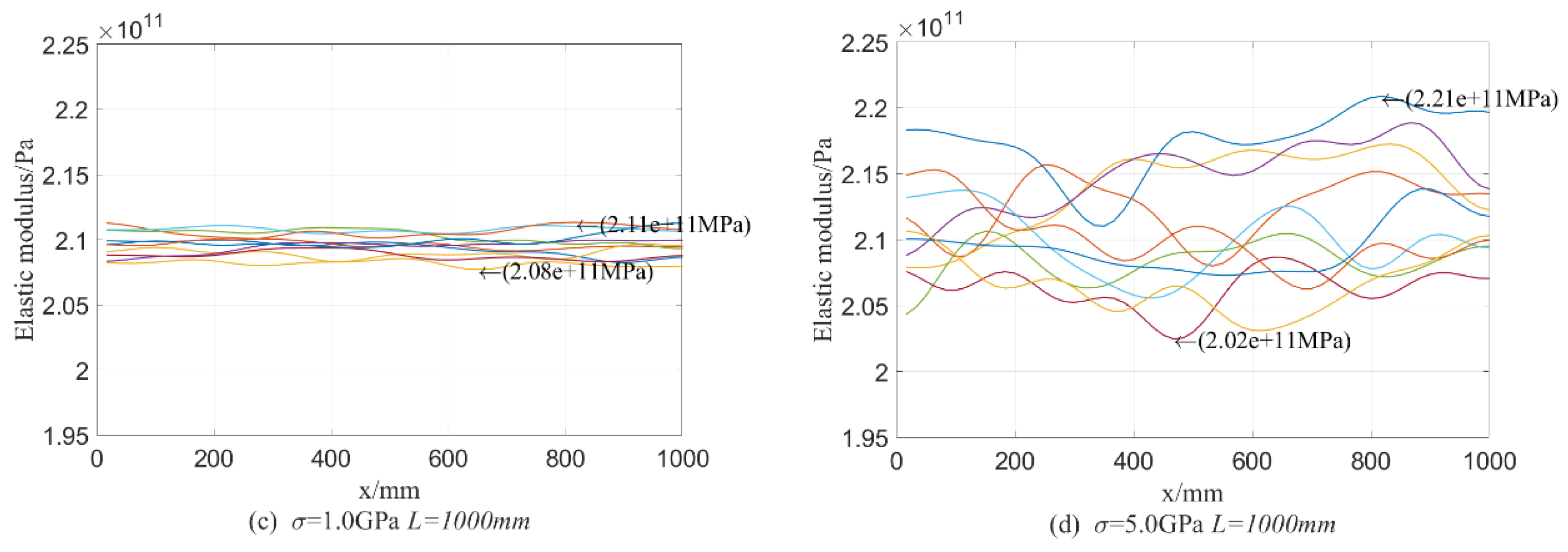
4.1.1. Test Data Analysis
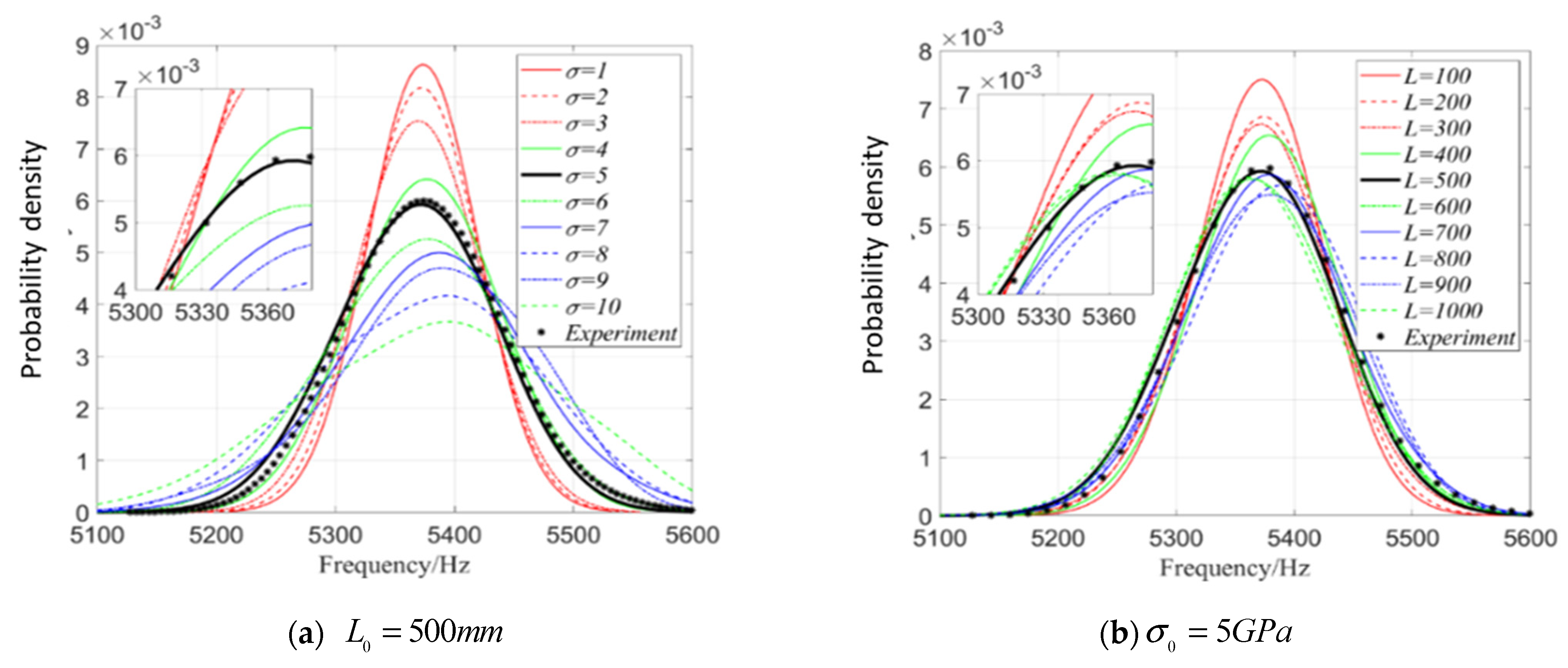
4.1.2. One-Dimensional Kernel Density Estimation
4.1.3. Multidimensional Kernel Density Estimation and Maximum Likelihood Estimation
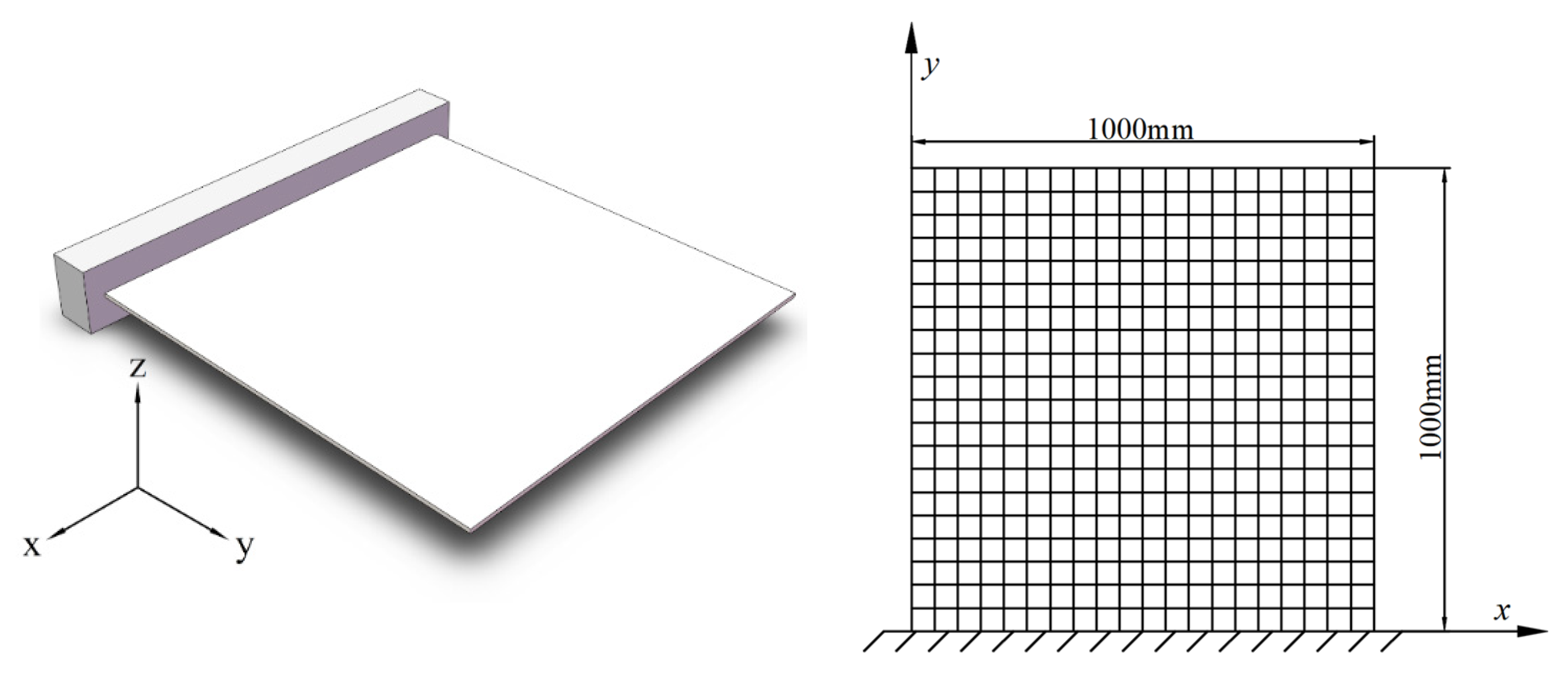
4.2. Example 2: Plate with Two-Dimensional Random Field
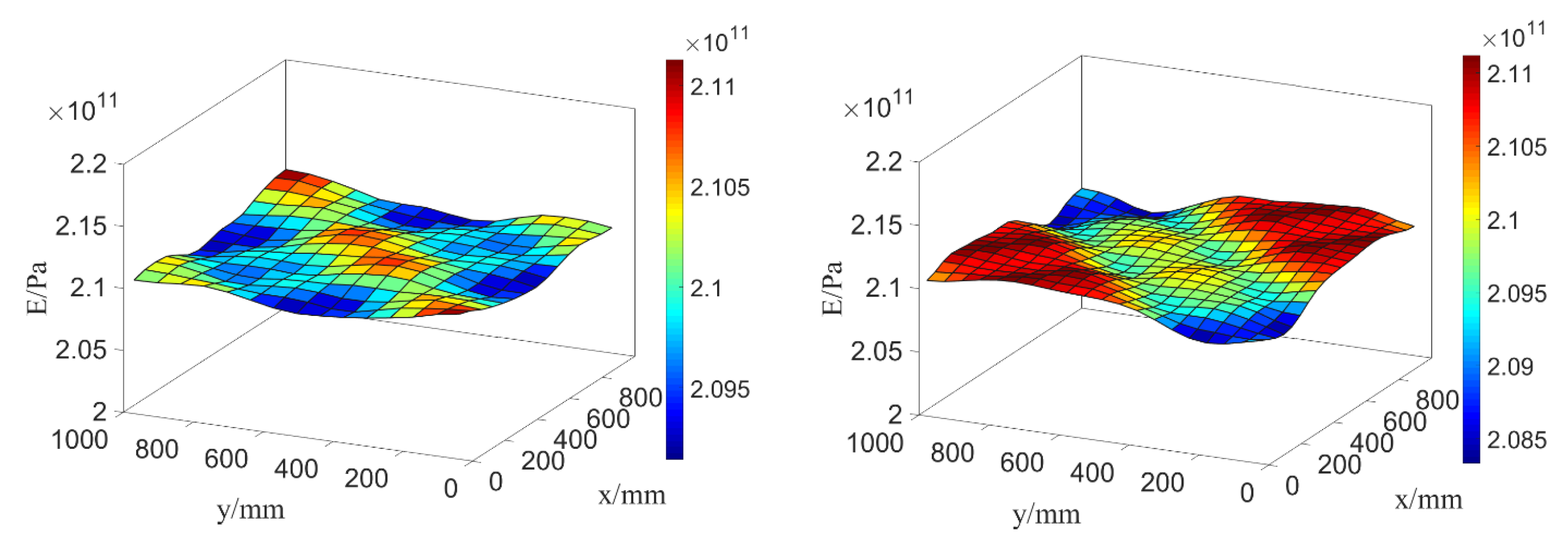
4.2.1. The Expansion and Distribution of Two-Dimensional Random Field
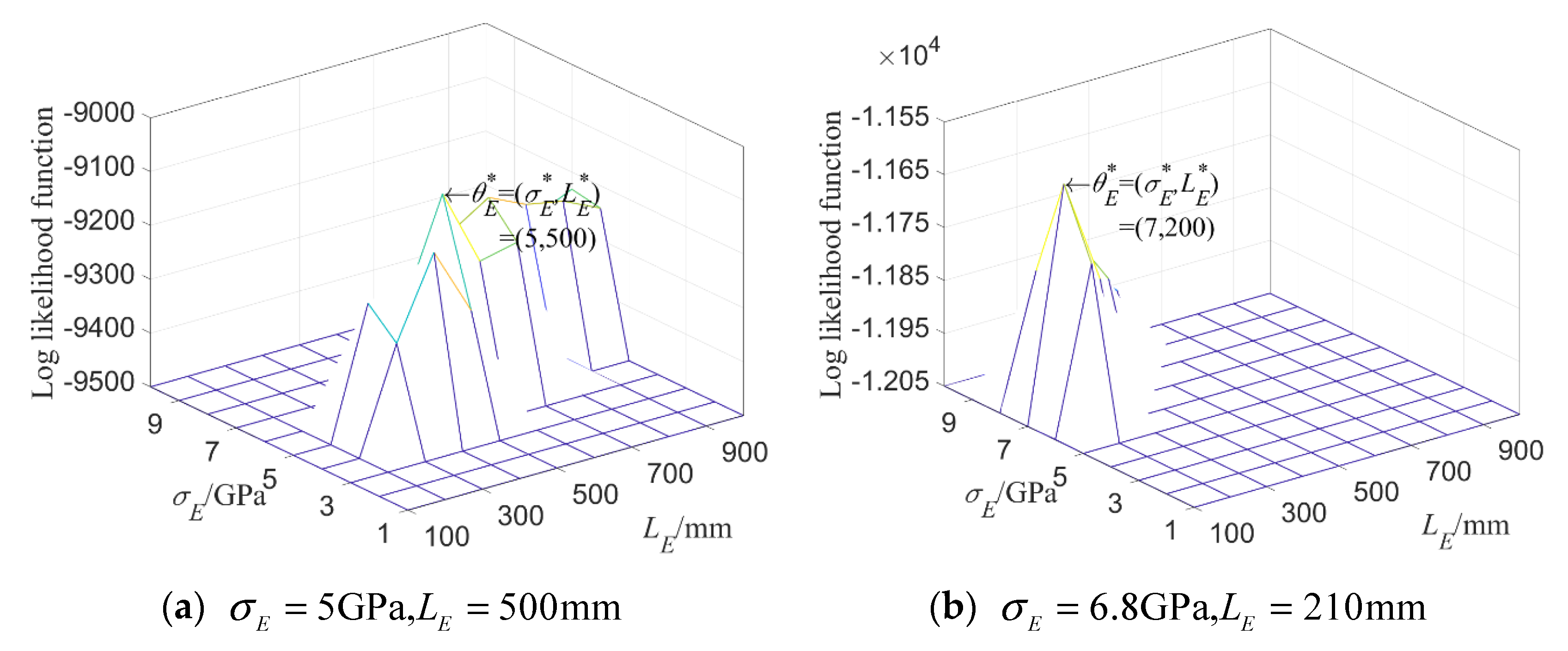
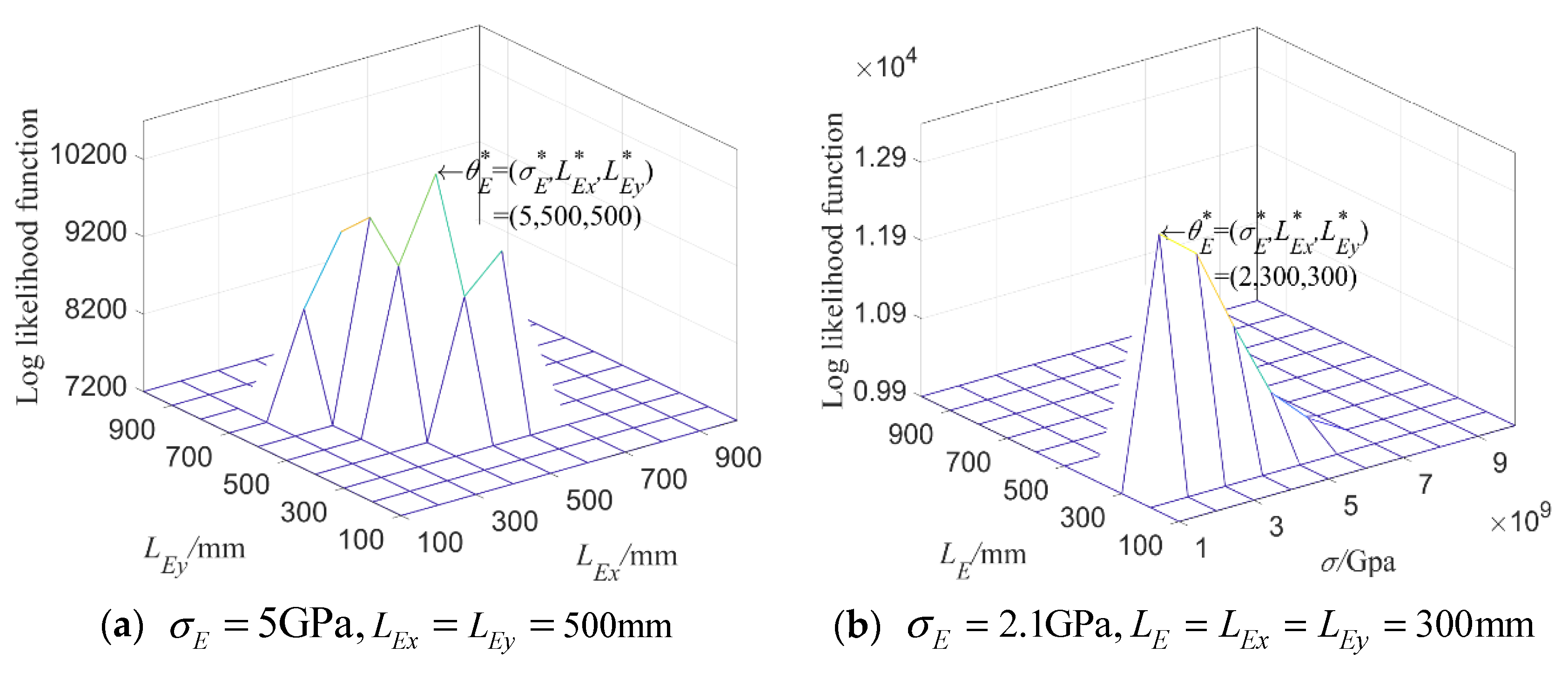
4.2.2. Kernel Density Estimation and Maximum Likelihood Estimation
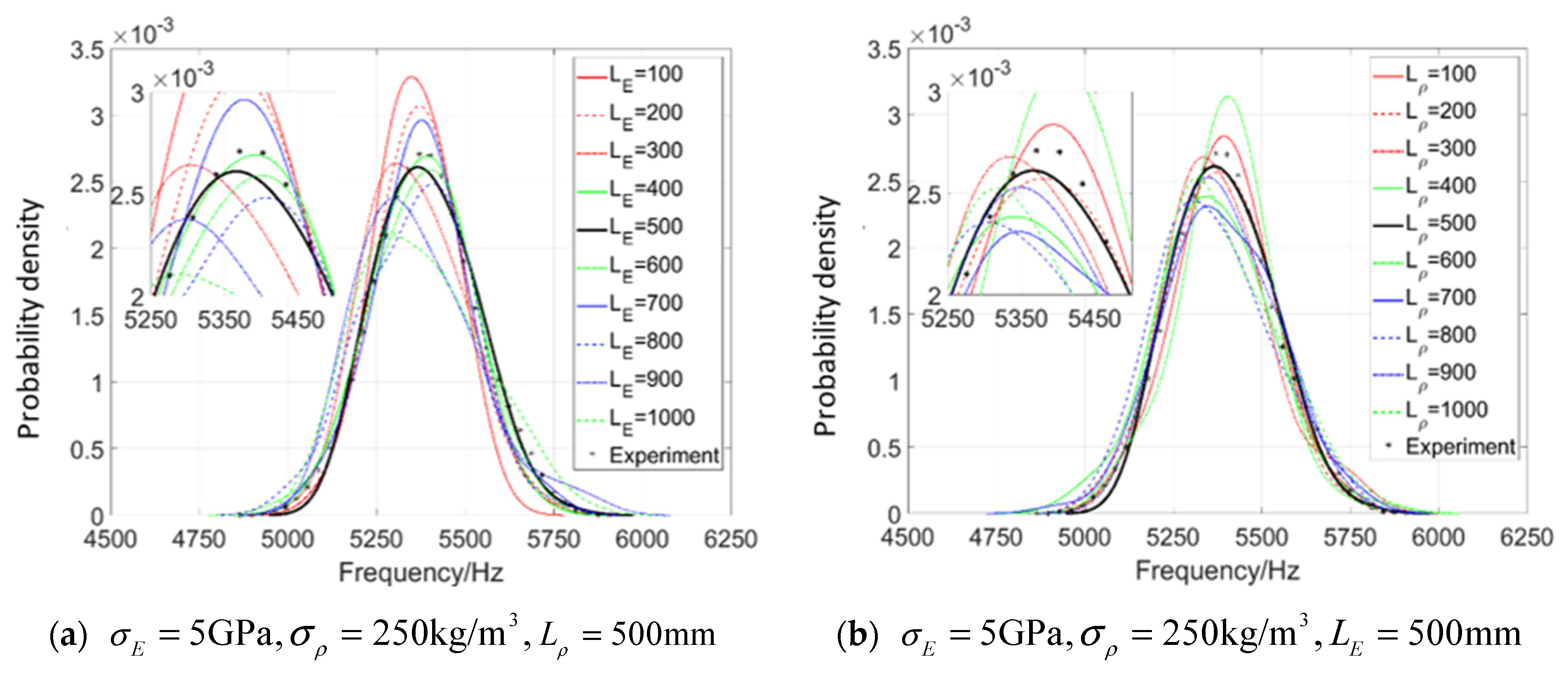
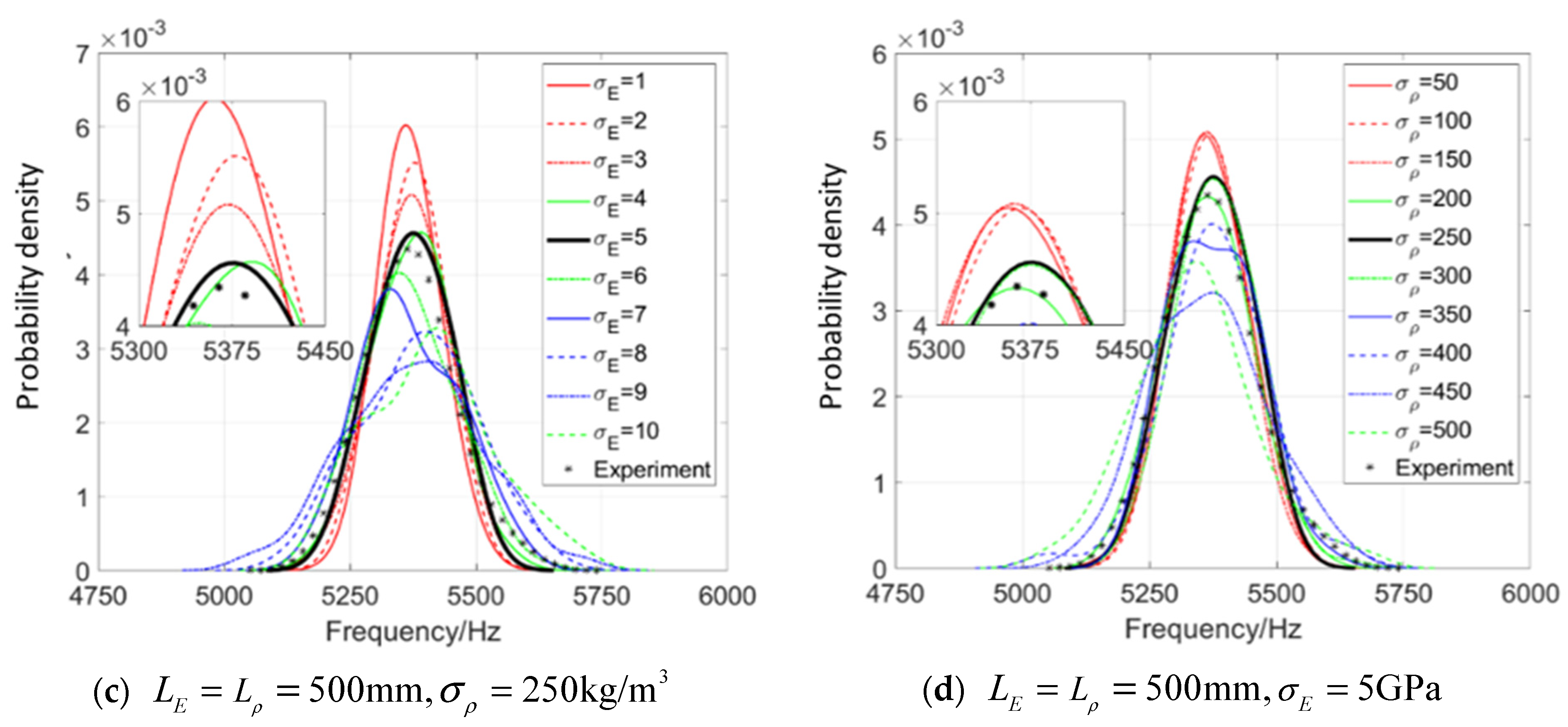
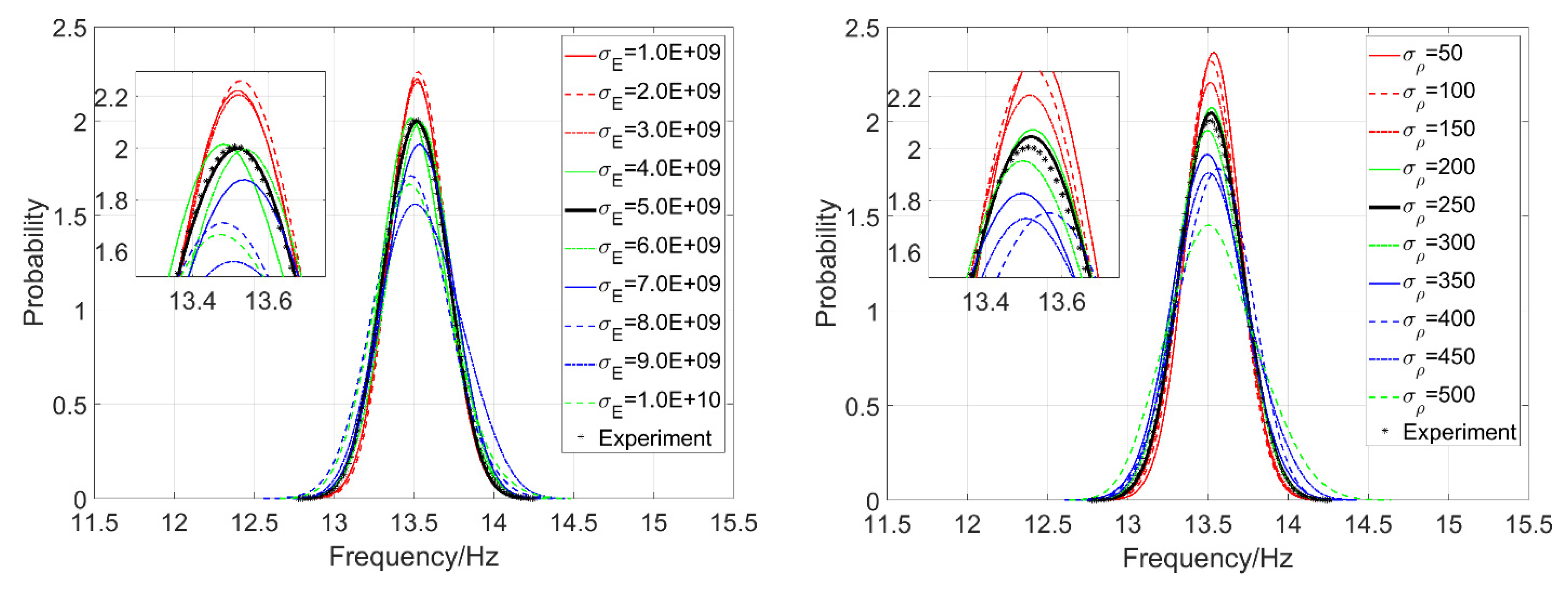
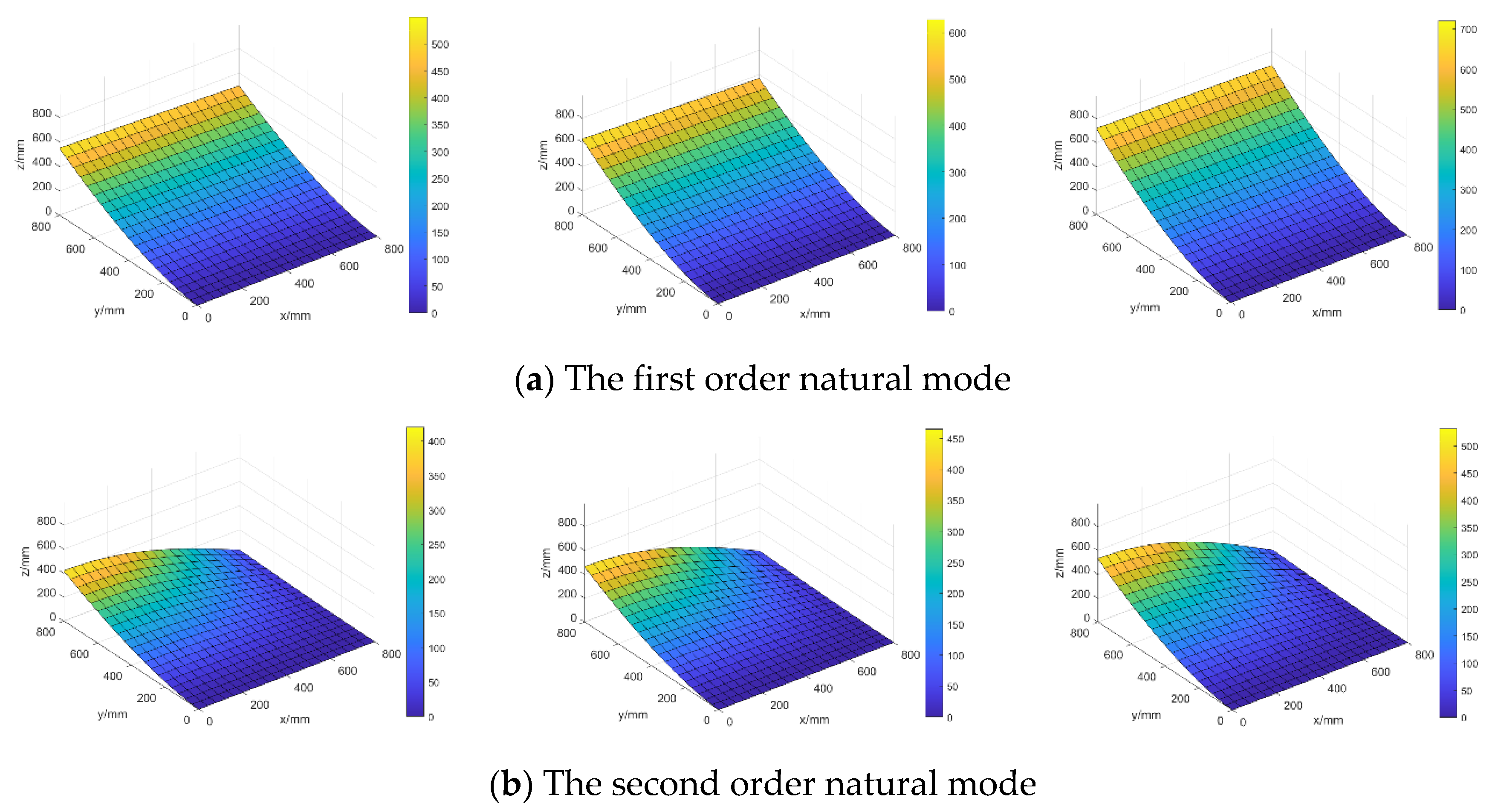
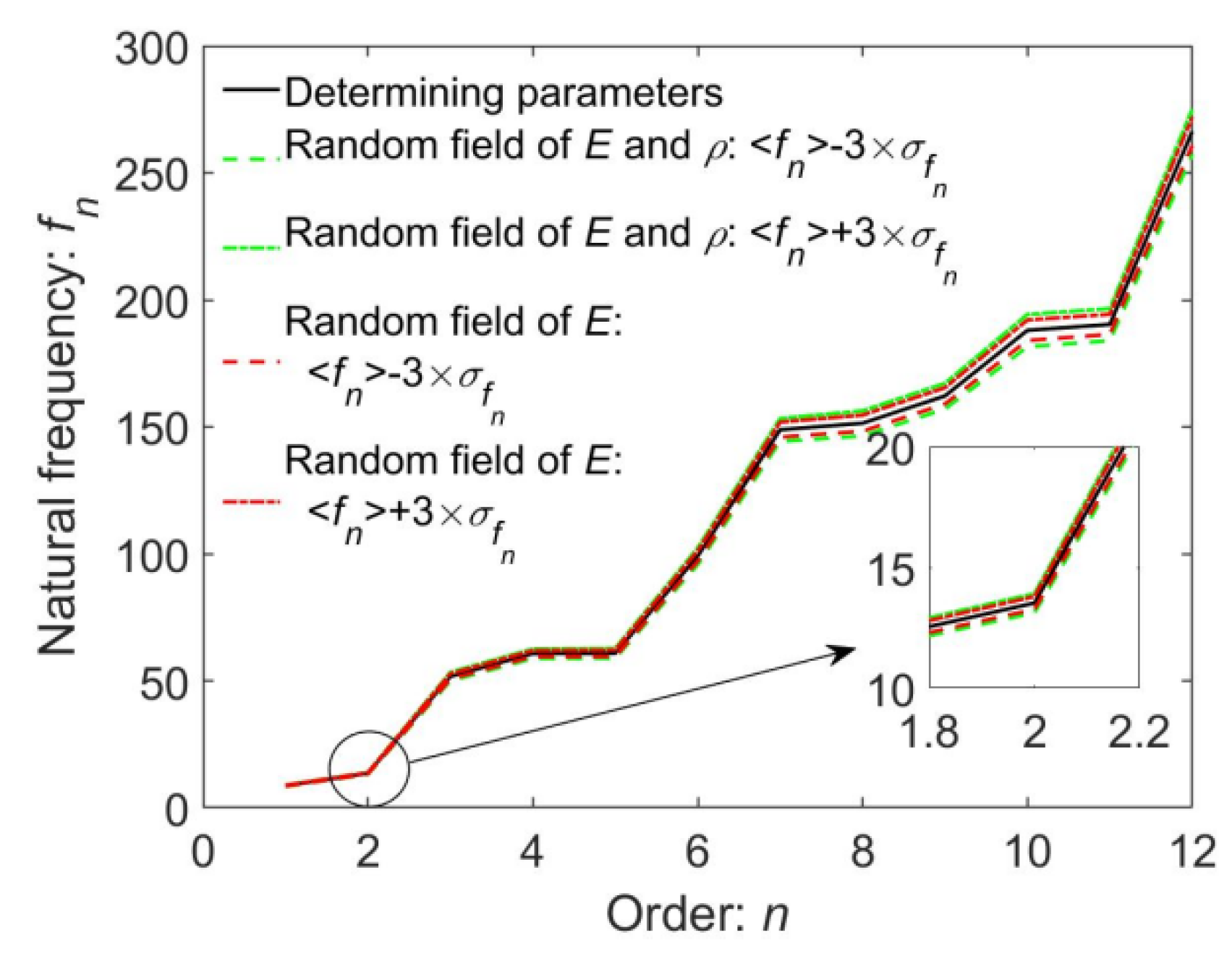
4.2.3. Investigation of the Random Characteristics
5. Conclusions
- (1)
- The parameter setting model based on random field theory can represent the spatially dependent uncertainty of structural parameters well, and the parameter setting model presented can describe the randomly varying characteristics of actual structural parameters.
- (2)
- The example shows that the parameter settings of the model can be quantified by the output response of the structural system; i.e., structural dynamic characteristics, such as the structural natural frequency, and the mean variance and autocorrelation distance of the parameter of the structure can also be obtained, which is very important to application of random field in engineering.
- (3)
- The proposed method can be extended to apply to other structural parameters and can also be used to establish and quantify the parameter setting model of random fields for other material parameters or structural parameters. The applicability and effectiveness of the proposed computational framework are evidently demonstrated through the numerical investigations on various practically motivated engineering structures.
- (4)
- Obviously, the simulation results are closer to reality when more parameters are considered with the random field. However, as the number of parameters considered increases, the computational effort increases exponentially. How to strike a valuable trade-off between them is an interesting area of future work.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xin, Y.; Hao, H.; Li, J.; Wang, Z.C.; Wan, H.P.; Ren, W.X. Bayesian based nonlinear model updating using instantaneous characteristics of structural dynamic responses. Eng. Struct. 2019, 183, 459–474. [Google Scholar] [CrossRef]
- Tisseur, F. Backward error and condition of polynomial eigenvalue problems. Linear Alg. Appl. 2000, 309, 339–361. [Google Scholar] [CrossRef]
- Collins, J.D.; Thomson, W.T. The eigenvalue problem for structural systems with statistical properties. AIAA J. 1969, 7, 642–648. [Google Scholar] [CrossRef]
- Gorman, D.J.; Yu, S.D. A review of the superposition method for computing free vibration eigenvalues of elastic structures. Comput. Struct. 2012, 104, 27–37. [Google Scholar] [CrossRef]
- De Lellis, S.; Statile, A.; Aglietti, G.S.; Richardson, G. Structural uncertainty estimation through a Craig-Bampton stochastic method optimization in satellites structures. J. Sound Vib. 2020, 469, 115123. [Google Scholar] [CrossRef]
- Mahadevan, S.; Haldar, A. Practical random field discretization in stochastic finite element analysis. Struct. Saf. 1991, 9, 283–304. [Google Scholar] [CrossRef]
- Jiang, L.; Liu, X.; Xiang, P.; Zhou, W. Train-bridge system dynamics analysis with uncertain parameters based on new point estimate method. Eng. Struct. 2019, 199, 109454. [Google Scholar] [CrossRef]
- Ma, J.; Gao, W.; Wriggers, P.; Chen, J.J. Structural dynamic optimal design based on the dynamic reliability. Eng. Struct. 2011, 33, 468–476. [Google Scholar] [CrossRef]
- Gao, W.; Wu, D.; Gao, K.; Chen, X.; Tin-Loi, F. Structural reliability analysis with imprecise random and interval fields. Appl. Math. Model. 2018, 55, 49–67. [Google Scholar] [CrossRef]
- Stavrev, A.; Stefanov, D.; Schillinger, D.; Rank, E. Comparison of eigenmode-based and random field-based imperfection modeling for the stochastic buckling analysis of I-section beam-colums. Int. J. Struct. Stab. Dyn. 2013, 13, 1350021. [Google Scholar] [CrossRef]
- Choi, C.K.; Yoo, H.H. Stochastic inverse method to identify parameter random fields in a structure. Struct. Multidiscip. Optim. 2016, 54, 1557–1571. [Google Scholar] [CrossRef]
- Ma, J.; Du, W.; Gao, W.; Wriggers, P.; Xue, X. Multiscale finite element analysis of uncertain-but-bounded heterogeneous materials at finite deformation. Finite Elem. Anal. Des. 2018, 149, 15–31. [Google Scholar] [CrossRef]
- Pacheco, J.N.; de Brito, J.; Chastre, C.; Evangelista, L. Uncertainty of shear resistance models: Influence of recycled concrete aggregate on beams with and without shear reinforcement. Eng. Struct. 2020, 204, 109905. [Google Scholar] [CrossRef]
- Padil, K.H.; Bakhary, N.; Abdulkareem, M.; Li, J.; Hao, H. Non-probabilistic method to consider uncertainties in frequency response function for vibration-based damage detection using Artificial Neural Network. J. Sound Vib. 2020, 467, 115069. [Google Scholar] [CrossRef]
- Wan, H.P.; Mao, Z.; Todd, M.D.; Ren, W.X. Analytical uncertainty quantification for modal frequencies with structural parameter uncertainty using a Gaussian process metamodel. Eng. Struct. 2014, 75, 577–589. [Google Scholar] [CrossRef]
- Venini, P.; Mariani, C. Free vibration of uncertain composite plates via stochastic Rayleith-Ritz approach. Comput. Struct. 1994, 64, 404–423. [Google Scholar]
- Hariri-Ardebili, M.A.; Seyed-Kolbadi, S.M.; Saouma, V.E.; Salamon, J.; Rajagopalan, B. Random finite element method for the seismic analysis of gravity dams. Eng. Struct. 2018, 171, 405–420. [Google Scholar] [CrossRef]
- Chen, J.J.; Che, J.W.; Sun, H.A.; Ma, H.B.; Cui, M.T. Probabilistic Dynamic analysis of truss structures. Struct. Eng. Mech. 2002, 13, 231–239. [Google Scholar] [CrossRef]
- Hakula, H.; Laaksonen, M. Multiparametric shell eigenvalue problems. Comput. Methods Appl. Mech. Eng. 2019, 343, 721–745. [Google Scholar] [CrossRef]
- Falsone, G.; Impollonia, N. A new approach for the stochastic analysis of finite element modelled structures with uncertain parameters. Comput. Methods Appl. Mech. Eng. 2002, 191, 5067–5085. [Google Scholar] [CrossRef]
- Wu, D.; Gao, W.; Song, C.; Tangaramvong, S. Probabilistic interval stability assessment for structures with mixed uncertainty. Struct. Saf. 2016, 58, 105–118. [Google Scholar] [CrossRef]
- Adhikari, S.; Phani, A.S. Random eigenvalue problems in structural dynamics: Experimental investigations. AIAA J. 2010, 48, 1085–1097. [Google Scholar] [CrossRef]
- Liu, W.K.; Belytschko, T.; Mani, A. Probabilistic finite elements for nonlinear structural dynamics. Comput. Methods Appl. Mech. Eng. 1986, 56, 61–81. [Google Scholar] [CrossRef]
- Borjigin, S.; Kim, C.W.; Chang, K.C.; Sugiura, K. Nonlinear dynamic response analysis of vehicle–bridge interactive system under strong earthquakes. Eng. Struct. 2018, 176, 500–521. [Google Scholar] [CrossRef]
- Daminski, M. Stochastic second-order perturbation approach to the stress-based finite element method. Int. J. Solids Struct. 2001, 38, 3831–3852. [Google Scholar] [CrossRef]
- Rashidi, S.; Ziaei-Rad, S. Experimental and numerical vibration analysis of wire rope isolators under quasi-static and dynamic loadings. Eng. Struct. 2017, 148, 328–339. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Chakraborty, S. Reliability of linear structures with parameter uncertainty under non-stationary earthquake. Struct. Saf. 2006, 28, 231–246. [Google Scholar] [CrossRef]
- Giaccu, G.F.; Caracoglia, L. Wind-load fragility analysis of monopole towers by layered stochastic-approximation-Monte-Carlo method. Eng. Struct. 2018, 174, 462–477. [Google Scholar] [CrossRef]
- Yan, B.; Ma, J.; Wu, D.; Wriggers, P. The analyses of dynamic response and reliability for failure dependent stochastic micro-resonator with thermoelastic coupling effects. Appl. Math. Model. 2019, 77, 1168–1187. [Google Scholar] [CrossRef]
- Stefanou, G.; Savvas, D.; Papadrakakis, M. Stochastic finite element analysis of composite structures based on material microstructure. Comput. Struct. 2015, 132, 384–392. [Google Scholar] [CrossRef]
- Ghanem, R.G.; Spanos, P.D. Stochastic Finite Elements: A Spectral Approach; Courier Corporation: Chelmsford, MA, USA, 2003. [Google Scholar]
- Wu, J.; Luo, Z.; Zhang, N.; Zhang, Y. A new uncertain analysis method and its application in vehicle dynamics. Mech. Syst. Signal Proc. 2015, 50, 659–675. [Google Scholar] [CrossRef]
- Huang, S.; Mahadevan, S.; Rebba, R. Collocation-based stochastic finite element analysis for random field problems. Probab. Eng. Eng. Mech. 2007, 22, 194–205. [Google Scholar] [CrossRef]
- Do, D.M.; Gao, W.; Song, C.; Beer, M. Interval spectral stochastic finite element analysis of structures with aggregationof random field and bounded parameters. Int. J. Numer. Methods Eng. 2016, 108, 1198–1229. [Google Scholar] [CrossRef]
- Feng, X.; Lu, Z.X.; Yang, Z.Y.; Guo, J.H. Analysis on the variances of material and structural properties based on random field theory. Probab. Eng. Eng. Mech. 2011, 26, 222–230. [Google Scholar] [CrossRef]
- Sepahvand, K.; Marburg, S. Stochastic dynamic analysis of structures with spatially uncertain material parameters. Int. J. Struct. Stab. Dyn. 2014, 14, 1440029. [Google Scholar] [CrossRef]
- Hurtado, J.E.; Barbat, A.H. Monte-carlo techniques in computational stochastic mechanics. Arch. Comput. Method Eng. 1998, 5, 3. [Google Scholar] [CrossRef]
- Stefanou, G.; Papadrakakis, M. Stochastic finite element analysis of shells with combined random material and geometric properties. Comput. Methods Appl. Mech. Eng. 2004, 193, 139–160. [Google Scholar] [CrossRef]
- Van Vinh, P.; van Chinh, N.; Tounsi, A. Static Bending and Buckling Analysis of Bi-Directional Functionally Graded Porous Plates Using an Improved First-Order Shear Deformation Theory and FEM. Eur. J. Mech.-A Solids 2022, 96, 104743. [Google Scholar] [CrossRef]
- Kong, F.; Dong, F.; Duan, M.; Habibi, M.; Safarpour, H.; Tounsi, A. On the Vibrations of the Electrorheological Sandwich Disk with Composite Face Sheets Considering Pre and Post-Yield Regions. Thin-Walled Struct. 2022, 179, 109631. [Google Scholar] [CrossRef]







| Input Parameter Setting of Test Samples of 500 Plates | The Maximal Value of Log Likelihood Function | Parameter Setting Estimated from | Mean Value and Mean Variance of the First Three Natural Frequencies Obtained from 500 Test Samples of 500 Plates | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (5, 500, 500) | 10,344.12 | 5 | 500 | 500 | 8.6185 | 0.0581 | 13.5240 | 0.0877 | 51.6952 | 0.3545 |
| (6, 300, 700) | 9190.03 | 6 | 300 | 700 | 8.6159 | 0.0659 | 13.5199 | 0.0969 | 51.6793 | 0.3957 |
| (2, 100, 700) | 13,712.95 | 2 | 100 | 700 | 8.6197 | 0.0131 | 13.5254 | 0.0183 | 51.7022 | 0.0776 |
| (9, 430, 650) | 8151.44 | 9 | 400 | 700 | 8.6204 | 0.1083 | 13.5271 | 0.1627 | 51.7069 | 0.6553 |
| Computational Results | Norm of Random Natural Modes | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Random Models | |||||||||
| Deterministic model | 6342.80 | 0 | 1635.00 | 0 | 399.12 | 0 | 296.67 | 0 | |
| Random field | 6346.67 | 94.82 | 1635.12 | 6.56 | 399.25 | 3.73 | 357.71 | 1010.50 | |
| Random fields and | 6347.82 | 134.34 | 1635.43 | 7.71 | 399.21 | 3.98 | 477.17 | 1249.14 | |
| Computational Results | Mean Value and Mean Variance of Natural Frequencies | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Random Models | |||||||||
| Deterministic model | 8.62 | 0 | 13.52 | 0 | 51.67 | 0 | 60.68 | 0 | |
| Random field of | 8.62 | 0.0583 | 13.53 | 0.0885 | 51.69 | 0.3580 | 60.69 | 0.3914 | |
| Random fields of and | 8.62 | 0.0906 | 13.52 | 0.1321 | 51.65 | 0.5651 | 60.62 | 0.6235 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, W.; Ma, J.; Zhou, C.; Yan, Y.; Wriggers, P. Uncertain Dynamic Characteristic Analysis for Structures with Spatially Dependent Random System Parameters. Materials 2023, 16, 1188. https://doi.org/10.3390/ma16031188
Du W, Ma J, Zhou C, Yan Y, Wriggers P. Uncertain Dynamic Characteristic Analysis for Structures with Spatially Dependent Random System Parameters. Materials. 2023; 16(3):1188. https://doi.org/10.3390/ma16031188
Chicago/Turabian StyleDu, Wenyi, Juan Ma, Changhu Zhou, Yongchun Yan, and Peter Wriggers. 2023. "Uncertain Dynamic Characteristic Analysis for Structures with Spatially Dependent Random System Parameters" Materials 16, no. 3: 1188. https://doi.org/10.3390/ma16031188
APA StyleDu, W., Ma, J., Zhou, C., Yan, Y., & Wriggers, P. (2023). Uncertain Dynamic Characteristic Analysis for Structures with Spatially Dependent Random System Parameters. Materials, 16(3), 1188. https://doi.org/10.3390/ma16031188






