Statistical Study of the Process Parameters for Achieving Continuous Consolidation of a Thermoplastic Composite
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material and Samples
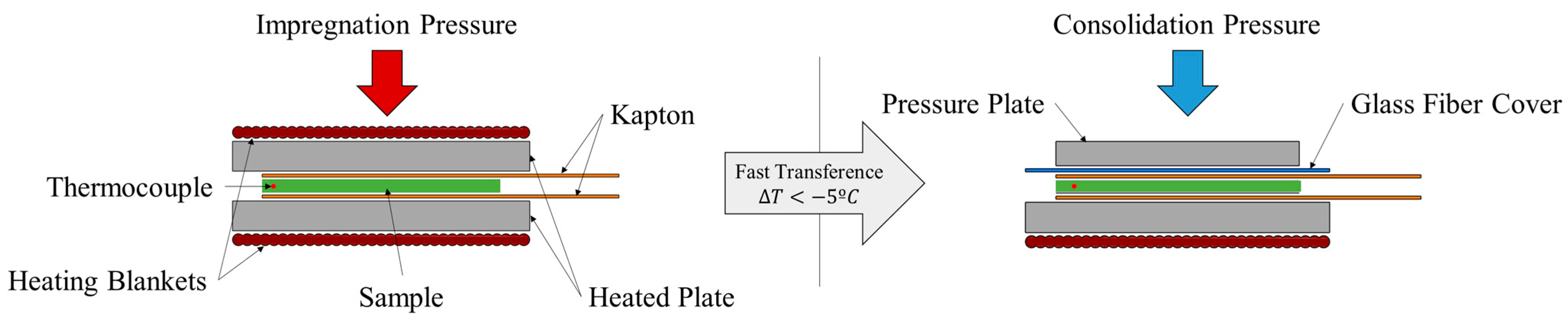
2.2. Experiment Setup Description
- Pre-heating and impregnation/forming phases;
- Consolidation phase;
2.2.1. Typical Process Parameters
- Forming temperature: The material supplier typically provided the recommended range for forming temperatures. For TC1225/T700 [25], this range is normally between 320 °C and 400 °C.
- Consolidation pressure: The consolidation pressure range could vary depending on the manufacturing process. From previous experiences with high-rate applications, good consolidation values were achieved in a range of pressures between 0.2 and 2 MPa [12].
- Time: Time is an indirect measure of the forming speed. It was feasible to approximate the forming speed by considering a standard length for the forming skids (counter molds) used in glide forming. Thus, for the impregnation/forming phase-assuming a skid length of 200 mm and forming speeds between 1 mm/s and 10 mm/s—forming equivalent time varied from 20 s to 200 s. For the consolidation phase, the equivalent time considering a 100 mm skid varied from 10 s to 100 s.
- Number of plies: The number of plies in the laminate, a key parameter in the design of the component, is typically within a range of 5 to 20 for secondary structures. However, in certain cases, local reinforcements may increase the number of plies up to 50. For the purposes of this study, a laminate with 20 plies was chosen.
- Impregnation pressure: Impregnation pressure, applied during the forming phase, is utilized to secure the cohesion of the plies while the material is at the appropriate forming temperature. This results in a greater degree of intimate contact among the plies and ensures that each fiber is fully impregnated by the thermoplastic matrix. Additionally, impregnation pressure is employed in shaping the component. Based on previous research, an appropriate value for this pressure was determined to be 4 kPa.
- Tool temperature: Tool temperature, which is typically below melting point and above the crystallization temperature, was set to 250 °C for this study.
2.2.2. Experimental Variables and Characterization
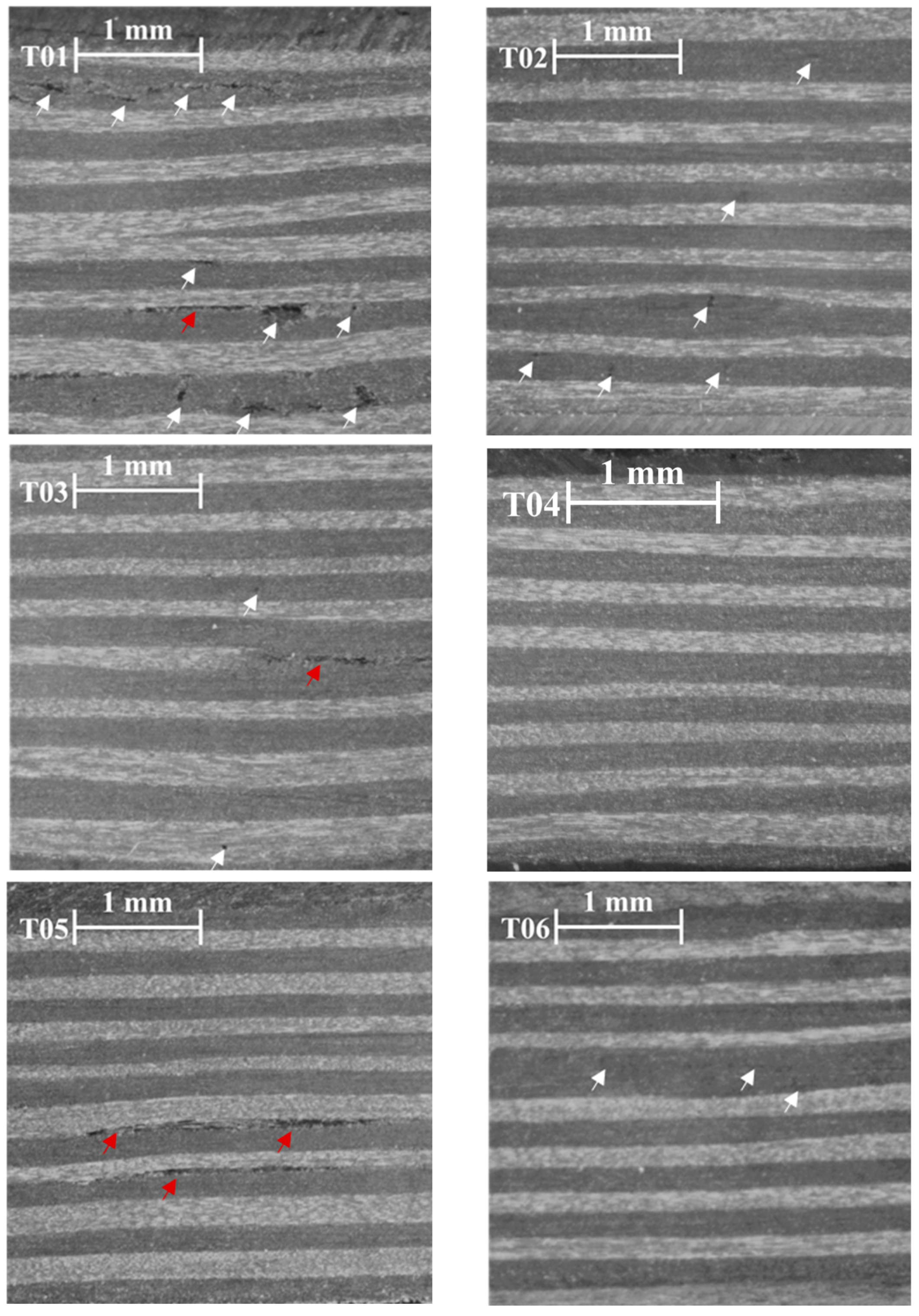
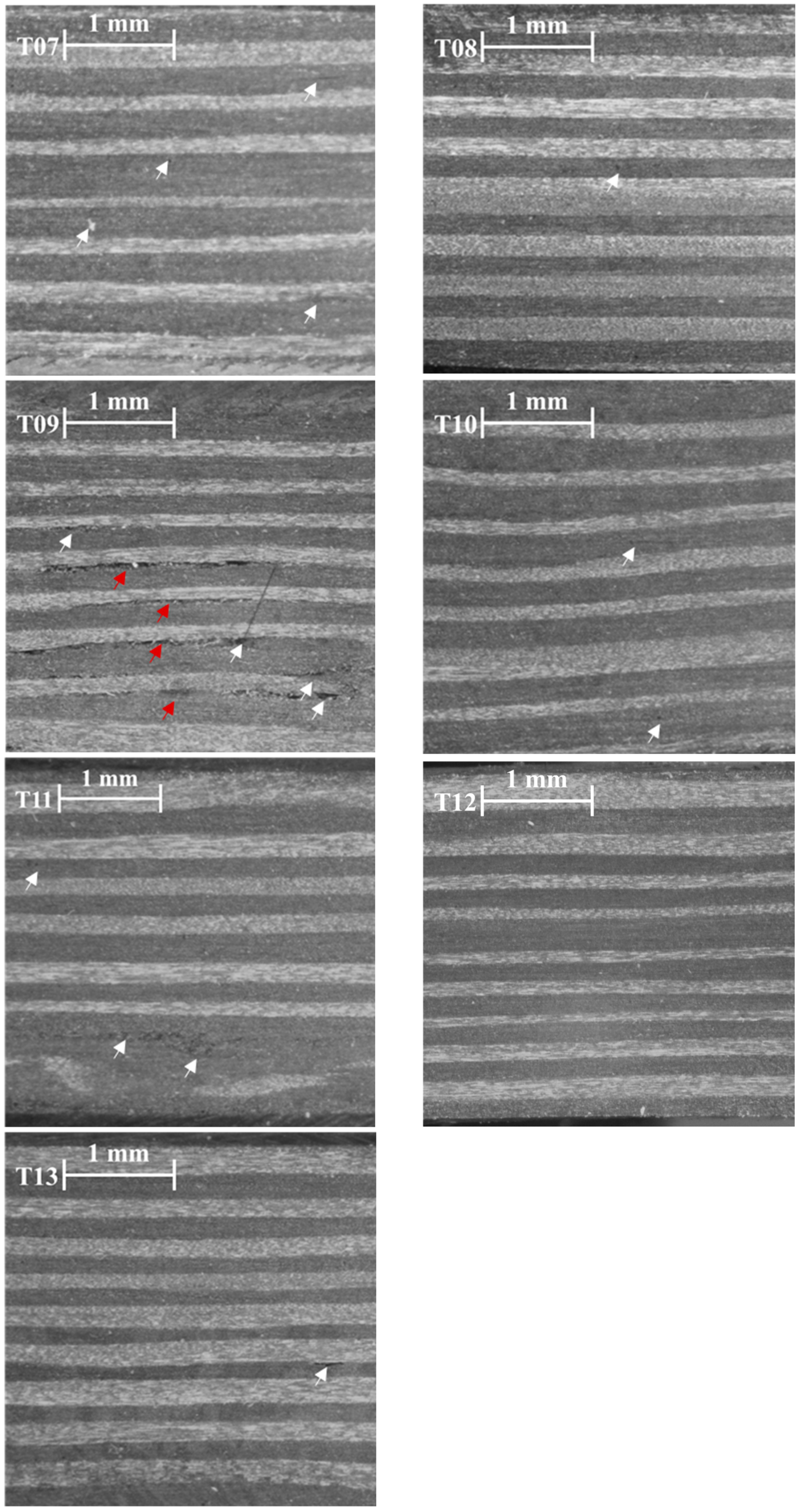
- Porosity: Porosity was quantified using the A-scan method via MUPE (manual ultrasound portable equipment). The transducer used was a mono-element straight beam transducer with a delay of 8.178 and a speed setting of 2713 m/s. The analysis involved comparing the sample attenuation to a reference standard. Micrographics were also utilized to provide a detailed examination of select samples. The methodology employed was in accordance with the Airbus AITM (Airbus Industries Test Methods) 6-4005 standard [26].
- Thickness: Thickness was measured using a micrometer and compared to the nominal thickness of a consolidated ply. The measured nominal thickness of the raw material was 0.170 mm.
2.3. Experiment Setup Description
2.4. Evaluation of the Models
3. Results
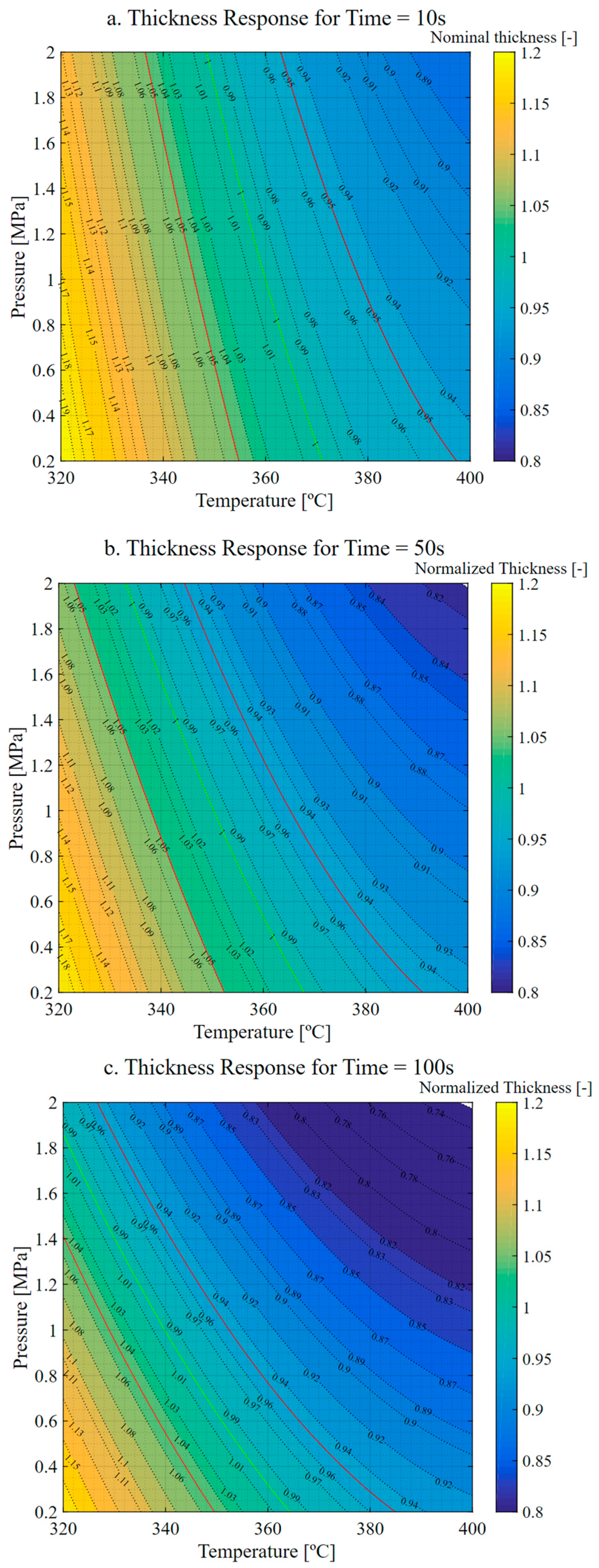
3.1. Thickness Model
3.1.1. Analysis of Variance
3.1.2. Response Surface Results
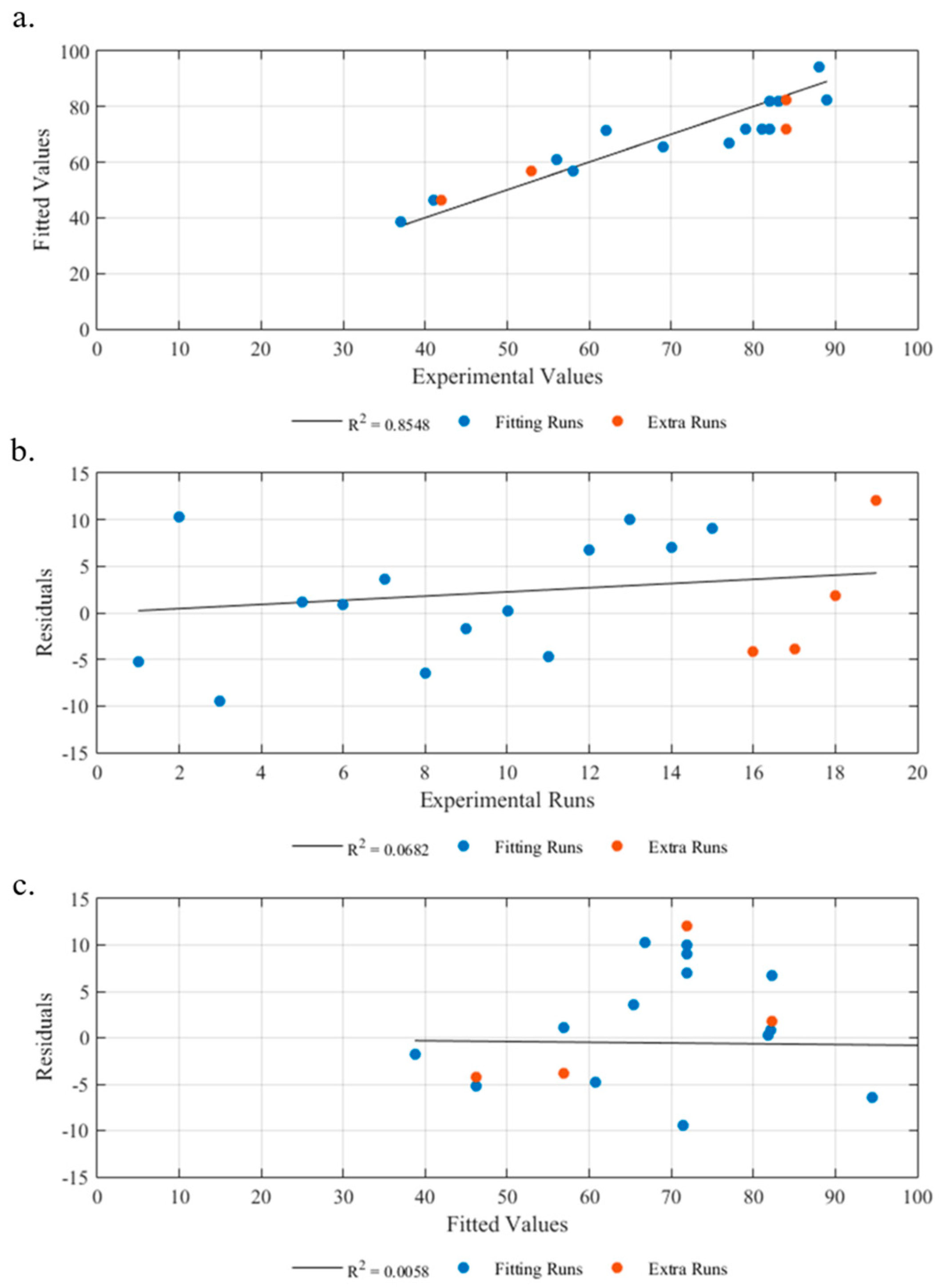
3.1.3. Diagnostic Model
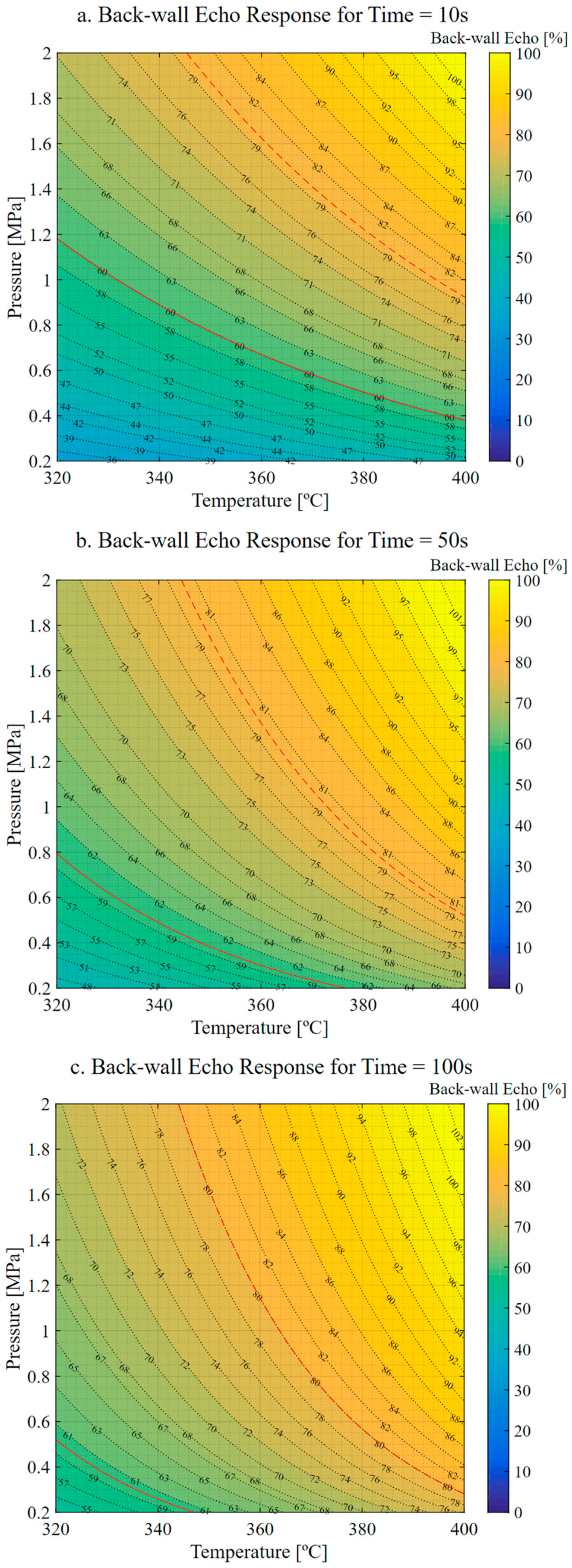
3.2. Backwall Echo Model
3.2.1. Analysis of Variance
3.2.2. Response Surface Results
3.2.3. Diagnostic Model
3.3. Micrographics
4. Discussion
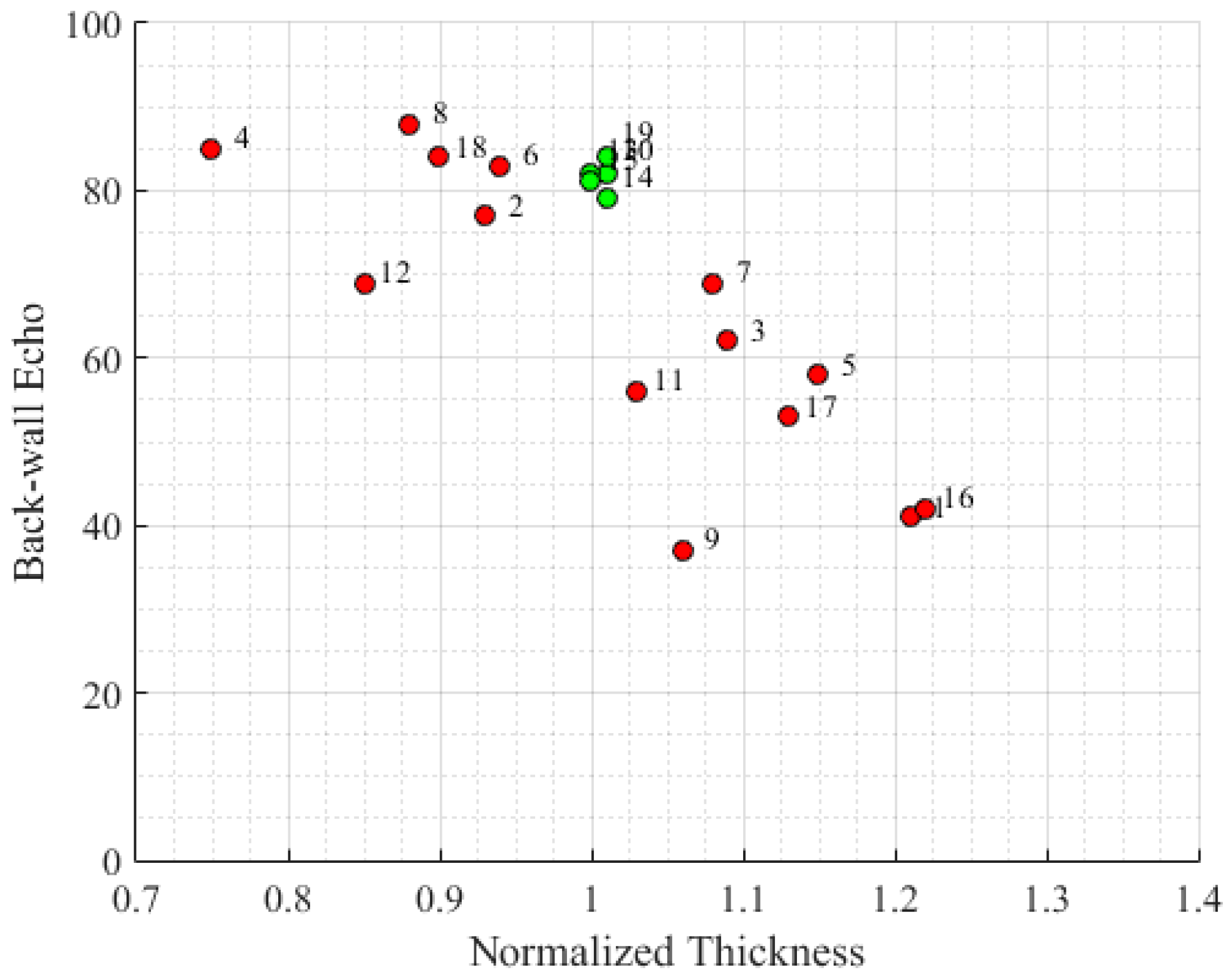
4.1. Relationship between Thickness and Porosity
4.2. Process Optimization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Biron, M. Thermoplastic Composites, in Thermoplastic and Thermoplastic Composites, 3rd ed.; William Andrew Publishing: Norwich, NY, USA, 2018; pp. 821–882. [Google Scholar]
- Steenkamer, A.; Sullivan, J.L. On the recyclability of a cyclic thermoplastic composite material. Compos. Part B Eng. 1998, 29, 745–752. [Google Scholar] [CrossRef]
- Pegoretti, A. Towards sustainable structural composites: A review on the recycling of continuous-fiber-reinforced thermoplastics. Adv. Ind. Eng. Polym. Res. 2021, 4, 105–115. [Google Scholar] [CrossRef]
- Martin, I.; Saenz del Castillo, D.; Fernandez, A.; Güemes, A. Advanced thermoplastic composite manufacturing by in-situ consolidation: A review. J. Compos. Sci. 2020, 4, 149–185. [Google Scholar] [CrossRef]
- Arquier, R.; Iliopoulos, I.; Réginier, G.; Miquelard-Garnier, G. Consolidation of continuous-carbon-fiber-reinforced PAEK composites: A review. Mater. Today Commun. 2022, 32, 104036. [Google Scholar] [CrossRef]
- Colton, J.M.; Muzzy, J.; Birger, S.; Yang, H.; Norpoth, L. Processing parameters for consolidating PEEK/carbon fibre (APC-2) composites. Polym. Compos. 1992, 13, 421–426. [Google Scholar] [CrossRef]
- Patou, J.; Bonnaire, R.; De Luycker, E.; Bernhart, G. Influence of consolidation process on voids and mechanical properties of powdered and commingled carbon/PPS laminates. Compos. Part. A Appl. Sci. Manuf. 2019, 17, 260–275. [Google Scholar] [CrossRef]
- Liu, F.; Li, T.; Xu, F.; Li, J.; Jiang, S. Microstructure, Tensile Property, and Surface Quality of Glass Fiber-Reinforced Polypropylene Parts by rapid heat cycle molding. Adv. Polym. Technol. 2020, 2020, 3161068. [Google Scholar] [CrossRef]
- Brufau, J.; Lorente, A.S. System for Forming Stacks of Composite Materials. U.S. Patent Application No. US2014/0290866A1, 17 October 2017. [Google Scholar]
- Brufau, J. System for Forming Stacks of Composite Materials. U.S. Patent Application No. US2016/0082675A1, 15 May 2018. [Google Scholar]
- Robins, B.G.; Berrios, I.; Redondo, J.B.; Rueda, M.C.C. Heat Blankets Assembly for Forming a Composite Charge. U.S. Patent Application No. US2019/0016040A1, 23 June 2020. [Google Scholar]
- Campos, D.; Brufau, J.; Biurrun, M.; Martín, A. A Review of the A+ Glide Forming Manufacturing Technology and its Adaptation to CFRP Thermoplastic Composite Materials. In Proceedings of the 5th International Conference & Exhibition on Thermoplastic Composites, Bremen, Germany, 13–14 October 2020. [Google Scholar]
- Enoki, S.; Kojima, K.; Mizuno, S.; Katayama, K.; Tanaka, K. High-speed compression molding of continuous carbon fiber reinforced polypropylene. WIT Trans. Built Environ. 2014, 137, 311–315. [Google Scholar]
- Piott, F.; Krämer, A.; Lück, A.; Hoffmann, L.; Mitschang, P.; Drummer, D. Increasing the performance of continuous compression moulding by local pressure adaption. Adv. Manuf. Polym. Comppos. Sci. 2021, 7, 1–14. [Google Scholar] [CrossRef]
- Christmann, M.; Medina, L.; Mitschang, P. Effects of inhomogeneous temperature distribution on the impregnation process of the continuous compression molding technology. J. Thermoplast. 2016, 30, 1285–1302. [Google Scholar] [CrossRef]
- Chih-Min, M.; Cheng-Tao, Y.; Bor-Wen, C. Optimization of stamp forming process for thermoplastic composites. Res. J. Appl. Sci. Eng. Technol. 2014, 7, 1568–1572. [Google Scholar]
- Brooks, R.A.; Wang, H.; Zerong, D.; Jie, X.; Song, Q.; Liu, H.; Dear, J.P.; Li, N. A review on stamp forming of continuous fibre-reinforced thermoplastics. Int. J. Lightweight Mater. Manuf. 2022, 5, 411–430. [Google Scholar] [CrossRef]
- McCool, R.; Murphy, A.; Wilson, R.; Jiang, Z.; Price, M.; Butterfield, J.; Hornsby, P. Thermoforming carbon fiber-reinforced thermoplastic composites. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2012, 226, 91–102. [Google Scholar]
- Tatsuno, D.; Yoneyyama, T.; Okamoto, M. Hot press forming of thermoplastic CFRP sheets. In Proceedings of the 17th International Conference on Metal Forming, Toyohashi, Japan, 16–19 September 2018. [Google Scholar]
- Yanagimoto, J.; Ikeuchi, K. Sheet forming process of carbon fiber reinforced plastics for lightweight parts. CIRP Annals Manuf. Tech. 2012, 61, 247–250. [Google Scholar] [CrossRef]
- Tukey, J.W. Exploratory Data Analysis, 1st ed.; Pearson: Readind, MA, USA, 1977. [Google Scholar]
- Kutner, M.; Nachtsheim, C.; Neter, J.; Li, W. Applied Linear Statistical Models, 4th ed.; McGraw-Hill Education: Homewood, IL, USA, 2004. [Google Scholar]
- Box, G.E.P.; Cox, D.R. An analysis of transformations. J. R. Statist. Soc. B 1964, 26, 211–252. [Google Scholar] [CrossRef]
- Khan, M.A.; Mitschang, P.; Schledjewski, R. Identification of some optimal parameters to achieve higher laminate quality through tape placement process. Adv. Polym. Technol. 2010, 29, 98–111. [Google Scholar] [CrossRef]
- Toray Advanced Composites. Toray Cetex TC1225 Product Data Sheet. 2019. Available online: https://www.toraytac.com/media/3bd72fac-0406-48e4-bfc4-2ffd2398ac0c/zipxIA/TAC/Documents/Data_sheets/Thermoplastic/UDtapes%2Cprepregsandlaminates/Toray-Cetex-TC1225_PAEK_PDS.pdf (accessed on 5 August 2023).
- AITM-6-4005; Ultrasonic Pulse-Echo Inspection of Carbon Fibre Plastic. Airbus Industries: Blagnac, France, 2018.
- Deignan, A.; Figiel, L.; McCarthy, M.A. Insights into complex rheological behaviour of carbon fibre/PEEK from a novel numerical methodology incorporating fibre friction and melt viscosity. Compos. Strct. 2018, 189, 614–626. [Google Scholar] [CrossRef]




| Property | TC1225/T700 |
|---|---|
| Type of composite | Unidirectional Prepreg |
| Type of reinforcement | T700 |
| Fiber areal weight (FAW) | |
| Resin content by weight (RC) | |
| Consolidated ply thickness (CPT) |
| Factor | Description | Low (−1) | Midpoint (0) | High (+1) |
|---|---|---|---|---|
| A | Temperature | 320 °C | 350 °C | 400 °C |
| B | Consolidation Pressure | 0.2 MPa | 1 MPa | 2 MPa |
| C | Consolidation Time | 10 s | 50 s | 100 s |
| Sample | Order | Factor | Normalized Thickness | Backwall Echo Amplitude (%) | ||
|---|---|---|---|---|---|---|
| A | B | C | ||||
| T01 | 19 | −1 | −1 | 0 | 1.21 ± 0.014 | 41 ± 1.132 |
| T02 | 9 | 1 | −1 | 0 | 0.93 ± 0.005 | 77 ± 1.729 |
| T03 | 1 | −1 | 1 | 0 | 1.09 ± 0.017 | 62 ± 1.729 |
| T04 | 18 | 1 | 1 | 0 | 0.75 ± 0.006 | 85 ± 0.653 |
| T05 | 13 | −1 | 0 | −1 | 1.15 ± 0.006 | 58 ± 2.356 |
| T06 | 10 | 1 | 0 | −1 | 0.94 ± 0.013 | 83 ± 2.848 |
| T07 | 15 | −1 | 0 | 1 | 1.08 ± 0.013 | 69 ± 2.848 |
| T08 | 5 | 1 | 0 | 1 | 0.88 ± 0.006 | 88 ± 2.848 |
| T09 | 7 | 0 | −1 | −1 | 1.06 ± 0.006 | 37 ± 1.960 |
| T10 | 8 | 0 | 1 | −1 | 1.01 ± 0.006 | 82 ± 2.356 |
| T11 | 14 | 0 | −1 | 1 | 1.03 ± 0.006 | 56 ± 4.573 |
| T12 | 2 | 0 | 1 | 1 | 0.85 ± 0.006 | 89 ± 1.729 |
| T13 | 16 | 0 | 0 | 0 | 1.00 ± 0.003 | 82 ± 1.802 |
| T14 | 3 | 0 | 0 | 0 | 1.01 ± 0.003 | 79 ± 1.802 |
| T15 | 6 | 0 | 0 | 0 | 1.00 ± 0.006 | 81 ± 1.820 |
| T16 | 12 | −1 | −1 | 0 | 1.22 ± 0.006 | 42 ± 3.638 |
| T17 | 17 | −1 | 0 | −1 | 1.13 ± 0.003 | 53 ± 5.696 |
| T18 | 4 | 0 | 1 | 1 | 0.90 ± 0.006 | 84 ± 2.356 |
| T19 | 11 | 0 | 0 | 0 | 1.01 ± 0.006 | 84 ± 1.820 |
| Type and Affected Parameters | Coefficients | p-Value | |||
|---|---|---|---|---|---|
| β0 | Constant | 5.7084 × 1000 | 0.0024 | ||
| β1 | Linear term of T | −2.2711 × 10−02 | 0.0153 | ||
| β2 | Linear term of P | −3.2726 × 10−02 | (0.1819) | ||
| β3 | Linear term of t | −5.3302 × 10−05 | (0.9088) | ||
| β4 | Interaction term of P·t | −7.8929 × 10−04 | 0.0607 | ||
| β5 | Squared term of T | 2.7073 × 10−05 | 0.0298 | ||
| R2 | 0.9582 | ||||
| adjR2 | 0.9349 | ||||
| p-Value (fstats) | 0.0000 | ||||
| Df | Sum Sq | Mean Sq | F Value | Pr (>F) | |
| FO (T, P, t) | 3 | 0.1754 | 0.0587 | 64.9335 | 0.0000 |
| TWI (P, t) | 1 | 0.0042 | 0.0042 | 4.6602 | 0.0592 |
| PQ (T) | 1 | 0.0059 | 0.0059 | 6.6430 | 0.0298 |
| Residuals | 9 | 0.0081 | 0.0009 | ||
| Type and Affected Parameters | Coefficients | p-Value | |||
|---|---|---|---|---|---|
| β0 | Constant | 2.4528 | 0.0001 | ||
| β1 | Linear term of T | 0.0046 | 0.0017 | ||
| β2 | Linear term of log(P) | 0.5175 | 0.0102 | ||
| β3 | Linear term of log(t) | 0.0607 | (0.1423) | ||
| β 4 | Interaction term of log(P)·log(t) | −0.0838 | 0.0823 | ||
| R2 | 0.8548 | ||||
| adjR2 | 0.7968 | ||||
| p-Value (fstats) | 0.0003 | ||||
| Df | Sum Sq | Mean Sq | F Value | Pr (>F) | |
| FO (T, log(P), log(t)) | 3 | 0.8534 | 0.2844 | 18.3873 | 0.0002 |
| TWI (log(P), log(t)) | 1 | 0.0576 | 0.0576 | 3.7284 | 0.0823 |
| Residuals | 10 | 0.1547 | 0.1547 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campos, D.; Maimí, P.; Martín, A. Statistical Study of the Process Parameters for Achieving Continuous Consolidation of a Thermoplastic Composite. Materials 2023, 16, 6723. https://doi.org/10.3390/ma16206723
Campos D, Maimí P, Martín A. Statistical Study of the Process Parameters for Achieving Continuous Consolidation of a Thermoplastic Composite. Materials. 2023; 16(20):6723. https://doi.org/10.3390/ma16206723
Chicago/Turabian StyleCampos, Daniel, Pere Maimí, and Alberto Martín. 2023. "Statistical Study of the Process Parameters for Achieving Continuous Consolidation of a Thermoplastic Composite" Materials 16, no. 20: 6723. https://doi.org/10.3390/ma16206723
APA StyleCampos, D., Maimí, P., & Martín, A. (2023). Statistical Study of the Process Parameters for Achieving Continuous Consolidation of a Thermoplastic Composite. Materials, 16(20), 6723. https://doi.org/10.3390/ma16206723







