CO2 Physisorption over an Industrial Molecular Sieve Zeolite: An Experimental and Theoretical Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Adsorbent Material
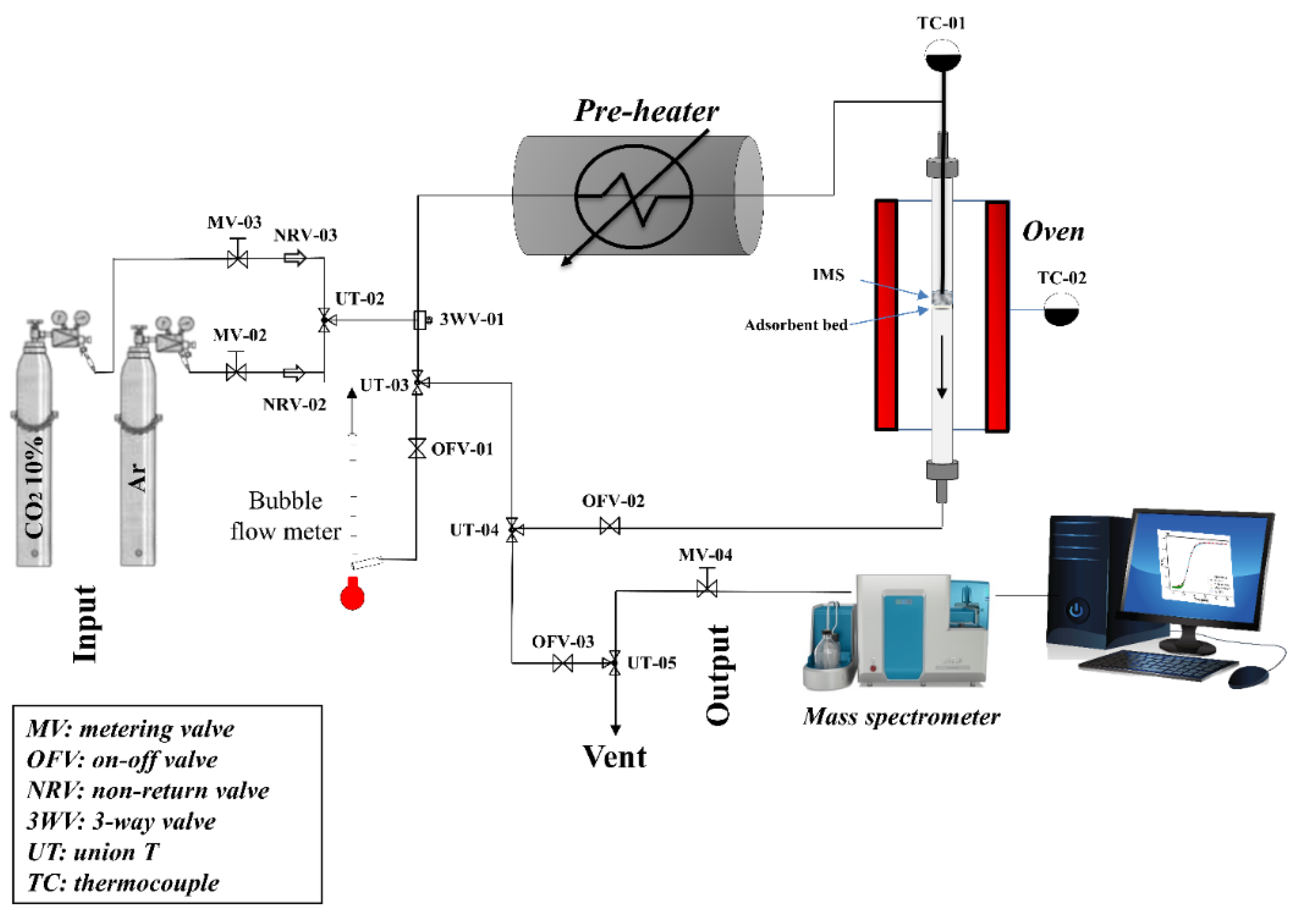
2.2. CO2 Adsorption Tests
3. Results and Discussion
3.1. Effect of the CO2 Feed Concentration
3.2. Effect of the Adsorption Temperature
3.3. Column Studies
3.4. Effect of Multiple Adsorption–Desorption Cycles
4. Conclusions
- By varying the initial CO2 feed concentration (or partial pressure), it was found that a higher feed concentration led to increased CO2 adsorption capacity. The CO2 adsorption isotherm could best be fitted to a Langmuir type isotherm and reached a plateau for CO2 feed concentrations that exceeded the value of 10 vol%.
- By varying the CO2 adsorption temperature, it was found that a higher temperature led to decreased CO2 adsorption capacity. This is indicative that CO2 is adsorbed via van der Waals forces, or, rather, via electrostatic interactions (i.e., physical adsorption).
- The Bangham model (i.e., pore diffusion) could best describe the adsorption kinetic behavior, as is usually the case in physical adsorption processes.
- The activation energy (Ea) was calculated at 32.9 kJ mol−1 and the adsorption enthalpy (ΔHo) at −21.8 kJ mol−1, indicating that CO2 adsorption over the IMS adsorbent is exothermic.
- The Thomas and Yoon–Nelson kinetic models were the most suitable to describe the adsorption process of CO2 on the IMS adsorbent during column studies.
- Lastly, the IMS adsorbent successfully maintained its high adsorption capacity (>200 mg g−1) after 10 consecutive adsorption–desorption cycles, with desorption/regeneration being carried out under mild conditions (200 °C for 15 min).
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Olabi, A.G.; Abdelkareem, M.A. Renewable Energy and Climate Change. Renew. Sustain. Energy Rev. 2022, 158, 112111. [Google Scholar] [CrossRef]
- Koytsoumpa, E.I.; Bergins, C.; Kakaras, E. The CO2 Economy: Review of CO2 Capture and Reuse Technologies. J. Supercrit. Fluids 2018, 132, 3–16. [Google Scholar] [CrossRef]
- Latsiou, A.I.; Charisiou, N.D.; Frontistis, Z.; Bansode, A.; Goula, M.A. CO2 Hydrogenation for the Production of Higher Alcohols: Trends in Catalyst Developments, Challenges and Opportunities. Catal. Today 2023, 420, 114179. [Google Scholar] [CrossRef]
- Choi, S.; Drese, J.H.; Jones, C.W. Adsorbent Materials for Carbon Dioxide Capture from Large Anthropogenic Point Sources. ChemSusChem 2009, 2, 796–854. [Google Scholar] [CrossRef]
- Gouveia, L.G.T.; Agustini, C.B.; Perez-Lopez, O.W.; Gutterres, M. CO2 Adsorption Using Solids with Different Surface and Acid-Base Properties. J. Environ. Chem. Eng. 2020, 8, 103823. [Google Scholar] [CrossRef]
- Tsiotsias, A.I.; Charisiou, N.D.; Harkou, E.; Hafeez, S.; Manos, G.; Constantinou, A.; Hussien, A.G.S.; Dabbawala, A.A.; Sebastian, V.; Hinder, S.J.; et al. Enhancing CO2 Methanation over Ni Catalysts Supported on Sol-Gel Derived Pr2O3-CeO2: An Experimental and Theoretical Investigation. Appl. Catal. B Environ. 2022, 318, 121836. [Google Scholar] [CrossRef]
- Dabbawala, A.A.; Ismail, I.; Vaithilingam, B.V.; Polychronopoulou, K.; Singaravel, G.; Morin, S.; Berthod, M.; Al Wahedi, Y. Synthesis of Hierarchical Porous Zeolite-Y for Enhanced CO2 Capture. Microporous Mesoporous Mater. 2020, 303, 110261. [Google Scholar] [CrossRef]
- Kumar, S.; Srivastava, R.; Koh, J. Utilization of Zeolites as CO2 capturing Agents: Advances and Future Perspectives. J. CO2 Util. 2020, 41, 101251. [Google Scholar] [CrossRef]
- Singh, G.; Lee, J.; Karakoti, A.; Bahadur, R.; Yi, J.; Zhao, D.; Albahily, K.; Vinu, A. Emerging Trends in Porous Materials for CO2 Capture and Conversion. Chem. Soc. Rev. 2020, 49, 4360–4404. [Google Scholar] [CrossRef] [PubMed]
- Rahmah, W.; Kadja, G.T.M.; Mahyuddin, M.H.; Saputro, A.G.; Dipojono, H.K.; Wenten, I.G. Small-Pore Zeolite and Zeotype Membranes for CO2 Capture and Sequestration—A Review. J. Environ. Chem. Eng. 2022, 10, 108707. [Google Scholar] [CrossRef]
- Zagho, M.M.; Hassan, M.K.; Khraisheh, M.; Al-Maadeed, M.A.A.; Nazarenko, S. A Review on Recent Advances in CO2 Separation Using Zeolite and Zeolite-like Materials as Adsorbents and Fillers in Mixed Matrix Membranes (MMMs). Chem. Eng. J. Adv. 2021, 6, 100091. [Google Scholar] [CrossRef]
- Murge, P.; Dinda, S.; Roy, S. Zeolite-Based Sorbent for CO2 Capture: Preparation and Performance Evaluation. Langmuir 2019, 35, 14751–14760. [Google Scholar] [CrossRef]
- Cavallo, M.; Dosa, M.; Porcaro, N.G.; Bonino, F.; Piumetti, M.; Crocella, V. Shaped Natural and Synthetic Zeolites for CO2 Capture in a Wide Temperature Range. J. CO2 Util. 2023, 67, 102335. [Google Scholar] [CrossRef]
- Tsiotsias, A.I.; Charisiou, N.D.; Yentekakis, I.V.; Goula, M.A. The Role of Alkali and Alkaline Earth Metals in the CO2 Methanation Reaction and the Combined Capture and Methanation of CO2. Catalysts 2020, 10, 812. [Google Scholar] [CrossRef]
- Georgiadis, A.G.; Charisiou, N.D.; Goula, M.A. Removal of Hydrogen Sulfide from Various Industrial Gases: A Review of the Most Promising Adsorbing Materials. Catalysts 2020, 10, 521. [Google Scholar] [CrossRef]
- Shen, J.; Sun, Q.; Cao, J.; Wang, P.; Jia, W.; Wang, S.; Zhao, P.; Wang, Z. A Lamellar Structure Zeolite LTA for CO2 Capture. N. J. Chem. 2022, 46, 6720–6728. [Google Scholar] [CrossRef]
- Davarpanah, E.; Armandi, M.; Hernández, S.; Fino, D.; Arletti, R.; Bensaid, S.; Piumetti, M. CO2 Capture on Natural Zeolite Clinoptilolite: Effect of Temperature and Role of the Adsorption Sites. J. Environ. Manag. 2020, 275, 111229. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Yi, H.; Tang, X.; Li, F.; Yuan, Q. Adsorption Separation of CO2/CH4 Gas Mixture on the Commercial Zeolites at Atmospheric Pressure. Chem. Eng. J. 2013, 229, 50–56. [Google Scholar] [CrossRef]
- De Aquino, T.F.; Estevam, S.T.; Viola, V.O.; Marques, C.R.M.; Zancan, F.L.; Vasconcelos, L.B.; Riella, H.G.; Pires, M.J.R.; Morales-Ospino, R.; Torres, A.E.B.; et al. CO2 Adsorption Capacity of Zeolites Synthesized from Coal Fly Ashes. Fuel 2020, 276, 118143. [Google Scholar] [CrossRef]
- Feng, L.; Shen, Y.; Wu, T.; Liu, B.; Zhang, D.; Tang, Z. Adsorption Equilibrium Isotherms and Thermodynamic Analysis of CH4, CO2, CO, N2 and H2 on NaY Zeolite. Adsorption 2020, 26, 1101–1111. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Z.; Li, P.; Yu, J.; Rodrigues, A.E. Experimental and Modeling Investigation on Post-Combustion Carbon Dioxide Capture Using Zeolite 13X-APG by Hybrid VTSA Process. Chem. Eng. J. 2012, 197, 151–161. [Google Scholar] [CrossRef]
- Pham, T.D.; Hudson, M.R.; Brown, C.M.; Lobo, R.F. Molecular Basis for the High CO2 Adsorption Capacity of Chabazite Zeolites. ChemSusChem 2014, 7, 3031–3038. [Google Scholar] [CrossRef] [PubMed]
- Shafeeyan, M.S.; Wan Daud, W.M.A.; Shamiri, A. A Review of Mathematical Modeling of Fixed-Bed Columns for Carbon Dioxide Adsorption. Chem. Eng. Res. Des. 2014, 92, 961–988. [Google Scholar] [CrossRef]
- Akinola, T.E.; Bonilla Prado, P.L.; Wang, M. Experimental Studies, Molecular Simulation and Process Modelling\simulation of Adsorption-Based Post-Combustion Carbon Capture for Power Plants: A State-of-the-Art Review. Appl. Energy 2022, 317, 119156. [Google Scholar] [CrossRef]
- Deng, Z.; Gopalan, A.; Sarkisov, L. In Silico Engineering of Ion-Exchanged Zeolites for High-Performance Carbon Capture in PSA Processes. Chem. Eng. J. 2023, 459, 141597. [Google Scholar] [CrossRef]
- Karka, S.; Kodukula, S.; Nandury, S.V.; Pal, U. Polyethylenimine-Modified Zeolite 13X for CO2 Capture: Adsorption and Kinetic Studies. ACS Omega 2019, 4, 16441–16449. [Google Scholar] [CrossRef] [PubMed]
- Georgiadis, A.G.; Charisiou, N.D.; Gaber, S.; Polychronopoulou, K.; Yentekakis, I.V.; Goula, M.A. Adsorption of Hydrogen Sulfide at Low Temperatures Using an Industrial Molecular Sieve: An Experimental and Theoretical Study. ACS Omega 2021, 6, 14774–14787. [Google Scholar] [CrossRef]
- Won, W.; Lee, S.; Lee, K.S. Modeling and Parameter Estimation for a Fixed-Bed Adsorption Process for CO2 Capture Using Zeolite 13X. Sep. Purif. Technol. 2012, 85, 120–129. [Google Scholar] [CrossRef]
- Faria, A.C.; Trujillano, R.; Rives, V.; Miguel, C.V.; Rodrigues, A.E.; Madeira, L.M. Cyclic Operation of CO2 Capture and Conversion into Methane on Ni-Hydrotalcite Based Dual Function Materials (DFMs). J. CO2 Util. 2023, 72, 102476. [Google Scholar] [CrossRef]
- Antzaras, A.N.; Heracleous, E.; Lemonidou, A.A. Sorption Enhanced–Chemical Looping Steam Methane Reforming: Optimizing the Thermal Coupling of Regeneration in a Fixed Bed Reactor. Fuel Process. Technol. 2020, 208, 106513. [Google Scholar] [CrossRef]
- Raganati, F.; Chirone, R.; Ammendola, P. CO2 Capture by Temperature Swing Adsorption: Working Capacity as Affected by Temperature and CO2 Partial Pressure. Ind. Eng. Chem. Res. 2020, 59, 3593–3605. [Google Scholar] [CrossRef]
- Wang, X.; Song, C. Carbon Capture from Flue Gas and the Atmosphere: A Perspective. Front. Energy Res. 2020, 8, 560849. [Google Scholar] [CrossRef]
- Li, Z.; Liu, P.; Ou, C.; Dong, X. Porous Metal-Organic Frameworks for Carbon Dioxide Adsorption and Separation at Low Pressure. ACS Sustain. Chem. Eng. 2020, 8, 15378–15404. [Google Scholar] [CrossRef]
- Hussin, F.; Aroua, M.K.; Yusoff, R. Adsorption of CO2 on Palm Shell Based Activated Carbon Modified by Deep Eutectic Solvent: Breakthrough Adsorption Study. J. Environ. Chem. Eng. 2021, 9, 105333. [Google Scholar] [CrossRef]
- Siakavelas, G.I.; Georgiadis, A.G.; Charisiou, N.D.; Yentekakis, I.V.; Goula, M.A. Cost-Effective Adsorption of Oxidative Coupling-Derived Ethylene Using a Molecular Sieve. Chem. Eng. Technol. 2021, 44, 2041–2048. [Google Scholar] [CrossRef]
- Raghav, S.; Kumar, D. Adsorption Equilibrium, Kinetics, and Thermodynamic Studies of Fluoride Adsorbed by Tetrametallic Oxide Adsorbent. J. Chem. Eng. Data 2018, 63, 1682–1697. [Google Scholar] [CrossRef]
- Chung Lau, L. Adsorption Isotherm, Kinetic, Thermodynamic and Breakthrough Curve Models of H2S Removal Using CeO2/NaOH/PSAC. Int. J. Petrochem. Sci. Eng. 2016, 1, 00009. [Google Scholar] [CrossRef]
- Xiao, Y.; Wang, S.; Wu, D.; Yuan, Q. Experimental and Simulation Study of Hydrogen Sulfide Adsorption on Impregnated Activated Carbon under Anaerobic Conditions. J. Hazard. Mater. 2008, 153, 1193–1200. [Google Scholar] [CrossRef] [PubMed]
- Mahmoud, M.A. Kinetics and Thermodynamics of Aluminum Oxide Nanopowder as Adsorbent for Fe (III) from Aqueous Solution. Beni Suef Univ. J. Basic Appl. Sci. 2015, 4, 142–149. [Google Scholar] [CrossRef]
- Zito, P.F.; Caravella, A.; Brunetti, A.; Drioli, E.; Barbieri, G. Estimation of Langmuir and Sips Models Adsorption Parameters for NaX and NaY FAU Zeolites. J. Chem. Eng. Data 2015, 60, 2858–2868. [Google Scholar] [CrossRef]
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing, K.S.W. Physisorption of Gases, with Special Reference to the Evaluation of Surface Area and Pore Size Distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef]
- Xie, M.; Leung, A.K.; Ng, C.W.W. Mechanisms of Hydrogen Sulfide Removal by Ground Granulated Blast Furnace Slag Amended Soil. Chemosphere 2017, 175, 425–430. [Google Scholar] [CrossRef] [PubMed]
- Jedli, H.; Almoneef, M.M.; Mbarek, M.; Jbara, A.; Slimi, K. Adsorption of CO2 onto Zeolite ZSM-5: Kinetic, Equilibrium and Thermodynamic Studies. Fuel 2022, 321, 124097. [Google Scholar] [CrossRef]
- Müller, B.R.; Calzaferri, G. Thin Mo(CO)6-Y-Zeolite Layers: Preparation and in Situ Transmission FTIR Spectroscopy. J. Chem. Soc. Faraday Trans. 1996, 92, 1633–1637. [Google Scholar] [CrossRef]
- Mall, I.D.; Srivastava, V.C.; Agarwal, N.K. Adsorptive Removal of Auramine-O: Kinetic and Equilibrium Study. J. Hazard. Mater. 2007, 143, 386–395. [Google Scholar] [CrossRef] [PubMed]
- Gong, H.; Liu, W.; Liu, L.; Goyal, N.; Xiao, P.; Li, G.; Wei, Y.; Du, T. In-Situ Synthesis of an Excellent CO2 Capture Material Chabazite. J. Taiwan Inst. Chem. Eng. 2019, 103, 160–166. [Google Scholar] [CrossRef]
- Lu, S.; Liu, Q.; Han, R.; Shi, J.; Guo, M.; Song, C.; Ji, N.; Lu, X.; Ma, D. Core-Shell Structured Y Zeolite/Hydrophobic Organic Polymer with Improved Toluene Adsorption Capacity under Dry and Wet Conditions. Chem. Eng. J. 2021, 409, 128194. [Google Scholar] [CrossRef]
- Song, T.; Liao, J.M.; Xiao, J.; Shen, L.H. Effect of Micropore and Mesopore Structure on CO2 Adsorption by Activated Carbons from Biomass. N. Carbon Mater. 2015, 30, 156–166. [Google Scholar] [CrossRef]
- Singh, V.K.; Kumar, E.A. Comparative Studies on CO2 Adsorption Kinetics by Solid Adsorbents. Energy Procedia 2016, 90, 316–325. [Google Scholar] [CrossRef]
- Cheng, H.; Song, H.; Toan, S.; Wang, B.; Gasem, K.A.M.; Fan, M.; Cheng, F. Experimental Investigation of CO2 Adsorption and Desorption on Multi-Type Amines Loaded HZSM-5 Zeolites. Chem. Eng. J. 2021, 406, 126882. [Google Scholar] [CrossRef]
- Ridha, F.N.; Webley, P.A. Entropic Effects and Isosteric Heats of Nitrogen and Carbon Dioxide Adsorption on Chabazite Zeolites. Microporous Mesoporous Mater. 2010, 132, 22–30. [Google Scholar] [CrossRef]
- Bohart, G.S.; Adams, E.Q. Some Aspects of the Behavior of Charcoal with Respect to Chlorine. J. Am. Chem. Soc. 1920, 42, 523–544. [Google Scholar] [CrossRef]
- Han, R.; Wang, Y.; Zhao, X.; Wang, Y.; Xie, F.; Cheng, J.; Tang, M. Adsorption of Methylene Blue by Phoenix Tree Leaf Powder in a Fixed-Bed Column: Experiments and Prediction of Breakthrough Curves. Desalination 2009, 245, 284–297. [Google Scholar] [CrossRef]
- Boonchuay, A.; Worathanakul, P. The Diffusion Behavior of CO2 Adsorption from a CO2/N2 Gas Mixture on Zeolite 5A in a Fixed-Bed Column. Atmosphere 2022, 13, 513. [Google Scholar] [CrossRef]
- Dima, J.B.; Ferrari, M.; Zaritzky, N. Mathematical Modeling of Fixed-Bed Columns Adsorption: Hexavalent Chromium onto Chitosan Flakes. Ind. Eng. Chem. Res. 2020, 59, 15378–15386. [Google Scholar] [CrossRef]
- Deng, Y.; Seville, J.P.K.; Bell, S.D.; Ingram, A.; Zhang, H.; Sweygers, N.; Dewil, R.; Baeyens, J.; Appels, L. Reviewing Fundamental CO2 Adsorption Characteristics of Zeolite and Activated Carbon by In-Situ Measurements with Radioactively Labelled CO2. Sep. Purif. Rev. 2022, 51, 318–329. [Google Scholar] [CrossRef]
- Montanari, T.; Busca, G. On the Mechanism of Adsorption and Separation of CO2 on LTA Zeolites: An IR Investigation. Vib. Spectrosc. 2008, 46, 45–51. [Google Scholar] [CrossRef]
- Martin-Calvo, A.; Parra, J.B.; Ania, C.O.; Calero, S. Insights on the Anomalous Adsorption of Carbon Dioxide in LTA Zeolites. J. Phys. Chem. C 2014, 118, 25460–25467. [Google Scholar] [CrossRef]
- Pokhrel, J.; Bhoria, N.; Wu, C.; Reddy, K.S.K.; Margetis, H.; Anastasiou, S.; George, G.; Mittal, V.; Romanos, G.; Karonis, D.; et al. Cu- and Zr-Based Metal Organic Frameworks and Their Composites with Graphene Oxide for Capture of Acid Gases at Ambient Temperature. J. Solid State Chem. 2018, 266, 233–243. [Google Scholar] [CrossRef]




| Characteristic | Value |
|---|---|
| Shape a | Spherical |
| Density (g dm−3) a | 1.36 |
| Bulk density (kg m−3) a | 700–750 |
| pH a | 8–11 |
| Melting point a | <1600 °C |
| Si/Al ratio b | 0.97 |
| Specific surface area (m2 g−1) c | 590 |
| Average pore size (nm) b | 1.73 |
| CO2 Feed Concentration (%) | Equilibrium Adsorption Capacity (mg g−1) |
|---|---|
| 0.2 | 53 |
| 0.5 | 73 |
| 1 | 100 |
| 2 | 142 |
| 5 | 183 |
| 10 | 204 |
| 20 | 204 |
| 50 | 204 |
| 100 | 205 |
| Model | Parameter | Value |
|---|---|---|
| Langmuir | 0.06 | |
| 211.8 | ||
| 0.979 | ||
| Freundlich | 71.66 | |
| 6.26 | ||
| 0.704 | ||
| Temkin | 2.98 | |
| 0.09 | ||
| 0.836 | ||
| DR | 2.3 × 10−5 | |
| 192.6 | ||
| 147.6 | ||
| 0.721 |
| Model | Parameter | 25 °C | 35 °C | 50 °C | 75 °C | 100 °C |
|---|---|---|---|---|---|---|
| PFO | 0.139 | 0.191 | 0.234 | 0.411 | 0.714 | |
| 206.92 | 164.40 | 117.51 | 65.66 | 34.59 | ||
| 203.69 | 162.23 | 116.28 | 65.14 | 34.46 | ||
| 0.979 | 0.970 | 0.977 | 0.970 | 0.979 | ||
| PSO | 7.7 × 10−4 | 1.5 × 10−3 | 2.7 × 10−3 | 1.0 × 10−2 | 3.8 × 10−2 | |
| 235.78 | 182.56 | 129.11 | 69.83 | 36.06 | ||
| 203.69 | 162.23 | 116.28 | 65.14 | 34.46 | ||
| 0.927 | 0.901 | 0.908 | 0.877 | 0.871 | ||
| WM | 21.18 | 15.11 | 10.52 | 4.38 | 1.73 | |
| 72.05 | 73.51 | 57.57 | 42.40 | 26.06 | ||
| 0.650 | 0.552 | 0.528 | 0.375 | 0.277 | ||
| Bangham | 0.058 | 0.074 | 0.116 | 0.230 | 0.550 | |
| 203.87 | 162.60 | 116.48 | 65.31 | 34.48 | ||
| 203.69 | 162.23 | 116.28 | 65.14 | 34.46 | ||
| 1.426 | 1.532 | 1.442 | 1.540 | 1.498 | ||
| 0.999 | 0.998 | 0.999 | 0.998 | 0.998 |
| Model | Fixed Parameter | Value | Estimated Parameter | 2 vol% CO2 | 5 vol% CO2 | 10 vol% CO2 |
|---|---|---|---|---|---|---|
| Adams–Bohart | 2.0 | 7.104 | 5.178 | 5.977 | ||
| 19.7 | 10.68 | 15.07 | 16.71 | |||
| 0.992 | 0.991 | 0.998 | ||||
| Thomas | 1.0 | 4.196 | 2.980 | 2.780 | ||
| 100.0 | 122.89 | 175.06 | 194.79 | |||
| 141.79 | 182.48 | 203.69 | ||||
| 0.998 | 0.999 | 0.996 | ||||
| Yoon–Nelson | - | - | 0.155 | 0.269 | 0.481 | |
| - | - | 33.28 | 19.40 | 11.23 | ||
| 0.998 | 0.999 | 0.996 |
| Cycle Number | CO2 Adsorption Capacity (mg g−1) | Cycle Number | CO2 Adsorption Capacity (mg g−1) |
|---|---|---|---|
| 1 | 204 | 6 | 200 |
| 2 | 202 | 7 | 202 |
| 3 | 202 | 8 | 203 |
| 4 | 200 | 9 | 205 |
| 5 | 205 | 10 | 203 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsiotsias, A.I.; Georgiadis, A.G.; Charisiou, N.D.; Goula, M.A. CO2 Physisorption over an Industrial Molecular Sieve Zeolite: An Experimental and Theoretical Approach. Materials 2023, 16, 6656. https://doi.org/10.3390/ma16206656
Tsiotsias AI, Georgiadis AG, Charisiou ND, Goula MA. CO2 Physisorption over an Industrial Molecular Sieve Zeolite: An Experimental and Theoretical Approach. Materials. 2023; 16(20):6656. https://doi.org/10.3390/ma16206656
Chicago/Turabian StyleTsiotsias, Anastasios I., Amvrosios G. Georgiadis, Nikolaos D. Charisiou, and Maria A. Goula. 2023. "CO2 Physisorption over an Industrial Molecular Sieve Zeolite: An Experimental and Theoretical Approach" Materials 16, no. 20: 6656. https://doi.org/10.3390/ma16206656
APA StyleTsiotsias, A. I., Georgiadis, A. G., Charisiou, N. D., & Goula, M. A. (2023). CO2 Physisorption over an Industrial Molecular Sieve Zeolite: An Experimental and Theoretical Approach. Materials, 16(20), 6656. https://doi.org/10.3390/ma16206656










