Measurement of Optical Properties of CH3NH3PbX3 (X = Br, I) Single Crystals Using Terahertz Time-Domain Spectroscopy
Abstract
1. Introduction
2. Experimental and Theoretical Details
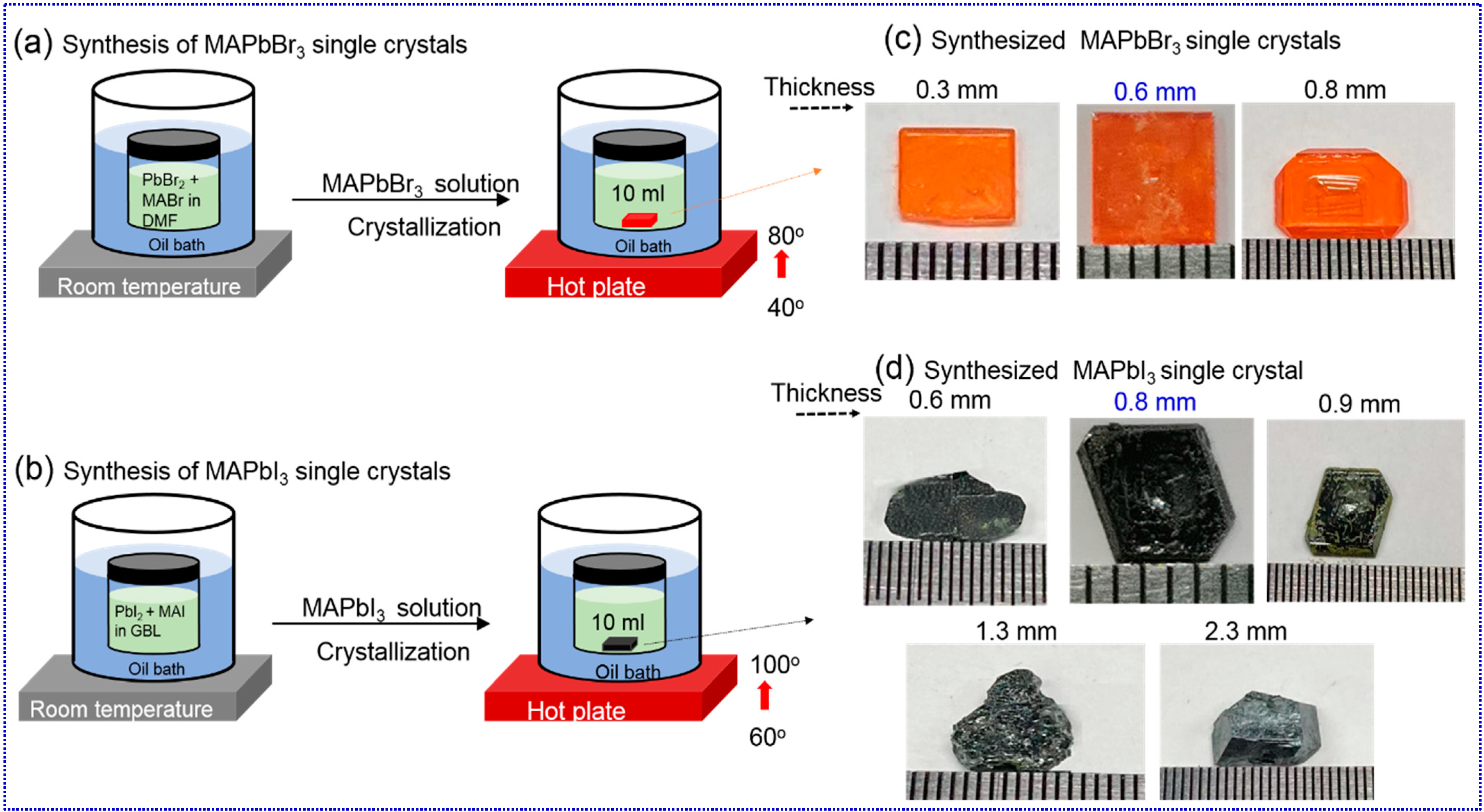
2.1. Materials’ Synthesis
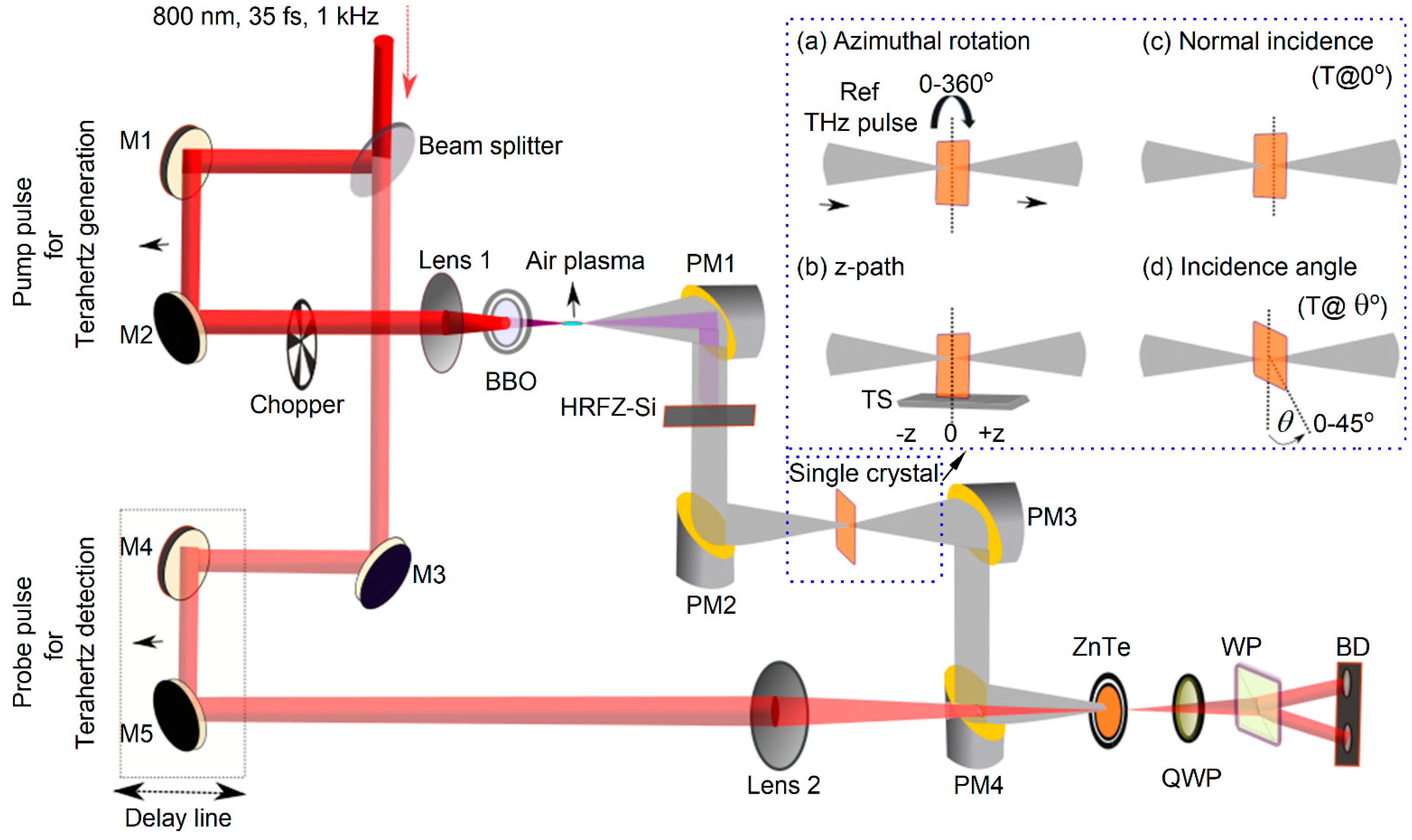
2.2. Experimental Details
2.3. Theoretical Equations for THz-Based Optical Parameters
3. Results and Discussions
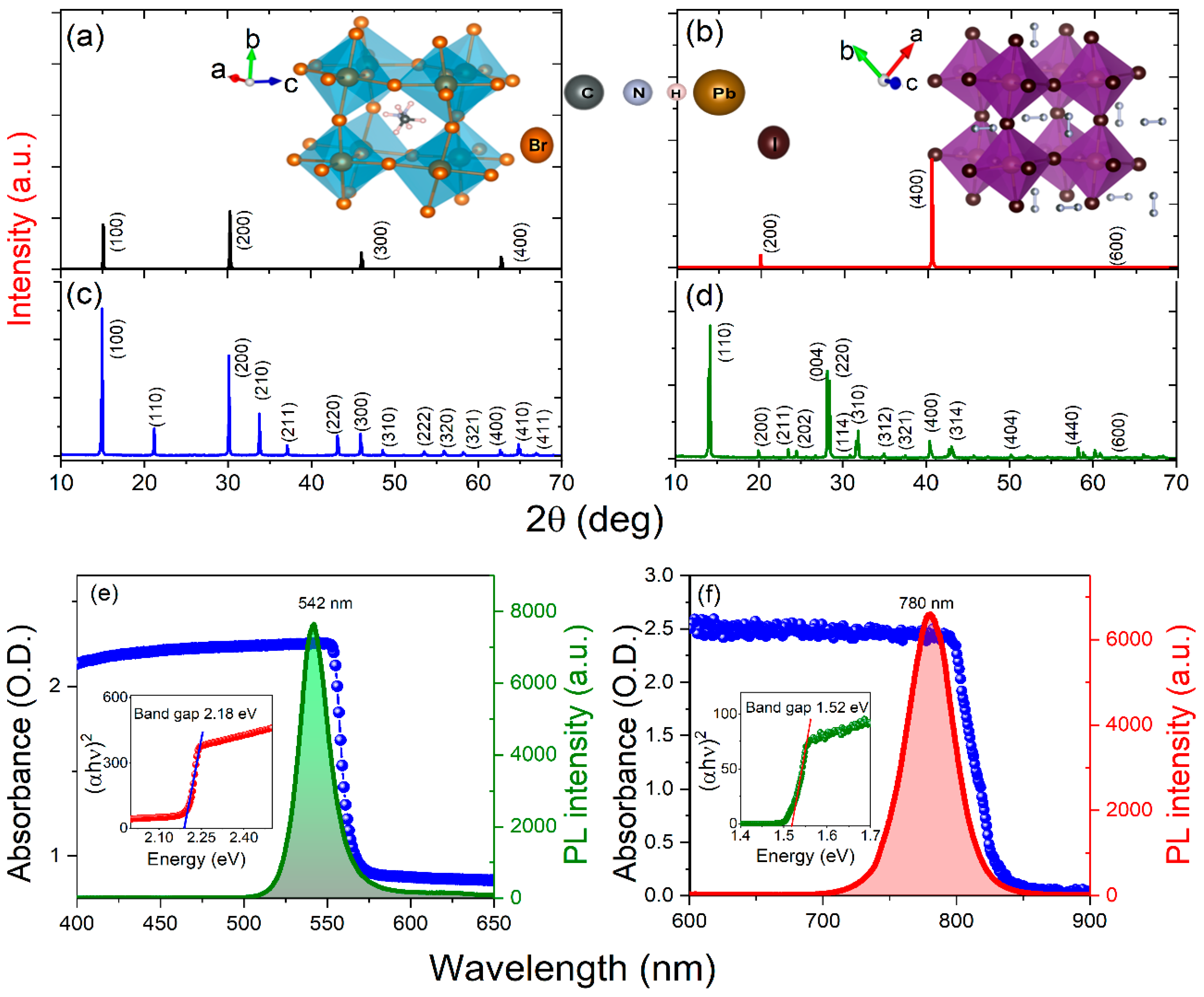
3.1. Structural Characterization and Optical Properties of PSCs
3.2. THz-TDS of PSCs
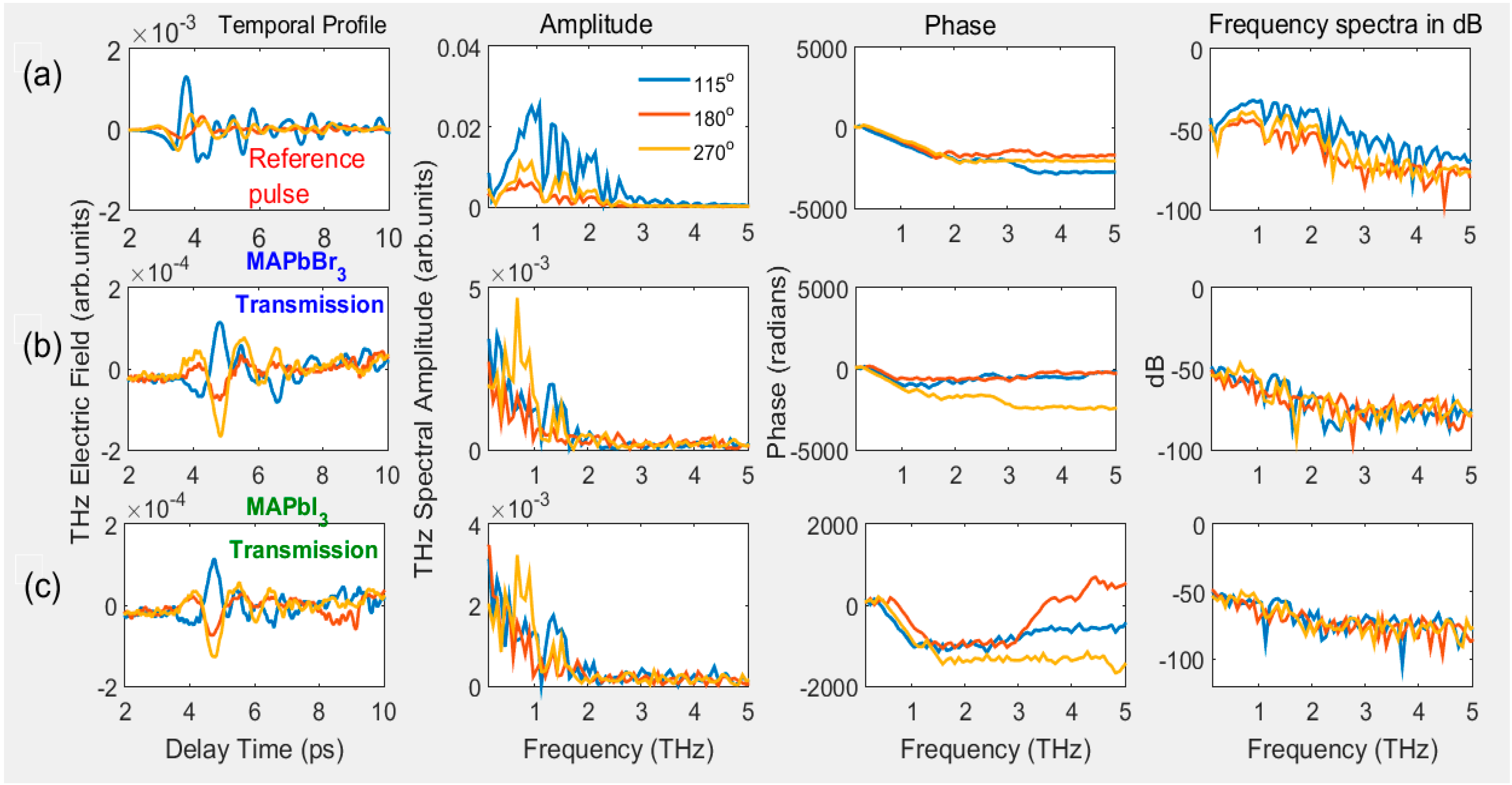
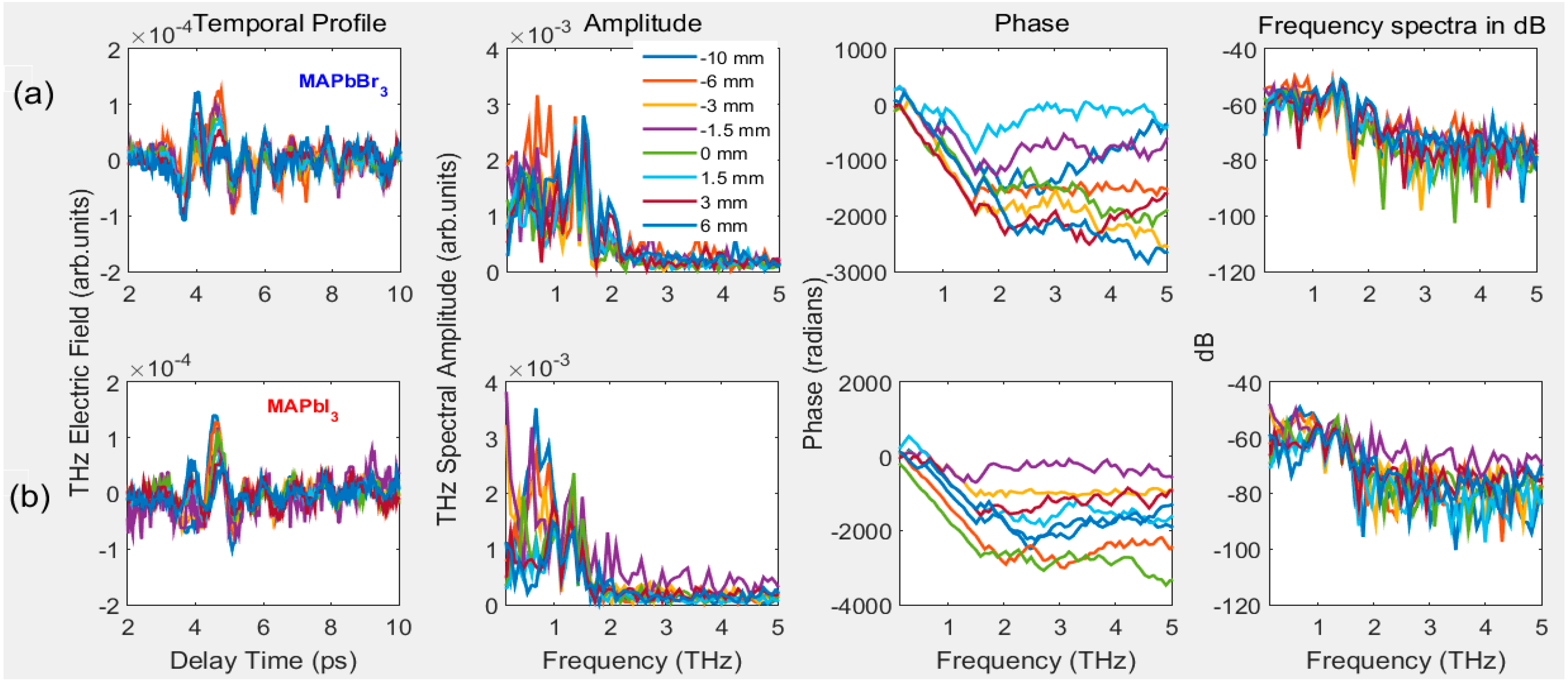
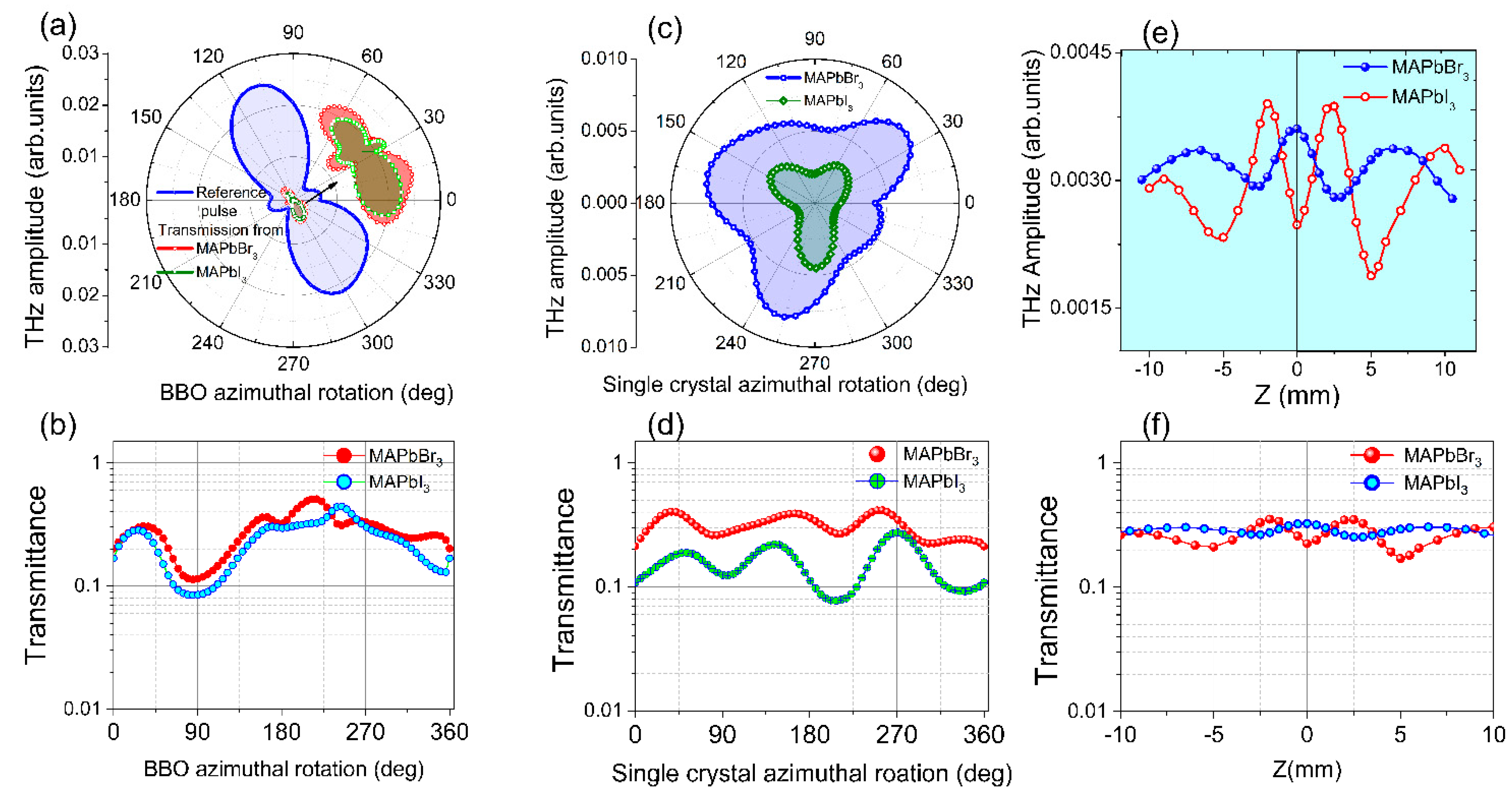
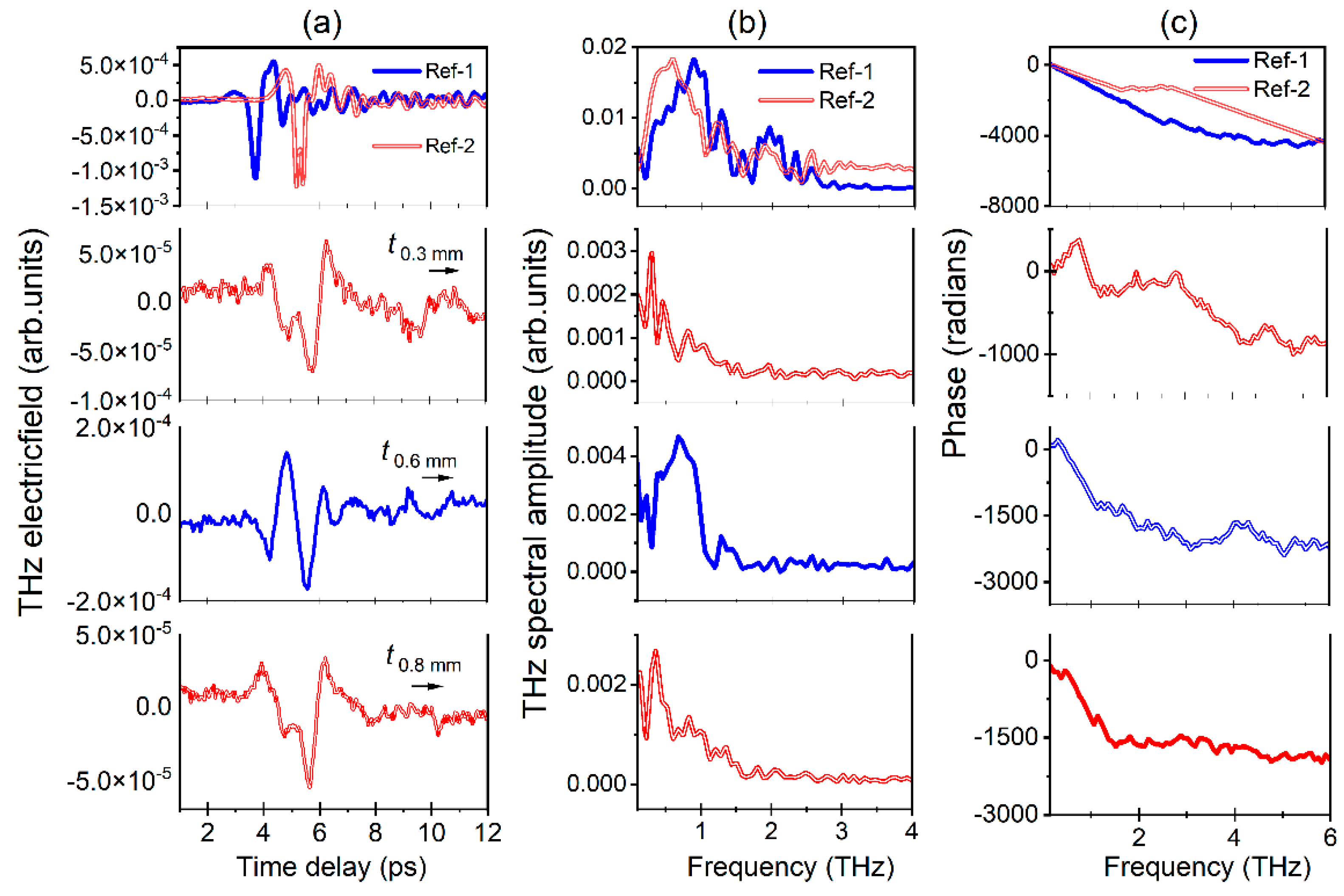
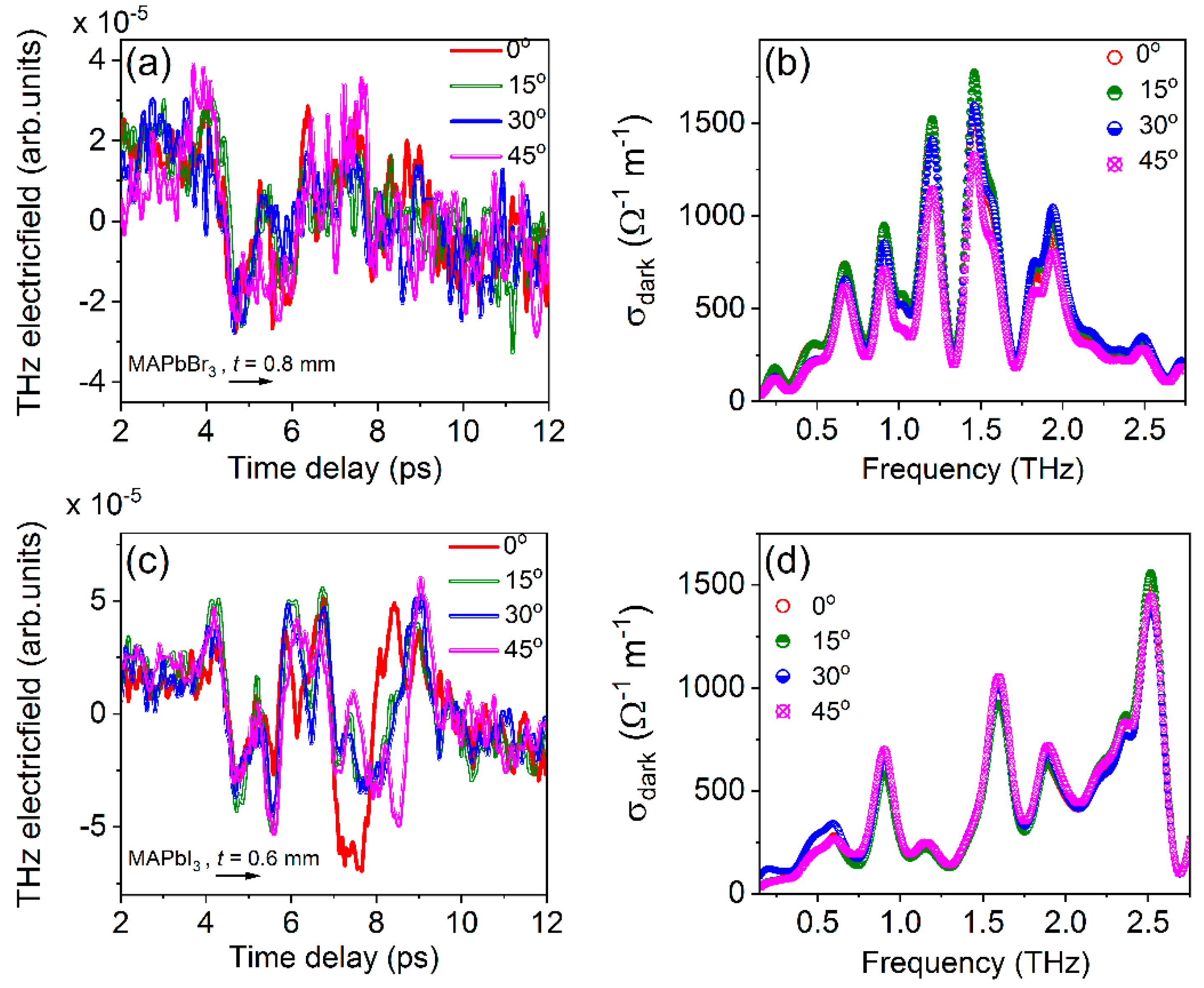
3.2.1. Optimization of Reference THz Pulse, THz-TDS of PSCs for Azimuthal Rotation, and Movement along the Z-Path
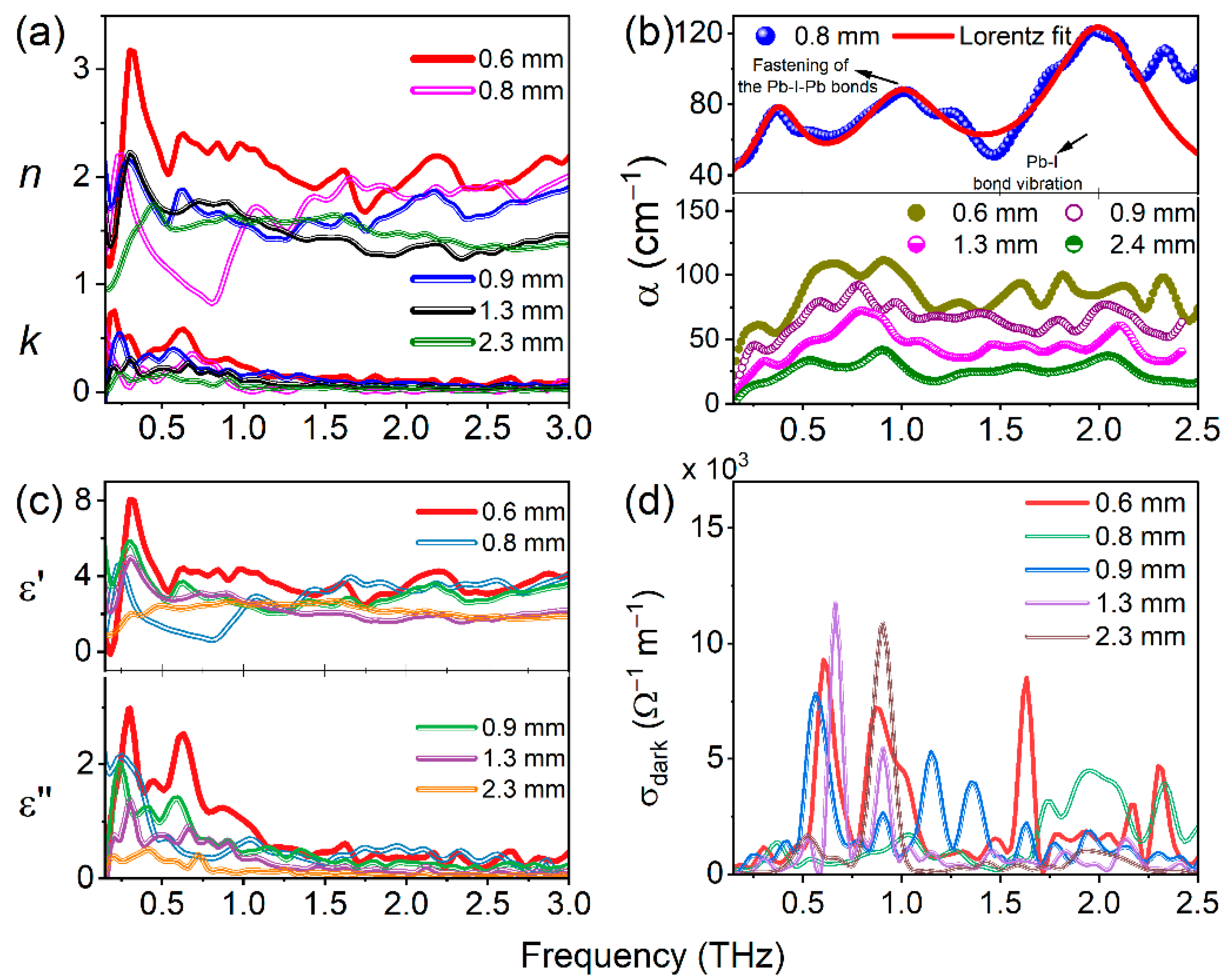
3.2.2. Measurements of THz Optical Properties with Varying Thicknesses of PSCs
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fedorov, V.Y.; Tzortzakis, S. Powerful Terahertz Waves from Long-Wavelength Infrared Laser Filaments. Light Sci. Appl. 2020, 9, 186. [Google Scholar] [CrossRef] [PubMed]
- Cook, D.J.; Hochstrasser, R.M. Intense Terahertz Pulses by Four-Wave Rectification in Air. Opt. Lett. 2000, 25, 1210–1212. [Google Scholar] [CrossRef] [PubMed]
- Heindl, M.B.; Kirkwood, N.; Lauster, T.; Lang, J.A.; Retsch, M.; Mulvaney, P.; Herink, G. Ultrafast Imaging of Terahertz Electric Waveforms Using Quantum Dots. Light Sci. Appl. 2022, 11, 31–33. [Google Scholar] [CrossRef] [PubMed]
- Roussel, E.; Szwaj, C.; Evain, C.; Steffen, B.; Gerth, C.; Jalali, B.; Bielawski, S. Phase Diversity Electro-Optic Sampling: A New Approach to Single-Shot Terahertz Waveform Recording. Light Sci. Appl. 2022, 11, 14. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Shi, C.; Zhu, Y.; Gu, M.; Zhuang, S. Terahertz Spectroscopy in Biomedical Field: A Review on Signal-to-Noise Ratio Improvement. PhotoniX 2020, 1, 12. [Google Scholar] [CrossRef]
- Chen, Z.; Segev, M. Highlighting Photonics: Looking into the next Decade. eLight 2021, 1, 2. [Google Scholar] [CrossRef]
- Lu, W.; Fan, Z.; Yang, Y.; Ma, J.; Lai, J.; Song, X.; Zhuo, X.; Xu, Z.; Liu, J.; Hu, X.; et al. Ultrafast Photothermoelectric Effect in Dirac Semimetallic Cd3As2 Revealed by Terahertz Emission. Nat. Commun. 2022, 13, 1623. [Google Scholar] [CrossRef]
- Rao, K.S.; Chaudhary, A.K.; Venkatesh, M.; Thirupugalmani, K.; Brahadeeswaran, S. DAST Crystal Based Terahertz Generation and Recording of Time Resolved Photoacoustic Spectra of N2O Gas at 0.5 and 1.5 THz Bands. Curr. Appl. Phys. 2016, 16, 777–783. [Google Scholar] [CrossRef]
- Jia, W.; Liu, M.; Lu, Y.; Feng, X.; Wang, Q.; Zhang, X.; Ni, Y.; Hu, F.; Gong, M.; Xu, X.; et al. Broadband Terahertz Wave Generation from an Epsilon-near-Zero Material. Light Sci. Appl. 2021, 10, 11. [Google Scholar] [CrossRef]
- Lin, K.; Xing, J.; Quan, L.N.; de Arquer, F.P.G.; Gong, X.; Lu, J.; Xie, L.; Zhao, W.; Zhang, D.; Yan, C.; et al. Perovskite Light-Emitting Diodes with External Quantum Efficiency Exceeding 20 per Cent. Nature 2018, 562, 245–248. [Google Scholar] [CrossRef]
- Deschler, F.; Price, M.; Pathak, S.; Klintberg, L.E.; Jarausch, D.D.; Higler, R.; Hüttner, S.; Leijtens, T.; Stranks, S.D.; Snaith, H.J.; et al. High Photoluminescence Efficiency and Optically Pumped Lasing in Solution-Processed Mixed Halide Perovskite Semiconductors. J. Phys. Chem. Lett. 2014, 5, 1421–1426. [Google Scholar] [CrossRef] [PubMed]
- Colella, S.; Mazzeo, M.; Rizzo, A.; Gigli, G.; Listorti, A. The Bright Side of Perovskites. J. Phys. Chem. Lett. 2016, 7, 4322–4334. [Google Scholar] [CrossRef] [PubMed]
- Syed, H.; Kong, W.; Mottamchetty, V.; Lee, K.J.; Yu, W.; Soma, V.R.; Yang, J.; Guo, C. Giant Nonlinear Optical Response in Triple Cation Halide Mixed Perovskite Films. Adv. Opt. Mater. 2020, 8, 1901766. [Google Scholar] [CrossRef]
- Chanana, A.; Liu, X.; Zhang, C.; Vardeny, Z.V.; Nahata, A. Ultrafast Frequency-Agile Terahertz Devices Using Methylammonium Lead Halide Perovskites. Sci. Adv. 2018, 4, eaar7353. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Yang, W.; Cheng, Y.; Dong, J.; Zhu, M.; Zhang, B.B.; Dubois, A.; Zhu, M.; Jie, W.; Xu, Y. Anisotropic Dielectric Behavior of Layered Perovskite-like Cs3Bi2I9crystals in the Terahertz Region. Phys. Chem. Chem. Phys. 2020, 22, 24555–24560. [Google Scholar] [CrossRef]
- Zhao, D.; Chia, E.E.M. Free Carrier, Exciton, and Phonon Dynamics in Lead-Halide Perovskites Studied with Ultrafast Terahertz Spectroscopy. Adv. Opt. Mater. 2020, 8, 1900783. [Google Scholar] [CrossRef]
- Nayak, D.; Vijayan, N.; Kumari, M.; Vashishtha, P.; Yadav, S.; Jewariya, M.; Chowdhury, D.R.; Gupta, G.; Pant, R.P. Elemental, Optical, and Time-Domain Terahertz Spectroscopy Studies on Methyl p-Hydroxybenzoate Single Crystal for THz Applications. J. Electron. Mater. 2021, 50, 6121–6127. [Google Scholar] [CrossRef]
- Xia, C.Q.; Poncé, S.; Peng, J.; Ulatowski, A.M.; Patel, J.B.; Wright, A.D.; Milot, R.L.; Kraus, H.; Lin, Q.; Herz, L.M.; et al. Ultrafast Photo-Induced Phonon Hardening Due to Pauli Blocking in MAPbI3single-Crystal and Polycrystalline Perovskites. J. Phys. Mater. 2021, 4, 44017. [Google Scholar] [CrossRef]
- Maeng, I.; Lee, S.; Tanaka, H.; Yun, J.; Wang, S.; Nakamura, M.; Kwon, Y.; Jung, M. Unique Phonon Modes of a CH 3 NH 3 PbBr 3 Hybrid Perovskite Fi Lm without the in Fl Uence of Defect Structures: An Attempt toward a Novel THz-Based Application. NPG Asia Mater. 2020, 12, 53. [Google Scholar] [CrossRef]
- Maeng, I.; Lee, Y.M.; Park, J.; Raga, S.R.; Kang, C.; Kee, C.S.; Yu, B.D.; Hong, S.; Ono, L.K.; Qi, Y.; et al. Significant THz Absorption in CH 3 NH 2 Molecular Defect-Incorporated Organic-Inorganic Hybrid Perovskite Thin Film. Sci. Rep. 2019, 9, 5811. [Google Scholar] [CrossRef]
- Saidaminov, M.I.; Abdelhady, A.L.; Murali, B.; Alarousu, E.; Burlakov, V.M.; Peng, W.; Dursun, I.; Wang, L.; He, Y.; MacUlan, G.; et al. High-Quality Bulk Hybrid Perovskite Single Crystals within Minutes by Inverse Temperature Crystallization. Nat. Commun. 2015, 6, 7586. [Google Scholar] [CrossRef] [PubMed]
- Duvillaret, L.; Garet, F.; Coutaz, J. A Reliable Method for Extraction of Material Parameters in Terahertz Time-Domain Spectroscopy. IEEE J. Sel. Top. Quantum Electron. 1996, 2, 739–746. [Google Scholar] [CrossRef]
- Withayachumnankul, W.; Naftaly, M. Fundamentals of Measurement in Terahertz Time-Domain Spectroscopy. J. Infrared Millim. Terahertz Waves 2014, 35, 610–637. [Google Scholar] [CrossRef]
- Yu, B.L.; Zeng, F.; Xing, Q.; Alfano, R.R. Probing Dielectric Relaxation Properties of Liquid CS2 with Terahertz Time-Domain Spectroscopy. Appl. Phys. Lett. 2003, 82, 4633–4635. [Google Scholar] [CrossRef]
- Nienhuys, H.K.; Sundström, V. Intrinsic Complications in the Analysis of Optical-Pump, Terahertz Probe Experiments. Phys. Rev. B Condens. Matter Mater. Phys. 2005, 71, 235110. [Google Scholar] [CrossRef]
- Lloyd-Hughes, J.; Jeon, T.-I. A Review of the Terahertz Conductivity of Bulk and Nano-Materials. J. Infrared Millim. Terahertz Waves 2012, 33, 871–925. [Google Scholar] [CrossRef]
- Wang, G.; Li, D.; Cheng, H.C.; Li, Y.; Chen, C.Y.; Yin, A.; Zhao, Z.; Lin, Z.; Wu, H.; He, Q.; et al. Wafer-Scale Growth of Large Arrays of Perovskite Microplate Crystals for Functional Electronics and Optoelectronics. Sci. Adv. 2015, 1, e1500613. [Google Scholar] [CrossRef]
- Chen, M.K.; Kim, J.H.; Yang, C.E.; Yin, S.S.; Hui, R.; Ruffin, P. Terahertz Generation in Multiple Laser-Induced Air Plasmas. Appl. Phys. Lett. 2008, 93, 2008–2010. [Google Scholar] [CrossRef]
- Yang, D.; Cheng, X.; Liu, Y.; Shen, C.; Xu, Z.; Zheng, X.; Jiang, T. Dielectric Properties of a CsPbBr3 Quantum Dot Solution in the Terahertz Region. Appl. Opt. 2017, 56, 2878. [Google Scholar] [CrossRef]
- Zou, B.; Li, Q.-Q.; Yang, Y.P.; Guo, H.-Z. Optically Tuned Dielectric Characteristics of SrTiO3/Si Thin Film in the Terahertz Range. Chinese Phys. B 2021, 30, 107802. [Google Scholar] [CrossRef]
- Sendner, M.; Nayak, P.K.; Egger, D.A.; Beck, S.; Mu, C.; Epding, B.; Kowalsky, W.; Kronik, L.; Snaith, H.J.; Pucci, A.; et al. Optical Phonons in Methylammonium Lead Halide Perovskites and Implications for Charge Transport†. Mater. Horizons 2016, 3, 613–620. [Google Scholar] [CrossRef]
- Zhao, D.; Skelton, J.M.; Hu, H.; La-O-Vorakiat, C.; Zhu, J.X.; Marcus, R.A.; Michel-Beyerle, M.E.; Lam, Y.M.; Walsh, A.; Chia, E.E.M. Low-Frequency Optical Phonon Modes and Carrier Mobility in the Halide Perovskite CH3NH3PbBr3 Using Terahertz Time-Domain Spectroscopy. Appl. Phys. Lett. 2017, 111, 201903. [Google Scholar] [CrossRef]
- La-O-Vorakiat, C.; Xia, H.; Kadro, J.; Salim, T.; Zhao, D.; Ahmed, T.; Lam, Y.M.; Zhu, J.X.; Marcus, R.A.; Michel-Beyerle, M.E.; et al. Phonon Mode Transformation Across the Orthohombic-Tetragonal Phase Transition in a Lead Iodide Perovskite CH3NH3PbI3: A Terahertz Time-Domain Spectroscopy Approach. J. Phys. Chem. Lett. 2016, 7, 1–6. [Google Scholar] [CrossRef]
- Maeng, I.; Matsuyama, A.; Yun, J.H.; Wang, S.; Kang, C.; Kee, C.S.; Nakamura, M.; Jung, M.C. Strong Linear Correlation between CH3NH2 Molecular Defect and THz-Wave Absorption in CH3NH3PbI3 Hybrid Perovskite Thin Film. Nanomaterials 2020, 10, 721. [Google Scholar] [CrossRef]
- La-O-Vorakiat, C.; Salim, T.; Kadro, J.; Khuc, M.T.; Haselsberger, R.; Cheng, L.; Xia, H.; Gurzadyan, G.G.; Su, H.; Lam, Y.M.; et al. Elucidating the Role of Disorder and Free-Carrier Recombination Kinetics in CH3 NH3 PbI3 Perovskite Films. Nat. Commun. 2015, 6, 7903. [Google Scholar] [CrossRef]
- Andrianov, A.V.; Aleshin, A.N.; Matyushkin, L.B. Terahertz Vibrational Modes in CH3 NH3 PbI3 and CsPbI3 Perovskite Films. JETP Lett. 2019, 109, 28–32. [Google Scholar] [CrossRef]
- Kim, H.; Hunger, J.; Cánovas, E.; Karakus, M.; Mics, Z.; Grechko, M.; Turchinovich, D.; Parekh, S.H.; Bonn, M. Direct Observation of Mode-Specific Phonon-Band Gap Coupling in Methylammonium Lead Halide Perovskites. Nat. Commun. 2017, 8, 687. [Google Scholar] [CrossRef] [PubMed]



| Materials/Methods | Regime (THz) | Each Row Represents Peak Positions of Phonon Vibrational Frequencies in THz | Ref. | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAPbBr3 thin films | ||||||||||
| Theory | 0.1-5.0 | 0.3 | 0.45 | 0.81 | 0.9 | 1.35 | 1.53 | 2.19 | 5.01 | [31] |
| Theory/Experiment | 0.25-3.0 | 1.5 | 2.0 | [32] | ||||||
| Theory | 0.25-2.75 | 1.3 | 2.25 | [16] | ||||||
| Theory/Experiment | 0.25-2.5 | 0.8 | 1.4 | 2.0 | [19] | |||||
| MAPbBr3 single crystals | ||||||||||
| Theory/Experiment | 0.25-2.5 | 0.2 | 0.59 | 0.71 | 0.93, 1.26 | 1.35 | 1.84 | 2.11, 2.29 | [19] | |
| Experiment | 0.1-3.0 | 0.38 | 0.53 | 1.05, 1.21 | 1.58 | 1.88 | 2.11 2.34 | This work | ||
| MAPbI3 thin films | ||||||||||
| Theory/Exp | 0.25-2.6 | 0.95 | 1.58 | 1.87 | [20] | |||||
| Experiment | 0.3-1.0 | 0.7 | [14] | |||||||
| Theory | 0.25-3.0 | 1.0 | 2.0 | [16] | ||||||
| Theory/Experiment | 0.25-3.0 | 1.05 | 2.25 | [33] | ||||||
| Theory/Experiment | 0-2.25 | 1.0 | 1.6 | 2.0 | [34] | |||||
| Theory/Experiment | 0.5-2.5 | 1.0 | 2.0 | [35] | ||||||
| Theory/Experiment | 0.25-3.0 | 0.95 | 1.92 | 2.7 | [36] | |||||
| Experiment | 0-3.0 | 1.0 | 2.0 | [37] | ||||||
| Experiment | 0.1-3.0 | 0.37 | 1.05 | 1.28 | 1.95 | 2.11 | 2.23 | Thiswork | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Konda, S.R.; Lin, Y.; Rajan, R.A.; Yu, W.; Li, W. Measurement of Optical Properties of CH3NH3PbX3 (X = Br, I) Single Crystals Using Terahertz Time-Domain Spectroscopy. Materials 2023, 16, 610. https://doi.org/10.3390/ma16020610
Konda SR, Lin Y, Rajan RA, Yu W, Li W. Measurement of Optical Properties of CH3NH3PbX3 (X = Br, I) Single Crystals Using Terahertz Time-Domain Spectroscopy. Materials. 2023; 16(2):610. https://doi.org/10.3390/ma16020610
Chicago/Turabian StyleKonda, Srinivasa Rao, Yucai Lin, Rahul A. Rajan, Weili Yu, and Wei Li. 2023. "Measurement of Optical Properties of CH3NH3PbX3 (X = Br, I) Single Crystals Using Terahertz Time-Domain Spectroscopy" Materials 16, no. 2: 610. https://doi.org/10.3390/ma16020610
APA StyleKonda, S. R., Lin, Y., Rajan, R. A., Yu, W., & Li, W. (2023). Measurement of Optical Properties of CH3NH3PbX3 (X = Br, I) Single Crystals Using Terahertz Time-Domain Spectroscopy. Materials, 16(2), 610. https://doi.org/10.3390/ma16020610









