Computational Fracture Evolution Analysis of Steel-Fiber-Reinforced Concrete Using Concrete Continuous Damage and Fiber Progressive Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
| Proportions of concrete mixtures (kg/m3) | |
| Material | Mixture ID |
| F1/F2 | |
| cement CEM I 42.5R | 380 |
| natural sand 0–2 mm | 220 |
| gravel 2–8 mm | 1611 |
| steel fibers | 25 |
| water | 167 |
| SP PE-220 % m.c. | 1 |
| VMA VM-500 % m.c. | 0.2 |
2.2. Mechanical Properties
2.3. Experimental Beam Tests
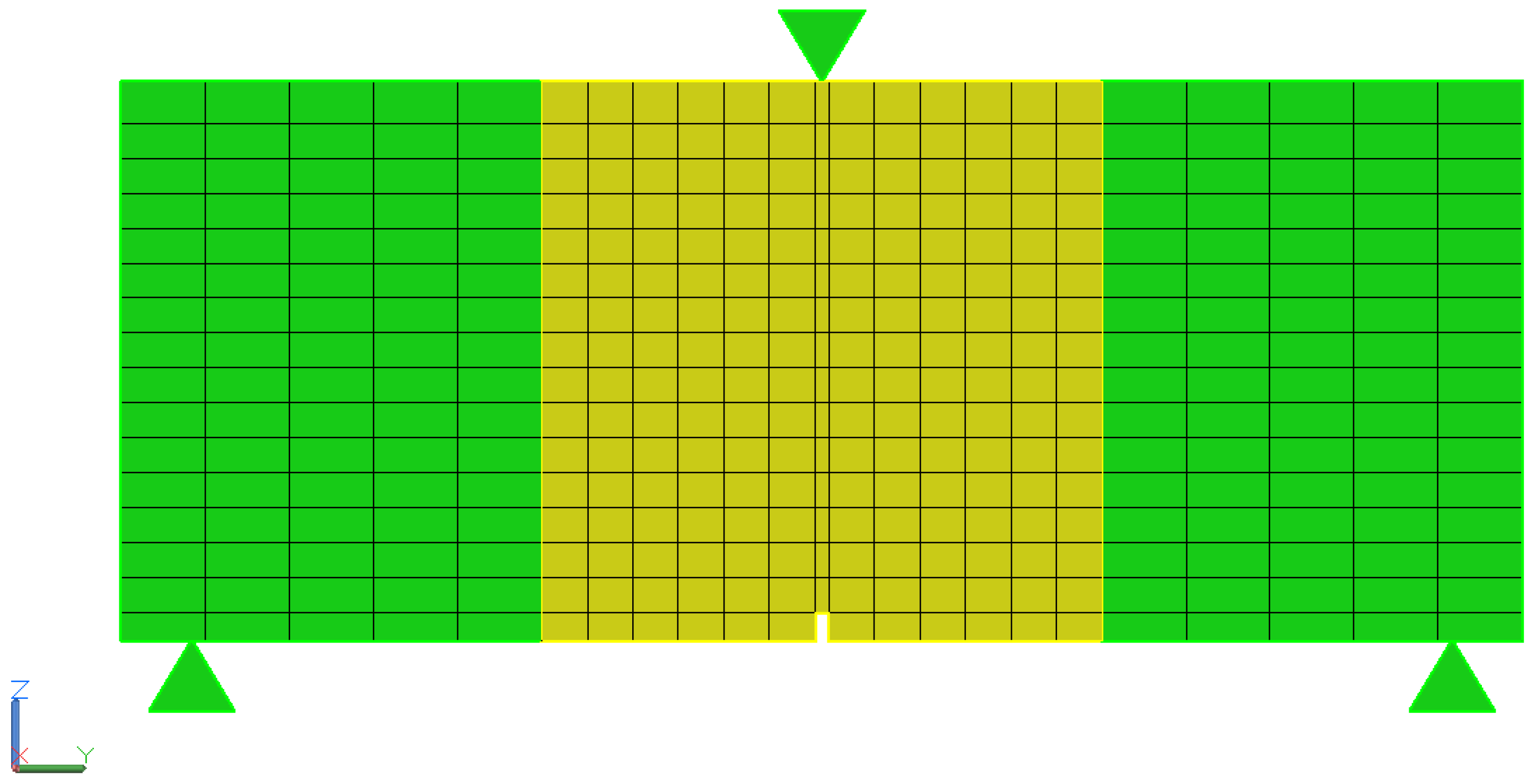
2.4. Numerical Analysis
Brief Description of the Methods Used in the Analysis
| Parameter | Value |
|---|---|
| Damage initiation criteria | maximum strain |
| Tensile strain limit | 0.1 |
| Damage evolution law | material properties degradation |
| Tensile and compressive stiffness reduction | 0.95 |
3. Results
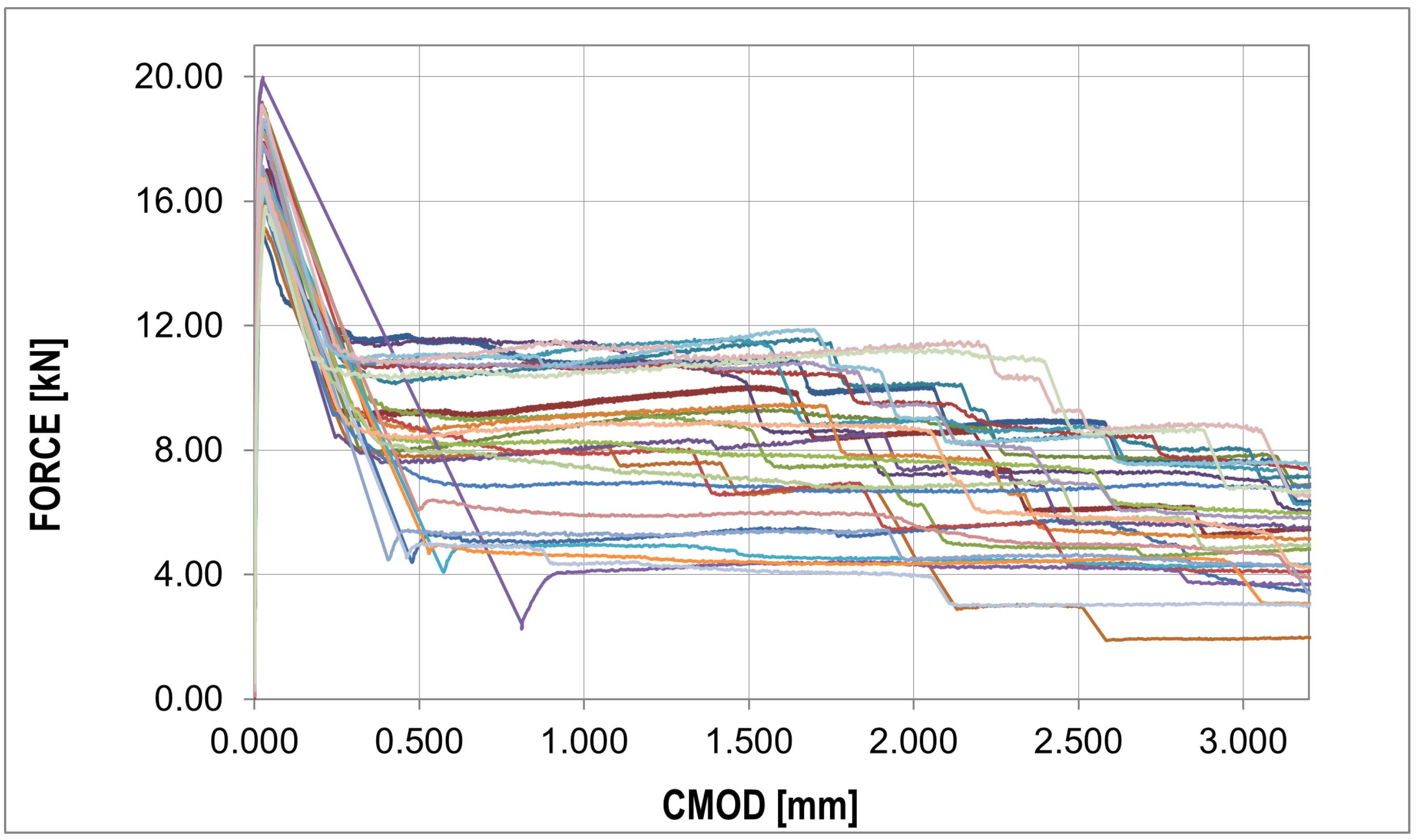
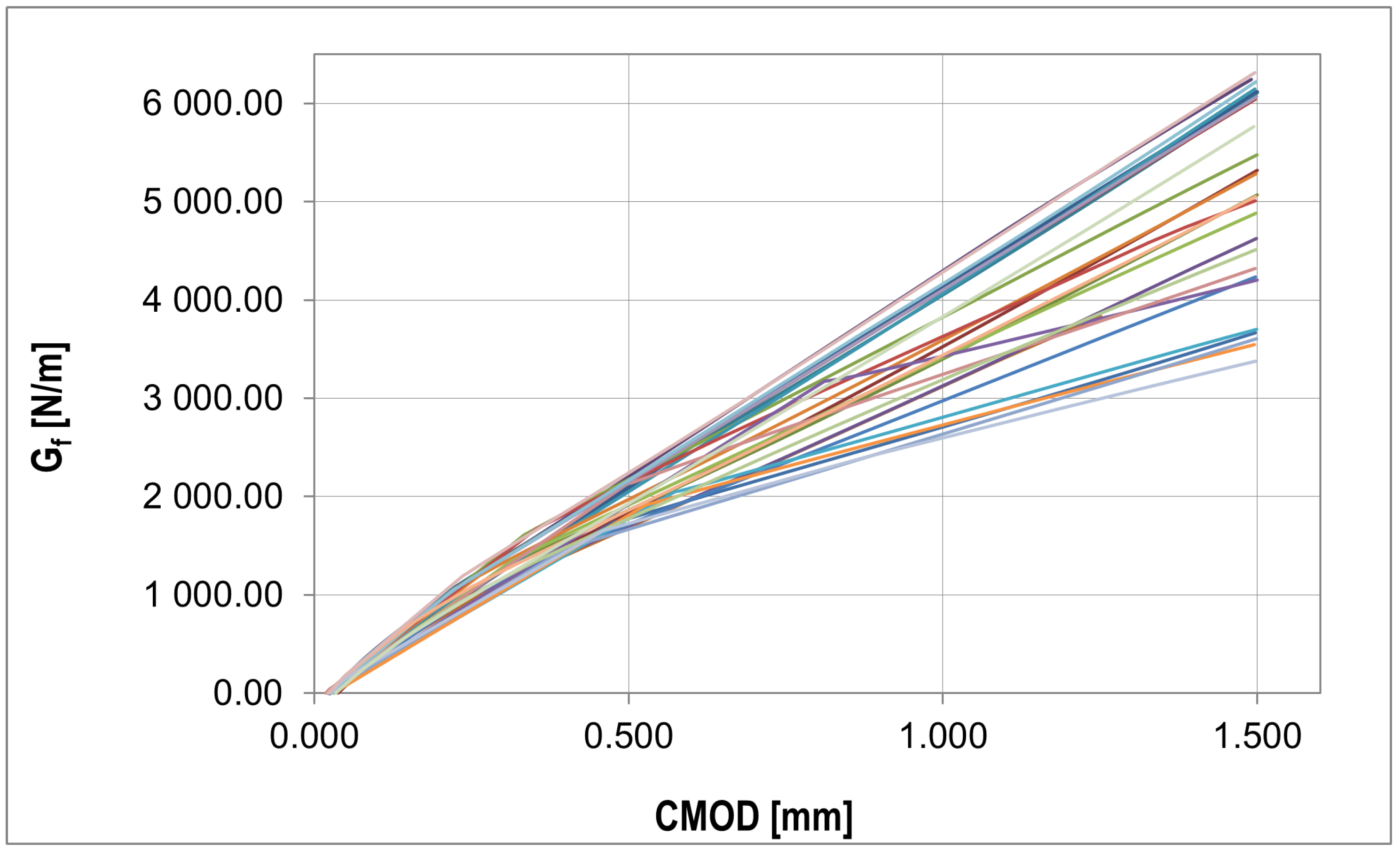
3.1. Experimental Results
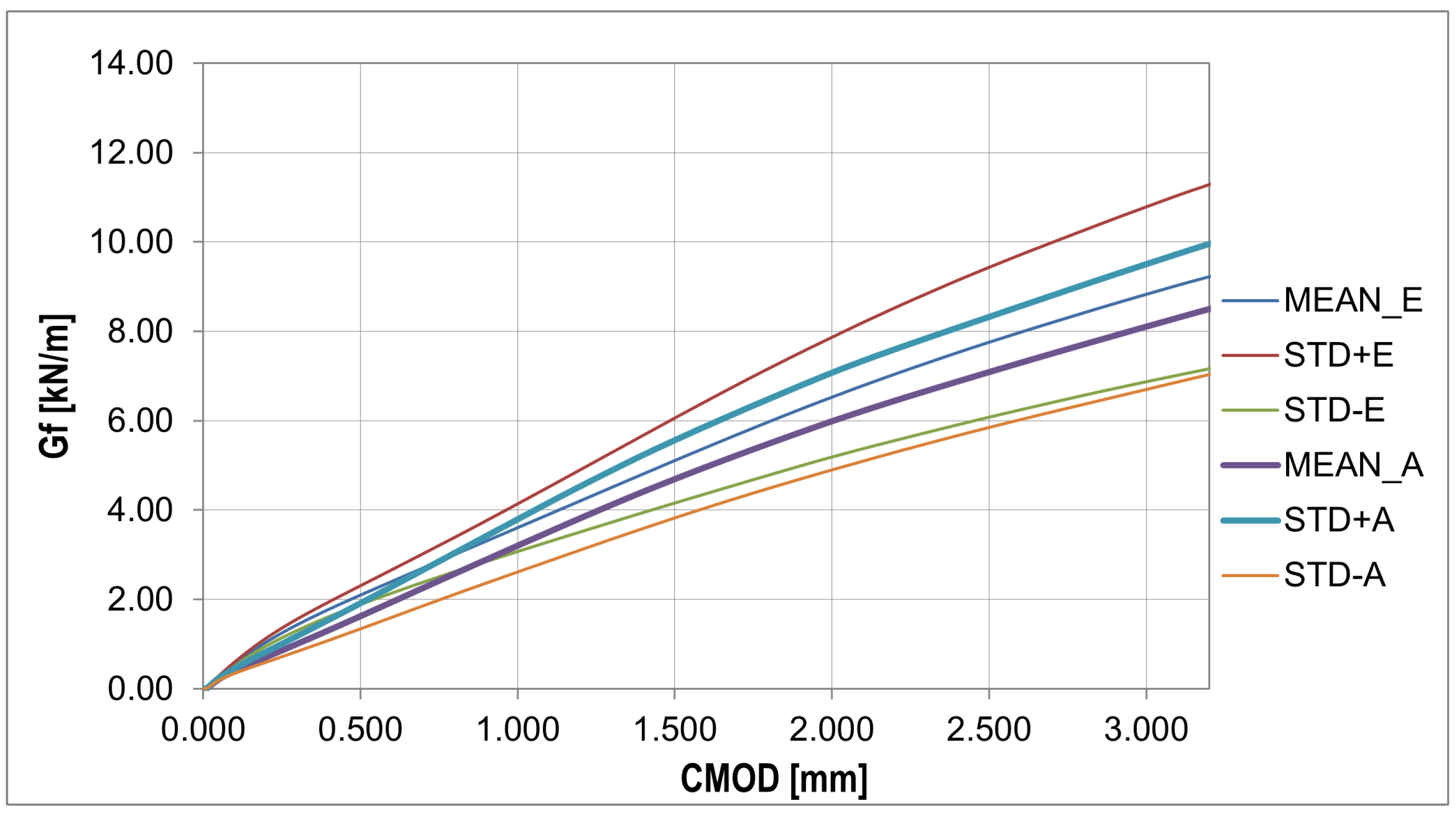
3.2. Numerical Results
4. Discussion and Conclusions
4.1. Discussion
4.2. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, S.J.; Won, J.P. Flexural behavior of precast reinforced concrete composite members reinforced with structural nano-synthetic and steel fibers. Compos. Struct. 2014, 118, 571–579. [Google Scholar] [CrossRef]
- Gdoutos, E.E.; Konsta-Gdoutos, M.S.; Danoglidis, P.A. Portland cement mortar nanocomposites at low carbon nanotube and carbon nanofiber content: A fracture mechanics experimental study. Cem. Concr. Compos. 2016, 70, 110–118. [Google Scholar] [CrossRef]
- Shah, S.P.; Swartz, S.E.; Ouyang, C. Fracture Mechanics of Concrete: Applications of Fracture Mechanics to Concrete, Rock and Other Quasi-Brittle Materials; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Xiao, J.; Han, N.; Li, Y.; Zhang, Z.; Shah, S.P. Review of recent developments in cement composites reinforced with fibers and nanomaterials. Front. Struct. Civ. Eng. 2021, 15, 1–19. [Google Scholar] [CrossRef]
- Pakravan, H.R.; Ozbakkaloglu, T. Synthetic fibers for cementitious composites: A critical and in-depth review of recent advances. Constr. Build. Mater. 2019, 207, 491–518. [Google Scholar] [CrossRef]
- Arslan, M.E. Effects of basalt and glass chopped fibers addition on fracture energy and mechanical properties of ordinary concrete: CMOD measurement. Constr. Build. Mater. 2016, 114, 383–391. [Google Scholar] [CrossRef]
- Jiang, C.; Fan, K.; Wu, F.; Chen, D. Experimental study on the mechanical properties and microstructure of chopped basalt fibre reinforced concrete. Mater. Des. 2014, 58, 187–193. [Google Scholar] [CrossRef]
- Tassew, S.; Lubell, A. Mechanical properties of glass fiber reinforced ceramic concrete. Constr. Build. Mater. 2014, 51, 215–224. [Google Scholar] [CrossRef]
- Shaikh, F.U.A. Review of mechanical properties of short fibre reinforced geopolymer composites. Constr. Build. Mater. 2013, 43, 37–49. [Google Scholar] [CrossRef] [Green Version]
- Almusallam, T.; Ibrahim, S.; Al-Salloum, Y.; Abadel, A.; Abbas, H. Analytical and experimental investigations on the fracture behavior of hybrid fiber reinforced concrete. Cem. Concr. Compos. 2016, 74, 201–217. [Google Scholar] [CrossRef]
- Das, S.; Sobuz, M.H.R.; Tam, V.W.; Akid, A.S.M.; Sutan, N.M.; Rahman, F.M. Effects of incorporating hybrid fibres on rheological and mechanical properties of fibre reinforced concrete. Constr. Build. Mater. 2020, 262, 120561. [Google Scholar] [CrossRef]
- Khan, M.; Cao, M.; Ali, M. Cracking behaviour and constitutive modelling of hybrid fibre reinforced concrete. J. Build. Eng. 2020, 30, 101272. [Google Scholar] [CrossRef]
- Cao, M.; Xie, C.; Guan, J. Fracture behavior of cement mortar reinforced by hybrid composite fiber consisting of CaCO3 whiskers and PVA-steel hybrid fibers. Compos. Part A Appl. Sci. Manuf. 2019, 120, 172–187. [Google Scholar] [CrossRef]
- Khan, M.; Cao, M. Effect of hybrid basalt fibre length and content on properties of cementitious composites. Mag. Concr. Res. 2021, 73, 487–498. [Google Scholar] [CrossRef]
- Saulat, H.; Cao, M.; Khan, M.M.; Khan, M.; Khan, M.M.; Rehman, A. Preparation and applications of calcium carbonate whisker with a special focus on construction materials. Constr. Build. Mater. 2020, 236, 117613. [Google Scholar] [CrossRef]
- Köksal, F.; Şahin, Y.; Gencel, O.; Yiğit, İ. Fracture energy-based optimisation of steel fibre reinforced concretes. Eng. Fract. Mech. 2013, 107, 29–37. [Google Scholar] [CrossRef]
- Eik, M.; Puttonen, J.; Herrmann, H. An orthotropic material model for steel fibre reinforced concrete based on the orientation distribution of fibres. Compos. Struct. 2015, 121, 324–336. [Google Scholar] [CrossRef]
- Caggiano, A.; Cremona, M.; Faella, C.; Lima, C.; Martinelli, E. Fracture behavior of concrete beams reinforced with mixed long/short steel fibers. Constr. Build. Mater. 2012, 37, 832–840. [Google Scholar] [CrossRef]
- Sun, X.; Zhao, K.; Li, Y.; Huang, R.; Ye, Z.; Zhang, Y.; Ma, J. A study of strain-rate effect and fiber reinforcement effect on dynamic behavior of steel fiber-reinforced concrete. Constr. Build. Mater. 2018, 158, 657–669. [Google Scholar] [CrossRef]
- Jin, L.; Zhang, R.; Tian, Y.; Dou, G.; Du, X. Experimental investigation on static and dynamic mechanical properties of steel fiber reinforced ultra-high-strength concretes. Constr. Build. Mater. 2018, 178, 102–111. [Google Scholar] [CrossRef]
- Germano, F.; Tiberti, G.; Plizzari, G. Post-peak fatigue performance of steel fiber reinforced concrete under flexure. Mater. Struct. 2016, 49, 4229–4245. [Google Scholar] [CrossRef]
- Abdallah, S.; Fan, M.; Rees, D.W. Bonding mechanisms and strength of steel fiber–reinforced cementitious composites: Overview. J. Mater. Civ. Eng. 2018, 30, 04018001. [Google Scholar] [CrossRef]
- Holschemacher, K.; Mueller, T.; Ribakov, Y. Effect of steel fibres on mechanical properties of high-strength concrete. Mater. Des. 2010, 31, 2604–2615. [Google Scholar] [CrossRef]
- Ho, H.V.; Choi, E.; Kang, J.W. Analytical bond behavior of cold drawn SMA crimped fibers considering embedded length and fiber wave depth. Rev. Adv. Mater. Sci. 2021, 60, 862–883. [Google Scholar] [CrossRef]
- Qing, L.; Yu, K.; Mu, R.; Forth, J.P. Uniaxial tensile behavior of aligned steel fibre reinforced cementitious composites. Mater. Struct. 2019, 52, 1–12. [Google Scholar] [CrossRef]
- Abdallah, S.; Fan, M.; Zhou, X. Effect of hooked-end steel fibres geometry on pull-out behaviour of ultra-high performance concrete. World Acad. Sci. Eng. Technol. Int. J. Civil Environ. Struct. Constr. Archit. Eng. 2016, 10, 1530–1535. [Google Scholar]
- Wille, K.; Naaman, A.E. Pullout Behavior of High-Strength Steel Fibers Embedded in Ultra-High-Performance Concrete. ACI Mater. J. 2012, 109. [Google Scholar]
- Bolander, J.E.; Eliáš, J.; Cusatis, G.; Nagai, K. Discrete mechanical models of concrete fracture. Eng. Fract. Mech. 2021, 257, 108030. [Google Scholar] [CrossRef]
- Cai, G.; Zhao, J.; Degée, H.; Vandoren, B. Shear capacity of steel fibre reinforced concrete coupling beams using conventional reinforcements. Eng. Struct. 2016, 128, 428–440. [Google Scholar] [CrossRef]
- Fu, Q.; Xu, W.; Huang, D.; He, J.; Zhang, L.; Kou, H.; Niu, D. Dynamic non-linear Mohr–Coulomb strength criterion for hybrid basalt–polypropylene fibre-reinforced concrete under impact loading. Arch. Civ. Mech. Eng. 2021, 21, 1–19. [Google Scholar] [CrossRef]
- Dmitriev, A.; Novozhilov, Y.; Mikhalyuk, D.; Lalin, V. Calibration and validation of the Menetrey-Willam constitutive model for concrete. Constr. Unique Build. Struct. 2020, 88, 1–22. [Google Scholar]
- Menetrey, P.; Willam, K. Triaxial failure criterion for concrete and its generalization. Struct. J. 1995, 92, 311–318. [Google Scholar]
- Puig Damians, I.; Olivella Pastallé, S.; Cots Corominas, C. Modelling of fiber-reinforced concrete and application case. In Proceedings of the 10th Workshop of CODE_BRIGHT Users. International Centre for Numerical Methods in Engineering (CIMNE), Berkeley, CA, USA, 18–20 May 2019; pp. 1–5. [Google Scholar]
- Vyas, G.; Pinho, S.; Robinson, P. Constitutive modelling of fibre-reinforced composites with unidirectional plies using a plasticity-based approach. Compos. Sci. Technol. 2011, 71, 1068–1074. [Google Scholar] [CrossRef] [Green Version]
- Bandeira, A.A.; Merighi, J.; Fortes, R.; Priszkulnik, S.; Pappalardo, A.; Haddad, M. Theoretical, computational and experimental analysis of concrete structures reinforced with carbon fiber. In Proceedings of the Fourth International Conference on FRP Composites in Civil Engineering (CICE2008), Zurich, Switzerland, 22–24 July 2008. [Google Scholar]
- Chi, Y.; Xu, L.; Yu, H.S. Plasticity model for hybrid fiber-reinforced concrete under true triaxial compression. J. Eng. Mech. 2014, 140, 393–405. [Google Scholar] [CrossRef]
- Ottosen, N.S. A failure criterion for concrete. J. Eng. Mech. Div. 1977, 103, 527–535. [Google Scholar] [CrossRef]
- Matos, L.M.; Barros, J.A.; Ventura-Gouveia, A.; Calcada, R.A. Constitutive model for fibre reinforced concrete by coupling the fibre and aggregate interlock resisting mechanisms. Cem. Concr. Compos. 2020, 111, 103618. [Google Scholar] [CrossRef]
- Pontes, M.F.; Pereira Junior, W.M.; Pituba, J.J.d.C. Numerical analysis on displacements of steel-fiber-reinforced concrete beams. Rev. IBracon Estruturas E Mater. 2020, 13. [Google Scholar] [CrossRef]
- Bahraq, A.A.; Al-Osta, M.A.; Ahmad, S.; Al-Zahrani, M.M.; Al-Dulaijan, S.O.; Rahman, M.K. Experimental and numerical investigation of shear behavior of RC beams strengthened by ultra-high performance concrete. Int. J. Concr. Struct. Mater. 2019, 13, 1–19. [Google Scholar] [CrossRef]
- Rhee, I. Failure Analysis of Steel Fiber-Reinforced Concrete T-Beams without Shear Stirrups. Appl. Sci. 2022, 12, 411. [Google Scholar] [CrossRef]
- Ab van den Bos, S.D.; Dai, Y.; BV, D.F. SF+ RC modelling using DIANA FEA. In Proceedings of the FRC2018: Fibre Reinforced Concrete: From Design to Structural Applications Joint ACI-fib-RILEM International Workshop, Desenzano, Italy, 28–30 June 2018. [Google Scholar]
- Li, Z.; Wu, M.; Wu, J.; Cui, Y.; Xue, X. Steel fibre reinforced concrete meso-scale numerical analysis. Adv. Civ. Eng. 2020, 2020, 2084646. [Google Scholar] [CrossRef]
- Cervenka, V.; Cervenka, J.; Pukl, R. ATENA-A tool for engineering analysis of fracture in concrete. Sadhana 2002, 27, 485–492. [Google Scholar] [CrossRef]
- Gambarelli, S.; Ožbolt, J. Meso-scale modeling of cfrp-confined concrete: Microplane-based approach. Fibers 2020, 8, 38. [Google Scholar] [CrossRef]
- Eliáš, J.; Vořechovskỳ, M.; Skoček, J.; Bažant, Z.P. Stochastic discrete meso-scale simulations of concrete fracture: Comparison to experimental data. Eng. Fract. Mech. 2015, 135, 1–16. [Google Scholar] [CrossRef]
- Kanellopoulos, A.; Farhat, F.A.; Nicolaides, D.; Karihaloo, B.L. Mechanical and fracture properties of cement-based bi-materials after thermal cycling. Cem. Concr. Res. 2009, 39, 1087–1094. [Google Scholar] [CrossRef]
- Bentur, A.; Mindess, S. Fibre Reinforced Cementitious Composites; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Karihaloo, B.L.; Abdalla, H.; Imjai, T. A simple method for determining the true specific fracture energy of concrete. Mag. Concr. Res. 2003, 55, 471–481. [Google Scholar] [CrossRef]
- Imjai, T.; Kefyalew, F.; Aosai, P.; Garcia, R.; Kim, B.; Abdalla, H.M.; Raman, S.N. A new equation to predict the shear strength of recycled aggregate concrete Z push-off specimens. Cem. Concr. Res. 2023, 169, 107181. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Xiang, Y. Crack growth and lifetime of concrete under long time loading. J. Eng. Mech. 1997, 123, 350–358. [Google Scholar] [CrossRef] [Green Version]
- Schauffert, E.A.; Cusatis, G.; Pelessone, D.; O’Daniel, J.L.; Baylot, J.T. Lattice discrete particle model for fiber-reinforced concrete. II: Tensile fracture and multiaxial loading behavior. J. Eng. Mech. 2012, 138, 834–841. [Google Scholar] [CrossRef]
- Cusatis, G.; Pelessone, D.; Mencarelli, A. Lattice discrete particle model (LDPM) for failure behavior of concrete. I: Theory. Cem. Concr. Compos. 2011, 33, 881–890. [Google Scholar] [CrossRef]
- Montero-Chacón, F.; Cifuentes, H.; Medina, F. Mesoscale characterization of fracture properties of steel fiber-reinforced concrete using a lattice–particle model. Materials 2017, 10, 207. [Google Scholar] [CrossRef]
- Kubissa, Wojciech and Jaskulski, Roman and Gil, Damian and Wilińska, Iwona Holistic Analysis of Waste Copper Slag Based Concrete by Means of EIPI Method. Buildings 2019, 10, 1. [CrossRef] [Green Version]
- Hoover, C.G.; Bažant, Z.P. Comprehensive concrete fracture tests: Size effects of types 1 & 2, crack length effect and postpeak. Eng. Fract. Mech. 2013, 110, 281–289. [Google Scholar]
- Hoover, C.G.; Bažant, Z.P.; Vorel, J.; Wendner, R.; Hubler, M.H. Comprehensive concrete fracture tests: Description and results. Eng. Fract. Mech. 2013, 114, 92–103. [Google Scholar] [CrossRef]
- Ansys® Academic Research Mechanical, Release 2021 R1, Help System, Material Reference, Material Damage; ANSYS Inc.: Canonsburg, PA, USA, 2021.
- Bathe, K.J. Finite Element Procedures; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Ansys® Academic Research Mechanical, Release 2021 R1, Help System, Structural Analysis Guide, Transient Dynamic Analysis; ANSYS Inc.: Canonsburg, PA, USA, 2021.
- Kim, M.O.; Bordelon, A. Determination of total fracture energy for fiber-reinforced concrete. Spec. Publ. 2015, 300, 1–16. [Google Scholar]






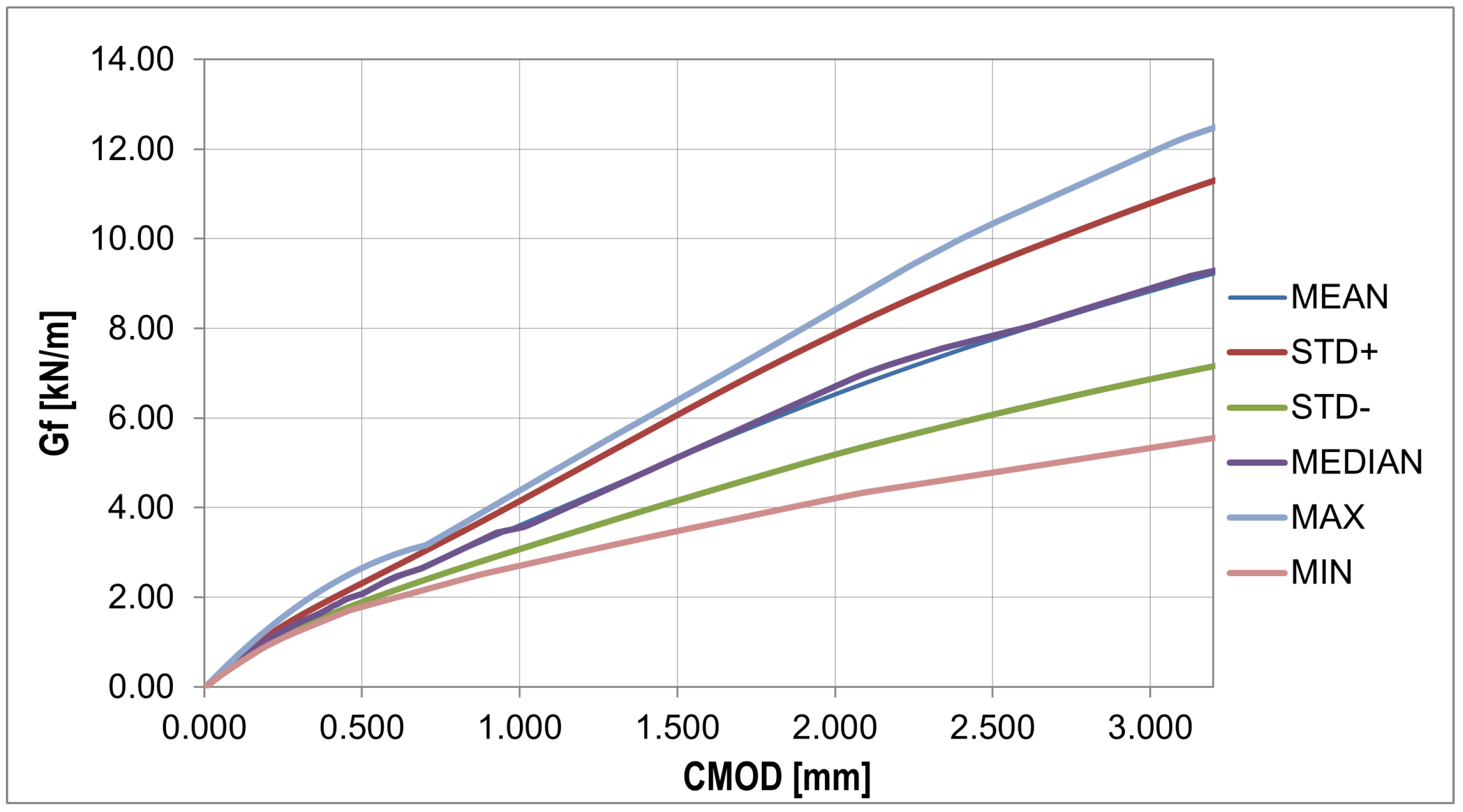


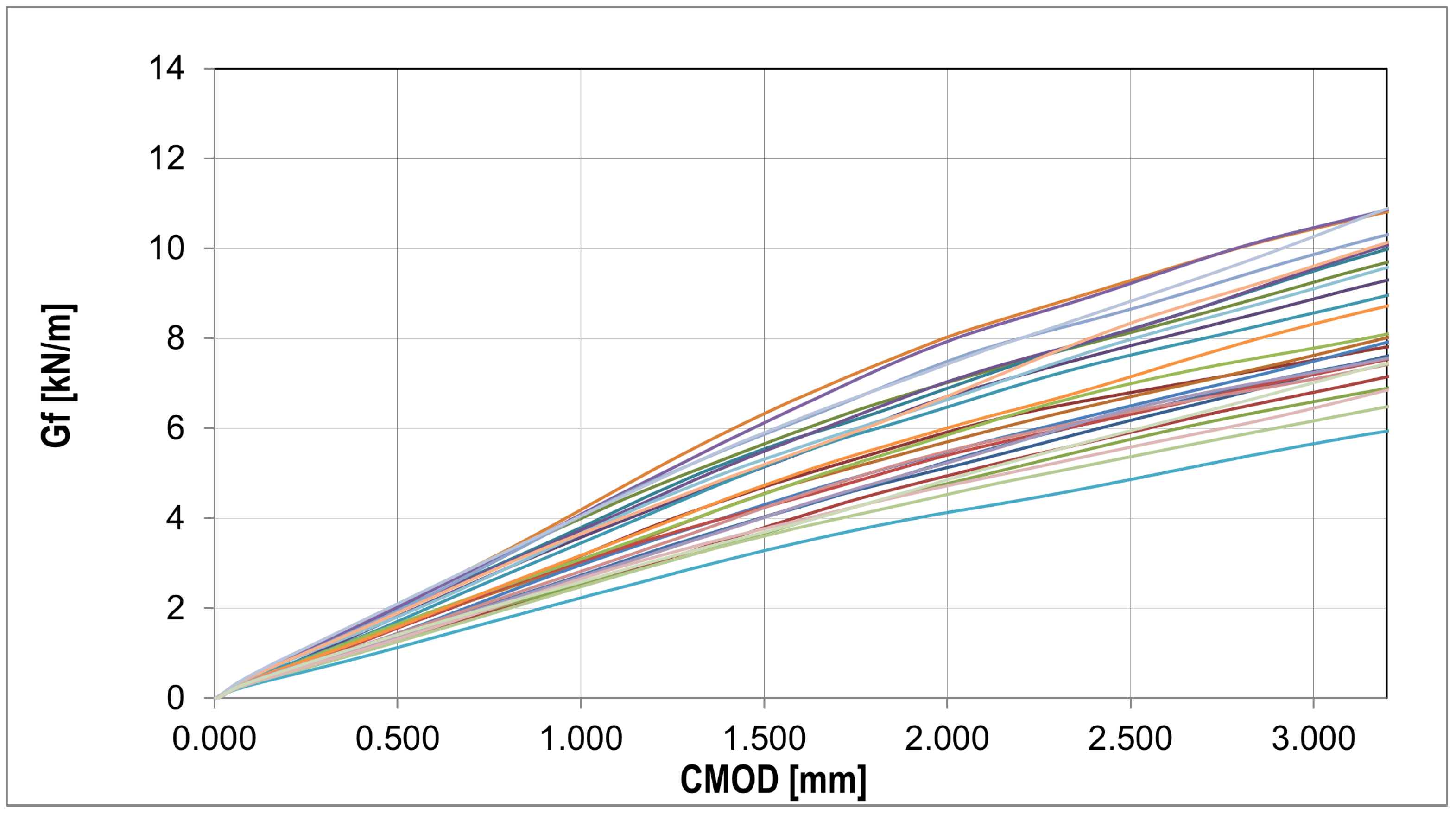
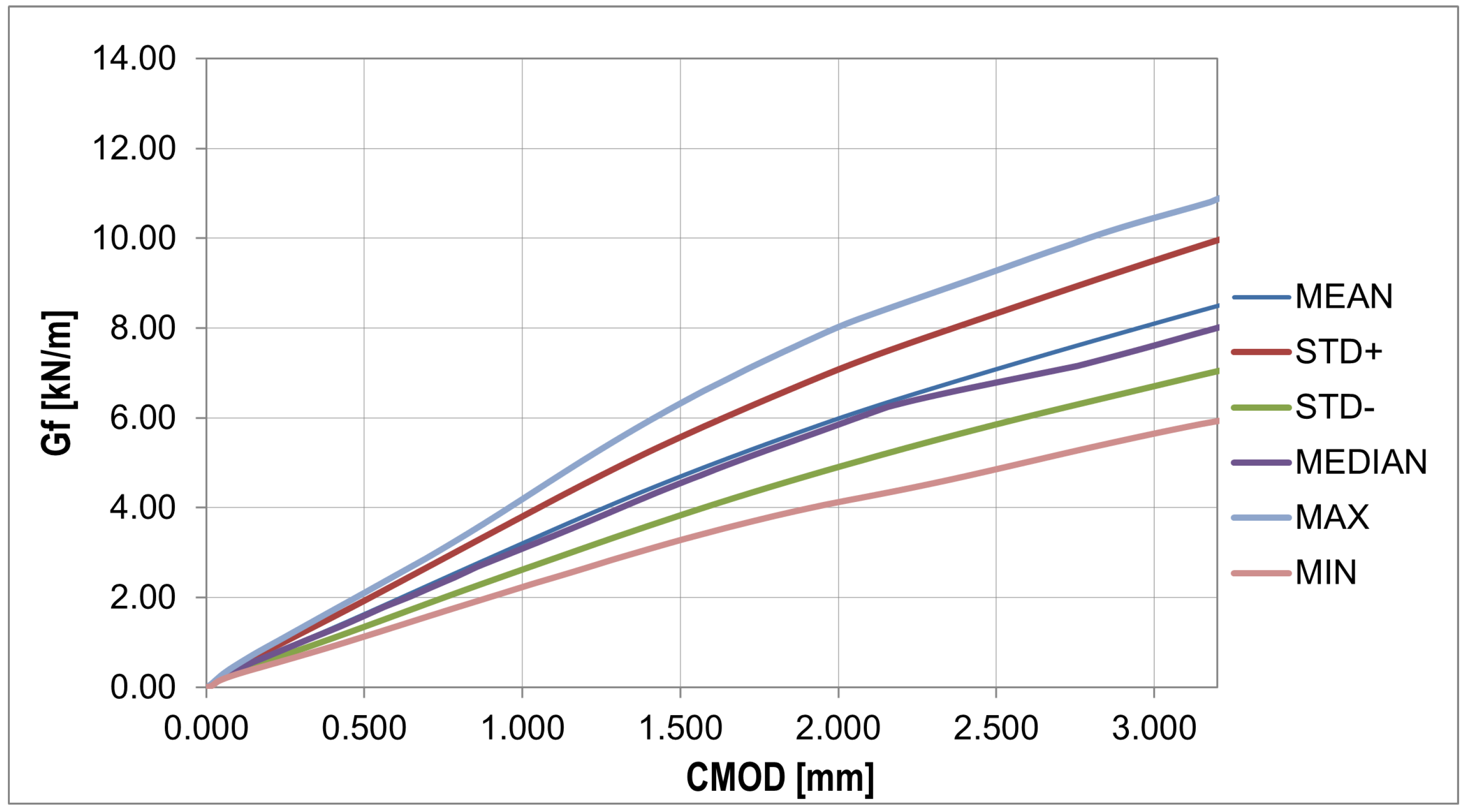
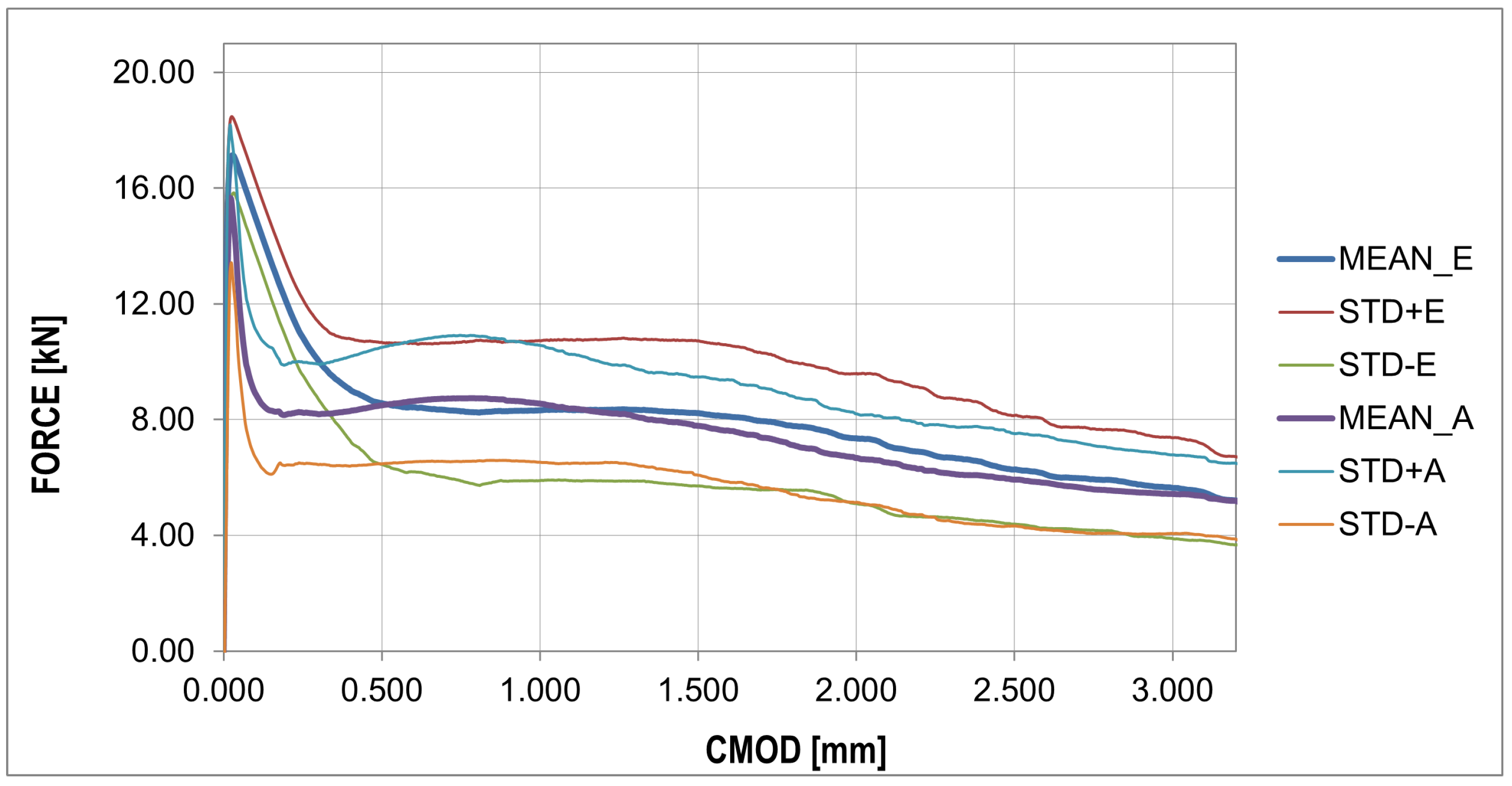
| Cement Type | Setting Time Start/End | Compr. Strength | Specific Surface Area (Blaine) | Specific Gravity | ||||
|---|---|---|---|---|---|---|---|---|
| (min) | (min) | (MPa) | (cm2/g) | (g/cm3) | (%) | (%) | (%) | |
| CEM I 42.5R | 176 | 231 | 57.9 | 3538 | 3.1 | 2.52 | 0.063 | 0.6 |
| Test | ID of Mixture | ||
|---|---|---|---|
| F1 | F2 | ave. F1 and F2 | |
| Flow (mm) | 360 | 350 | class F2 |
| Compressive strength 28 days (MPa) | 62.46 [1.58] | 62.4 [1.25] | 62.43 [1.36] |
| Compressive strength 134 days (MPa) | 51.98 [0.82] | 52.42 [1.50] | 52.2 [1.22] |
| Flexural strength 134 days (MPa) | 5.58 [0.14] | 5.73 [0.08] | 5.66 [0.13] |
| Parameter | Value |
|---|---|
| Concrete density | 2500 |
| Concrete Young’s modulus | 41.545 GPa |
| Concrete Poisson’s ratio | 0.18 |
| SF density | 7850 |
| SF Young’s modulus | 4 GPa |
| SF Poisson’s ratio | 0.3 |
| Parameter | Value |
|---|---|
| Uniaxial compressive strength | 62.4 MPa |
| Uniaxial tensile strength | 6.25 GPa |
| Biaxial compressive strength | 74.9 MPa |
| Dilatancy angle | 30 deg |
| Softening | exponential |
| Plastic strain at uniaxial compressive strength | 0.002 |
| Plastic strain at transition form power law to exponential softening | 0.0035 |
| Relative stress at start of nonlinear hardening | 0.3 |
| Residual relative stress at | 0.75 |
| Residual compressive relative stress | 0.2 |
| Mode 1 area specific fracture energy | 100 N/m |
| Residual tensile relative stress | 0.1 |
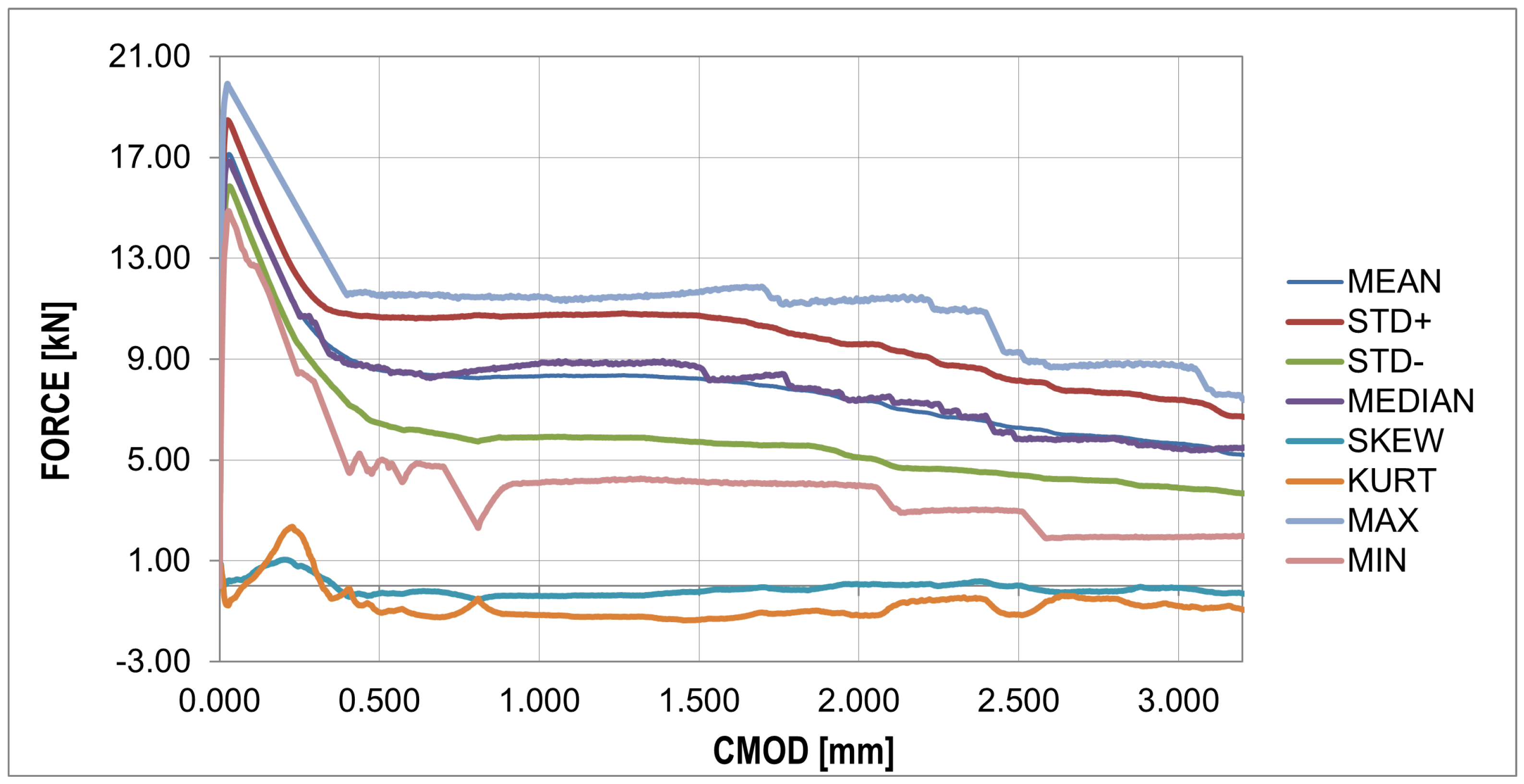
| Plain Concrete (PC) | FRC | |||||
|---|---|---|---|---|---|---|
| Statistic | CMOD | |||||
| (MPa) | (mm) | (MPa) | (MPa) | (N/mm) | (MPa) | |
| mean | 6.247 | 0.027 | 2.903 | 2.988 | 4.869 | 36.794 |
| std.dev. | 0.472 | 0.005 | 0.957 | 0.958 | 1.000 | 108.304 |
| coeff. of var. | 7.55% | 17.34% | 32.95% | 32.08% | 20.54% | 294.35% |
| skewness | 0.252 | 0.554 | −0.464 | −0.297 | 0.044 | 0.447 |
| kurtosis | −0.699 | 0.085 | −0.847 | −1.468 | −1.463 | 0.368 |
| median | 6.105 | 0.026 | 2.996 | 3.194 | 4.883 | 52.152 |
| (0.95,4) | 6.000 | 3.600 | 5.600 | 6.000 | 2.000 | 6.000 |
| Shapiro–Wilk | 0.966 | 0.963 | 0.963 | 0.899 | 0.941 | 0.968 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pokorska, I.; Poński, M.; Kubissa, W.; Libura, T.; Brodecki, A.; Kowalewski, Z. Computational Fracture Evolution Analysis of Steel-Fiber-Reinforced Concrete Using Concrete Continuous Damage and Fiber Progressive Models. Materials 2023, 16, 5635. https://doi.org/10.3390/ma16165635
Pokorska I, Poński M, Kubissa W, Libura T, Brodecki A, Kowalewski Z. Computational Fracture Evolution Analysis of Steel-Fiber-Reinforced Concrete Using Concrete Continuous Damage and Fiber Progressive Models. Materials. 2023; 16(16):5635. https://doi.org/10.3390/ma16165635
Chicago/Turabian StylePokorska, Iwona, Mariusz Poński, Wojciech Kubissa, Tomasz Libura, Adam Brodecki, and Zbigniew Kowalewski. 2023. "Computational Fracture Evolution Analysis of Steel-Fiber-Reinforced Concrete Using Concrete Continuous Damage and Fiber Progressive Models" Materials 16, no. 16: 5635. https://doi.org/10.3390/ma16165635
APA StylePokorska, I., Poński, M., Kubissa, W., Libura, T., Brodecki, A., & Kowalewski, Z. (2023). Computational Fracture Evolution Analysis of Steel-Fiber-Reinforced Concrete Using Concrete Continuous Damage and Fiber Progressive Models. Materials, 16(16), 5635. https://doi.org/10.3390/ma16165635






