Deformation-Induced Surface Roughening of an Aluminum–Magnesium Alloy: Experimental Characterization and Crystal Plasticity Modeling
Abstract
:1. Introduction
2. Experiments
2.1. Opening Remarks
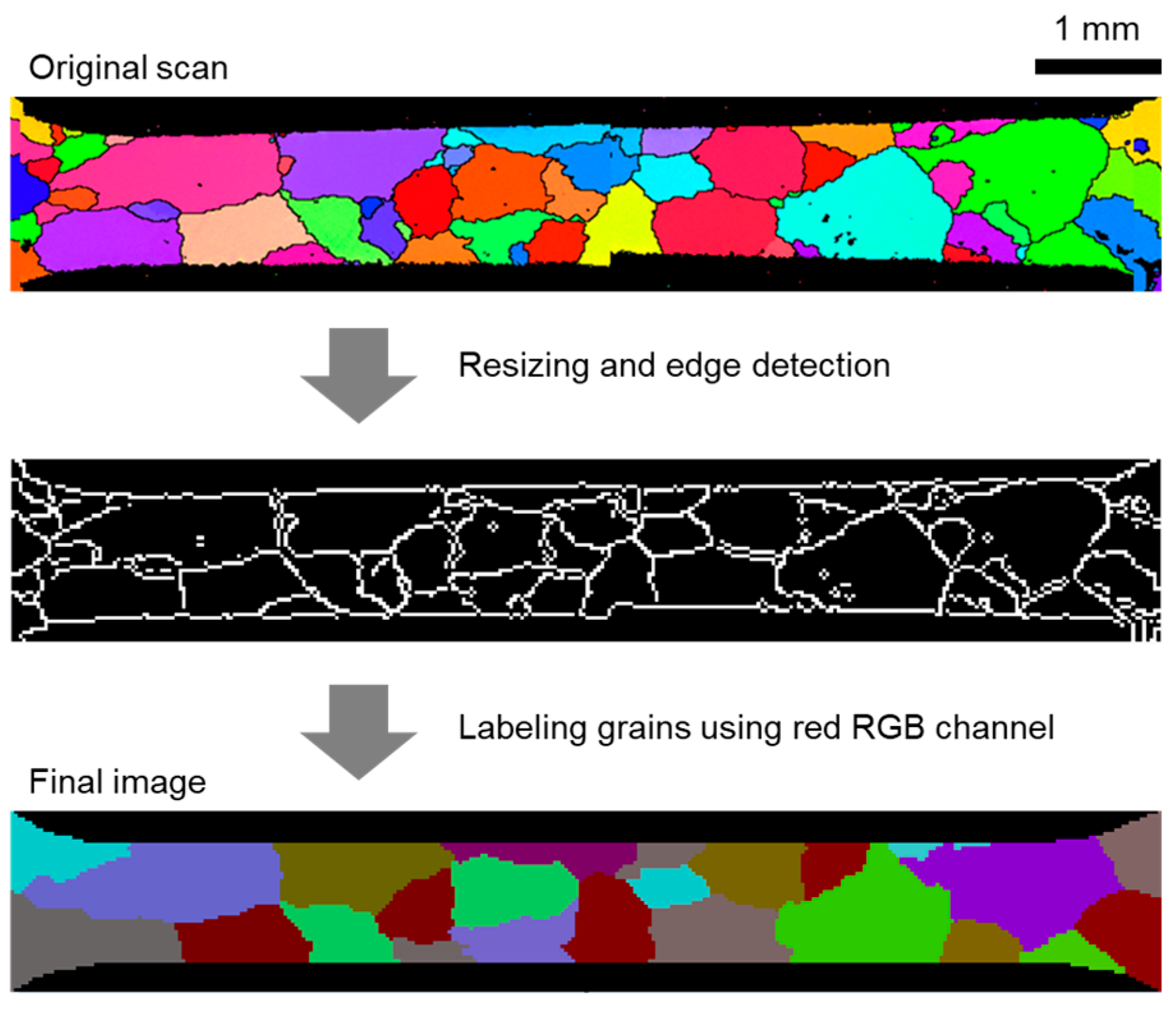
2.2. Specimen Preparation
- An AA5052-O sheet of 0.5 mm thickness is prestrained in uniaxial tension to 10% nominal strain.
- The plate is heat-treated at 450 °C for 1 h.
- Tensile specimens of the geometry shown in Figure 1 are cut from the plate.
- The tensile specimen thickness is reduced from 0.5 mm to 0.134 mm by polishing.
- The top and bottom faces of the tensile specimen are polished, in preparation for the tensile experiment.
2.3. Experimental Setup
3. Modeling
3.1. Crystal Plasticity Finite Element (CPFE) Model Overview
| Parameter | Symbol | Value | Unit | Comment |
|---|---|---|---|---|
| Aluminum crystal elastic constants | 107,300 | Mpa | [59] | |
| 60,900 | Mpa | [59] | ||
| 56,600 | Mpa | [59] | ||
| Initial slip resistance | 51.3 | Mpa | Optimization | |
| Shear modulus | 26,100 | Mpa | [58] | |
| Burgers vector | 0.286 | nm | [58] | |
| Trapping rate coefficient | 6.376 × 107 | m−1 | Optimization | |
| Activation barrier | 0.005283 | - | Optimization | |
| Drag stress | 1535 | Mpa | Optimization | |
| Dislocation recovery rate | 16 | - | [58] |
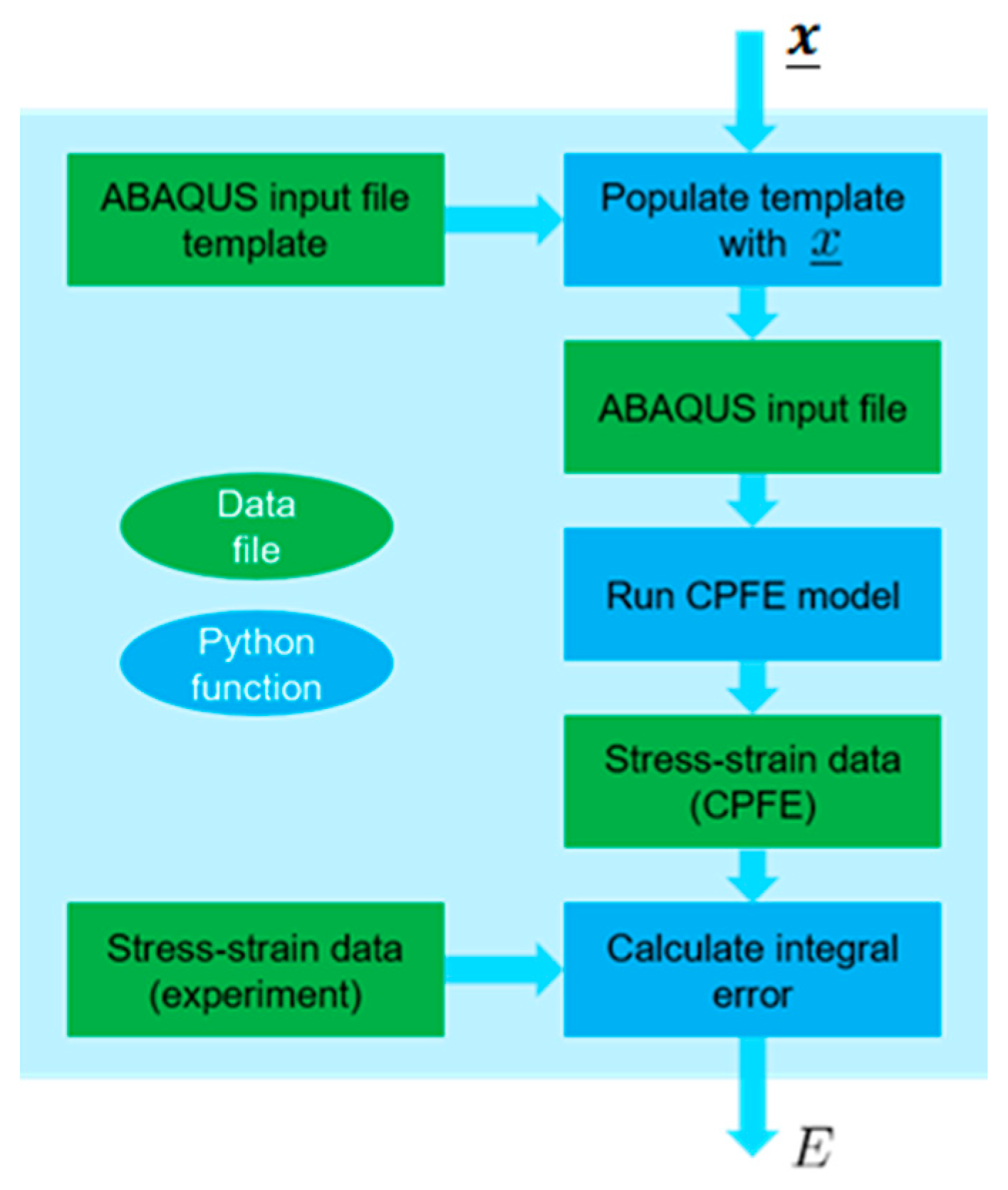
3.2. Identification of Material Properties
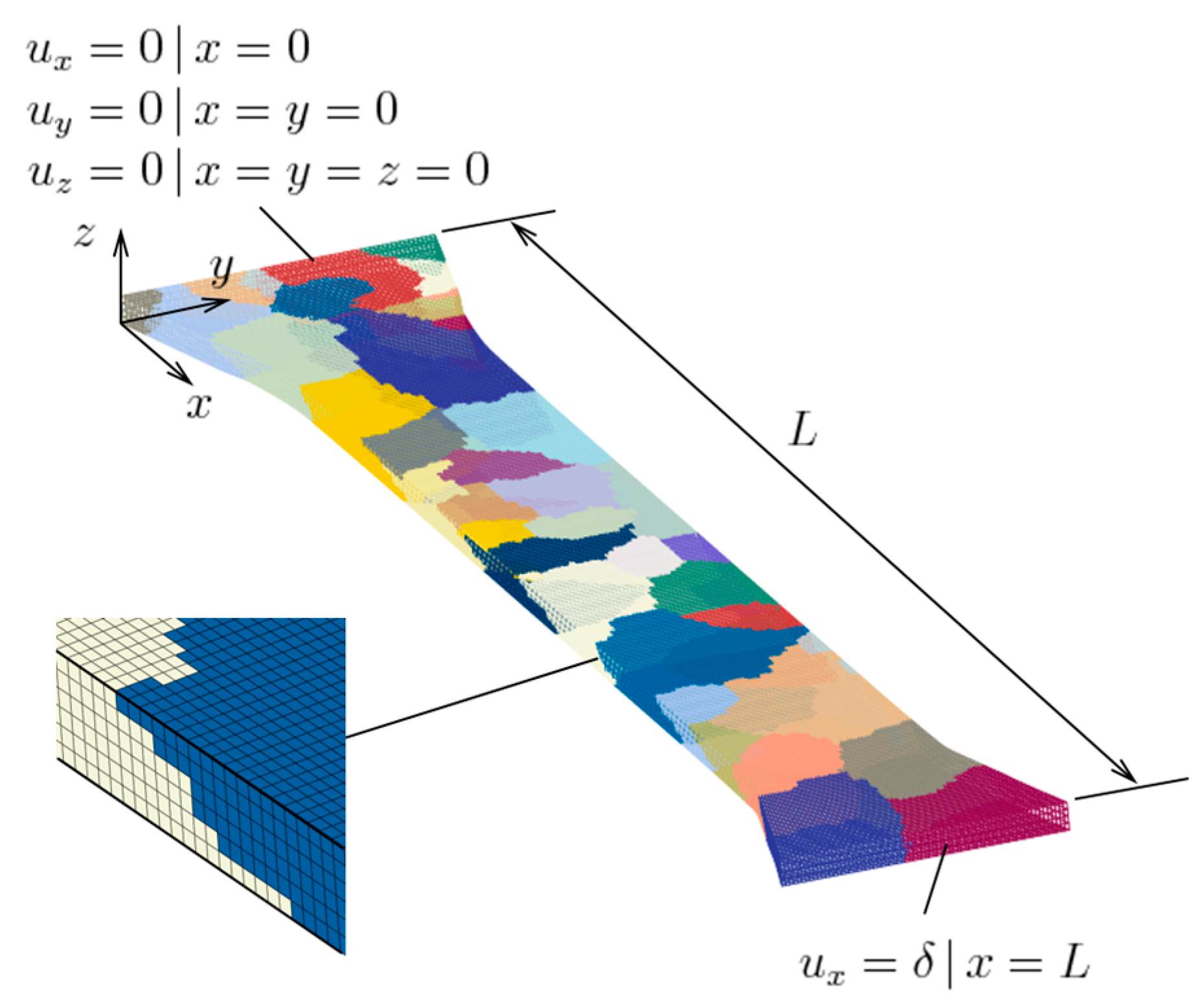
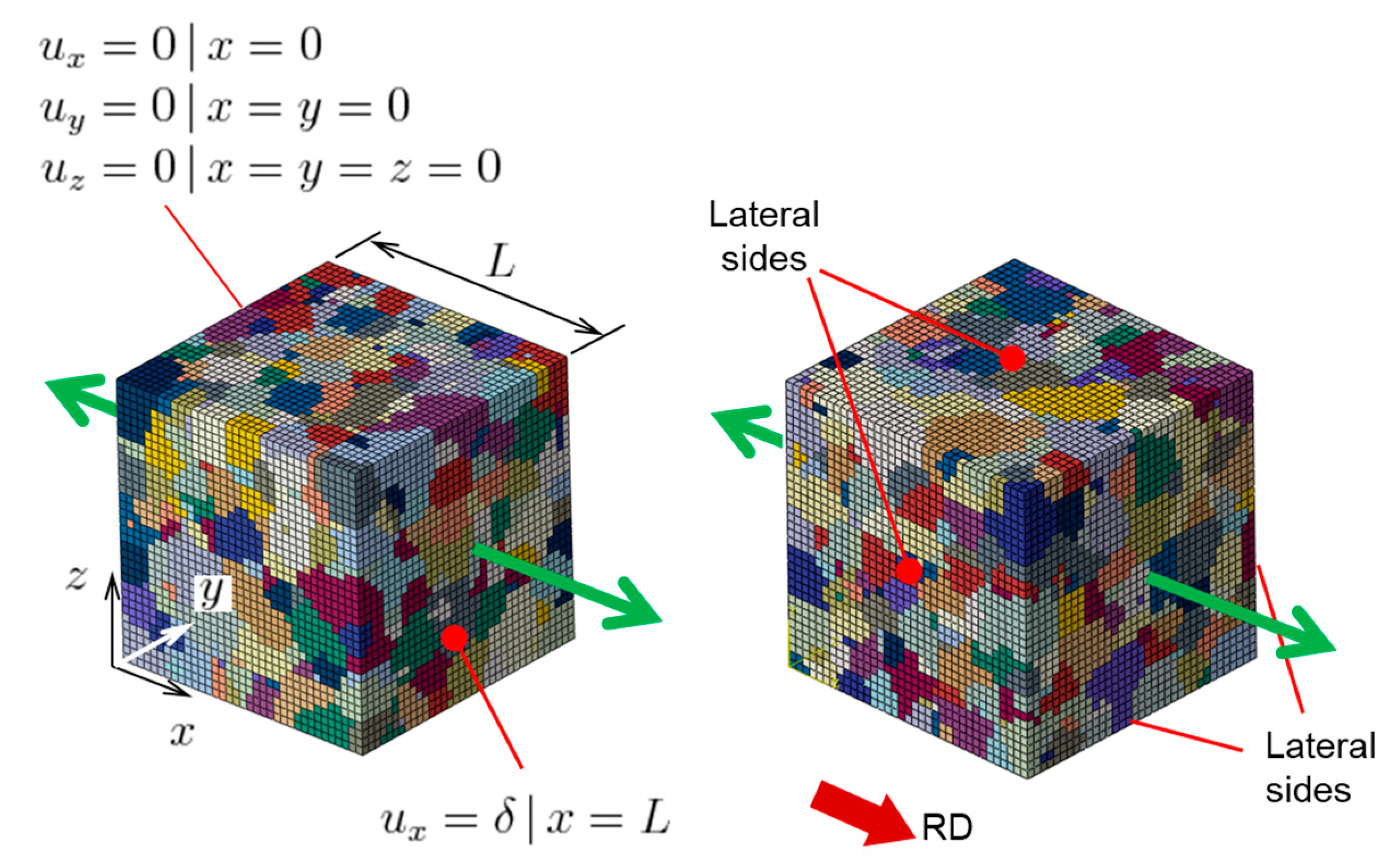
3.3. Mesh Construction
3.4. Finite Element Model
4. Comparison between Experiment and Model
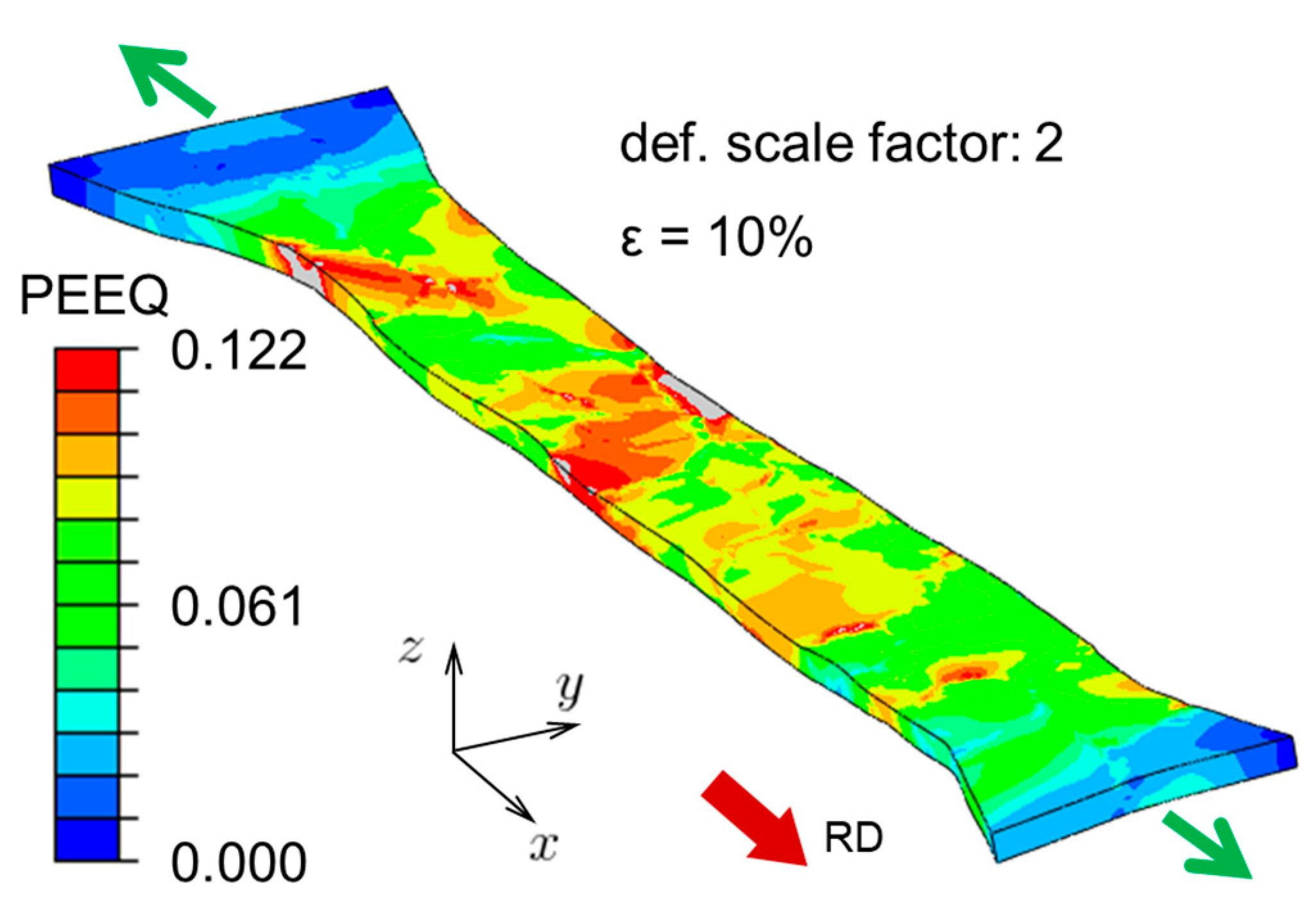
4.1. Shape of Deformed Specimen
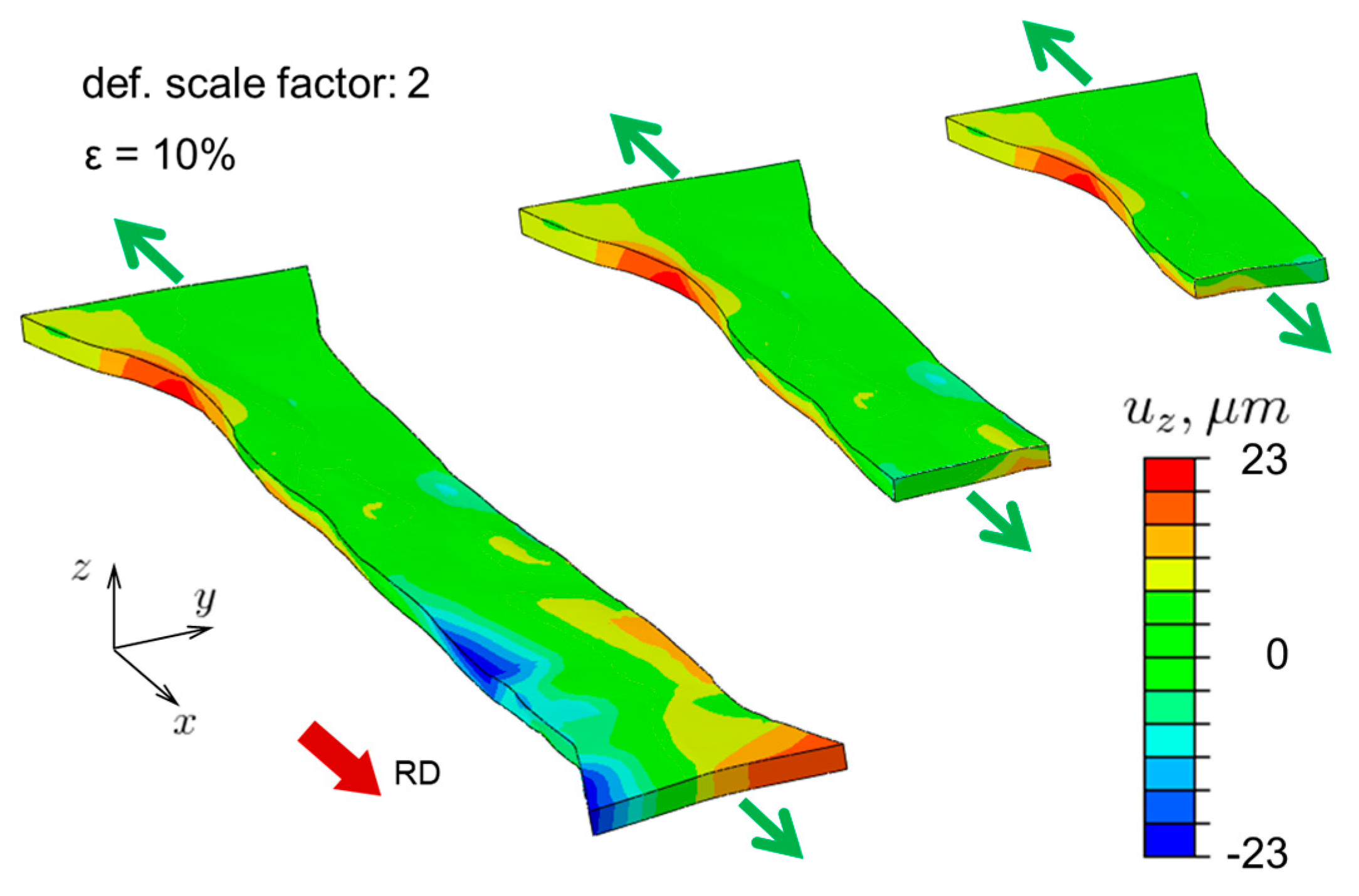
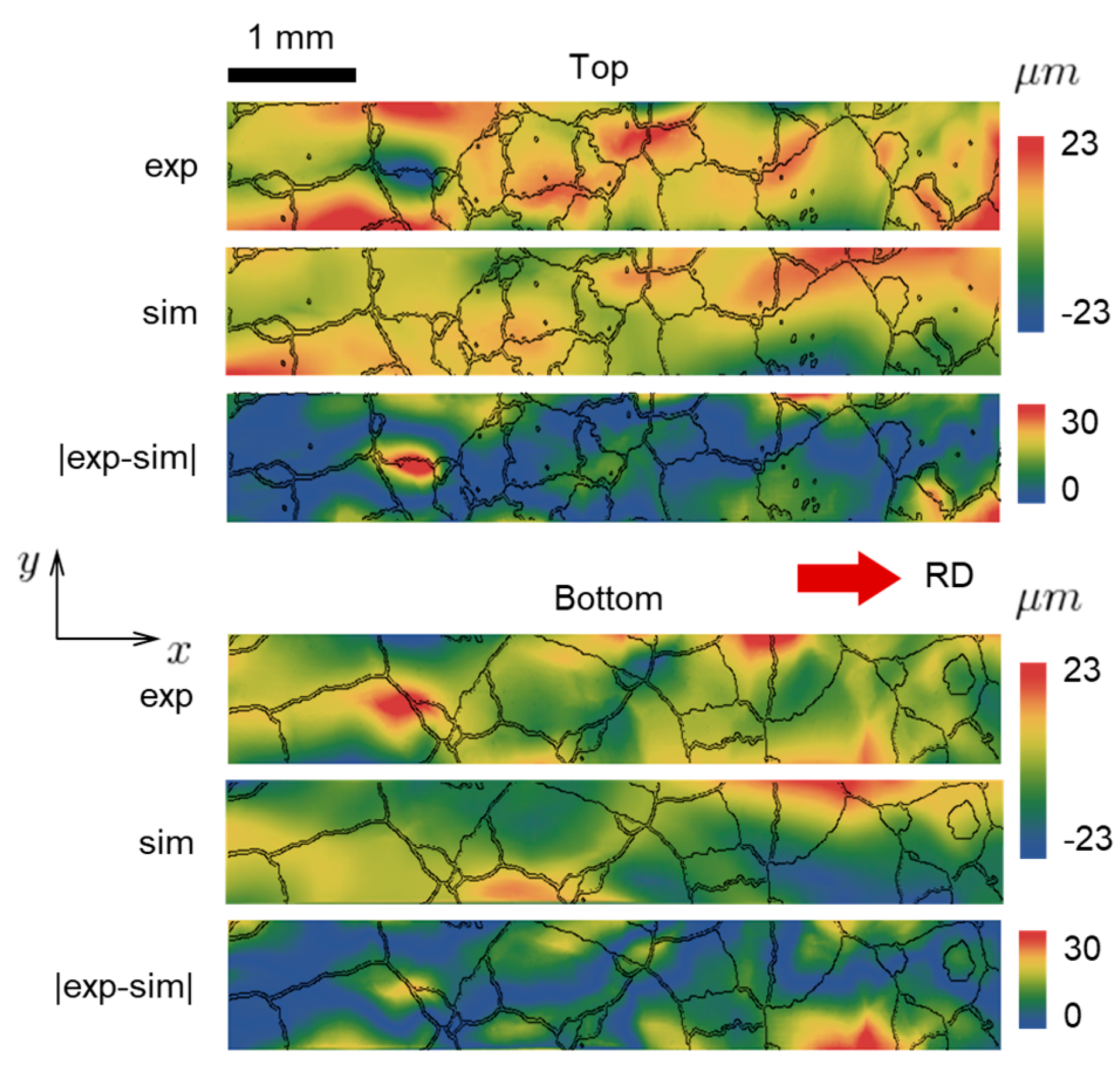
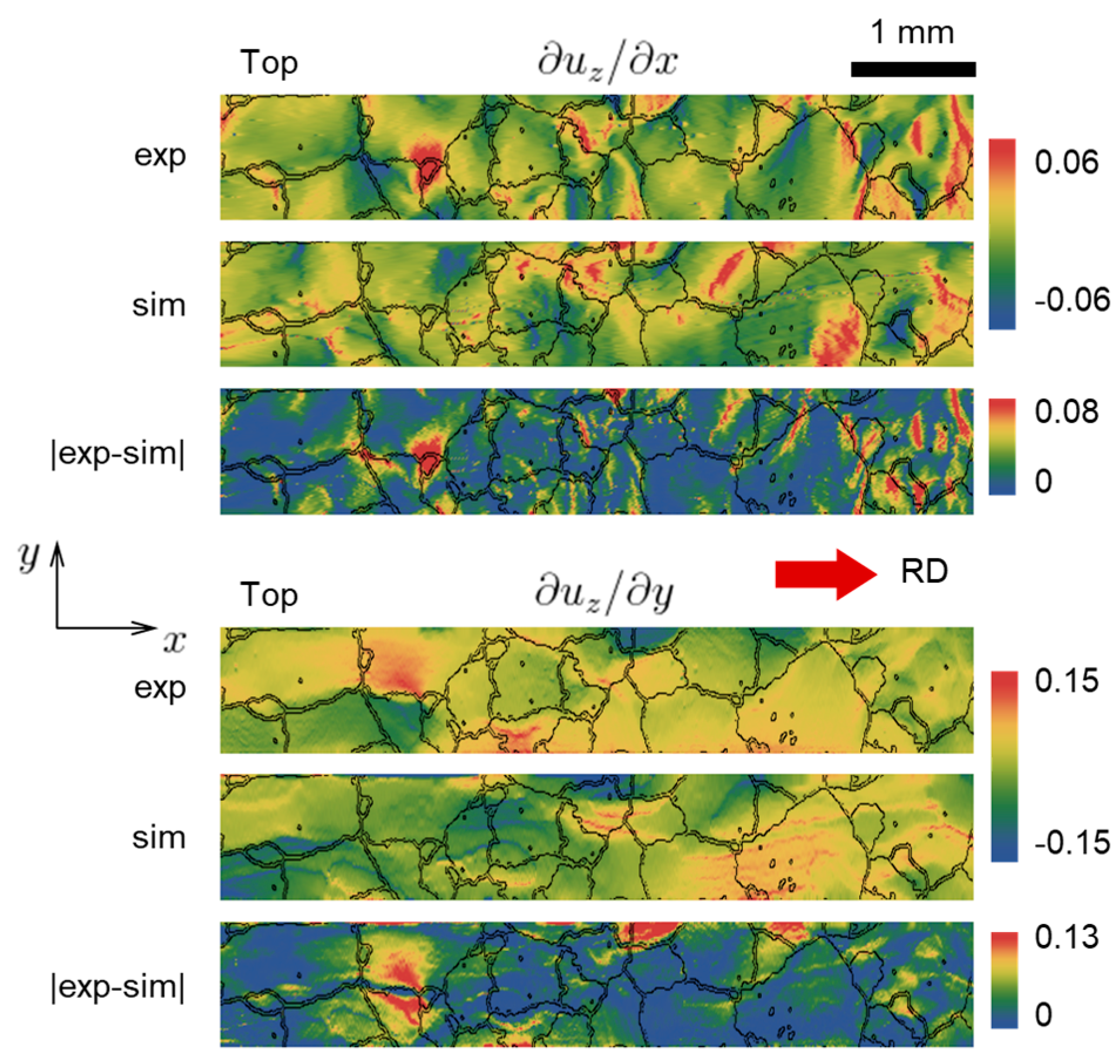
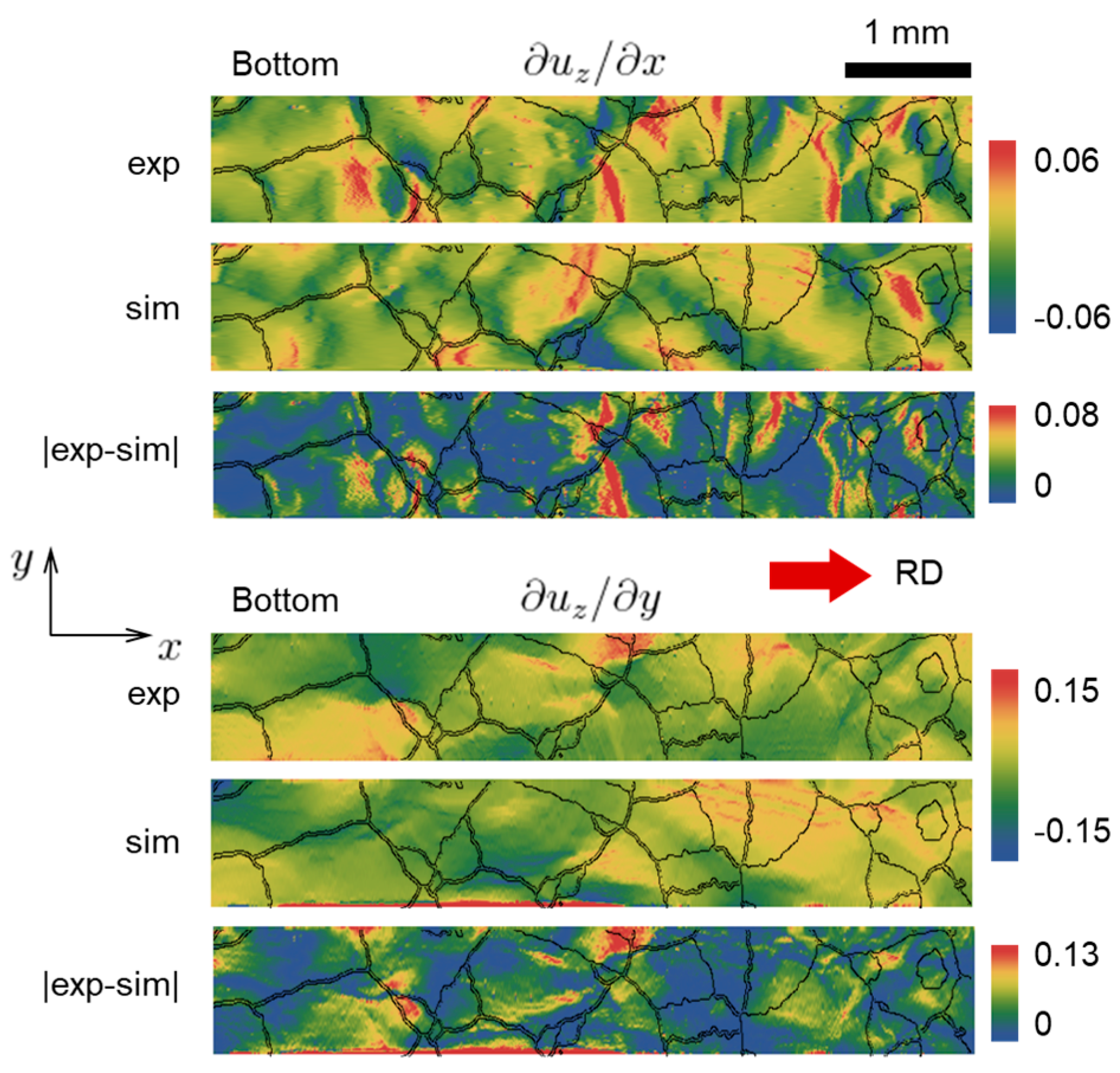
4.2. Surface Topography
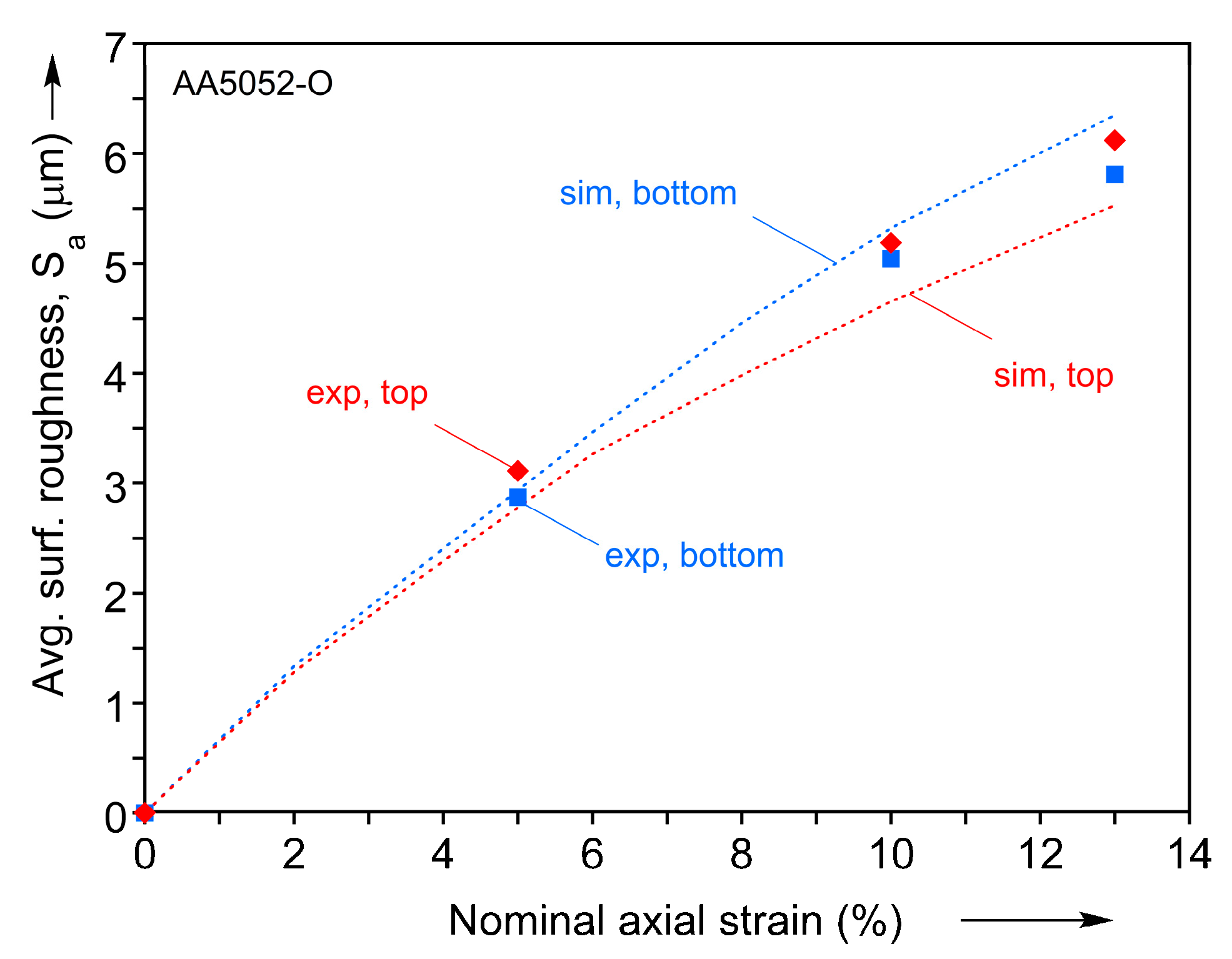
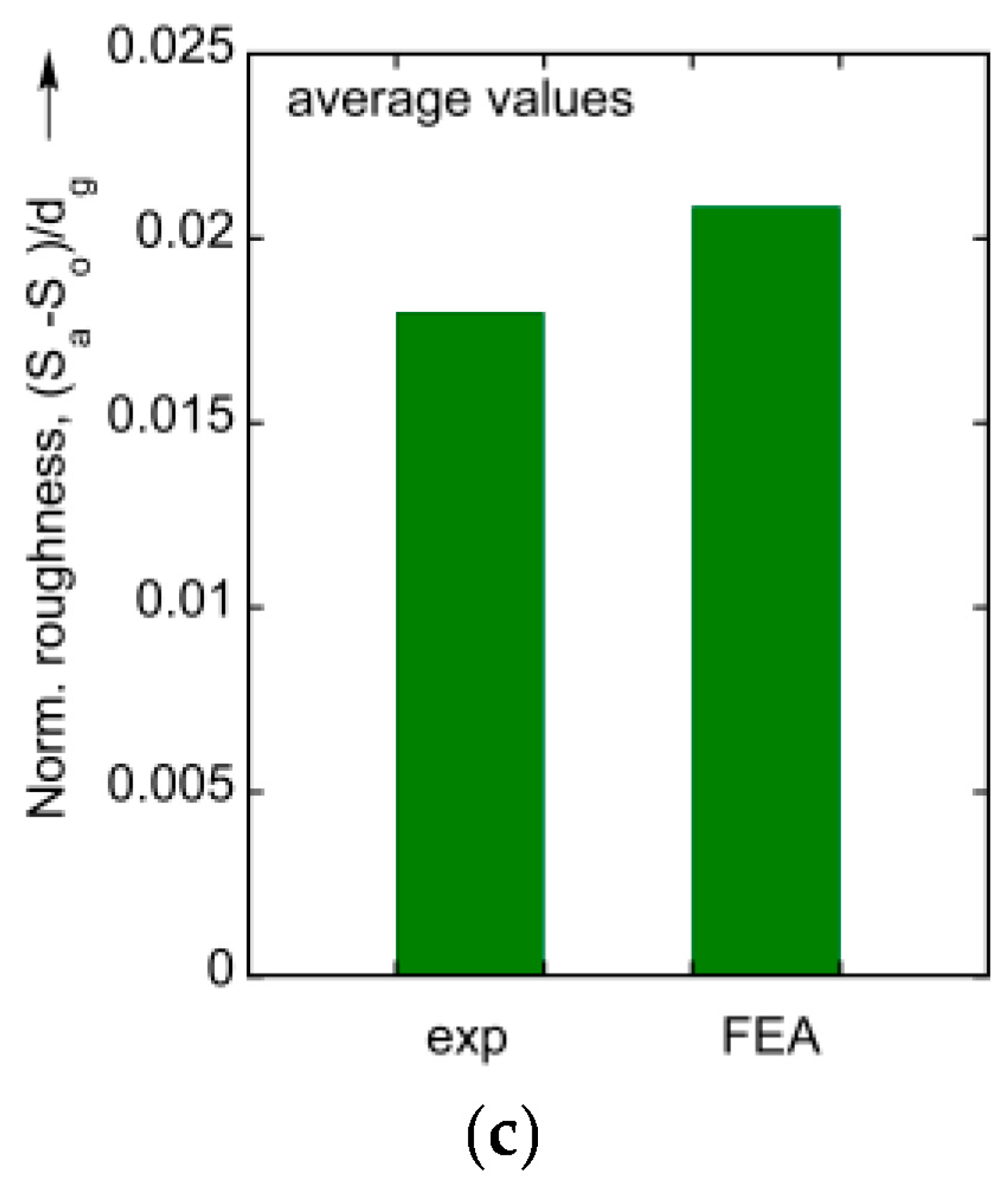
4.3. Average Surface Roughness
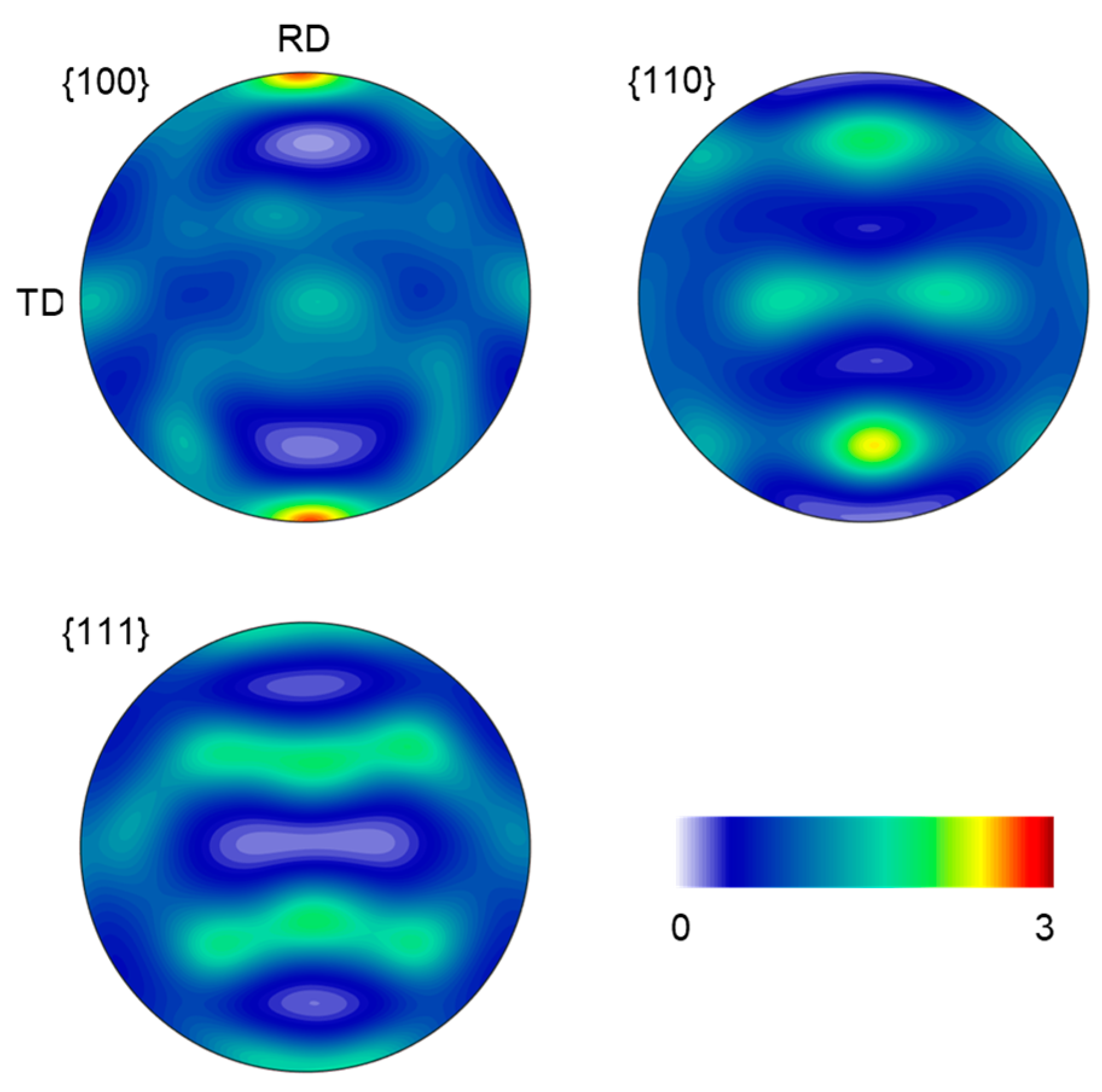
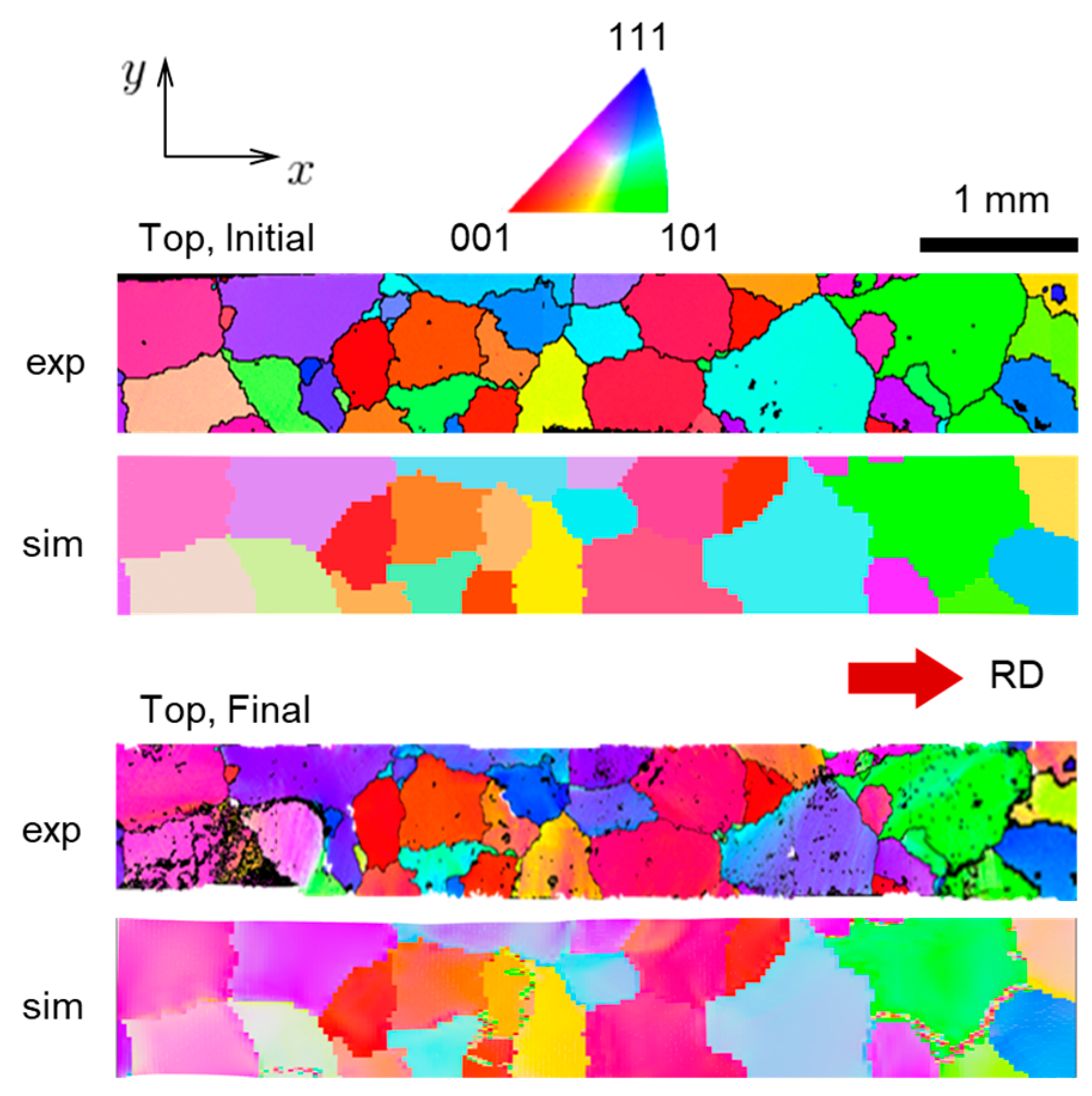
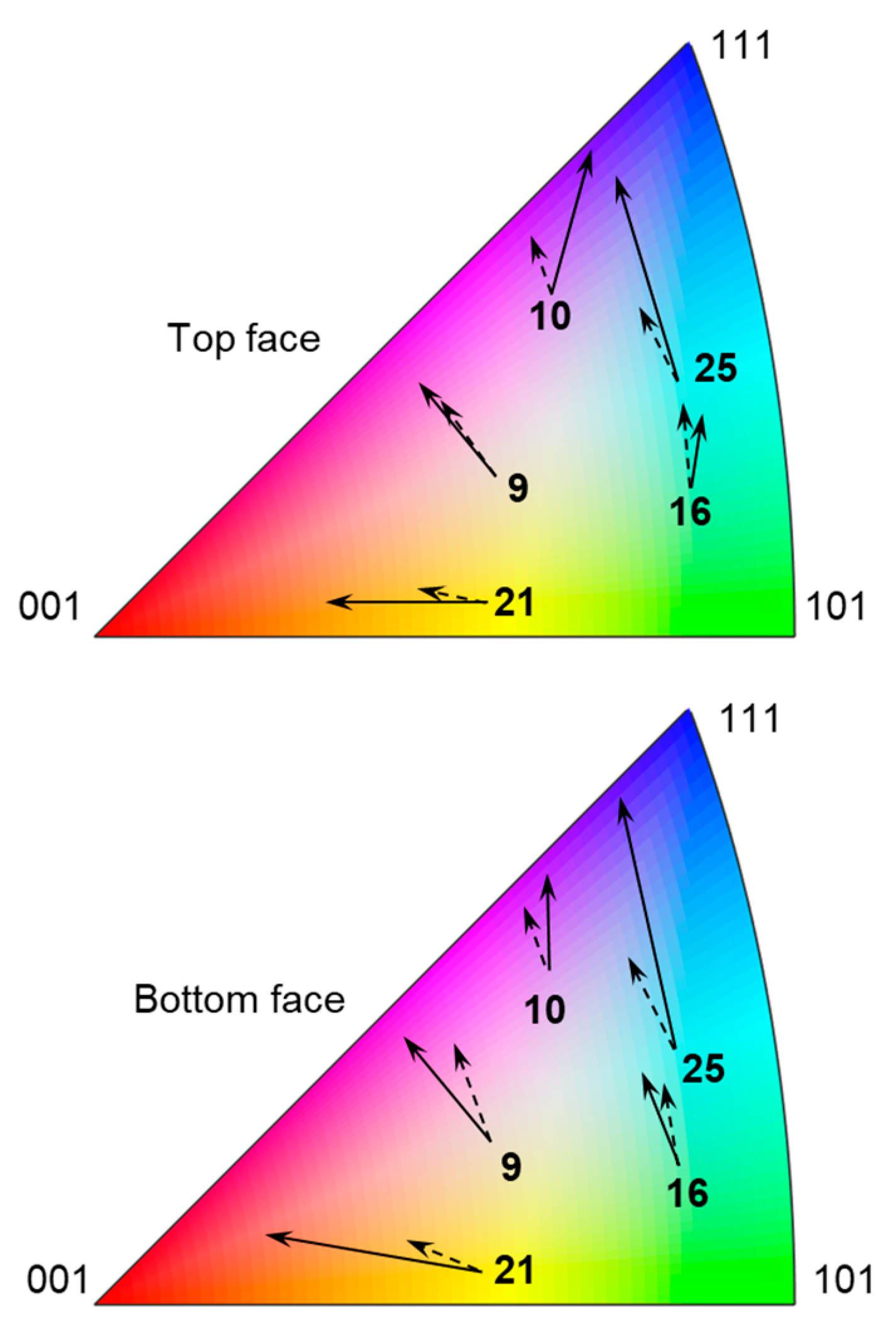
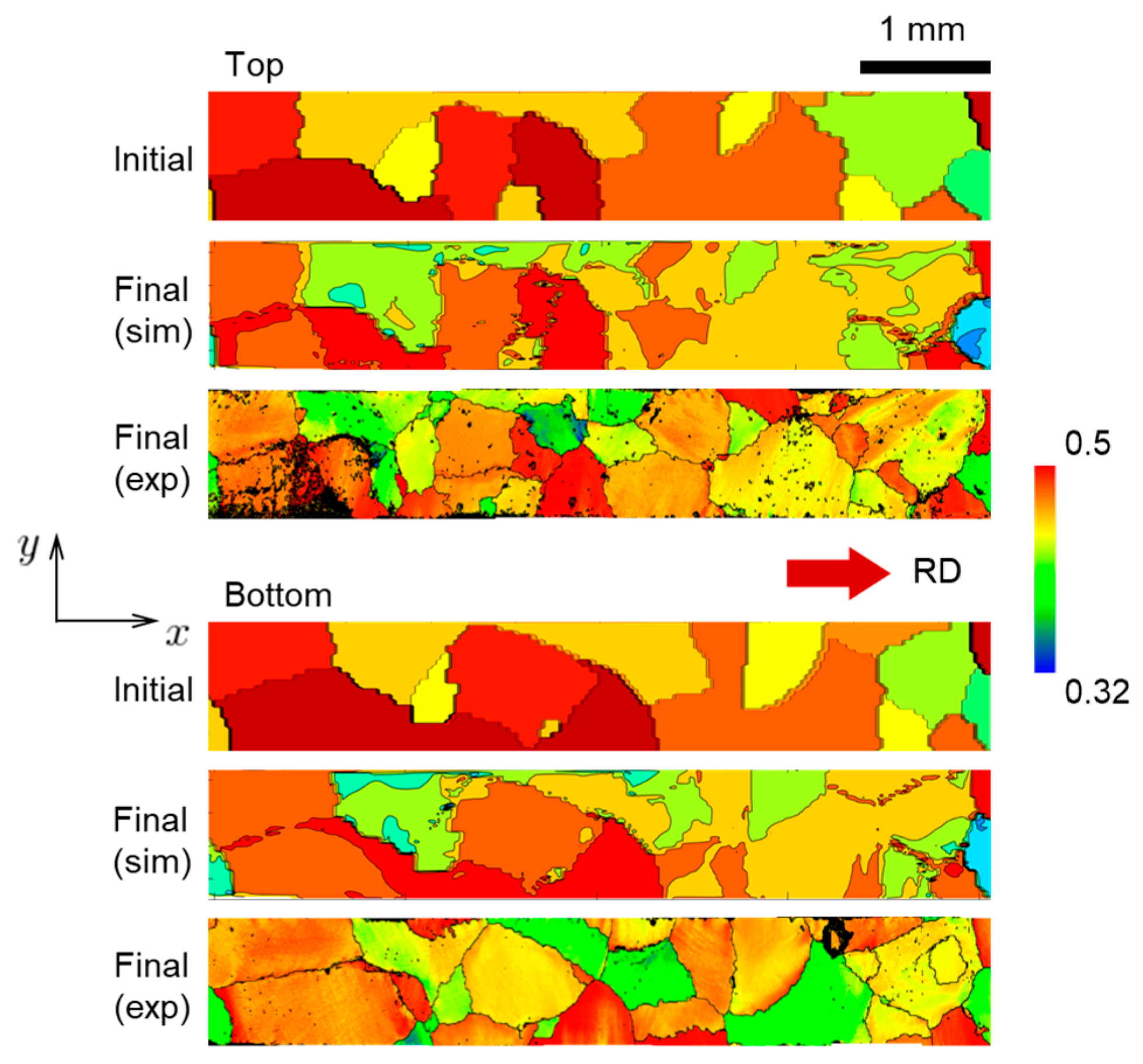
4.4. Texture Evolution during Testing
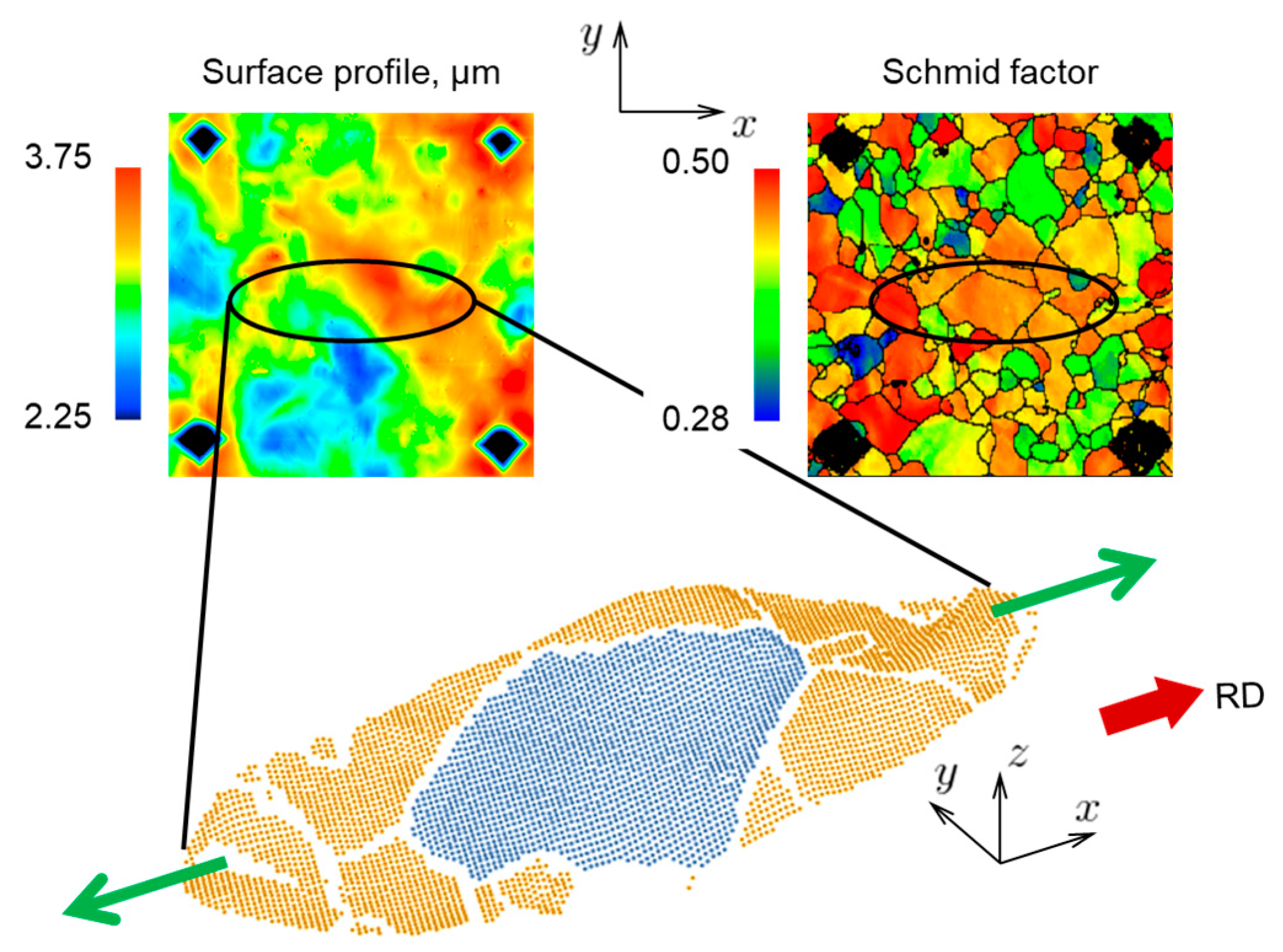
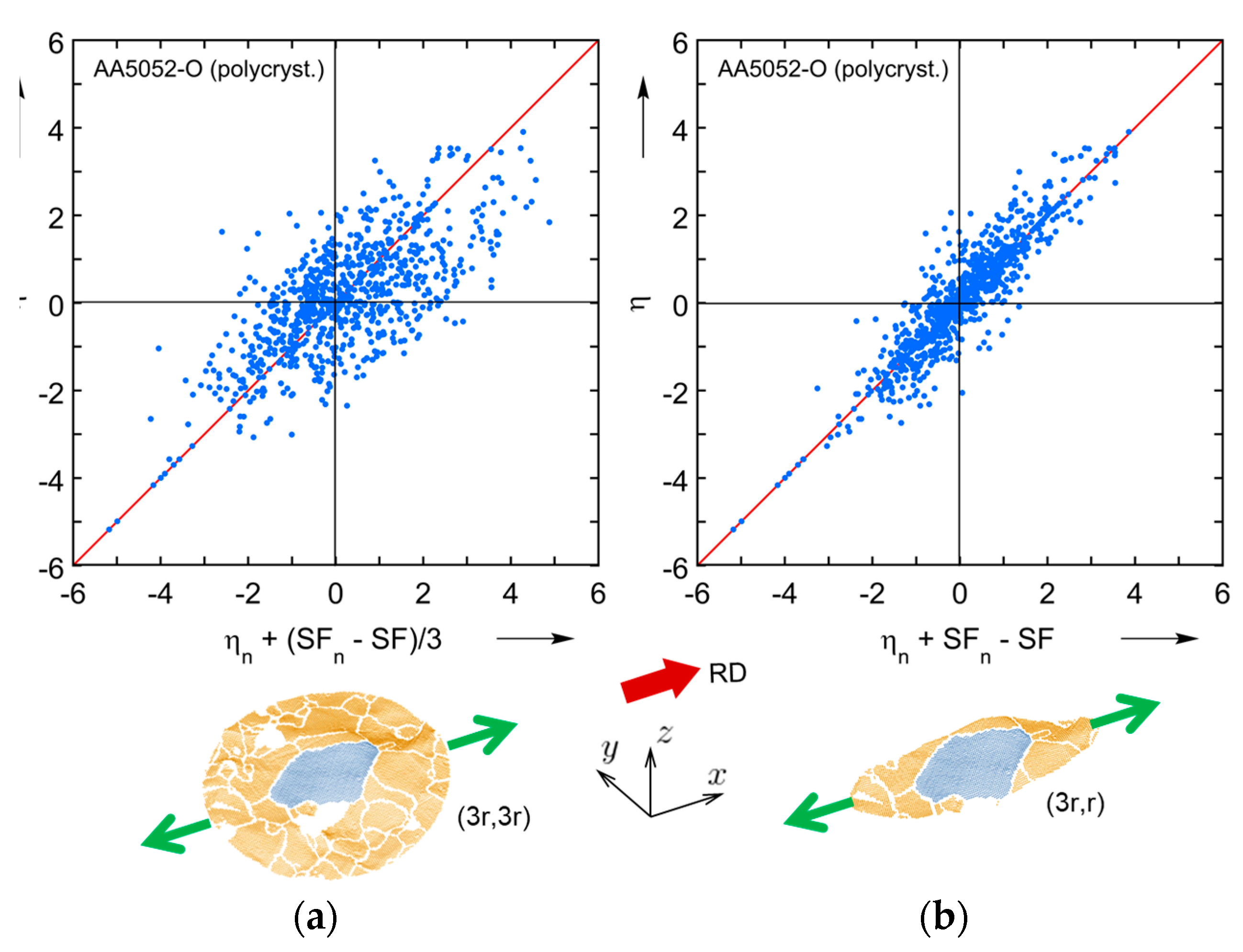
5. Analysis of Roughness Statistics
Modeling Surface Roughening in a Polycrystal
- Ratio of average elevation within the grain (, where is the area of the given grain) to the average surface roughness of the specimen (, see Equation (13)):
- Ratio of average roughness within the grain () to the average surface roughness of the specimen ():
- Average Schmid factor of the grain (SF) with respect to the loading axis.
- Relative grain size:where is an effective radius of the given grain and is the average effective radius among all grains.
6. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Yoshida, K. Effects of grain-scale heterogeneity on surface roughness and sheet metal necking. Int. J. Mech. Sci. 2014, 83, 48–56. [Google Scholar] [CrossRef]
- Zwicker, M.F.R.; Bay, N.; Nielsen, C.V. A new test for sheet metal asperity flattening under varying subsurface strain conditions. Tribol. Int. 2023, 180, 108249. [Google Scholar] [CrossRef]
- Becker, R. Effects of strain localization on surface roughening during sheet forming. Acta Mater. 1998, 46, 1385–1401. [Google Scholar] [CrossRef]
- Raabe, D.; Sachtleber, M.; Weiland, H.; Scheele, G.; Zhao, Z. Grain-scale micromechanics of polycrystal surfaces during plastic straining. Acta Mater. 2003, 51, 1539–1560. [Google Scholar] [CrossRef]
- Wilson, W.R.D.; Lee, W. Mechanics of Surface Roughening in Metal Forming Processes. J. Manuf. Sci. Eng. 2000, 123, 279–283. [Google Scholar] [CrossRef]
- Van Tijum, R.; Vellinga, W.P.; De Hosson, J.T.M. Surface roughening of metal–polymer systems during plastic deformation. Acta Mater. 2007, 55, 2757–2764. [Google Scholar] [CrossRef]
- Osakada, K.; Oyane, M. On the Roughening of Free Surface in Deformation Processes. Bull. JSME 1971, 14, 171–177. [Google Scholar] [CrossRef] [Green Version]
- Yamaguchi, K.; Mellor, P.B. Thickness and grain size dependence of limit strains in sheet metal stretching. Int. J. Mech. Sci. 1976, 18, 85–90. [Google Scholar] [CrossRef]
- Mahmudi, R.; Mehdizadeh, M. Surface roughening during uniaxial and equi-biaxial stretching of 70–30 brass sheets. J. Mater. Process. Technol. 1998, 80–81, 707–712. [Google Scholar] [CrossRef]
- Tadros, A.K.; Mellor, P.B. An experimental study of the in-plane stretching of sheet metal. Int. J. Mech. Sci. 1978, 20, 121–133. [Google Scholar] [CrossRef]
- Lee, P.S.; Piehler, H.R.; Adams, B.L.; Jarvis, G.; Hampel, H.; Rollett, A.D. Influence of surface texture on orange peel in aluminum. J. Mater. Process. Technol. 1998, 80–81, 315–319. [Google Scholar] [CrossRef]
- Banovic, S.W.; Foecke, T. Evolution of strain-induced microstructure and texture in commercial aluminum sheet under balanced biaxial stretching. Metall. Mater. Trans. A 2003, 34, 657–671. [Google Scholar] [CrossRef]
- Beaudoin, A.J.; Bryant, J.D.; Korzekwa, D.A. Analysis of ridging in aluminum auto body sheet metal. Metall. Mater. Trans. A 1998, 29, 2323–2332. [Google Scholar] [CrossRef]
- Muhammad, W.; Ali, U.; Brahme, A.P.; Kang, J.; Mishra, R.K.; Inal, K. Experimental analyses and numerical modeling of texture evolution and the development of surface roughness during bending of an extruded aluminum alloy using a multiscale modeling framework. Int. J. Plast. 2019, 117, 93–121. [Google Scholar] [CrossRef]
- Rossiter, J.; Brahme, A.; Inal, K.; Mishra, R. Numerical analyses of surface roughness during bending of FCC single crystals and polycrystals. Int. J. Plast. 2013, 46, 82–93. [Google Scholar] [CrossRef]
- Stoudt, M.R.; Levine, L.E.; Creuziger, A.; Hubbard, J.B. The fundamental relationships between grain orientation, deformation-induced surface roughness and strain localization in an aluminum alloy. Mater. Sci. Eng. A 2011, 530, 107–116. [Google Scholar] [CrossRef]
- Wittridge, N.J.; Knutsen, R.D. A microtexture based analysis of the surface roughening behaviour of an aluminium alloy during tensile deformation. Mater. Sci. Eng. A 1999, 269, 205–216. [Google Scholar] [CrossRef]
- Wu, P.D.; Lloyd, D.J. Analysis of surface roughening in AA6111 automotive sheet. Acta Mater. 2004, 52, 1785–1798. [Google Scholar] [CrossRef]
- Zhao, Z.; Radovitzky, R.; Cuitiño, A. A study of surface roughening in fcc metals using direct numerical simulation. Acta Mater. 2004, 52, 5791–5804. [Google Scholar] [CrossRef]
- Zhao, Z.; Ramesh, M.; Raabe, D.; Cuitiño, A.M.; Radovitzky, R. Investigation of three-dimensional aspects of grain-scale plastic surface deformation of an aluminum oligocrystal. Int. J. Plast. 2008, 24, 2278–2297. [Google Scholar] [CrossRef]
- Lo, S.-W.; Horng, T.-C. Surface Roughening and Contact Behavior in Forming of Aluminum Sheet. J. Tribol. 1999, 121, 224–233. [Google Scholar] [CrossRef]
- Wittridge, N.J. A Microtexture Based Analysis of Surface Roughening in Ductile Metals during Tensile Deformation. Ph.D. Thesis, University of Cape Town, Cape Town, South Africa, 1998. [Google Scholar]
- Romanova, V.; Balokhonov, R.; Zinovieva, O.; Shakhidjanov, V. Numerical study of the surface hardening effect on the deformation-induced roughening in titanium polycrystals. Comput. Mater. Sci. 2016, 116, 96–102. [Google Scholar] [CrossRef]
- Kubo, M.; Hama, T.; Tsunemi, Y.; Nakazawa, Y.; Takuda, H. Influence of Strain Ratio on Surface Roughening in Biaxial Stretching of IF Steel Sheets. ISIJ Int. 2018, 58, 704–713. [Google Scholar] [CrossRef] [Green Version]
- Dong, W.; Wang, D.; Wang, Z.; Lin, Q. Effect of Pre-strain on Surface Roughening and Frictional Behavior of DP590 High-Strength Steel. J. Mater. Eng. Perform. 2023, 32, 5317–5328. [Google Scholar] [CrossRef]
- Furushima, T.; Tsunezaki, H.; Manabe, K.; Alexsandrov, S. Ductile fracture and free surface roughening behaviors of pure copper foils for micro/meso-scale forming. Int. J. Mach. Tools Manuf. 2014, 76, 34–48. [Google Scholar] [CrossRef]
- Luo, L.; Jiang, Z.; Wei, D.; Manabe, K.; Zhao, X.; Wu, D.; Furushima, T. Effects of surface roughness on micro deep drawing of circular cups with consideration of size effects. Finite Elem. Anal. Des. 2016, 111, 46–55. [Google Scholar] [CrossRef] [Green Version]
- Meng, B.; Fu, M.W. Size effect on deformation behavior and ductile fracture in microforming of pure copper sheets considering free surface roughening. Mater. Des. 2015, 83, 400–412. [Google Scholar] [CrossRef]
- Guan, Y.; Chen, B.; Zou, J.; Britton, T.B.; Jiang, J.; Dunne, F.P.E. Crystal plasticity modelling and HR-DIC measurement of slip activation and strain localization in single and oligo-crystal Ni alloys under fatigue. Int. J. Plast. 2017, 88, 70–88. [Google Scholar] [CrossRef] [Green Version]
- Lim, H.; Carroll, J.D.; Battaile, C.C.; Buchheit, T.E.; Boyce, B.L.; Weinberger, C.R. Grain-scale experimental validation of crystal plasticity finite element simulations of tantalum oligocrystals. Int. J. Plast. 2014, 60, 1–18. [Google Scholar] [CrossRef]
- Vasilev, E.; Knezevic, M. Role of microstructural heterogeneities in damage formation and fracture of oligocrystalline Mg under tensile loading. Mater. Sci. Eng. A 2021, 827, 142096. [Google Scholar] [CrossRef]
- Lee, G.M.; Lee, J.U.; Park, S.H. Effects of surface roughness on bending properties of rolled AZ31 alloy. J. Magnes. Alloy. 2023, 11, 1224–1235. [Google Scholar] [CrossRef]
- Furushima, T.; Hirose, Y.; Tada, K.; Manabe, K. Development of compact marchiniak testing apparatus for in-situ microscopic observation of surface roughening. Procedia Eng. 2017, 207, 1946–1951. [Google Scholar] [CrossRef]
- Zhang, Z.; Lunt, D.; Abdolvand, H.; Wilkinson, A.J.; Preuss, M.; Dunne, F.P.E. Quantitative investigation of micro slip and localization in polycrystalline materials under uniaxial tension. Int. J. Plast. 2018, 108, 88–106. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Xu, W.; Niu, T.; Chen, Y. Roughness evolution of constrained surface based on crystal plasticity finite element model and coupled Eulerian-Lagrangian method. Comput. Mater. Sci. 2022, 201, 110900. [Google Scholar] [CrossRef]
- Shenoy, M.; Tjiptowidjojo, Y.; McDowell, D. Microstructure-sensitive modeling of polycrystalline IN 100. Int. J. Plast. 2008, 24, 1694–1730. [Google Scholar] [CrossRef]
- Zhang, P.; Karimpour, M.; Balint, D.; Lin, J. Three-dimensional virtual grain structure generation with grain size control. Mech. Mater. 2012, 55, 89–101. [Google Scholar] [CrossRef]
- Baudoin, P.; Hama, T.; Takuda, H. Influence of critical resolved shear stress ratios on the response of a commercially pure titanium oligocrystal: Crystal plasticity simulations and experiment. Int. J. Plast. 2019, 115, 111–131. [Google Scholar] [CrossRef]
- Knysh, P.; Sasaki, K.; Furushima, T.; Knezevic, M.; Korkolis, Y.P. A shape interpolation procedure: Application to creating explicit grain structure models based on partial data sets. Comput. Mater. Sci. 2019, 167, 42–51. [Google Scholar] [CrossRef]
- Hinkle, A.R.; Nöhring, W.G.; Leute, R.; Junge, T.; Pastewka, L. The emergence of small-scale self-affine surface roughness from deformation. Sci. Adv. 2023, 6, eaax0847. [Google Scholar] [CrossRef] [Green Version]
- Papanikolaou, S.; Song, H.; Van der Giessen, E. Obstacles and sources in dislocation dynamics: Strengthening and statistics of abrupt plastic events in nanopillar compression. J. Mech. Phys. Solids 2017, 102, 17–29. [Google Scholar] [CrossRef] [Green Version]
- Ardeljan, M.; Beyerlein, I.J.; Knezevic, M. Effect of dislocation density-twin interactions on twin growth in AZ31 as revealed by explicit crystal plasticity finite element modeling. Int. J. Plast. 2017, 99, 81–101. [Google Scholar] [CrossRef]
- Ardeljan, M.; Knezevic, M.; Nizolek, T.; Beyerlein, I.J.; Mara, N.A.; Pollock, T.M. A study of microstructure-driven strain localizations in two-phase polycrystalline HCP/BCC composites using a multi-scale model. Int. J. Plast. 2015, 74, 35–57. [Google Scholar] [CrossRef]
- Zecevic, M.; Knezevic, M. A new visco-plastic self-consistent formulation implicit in dislocation-based hardening within implicit finite elements: Application to high strain rate and impact deformation of tantalum. Comput. Methods Appl. Mech. Eng. 2018, 341, 888–916. [Google Scholar] [CrossRef]
- Knysh, P.; Korkolis, Y.P. Blackbox: A procedure for parallel optimization of expensive black-box functions. arXiv 2016, arXiv:1605.00998. [Google Scholar]
- Vander Voort, G.F.; Lampman, S.R.; Sanders, B.R.; Anton, G.J.; Polakowski, C.; Kinson, J.; Muldoon, K.; Henry, S.D.; Scott, W.W., Jr. Metallography and Microstructures. In ASM Handbook; ASM International: Novelty, OH, USA, 2004; Volume 9, pp. 40002–44073. [Google Scholar]
- ASTM E112-13; Standard Test Methods for Determining Average Grain Size. ASTM International: Philadelphia, PA, USA, 2013.
- Keyence. KEYENCE VK-X100 Specifications; Keyence: Osaka, Japan, 2023. [Google Scholar]
- Kalidindi, S.R.; Bronkhorst, C.A.; Anand, L. Crystallographic texture evolution in bulk deformation processing of FCC metals. J. Mech. Phys. Solids 1992, 40, 537–569. [Google Scholar] [CrossRef]
- Ardeljan, M.; Beyerlein, I.J.; Knezevic, M. A dislocation density based crystal plasticity finite element model: Application to a two-phase polycrystalline HCP/BCC composites. J. Mech. Phys. Solids 2014, 66, 16–31. [Google Scholar] [CrossRef]
- Knysh, P.; Korkolis, Y.P. Determination of the fraction of plastic work converted into heat in metals. Mech. Mater. 2015, 86, 71–80. [Google Scholar] [CrossRef]
- Knezevic, M.; Zecevic, M.; Beyerlein, I.J.; Lebensohn, R.A. A numerical procedure enabling accurate descriptions of strain rate-sensitive flow of polycrystals within crystal visco-plasticity theory. Comput. Methods Appl. Mech. Eng. 2016, 308, 468–482. [Google Scholar] [CrossRef] [Green Version]
- Korkolis, Y.P.; Mitchell, B.R.; Locke, M.R.; Kinsey, B.L. Plastic flow and anisotropy of a low-carbon steel over a range of strain-rates. Int. J. Impact. Eng. 2018, 121, 157–171. [Google Scholar] [CrossRef]
- Roy, B.K.; Korkolis, Y.P.; Arai, Y.; Araki, W.; Iijima, T.; Kouyama, J. Plastic deformation of AA6061-T6 at elevated temperatures: Experiments and modeling. Int. J. Mech. Sci. 2022, 216, 106943. [Google Scholar] [CrossRef]
- Hall, E.O. The Deformation and Ageing of Mild Steel: III Discussion of Results. Proc. Phys. Soc. Sect. B 1951, 64, 747. [Google Scholar] [CrossRef]
- Petch, N.J. The cleavage strength of polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
- Ferreri, N.C.; Feng, Z.; Savage, D.J.; Brown, D.W.; Clausen, B.; Sisneros, T.A.; Knezevic, M. In-situ high-energy X-ray diffraction and crystal plasticity modeling to predict the evolution of texture, twinning, lattice strains and strength during loading and reloading of beryllium. Int. J. Plast. 2022, 150, 103217. [Google Scholar] [CrossRef]
- Zecevic, M.; Knezevic, M. A dislocation density based elasto-plastic self-consistent model for the prediction of cyclic deformation: Application to AA6022-T4. Int. J. Plast. 2015, 72, 200–217. [Google Scholar] [CrossRef] [Green Version]
- Simmons, G.; Wang, H. Single Crystal Elastic Constants and Calculated Aggregate Properties: A Handbook, 2nd ed.; MIT Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Guery, A.; Hild, F.; Latourte, F.; Roux, S. Identification of crystal plasticity parameters using DIC measurements and weighted FEMU. Mech. Mater. 2016, 100, 55–71. [Google Scholar] [CrossRef] [Green Version]
- Eghtesad, A.; Barrett, T.J.; Knezevic, M. Compact reconstruction of orientation distributions using generalized spherical harmonics to advance large-scale crystal plasticity modeling: Verification using cubic, hexagonal, and orthorhombic polycrystals. Acta Mater. 2018, 155, 418–432. [Google Scholar] [CrossRef]
- Knysh, P.; Korkolis, Y.P. Identification of the post-necking hardening response of rate- and temperature-dependent metals. Int. J. Solids Struct. 2017, 115, 149–160. [Google Scholar] [CrossRef]
- Feather, W.G.; Lim, H.; Knezevic, M. A numerical study into element type and mesh resolution for crystal plasticity finite element modeling of explicit grain structures. Comput. Mech. 2021, 67, 33–55. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Baudoin, P.; Kyoto University, Kyoto, Japan; Hama, T.; Kyoto University, Kyoto, Japan. Private communication, 2018.
- Hosford, W.F. Mechanical Behavior of Materials; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Groeber, M.A.; Jackson, M.A. DREAM.3D: A Digital Representation Environment for the Analysis of Microstructure in 3D. Integr. Mater. Manuf. Innov. 2014, 3, 56–72. [Google Scholar] [CrossRef] [Green Version]
- Knezevic, M.; Drach, B.; Ardeljan, M.; Beyerlein, I.J. Three dimensional predictions of grain scale plasticity and grain boundaries using crystal plasticity finite element models. Comput. Methods Appl. Mech. Eng. 2014, 277, 239–259. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Anand, L. Thermodynamics applied to gradient theories involving the accumulated plastic strain: The theories of Aifantis and Fleck and Hutchinson and their generalization. J. Mech. Phys. Solids 2009, 57, 405–421. [Google Scholar] [CrossRef]








| Grain Number | |||
|---|---|---|---|
| 1 | 343.1 | 36.2 | 58.7 |
| 2 | 170.4 | 7.5 | 78.5 |
| 3 | 155 | 30.6 | 3.6 |
| 4 | 122.1 | 37.9 | 0.5 |
| 5 | 37.9 | 23.7 | 84.3 |
| 6 | 342.9 | 20.6 | 81.4 |
| 7 | 33.1 | 23.1 | 56.9 |
| 8 | 44.3 | 43.6 | 37.9 |
| 9 | 192 | 38 | 80.8 |
| 10 | 235.8 | 38.7 | 38.9 |
| 11 | 227.7 | 32.4 | 36.1 |
| 12 | 322.2 | 30.7 | 46.8 |
| 13 | 82.8 | 25.7 | 30.8 |
| 14 | 247.4 | 26.5 | 14.3 |
| 15 | 328.5 | 41.5 | 54.4 |
| 16 | 215.5 | 11.4 | 23.8 |
| 17 | 354.9 | 42.7 | 5.6 |
| 18 | 169.4 | 19.3 | 83.3 |
| 19 | 258.1 | 51 | 45.5 |
| 20 | 340.4 | 36.1 | 17.9 |
| 21 | 233.7 | 48.4 | 58.1 |
| 22 | 209.9 | 41.4 | 7.1 |
| 23 | 38.5 | 25.7 | 15 |
| 24 | 185.8 | 16.9 | 60.4 |
| 25 | 37.7 | 14.8 | 40.8 |
| 26 | 202.9 | 29.6 | 76.9 |
| 27 | 7.3 | 33.8 | 83.9 |
| 28 | 89.1 | 14.4 | 53.3 |
| 29 | 302.1 | 19.6 | 76.5 |
| 30 | 352 | 10.7 | 54 |
| 31 | 283.2 | 24.4 | 9 |
| 32 | 314.7 | 33.3 | 36.4 |
| 33 | 229.9 | 28.8 | 84.7 |
| 34 | 181 | 43.6 | 53.4 |
| 35 | 77.8 | 51 | 53.2 |
| 36 | 337.2 | 15.8 | 48.8 |
| 37 | 154.4 | 10.2 | 7.2 |
| 38 | 263.7 | 6.1 | 6.9 |
| Grain Number | Δ (Top) | Δ (Bottom) |
|---|---|---|
| 9 | 0.12 | 0.20 |
| 10 | 0.49 | 0.26 |
| 16 | 0.13 | 0.11 |
| 21 | 0.36 | 0.43 |
| 25 | 0.42 | 0.42 |
| Average | 0.29 | |
| Shape | Semi-Axes | Relation |
|---|---|---|
 | ||
 | ||
 | ||
 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korkolis, Y.P.; Knysh, P.; Sasaki, K.; Furushima, T.; Knezevic, M. Deformation-Induced Surface Roughening of an Aluminum–Magnesium Alloy: Experimental Characterization and Crystal Plasticity Modeling. Materials 2023, 16, 5601. https://doi.org/10.3390/ma16165601
Korkolis YP, Knysh P, Sasaki K, Furushima T, Knezevic M. Deformation-Induced Surface Roughening of an Aluminum–Magnesium Alloy: Experimental Characterization and Crystal Plasticity Modeling. Materials. 2023; 16(16):5601. https://doi.org/10.3390/ma16165601
Chicago/Turabian StyleKorkolis, Yannis P., Paul Knysh, Kanta Sasaki, Tsuyoshi Furushima, and Marko Knezevic. 2023. "Deformation-Induced Surface Roughening of an Aluminum–Magnesium Alloy: Experimental Characterization and Crystal Plasticity Modeling" Materials 16, no. 16: 5601. https://doi.org/10.3390/ma16165601
APA StyleKorkolis, Y. P., Knysh, P., Sasaki, K., Furushima, T., & Knezevic, M. (2023). Deformation-Induced Surface Roughening of an Aluminum–Magnesium Alloy: Experimental Characterization and Crystal Plasticity Modeling. Materials, 16(16), 5601. https://doi.org/10.3390/ma16165601








