Thermodynamic and Ab Initio Design of Multicomponent Alloys Based on (Fe50Mn30Co10Cr10)-xBx (x = 0, 5, 7, 10, and 15 at.%)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Phase Prediction with Empiric Parameters
2.2. Thermodynamic CALPHAD Calculations: Phase Diagram Prediction
2.3. Ab Initio DFT Solid Solution Modelling
3. Results
3.1. Empiric Formation Phase Rule Analysis
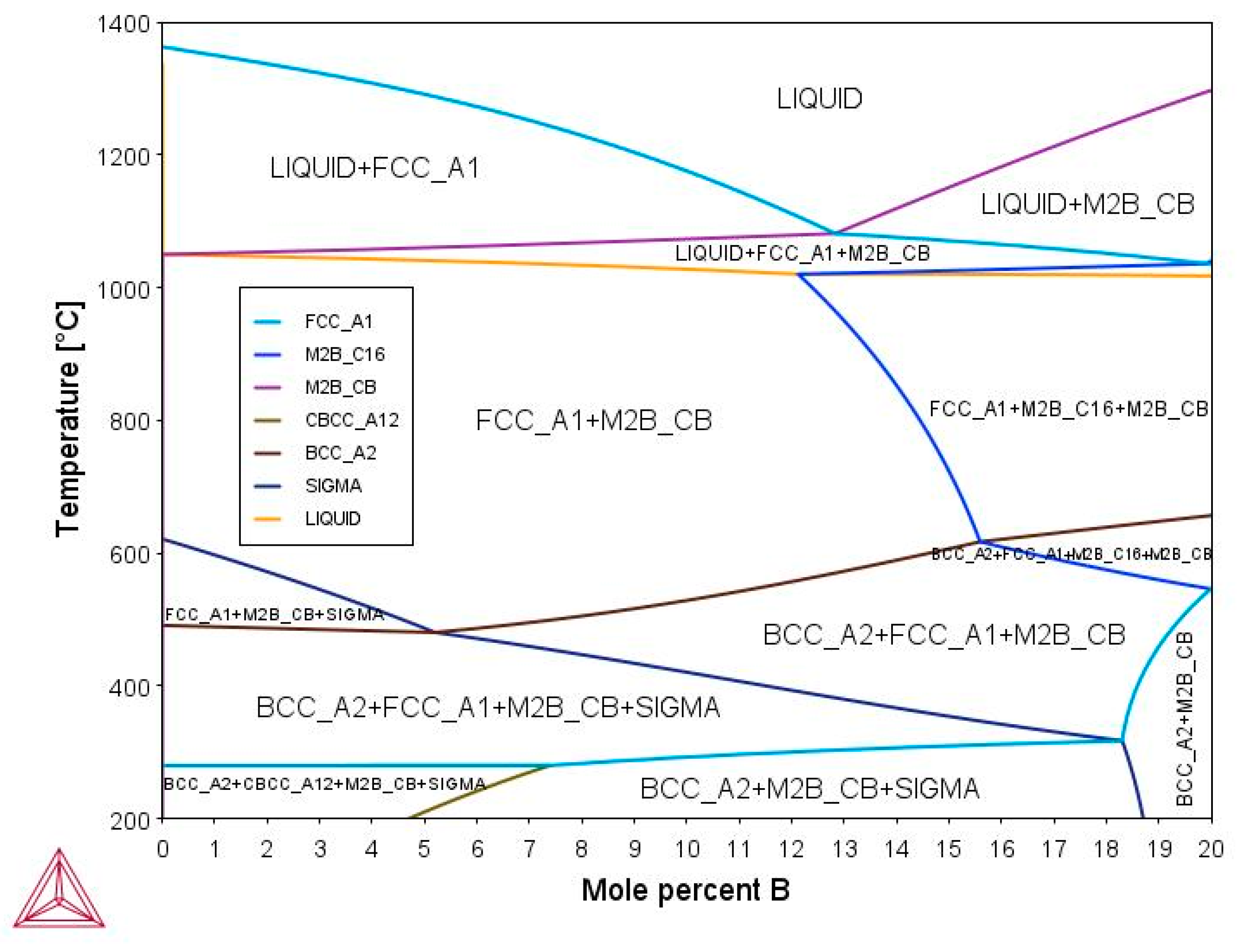
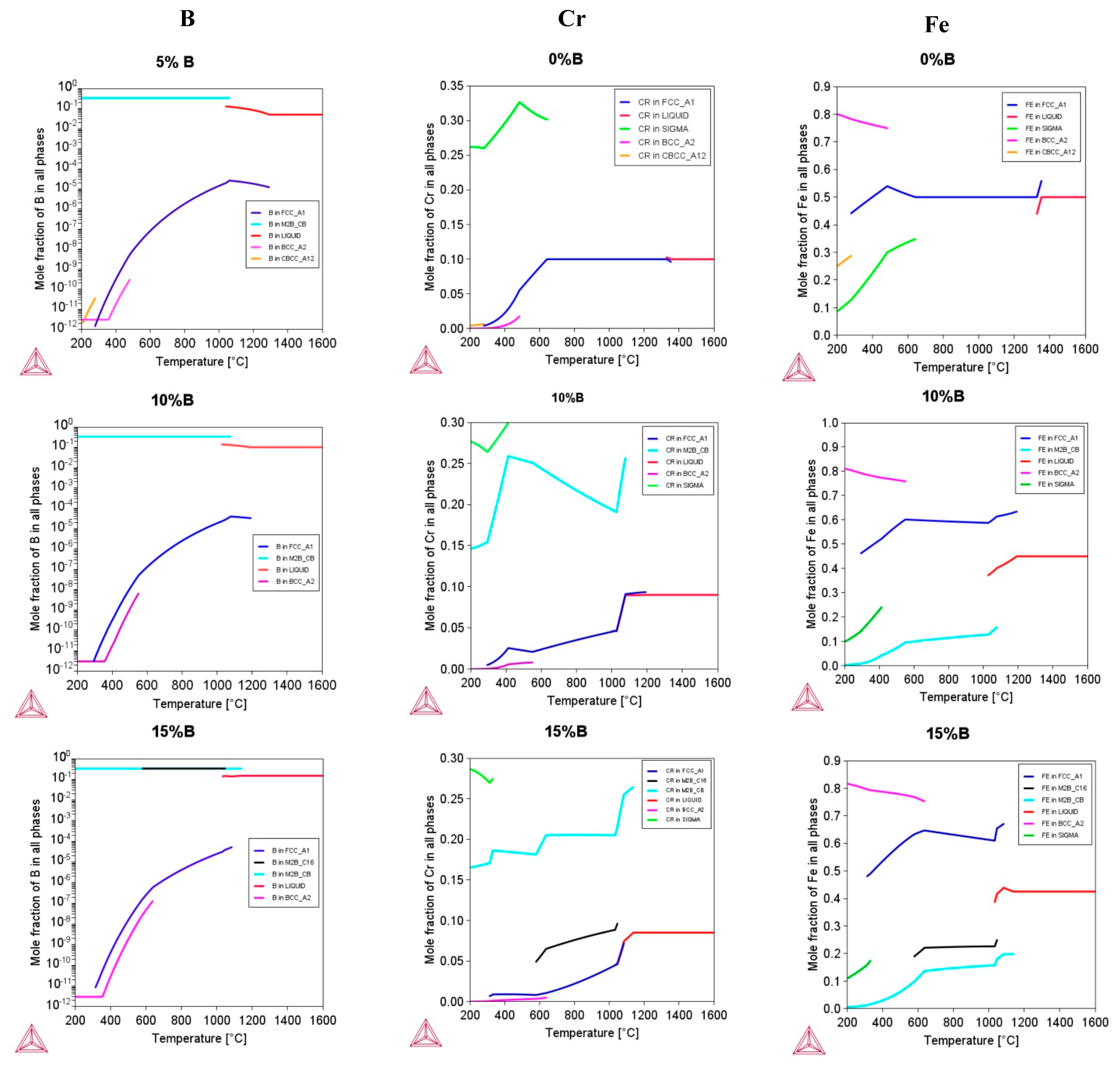
3.2. Phase Diagram Prediction for (Fe50Mn30Cr10Co10)-xBx (x = 0, 5, 7, 10, and 15 at.%)
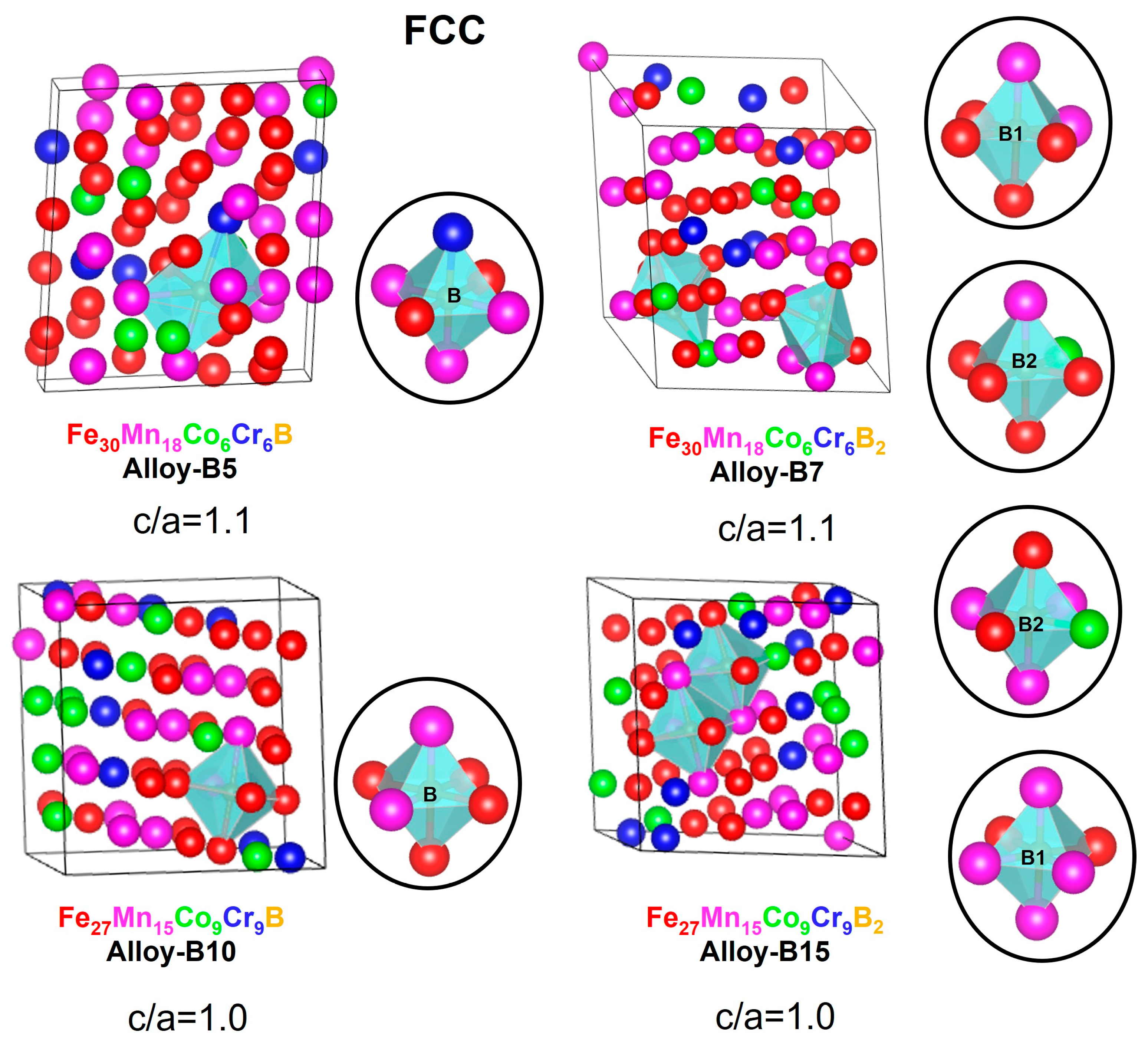
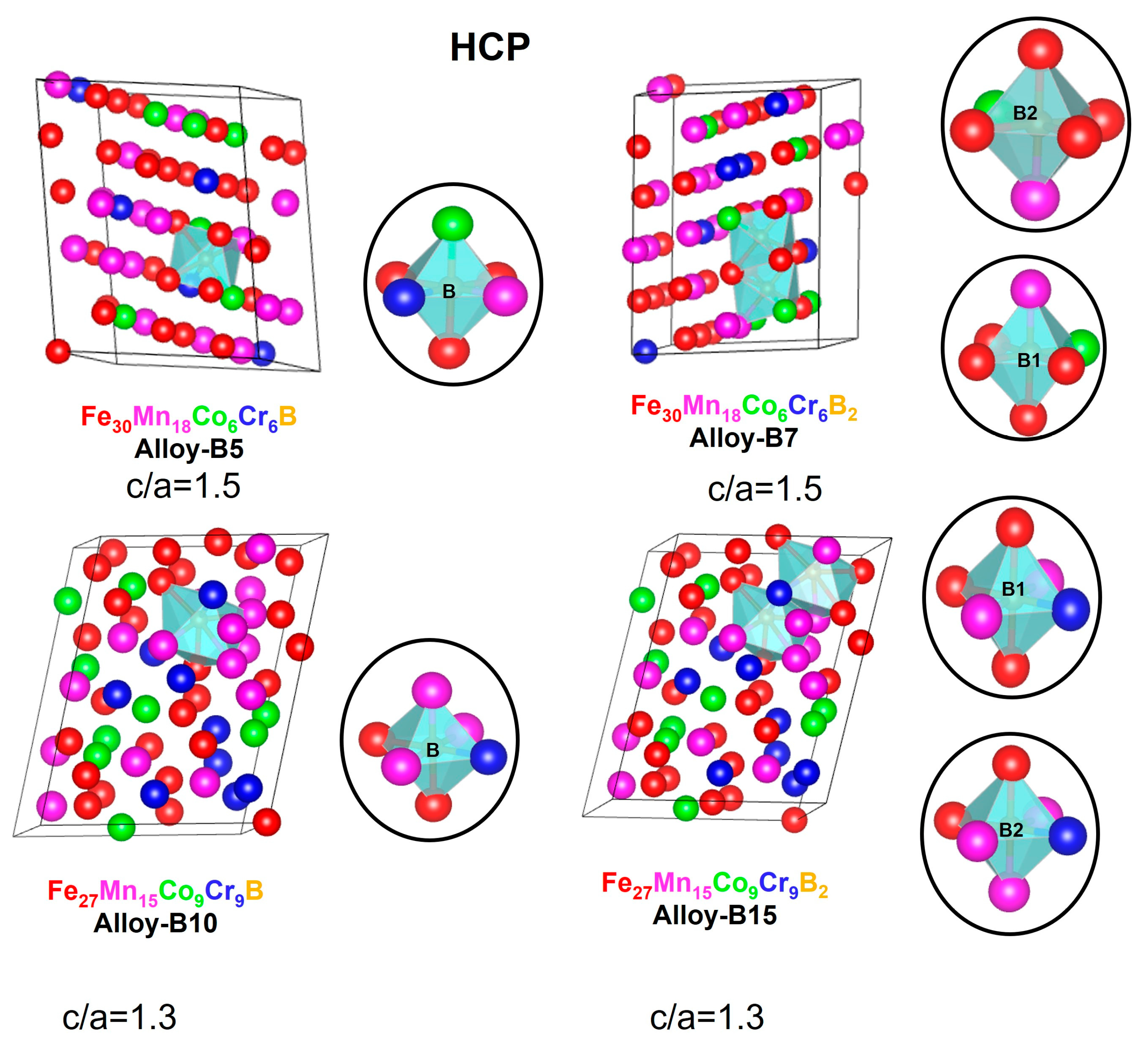
3.3. Structure, Stability, Magnetic Role, and SFE for the Design Alloys (Fe50Mn30Cr10Co10)-xBx (x = 0, 5, 7, 10, and 15 at.%)
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cai, Z.; Cui, X.; Liu, Z.; Li, Y.; Dong, M.; Jin, G. Microstructure and Wear Resistance of Laser Cladded Ni-Cr-Co-Ti-V High-Entropy Alloy Coating after Laser Remelting Processing. Opt. Laser Technol. 2018, 99, 276–281. [Google Scholar] [CrossRef]
- Ye, Q.; Feng, K.; Li, Z.; Lu, F.; Li, R.; Huang, J.; Wu, Y. Microstructure and Corrosion Properties of CrMnFeCoNi High Entropy Alloy Coating. Appl. Surf. Sci. 2017, 396, 1420–1426. [Google Scholar] [CrossRef]
- Miracle, D.B. High Entropy Alloys as a Bold Step Forward in Alloy Development. Nat. Commun. 2019, 10, 1805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miracle, D.B.; Senkov, O.N. A Critical Review of High Entropy Alloys and Related Concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef] [Green Version]
- Khan, N.A.; Akhavan, B.; Zhou, H.; Chang, L.; Wang, Y.; Sun, L.; Bilek, M.M.; Liu, Z. High Entropy Alloy Thin Films of AlCoCrCu0.5FeNi with Controlled Microstructure. Appl. Surf. Sci. 2019, 495, 143560. [Google Scholar] [CrossRef]
- Joseph, J.; Jarvis, T.; Wu, X.; Stanford, N.; Hodgson, P.; Fabijanic, D.M. Comparative Study of the Microstructures and Mechanical Properties of Direct Laser Fabricated and Arc-Melted AlxCoCrFeNi High Entropy Alloys. Mater. Sci. Eng. A 2015, 633, 184–193. [Google Scholar] [CrossRef]
- Ron, T.; Shirizly, A.; Aghion, E. Additive Manufacturing Technologies of High Entropy Alloys (HEA): Review and Prospects. Materials 2023, 16, 2454. [Google Scholar] [CrossRef]
- Savage, N. Striking a Balance with High Entropy Alloys. Nat. Commun. 2021, 67, 64–66. [Google Scholar]
- George, E.P.; Raabe, D.; Ritchie, R.O. High-Entropy Alloys. Nat. Rev. Mater. 2019, 4, 515–534. [Google Scholar] [CrossRef]
- Yeh, M.C.G.J.; Liaw, P.K.; Zhang, Y. High-Entropy Alloys; Gao, M.C., Yeh, J.-W., Liaw, P.K., Zhang, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 9783319270111. [Google Scholar]
- Zhang, Y.; Zuo, T.T.; Tang, Z.; Gao, M.C.; Dahmen, K.A.; Liaw, P.K.; Lu, Z.P. Microstructures and Properties of High-Entropy Alloys. Prog. Mater. Sci. 2014, 61, 1–93. [Google Scholar] [CrossRef]
- Xin, Y.; Li, S.; Qian, Y.; Zhu, W.; Yuan, H.; Jiang, P.; Guo, R.; Wang, L. High-Entropy Alloys as a Platform for Catalysis: Progress, Challenges, and Opportunities. ACS Catal. 2020, 10, 11280–11306. [Google Scholar] [CrossRef]
- Li, K.; Chen, W. Recent Progress in High-Entropy Alloys for Catalysts: Synthesis, Applications, and Prospects. Mater. Today Energy 2021, 20, 100638. [Google Scholar] [CrossRef]
- Tomboc, G.M.; Kwon, T.; Joo, J.; Lee, K. High Entropy Alloy Electrocatalysts: A Critical Assessment of Fabrication and Performance. J. Mater. Chem. A Mater. 2020, 8, 14844–14862. [Google Scholar] [CrossRef]
- Sun, Y.; Dai, S. High-Entropy Materials for Catalysis: A New Frontier. Sci. Adv. 2021, 7, eabg1600. [Google Scholar] [CrossRef]
- Wang, X.; Guo, W.; Fu, Y. High-Entropy Alloys: Emerging Materials for Advanced Functional Applications. J. Mater. Chem. A Mater. 2021, 9, 663–701. [Google Scholar]
- Amiri, A.; Shahbazian-Yassar, R. Recent Progress of High-Entropy Materials for Energy Storage and Conversion. J. Mater. Chem. A Mater. 2021, 9, 782–823. [Google Scholar] [CrossRef]
- Fu, M.; Ma, X.; Zhao, K.; Li, X.; Su, D. High-Entropy Materials for Energy-Related Applications. Iscience 2021, 24, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Akinwekomi, A.D.; Akhtar, F. Bibliometric Mapping of Literature on High-Entropy/Multicomponent Alloys and Systematic Review of Emerging Applications. Entropy 2022, 24, 329. [Google Scholar] [CrossRef]
- Wang, B.; Yao, Y.; Yu, X.; Wang, C.; Wu, C.; Zou, Z. Understanding the Enhanced Catalytic Activity of High Entropy Alloys: From Theory to Experiment. J. Mater. Chem. A Mater. 2021, 9, 19410–19438. [Google Scholar] [CrossRef]
- Yang, F.; Wang, J.; Zhang, Y.; Wu, Z.; Zhang, Z.; Zhao, F.; Huot, J.; Grobivć Novaković, J.; Novaković, N. Recent Progress on the Development of High Entropy Alloys (HEAs) for Solid Hydrogen Storage: A Review. Int. J. Hydrogen Energy 2022, 47, 11236–11249. [Google Scholar] [CrossRef]
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural Development in Equiatomic Multicomponent Alloys. Mater. Sci. Eng. A 2004, 375–377, 213–218. [Google Scholar] [CrossRef]
- Cantor, B. Multicomponent and High Entropy Alloys. Entropy 2014, 16, 4749–4768. [Google Scholar] [CrossRef] [Green Version]
- Yeh, J.; Chen, S.; Gan, J.; Lin, S. Communications: Formation of Simple Crystal Structures in Cu-Co-Ni-Cr-Al-Fe-Ti-V Alloys with Multiprincipal Metallic Elements. Metall. Mater. Trans. A 2004, 35, 2533–2536. [Google Scholar]
- Yeh, J.W. Alloy Design Strategies and Future Trends in High-Entropy Alloys. JOM 2013, 65, 1759–1771. [Google Scholar] [CrossRef]
- Mújica Roncery, L.; Weber, S.; Theisen, W. Nucleation and Precipitation Kinetics of M23C6 and M2N in an Fe-Mn-Cr-C-N Austenitic Matrix and Their Relationship with the Sensitization Phenomenon. Acta Mater. 2011, 59, 6275–6286. [Google Scholar] [CrossRef]
- Chmielak, L.; Mujica Roncery, L.; Niederhofer, P.; Weber, S.; Theisen, W. CrMnFeCoNi High Entropy Alloys with Carbon and Nitrogen: Mechanical Properties, Wear and Corrosion Resistance. SN Appl. Sci. 2021, 3, 835. [Google Scholar] [CrossRef]
- Li, Z.; Tasan, C.C.; Springer, H.; Gault, B.; Raabe, D. Interstitial Atoms Enable Joint Twinning and Transformation Induced Plasticity in Strong and Ductile High-Entropy Alloys. Sci. Rep. 2017, 7, 40704. [Google Scholar] [CrossRef] [Green Version]
- Seol, J.B.; Bae, J.W.; Li, Z.; Han, J.C.; Kim, J.G.; Raabe, D.; Kim, H.S. Boron Doped Ultrastrong and Ductile High-Entropy Alloys. Acta Mater. 2018, 151, 366–376. [Google Scholar] [CrossRef]
- Hu, M.; Ouyang, X.; Yin, F.; Zhao, X.; Zhang, Z.; Wang, X. Effect of Boronizing on the Microstructure and Mechanical Properties of CoCrFeNiMn High-Entropy Alloy. Materials 2023, 16, 3754. [Google Scholar] [CrossRef]
- Aguilar-Hurtado, J.Y.; Vargas-Uscategui, A.; Zambrano-Mera, D.; Palma-Hillerns, R. The Effect of Boron Content on the Microstructure and Mechanical Properties of Fe50-XMn30Co10Cr10BX (X = 0, 0.3, 0.6 and 1.7 wt%) Multi-Component Alloys Prepared by Arc-Melting. Mater. Sci. Eng. A 2019, 748, 244–252. [Google Scholar] [CrossRef]
- Aguilar-Hurtado, J.Y.; Vargas-Uscategui, A.; Paredes-Gil, K.; Palma-Hillerns, R.; Tobar, M.J.; Amado, J.M. Boron Addition in a Non-Equiatomic Fe50Mn30Co10Cr10 Alloy Manufactured by Laser Cladding: Microstructure and Wear Abrasive Resistance. Appl. Surf. Sci. 2020, 515, 146084. [Google Scholar] [CrossRef]
- Ding, J.; Yu, Q.; Asta, M.; Ritchie, R.O. Tunable Stacking Fault Energies by Tailoring Local Chemical Order in CrCoNi Medium-Entropy Alloys. Proc. Natl. Acad. Sci. USA 2018, 115, 8919–8924. [Google Scholar] [CrossRef] [Green Version]
- Lu, J.; Hultman, L.; Holmström, E.; Antonsson, K.H.; Grehk, M.; Li, W.; Vitos, L.; Golpayegani, A. Stacking Fault Energies in Austenitic Stainless Steels. Acta Mater. 2016, 111, 39–46. [Google Scholar] [CrossRef]
- Lee, T.H.; Kim, S.D.; Ha, H.Y.; Jang, J.H.; Moon, J.; Kang, J.Y.; Lee, C.H.; Park, S.J.; Woo, W.; Shin, J.H.; et al. Screw Dislocation Driven Martensitic Nucleation: A Step toward Consilience of Deformation Scenario in Fcc Materials. Acta Mater. 2019, 174, 342–350. [Google Scholar] [CrossRef]
- Liu, S.F.; Wu, Y.; Wang, H.T.; He, J.Y.; Liu, J.B.; Chen, C.X.; Liu, X.J.; Wang, H.; Lu, Z.P. Stacking Fault Energy of Face-Centered-Cubic High Entropy Alloys. Intermetallics 2018, 93, 269–273. [Google Scholar] [CrossRef]
- Pierce, D.T.; Jiménez, J.A.; Bentley, J.; Raabe, D.; Oskay, C.; Wittig, J.E. The Influence of Manganese Content on the Stacking Fault and Austenite/ε-Martensite Interfacial Energies in Fe-Mn-(Al-Si) Steels Investigated by Experiment and Theory. Acta Mater. 2014, 68, 238–253. [Google Scholar] [CrossRef]
- Roncery, L.M.; Weber, S.; Theisen, W. Development of Mn-Cr-(C-N) Corrosion Resistant Twinning Induced Plasticity Steels: Thermodynamic and Diffusion Calculations, Production, and Characterization. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2010, 41, 2471–2479. [Google Scholar] [CrossRef]
- Olson, G.B.; Cohen, M. A General Mechanism of Martensitic Nucleation: Part I. General Concepts and the FCC → HCP Transformation. Metall. Trans. A 1976, 7, 1897–1904. [Google Scholar] [CrossRef]
- Olson, G.B.; Cohen, M. A General Mechanism of Martensitic Nucleation: Part III. Kinetics of Martensitic Nucleation. Metall. Trans. A 1976, 7, 1915–1923. [Google Scholar] [CrossRef]
- King, D.J.M.; Middleburgh, S.C.; McGregor, A.G.; Cortie, M.B. Predicting the Formation and Stability of Single Phase High-Entropy Alloys. Acta Mater. 2016, 104, 172–179. [Google Scholar] [CrossRef]
- Widom, M. Modeling the Structure and Thermodynamics of High-Entropy Alloys. J. Mater. Res. 2018, 33, 2881–2898. [Google Scholar] [CrossRef] [Green Version]
- Tian, F. A Review of Solid-Solution Models of High-Entropy Alloys Based on Ab Initio Calculations. Front. Mater. 2017, 4, 36. [Google Scholar] [CrossRef] [Green Version]
- Beyramali Kivy, M.; Asle Zaeem, M.; Lekakh, S. Investigating Phase Formations in Cast AlFeCoNiCu High Entropy Alloys by Combination of Computational Modeling and Experiments. Mater. Des. 2017, 127, 224–232. [Google Scholar] [CrossRef]
- Reuter, K.; Stampf, C.; Scheffler, M. Ab Initio Atomistic Thermodynamics and Statistical Mechanics of Surface Properties and Functions. Handb. Mater. Model. 2005, 1, 149–194. [Google Scholar]
- Okamoto, N.L.; Fujimoto, S.; Kambara, Y.; Kawamura, M.; Chen, Z.M.T.; Matsunoshita, H.; Tanaka, K.; Inui, H.; George, E.P. Size Effect, Critical Resolved Shear Stress, Stacking Fault Energy, and Solid Solution Strengthening in the CrMnFeCoNi High-Entropy Alloy. Sci. Rep. 2016, 6, 35863. [Google Scholar] [CrossRef]
- Denteneer, P.J.H.; Soler, J.M. Energetics of Point and Planar Defects in Aluminium from First-Principles Calculations. Solid State Commun. 1991, 78, 857–861. [Google Scholar] [CrossRef]
- Denteneer, P.J.H.; Haeringen, W. van Stacking Fault Energies in Semiconductors from Firts-Principles Calculations. J. Phys. C Solid State Phys. 1987, 20, 883–887. [Google Scholar] [CrossRef]
- Ikeda, Y.; Grabowski, B.; Körmann, F. Ab Initio Phase Stabilities and Mechanical Properties of Multicomponent Alloys: A Comprehensive Review for High Entropy Alloys and Compositionally Complex Alloys. Mater. Charact. 2019, 147, 464–511. [Google Scholar] [CrossRef]
- Zaddach, A.J.; Niu, C.; Koch, C.C.; Irving, D.L. Mechanical Properties and Stacking Fault Energies of NiFeCrCoMn High-Entropy Alloy. J. Miner. Metal Mater. Soc. 2013, 65, 1780–1789. [Google Scholar] [CrossRef]
- Li, Z.; Körmann, F.; Grabowski, B.; Neugebauer, J.; Raabe, D. Ab Initio Assisted Design of Quinary Dual-Phase High-Entropy Alloys with Transformation-Induced Plasticity. Acta Mater. 2017, 136, 262–270. [Google Scholar] [CrossRef]
- Raabe, D.; Roters, F.; Neugebauer, J.; Gutierrez-Urrutia, I.; Hickel, T.; Bleck, W.; Schneider, J.M.; Wittig, J.E.; Mayer, J. Ab Initio-Guided Design of Twinning-Induced Plasticity Steels. MRS Bull. 2016, 41, 320–325. [Google Scholar] [CrossRef] [Green Version]
- Ma, D.; Grabowski, B.; Körmann, F.; Neugebauer, J.; Raabe, D. Ab Initio Thermodynamics of the CoCrFeMnNi High Entropy Alloy: Importance of Entropy Contributions beyond the Configurational One. Acta Mater. 2015, 100, 90–97. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y. Prediction of High-Entropy Stabilized Solid-Solution in Multi-Component Alloys. Mater. Chem. Phys. 2012, 132, 233–238. [Google Scholar] [CrossRef]
- Gao, M.C. Computational Thermodynamic and Kinetic Modeling of High-Entropy Alloys and Amorphous Alloys. JOM 2012, 64, 828–829. [Google Scholar] [CrossRef]
- Choi, W.; Jo, Y.H.; Sohn, S.S.; Lee, S.; Lee, B. Understanding the Physical Metallurgy of the CoCrFeMnNi High-Entropy Alloy: An Atomistic Simulation Study. NPJ Comput. Mater. 2018, 4, 1. [Google Scholar] [CrossRef] [Green Version]
- Yin, B.; Curtin, W.A. First-Principles-Based Prediction of Yield Strength in the RhIrPdPtNiCu High-Entropy Alloy. NPJ Comput. Mater. 2019, 5, 14. [Google Scholar] [CrossRef] [Green Version]
- Tamm, A.; Aabloo, A.; Klintenberg, M.; Stocks, M.; Caro, A. Atomic-Scale Properties of Ni-Based FCC Ternary, and Quaternary Alloys. Acta Mater. 2015, 99, 307–312. [Google Scholar] [CrossRef] [Green Version]
- Van De Walle, A. Methods for First-Principles Alloy Thermodynamics. JOM 2013, 65, 1523–1532. [Google Scholar] [CrossRef]
- Manu, B.R.; Gupta, A.; Jayatissa, A.H. Tribological Properties of 2D Materials and Composites—A Review of Recent Advances. Materials 2021, 14, 1630. [Google Scholar] [CrossRef]
- He, J.Y.; Wang, H.; Huang, H.L.; Xu, X.D.; Chen, M.W.; Wu, Y.; Liu, X.J.; Nieh, T.G.; An, K.; Lu, Z.P. A Precipitation-Hardened High-Entropy Alloy with Outstanding Tensile Properties. Acta Mater. 2016, 102, 187–196. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Wang, Z.M. (Eds.) High-Efficiency Solar Cells; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 9783319019871. [Google Scholar]
- Tian, F.; Varga, L.K.; Chen, N.; Shen, J.; Vitos, L. Empirical Design of Single-Phase High-Entropy Alloys with High Hardness. Intermetallics 2015, 58, 1–6. [Google Scholar] [CrossRef]
- Dong, Y.; Lu, Y.; Jiang, L.; Wang, T.; Li, T. Effects of Electro-Negativity on the Stability of Topologically Close-Packed Phase in High Entropy Alloys. Intermetallics 2014, 52, 105–109. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y.J.; Lin, J.P.; Chen, G.L.; Liaw, P.K. Solid-Solution Phase Formation Rules for Multi-Component Alloys. Adv. Eng. Mater. 2008, 10, 534–538. [Google Scholar] [CrossRef]
- Martin, P.; Madrid-Cortes, C.E.; Cáceres, C.; Araya, N.; Aguilar, C.; Cabrera, J.M. HEAPS: A User-Friendly Tool for the Design and Exploration of High-Entropy Alloys Based on Semi-Empirical Parameters. Comput. Phys. Commun. 2022, 278, 108398. [Google Scholar] [CrossRef]
- Hirth, J.P. Thermodynamics of Stacking Faults. Metall. Trans. 1970, 1, 2367–2374. [Google Scholar] [CrossRef]
- Allain, S.; Chateau, J.P.; Bouaziz, O.; Migot, S.; Guelton, N. Correlations between the Calculated Stacking Fault Energy and the Plasticity Mechanisms in Fe–Mn–C Alloys. Mater. Sci. Eng. A 2004, 387–389, 158–162. [Google Scholar] [CrossRef]
- Nakano, J.; Jacques, P.J. Effects of the Thermodynamic Parameters of the Hcp Phase on the Stacking Fault Energy Calculations in the Fe-Mn and Fe-Mn-C Systems. CALPHAD Comput. Coupling Phase Diagr. Thermochem. 2010, 34, 167–175. [Google Scholar] [CrossRef]
- Zunger, A.; Wei, S.H.; Ferreira, L.G.; Bernard, J.E. Special Quasirandom Structures. Phys. Rev. Lett. 1990, 65, 353–356. [Google Scholar] [CrossRef] [Green Version]
- Van De Walle, A.; Tiwary, P.; De Jong, M.; Olmsted, D.L.; Asta, M.; Dick, A.; Shin, D.; Wang, Y.; Chen, L.Q.; Liu, Z.K. Efficient Stochastic Generation of Special Quasirandom Structures. Calphad 2013, 42, 13–18. [Google Scholar] [CrossRef]
- Tasndi, F.; Wang, F.; Odén, M.; Abrikosov, I.A. Special Quasirandom Structure Method in Application for Advanced Properties of Alloys: A study on Ti0.5Al0.5N and TiN/Ti0.5Al0.5N multilayer. Comput. Mater. Sci. 2015, 103, 194–199. [Google Scholar] [CrossRef]
- De Jong, M.; Qi, L.; Olmsted, D.L.; Van De Walle, A.; Asta, M. Calculations of Planar Defect Energies in Substitutional Alloys Using the Special-Quasirandom-Structure Approach. Phys. Rev. B Condens. Matter Mater. Phys. 2016, 93, 094101. [Google Scholar] [CrossRef] [Green Version]
- Jiang, C.; Wolverton, C.; Sofo, J.; Chen, L.Q.; Liu, Z.K. First-Principles Study of Binary Bcc Alloys Using Special Quasirandom Structures. Phys. Rev. B Condens. Matter Mater. Phys. 2004, 69, 214202. [Google Scholar] [CrossRef] [Green Version]
- Shin, D.; Van De Walle, A.; Wang, Y.; Liu, Z.K. First-Principles Study of Ternary Fcc Solution Phases from Special Quasirandom Structures. Phys. Rev. B Condens. Matter Mater. Phys. 2007, 76, 144204. [Google Scholar] [CrossRef] [Green Version]
- Van de Walle, A.; Asta, M.; Ceder, G. The Alloy Theoretic Automated Toolkit: A User Guide. Calphad 2002, 26, 539–553. [Google Scholar] [CrossRef] [Green Version]
- Takeuchi, A.; Inoue, A. Classification of Bulk Metallic Glasses by Atomic Size Difference, Heat of Mixing and Period of Constituent Elements and Its Application to Characterization of the Main Alloying Element. Mater. Trans. 2005, 46, 2817–2829. [Google Scholar] [CrossRef] [Green Version]
- Kresse, G.; Furthmüller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Norm-Conserving and Ultrasoft Pseudopotentials for First-Row and Transition Elements. J. Phys. Condens. Matter 1994, 6, 8245–8257. [Google Scholar] [CrossRef]
- Adamo, C.; Cossi, M.; Barone, V. An Accurate Density Functional Method for the Study of Magnetic Properties: The PBE0 Model. J. Mol. Struct. Theochem 1999, 493, 145–157. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew–Burke–Ernzerhof Exchange-Correlation Functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef] [Green Version]
- Csonka, G.I.; Perdew, J.P.; Ruzsinszky, A.; Philipsen, P.H.T.; Lebègue, S.; Paier, J.; Vydrov, O.A.; Ángyán, J.G. Assessing the Performance of Recent Density Functionals for Bulk Solids. Phys. Rev. B Condens. Matter Mater. Phys. 2009, 79, 155107. [Google Scholar] [CrossRef]
- Torres-Mejia, L.G.; Paredes-Gil, K.; Parra-Vargas, C.A.; Lentz, J.; Weber, S.; Mujica.-Roncery, L. Effect of Deformation on Magnetic Properties of C+N Austenitic Steel. Metall. Mater. Trans. A, 2023; submitted. [Google Scholar]
- Zhao, S.; Stocks, G.M.; Zhang, Y. Stacking Fault Energies of Face-Centered Cubic Concentrated Solid Solution Alloys. Acta Mater. 2017, 134, 334–345. [Google Scholar] [CrossRef]
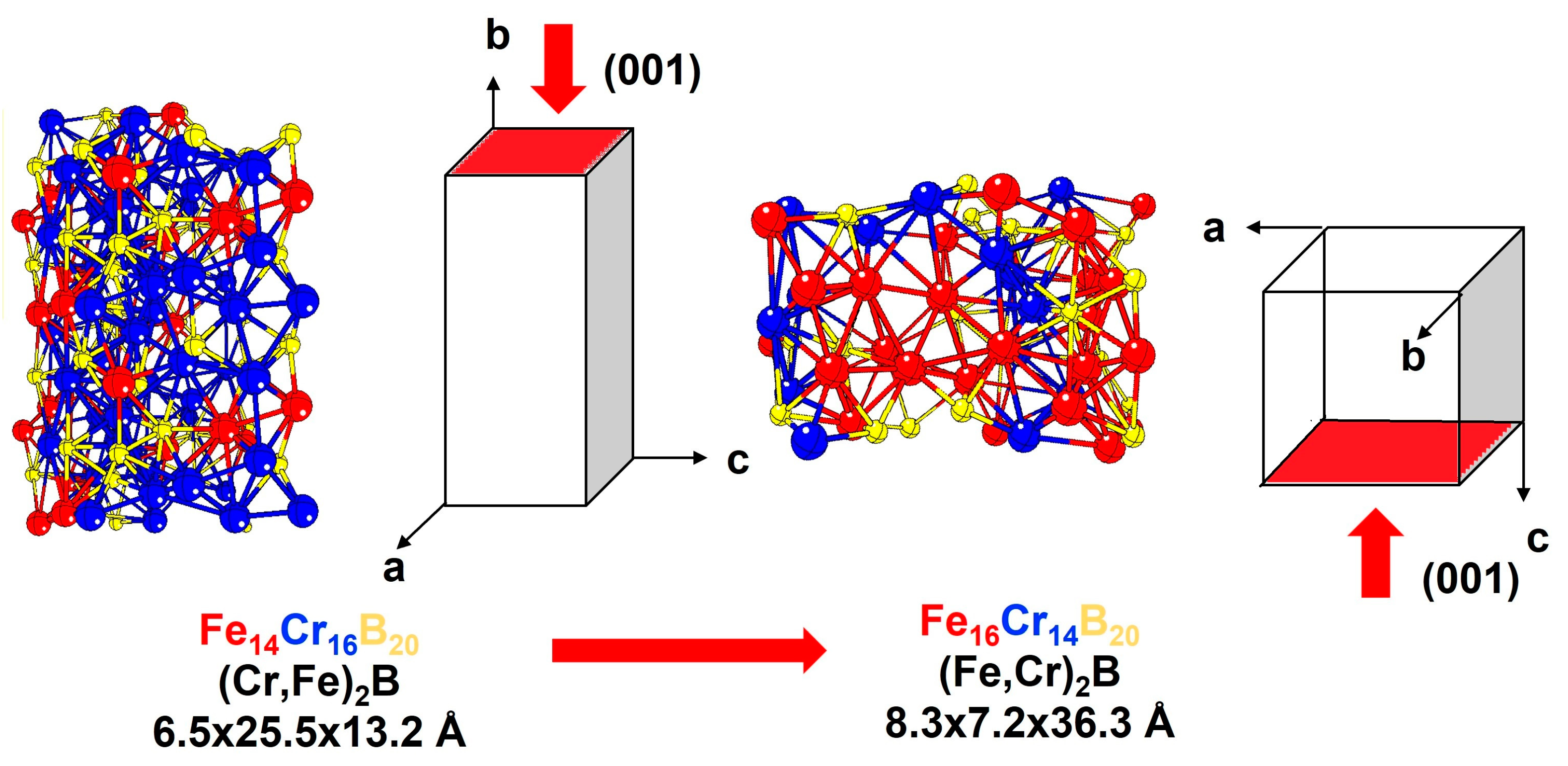
- Goldfarb, I.; Kaplan, W.D.; Ariely, S.; Bamberger, M. Fault-Induced Polytypism in (Cr, Fe)2B. Philos. Mag. A Phys. Condens. Matter Struct. Defects Mech. Prop. 1995, 72, 963–979. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, G.J.; Dai, P.Q. Evolution of the Microstructure and Properties of Laser-Clad FeCrNiCoBx High-Entropy Alloy Coatings. Mater. Sci. Technol. 2016, 32, 1666–1672. [Google Scholar] [CrossRef]
- Wu, X.; Li, Z.; Rao, Z.; Ikeda, Y.; Dutta, B.; Körmann, F.; Neugebauer, J.; Raabe, D. Role of Magnetic Ordering for the Design of Quinary TWIP-TRIP High Entropy Alloys. Phys. Rev. Mater. 2020, 4, 033601. [Google Scholar] [CrossRef] [Green Version]
- Egilmez, M.; Abuzaid, W. Magnetic, Electrical and Mechanical Properties of Fe40Mn40Co10Cr10 High Entropy Alloy. Sci. Rep. 2021, 11, 8048. [Google Scholar] [CrossRef]
- Niu, C.; Zaddach, A.J.; Koch, C.C.; Irving, D.L. First Principles Exploration of Near-Equiatomic NiFeCrCo High Entropy Alloys. J. Alloys Compd. 2016, 672, 510–520. [Google Scholar] [CrossRef] [Green Version]
- Jin, H.W.; Park, C.G.; Kim, M.C. In Situ TEM Heating Studies on the Phase Transformation of Metastable Phases in Fe-Cr-B Alloy Spray Coatings. Mater. Sci. Eng. A 2001, 304, 321–326. [Google Scholar] [CrossRef]
- Sorour, A.A.; Chromik, R.R.; Gauvin, R.; Jung, I.H.; Brochu, M. Understanding the Solidification and Microstructure Evolution during CSC-MIG Welding of Fe-Cr-B-Based Alloy. Mater. Charact. 2013, 86, 127–138. [Google Scholar] [CrossRef]

| Criteria | Parameters | Range |
|---|---|---|
| MC1 | ||
| MC2 | ||
| MC7 | ||
| ≤ 6.6% | ||
| ≤ 3.3% |
| Nomenclature | Exact Composition (at.%) | 60 Atoms’ FCC and HCP Supercell Composition |
|---|---|---|
| Alloy-B0 | Fe50Mn30Co10Cr10 | Fe30Mn18Co6Cr6 |
| Alloy-B5 | Fe48Mn27Co10Cr10B5 | Fe30Mn18Co6Cr6B |
| Alloy-B7 | Fe48Mn27Co9Cr9B7 | Fe30Mn18Co6Cr6B2 |
| Alloy-B10 | Fe45Mn27Co9Cr9B10 | Fe27Mn15Co9Cr9B |
| Alloy-B15 | Fe42Mn25Co9Cr9B15 | Fe27Mn15Co9Cr9B2 |
| Nomenclature | ∆Smix (J/mol*K) | ∆Hmix (kJ/mol) | VEC | ∆XP | δr (%) | Ω | Tm (K) |
|---|---|---|---|---|---|---|---|
| Alloy-B0 | 9.71 | −0.92 | 7.60 | 0.132 | 3.83 | 18.54 | 1756 |
| Alloy-B5 | 10.94 | −6.19 | 7.38 | 0.143 | 8.75 | 3.17 | 1792 |
| Alloy-B7 | 11.02 | −8.07 | 7.29 | 0.148 | 10.06 | 2.46 | 1799 |
| Alloy-B10 | 11.45 | −10.86 | 7.14 | 0.155 | 11.73 | 1.91 | 1815 |
| Alloy-B15 | 11.88 | −15.02 | 6.91 | 0.163 | 13.96 | 1.46 | 1848 |
| Nomenclature | MC1 (∆Hmix-δr) | MC2 (Ω-δr) | MC7 (T/Tm-δr-∆Hmix) | IMF1 (∆XP) |
|---|---|---|---|---|
| Alloy-B0 | SS | SS | IM(0.5 < T/Tm < 0.9) | Uncertain |
| Alloy-B5 | IM/BMG | IM | IM(0.5 < T/Tm < 0.9) | TCP phase |
| Alloy-B7 | IM/BMG | IM | IM(0.5 < T/Tm < 0.9) | TCP phase |
| Alloy-B10 | IM/BMG | IM | IM(0.5 < T/Tm < 0.9) | TCP phase |
| Alloy-B15 | IM/BMG | IM | IM(0.5 < T/Tm < 0.9) | TCP phase |
| Alloys | (J/mol) | (J/mol) | (J/mol) | (Å) | (mol/m2) | SFE (mJ/m2) |
|---|---|---|---|---|---|---|
| Alloy-B0 | −7327.51 | −7088.64 | 239 | 3.6 | 2.96 × 10−5 | 24.19 |
| Alloy-B5 | −15,300.30 | −14,855.36 | 445 | 3.6 | 2.96 × 10−5 | 36.34 |
| Alloy-B7 | −17,181.93 | −16,360.73 | 821 | 3.6 | 2.96 × 10−5 | 56.61 |
| Alloy-B10 | −17,059.02 | −16,206.17 | 853 | 3.6 | 2.96 × 10−5 | 60.48 |
| Alloy-B15 | −16,824.66 | −15,911.14 | 913 | 3.6 | 2.96 × 10−5 | 64.08 |
| Phase | Alloys | RMSD All Atoms | RMSD All Cr | RMSD All Mn | RMSD All Fe | RMSD All Co |
|---|---|---|---|---|---|---|
| FCC | alloy-B5 vs. alloy-B7 | 2.824 | 4.758 | 2.705 | 2.163 | 3.505 |
| HCP | alloy-B5 vs. alloy-B7 | 2.209 | 0.671 | 3.041 | 2.007 | 0.666 |
| FCC | alloy-B10 vs. alloy-B15 | 2.247 | 0.546 | 2.205 | 1.726 | 4.039 |
| HCP | alloy-B10 vs. alloy-B15 | 1.656 | 0.441 | 0.333 | 2.437 | 0.310 |
| Alloys | E Total FCC (eV) | E Total HCP (eV) | EAFM (eV) | EFM (eV) | EAFM/FM (eV) |
|---|---|---|---|---|---|
| Alloy-B0 | −487.98 | −502.23 | −494.87 | −495.91 | −494.64 |
| Alloy-B5 | −500.22 | −505.97 | −506.97 | −507.22 | −506.85 |
| Alloy-B7 | −514.69 | −521.81 | −513.21 | −513.84 | −513.08 |
| Alloy-B10 | −506.49 | −504.27 | −506.76 | −506.85 | −506.53 |
| Alloy-B15 | −513.18 | −511.34 | −515.10 | −515.23 | −514.99 |
| Alloys | ∆Hf (kJ/mol), FCC | ∆Hf (kJ/mol), HCP |
|---|---|---|
| Alloy-B0 | −14.09 | −14.19 |
| Alloy-B5 | −14.08 | −14.24 |
| Alloy-B7 | −14.44 | −14.33 |
| Alloy-B10 | −14.26 | −14.18 |
| Alloy-B15 | −14.39 | −14.34 |
| Alloys | ΔEHCP-FCC (eV) | SFEANNI (mJ/m2) | SFEANNI+M2B (mJ/m2) |
|---|---|---|---|
| Alloy-B0 | 6.66 | 20.74 | - |
| Alloy-B5 | 5.75 | 18.34 | - |
| Alloy-B7 | 7.11 | 23.00 | - |
| Alloy-B10 | 2.22 | 6.18 | 52.55 |
| Alloy-B15 | 1.84 | 5.07 | 51.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vargas-Osorio, R.; Torres-Mejia, L.G.; Mujica-Roncery, L.; Aguilar-Hurtado, J.Y.; Paredes-Gil, K. Thermodynamic and Ab Initio Design of Multicomponent Alloys Based on (Fe50Mn30Co10Cr10)-xBx (x = 0, 5, 7, 10, and 15 at.%). Materials 2023, 16, 5579. https://doi.org/10.3390/ma16165579
Vargas-Osorio R, Torres-Mejia LG, Mujica-Roncery L, Aguilar-Hurtado JY, Paredes-Gil K. Thermodynamic and Ab Initio Design of Multicomponent Alloys Based on (Fe50Mn30Co10Cr10)-xBx (x = 0, 5, 7, 10, and 15 at.%). Materials. 2023; 16(16):5579. https://doi.org/10.3390/ma16165579
Chicago/Turabian StyleVargas-Osorio, Rodrigo, Laura Gabriela Torres-Mejia, Lais Mujica-Roncery, Jose Y. Aguilar-Hurtado, and Katherine Paredes-Gil. 2023. "Thermodynamic and Ab Initio Design of Multicomponent Alloys Based on (Fe50Mn30Co10Cr10)-xBx (x = 0, 5, 7, 10, and 15 at.%)" Materials 16, no. 16: 5579. https://doi.org/10.3390/ma16165579
APA StyleVargas-Osorio, R., Torres-Mejia, L. G., Mujica-Roncery, L., Aguilar-Hurtado, J. Y., & Paredes-Gil, K. (2023). Thermodynamic and Ab Initio Design of Multicomponent Alloys Based on (Fe50Mn30Co10Cr10)-xBx (x = 0, 5, 7, 10, and 15 at.%). Materials, 16(16), 5579. https://doi.org/10.3390/ma16165579







