The Influence of Ni Addition in the Mechanism of CO2 Electroreduction on Cu Crystals—Mechanistic Insight from DFT Simulations
Abstract
1. Introduction
2. Aim and Scope
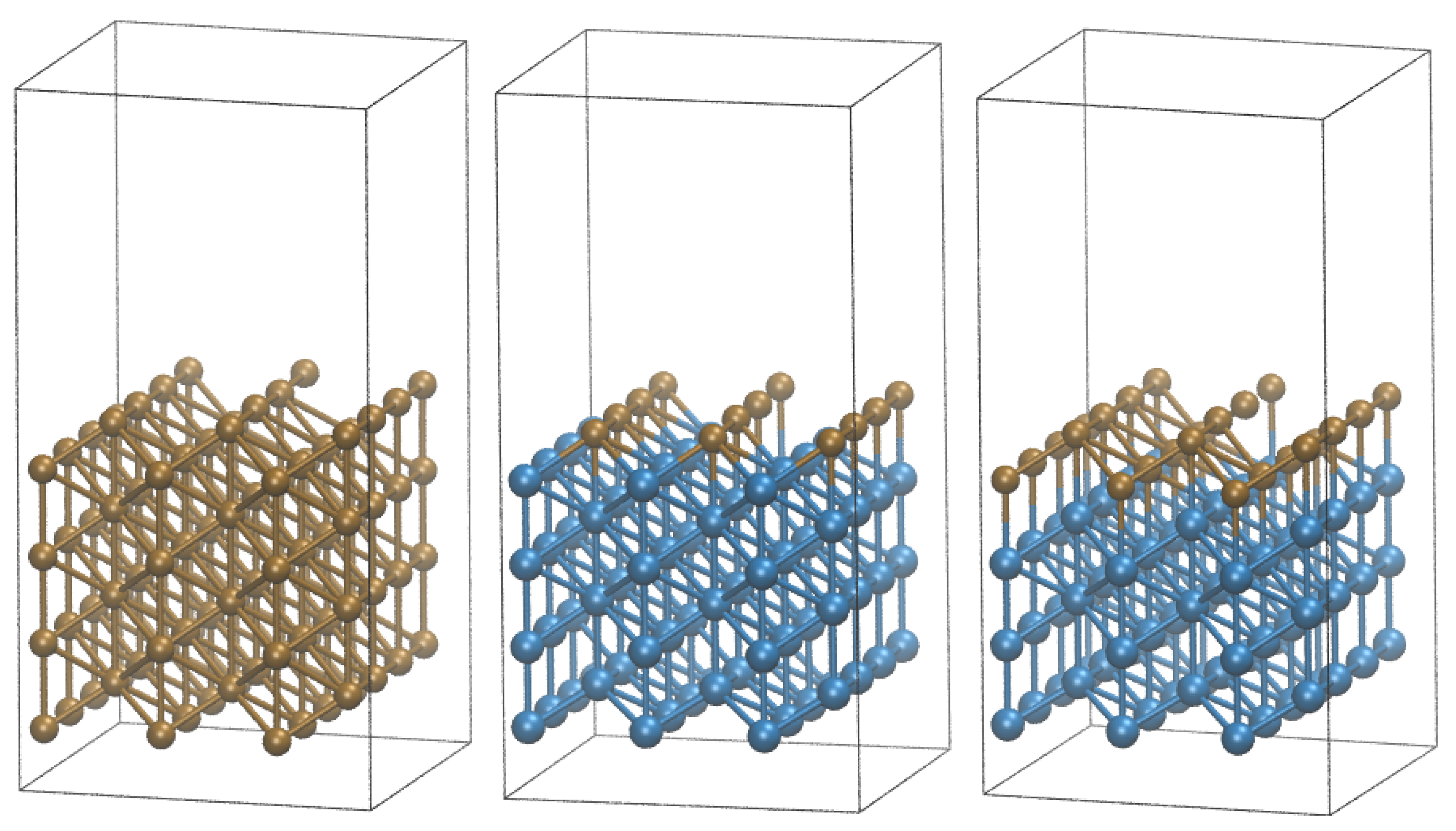
3. Model and Computational Details
4. Results
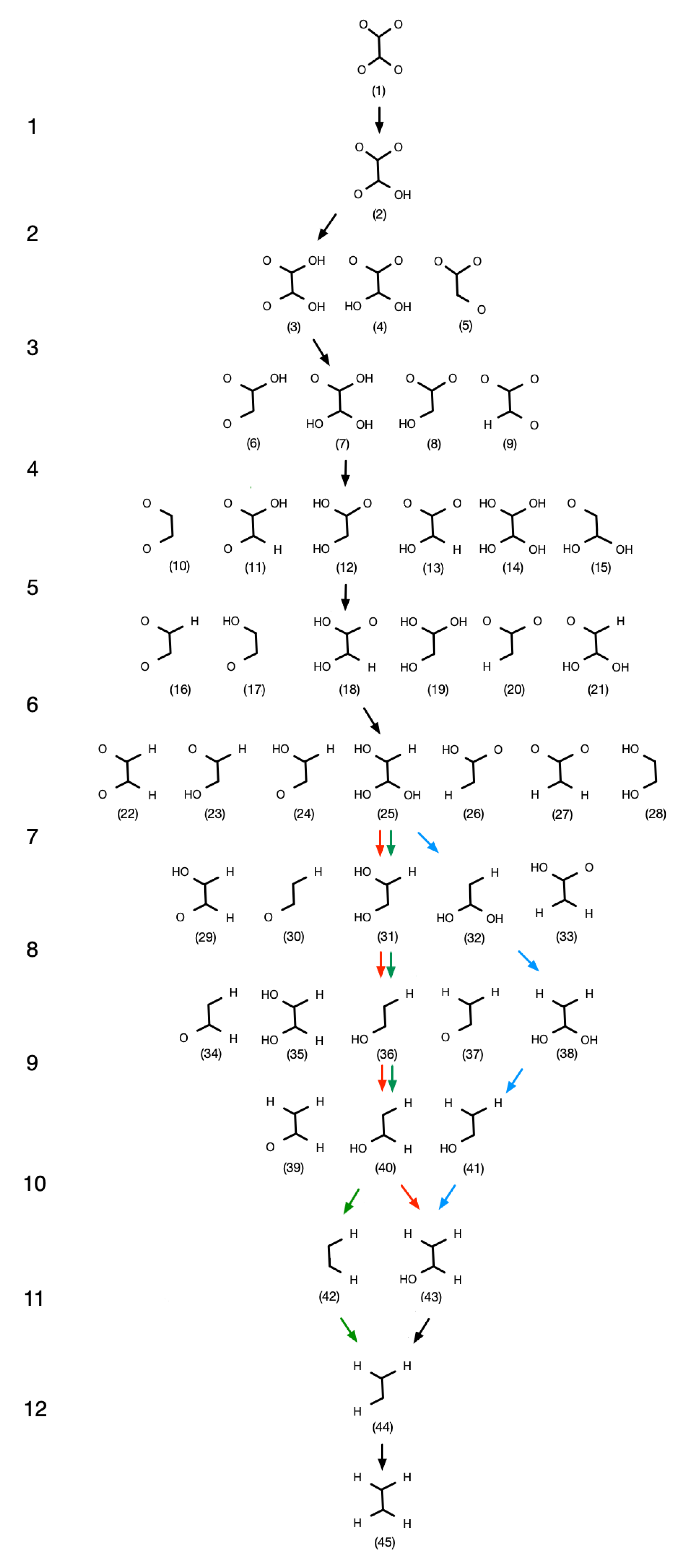
4.1. Pathways
4.2. Pure Cu Catalyst
4.3. Cu-Ni Bimetallic Surfaces
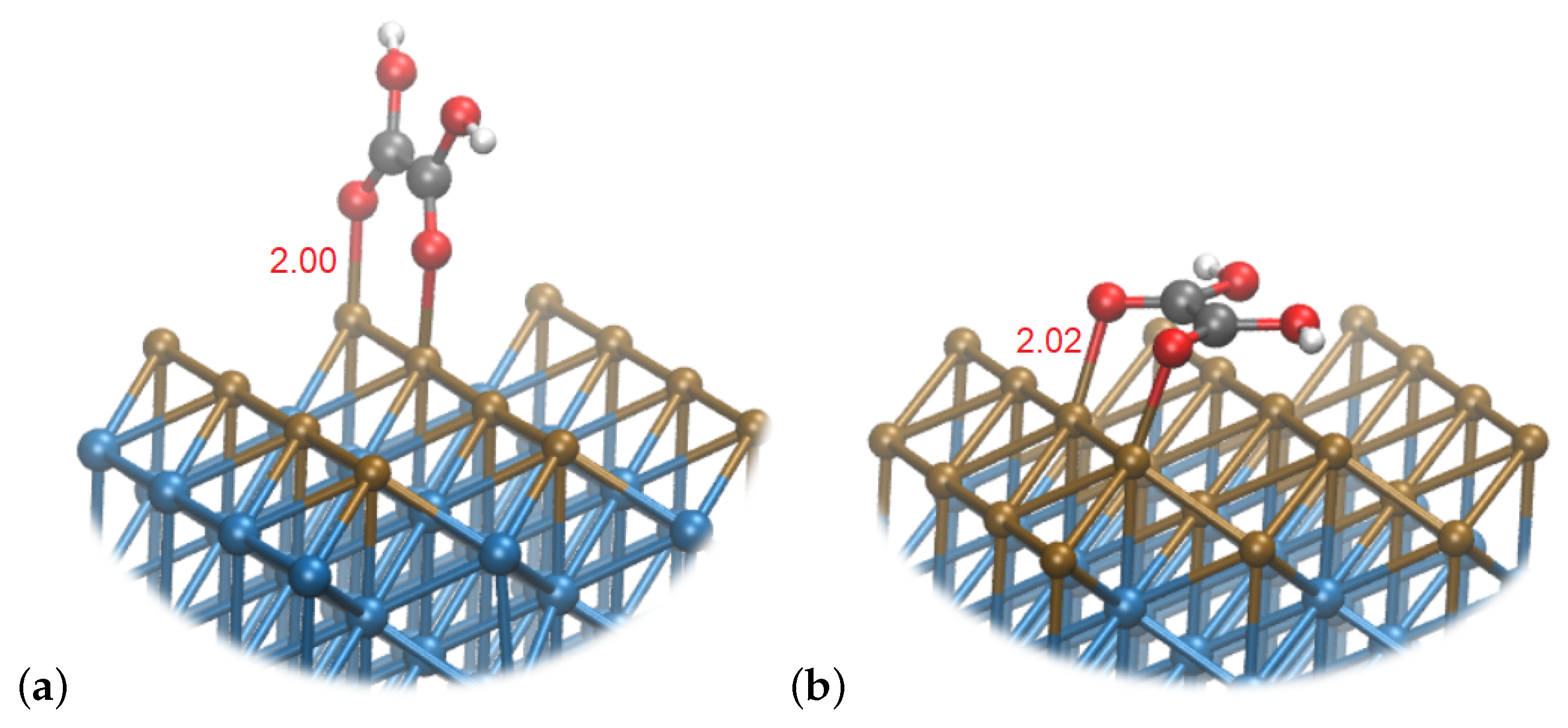
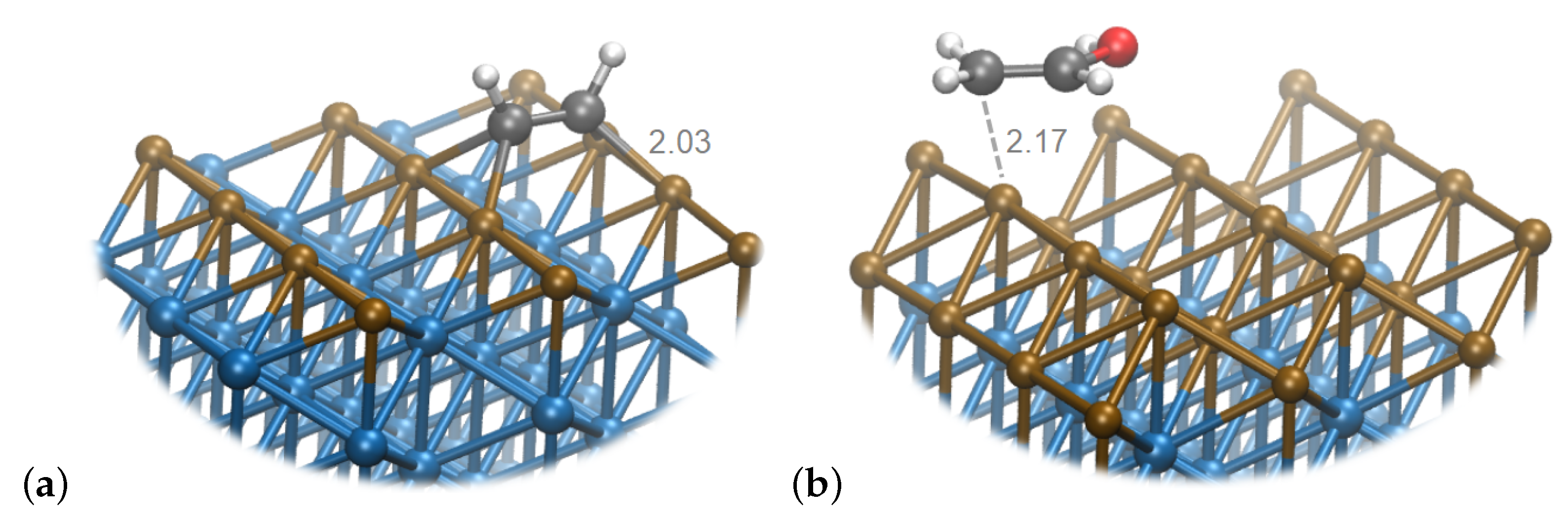
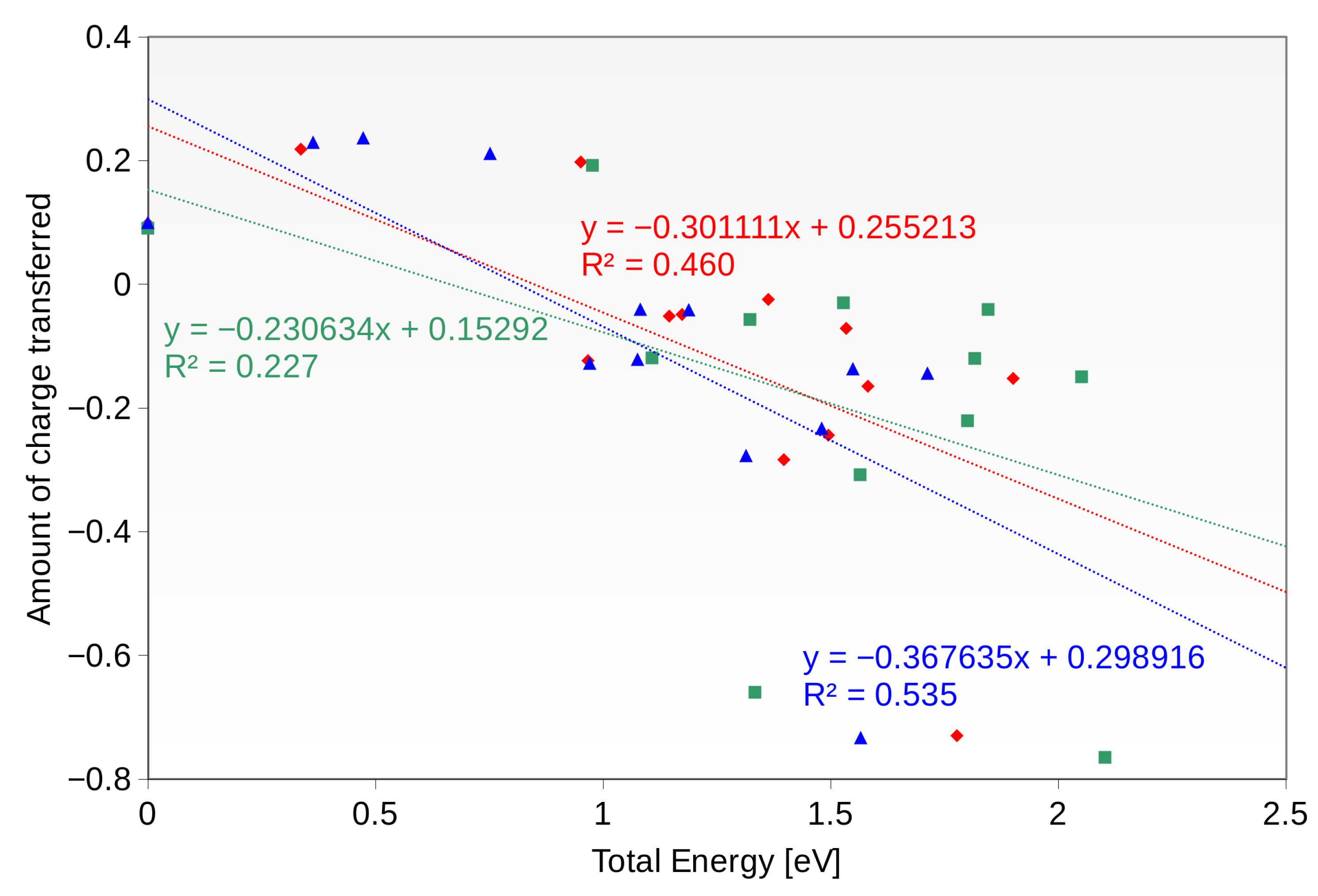
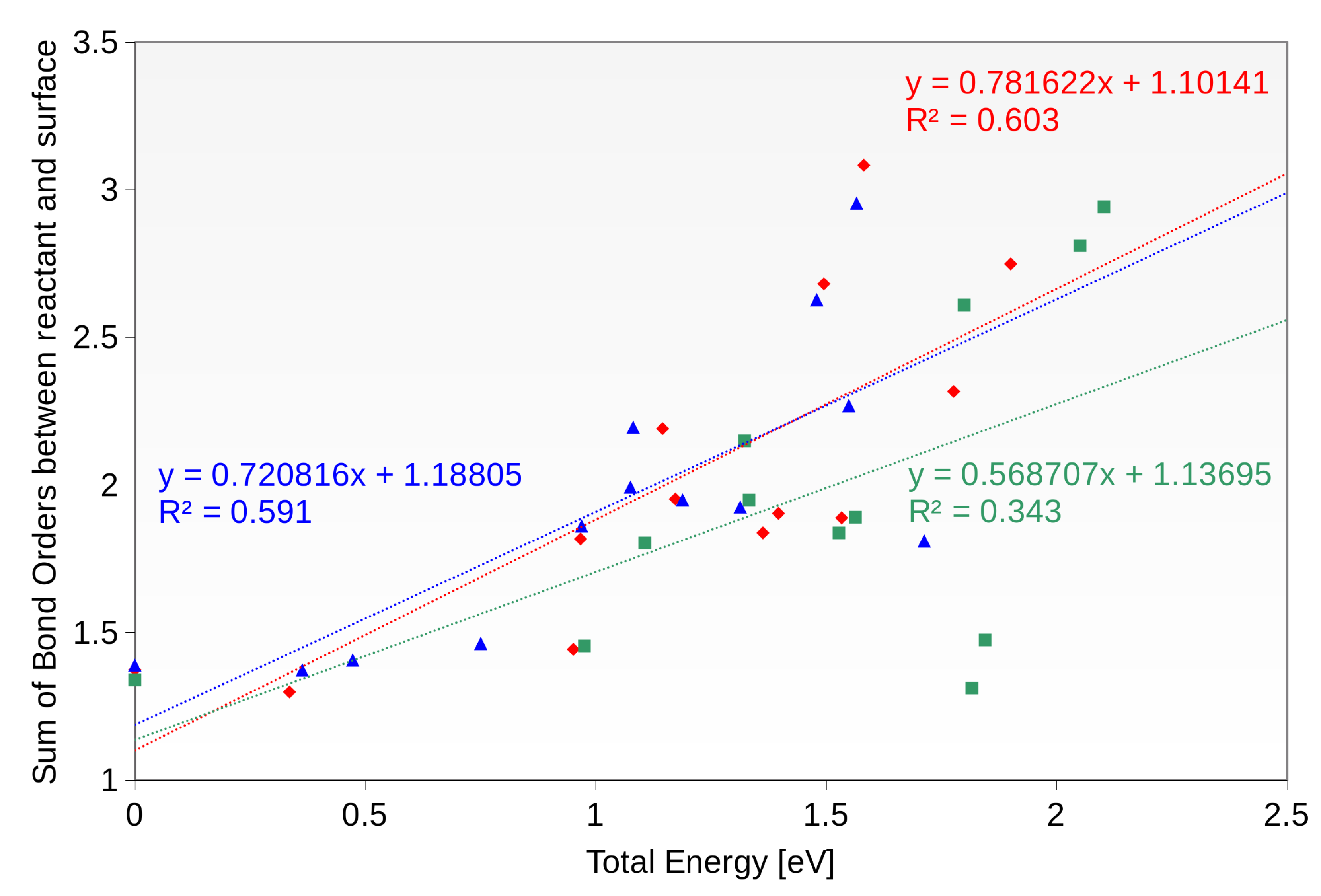
5. Interactions with the Surface
6. Discussion
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maginn, E.J. What to Do with CO2. J. Phys. Chem. Lett. 2010, 1, 3478–3479. [Google Scholar] [CrossRef]
- Zhu, Q. Developments on CO2-utilization technologies. Clean Energy 2019, 3, 85–100. [Google Scholar] [CrossRef]
- Alper, E.; Yuksel Orhan, O. CO2 utilization: Developments in conversion processes. Petroleum 2017, 3, 109–126. [Google Scholar] [CrossRef]
- Li, Y.; Hwa Chan, S.; Sun, Q. Heterogeneous catalytic conversion of CO2: A comprehensive theoretical review. Nanoscale 2015, 7, 8663–8683. [Google Scholar] [CrossRef]
- Parigi, D.; Giglio, E.; Soto, A.; Santarelli, M. Power-to-fuels through carbon dioxide Re-Utilization and high-temperature electrolysis: A technical and economical comparison between synthetic methanol and methane. J. Clean. Prod. 2019, 226, 679–691. [Google Scholar] [CrossRef]
- Palys, M.J.; Daoutidis, P. Power-to-X: A review and perspective. Comput. Chem. Eng. 2022, 165, 107948. [Google Scholar] [CrossRef]
- Ran, J.; Jaroniec, M.; Qiao, S.Z. Cocatalysts in Semiconductor-based Photocatalytic CO2 Reduction: Achievements, Challenges, and Opportunities. Adv. Mater. 2018, 30, 1704649. [Google Scholar] [CrossRef] [PubMed]
- Owusu, P.A.; Asumadu-Sarkodie, S. A review of renewable energy sources, sustainability issues and climate change mitigation. Cogent Eng. 2016, 3, 1167990. [Google Scholar] [CrossRef]
- Hori, Y. Electrochemical CO2 Reduction on Metal Electrodes. In Modern Aspects of Electrochemistry; Springer: New York, NY, USA, 2008; pp. 89–189. [Google Scholar] [CrossRef]
- Nitopi, S.; Bertheussen, E.; Scott, S.B.; Liu, X.; Engstfeld, A.K.; Horch, S.; Seger, B.; Stephens, I.E.; Chan, K.; Hahn, C.; et al. Progress and Perspectives of Electrochemical CO2 Reduction on Copper in Aqueous Electrolyte. Chem. Rev. 2019, 119, 7610–7672. [Google Scholar] [CrossRef]
- Bagger, A.; Ju, W.; Varela, A.S.; Strasser, P.; Rossmeisl, J. Electrochemical CO2 Reduction: A Classification Problem. ChemPhysChem 2017, 18, 3266–3273. [Google Scholar] [CrossRef]
- Sharifian, R.; Wagterveld, R.M.; Digdaya, I.A.; Xiang, C.; Vermaas, D.A. Electrochemical carbon dioxide capture to close the carbon cycle. Energy Environ. Sci. 2021, 14, 781–814. [Google Scholar] [CrossRef]
- Tan, X.; Yu, C.; Ren, Y.; Cui, S.; Li, W.; Qiu, J. Recent advances in innovative strategies for the CO2 electroreduction reaction. Energy Environ. Sci. 2021, 14, 765–780. [Google Scholar] [CrossRef]
- Zhang, S.; Fan, Q.; Xia, R.; Meyer, T.J. CO2 Reduction: From Homogeneous to Heterogeneous Electrocatalysis. Accounts Chem. Res. 2020, 53, 255–264. [Google Scholar] [CrossRef] [PubMed]
- Bu, Y.F.; Zhao, M.; Zhang, G.X.; Zhang, X.; Gao, W.; Jiang, Q. Electroreduction of CO2 on Cu Clusters: The Effects of Size, Symmetry, and Temperature. ChemElectroChem 2019, 6, 1831–1837. [Google Scholar] [CrossRef]
- Dong, H.; Li, Y.; Jiang, D.E. First-Principles Insight into Electrocatalytic Reduction of CO2 to CH4 on a Copper Nanoparticle. J. Phys. Chem. C 2018, 122, 11392–11398. [Google Scholar] [CrossRef]
- Xu, H.; Rebollar, D.; He, H.; Chong, L.; Liu, Y.; Liu, C.; Sun, C.J.; Li, T.; Muntean, J.V.; Winans, R.E.; et al. Highly selective electrocatalytic CO2 reduction to ethanol by metallic clusters dynamically formed from atomically dispersed copper. Nat. Energy 2020, 5, 623–632. [Google Scholar] [CrossRef]
- He, J.; Johnson, N.J.J.; Huang, A.; Berlinguette, C.P. Electrocatalytic Alloys for CO2 Reduction. ChemSusChem 2018, 11, 48–57. [Google Scholar] [CrossRef]
- Kim, D.; Resasco, J.; Yu, Y.; Asiri, A.M.; Yang, P. Synergistic geometric and electronic effects for electrochemical reduction of carbon dioxide using gold–copper bimetallic nanoparticles. Nat. Commun. 2014, 5, 3066. [Google Scholar] [CrossRef]
- Li, M.; Wang, J.; Li, P.; Chang, K.; Li, C.; Wang, T.; Jiang, B.; Zhang, H.; Liu, H.; Yamauchi, Y.; et al. Mesoporous palladium–copper bimetallic electrodes for selective electrocatalytic reduction of aqueous CO2 to CO. J. Mater. Chem. A 2016, 4, 4776–4782. [Google Scholar] [CrossRef]
- Minati, L.; Speranza, G.; Calliari, L.; Micheli, V.; Baranov, A.; Fanchenko, S. The Influence of Metal Nanoparticle Size Distribution in Photoelectron Spectroscopy. J. Phys. Chem. A 2008, 112, 7856–7861. [Google Scholar] [CrossRef]
- Siegel, J.; Kvítek, O.; Ulbrich, P.; Kolská, Z.; Slepička, P.; Švorčík, V. Progressive approach for metal nanoparticle synthesis. Mater. Lett. 2012, 89, 47–50. [Google Scholar] [CrossRef]
- Sharma, G.; Kumar, A.; Sharma, S.; Naushad, M.; Prakash Dwivedi, R.; ALOthman, Z.A.; Mola, G.T. Novel development of nanoparticles to bimetallic nanoparticles and their composites: A review. J. King Saud Univ.-Sci. 2019, 31, 257–269. [Google Scholar] [CrossRef]
- Kuhl, K.P.; Cave, E.R.; Abram, D.N.; Jaramillo, T.F. New insights into the electrochemical reduction of carbon dioxide on metallic copper surfaces. Energy Environ. Sci. 2012, 5, 7050–7059. [Google Scholar] [CrossRef]
- Klier, K. Methanol Synthesis. In Advances in Catalysis; Elsevier: Amsterdam, The Netherlands, 1982; pp. 243–313. [Google Scholar] [CrossRef]
- Peterson, A.A.; Abild-Pedersen, F.; Studt, F.; Rossmeisl, J.; Nørskov, J.K. How copper catalyzes the electroreduction of carbon dioxide into hydrocarbon fuels. Energy Environ. Sci. 2010, 3, 1311–1315. [Google Scholar] [CrossRef]
- Fan, L.; Xia, C.; Yang, F.; Wang, J.; Wang, H.; Lu, Y. Strategies in catalysts and electrolyzer design for electrochemical CO2 reduction toward C2 products. Sci. Adv. 2020, 6, eaay3111. [Google Scholar] [CrossRef]
- Zhou, Y.; Yeo, B.S. Formation of C–C bonds during electrocatalytic CO2 reduction on non-copper electrodes. J. Mater. Chem. A 2020, 8, 23162–23186. [Google Scholar] [CrossRef]
- Zhu, W.; Tackett, B.M.; Chen, J.G.; Jiao, F. Bimetallic Electrocatalysts for CO2 Reduction. Top. Curr. Chem. 2018, 376. [Google Scholar] [CrossRef]
- Ruiz-López, E.; Gandara-Loe, J.; Baena-Moreno, F.; Reina, T.R.; Odriozola, J.A. Electrocatalytic CO2 conversion to C2 products: Catalysts design, market perspectives and techno-economic aspects. Renew. Sustain. Energy Rev. 2022, 161, 112329. [Google Scholar] [CrossRef]
- Calle-Vallejo, F.; Koper, M.T.M. Theoretical Considerations on the Electroreduction of CO to C2 Species on Cu(100) Electrodes. Angew. Chem. Int. Ed. 2013, 52, 7282–7285. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B-Condens. Matter Mater. Phys. 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B-Condens. Matter Mater. Phys. 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865, Erratum in Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- VTSTTools 3.1; Henkelman Group, University of Texas: Austin, TX, USA; Available online: http://theory.cm.utexas.edu (accessed on 19 June 2023).
- Mathew, K.; Sundararaman, R.; Letchworth-Weaver, K.; Arias, T.A.; Hennig, R.G. Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways. J. Chem. Phys. 2014, 140, 084106. [Google Scholar] [CrossRef]
- Manz, T.A.; Limas, N.G. Introducing DDEC6 atomic population analysis: Part 1. Charge partitioning theory and methodology. RSC Adv. 2016, 6, 47771–47801. [Google Scholar] [CrossRef]
- Limas, N.G.; Manz, T.A. Introducing DDEC6 atomic population analysis: Part 2. Computed results for a wide range of periodic and nonperiodic materials. RSC Adv. 2016, 6, 45727–45747. [Google Scholar] [CrossRef]
- Manz, T.A. Introducing DDEC6 atomic population analysis: Part 3. Comprehensive method to compute bond orders. RSC Adv. 2017, 7, 45552–45581. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dziadyk-Stopyra, E.; Tranca, I.; Smykowski, D.; Szyja, B.M. The Influence of Ni Addition in the Mechanism of CO2 Electroreduction on Cu Crystals—Mechanistic Insight from DFT Simulations. Materials 2023, 16, 5138. https://doi.org/10.3390/ma16145138
Dziadyk-Stopyra E, Tranca I, Smykowski D, Szyja BM. The Influence of Ni Addition in the Mechanism of CO2 Electroreduction on Cu Crystals—Mechanistic Insight from DFT Simulations. Materials. 2023; 16(14):5138. https://doi.org/10.3390/ma16145138
Chicago/Turabian StyleDziadyk-Stopyra, Elżbieta, Ionut Tranca, Daniel Smykowski, and Bartłomiej M. Szyja. 2023. "The Influence of Ni Addition in the Mechanism of CO2 Electroreduction on Cu Crystals—Mechanistic Insight from DFT Simulations" Materials 16, no. 14: 5138. https://doi.org/10.3390/ma16145138
APA StyleDziadyk-Stopyra, E., Tranca, I., Smykowski, D., & Szyja, B. M. (2023). The Influence of Ni Addition in the Mechanism of CO2 Electroreduction on Cu Crystals—Mechanistic Insight from DFT Simulations. Materials, 16(14), 5138. https://doi.org/10.3390/ma16145138







