Simplified Calculation Model and Experimental Validation of the Force Transfer Ratio of Steel–Concrete Joint of Hybrid Box Girder
Abstract
1. Introduction
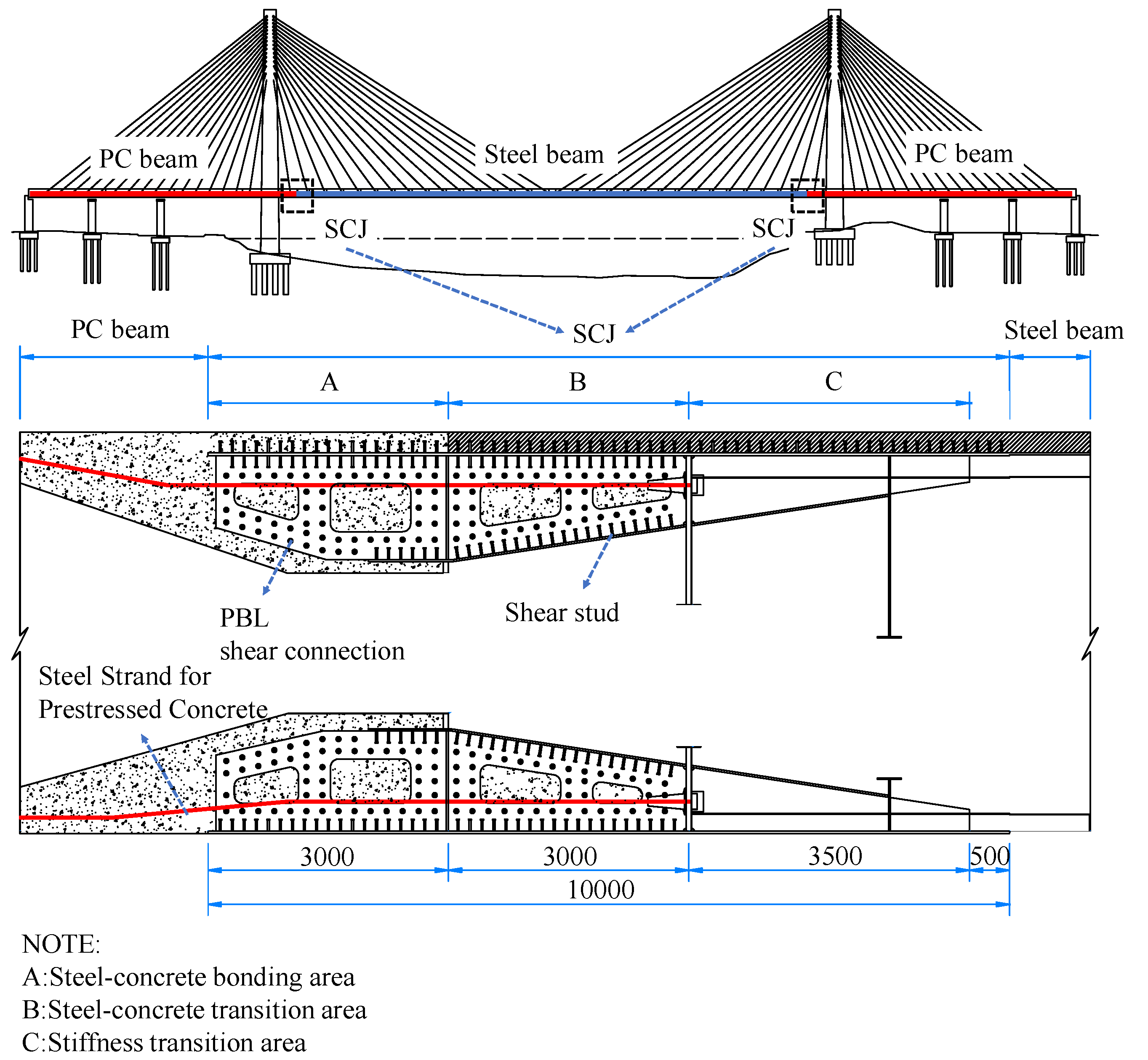
2. Experimental Program
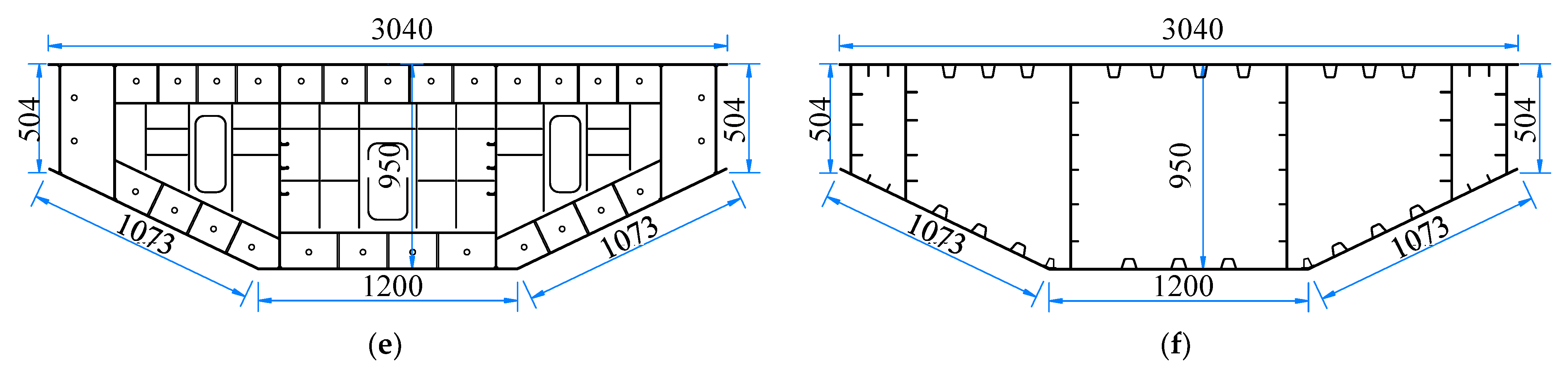
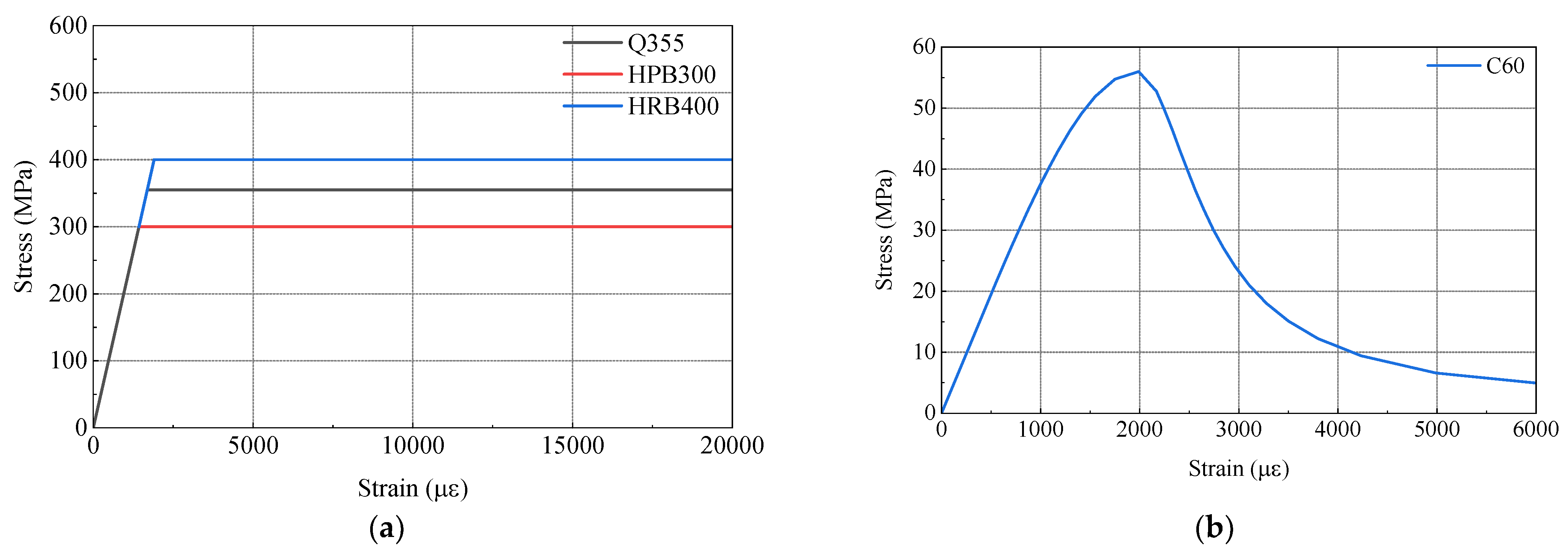
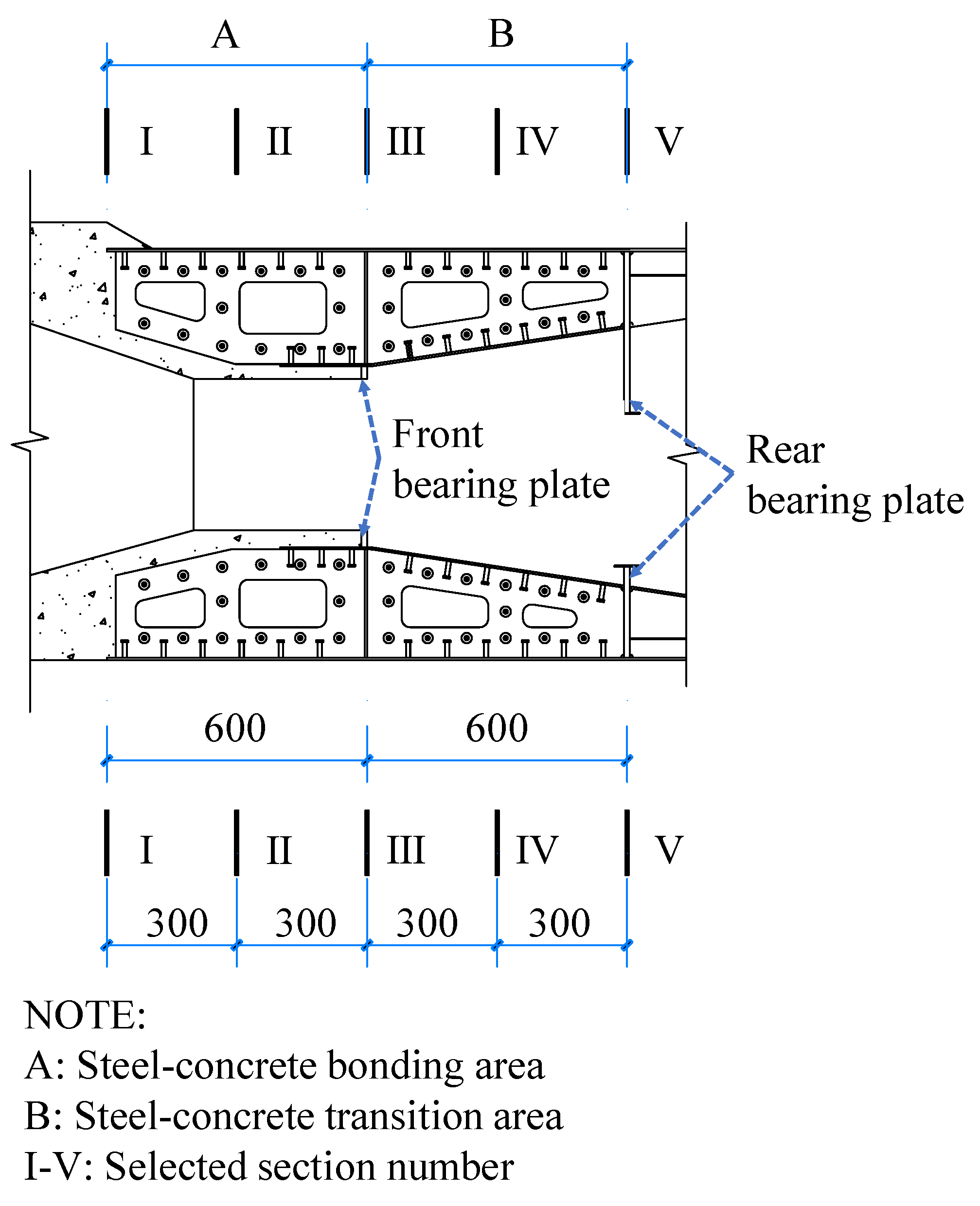
2.1. Test Model Design
2.2. Loading Program
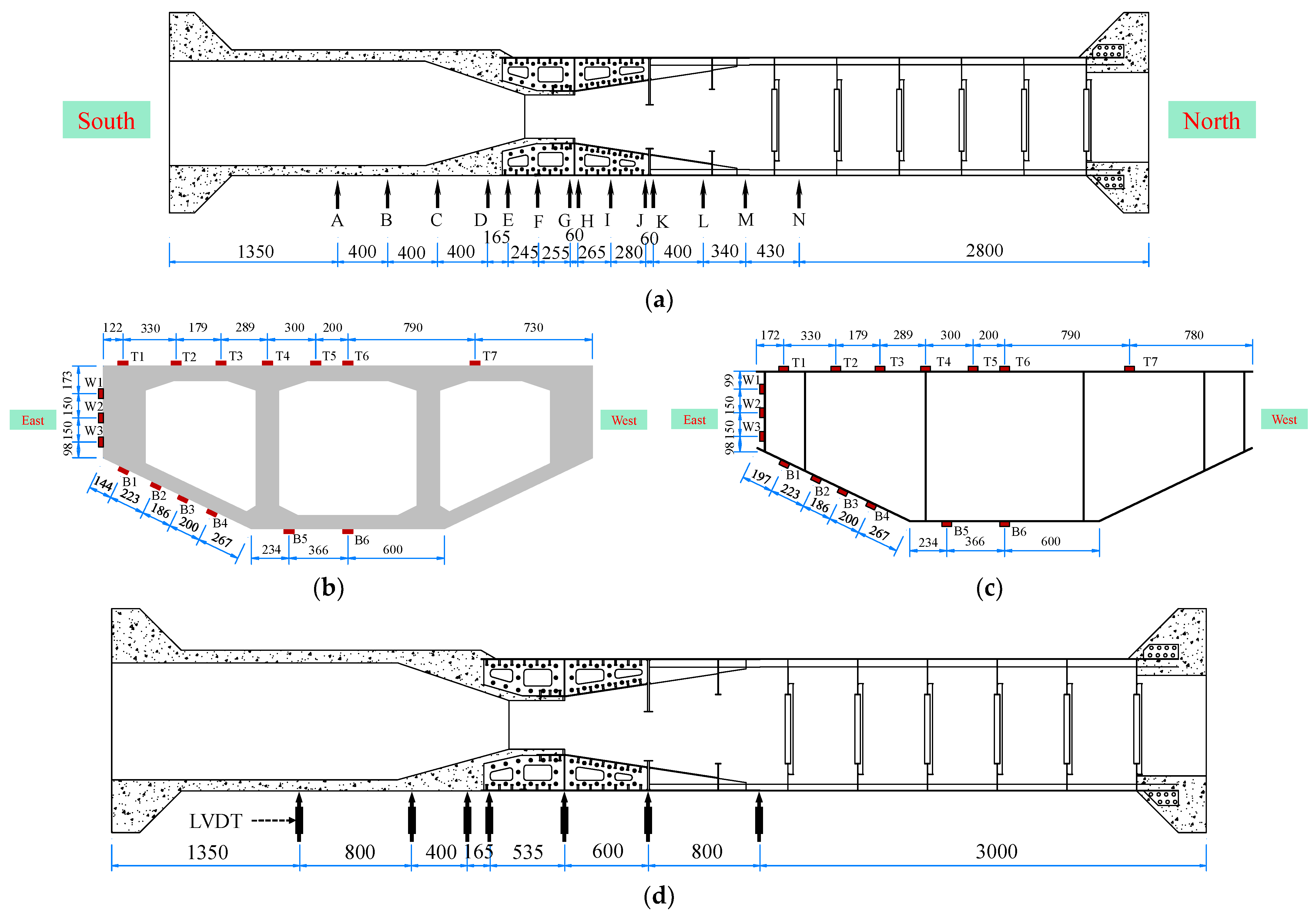
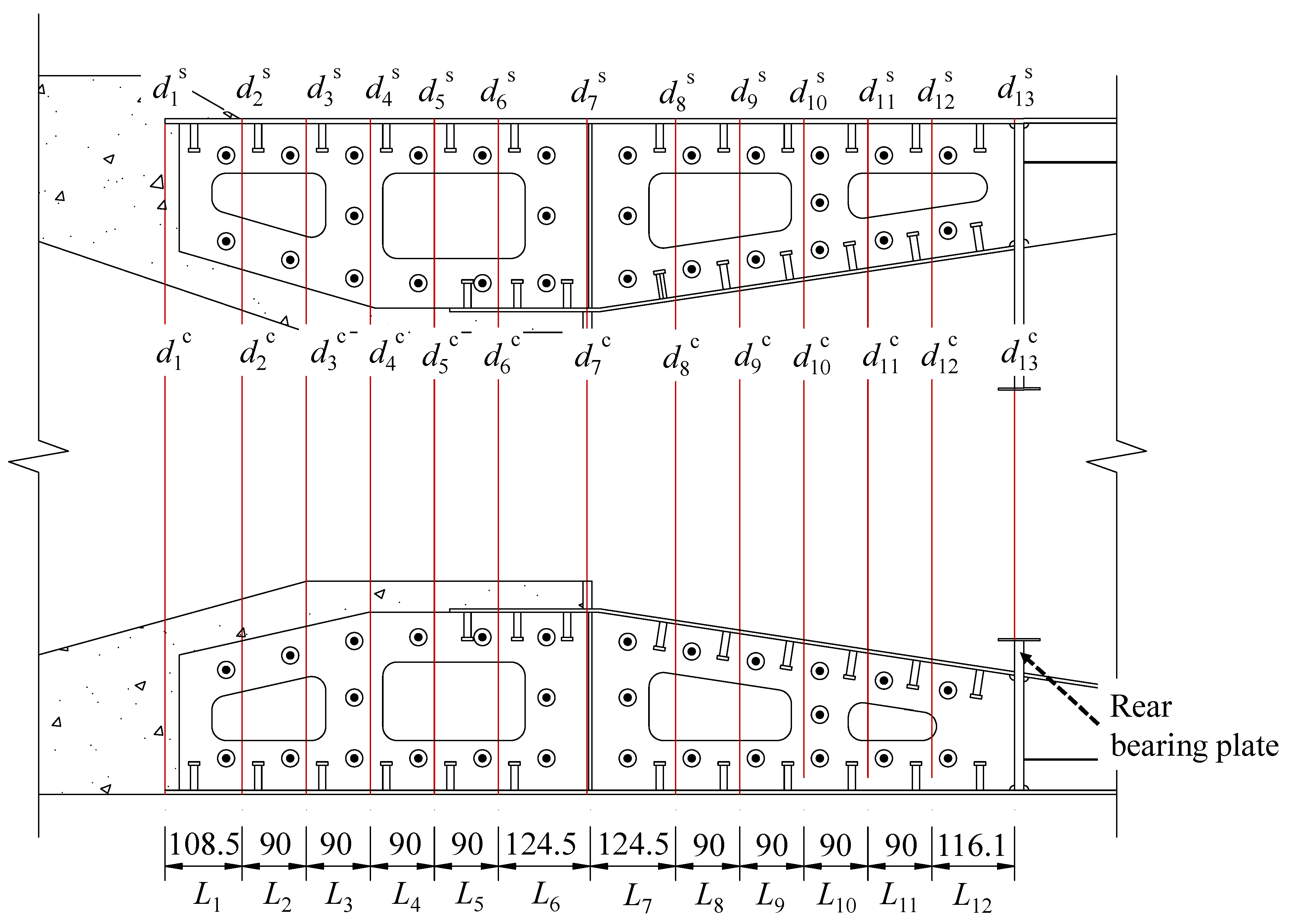
2.3. Measurement Programs
3. Results
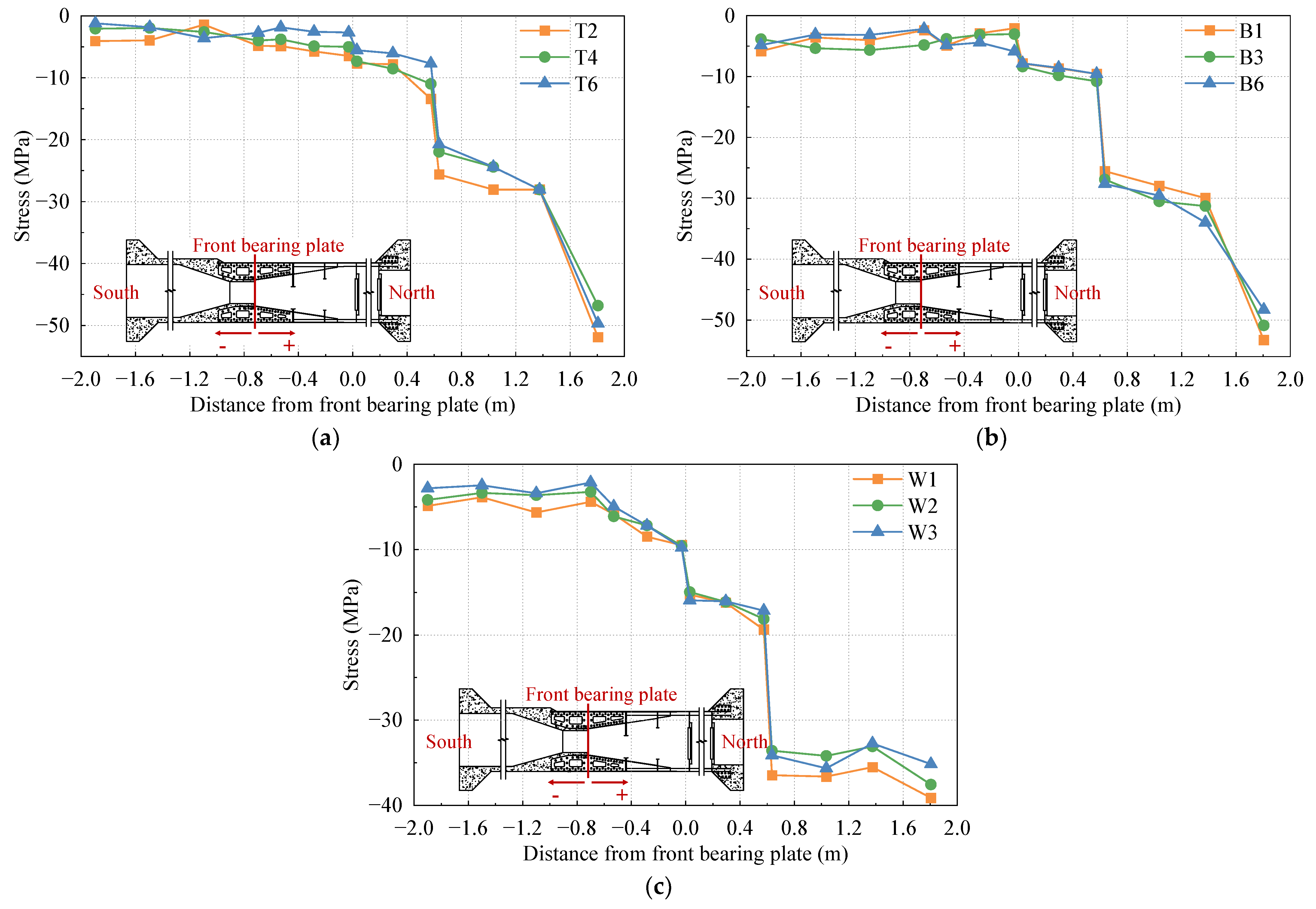
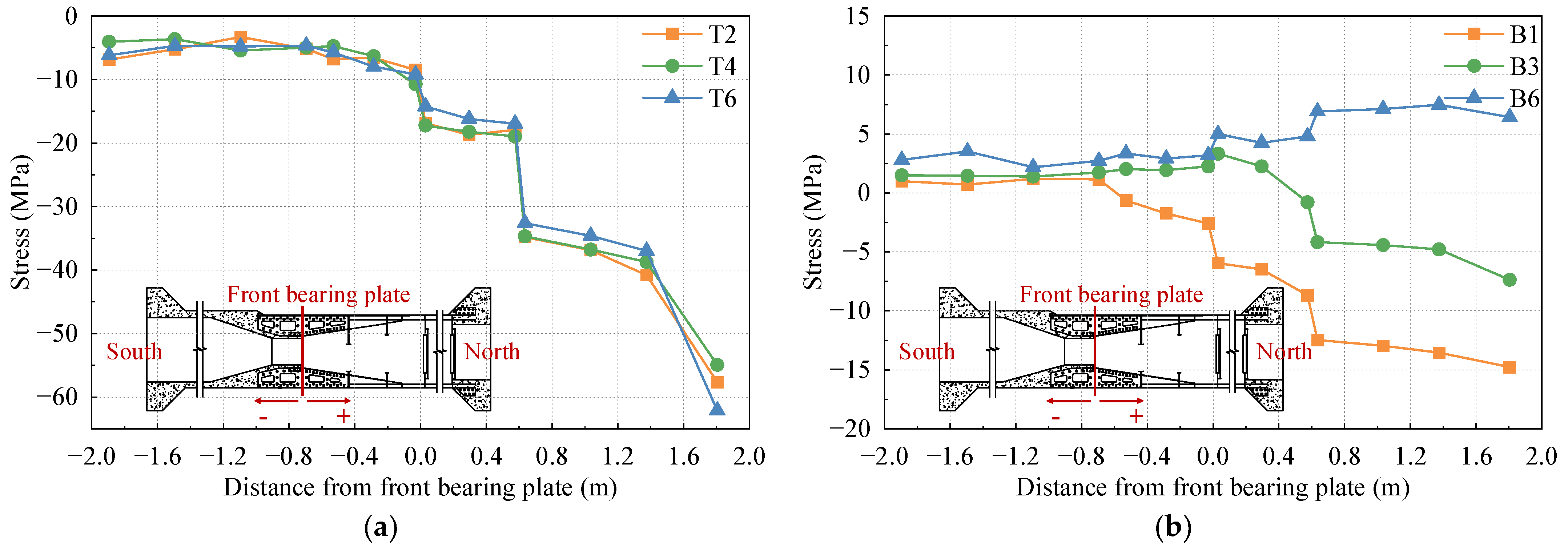
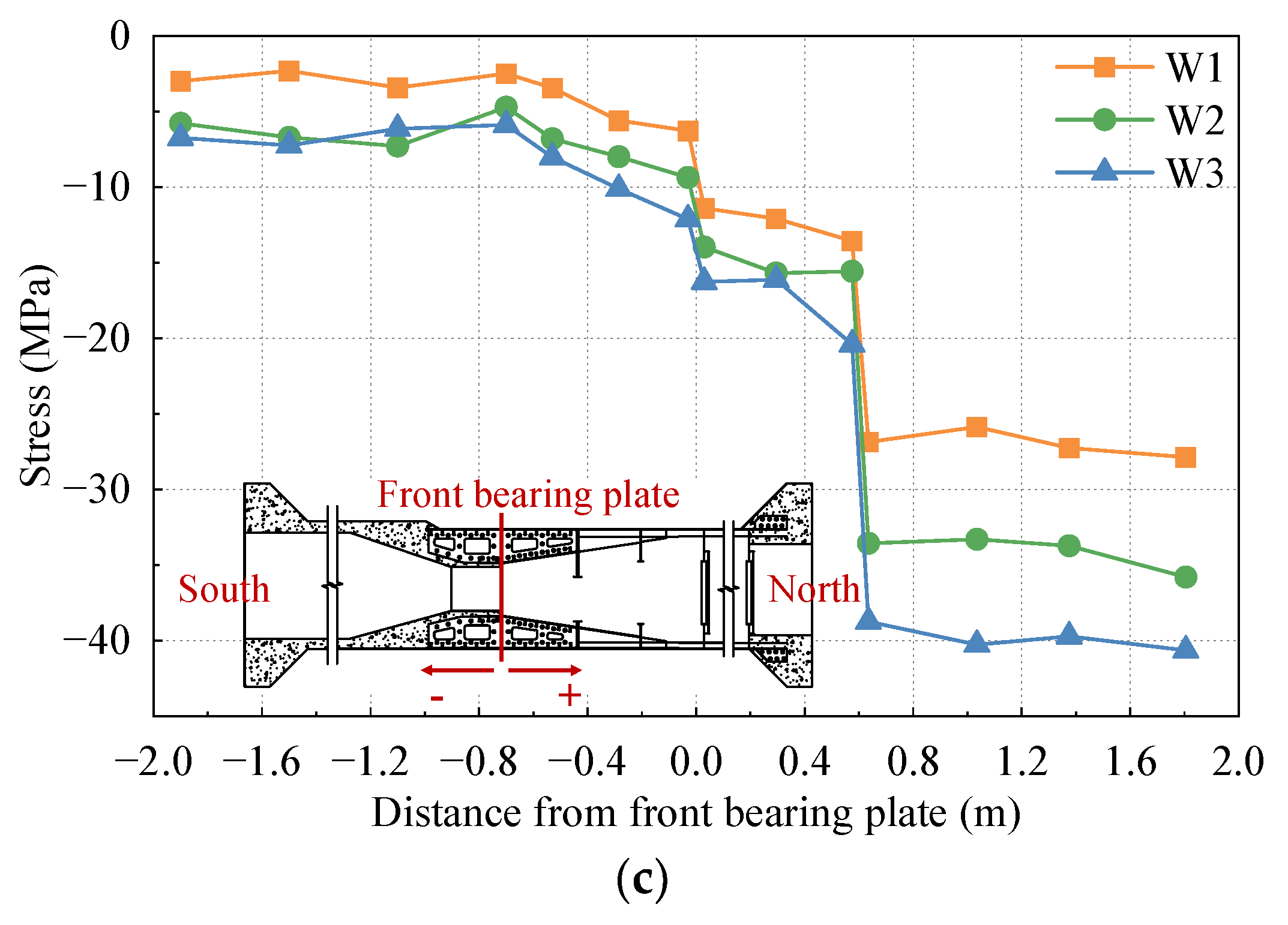
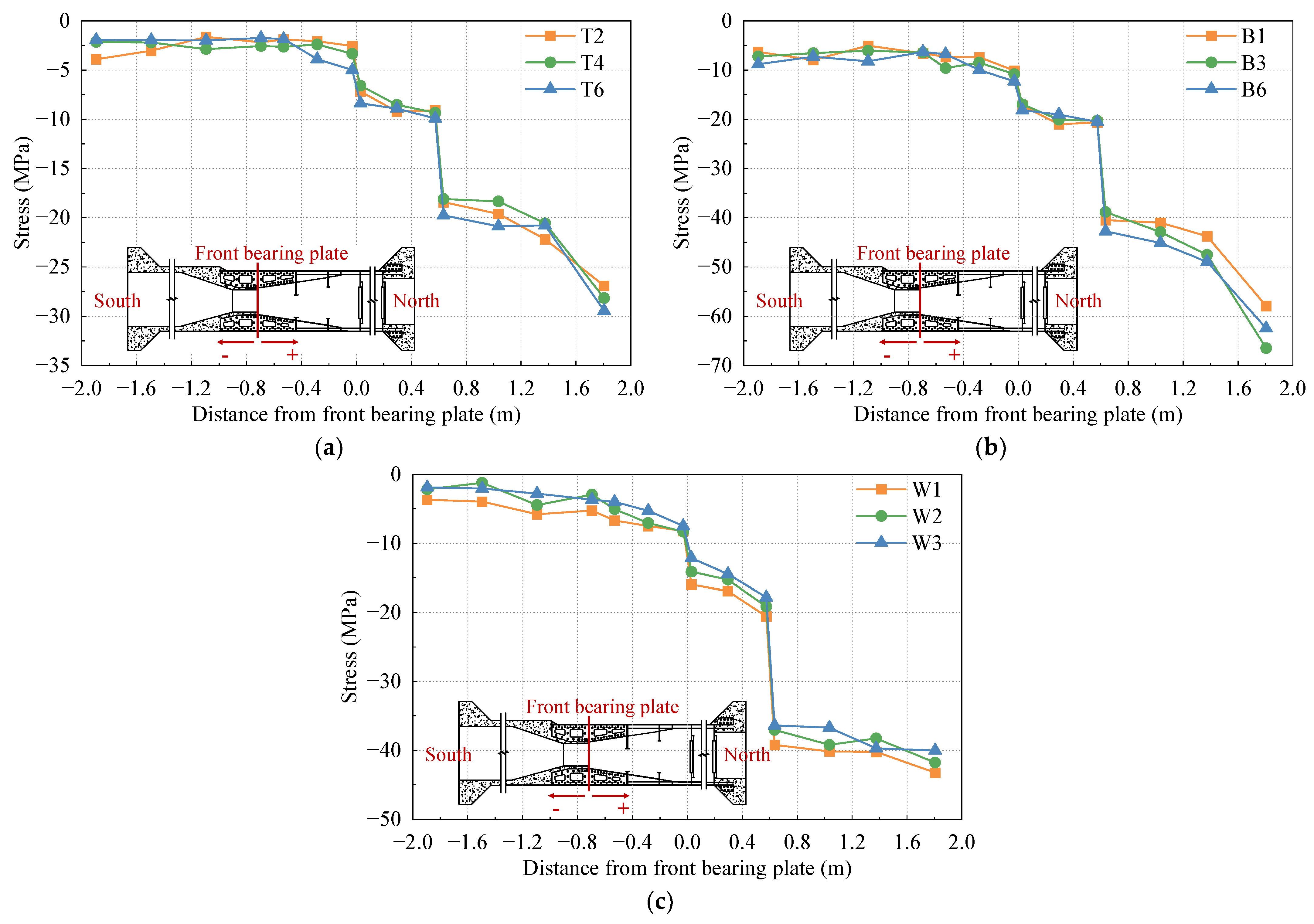
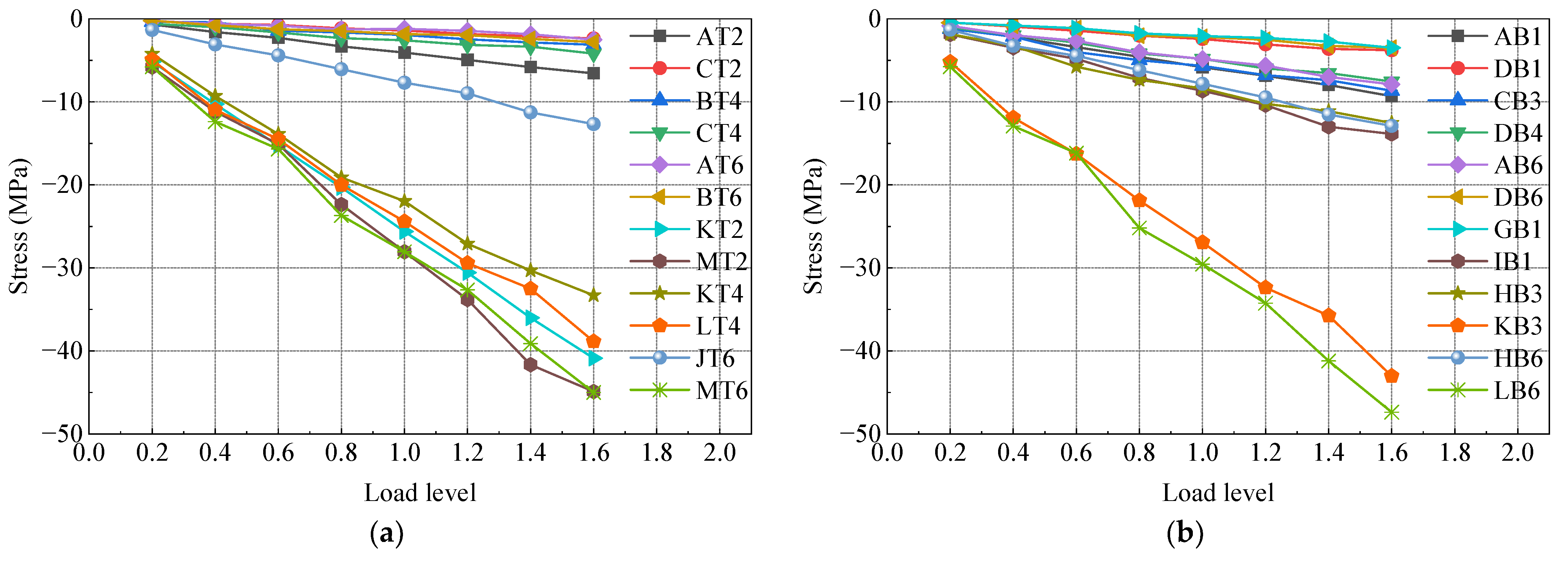
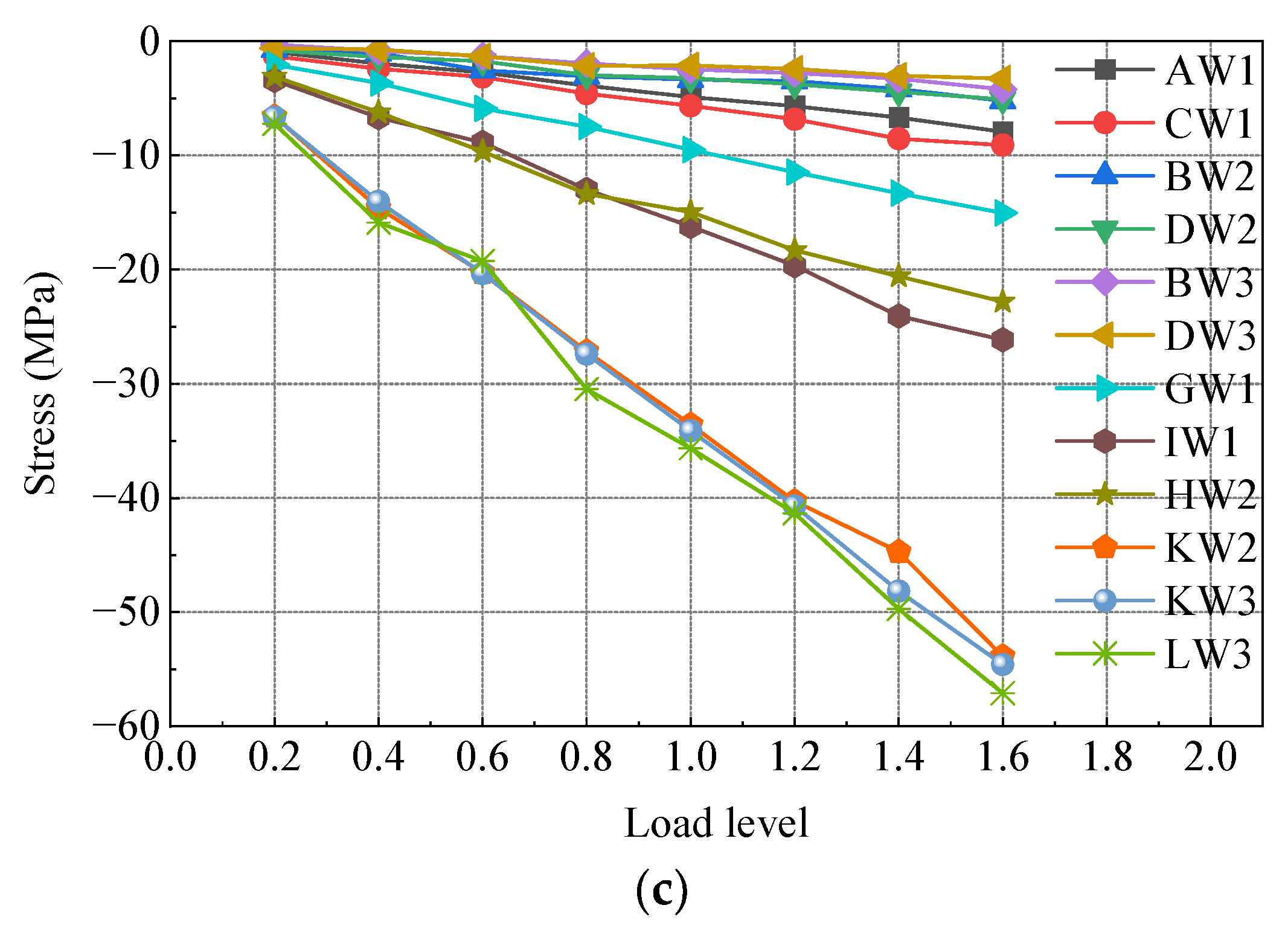
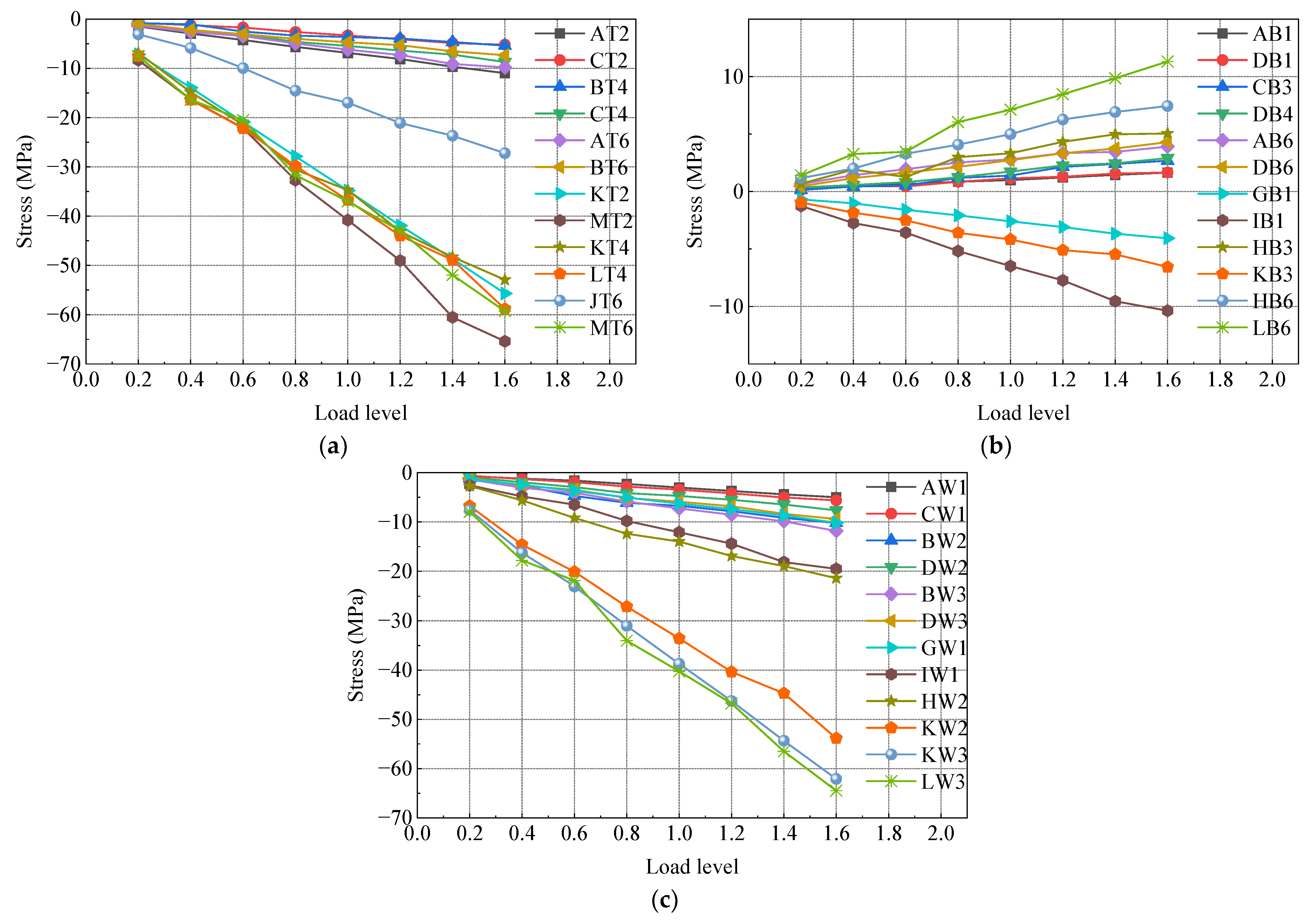
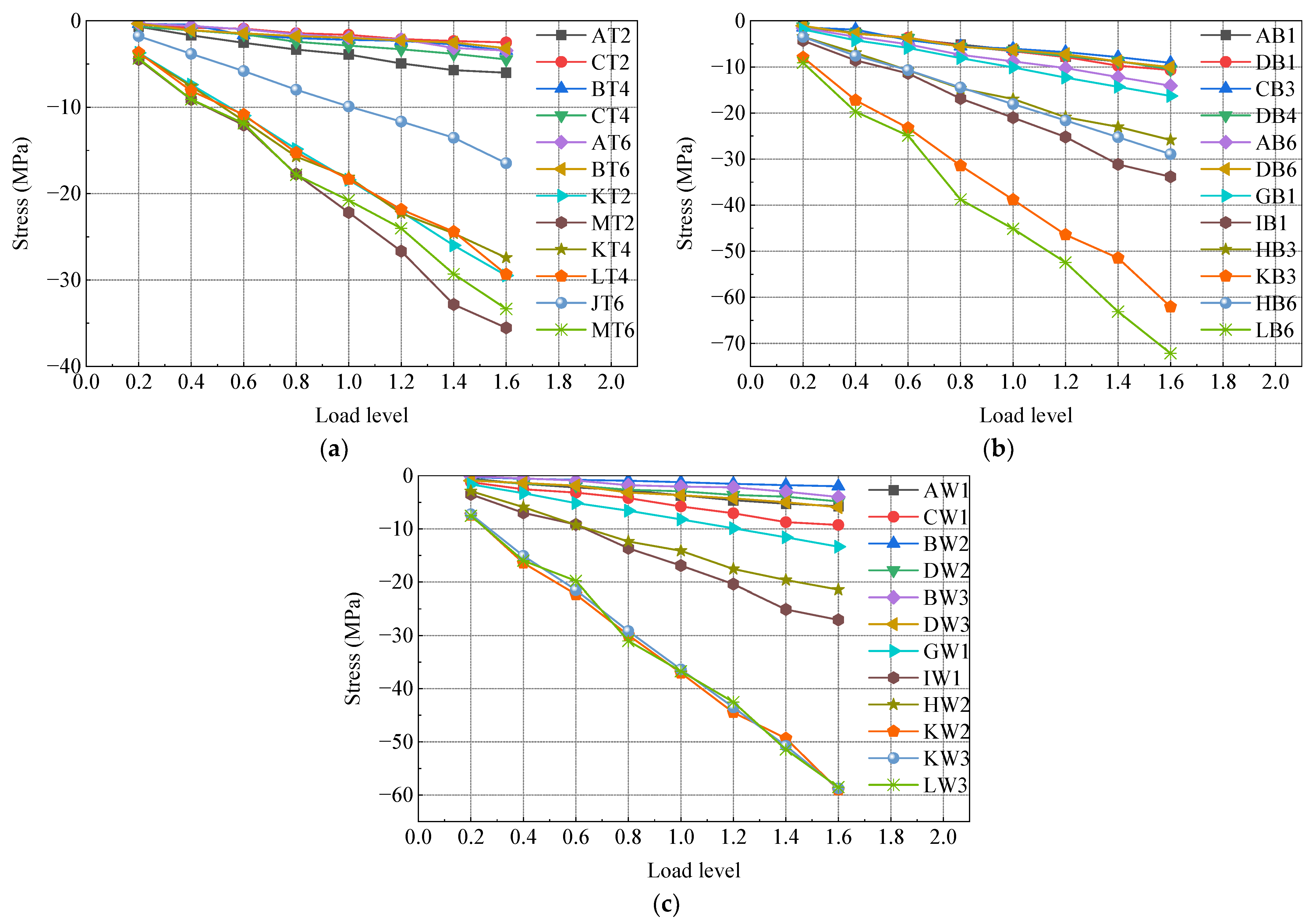
3.1. Stress Distribution in the Longitudinal Direction
- Tensile stress is considered positive, while compressive stress is considered negative;
- The analysis is based on the position of the front bearing plate of the SCJ as the coordinate origin. Positive values indicate the direction toward the steel box beam side, while negative values indicate the direction toward the PC box beam side;
- A distance of −0.6 m from the front bearing plate corresponds to the intersection between the PC box beam and the SCJ;
- The position of the rear bearing plate is located at a distance of 0.6 m from the front bearing plate;
- A distance of 1.4 m from the front bearing plate corresponds to the intersection between the SCJ and the steel box beam.
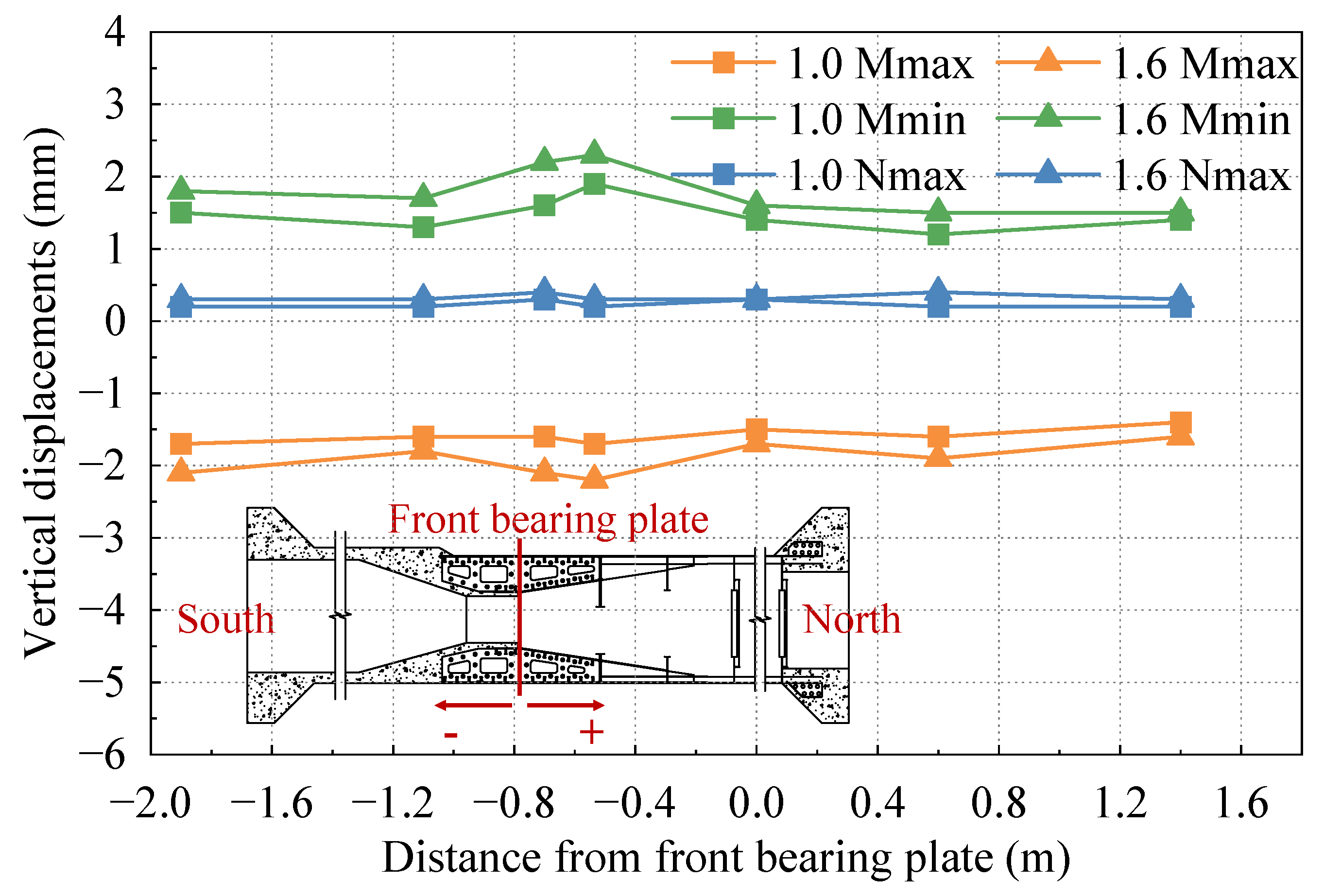
3.2. Vertical Displacement
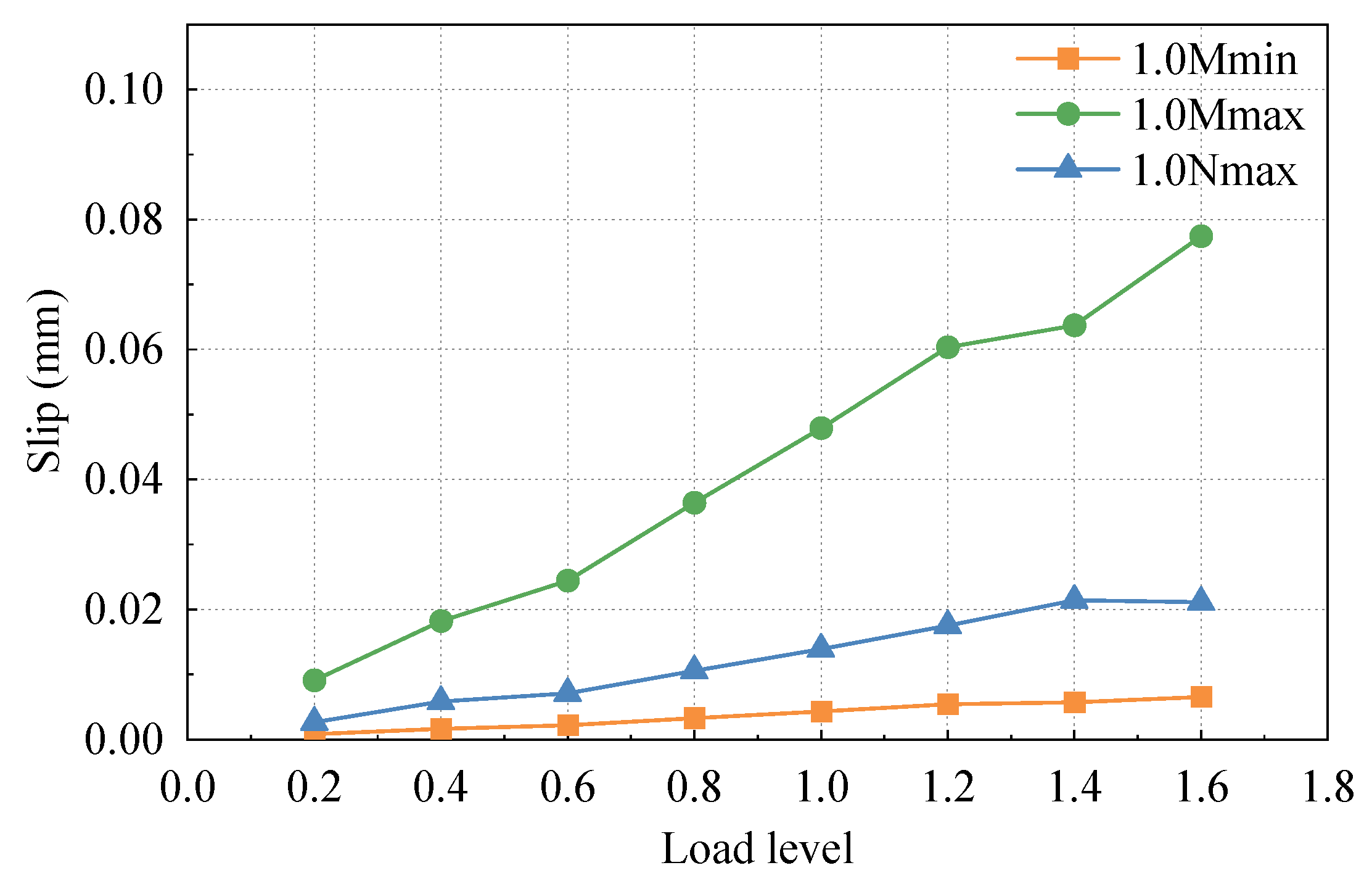
3.3. Relative Slip of Steel and Concrete
3.4. Model Carrying Capacity Analysis
4. Finite Element Analysis
4.1. Finite Element Model
4.2. Finite Element Model Validation
4.3. Analysis of the Axial Force Transfer Mechanism of Concrete and Steel Structures
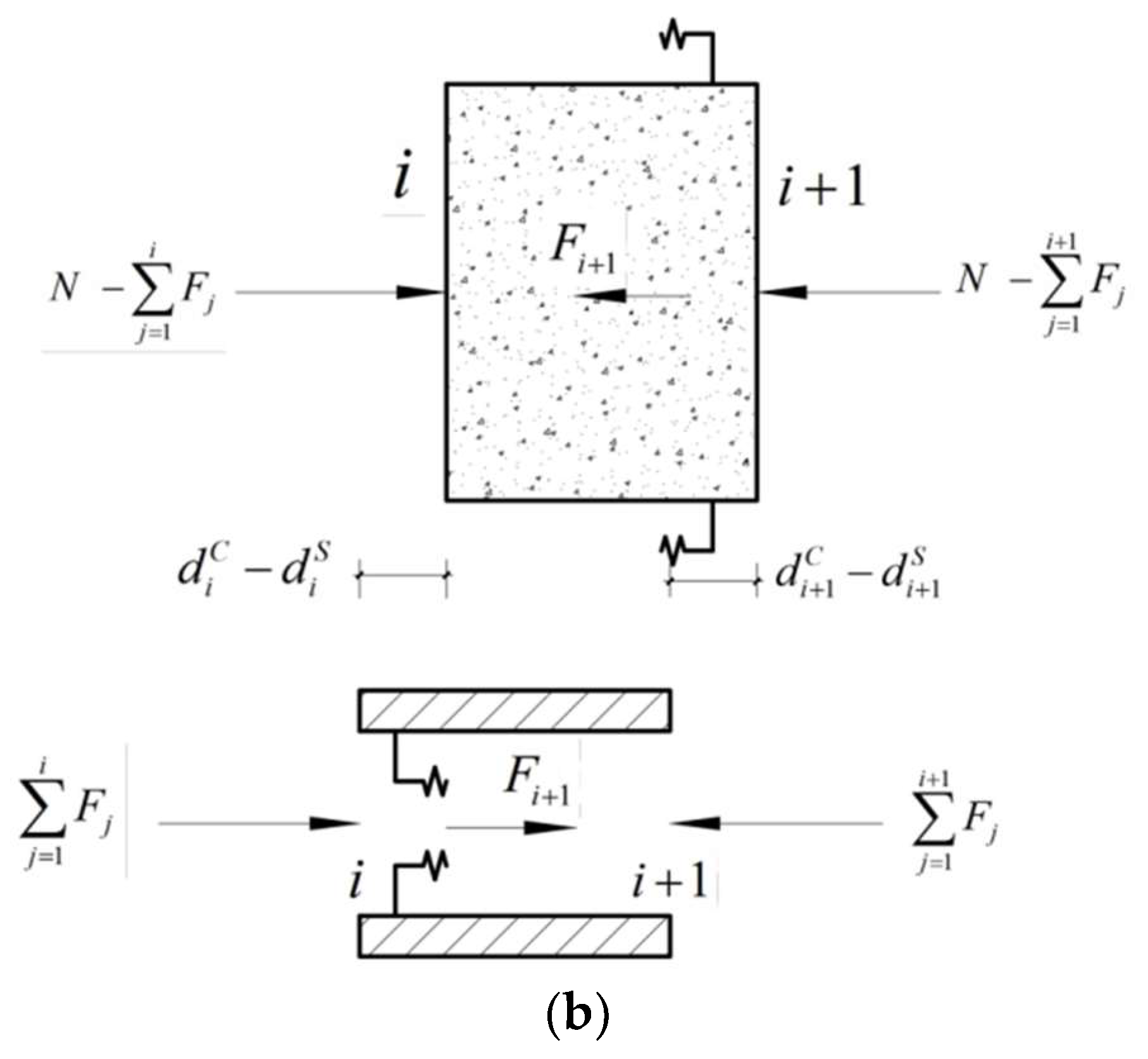
5. Simplified Calculation Model of the SCJ Axial Force Transfer Ratio
5.1. Calculation Method and Basic Assumptions
- Both steel and concrete are assumed to be isotropic elastomers within the elastic force range;
- The steel and concrete structures along the longitudinal bridge direction conform to the assumption of flat sections;
- The shear joint is represented by an equivalent spring, where the shear force is proportional to the relative slip between the steel and concrete, disregarding the nonlinearity of the shear joint;
- Adhesive friction between the steel and concrete is neglected;
- Structural bending and shear deformation are disregarded;
- The force transfer effect of the front bearing plate is ignored.
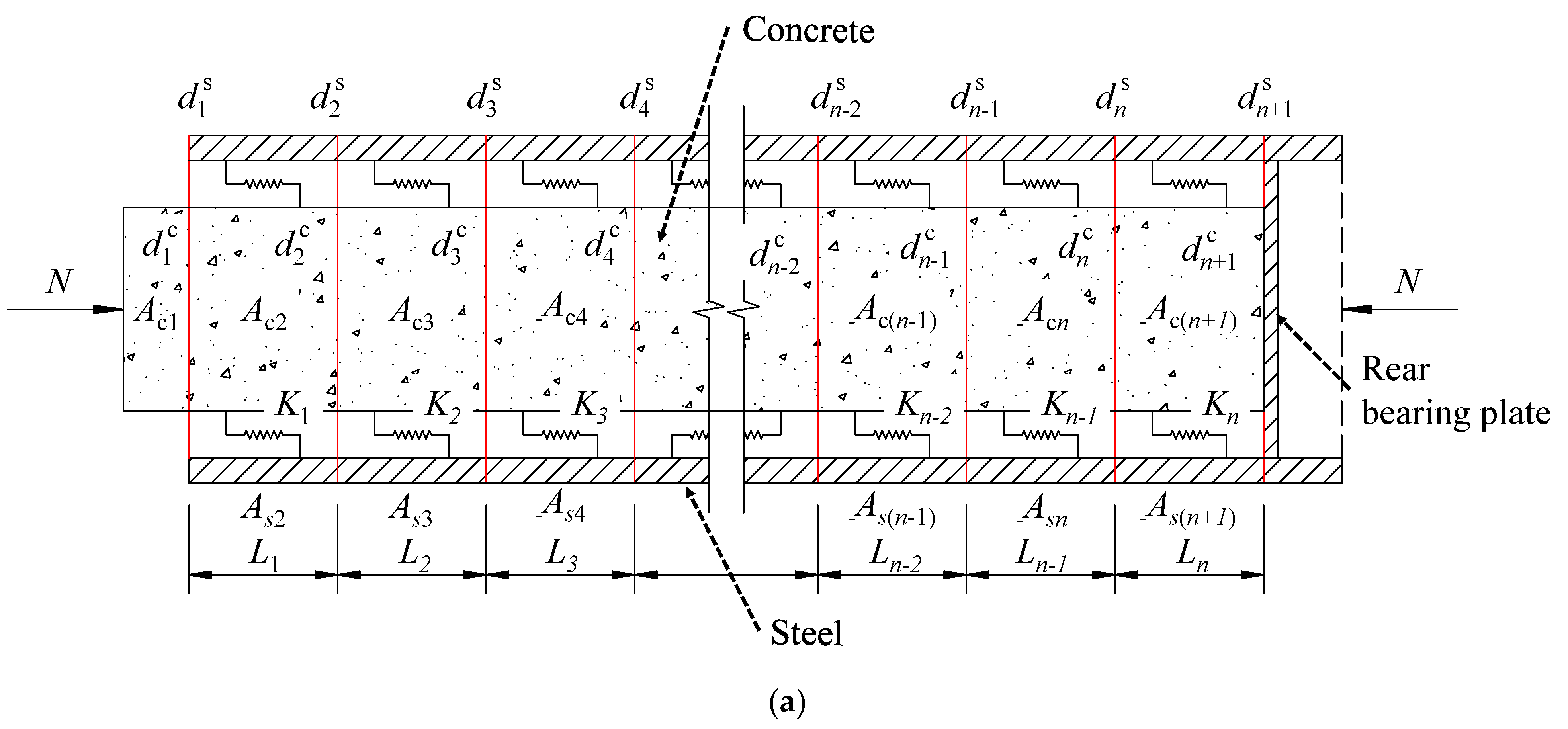
5.2. Theoretical Model of Deformation Coordination
5.3. Solution of the Deformation Coordination Theory Model
- 1.
- Divide the SCJ into n sections, calculate the equivalent stiffness Ki of each section according to Equations (8)–(11), and obtain the end displacement dsn+1 of the steel and the stiffness Khc of the rear bearing plate according to Equations (12) and (13);
- 2.
- Combining Equations (4), (5), and (11), the following derivations and simplifications are made:
- 3.
- Write the system of equations in step 2 in matrix form:[K] is the generalized stiffness matrix.
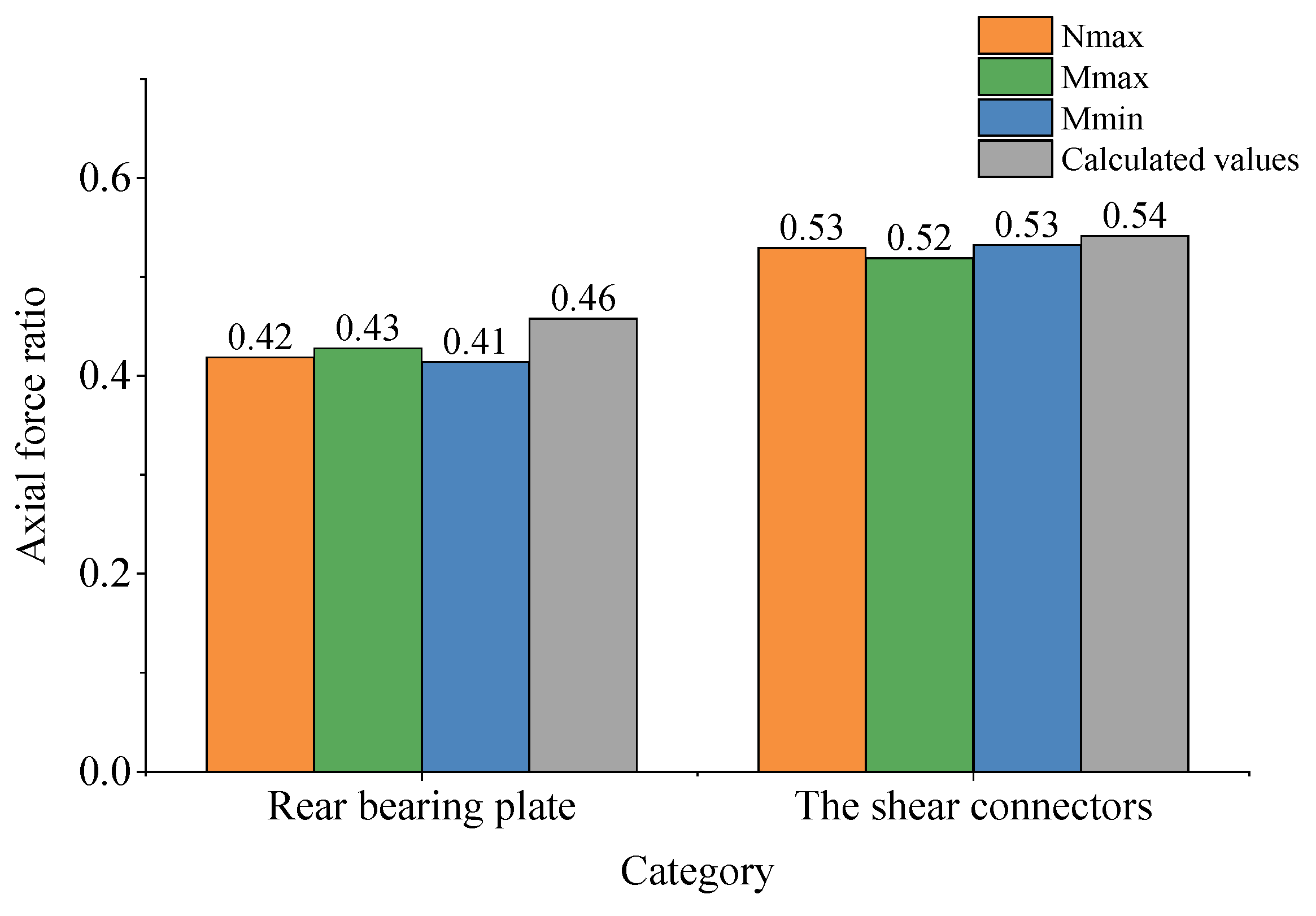
5.4. Validation of the Calculation Method
6. Conclusions
- (1)
- The tested steel–concrete joint model, which did not consider the shear torsion effect and was subjected to 1.0 times the design load, exhibited continuous and smooth vertical deformation. The slip between the steel and concrete was minimal and linearly increased. Moreover, all members remained in an elastic working state even when subjected to 1.6 times the load. These findings indicate that the tested SCJ model possesses high safety, reliability, and an ample safety reserve.
- (2)
- The measured data in the test model aligned well with the theoretically calculated values through finite element analysis, affirming the reliability of the finite element model for further analysis of the test.
- (3)
- Through the finite element analysis of the test model, it was observed that the force transmission ratios of the steel–concrete joint members did not exhibit significant changes under different cases. They considered axial force and bending moment but excluded shear force and torsion. The rear bearing plate emerged as the primary axial force transfer member and was responsible for approximately 42% of the axial force transmission. The front bearing plate played a minor role, accounting for only about 7% of the transfer. The force transfer in other sections did not exhibit abrupt changes, indicating relatively smooth force transmission within the steel–cement combination zone and steel–cement transition zone.
- (4)
- A simplified calculation model for the axial force transfer ratio of the steel–concrete joint was proposed based on the deformation coordination theory. The results of the simplified calculation demonstrated a close agreement between the axial force transfer ratio of the shear connectors obtained through finite element analysis and the simplified calculation. However, the simplified calculation yielded higher values for the rear bearing plate compared to the finite element results. Nevertheless, the higher transfer ratio for the rear bearing plate provides an added safety margin for its design. Therefore, the proposed method has valuable implications for estimating the steel–concrete joint transfer ratio, calculating and designing shear connectors, and conducting local verification of the bearing plate.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rahnavard, R.; Rebelo, C.; Craveiro, H.D.; Napolitano, R. Understanding the cyclic performance of composite steel-concrete connections on steel bridges. Eng. Struct. 2020, 224, 111213. [Google Scholar] [CrossRef]
- Li, F.; Qu, Y.; Wang, J. Bond life degradation of steel strand and concrete under combined corrosion and fatigue. Eng. Fail. Anal. 2017, 80, 186–196. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, W.; Liu, X. Assessment of diagonal macrocrack-induced debonding mechanisms in FRP-strengthened RC beams. J. Compos. Constr. 2022, 26, 4022056. [Google Scholar] [CrossRef]
- Huang, H.; Li, M.; Zhang, W.; Yuan, Y. Seismic behavior of a friction-type artificial plastic hinge for the precast beam–column connection. Archiv. Civ. Mech. Eng. 2022, 22. [Google Scholar] [CrossRef]
- Yao, Y.; Yan, M.; Shi, Z.; Wang, Y.; Bao, Y. Mechanical behavior of an innovative steel–concrete joint for long-span railway hybrid box girder cable-stayed bridges. Eng. Struct. 2021, 239, 112358. [Google Scholar] [CrossRef]
- Leonhardt, F. Cable stayed bridges with prestressed concrete. PCI J. 1987, 32, 52–80. [Google Scholar] [CrossRef]
- Volke, E. The current pressure in the case of the Nordbrucke Mannheim-Ludwigshafen (Kurt-Schumacher bridge). Teil 1973, 1, 97–104. [Google Scholar]
- Virlogeux, M. The Normandie Bridge, France: A new record for cable-stayed bridges. Struct. Eng. Int. 1994, 4, 208–213. [Google Scholar] [CrossRef]
- Pipinato, A. Case study: The Russky bridge. In Innovative Bridge Design Handbook; Elsevier: Amsterdam, The Netherlands, 2016; pp. 671–680. [Google Scholar]
- Nakamura, S. New structural forms for steel/concrete composite bridges. Struct. Eng. Int. 2000, 10, 45–50. [Google Scholar] [CrossRef]
- Cheng, X.; Nie, X.; Fan, J. Structural performance and strength prediction of steel-to-concrete box girder deck transition zone of hybrid steel-concrete cable-stayed bridges. J. Bridge Eng. 2016, 21, 4016083. [Google Scholar] [CrossRef]
- Wang, H.; Wu, S. Influence of Fatigue Damage on Criticality Cell Ultimate Load Capacity of Steel–Concrete Composite Section. Buildings 2023, 13, 1254. [Google Scholar] [CrossRef]
- Zhang, D.L.; Bao, Y.W.; Gao, J.H.; Xiao, L.; Li, X.Z. In Research on Load Transfer Mechanism of Steel-Concrete Joint Section of Hybrid Beam Cable-Stayed Bridge. Adv. Mater. Res. 2013, 639, 216–219. [Google Scholar] [CrossRef]
- Zhou, Y.; Pu, Q.; Shi, Z.; Gou, H.-Y.; Yang, S.-L. Experimental Study on Fatigue Performance of Steel-Concrete Joint Section of Hybrid Girder Cable-Stayed Bridge. Adv. Steel. Constr. 2022, 18, 536–543. [Google Scholar]
- He, S.; Mosallam, A.S.; Fang, Z.; Liu, L. Structural evaluation of steel–concrete joint with UHPC grout in single cable–plane hybrid cable-stayed bridges. J. Bridge Eng. 2019, 24, 4019022. [Google Scholar] [CrossRef]
- He, J.; Liu, Y.; Pei, B. Experimental study of the steel-concrete connection in hybrid cable-stayed bridges. J. Perform. Constr. Fac. 2014, 28, 559–570. [Google Scholar] [CrossRef]
- Chen, K.; Wang, J.; An, Q. Model tests on steel-concrete joining section of main girder of a cable-stayed bridge. China Civ. Eng. J. 2006, 39, 86–90. [Google Scholar]
- Huang, C. Experimental Study and Theoretical Analysis of Mechanical Behavior of Steel-Concrete Joint Section of Hybrid Girder Cable-Stayed Bridge. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2012. [Google Scholar]
- Yang, S.; Pu, Q.; Shi, Z.; Hong, Y. Mechanical behavior of steel–concrete composite joints in railway hybrid cable-stayed bridges. J. Constr. Steel Res. 2020, 173, 106242. [Google Scholar] [CrossRef]
- Xin, H.; Liu, Y.; He, J.; Zhang, Y. Experimental and analytical study on stiffened steel segment of hybrid structure. J. Constr. Steel Res. 2014, 100, 237–258. [Google Scholar] [CrossRef]
- JTG/T D64-01—2015; L. CCCC Highway Consultants Co. Specifications for Design and Construction of Highway Steel-concrete Composite Bridge; China Communications Press: Beijing, China, 2015.
- Huang, H.; Guo, M.; Zhang, W.; Zeng, J.; Yang, K.; Bai, H. Numerical investigation on the bearing capacity of RC columns strengthened by HPFL-BSP under combined loadings. J. Build. Eng. 2021, 39, 102266. [Google Scholar] [CrossRef]
- Huang, H.; Li, M.; Yuan, Y.; Bai, H. Theoretical analysis on the lateral drift of precast concrete frame with replaceable artificial controllable plastic hinges. J. Build. Eng. 2022, 62, 105386. [Google Scholar] [CrossRef]
- Feng-jiang, Q.; Xu-hong, Z.; Bo-wen, L.; Jin, D.; Xi, T.; Liang-jin, X.; Yang, Z. Experiment on Steel-concrete Joint do Hybrid Girder of a Long-span Self-anchored Suspension Bridge. China J. Highw. Transp. 2018, 31, 52–64. [Google Scholar]
- L. CCCC Highway Consultants Co. General Code for Design of Highway Bridges and Culverts; China Communications Press: Beijing, China, 2015. [Google Scholar]
- Ding, F.; Wu, X.; Xiang, P.; Yu, Z. New damage ratio strength criterion for concrete and lightweight aggregate concrete. ACI Struct. J. 2021, 118, 165–178. [Google Scholar]
- Rabbat, B.G.; Russell, H.G. Friction coefficient of steel on concrete or grout. J. Struct. Eng. 1985, 111, 505–515. [Google Scholar] [CrossRef]
- Yin, G.; Ding, F.; Wang, H.; Bai, Y.; Liu, X.-m. Connection performance in steel–concrete composite truss bridge structures. J. Bridge Eng. 2017, 22, 4016126. [Google Scholar] [CrossRef]
- Shangguan, B.; Su, Q.; Casas, J.R.; Su, H.; Wang, S.; Zhao, R. Modeling and Testing of a Composite Steel-Concrete Joint for Hybrid Girder Bridges. Materials 2023, 16, 3265. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Wang, W.; Wu, S. Study on Load-Slip Curve of a PBL Shear Key at a Steel-Concrete Composite Joint. Appl. Sci. 2023, 13, 6165. [Google Scholar] [CrossRef]
- Wang, W.; Yi, Z.; Tian, B.; Zhang, Y.; Lu, S. Nonlinear Finite Element Analysis of PBL Shear Connectors in Hybrid Structures. In Structures; Elsevier: Amsterdam, The Netherlands, 2021; pp. 4642–4654. [Google Scholar]
- Zhang, Q.; Jia, D.; Bao, Y.; Cheng, Z.; Xiao, L.; Bu, Y. Internal force transfer effect-based fatigue damage evaluation for PBL shear connector groups. J. Constr. Steel Res. 2018, 148, 469–478. [Google Scholar] [CrossRef]
- Qinghua, Z.; Qiao, L.; Yizhi, B. Load transmission mechanism of PBL shear connector group (Ⅰ)—Theoretical model. China Civ. Eng. J. 2011, 44, 71–77. [Google Scholar]
- Lin, Z.-F.; Liu, Y.-Q.; He, J. Research on Calculation Method of Shear Stiffness for Headed Stud Connectors. Eng. Mech. 2014, 31, 85–90. [Google Scholar]
- Pu, Q.; Yang, S.; Shi, Z.; Hong, Y.; Zhou, Y. Fatigue performance of an innovative steel–concrete joint in long-span railway hybrid box girder cable-stayed bridges. J. Bridge Eng. 2021, 26, 4020129. [Google Scholar] [CrossRef]








| Bridge Name | Country | Main Span (m) | Year |
|---|---|---|---|
| Russian Island Bridge | Russia | 1104 | 2012 |
| Stonecutters Bridge | China | 1018 | 2009 |
| Qingshan Yangtze River Bridge | China | 938 | 2020 |
| Erdong Yangtze River Bridge | China | 926 | 2010 |
| Jiayu Yangtze River Highway Bridge | China | 920 | 2019 |
| Dodoro Bridge | Japan | 890 | 1999 |
| Normandy Bridge | France | 856 | 1995 |
| Chizhou Yangtze River Highway Bridge | China | 828 | 2019 |
| Shishou Yangtze River Bridge | China | 820 | 2019 |
| Jiujiang Second Bridge | China | 818 | 2013 |
| Bridge Name | Parameter Similarity Ratio |
|---|---|
| Model size | 1/5 |
| Cross-sectional area | 1/25 |
| Cross-sectional moment of inertia | 1/625 |
| Axial force | 1/25 |
| Bending moment | 1/125 |
| Stress | 1/1 |
| Component | Variable | Actual Bridge | Test Model |
|---|---|---|---|
| Top plate | Plate thickness | 33 mm | 6 mm |
| Base plate | Plate thickness | 30 mm | 6 mm |
| Center web | Plate thickness | 30 mm | 6 mm |
| Center side web | Plate thickness | 30 mm | 6 mm |
| Side webs | Plate thickness | 30 mm | 6 mm |
| Bearing plate | Plate thickness | 64 mm | 12 mm |
| PBL connectors | Diameter of the steel plate opening | 60 mm | 24 mm |
| PBL connectors | Diameter of penetration reinforcement | 25 mm | 10 mm |
| Shear studs | Specification | ϕ22 × 150 mm | ϕ10 × 40 mm |
| Material | Actual Bridge | Test Model |
|---|---|---|
| Steel | Q345qD | Q355B |
| Concrete | C60 | C60 |
| Steel bars | HPB300 | HPB300 |
| Steel bars | HRB400 | HRB400 |
| Shear studs | ML15 | ML15 |
| Steel Plate Thickness (mm) | Yield Strength (Mpa) | Tensile Strength (Mpa) | Elongation after Fracture (%) |
|---|---|---|---|
| 4 | 463 | 568 | 30 |
| 6 | 433 | 479 | 28.5 |
| 8 | 409 | 498 | 30.5 |
| 12 | 434 | 570 | 27.5 |
| Serial Number | Length (mm) | Width (mm) | Height (mm) | Damage Load (kN) | Compressive Strength (Mpa) | Average Compressive Strength (Mpa) |
|---|---|---|---|---|---|---|
| 1 | 148 | 147 | 148 | 1519.6 | 69.8 | 69.1 |
| 2 | 149 | 149 | 152 | 1468.4 | 66.1 | |
| 3 | 148 | 150 | 150 | 1580.5 | 71.2 |
| Type of Working Condition | Axial Force (kN) | Bending Moment (kN-m) | Shear Force (kN) | Torque (kN-m) |
|---|---|---|---|---|
| Maximum shaft force | −74,673.57 | −4228.85 | −22,489.47 | −131.57 |
| Minimum shaft force | −54,027.58 | −657.18 | 40,272.85 | −136.91 |
| Maximum positive shear | −63,532.42 | 701.91 | 51,729.39 | 362.86 |
| Maximum negative shear | −64,686.62 | −6071.63 | −22,770.58 | −631.31 |
| Maximum positive bending moment | −56,062.51 | −571.15 | 74,856.05 | 362.86 |
| Maximum negative bending moment | −72,461.53 | −4366.84 | −54,962.33 | −131.32 |
| Load Case | The Total Force of the Top Jack | The Total Force of the Bottom Jack |
|---|---|---|
| 1.0 times the maximum axial force (1.0 Nmax) | 1255.38 | 1731.56 |
| 1.6 times the maximum axial force (1.6 Nmax) | 2008.61 | 2770.50 |
| 1.0 times the maximum positive bending moment (1.6 Mmax) | 1794.00 | 448.50 |
| 1.6 times the maximum positive bending moment (1.6 Mmax) | 2870.40 | 717.60 |
| 1.0 times the maximum negative bending moment (1.6 Mmin) | 899.52 | 1998.94 |
| 1.6 times the maximum negative bending moment (1.6 Mmin) | 1439.24 | 3198.30 |
| Load Case | Load Level | Single Top Jack Applied Load | Single Bottom Jack Applied Load |
|---|---|---|---|
| The maximum axial force | 0.2 P | 25.11 | 34.63 |
| 0.4 P | 50.22 | 69.26 | |
| 0.6 P | 75.32 | 103.89 | |
| 0.8 P | 100.43 | 138.52 | |
| 1.0 P | 125.54 | 173.16 | |
| 1.2 P | 150.65 | 207.79 | |
| 1.4 P | 175.75 | 242.42 | |
| 1.6 P | 200.86 | 277.05 | |
| The maximum positive bending moment | 0.2 P | 35.88 | 8.97 |
| 0.4 P | 71.76 | 17.94 | |
| 0.6 P | 107.64 | 26.91 | |
| 0.8 P | 143.52 | 35.88 | |
| 1.0 P | 179.4 | 44.85 | |
| 1.2 P | 215.28 | 53.82 | |
| 1.4 P | 251.16 | 62.79 | |
| 1.6 P | 287.04 | 71.76 | |
| The maximum negative bending moment | 0.2 P | 17.99 | 39.98 |
| 0.4 P | 35.98 | 79.96 | |
| 0.6 P | 53.97 | 119.94 | |
| 0.8 P | 71.96 | 159.92 | |
| 1.0 P | 89.95 | 199.89 | |
| 1.2 P | 107.94 | 239.87 | |
| 1.4 P | 125.93 | 279.85 | |
| 1.6 P | 143.92 | 319.83 |
| Case | Type | Ⅴ-Right | Ⅴ-Left | Ⅳ | Ⅲ-Right | Ⅲ-Left | Ⅱ | Ⅰ |
|---|---|---|---|---|---|---|---|---|
| 1.0 Nmax | Concrete | 0 | 41.90% | 55.49% | 58.70% | 63.85% | 75.97% | 100% |
| Steel | 100% | 58.10% | 44.51% | 41.30% | 36.15% | 24.03% | 0 | |
| 1.0 Mmax | Concrete | 0 | 42.81% | 55.99% | 58.89% | 64.15% | 76.82% | 100% |
| Steel | 100% | 57.19% | 44.01% | 41.11% | 35.85% | 23.18% | 0 | |
| 1.0 Mmin | Concrete | 0 | 41.43% | 55.02% | 57.68% | 63.01% | 75.04% | 100% |
| Steel | 100% | 58.57% | 44.98% | 42.32% | 36.99% | 24.96% | 0 |
| Segment i | Length Li (mm) | Number of Shear Studs | Number of PBL | Total Stiffness (kN/mm) | Aci+1 (mm2) | Asi+1 (mm2) |
|---|---|---|---|---|---|---|
| 1 | 108.5 | 153 | 54 | 62,595.41 | 1,979,677.02 | 95,149.77 |
| 2 | 90 | 124 | 54 | 57,403.47 | 2,006,623.15 | 98,698.38 |
| 3 | 90 | 128 | 81 | 75,721.33 | 1,989,173.64 | 100,143.78 |
| 4 | 90 | 219 | 54 | 74,411.55 | 1,989,173.73 | 102,380.3 |
| 5 | 90 | 167 | 54 | 65,101.87 | 1,989,173.73 | 128,281.52 |
| 6 | 124.5 | 174 | 81 | 83,956.82 | 1,989,173.73 | 128,268.09 |
| 7 | 124.5 | 184 | 81 | 85,747.14 | 1,515,175.06 | 120,476.9 |
| 8 | 90 | 188 | 54 | 68,861.55 | 1,445,307.86 | 118,083.41 |
| 9 | 90 | 205 | 54 | 71,905.10 | 1,375,440.66 | 115,656.62 |
| 10 | 90 | 184 | 81 | 85,747.14 | 1,305,573.46 | 113,273.01 |
| 11 | 90 | 184 | 54 | 68,145.42 | 1,235,706.26 | 110,836.35 |
| 12 | 116.1 | 213 | 54 | 73,337.36 | 1,144,551.06 | 107,727.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zeng, H.; Wu, X.; Yu, F. Simplified Calculation Model and Experimental Validation of the Force Transfer Ratio of Steel–Concrete Joint of Hybrid Box Girder. Materials 2023, 16, 5091. https://doi.org/10.3390/ma16145091
Wang H, Zeng H, Wu X, Yu F. Simplified Calculation Model and Experimental Validation of the Force Transfer Ratio of Steel–Concrete Joint of Hybrid Box Girder. Materials. 2023; 16(14):5091. https://doi.org/10.3390/ma16145091
Chicago/Turabian StyleWang, Haibo, Haozhe Zeng, Xun Wu, and Fangcong Yu. 2023. "Simplified Calculation Model and Experimental Validation of the Force Transfer Ratio of Steel–Concrete Joint of Hybrid Box Girder" Materials 16, no. 14: 5091. https://doi.org/10.3390/ma16145091
APA StyleWang, H., Zeng, H., Wu, X., & Yu, F. (2023). Simplified Calculation Model and Experimental Validation of the Force Transfer Ratio of Steel–Concrete Joint of Hybrid Box Girder. Materials, 16(14), 5091. https://doi.org/10.3390/ma16145091






