Experimental Research on the Bond Performance between SMAF-ECC Composites and Steel Bar
Abstract
1. Introduction
2. Test Overview
2.1. Test Material
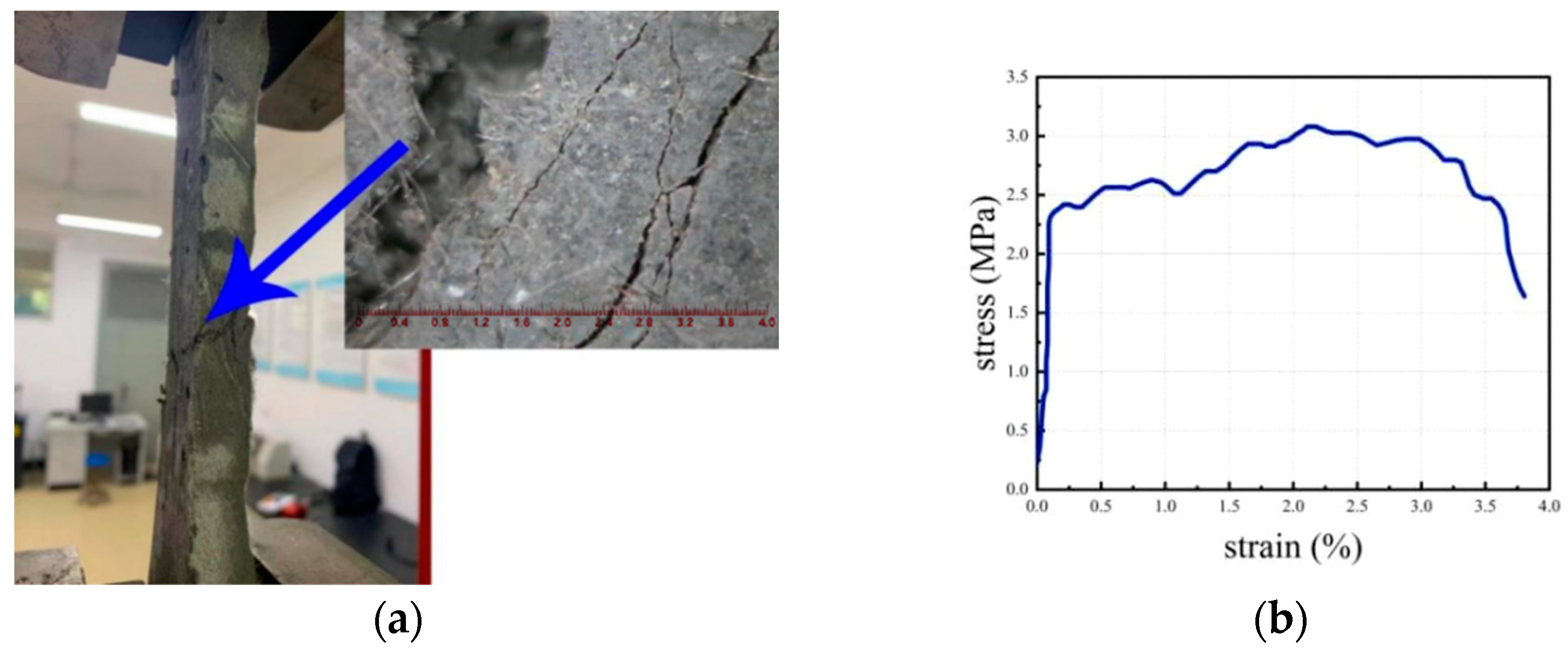
2.1.1. Engineered Cementitious Composites (ECC)
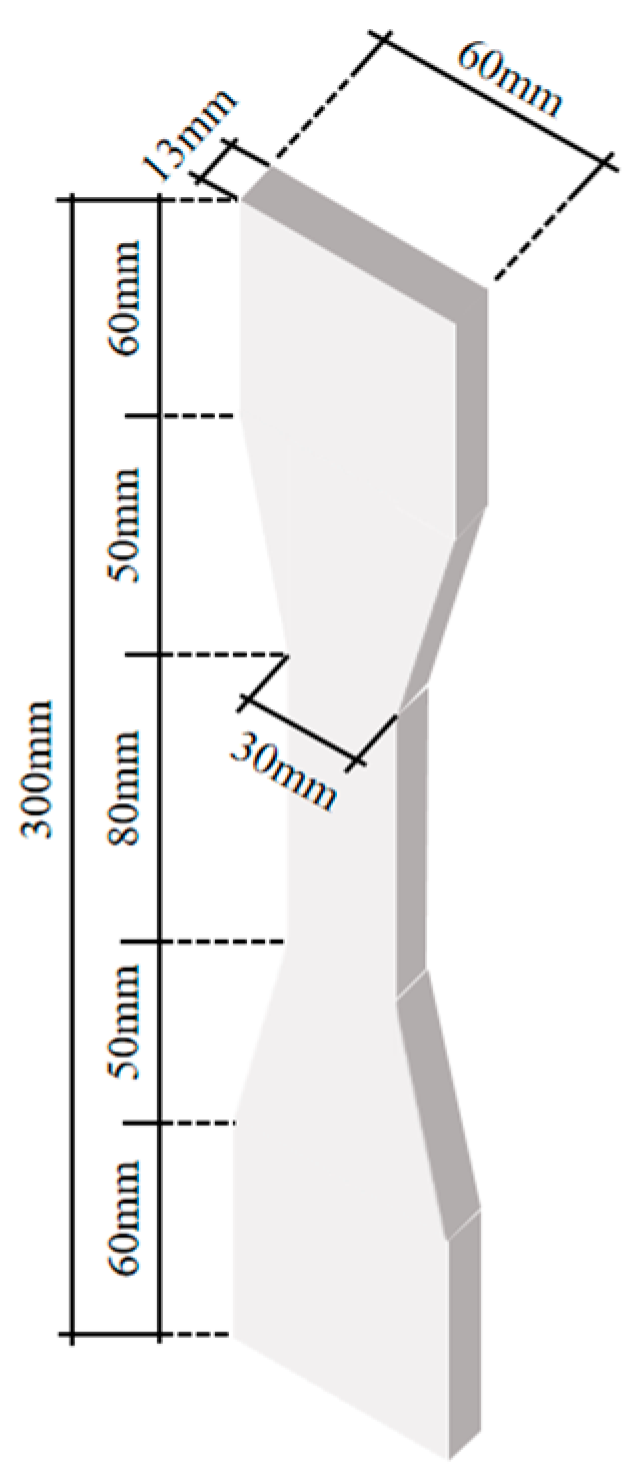
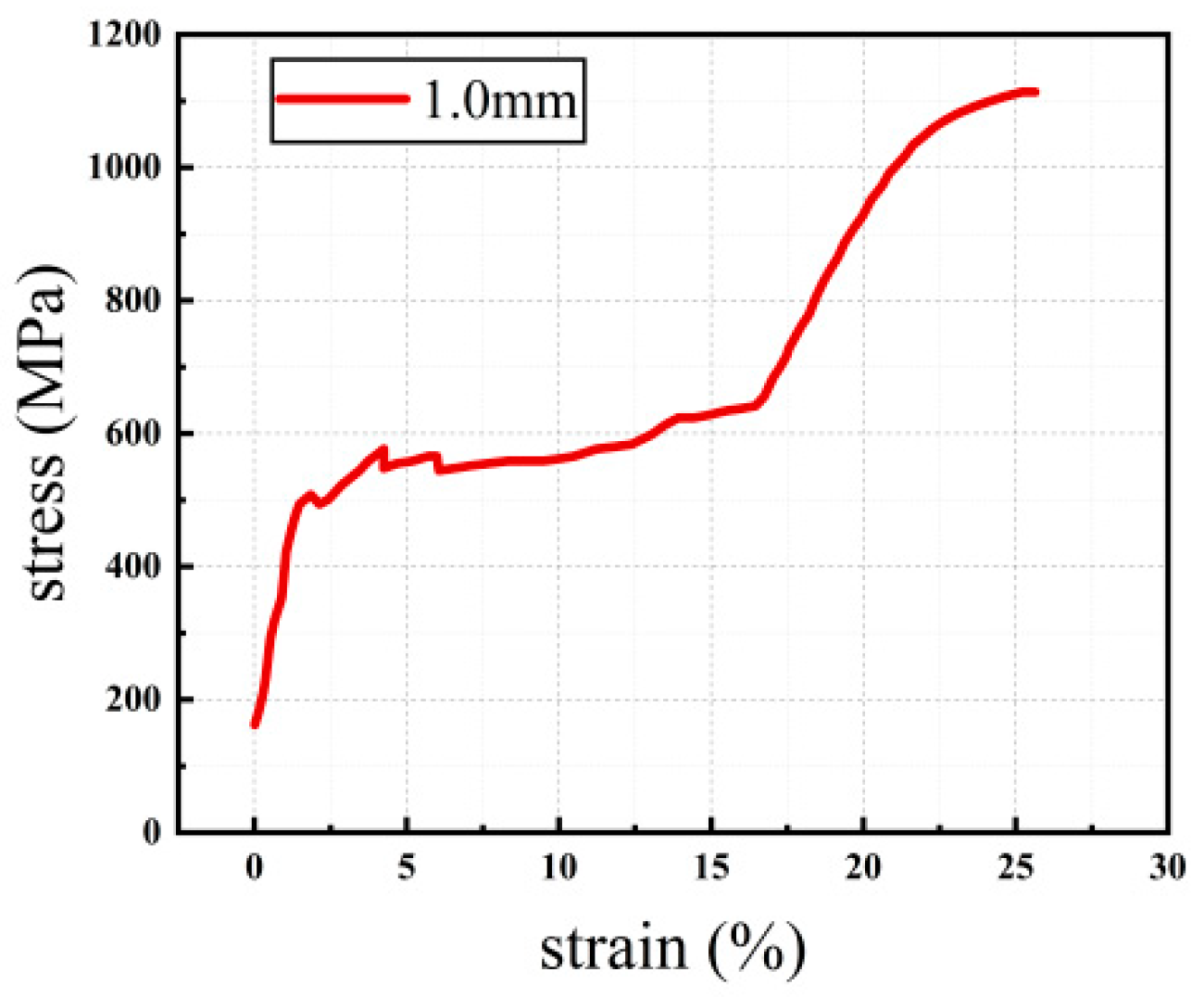
2.1.2. Shape Memory Alloy (SMA)
2.1.3. Steel Bar
2.2. Design of Tensile Test
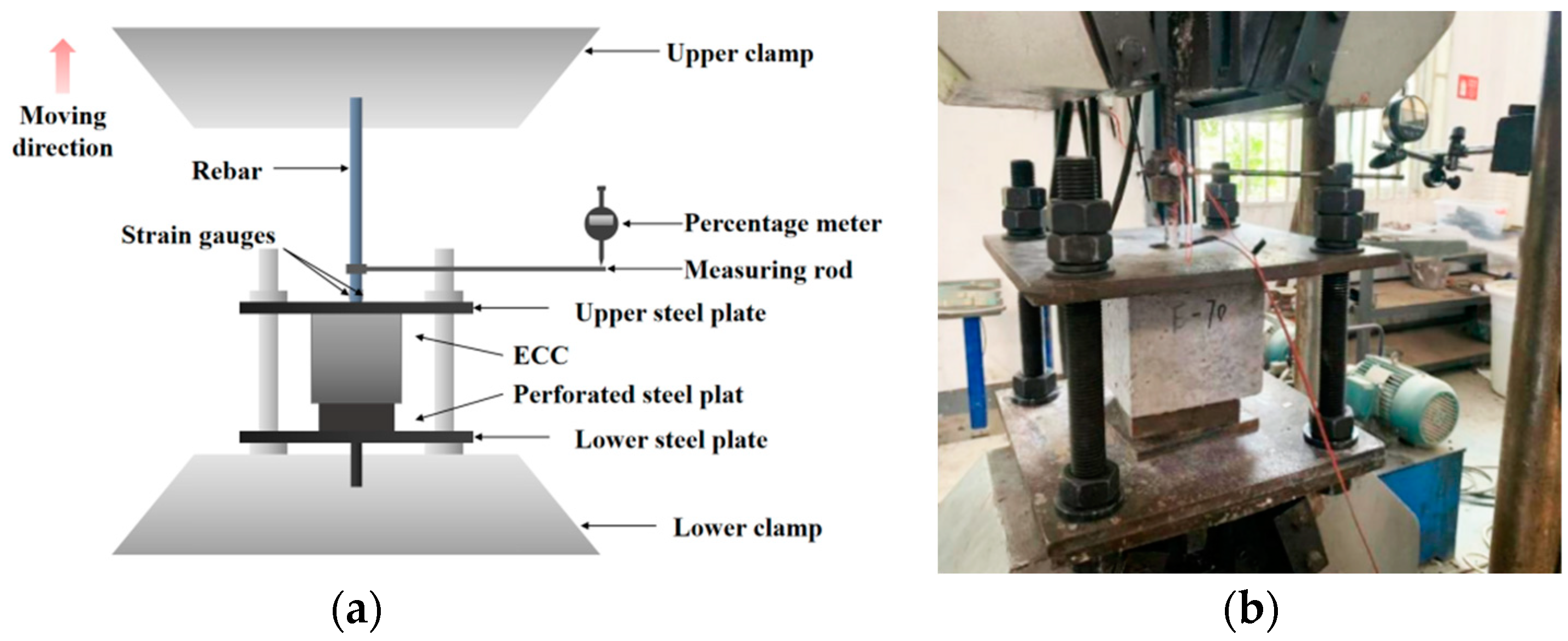
2.3. Test Loading and Measuring Devices
3. Test Results and Analysis
3.1. Test Material
3.2. Bond Strength
3.2.1. Test Results
3.2.2. Influencing Factors
Diameter of the Steel Bar
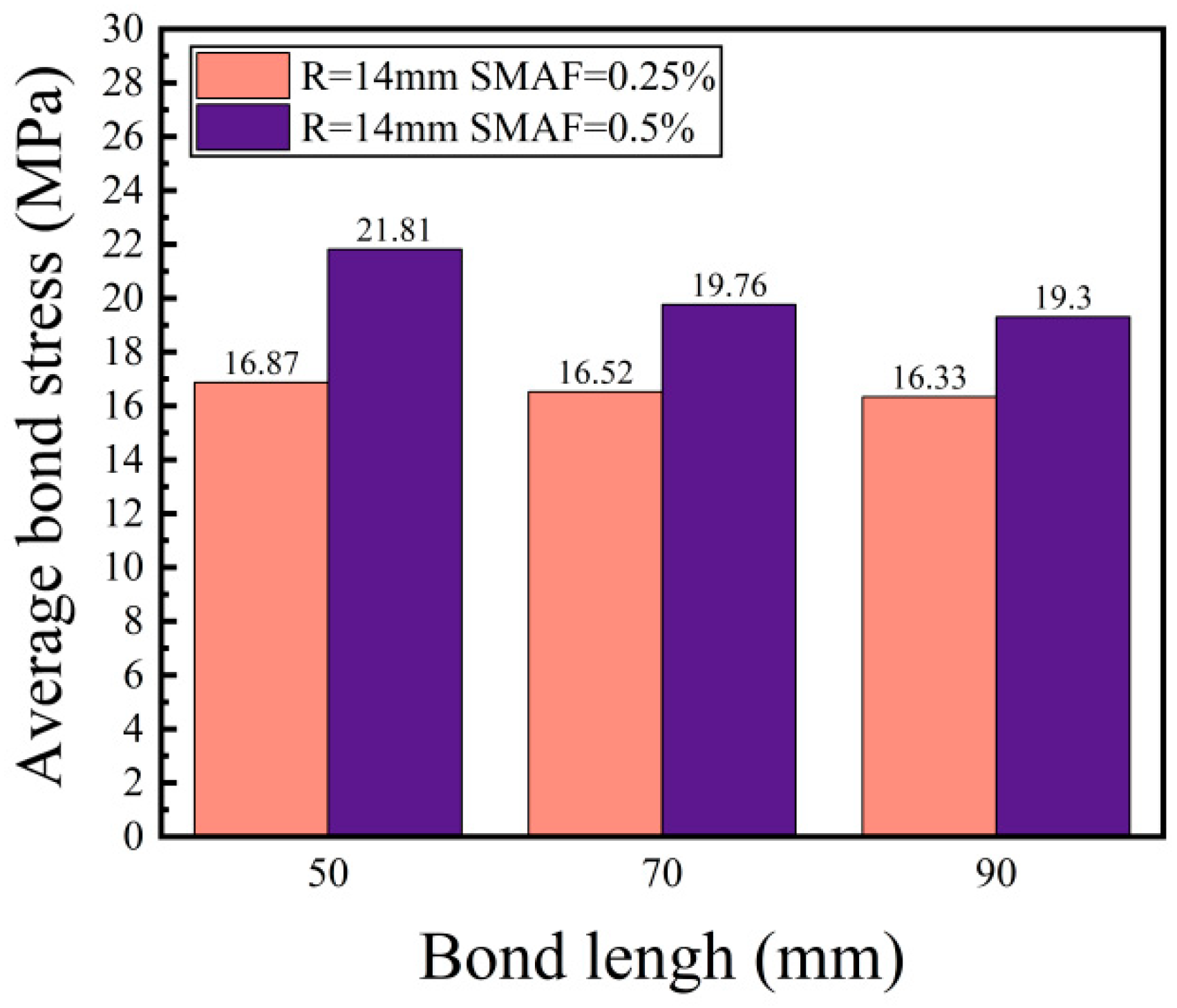
Bond Length
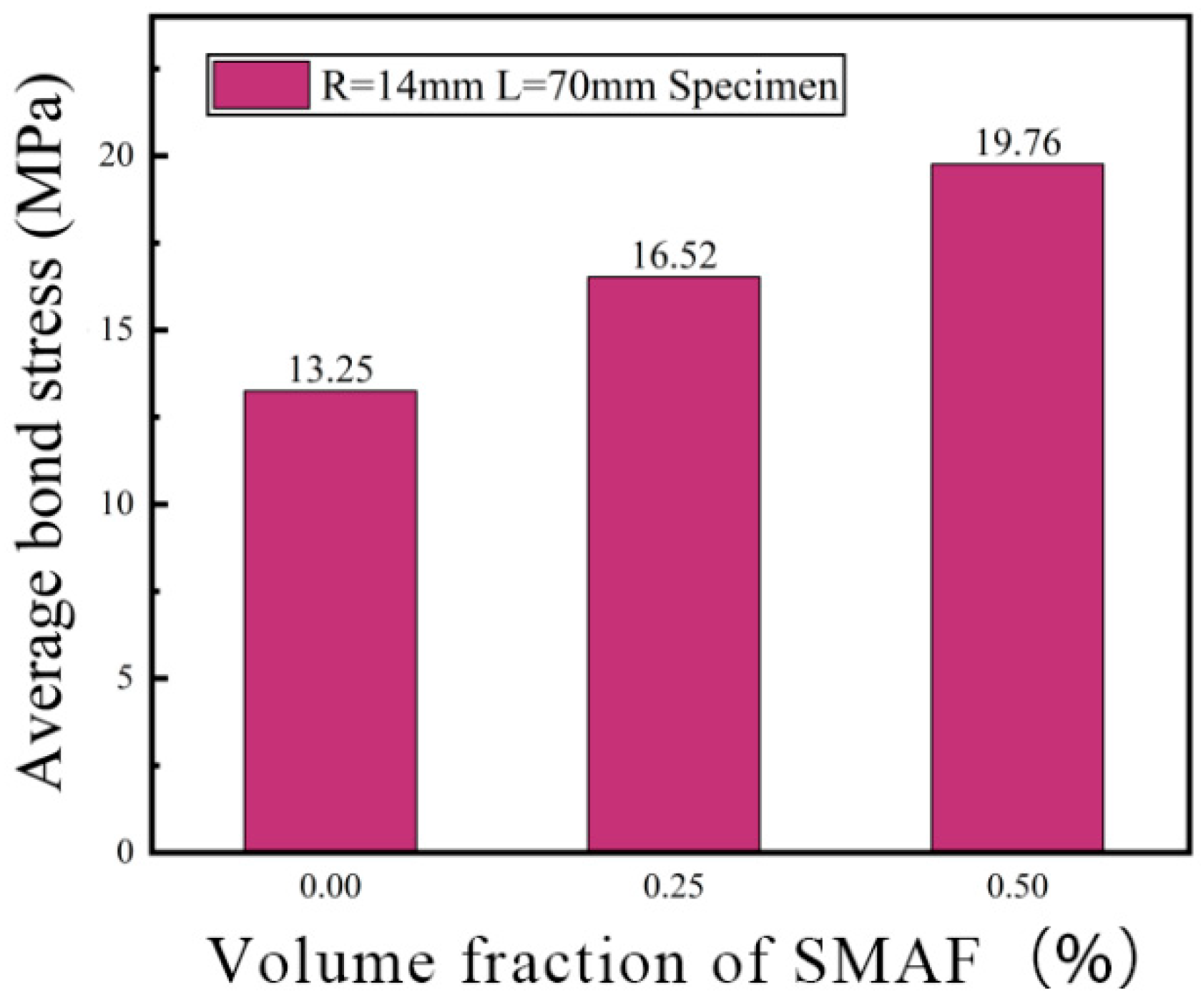
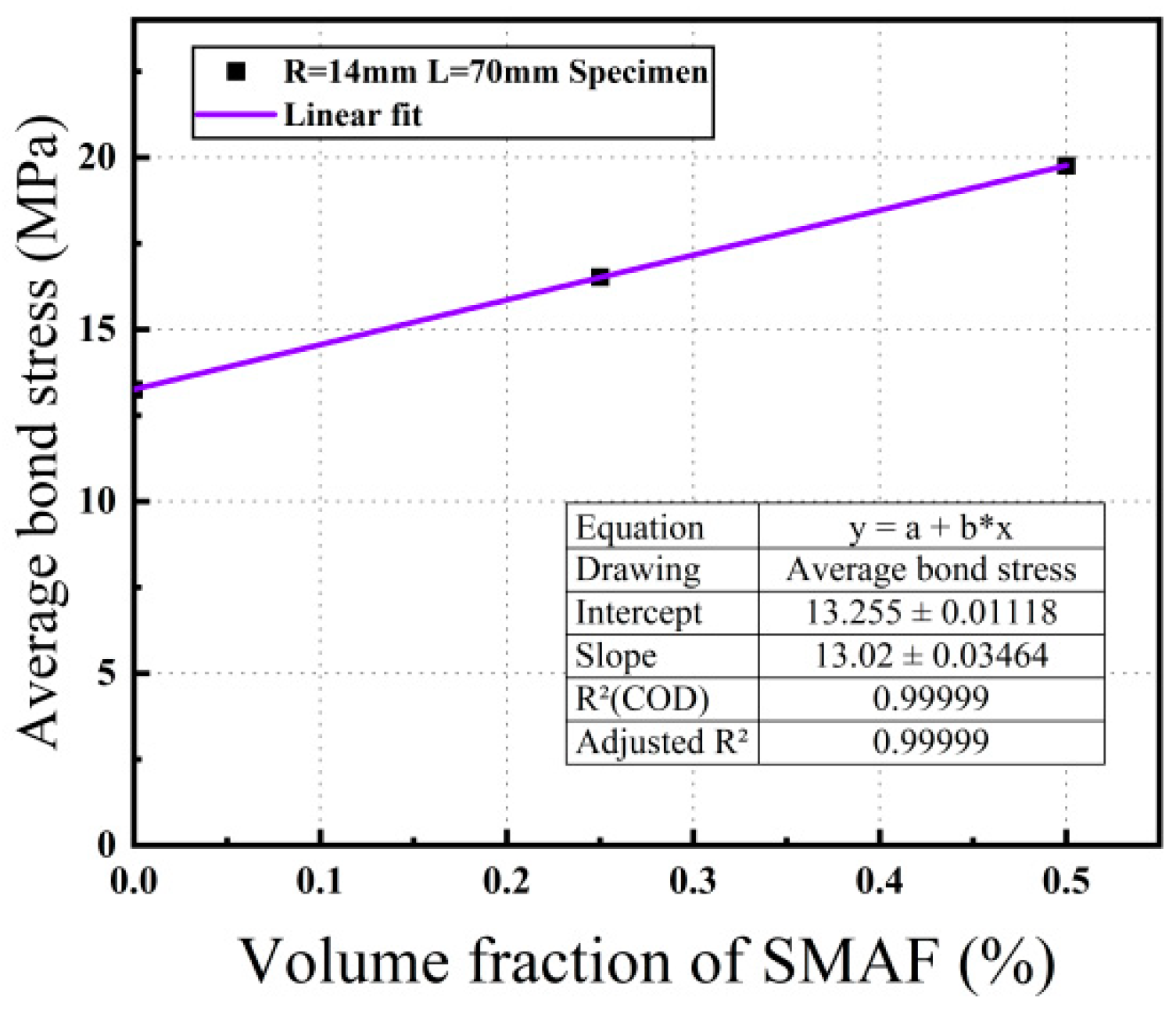
Volume Fraction of SMAF
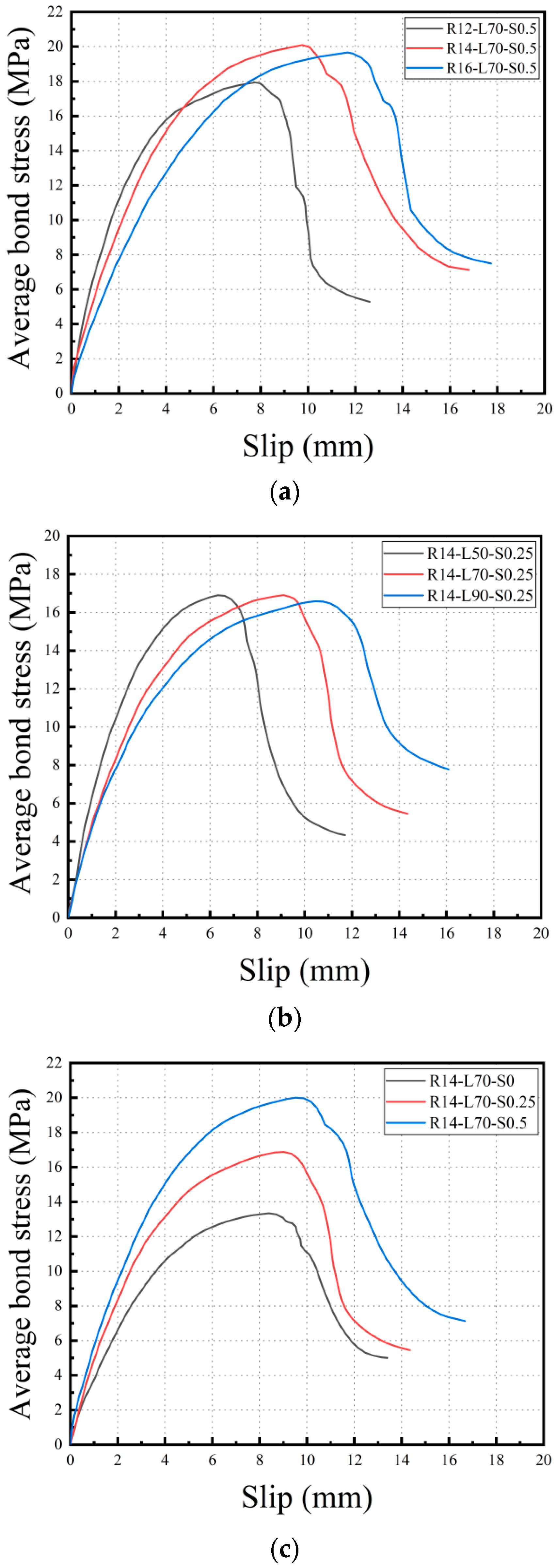
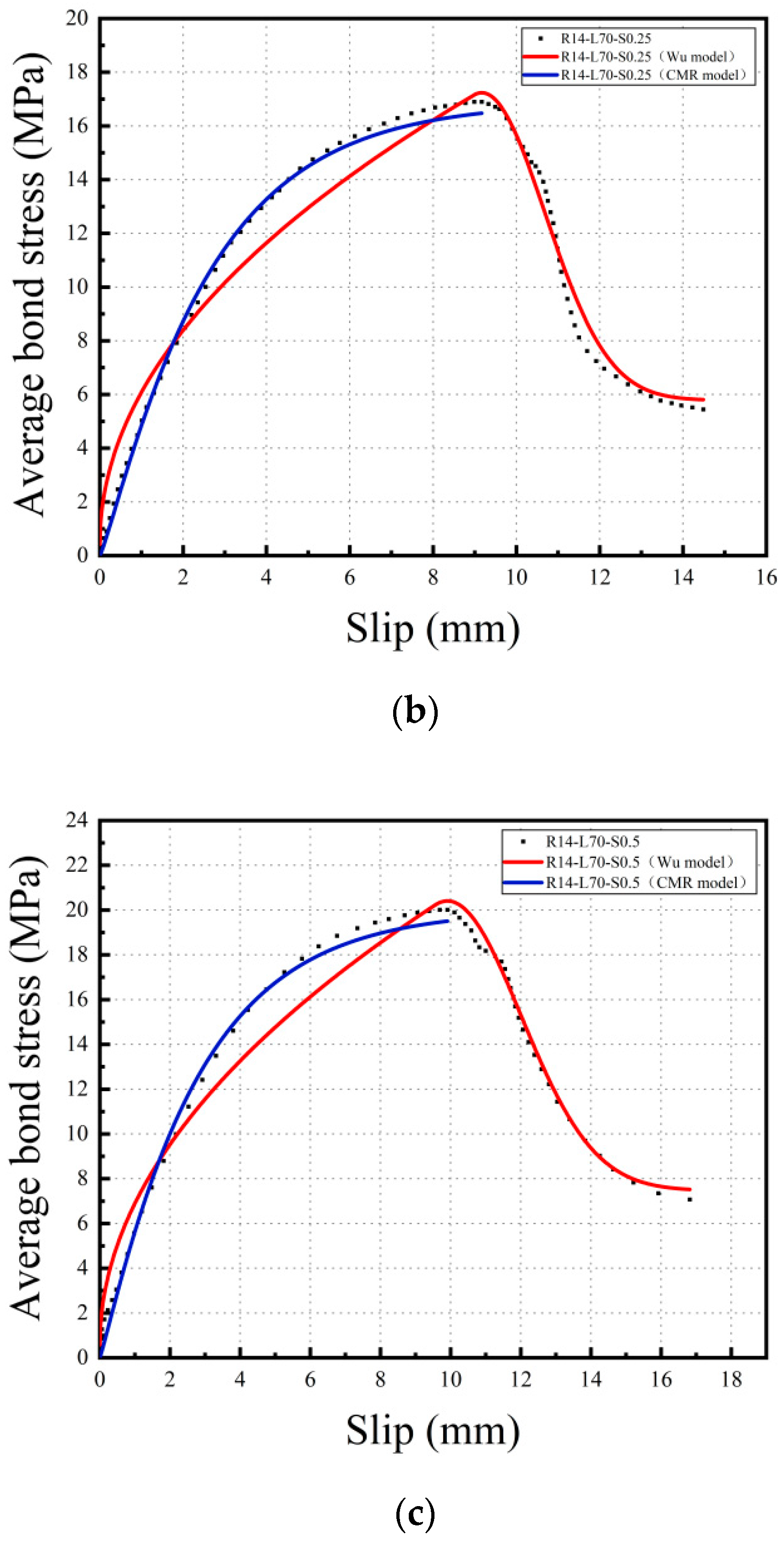
3.3. Bond-Slip Relationship
- (1)
- The initial cracking stage: the bond-slip curve appears as a straight line. At this stage, the bond between the steel bar and the matrix is mainly controlled by chemical adhesion forces. Despite the fact that several micro-cracks propagate from the top of the protruding ribs, most of the cracks remain in their original or undeveloped state due to the low level of the applied load. The action of the SMA and PVA fibers at this stage has not been activated.
- (2)
- The stable crack extension stage: the bond-slip curve enters a non-linear rising phase with a decreasing slope. In this stage, force transfer is primarily controlled by the mechanical interlocking force between the rib of the reinforcing steel and the matrix. As the applied load increases, the micro-cracks in the specimen begin to expand continuously at the matrix and rib of the reinforcing steel, leading to the development of multiple fine cracks, thus causing a continuous softening of the bond reaction. During this period, the cracks in the specimen have a certain width, and the bridging effect of SMA and PVA fibers in the matrix helps to suppress crack propagation, allowing the specimen to achieve a higher maximum bond strength.
- (3)
- The unstable crack propagation stage: the bond-slip curve enters the descending phase. Micro-cracks in the specimen gradually develop and accumulate, forming large cracks, and the speed of crack propagation becomes unstable. The load-carrying capacity of the specimen continuously decreases until shear failure occurs.
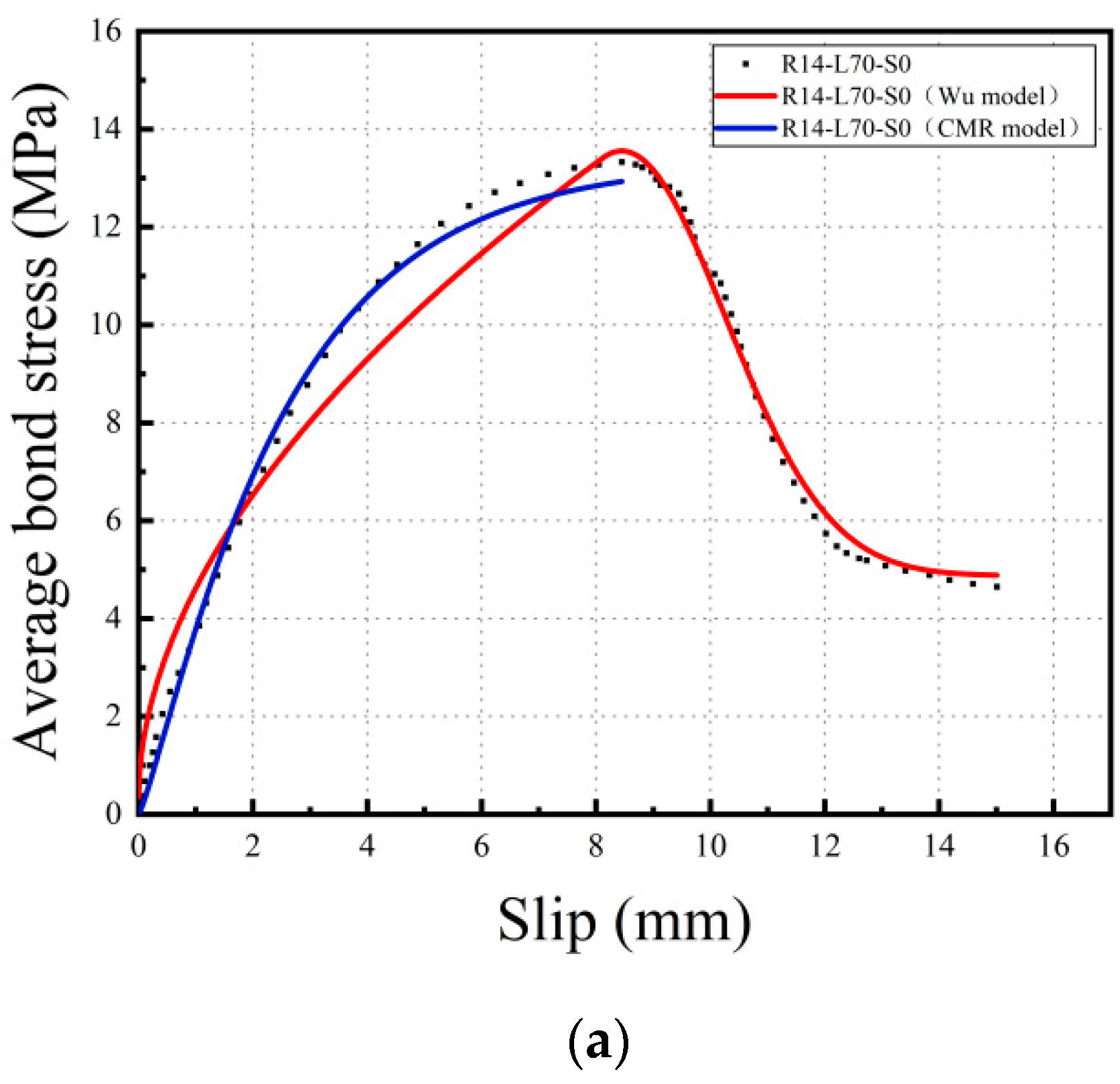
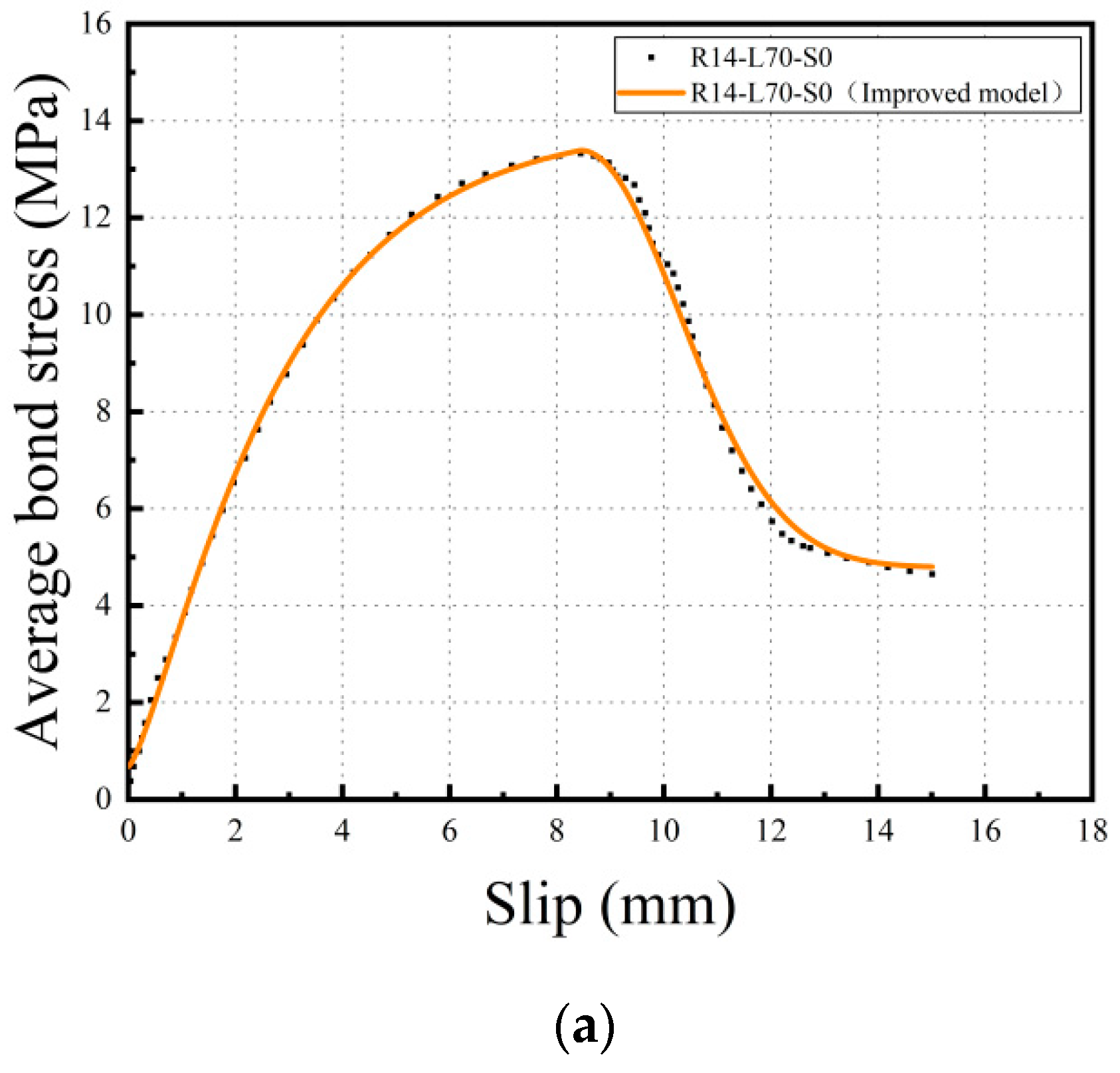
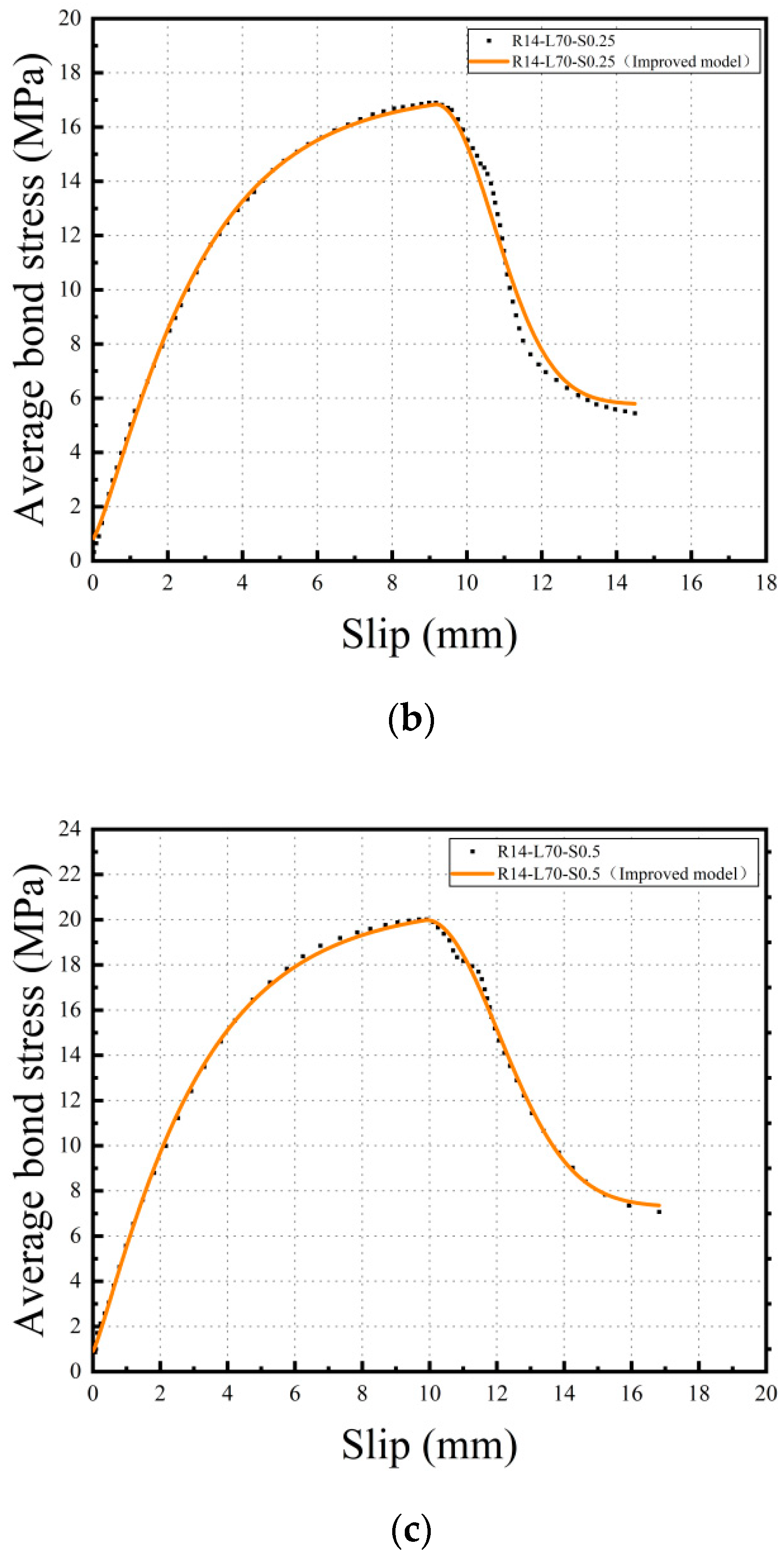
3.4. Bond-Slip Constitutive Model
4. Conclusions
- The failure mode of the pull-out specimens is mainly steel bar pull-out failure, and no through-cracks appeared in the SMAF-ECC matrix when the specimens failed, indicating good tensile capacity of the matrix; the specimens with SMAF have significantly improved bond strength compared with those without SMAF, with the specimen of steel bar diameter 12 mm, bond length 70 mm, and SMAF volume fraction 0.5% showing the largest increase in bond strength, reaching 52.96%.
- Within the scope of the experiment, it was found that as the diameter of the steel bar increased, the rib height relatively decreased, the rib spacing relatively increased, and the mechanical interlocking force decreased, resulting in a decrease in bond strength. When the bond length exceeded the effective bond length, an increase in bond length would lead to a smaller increase in tensile load than in bond area, a more uneven distribution of bond stress, and greater radial shrinkage of the reinforcing steel, thereby causing a decrease in bond strength. Increasing the volume fraction of SMAF effectively enhanced the crack resistance of the ECC matrix, as well as the shear and tensile strength of the matrix, thus improving the bond strength.
- Based on the experimental data, the bond-slip curve between the steel rebar and SMAF-ECC matrix was obtained. An improved bond-slip constitutive model was proposed by introducing the SMAF fiber content influence coefficient to the existing model. Curve fitting analysis shows that the improved bond-slip constitutive model curve matches the experimentally obtained bond-slip curve well, with a determination coefficient of 0.99.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, Z.; Shi, X. Principle and Analysis of Reinforced Concrete; Tsinghua University Publication: Beijing, China, 2003. [Google Scholar]
- Chu, S.H.; Unluer, C.; Yoo, D.Y.; Sneed, L.; Kwan, A.K.H. Bond of steel reinforcing bars in self-prestressed hybrid steel fiber reinforced concrete. Eng. Struct. 2023, 291, 116390. [Google Scholar] [CrossRef]
- He, S.; Guan, P.; Wang, Q.; Fang, Z.; Mosallam, A. Investigation on structural performance of perfobond strip connector group in steel-concrete joints. Eng. Struct. 2021, 242, 112571. [Google Scholar] [CrossRef]
- Ding, Y.; Mao, W.H.; Wei, W.; Liu, J.P.; Chen, Y.F. Bond behavior and anchorage length of deformed bars in steel-polyethylene hybrid fiber engineered cementitious composites. Eng. Struct. 2022, 252, 113675. [Google Scholar] [CrossRef]
- Chao, S.H.; Naaman, A.E.; Parra-Montesinos, G.J. Bond behavior of reinforcing bars in tensile strain-hardening fiber-reinforced cement composites. ACI Struct. J. 2009, 106, 897. [Google Scholar]
- Li, V.C. ECC-tailored composites through micromechanical modeling. In Fiber Reinforced Concrete: Present and the Future; Banthia, N., Bentur, A., Mufti, A., Eds.; CSCE: Monteal, QC, Canada, 1998; pp. 64–97. [Google Scholar]
- Li, V.C.; Wang, S.; Wu, C. Tensile strain-hardening behavior of polyvinyl alcohol engineered cementitious composite (PVA-ECC). Mater. J. 2001, 98, 483–492. [Google Scholar]
- Lin, Z.; Kanda, T.; Li, V.C. On interface property characterization and performance of fiber reinforced cementitious composites. Concr. Sci. Eng. 1999, 1, 173–184. [Google Scholar]
- Li, H.; Xu, S.; Leung, C.K.Y. Tensile and flexural properties of ultra high toughness cemontious composite. J. Wuhan Univ. Technol. Mat. Sci. Edit. 2009, 24, 677–683. [Google Scholar] [CrossRef]
- Li, V.C.; Fischer, G.; Kim, Y.; Lepech, M.D.; Qian, S.; Weimann, M.; Wang, S. Durable Link Slabs for Jointless Bridge Decks Based on Strain-Hardening Cementitious Composites; National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 2003. [Google Scholar]
- Cui, D. Research on Shape Memory Alloy and Its Intelligent Concrete Structure; Dalian University of Technology: Dalian, China, 2007. (In Chinese) [Google Scholar]
- Hu, J.W. Cyclic Behavior of Superelastic Shape Memory Alloys (SMAs) under Various Loading Conditions. Urban Sci. 2018, 7, 5–9. [Google Scholar]
- Qian, H.; Zhang, Q.; Zhang, X.; Deng, E.; Gao, J. Experimental Investigation on Bending Behavior of Existing RC Beam Retrofitted with SMA-ECC Composites Materials. Materials 2021, 15, 12. [Google Scholar] [CrossRef]
- Hung, C.C.; Yen, W.M.; Yu, K.H. Vulnerability and improvement of reinforced ECC flexural members under displacement reversals: Experimental investigation and computational analysis. Constr. Build. Mater. 2016, 107, 287–298. [Google Scholar] [CrossRef]
- Choi, E.; Kim, H.S.; Nam, T.H. Effect of crimped SMA fiber geometry on recovery stress and pullout resistance. Compos. Struct. 2020, 247, 112466. [Google Scholar] [CrossRef]
- Choi, E.; Ostadrahimi, A.; Lee, J.H. Pullout resistance of crimped reinforcing fibers using cold-drawn NiTi SMA wires. Constr. Build. Mater. 2020, 265, 120858. [Google Scholar] [CrossRef]
- Wang, P. The Pullout Experimental Study on Knotted Shape Memory Alloy Fiber Composite. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2007. (In Chinese). [Google Scholar]
- Luo, C. Experimental Study on Controlled V-shaped Notch Propagation in Matrix by Knotted Shape Memory Alloy Fibers. Master’s Dissertation, Beijing Jiaotong University, Beijing, China, 2009. (In Chinese). [Google Scholar]
- Shajil, N.; Srinivasan, S.M.; Santhanam, M. An experimental study on self-centering and ductility of pseudo-elastic shape memory alloy (PESMA) fiber reinforced beam and beam-column joint specimens. Mater. Struct. 2016, 49, 783–793. [Google Scholar] [CrossRef]
- Ali, M.A.E.M.; Soliman, A.M.; Nehdi, M.L. Hybrid-fiber reinforced engineered cementitious composite under tensile and impact loading. Mater. Des. 2017, 117, 139–149. [Google Scholar] [CrossRef]
- Ali, M.A.; Nehdi, M.L. Experimental investigation on mechanical properties of shape memory alloy fibre-reinforced ECC composite. In The International Conference on Civil and Architecture Engineering; In Proceedings of the 11th International Conference on Civil and Architecture Engineering; Military Technical College: Cairo, Egypt, 2016; Volume 1, pp. 1–11. [Google Scholar]
- Yang, Z.; Du, Y.; Liang, Y.; Ke, X. Mechanical Behavior of Shape Memory Alloy Fibers Embedded in Engineered Cementitious Composite Matrix under Cyclic Pullout Loads. Materials 2022, 15, 4531. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Deng, T.; Li, J.; Xu, C. Experimental Study on Self-Centering Performance of the SMA Fiber Reinforced ECC Composite Beam. Materials 2022, 15, 3062. [Google Scholar] [CrossRef] [PubMed]
- Tian, J.; Wu, X.; Wang, W.-W.; Hu, S.; Tan, X.; Du, Y.; Zheng, Y.; Sun, C. Experimental study and mechanics model of ECC-to-concrete bond interface under tensile loading. Compos. Struct. 2022, 285, 115203. [Google Scholar] [CrossRef]
- Cai, J.; Pan, J.; Tan, J.; Li, X. Bond behaviours of deformed steel rebars in engineered cementitious composites (ECC) and concrete. Constr. Build. Mater. 2020, 252, 119082. [Google Scholar] [CrossRef]
- Liu, H.; Liu, Y.; Li, A.; Lei, H. Experimental study on the bond performance of deformed steel bar in ultrahigh performance concrete. Case Stud. Constr. Mater. 2023, 18, e01874. [Google Scholar] [CrossRef]
- Yoo, D.Y.; Shin, H.O. Bond performance of steel rebar embedded in 80–180 MPa ultra-high-strength concrete. Cem. Concr. Compos. 2018, 93, 206–217. [Google Scholar] [CrossRef]
- Jiu, Y.; Nan, D.; Hao, D. Experimental study on the adhesion performance of shape memory alloy fibers in highly ductile cementitious composites. Ind. Constr. 2021, 51, 188–196. (In Chinese) [Google Scholar]
- JC/T2461-2018; Standard Test Method for the Mechanical Properties of Ductile Fiber Reinforced Cementitious Composites. China Building Industry Press: Beijing, China, 2018.
- Fathi, H.; Shokrieh, M.M.; Saeedi, A. Effect of tensile loading rate on interfacial properties of SMA/polymer composites. Compos. Part B Eng. 2020, 183, 107730. [Google Scholar] [CrossRef]
- GB 50152–92; Number Standard Methods for Testing of Concrete Structures. China Architecture & Building Press: Beijing, China, 2012.
- JGJ 55–2011; Specification for Mix Proportion Fesign of Ordinary Concrete. China Architecture & Building Press: Beijing, China, 2011.
- Butler, L.; West, J.S.; Tighe, S.L. The effect of recycled concrete aggregate properties on the bond strength between RCA concrete and steel reinforcement. Cem. Concr. Res. 2011, 41, 1037–1049. [Google Scholar] [CrossRef]
- Krstulovic-Opara, N.; Watson, K.A.; LaFave, J.M. Effect of increased tensile strength and toughness on reinforcing-bar bond behavior. Cem. Concr. Compos. 1994, 16, 129–141. [Google Scholar] [CrossRef]
- Wang, W. Experimental Study on the Anchorage Performance of Ceramic Concrete Bonded to Steel Reinforcement. Master’s Dissertation, Guangxi University, Nanning, China, 2005. [Google Scholar]
- Soroushian, P.; Bayasi, Z. Local bond behaviour of deformed bars in steel fibre reinforced concrete joints. Mag. Concr. Res. 1990, 42, 91–95. [Google Scholar] [CrossRef]
- Mi, Y. Experimental and Theoretical Study on the Bonding Performance of FRP Tendons with ECC. Master’s Dissertation, Southeast University, Nanjing, China, 2015. (In Chinese). [Google Scholar]
- Lin, R.; Yu, X.; Qin, C.; Ju, Y. Study on the bonding performance between reactive powder concrete and steel bar. J. Phys. Conf. Ser. IOP Publ. 2022, 2368, 012034. [Google Scholar] [CrossRef]
- Ali, M.; Nehdi, M.L. Innovative crack-healing hybrid fiber reinforced engineered cementitious composite. Constr. Build. Mater. 2017, 150, 689–702. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, X.; Zheng, J.; Hu, Y.; Li, Q. Experimental study on the bond behavior of deformed bars embedded in concrete subjected to lateral tension. Mater. Struct. 2014, 47, 1647–1668. [Google Scholar] [CrossRef]
- Cosenza, E.; Manfredi, G.; Realfonzo, R. Behavior and modeling of bond of FRP rebars to concrete. J. Compos. Constr. 1997, 1, 40–51. [Google Scholar] [CrossRef]





| Cement /kg | Fly Ash /kg | Sand Cement Ratio | Water Cement Ratio | Water Reducing Agent/kg | Fiber Admixture * (%) |
|---|---|---|---|---|---|
| 1.0 | 2.4 | 0.36 | 0.25 | 0.0082 | 2.0 |
| Diameter (mm) | Starting Point of Stress Platform | Ending Point of Stress Platform | Tensile Strength a (MPa) | Ultimate Strain b (%) | ||
|---|---|---|---|---|---|---|
| Strain (%) | Stress (MPa) | Strain (%) | Stress (MPa) | |||
| 1.0 | 1.55 | 441.86 | 16.29 | 589.63 | 1111.01 | 25.53 |
| Diameter (mm) | Yield Strength (MPa) | Tensile Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|---|
| 12 | 470 ± 1 | 589 ± 2 | 182 ± 1 |
| 14 | 464 ± 1 | 579 ± 1 | 185 ± 1 |
| 16 | 471 ± 1 | 568 ± 2 | 181 ± 8 |
| Specimen | Steel Bar Diameter | Bond Length | Volume Fraction of SMAF |
|---|---|---|---|
| R12-L70-S0 | 12 mm | 70 mm | 0% |
| R14-L70-S0 | 14 mm | 70 mm | 0% |
| R16-L70-S0 | 16 mm | 70 mm | 0% |
| R14-L50-S0.25 | 14 mm | 50 mm | 0.25% |
| R14-L90-S0.25 | 14 mm | 90 mm | 0.25% |
| R14-L70-S0.25 | 14 mm | 70 mm | 0.25% |
| R12-L70-S0.5 | 12 mm | 70 mm | 0.50% |
| R14-L70-S0.5 | 14 mm | 70 mm | 0.50% |
| R16-L70-S0.5 | 16 mm | 70 mm | 0.50% |
| R14-L50-S0.5 | 14 mm | 50 mm | 0.50% |
| R14-L90-S0.5 | 14 mm | 90 mm | 0.50% |
| Specimen | Ultimate Load/N | Bond Strength/MPa | Failure Mode |
|---|---|---|---|
| R12-L70-S0 | 36,050.43 | 13.67 | Pull Out Failure |
| R14-L70-S0 | 40,777.92 | 13.25 | Pull Out Failure |
| R16-L70-S0 | 45,910.13 | 13.05 | Pull Out Splitting Failure |
| R14-L50-S0.25 | 37,084.43 | 16.87 | Pull Out Failure |
| R14-L90-S0.25 | 64,597.40 | 16.33 | Pull Out Failure |
| R14-L70-S0.25 | 50,840.08 | 16.52 | Pull Out Failure |
| R12-L70-S0.5 | 52,189.12 | 20.91 | Pull Out Failure |
| R14-L70-S0.5 | 60,812.71 | 19.76 | Pull Out Failure |
| R16-L70-S0.5 | 67,863.74 | 19.62 | Pull Out Splitting Failure |
| R14-L50-S0.5 | 45,941.06 | 20.90 | Pull Out Failure |
| R14-L90-S0.5 | 76,374.85 | 19.30 | Pull Out Failure |
| Specimen | Wu Parameter | CMR Parameter | ||||
|---|---|---|---|---|---|---|
| α | β | R2 | Sr | p | R2 | |
| R14-L70-S0 | 0.535 | −10.789 | 0.97 | 2.287 | 1.214 | 0.99 |
| R14-L70-S0.25 | 0.493 | −18.130 | 0.96 | 2.392 | 1.163 | 0.99 |
| R14-L70-S0.5 | 0.503 | −11.241 | 0.97 | 2.623 | 1.104 | 0.99 |
| Specimen | Modified Model Parameter | |||
|---|---|---|---|---|
| Sr | p | β | R2 | |
| R14-L70-S0 | 2.417 | 1.368 | −10.437 | 0.99 |
| R14-L70-S0.25 | 2.440 | 1.313 | −17.896 | 0.99 |
| R14-L70-S0.5 | 2.795 | 1.209 | −10.781 | 0.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Z.; Li, S.; Gao, F.; Wang, R. Experimental Research on the Bond Performance between SMAF-ECC Composites and Steel Bar. Materials 2023, 16, 5037. https://doi.org/10.3390/ma16145037
Yang Z, Li S, Gao F, Wang R. Experimental Research on the Bond Performance between SMAF-ECC Composites and Steel Bar. Materials. 2023; 16(14):5037. https://doi.org/10.3390/ma16145037
Chicago/Turabian StyleYang, Zhao, Shuai Li, Feng Gao, and Rui Wang. 2023. "Experimental Research on the Bond Performance between SMAF-ECC Composites and Steel Bar" Materials 16, no. 14: 5037. https://doi.org/10.3390/ma16145037
APA StyleYang, Z., Li, S., Gao, F., & Wang, R. (2023). Experimental Research on the Bond Performance between SMAF-ECC Composites and Steel Bar. Materials, 16(14), 5037. https://doi.org/10.3390/ma16145037






