Bond Behavior of Plain Bars in Concrete under Reversed Cyclic Loading
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
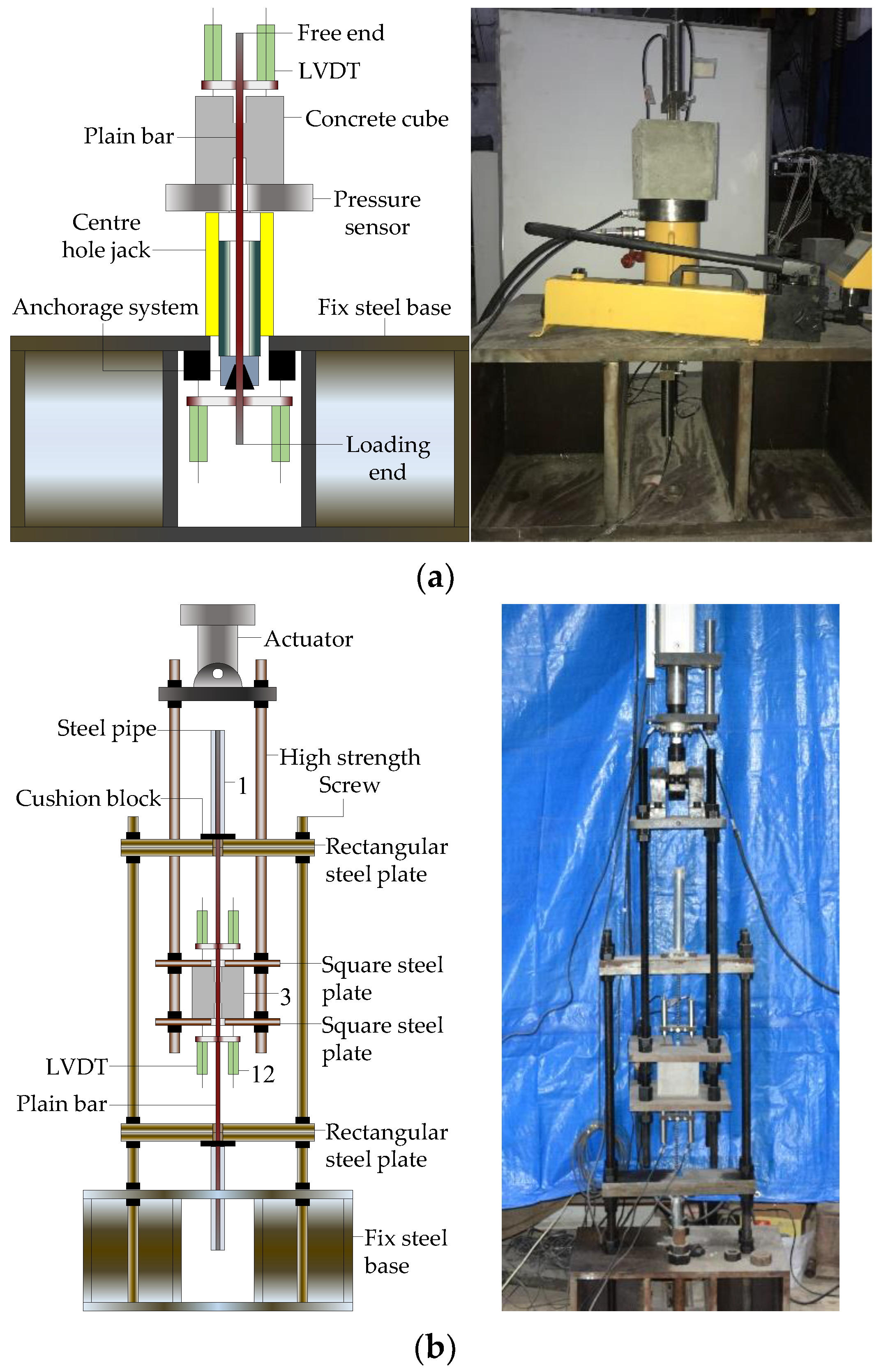
2.2. Bonding Specimens
2.3. Test Devices and Procedures
3. Results and Discussions
3.1. Failure Mode
3.2. Bond Stress–Slip Curves
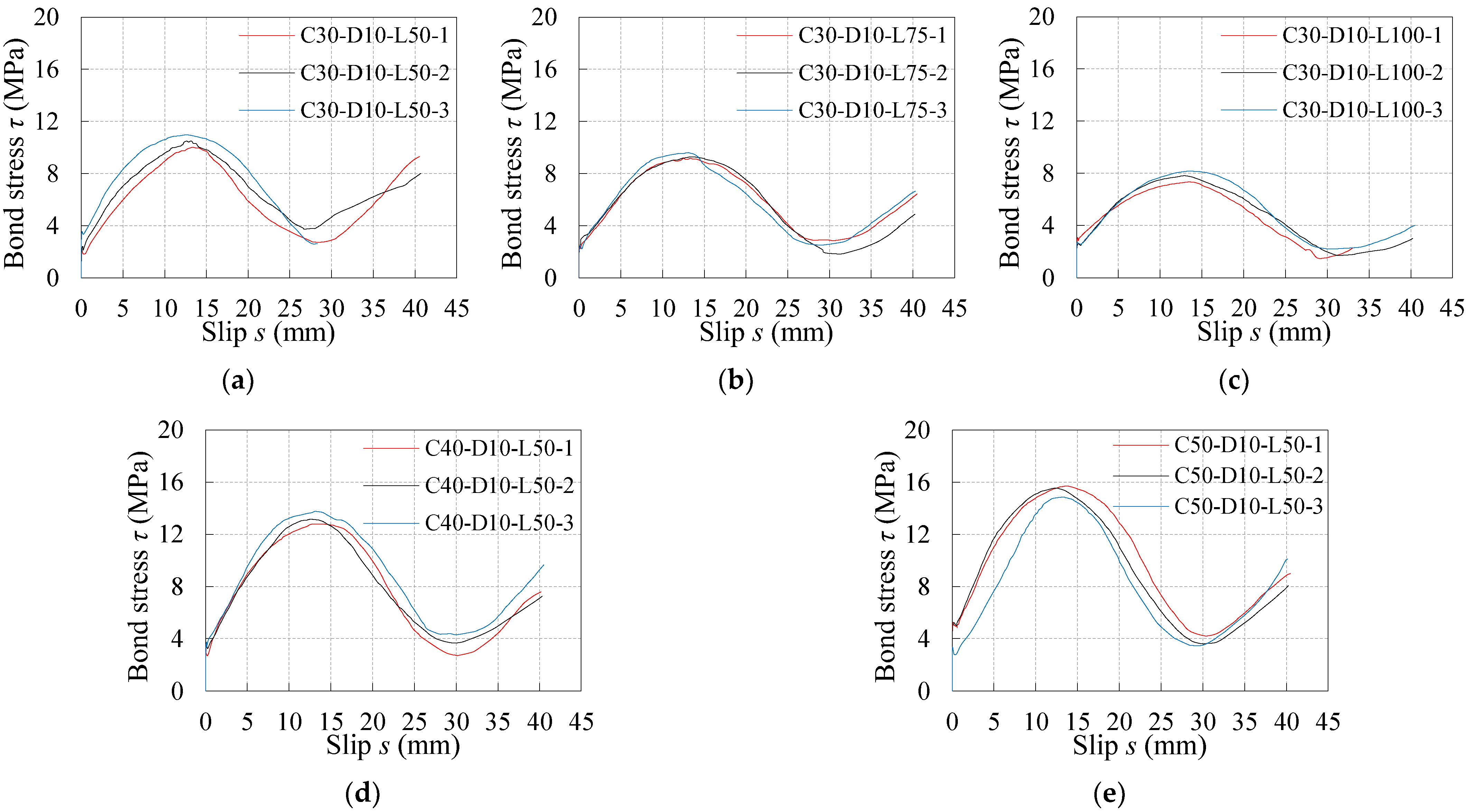
3.2.1. Bond Stress–Slip Curves under Monotonic Loading
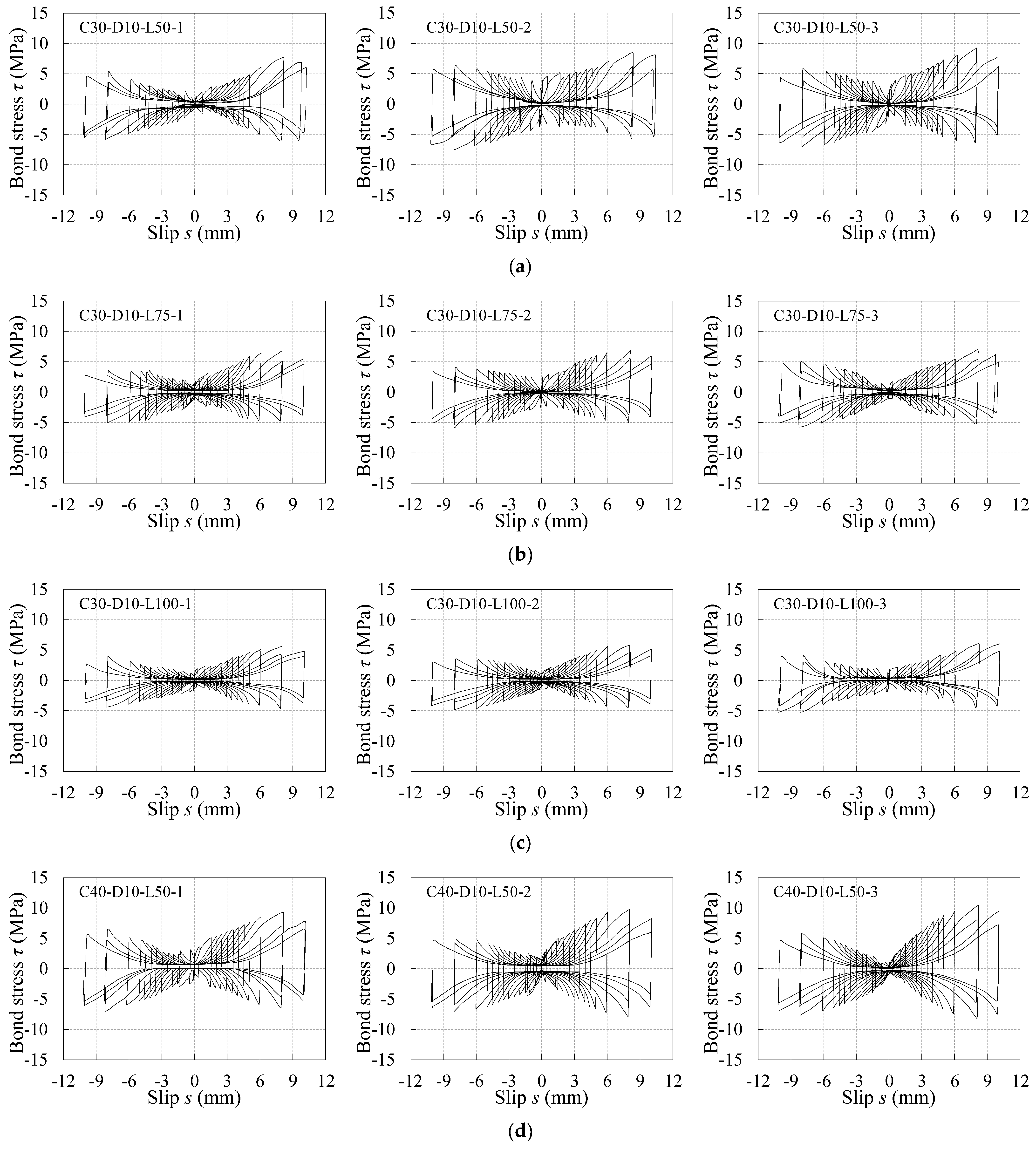
3.2.2. Bond Stress–Slip Curves under Reversed Cyclic Loading
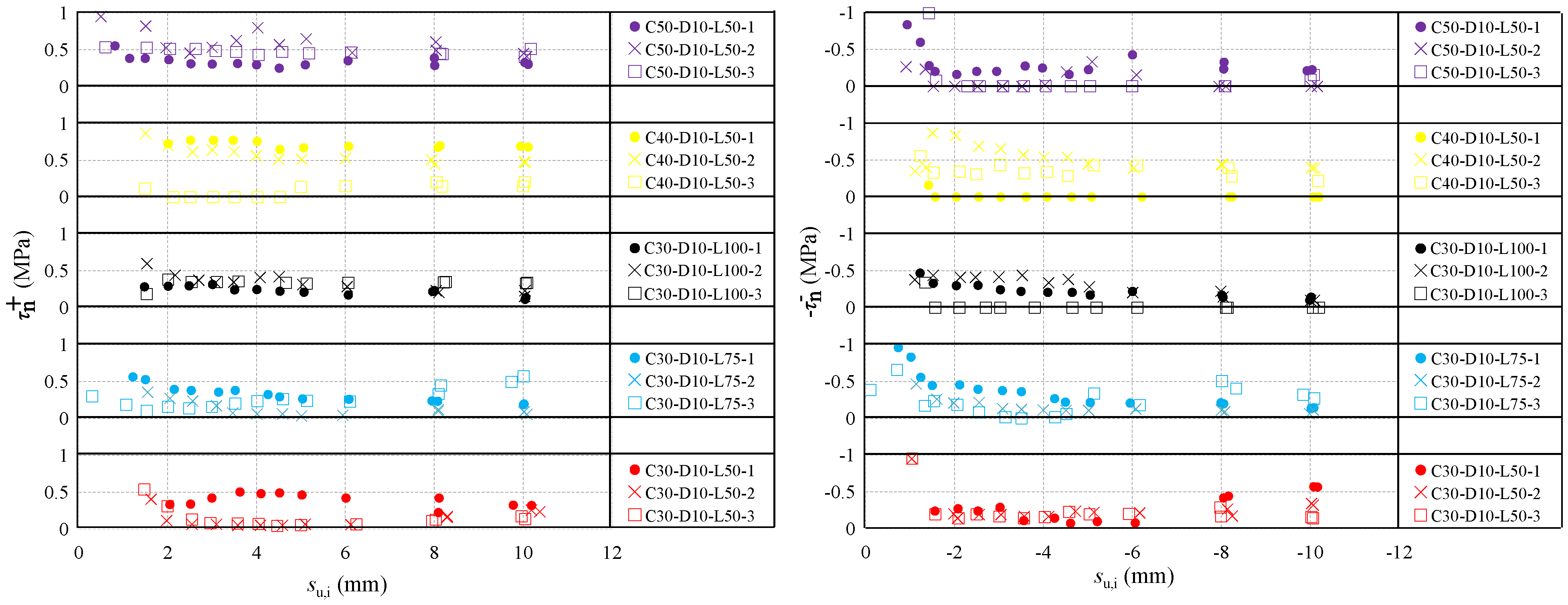
3.3. The Influence of Test Parameters on the Bond Performance
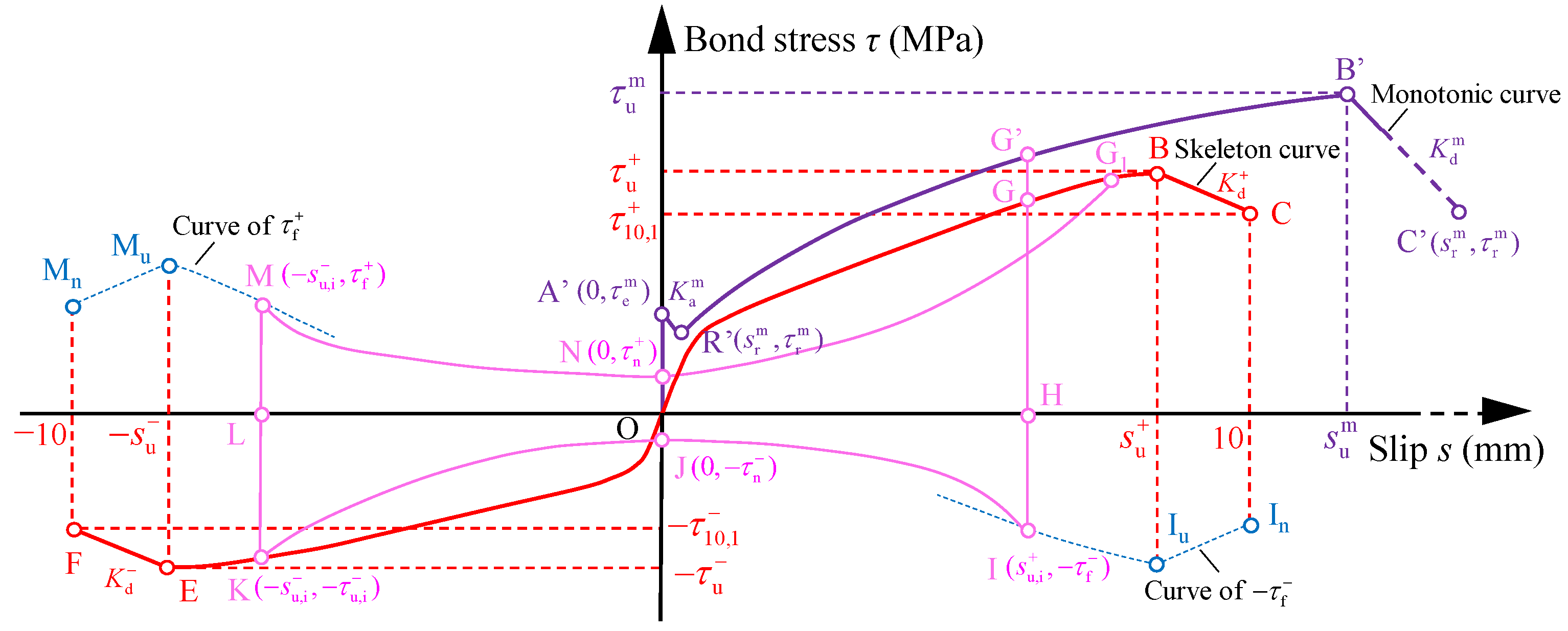
4. Analytical Model of Bond Stress-Slip Curve
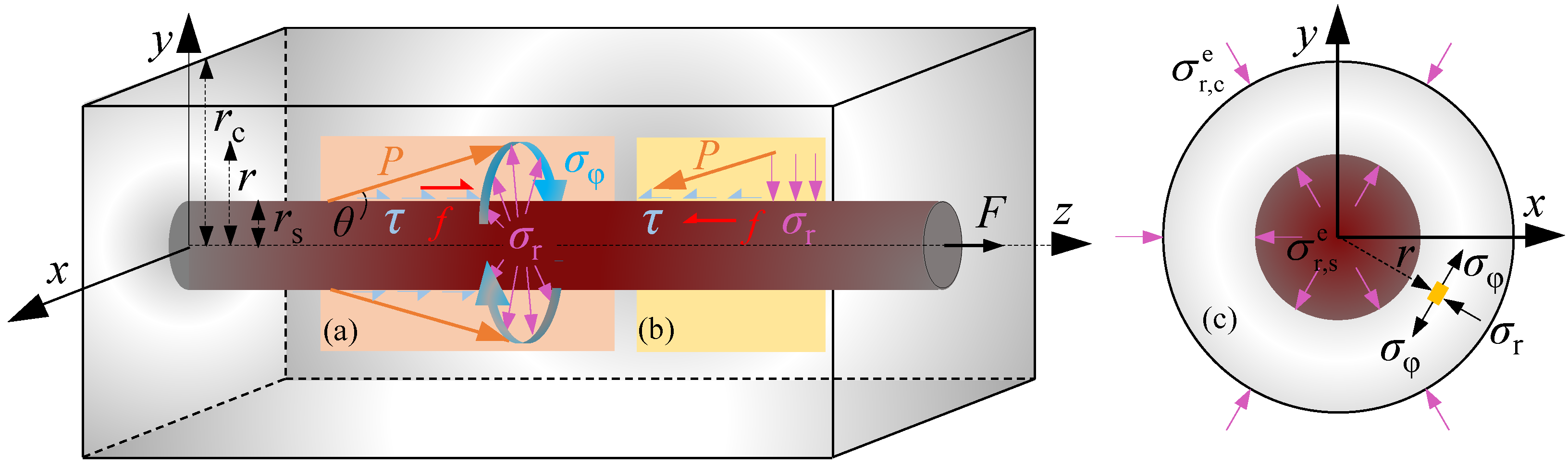
4.1. Elastic Analysis on Bond Stress
4.2. Monotonic and Skeleton Curves
4.2.1. Elastic Stage of Monotonic Curve
4.2.2. Abrupt Stage of Monotonic Curve
4.2.3. Strengthening Stage of Monotonic Curve and Ascent Stage of Skeleton Curve
4.2.4. Degradation Stages of Monotonic and Skeleton Curves
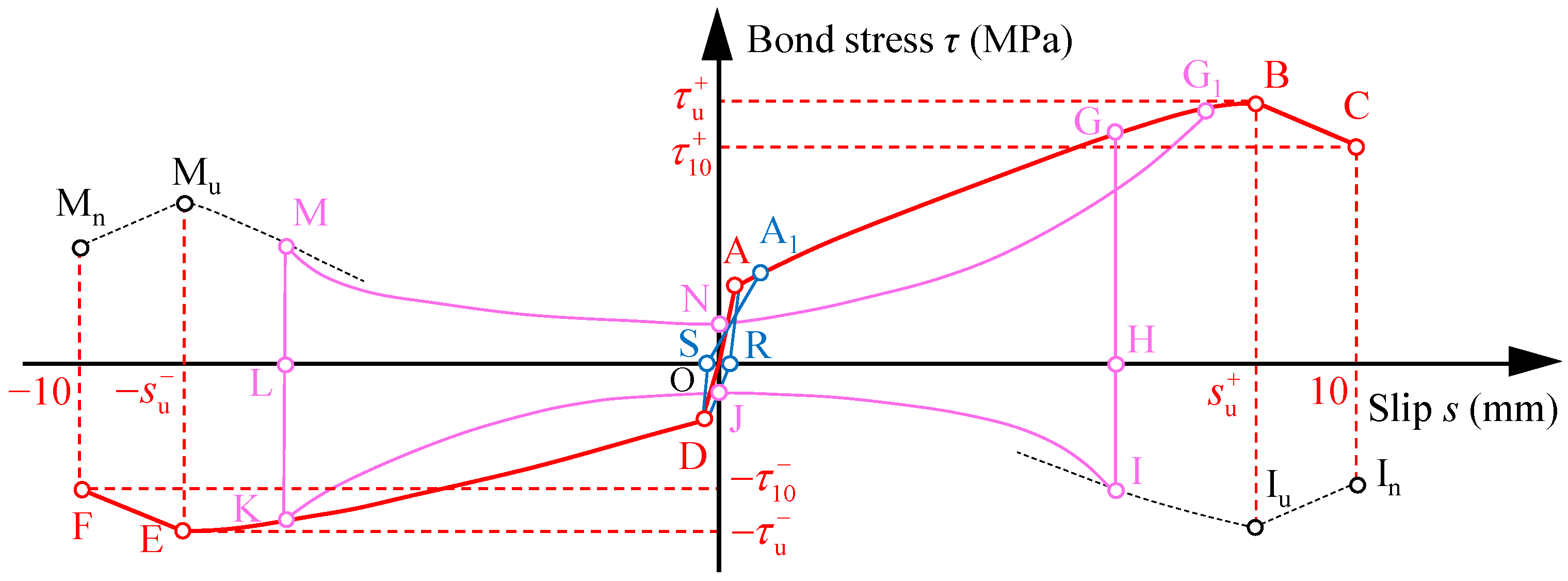
4.3. Hysteresis Loop
4.3.1. Bond Stresses and
4.3.2. Bond Stresses and
4.3.3. Decrease and Re-Increase Branches
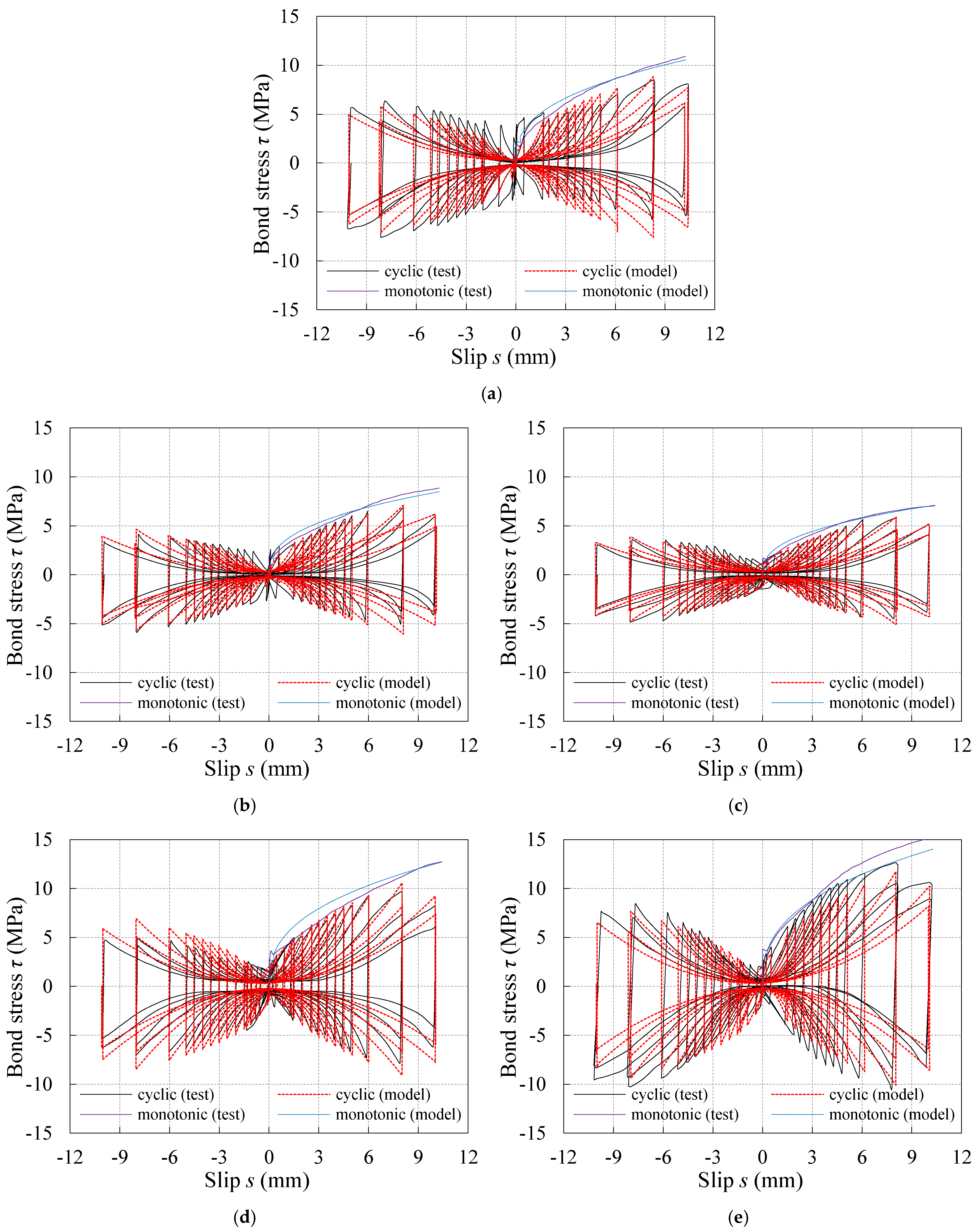
4.4. Verification of the Proposed Model
5. Conclusions
- The bond stress–slip curves under monotonic loading present as an attenuated sine curve; the bond stress–slip curves under reversed cyclic loading present as the butterfly shape and are roughly symmetrical about the origin;
- The maximum bond stress of plain bar in concrete decreases with the increase in embedment length, and increases with the increase in concrete compression strength, whether the specimens are subjected to monotonic loading or reversed cyclic loading.
- The maximum bond stress and corresponding slip of plain bar in concrete under reversed cyclic loading are lower than that under monotonic loading for the specimens with the same concrete compression strength and embedment length, which illustrates that the reversed cyclic loading leads to the degeneration of bond behavior;
- The analytical solutions for the bond stresses at the characteristic points were derived based on the elasticity, which could reflect the influence of the laws of concrete compression strength and embedment length;
- The bond stress–slip model was proposed, which was suitable for predicting the bond stress–slip curves of plain bars in concrete under both monotonic loading and reversed cyclic loading.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hertanto, E. Seismic Assessment of pre-1970s Reinforced Concrete Structures. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 2005. [Google Scholar]
- Hu, Z.; Shah, Y.I.; Yao, P. Experimental and numerical study on interface bond strength and anchorage performance of steel bars within prefabricated concrete. Materials 2021, 14, 3713. [Google Scholar] [CrossRef]
- Tang, C.-W.; Cheng, C.-K. Modeling local bond stress–slip relationships of reinforcing bars embedded in concrete with different strengths. Materials 2020, 13, 3701. [Google Scholar] [CrossRef]
- Arani, K.K.; Marefat, M.S.; Amrollahi-Biucky, A.; Khanmohammadi, M. Experimental seismic evaluation of old concrete columns reinforced by plain bars. Struct. Des. Tall Spec. Build. 2010, 22, 267–290. [Google Scholar] [CrossRef]
- Xiao, J.; Falkner, H. Bond behaviour between recycled aggregate concrete and steel rebars. Constr. Build. Mater. 2007, 21, 395–401. [Google Scholar] [CrossRef]
- Hossain, K.M.A. Bond characteristics of plain and deformed bars in lightweight pumice concrete. Constr. Build. Mater. 2008, 22, 1491–1499. [Google Scholar] [CrossRef]
- Li, F.; Yu, K.; Ding, X.; Li, C. Bond properties of plain steel bar in concrete with machine-made sand. Appl. Mech. Mater. 2013, 438–439, 20–24. [Google Scholar] [CrossRef]
- Wu, Z.; Deng, M.; Zhang, Y.; Chen, H.; Liu, J.; Tian, T. Bond behavior of plain bar in highly ductile fiber-reinforced concrete (HDC) subjected to monotonic and repeated loading. J. Build. Eng. 2023, 72, 106593. [Google Scholar] [CrossRef]
- Purnomo, H.; Chalid, M.; Pamudji, G.; Arrifian, T.W. Bond–slip relationship between sand-coated polypropylene coarse aggregate concrete and plain rebar. Materials 2022, 15, 2643. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, X.; Wu, Z.; Abdellahi, M.M. Bond-slip response of plain bars embedded in self-compacting lightweight aggregate concrete under lateral tensions. J. Mater. Civ. Eng. 2017, 29, 04017084. [Google Scholar] [CrossRef]
- Faleschini, F.; Santamaria, A.; Zanini, M.A.; San José, J.T.; Pellegrino, C. Bond between steel reinforcement bars and Electric Arc Furnace slag concrete. Mater. Struct. 2017, 50, 170. [Google Scholar] [CrossRef]
- Deng, M.; Pan, J.; Sun, H. Bond behavior of steel bar embedded in Engineered Cementitious Composites under pullout load. Constr. Build. Mater. 2018, 168, 705–714. [Google Scholar] [CrossRef]
- Shang, H.; Zhao, T.; Cao, W. Bond behavior between steel bar and recycled aggregate concrete after freeze-thaw cycles. Cold Reg. Sci. Technol. 2015, 118, 38–44. [Google Scholar] [CrossRef]
- Ma, Y.; Guo, Z.; Wang, L.; Zhang, J. Experimental investigation of corrosion effect on bond behavior between reinforcing bar and concrete. Constr. Build. Mater. 2017, 152, 240–249. [Google Scholar] [CrossRef]
- Robuschi, S.; Sumearll, J.; Fernandez, I.; Lundgren, K. Bond of naturally corroded, plain reinforcing bars in concrete. Struct. Infrastruct. Eng. 2020, 102, 792–808. [Google Scholar] [CrossRef]
- Fabbrocino, G.; Verderame, G.M.; Manfredi, G. Experimental behaviour of anchored smooth rebars in old type reinforced concrete buildings. Eng. Struct. 2005, 27, 1575–1585. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, W.; Zheng, J.; Wu, Z.; Hu, Y.; Li, Q. Bond behavior of plain round bars embedded in concrete subjected to lateral tension. Constr. Build. Mater. 2014, 54, 17–26. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, X.; Zheng, J.; Hu, Y.; Li, Q. Bond behavior of plain round bars embedded in concrete subjected to biaxial lateral tensile-compressive stresses. J. Struct. Eng. 2014, 140, 04013089. [Google Scholar] [CrossRef]
- Xu, F.; Wu, Z.; Zheng, J.; Hu, Y.; Li, Q. Bond behavior of plain round bars in concrete under complex lateral pressures. ACI Struct. J. 2014, 111, 15–25. [Google Scholar] [CrossRef]
- Li, X.; Wu, Z.; Zheng, J.; Dong, W. Effect of loading rate on the bond behavior of plain round bars in concrete under lateral pressure. Constr. Build. Mater. 2015, 94, 826–836. [Google Scholar] [CrossRef]
- Li, X.; Wu, Z.; Zheng, J.; Cao, Q. Rate-dependent bond performance of plain bars in concrete under biaxial transverse tensions. Eng. Struct. 2020, 216, 110740. [Google Scholar] [CrossRef]
- Melo, J.; Rossetto, T.; Varum, H. Experimental study of bond-slip in RC structural elements with plain bars. Mater. Struct. 2015, 48, 2367–2381. [Google Scholar] [CrossRef]
- Xing, G.; Zhou, C.; Wu, T.; Liu, B. Experimental study on bond behavior between plain reinforcing bars and concrete. Adv. Mater. Sci. Eng. 2015, 2015, 604280. [Google Scholar] [CrossRef]
- Cairns, J. Local bond–slip model for plain surface reinforcement. Struct. Concr. 2021, 22, 666–675. [Google Scholar] [CrossRef]
- Eligehausen, R.; Popov, E.P.; Bertero, V.V. Local and Bond Stress-Slip Relationships of Deformed Bars under Generalized Excitations; Report no. UCB/EERC 83-23; EERC University of California: Berkeley, CA, USA, 1983. [Google Scholar]
- Zhang, X.; Wu, Z.; Zheng, J.; Dong, W.; Bouchair, A. Ultimate bond strength of plain round bars embedded in concrete subjected to uniform lateral tension. Constr. Build. Mater. 2016, 117, 163–170. [Google Scholar] [CrossRef]
- Pan, J.; Deng, M.; Sun, H. Bond behavior of plain round bar embedded in high ductile concrete under monotonic and cyclic loading. Struct. Concr. 2021, 24, 3446–3460. [Google Scholar] [CrossRef]
- Verderame, G.M.; Ricci, P.; Carlo, G.D.; Manfredi, G. Cyclic bond behaviour of plain bars. Part I: Experimental investigation. Constr. Build. Mater. 2009, 23, 3499–3511. [Google Scholar] [CrossRef]
- Verderame, G.M.; Carlo, G.D.; Ricci, P.; Fabbrocino, G. Cyclic bond behaviour of plain bars. Part II: Analytical investigation. Constr. Build. Mater. 2009, 23, 3512–3522. [Google Scholar] [CrossRef]
- Xa, S.; Nie, B.; Li, A. Bond properties for plain bars in frost-damaged concrete. Mag. Concr. Res. 2019, 71, 975–988. [Google Scholar] [CrossRef]
- Xu, S.; Li, A.; Wang, H. Bond properties for deformed steel bar in frost-damaged concrete under monotonic and reversed cyclic loading. Constr. Build. Mater. 2017, 148, 344–358. [Google Scholar] [CrossRef]
- Hu, X.; Peng, G.; Niu, D.; Wang, J. Bond properties of deformed steel bars in concrete during construction under reversed cyclic loading. Constr. Build. Mater. 2019, 223, 817–829. [Google Scholar] [CrossRef]
- Shen, D.; Wen, C.; Zhu, P.; Li, M.; Ojha, B.; Li, C. Bond behavior between basalt fiber-reinforced polymer bars and concrete under cyclic loading. Constr. Build. Mater. 2020, 258, 119518. [Google Scholar] [CrossRef]
- Zhao, J.; Li, X.; Zhang, X. Experimental and theoretical research on bond performance between CFRP bar and concrete under monotonic and reversed cyclic loading. Eng. Struct. 2021, 246, 112994. [Google Scholar] [CrossRef]
- Cai, G. Seismic Performance and Evaluation of Resilient Circular Concrete Columns. Ph.D. Thesis, Kobe University, Kobe, Japan, 2014. [Google Scholar]
- Sargsyan, G.; Cai, G.; Takeuchi, T.; Sun, Y. Seismic behaviour and assessment of drift-hardening concrete columns. In Proceedings of the 16th World Conference on Earthquake (16WCEE), Santiago, Chile, 9–13 January 2017. [Google Scholar]
- Grigor, S. Cyclic Behavior and Evaluation of Drift-Hardening Concrete Columns. Ph.D. Thesis, Kobe University, Kobe, Japan, 2017. [Google Scholar]
- Liu, Z.; Zhao, H.; Sun, Y.; Han, R.; Zhao, Q. Seismic performance of circular concrete columns reinforced by PC Strands. J. Adv. Concr. Technol. 2020, 18, 256–271. [Google Scholar] [CrossRef]
- JGJ 55—2011; Specification for Mix Proportion Design of Ordinary Concrete. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China; China Architecture and Building Press: Beijing, China, 2011.
- GB/T 50081—2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China; China Architecture and Building Press: Beijing, China, 2019.
- GB/T 228.1—2021; Metallic Materials-Tensile Testing—Part 1: Method of Test at Room Temperature. Standardization Administration of the People’s Republic of China: Beijing, China; Standards Press of China: Beijing, China, 2021.
- ASTM D7913/D7913M-14; Standard Test Method for Bond Strength of Fiber Reinforced Polymer Matrix Composite Bars to Concrete by Pull-Out Testing. ASTM International: West Conshohocken, PA, USA, 2014.
- Rabinowicz, E. Friction and Wear of Materials, 2nd ed.; John Wiley & Sons Inc.: New York, NY, USA, 1995. [Google Scholar]
- Zhao, W.; Xiao, J. On bond-slip constitutive model between ribbed steel bars and concrete. Eng. Mech. 2011, 28, 164–171. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity, 3rd ed.; McGraw-Hill Book Co.: Singapore, 1982. [Google Scholar]
- GB 50010-2010; Code for Design of Concrete Structure. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China; China Architecture and Building Press: Beijing, China, 2015.
- Feldman, L.R.; Bartlett, F.M. Bond stress along plain steel reinforcing bars in pullout specimens. ACI Struct. J. 2007, 104, 685–692. [Google Scholar] [CrossRef]










| Grade | Water (kg/m3) | Cement (kg/m3) | Sand (kg/m3) | Gravel (kg/m3) | Superplasticizer (kg/m3) | fcu (MPa) | SD (MPa) |
|---|---|---|---|---|---|---|---|
| C30 | 215 | 347 | 699 | 1139 | - | 36.2 | 0.668 |
| C40 | 215 | 448 | 591 | 1146 | - | 50.0 | 0.648 |
| C50 | 148 | 375 | 760 | 1115 | 2.6 | 60.5 | 0.510 |
| Specimen Groups | Concrete Grade | d (mm) | l (mm) | fcu (MPa) | Number |
|---|---|---|---|---|---|
| C30-D10-L50 | C30 | 10 | 50 | 36.2 | 6 |
| C30-D10-L75 | C30 | 10 | 75 | 36.2 | 6 |
| C30-D10-L100 | C30 | 10 | 100 | 36.2 | 6 |
| C40-D10-L50 | C40 | 10 | 50 | 50.0 | 6 |
| C50-D10-L50 | C50 | 10 | 50 | 60.5 | 6 |
| Specimens | (MPa) | (MPa) | (MPa) | (MPa) | (mm) | (MPa) | (mm) | (MPa) | (MPa) | φ | ζ | (MPa) | (MPa) | αm | α+ | α− | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Test | Mean | Test | Mean | Test | Mean | Test | Mean | |||||||||||||
| C30-D10-L50-1 | 2.11 | 2.20 | 1.85 | 0.23 | 11.32 | 11.87 | 13.34 | 3.12 | 27.79 | 7.76 | 8.50 | 5.88 | 6.85 | 0.76 | 0.72 | 6.91 | 5.48 | 0.457 | 0.653 | 0.416 |
| C30-D10-L50-2 | 1.94 | 1.73 | 0.23 | 11.87 | 13.15 | 4.22 | 26.73 | 8.47 | 7.61 | 0.90 | 8.10 | 6.74 | 0.412 | 0.410 | 0.325 | |||||
| C30-D10-L50-3 | 2.56 | 2.24 | 0.26 | 12.41 | 12.57 | 2.94 | 27.91 | 9.28 | 7.06 | 0.76 | 6.91 | 6.43 | 0.315 | 0.464 | 0.322 | |||||
| C30-D10-L75-1 | 1.79 | 1.77 | 1.53 | 0.36 | 9.17 | 9.35 | 13.30 | 2.87 | 30.61 | 6.72 | 6.89 | 5.12 | 5.59 | 0.76 | 0.74 | 5.51 | 4.11 | 0.391 | 0.399 | 0.318 |
| C30-D10-L75-2 | 2.03 | 1.85 | 0.20 | 9.28 | 13.29 | 1.83 | 31.27 | 6.94 | 5.89 | 0.85 | 5.95 | 5.14 | 0.363 | 0.389 | 0.343 | |||||
| C30-D10-L75-3 | 1.49 | 1.22 | 0.32 | 9.61 | 13.09 | 2.52 | 28.84 | 7.02 | 5.78 | 0.82 | 6.25 | 4.98 | 0.375 | 0.569 | 0.390 | |||||
| C30-D10-L100-1 | 1.38 | 1.51 | 1.13 | 0.30 | 6.83 | 7.23 | 13.42 | 1.41 | 29.76 | 5.61 | 5.84 | 4.47 | 4.85 | 0.80 | 0.81 | 4.83 | 3.71 | 0.317 | 0.456 | 0.384 |
| C30-D10-L100-2 | 1.69 | 1.49 | 0.30 | 7.27 | 12.88 | 1.58 | 31.33 | 5.80 | 4.85 | 0.84 | 5.15 | 4.22 | 0.346 | 0.433 | 0.373 | |||||
| C30-D10-L100-3 | 1.48 | 1.31 | 0.28 | 7.60 | 13.44 | 2.04 | 30.79 | 6.11 | 5.24 | 0.86 | 6.00 | 4.94 | 0.359 | 0.539 | 0.579 | |||||
| C40-D10-L50-1 | 3.01 | 2.84 | 2.68 | 0.20 | 12.79 | 13.24 | 12.96 | 2.70 | 30.14 | 9.29 | 9.81 | 7.06 | 7.28 | 0.76 | 0.74 | 7.80 | 6.07 | 0.382 | 0.421 | 0.478 |
| C40-D10-L50-2 | 3.58 | 3.23 | 0.25 | 13.16 | 12.68 | 3.67 | 29.72 | 9.73 | 7.04 | 0.72 | 8.25 | 6.40 | 0.414 | 0.401 | 0.349 | |||||
| C40-D10-L50-3 | 1.94 | 1.64 | 0.36 | 13.76 | 13.11 | 4.30 | 30.06 | 10.42 | 7.75 | 0.74 | 9.52 | 6.97 | 0.388 | 0.466 | 0.350 | |||||
| C50-D10-L50-1 | 2.75 | 3.20 | 2.52 | 0.28 | 14.87 | 15.38 | 13.39 | 3.47 | 28.79 | 12.14 | 12.52 | 10.41 | 10.12 | 0.86 | 0.81 | 10.57 | 8.55 | 0.359 | 0.445 | 0.446 |
| C50-D10-L50-2 | 3.80 | 3.64 | 0.25 | 15.55 | 12.54 | 3.61 | 29.85 | 12.65 | 10.26 | 0.81 | 10.61 | 9.56 | 0.352 | 0.401 | 0.462 | |||||
| C50-D10-L50-3 | 3.03 | 2.80 | 0.22 | 15.71 | 13.62 | 4.22 | 30.59 | 12.77 | 9.70 | 0.76 | 11.36 | 8.44 | 0.422 | 0.439 | 0.424 | |||||
| Mean value | 0.269 | 13.12 | 29.61 | 0.800 | 0.763 | 0.377 | 0.459 | 0.397 | ||||||||||||
| SD | 0.050 | 0.332 | 1.347 | 0.052 | 0.038 | 0.039 | 0.074 | 0.072 | ||||||||||||
| Specimens | (MPa) | Error(%) | (MPa) | Error(%) | (MPa) | Error(%) | (MPa) | Error(%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Test | Calculated | Test | Calculated | Test | Calculated | Test | Calculated | |||||
| C30-D10-L50 | 2.20 | 2.34 | 6.43 | 11.87 | 11.60 | −2.22 | 8.50 | 8.85 | 4.11 | 6.85 | 7.08 | 3.39 |
| C30-D10-L75 | 1.77 | 1.88 | 5.91 | 9.35 | 9.28 | −0.75 | 6.89 | 7.08 | 2.73 | 5.59 | 5.67 | 1.27 |
| C30-D10-L100 | 1.51 | 1.56 | 3.17 | 7.23 | 7.73 | 6.93 | 5.84 | 5.90 | 1.00 | 4.85 | 4.72 | −2.73 |
| C40-D10-L50 | 2.84 | 2.80 | −1.53 | 13.24 | 13.86 | 4.70 | 9.81 | 10.57 | 7.74 | 7.28 | 8.46 | 16.18 |
| C50-D10-L50 | 3.20 | 3.11 | −2.74 | 15.38 | 15.39 | 0.08 | 12.52 | 11.74 | −6.22 | 10.12 | 9.39 | −7.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Yin, L.; Li, X.; Yue, X. Bond Behavior of Plain Bars in Concrete under Reversed Cyclic Loading. Materials 2023, 16, 4836. https://doi.org/10.3390/ma16134836
Zhao J, Yin L, Li X, Yue X. Bond Behavior of Plain Bars in Concrete under Reversed Cyclic Loading. Materials. 2023; 16(13):4836. https://doi.org/10.3390/ma16134836
Chicago/Turabian StyleZhao, Jun, Lu Yin, Xiaopeng Li, and Xinjie Yue. 2023. "Bond Behavior of Plain Bars in Concrete under Reversed Cyclic Loading" Materials 16, no. 13: 4836. https://doi.org/10.3390/ma16134836
APA StyleZhao, J., Yin, L., Li, X., & Yue, X. (2023). Bond Behavior of Plain Bars in Concrete under Reversed Cyclic Loading. Materials, 16(13), 4836. https://doi.org/10.3390/ma16134836






