Abstract
Biomaterials play a crucial role in enhancing human health and quality of life. They are employed in applications such as tissue substitution, diagnostic tools, medical supplies, therapeutic treatments, regenerative medicine, and radiation dosimetric studies. However, their predisposition to proton therapy, which is a trending treatment in the world, has not been adequately studied. Ceramic biomaterials, known for their hardness and durability, offer versatile uses, especially in bone tissue replacements. The wide range of physical, mechanical, and chemical properties exhibited by ceramics has spurred extensive research, development, and application in this field. This study focuses on investigating and analyzing the ionization, recoils, phonon release, collision events, and lateral scattering properties of ceramic biomaterials that closely resemble bone tissue in proton therapy applications. Monte Carlo (MC) Transport of Ions in Matter (TRIM) simulation tools were utilized for this analysis. The results showed that Silicon dioxide exhibited the Bragg peak position closest to bone tissue, with a deviation of 10.6%. The average recoils differed by 1.7%, and the lateral scattering differed by 3.6%. The main innovation of this study lies in considering interactions such as recoil, collision events, phonon production, and lateral scattering when selecting biomaterials, despite their limited digitization and understanding. By evaluating all these interactions, the study aimed to identify the most suitable ceramic biomaterial to replace bone tissue in proton therapy.
1. Introduction
Proton therapy is thought to have greater potential to preserve healthy tissue than conventional photon therapy [1]. Providing overdose to deep-seated or radiation-resistant tumors and less radiation to the healthy tissue around the tumor are the most important advantages of this approach [2,3]. This provides most of the energy of a single-energy proton beam, leaving the peak Linear Energy Transfer (LET) depth within a narrow depth range known as the Bragg peak [4]. Due to the narrow depth range of the Bragg peak, it delivers a therapeutic dose that is highly compatible with the target volume, with minimal lateral scattering [5,6] and an input dose much lower than is possible with photon therapy [7]. The success of proton therapy depends on the correct LET measurement and the accuracy of the LET value obtained with the help of semi-analytical pencil beam algorithms [8].
The accuracy of the LET calculation algorithm in proton therapy is critical in terms of taking full advantage of the ballistic (focus on target) potential of protons. Monte Carlo (MC) proton transport simulation is considered the most accurate approach [9,10]. The expected medical benefit of MC simulation is better to control the administered doses with a reduction in treatment toxicity due to the proton therapy margin reduction [11]. This control is performed by using phantoms. It is generally accepted that these phantoms give accurate results in measurements and that the phantom structure is related to tissue equivalence [12].
Bioceramics used as phantoms can be of synthetic or natural origin, designed to bond with bone, and emerged as an alternative to metallic implants [13,14,15]. They are important in the field of biomedicine because of their good and compatible physico-chemical properties with certain parts of the human body [16,17,18]. Ceramic applications, especially in the 20th century, have been widely preferred in the field of medicine due to the advances in processing technology [19,20,21]. They are preferred over metal-based biomaterials because of their excellent biocompatibility, poor degradability, high melting temperature, non-corrosive, better mechanical properties, and poor plasticity [16]. Bioceramics are hard and brittle and have low fracture toughness with elastic modulus compared to bone [12,22,23]. Synthetic bioceramics such as alumina, zirconia, titania, and bioactive glasses/glass ceramics are used in dentistry, orthopedics, calcified tissues, implants, coatings, medical sensors, and many other applications [24]. The use of bioceramics also provides a new horizon in the context of hard tissue repair and regeneration [25]. The main innovation of this study lies in considering interactions such as recoil, collision events, phonon production, and lateral scattering when selecting biomaterials, despite their limited digitization and understanding. By evaluating all these interactions, the study aimed to identify the most suitable ceramic biomaterial to replace bone tissue in proton therapy.
2. Material and Method
Ceramic materials used as biomaterials in this study, namely, alumina (Al2O3), silicon dioxide (SiO2), titanium dioxide (TiO2), and zirconium dioxide (ZrO2) were simulated by MC TRIM to be compared with bone tissue. Mass densities (g/cm3), atomic number density (×1022 atoms/cm3), and basic chemical compositions in percent (%) of ceramic biomaterials are given in Table 1. The TRIM simulation program determined these percentages according to the ICRU-276 report [26].

Table 1.
Atomic and mass percent, atomic number, and mass density values of ceramic biomaterials selected from the MC TRIM system library [27].
The phantom in Figure 1 was formed from these ceramic biomaterials in a volume of 15 × 15 × 15 and was bombarded with a pencil beam of 10⁶ protons at therapeutic energies (60, 80, 100, 120, 140, and 160 MeV). The energy employed in this study is set at the average therapeutic energy level and was administered in increments of 20 MeV on average. The purpose of these increments is to facilitate progress in material scanning, covering an average area below 2 cm. To obtain the desired calculation parameters, the average application time at each energy level was considered through the use of the TRIM simulation program. These calculation parameters are determined by TRIM, incorporating probability calculations due to the nature of MC simulations.
Figure 1.
In the MC TRIM system, the figure shows the shape and size of the phantom formed from the ceramic biomaterial and the direction of progression of the proton beam.
The MC TRIM simulation system used in this study can calculate all interactions of the proton beam inside the phantom [27]. The energy of the proton beam, the number of particles, the selected phantom type and geometry and the parameters to be calculated can be entered from the MC TRIM screen [27]. MC TRIM can calculate all kinetic events related to energy dissipation processes of the proton beam, such as damage, scattering, ionization, voids in the crystal structure of ceramic biomaterials, phonon production, and recoil in the selected ceramic phantom [27]. Furthermore, it can track and record the target atomic cascades in selected ceramic phantoms in detail [28].
The important innovations provided in this study are the parameters of recoils and collision events. These parameters are expressed by the Kinchin–Pease theory. It is used to calculate the displacements of proton beams and atoms of ceramic biomaterials [29]. The displacement with the Norgett, Robinson, and Torrens [30] model is used to calculate the number of primary impact atoms. Number of displaced atoms Nv, Norgett, Robinson, and Torrens model:
In Equation (1), while Ev refers the damage energy, Ed is for the threshold displacement energy [29]. Recoils and collision events parameters are calculated with the help of Equation (1).
The other concept that this study focuses on is the lateral scattering parameter. This parameter xi is the projection range of the “i” ion on the x-axis; Σi xi = sum of ion projection ranges; Σi xi/N = mean projection range of N ions and <x> = mean projection range of all ions [28]. Considering the transverse coordinate “y” in the same way, only the distance in the XY plane is considered [28]. Therefore, the lateral scattering is:
σ = [(Σi xi2)/N − Rp2]1/2 = <(Δxi)2>1/2
It is defined as given in Equation (2). For a normal sent projectile proton beam, the cylindrical symmetry of the gap distribution can be assumed, so the average lateral reflected range is zero (i.e., Ry = 0) [13]. Moreover, the ranges predicted by Y and Z are averaged to increase the accuracy of the calculation [28]. Therefore, the lateral scattering is expressed as given in Equation (3):
σy = [Σi ((|yi| + |zi|)/2)2/N]1/2
3. Results
3.1. Bragg Cure
The Bragg peak position and amplitude formed (electronvolt (eV) and Angstrom (A)) in Al2O3, SiO2, TiO2, ZrO2, and bone phantoms of the proton beam with 60–160 MeV energy obtained from this study are shown in Table 2. For every 20 MeV energy increase in the proton beam, the Bragg peak range increased 29.5% in Al2O3, 28.7% in bone, 28.5% in SiO2, 27.7% in TiO2, and 27.2% in ZrO2. The Bragg peak range is average, respectively, for the ceramic biomaterial closest to the bone; SiO2 with a difference of 10.6%, TiO2 with a difference of 45.2%, Al2O3 with a difference of 46.9%, and ZrO2 with a difference of 53.6% were obtained. When Bragg peak amplitude was compared with bone, the closest ceramic biomaterial value was formed in SiO2 biomaterial with an average difference of 3.2%. In other biomaterials, the average differences are, respectively, TiO2 45.2%, Al2O3 46.9%, and ZrO2 53.6%.

Table 2.
Bragg peak positions and Bragg peak amplitudes formed by the proton beam in phantoms formed from ceramic biomaterials with the help of MC TRIM system.
Simulation outputs of SiO2 biomaterial, which is the ceramic biomaterial that gives the closest value to hard tissue in ionization results are given in Figure 2.
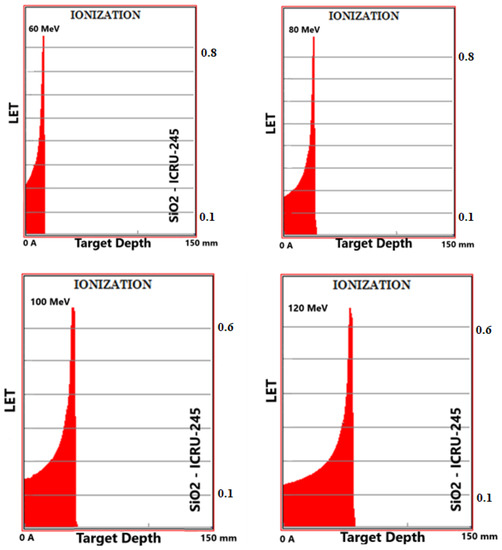
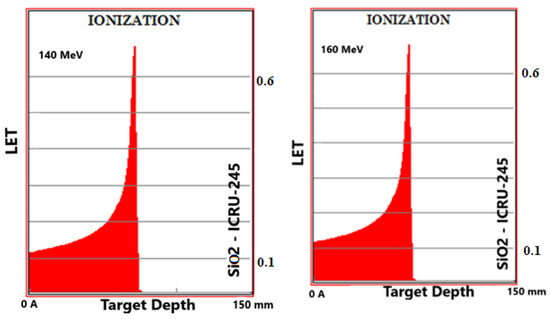
Figure 2.
MC TRIM simulation output figures of ionization (LET (ev/A)) values in SiO2 ceramic biomaterial of a 106-particle proton beam with 60–160 MeV energy.
3.2. Recoils
The recoils peak (eV/A-ion) formed by the proton beam in selected ceramic and bone phantoms and the percentage contribution of the atoms forming the phantoms to this peak are given in Table 3. The average recoil value of bone tissue in six energy ranges was 0.2697 eV/A-ion. The average contribution of atoms to these average recoils value is, respectively. It is composed of 27.2% H, 22.4% C, 32.7% O, 2.2% N, 0.2% Mg, 4.9% P, 0.2% S, and 10.2% Ca. The average recoil value of the Al2O3 phantom in six energy ranges was 0.345 eV/A-ion. The contribution of atoms to these average recoils value is, respectively, composed of 49.1% Al and 50.9% O. The average recoil values of SiO2, TiO2, and ZrO2 phantoms in six energy ranges were 0.265, 0.352, and 0.346 eV/A-ion, respectively. The contribution of atoms to these average recoils value consisted of 46.5% Si and 53.5% O in the SiO2 phantom, 52.5% Ti and 47.5% O in the TiO2 phantom, and 63.9% Z and 36.1% O in the ZrO2 phantom.

Table 3.
The total recoil value in the ceramic biomaterials of the proton beam in the energy range and the percentage contribution of the atoms forming the ceramic biomaterials to this amplitude.
Simulation outputs of SiO2 biomaterial, which is the ceramic biomaterial that gives the closest value to hard tissue in recoil results are given in Figure 3.
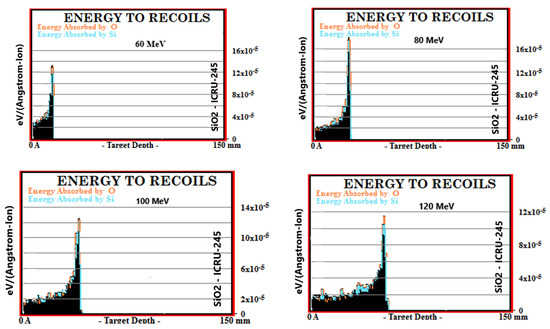
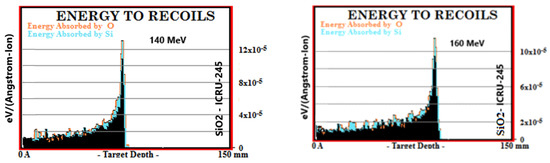
Figure 3.
MC TRIM simulation output figures of recoils values in SiO2 ceramic biomaterial of a 106-particle proton beam with 60–160 MeV energy.
3.3. Phonon Production
The phonon production (Phonons/(A-Ion)) of the proton beam in the 60–160 MeV energy range, consisting of Al2O3, SiO2, TiO2, and ZrO2 ion and recoil-induced interactions in bone phantoms, is given in Table 4. Both ion and recoils were evaluated by comparing ceramic biomaterials with bone by multiplying by 104 for the phonon production numbers with recoil to be meaningful. The ion-induced phonon production in the bone phantom was 0.73 × 104 Phonons/(A-Ion) on average. In the six energy ranges of Al2O3, SiO2, TiO2, and ZrO2 phantoms, the ion-derived phonon production values were, respectively, 1.05, 0.73, 1.03, and 0.97 × 104 Phonons/(A-Ion) made of biomaterial. The difference in the remaining biomaterials is average, respectively, occurring at 33.3% in ZrO2, 40.6% in TiO2, and 43.9% in Al2O3. As the energy of the proton beam increased, the ion-induced phonon production increased by an average of 10.6% in the bone phantom. This increase in Al2O3, SiO2, TiO2, and ZrO2 phantoms, respectively, 11.2%, 9.7%, 9.6%, and 10.8%. In the bone phantom, the phonon production from recoils was realized as 1.35 × 104 Phonons/(A-Ion) on average. Recoil-induced phonon production values of Al2O3, SiO2, TiO2, and ZrO2 phantoms in six energy ranges were, respectively, 2.64, 1.95, 2.73, and 2.82 × 104 Phonons/(A-Ion). In ion-derived phonon production, the biomaterial closest to the bone consisted of SiO2 biomaterial with an average difference of 44.2%. The difference in the remaining biomaterials is average, respectively. It formed 95.5% in Al2O3, 102.1% in TiO2, and 108.3% in ZrO2. As the energy of the proton beam increased, the phonon production from recoils increased by an average of 10.7% in the bone phantom. This increase in Al2O3, SiO2, TiO2, and ZrO2 phantoms, respectively, was 11.9%, 9.8%, 9.6%, and 7.6%.

Table 4.
Phonon production consisting of interactions originating from ions and recoils in the ceramic biomaterial phantoms of the proton beam in the energy range.
Simulation outputs of SiO2 biomaterial, which is the ceramic biomaterial that gives the closest value to hard tissue in phonon production results are given in Figure 4.
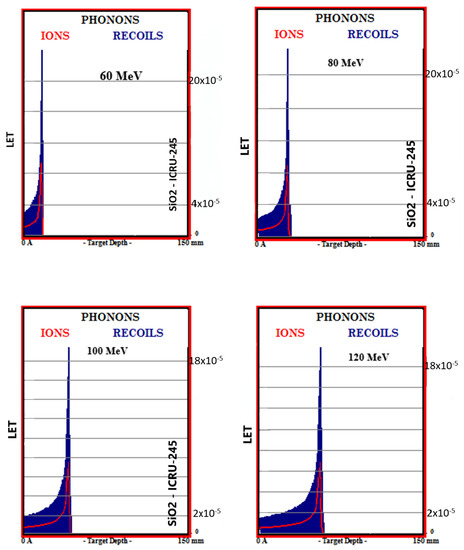
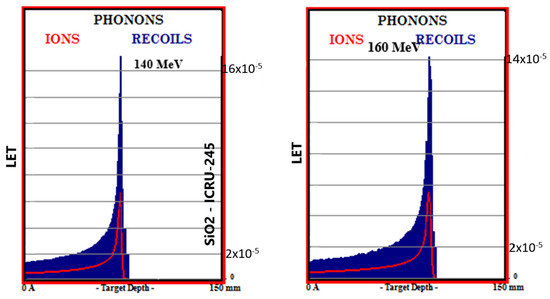
Figure 4.
MC TRIM simulation output figures of phonon production in SiO2 ceramic biomaterial of a 106-particle proton beam with 60–160 MeV energy.
3.4. Collision Events
Total collision events (Number/(A-Ion)) caused by the ionization and recoil interactions of the proton beam in the 60–160 MeV energy range with collisions with atoms in Al2O3, SiO2, TiO2, ZrO2, and bone phantoms are given in Table 5. With the 20 MeV energy increase in the proton beam, an increase in the values of collision events occurred in bone 13.2%, Al2O3 12.6%, SiO2 13.6%, TiO2 13.7%, and ZrO2 13.1%. In total target vacancies, the closest ceramic biomaterial to the bone was Al2O3 with a 1.2% difference. The differences between the remaining ceramic biomaterials and bone are, respectively, 1.9% in TiO2, 11.7% in ZrO2, and 18.4% in SiO2. In total target displacements, the closest biomaterial to the bone was Al2O3 with a difference of 1.8%. The differences between the remaining biomaterials and bone are, respectively; It was 3.4% in TiO2, 13.2% in ZrO2, and 19.4% in SiO2. In total target replacement collisions, the ceramic biomaterial closest to the bone was Al2O3.

Table 5.
Total collision events values formed by proton beam in phantoms formed from ceramic biomaterials with the help of MC TRIM system.
Simulation outputs of SiO2 biomaterial, which is the ceramic biomaterial that gives the closest value to hard tissue in total collision events values, are given in Figure 5.
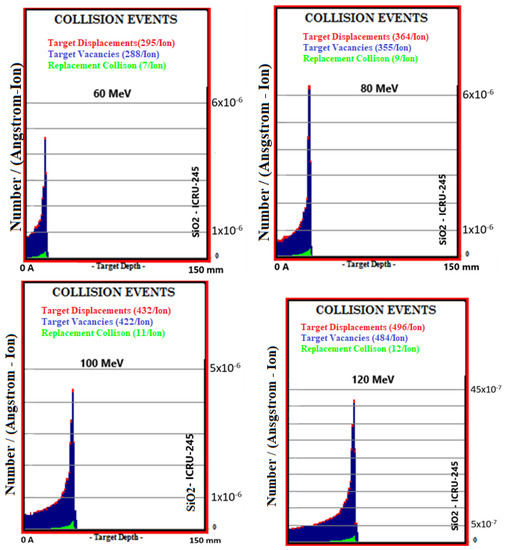
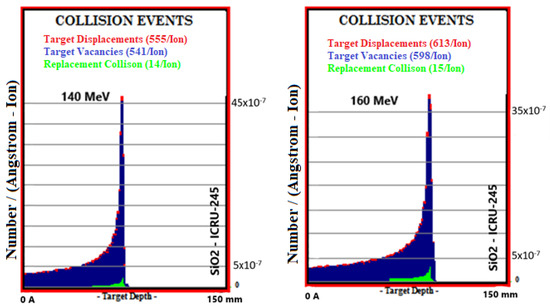
Figure 5.
MC TRIM simulation output figures of total collision events values in SiO2 ceramic biomaterial of a 106-particle proton beam with 60–160 MeV energy.
3.5. Lateral Straggle
The lateral straggle formed in the beam direction as a result of interactions between Al2O3, SiO2, TiO2, ZrO2, and bone phantoms of proton beams in the 60–160 MeV energy range is given in Figure 6. The proton beam formed in the bone phantom with an average of 1.310 mm lateral straggle and there was an 81.4% increase between the lowest range and the largest range. While the mean lateral straggle was 1.357 mm in the SiO2 phantom, there was an 80.7% increase between the lowest range and the largest range. In the ZrO2 phantom, the mean lateral straggle was 1.159 mm, while there was an 80.6% increase between the lowest range and the largest range. In the TiO2 phantom, the mean lateral straggle was 0.961 mm, while there was an 80.6% increase between the lowest range and the largest range. While the average lateral straggle was 0.805 mm in the Al2O3 phantom, there was an increase of 81.1% between the lowest range and the largest range. Ceramic biomaterials closest to the bone in lateral straggle are, respectively; It was found as SiO2, ZrO2, TiO2, and Al2O3.
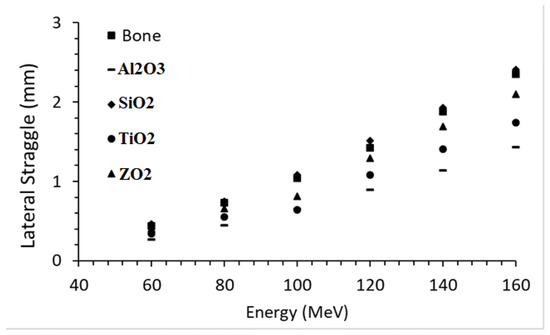
Figure 6.
Lateral straggle formed in the beam direction while moving through ceramic and bone biomaterials of the proton beam in the energy range.
4. Discussion
In this study, the Bragg peak range, Bragg peak amplitude, recoils, collision event values, phonon formation, and lateral straggle lengths of the therapeutic energy proton beam were calculated in four different ceramic phantoms and compared with the bone phantom. A proton beam was used in this study, especially since the effect of LET on biological properties and lateral dose distribution may differ between selected ion beam types [31]. The ion type to be selected can be customized by considering these differences and the target tissue with different properties [32]. At this point, it has been a critical issue to investigate the biomaterials closest to the selected hard tissue, i.e., bone. For this reason, bone and four different ceramic biomaterials were selected for the phantom material and compared with bone. As presented in Table 1, the properties of ceramic biomaterials in the MC TRIM simulation system are given. The results obtained with these calculations are compared in Table 2. At the Bragg peak position, the ceramic biomaterial closest to the bone was SiO2 with a difference of 10.6%. There is a difference of 47.9% between the atomic density of SiO2 and bone biomaterials and 25.4% between their densities. The ceramic biomaterial, which had the biggest difference with bone, was ZrO2 with a 53.7% difference. There is a 37.8% difference between the atomic densities of ZrO2 and bone biomaterials and a 207% difference between their densities. Thus, it has been observed that the Bragg peak range is largely due to density. Among the selected ceramic biomaterials, it was observed that SiO2 was the closest to the bone with a mean Bragg peak amplitude of 3.2%, while the farthest was TiO2 with a 56.2% difference. At this point, SiO2 was the closest ceramic biomaterial to the bone in Bragg peak location and amplitude. Ionization interactions constitute almost all of the total interactions. Accordingly, the recoil peak is approximately 103 times less than the Bragg peak. Recoil interactions are the main reason for both heavy ion treatment close to critical points, deviations in the direction of the ion beam’s progression within the target, and secondary ion and phonon formations that occur as a result of these two conditions. The mean recoil value closest to the bone was formed in the SiO2 ceramic phantom with a difference of 1.7%. It was seen that the biggest contribution to the recoil value was related to the mass percentage of the atom forming the biomaterial, as given in Table 3. Since the percentages of O in bone, Al2O3 and SiO2 biomaterials and Z atom in Ti, and ZrO2 biomaterials in TiO2 biomaterials are high, the greatest contribution to the recoil’s interaction came from these atoms. These results agreed with the literature [29]. Phonons produced from all interactions of the proton beam in ceramic biomaterials were investigated by considering SRIM MC [29], similar to this study [33]. In particular, the produced phonons were found to be compatible with the literature [29]. SiO2 was the closest ceramic biomaterial to bone in ion and recoil-based phonon production. When the remaining biomaterials are evaluated, respectively, they are listed as TiO2 and Al2O3. In experimental studies, diverse types of biomaterials were investigated in experimental studies with the help of heavy ion beams [34]. It is a known fact that the energy coming from the phonons increases the total dose. This increase may also occur at points further away from the intended interaction point. This may cause damage to healthy tissues and may pose a risk of secondary cancer. In this study, ceramic biomaterials were investigated with the help of a simulation system since there was no experimental ion line. Similar properties were investigated using liquid biomaterials in our previous study [35]. In particular, the interaction of ion beams passing through layers and structures with different properties has revealed the importance of choosing the closest biomaterials to biological tissues. These studies have been the subject of research not only in heavy ions but also in conventional beams [36]. The effect of Al2O3 and ZrO2 ceramic biomaterials on the dose was investigated with the help of different ionizing rays and MC [37]. In the collision events presented in Table 5, the ceramic biomaterials that give the closest result to the bone are, respectively, Al2O3, TiO2, ZrO2, and SiO2. Therefore, the closest crystal structure to bone was found to be Al2O3. Considering the lateral scattering values in the selected phantoms, the closest biomaterial to bone was SiO2 with a difference of 3.6%. Lateral scattering increased by an average of 0.389 mm for each 20 MeV energy increase in the proton beam in SiO2 ceramic biomaterial. This mean increase was 0.382 mm in bone, 0.339 in ZrO2, 0.280 in TiO2, and 0.232 mm in Al2O3. Lateral scatter. It is a parameter that should be considered in the treatment of tumors close to critical tissues [38,39,40]. In our previous studies, besides the layered biological structures, the contribution of the biomaterials placed between the biological structures to the lateral scattering was investigated [3]. The effects of therapeutic biomaterials on lateral scattering have been investigated, especially in organs such as the brain, where critical tissues are concentrated [40]. In addition, lateral scattering has also been evaluated in terms of different heavy ion species in similar biomaterials [2]. It was found to be compatible with this study. Additive manufacturing, also known as 3D printing, is a relatively new technique for creating scaffolds with customizable pore shapes and sizes [41]. Chuck Hall introduced the concept in 1986, and it has since revolutionized tissue engineering [41]. By using medical imaging data, personalized scaffolds can be produced to accurately fill injury sites and potentially reconstruct entire organs with complex microstructures [41]. Recent studies highlight the promising applications of additive manufacturing in creating functional tissue scaffolds [42,43]. Bioprinting is an innovative method introduced in the last decade for creating living tissues. It utilizes bioprinters to distribute cells and extracellular matrix components with precision. This exclusive advantage of 3D bioprinting is highlighted in recent research by Santoni et al. [42]. Additive manufacturing methods such as 3D printing offer precise control over pore shape, size, and distribution in scaffolds, allowing easy adjustment of their physicochemical properties [41]. Studies by Jin et al. [44] and Büyük et al. [45] have explored how modifying strand distance, diameter, and stacking pattern in 3D-printed bone scaffolds can regulate their degradation.
5. Conclusions
In this study, the interaction of a proton beam with bioceramics, ionization, rebound, collision phenomenon, phonon production, and lateral scattering was investigated with the help of TRIM MC. Phonon production resulting from ionization and recoil interactions was investigated and found to be compatible with the literature. The change properties in the crystal structure of bioceramics, when bombarded with a proton beam, were investigated with collision event parameters and presented as an innovation in this study. The main innovation of this study is to examine the reactions of ceramic biomaterials, which are bone-equivalent biomaterials, to proton therapy in both electron and atomic dimensions. In addition, the results of lateral scattering in the proton beam as a result of ionization and recoil interactions are examined and discussed with similar studies in the literature. As a result of the obtained results and studies in the literature, ceramic biomaterials, which are thought to be close to bone tissue, were compared. The disparity in the Bragg peak position of the proton beam within ceramic biomaterials is believed to stem from the presence of minute air spaces found in biological materials such as bone, as well as disparities in crystal structures. Furthermore, it has been observed that denser materials, despite having a density similar to that of bone, are likely to exhibit these distinctions. Since the energy and particle number of the sent proton beam is at the treatment level, it has been evaluated that it will not cause physical damage such as a fracture in the bone or in the ceramic biomaterial. So much so that, with the beams with proton beam properties in this study, treatments are still ongoing today. However, the main innovation of this study is how many atoms in each ceramic biomaterial are removed from the crystal structure and what interactions result in energy depletion. It is recommended that these calculations be made for different heavy ions as well. Considering the importance of investigating ceramic biomaterials closest to the bone tissue in radiotherapy, different ceramic biomaterials were evaluated.
Author Contributions
Conceptualization, F.E. and T.A.; Methodology, F.E.; Software, T.A and K.A.; Validation, F.E. and K.A.; Formal Analysis, F.E.; Investigation, F.E.; Resources, T.A. and K.A.; Data Curation, T.A. and K.A.; Writing—Original Draft Preparation, F.E.; Writing—Review & Editing, T.A. and K.A.; Visualization, F.E.; Supervision, F.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, Q.; Adair, A.H.; Deng, Y.; Chen, H.; Moyers, M.; Lin, J.; Yepes, P.P. A track repeating algorithm for intensity modulated carbon ion therapy. Phys. Med. Biol. 2019, 64, 095026. [Google Scholar] [CrossRef]
- Ekinci, F.; Bostanci, G.E.; Dağli, Ö.; Güzel, M.S. Analysis of Bragg curve parameters and lateral straggle for proton and carbon beams. In Communications Faculty of Sciences University of Ankara Series A2-A3 Physical Sciences and Engineering; Ankara University: Ankara, Turkey, 2021; Volume 63, pp. 32–41. [Google Scholar] [CrossRef]
- Bölükdemiïr, M.H.; Ekiïnciï, F. The Effect of the Second Peak formed in Biomaterials used in a Slab Head Phantom on the Proton Bragg Peak. Polite-Derg. 2019, 23, 129–136. [Google Scholar] [CrossRef]
- Vásquez, A.C.; Runz, A.; Echner, G.; Sroka-Perez, G.; Karger, C.P. Comparison of two respiration monitoring systems for 4D imaging with a Siemens CT using a new dynamic breathing phantom. Phys. Med. Biol. 2012, 57, N131–N143. [Google Scholar] [CrossRef] [PubMed]
- Perrin, R.L.; Zakova, M.; Peroni, M.; Bernatowicz, K.; Bikis, C.; Knopf, A.K.; Safai, S.; Fernandez-Carmona, P.; Tscharner, N.; Weber, D.C.; et al. An anthropomorphic breathing phantom of the thorax for testing new motion mitigation techniques for pencil beam scanning proton therapy. Phys. Med. Biol. 2017, 62, 2486–2504. [Google Scholar] [CrossRef] [PubMed]
- Lourenço, A.; Wellock, N.; Thomas, R.; Homer, M.; Bouchard, H.; Kanai, T.; MacDougall, N.; Royle, G.; Palmans, H. Theoretical and experimental characterization of novel water-equivalent plastics in clinical high-energy carbon-ion beams. Phys. Med. Biol. 2016, 61, 7623–7638. [Google Scholar] [CrossRef]
- Arib, M.; Medjadj, T.; Boudouma, Y. Study of the influence of phantom material and size on the calibration of ionization chambers in terms of absorbed dose to water. J. Appl. Clin. Med. Phys. 2006, 7, 55–64. [Google Scholar] [CrossRef] [PubMed]
- Samson, D.O.; Jafri, M.Z.M.; Shukri, A.; Hashim, R.; Sulaiman, O.; Aziz, M.Z.A.; Yusof, M.F.M. Measurement of radiation attenuation parameters of modified defatted soy flour–soy protein isolate-based mangrove wood particleboards to be used for CT phantom production. Radiat. Environ. Biophys. 2020, 59, 483–501. [Google Scholar] [CrossRef]
- Widesott, L.; Lorentini, S.; Fracchiolla, F.; Farace, P.; Schwarz, M. Improvements in pencil beam scanning proton therapy dose calculation accuracy in brain tumor cases with a commercial Monte Carlo algorithm. Phys. Med. Biol. 2018, 63, 145016. [Google Scholar] [CrossRef]
- Gardner, R.P.; Verghese, K. Use of Monte Carlo Methods in the Calibration and Design Optimization of Radiation Ganges and Analyzers. Isot. Isot. Environ. Health Stud. 1983, 19, 329–335. [Google Scholar] [CrossRef]
- Maneval, D.; Ozell, B.; Després, P. pGPUMCD: An efficient GPU-based Monte Carlo code for accurate proton dose calculations. Phys. Med. Biol. 2019, 64, 085018. [Google Scholar] [CrossRef]
- Kaur, M.; Singh, K. Review on titanium and titanium based alloys as biomaterials for orthopaedic applications. Mater. Sci. Eng. C 2019, 102, 844–862. [Google Scholar] [CrossRef]
- Pina, S.; Rebelo, R.; Correlo, V.M.; Oliveira, J.M.; Reis, R.L. Bioceramics for osteochondral tissue engineering and regeneration. Adv. Exp. Med. Biol. 2018, 1058, 53–75. [Google Scholar] [CrossRef] [PubMed]
- Tarasova, N.; Bedarkova, A.; Animitsa, I. Novel Pr-Doped BaLaInO4 Ceramic Material with Layered Structure for Proton-Conducting Electrochemical Devices. Appl. Sci. 2023, 13, 1328. [Google Scholar] [CrossRef]
- Jastrzębska, I.; Piwowarczyk, A. Traditional vs. Automated Computer Image Analysis—A Comparative Assessment of Use for Analysis of Digital SEM Images of High-Temperature Ceramic Material. Materials 2023, 16, 812. [Google Scholar] [CrossRef]
- Punj, S.; Singh, J.; Singh, K. Ceramic biomaterials: Properties, state of the art and future prospectives. Ceram. Int. 2021, 47, 28059–28074. [Google Scholar] [CrossRef]
- Rafikova, G.; Piatnitskaia, S.; Shapovalova, E.; Chugunov, S.; Kireev, V.; Ialiukhova, D.; Bilyalov, A.; Pavlov, V.; Kzhyshkowska, J. Interaction of Ceramic Implant Materials with Immune System. Int. J. Mol. Sci. 2023, 24, 4200. [Google Scholar] [CrossRef]
- Ellakany, P.; Madi, M.; Aly, N.M.; Alshehri, T.; Alameer, S.T.; Al-Harbi, F.A. Influences of Different CAD/CAM Ceramic Compositions and Thicknesses on the Mechanical Properties of Ceramic Restorations: An In Vitro Study. Materials 2023, 16, 646. [Google Scholar] [CrossRef]
- Rieger, W. Ceramics in Orthopedics-30 Years of Evolution and Experience. In World Tribology Forum in Arthroplasty; Hans Huber Verlag Bern: Bern, Switzerland, 2001; pp. 283–294. [Google Scholar]
- Vdoviaková, K.; Jenca, A.; Jenca, A.; Danko, J.; Kresáková, L.; Simaiová, V.; Reichel, P.; Rusnák, P.; Pribula, J.; Vrzgula, M.; et al. Regenerative Potential of Hydroxyapatite-Based Ceramic Biomaterial on Mandibular Cortical Bone: An In Vivo Study. Biomedicines 2023, 11, 877. [Google Scholar] [CrossRef]
- Dec, P.; Modrzejewski, A.; Pawlik, A. Existing and Novel Biomaterials for Bone Tissue Engineering. Int. J. Mol. Sci. 2022, 24, 529. [Google Scholar] [CrossRef]
- Kurinjinathan, P.; Arul, K.T.; Ramya, J.R. Cobalt Ions Doped Bioactive Ceramics for Biosensor Biomedical Applications. Int. J. Curr. Res. Rev. 2018, 10, 49–52. [Google Scholar] [CrossRef]
- Ricciotti, L.; Apicella, A.; Perrotta, V.; Aversa, R. Geopolymer Materials for Bone Tissue Applications: Recent Advances and Future Perspectives. Polymers 2023, 15, 1087. [Google Scholar] [CrossRef]
- Danewalia, S.; Singh, K. Bioactive glasses and glass-ceramics for hyperthermia treatment of cancer: State-of-art, challenges, and future perspectives. Mater. Today Bio 2021, 10, 100100. [Google Scholar] [CrossRef]
- Kargozar, S.; Singh, R.K.; Kim, H.-W.; Baino, F. “Hard” ceramics for “Soft” tissue engineering: Paradox or opportunity? Acta Biomater. 2020, 115, 1–28. [Google Scholar] [CrossRef] [PubMed]
- ICRU. Report 46; Photon, Electron, Proton and Neutron Interaction Data for Body Tissues; International Commission on Radiation Units and Measurements: Bethesda, MD, USA, 1992; Volume 24, Issue 1. [Google Scholar]
- Ziegler, J.F. SRIM The Stopping and Range of Ion in Matter. Publisher of Website. Available online: https://www.srim.org (accessed on 19 October 2021).
- Foster, D.G.; Artur, E.D. Avarege Neutronic Properties of “Prompt” Fission Poducts; LA-9168-MS:DE32:009080, Los Alamos National Laboratory Report; Los Alamos National Laboratory: Santa Fe, NM, USA, 1982. [Google Scholar]
- Qi, M.; Yang, Q.; Chen, X.; Yang, J.D.L. Fast Calculation of Mont Carlo Ion Transport Code. J. Phys. Conf. Ser. 2021, 1739, 012030. [Google Scholar] [CrossRef]
- Groom, D.E.; Klein, S.R. Passage of particles through matter. Eur. Phys. J. C 2000, 15, 163–173. [Google Scholar] [CrossRef]
- Loeffler, J.S.; Durante, M. Charged particle therapy—Optimization, challenges and future directions. Nat. Rev. Clin. Oncol. 2013, 10, 411–424. [Google Scholar] [CrossRef]
- Uhl, M.; Mattke, M.; Welzel, T.; Roeder, F.; Oelmann, J.; Habl, G.; Jensen, A.; Ellerbrock, M.; Jäkel, O.; Haberer, T.; et al. Highly effective treatment of skull base chordoma with carbon ion irradiation using a raster scan technique in 155 patients: First long-term results. Cancer 2014, 120, 3410–3417. [Google Scholar] [CrossRef] [PubMed]
- Mattei, I.; Bini, F.; Collamati, F.; De Lucia, E.; Frallicciardi, P.M.; Iarocci, E.; Mancini-Terracciano, C.; Marafini, M.; Muraro, S.; Paramatti, R.; et al. Secondary radiation measurements for particle therapy applications: Prompt photons produced by4He,12C and16O ion beams in a PMMA target. Phys. Med. Biol. 2017, 62, 1438–1455. [Google Scholar] [CrossRef]
- Pinto, M.; Bajard, M.; Brons, S.; Chevallier, M.; Dauvergne, D.; Dedes, G.; De Rydt, M.; Freud, N.; Krimmer, J.; La Tessa, C.; et al. Absolute prompt-gamma yield measurements for ion beam therapy monitoring. Phys. Med. Biol. 2014, 60, 565–594. [Google Scholar] [CrossRef] [PubMed]
- Mattei, I.; Battistoni, G.; Bini, F.; Collamati, F.; De Lucia, E.; Durante, M.; Faccini, R.; La Tessa, C.; Marafini, M.; Piersanti, L.; et al. Prompt-γ production of 220 MeV/u12C ions interacting with a PMMA target. J. Instrum. 2015, 10, P10034. [Google Scholar] [CrossRef]
- Sato, E.; Shigemitsu, R.; Mito, T.; Yoda, N.; Rasmussen, J.; Sasaki, K. The effects of bone remodeling on biomechanical behavior in a patient with an implant-supported overdenture. Comput. Biol. Med. 2021, 129, 104173. [Google Scholar] [CrossRef] [PubMed]
- Akyol, O.; Dirican, B.; Toklu, T.; Eren, H.; Olgar, T. Investigating the effect of dental implant materials with different densities on radiotherapy dose distribution using Monte-Carlo simulation and pencil beam convolution algorithm. Dentomaxillofacial Radiol. 2019, 48, 20180267. [Google Scholar] [CrossRef] [PubMed]
- Haettner, E.; Iwase, H.; Krämer, M.; Kraft, G.; Schardt, D. Experimental study of nuclear fragmentation of 200 and 400 MeV/u12C ions in water for applications in particle therapy. Phys. Med. Biol. 2013, 58, 8265–8279. [Google Scholar] [CrossRef]
- Grün, R.; Friedrich, T.; Kramer, M.; Zink, K.; Durante, M.; Engenhart-Cabillic, R.; Scholz, M. Assessment of potential advantages of relevant ions for particle therapy: A model based study. Med. Phys. 2015, 42, 1037–1047. [Google Scholar] [CrossRef]
- Ekinci, F.; Bostanci, E.; Güzel, M.S.; Dagli, O. Effect of different embolization materials on proton beam stereotactic radiosurgery Arteriovenous Malformation dose distributions using the Monte Carlo simulation code. J. Radiat. Res. Appl. Sci. 2022, 15, 191–197. [Google Scholar] [CrossRef]
- Tajvar, S.; Hadjizadeh, A.; Samandari, S.S. Scaffold degradation in bone tissue engineering: An overview. Int. Biodeterior. Biodegradation 2023, 180, 105599. [Google Scholar] [CrossRef]
- Santoni, S.; Gugliandolo, S.G.; Sponchioni, M.; Moscatelli, D.; Colosimo, B.M. 3D bioprinting: Current status and trends—A guide to the literature and industrial practice. Bio-Des. Manuf. 2021, 5, 14–42. [Google Scholar] [CrossRef]
- Yi, H.-G.; Kim, H.; Kwon, J.; Choi, Y.-J.; Jang, J.; Cho, D.-W. Application of 3D bioprinting in the prevention and the therapy for human diseases. Signal Transduct. Target. Ther. 2021, 6, 177. [Google Scholar] [CrossRef]
- Jin, H.; Zhuo, Y.; Sun, Y.; Fu, H.; Han, Z. Microstructure design and degradation performance in vitro of three-dimensional printed bioscaffold for bone tissue engineering. Adv. Mech. Eng. 2019, 11, 1687814019883784. [Google Scholar] [CrossRef]
- Büyük, N.I.; Aksu, D.; Köse, G.T. Effect of different pore sizes of 3D printed PLA-based scaffold in bone tissue engineering. Int. J. Polym. Mater. Polym. Biomater. 2022, 72, 1021–1031. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).