Creep Monitoring of Submersible Observation Windows Using Mueller Matrix Imaging
Abstract
1. Introduction
2. Materials and Methods
2.1. Material
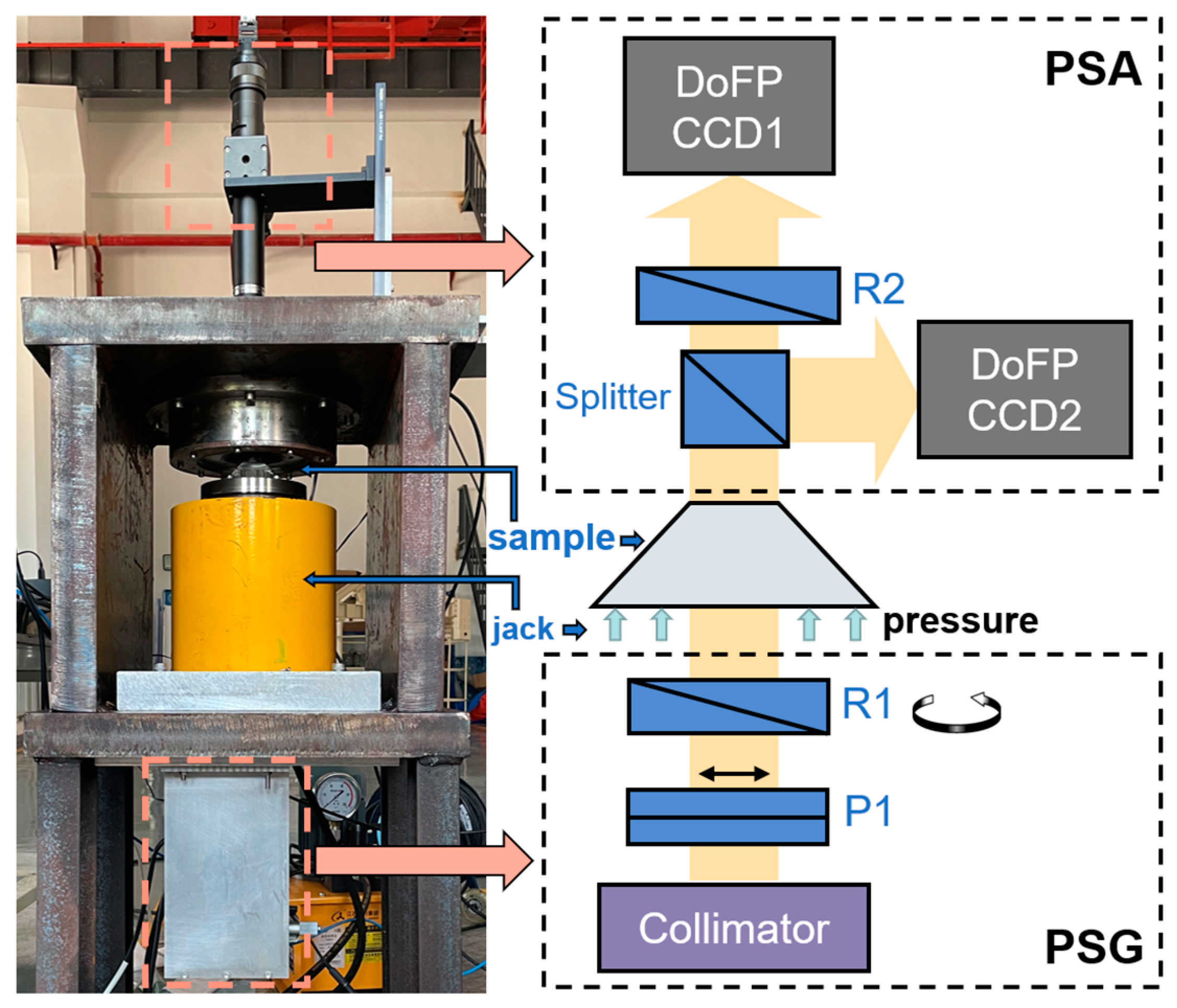
2.2. Experimental Setup
2.3. Calibration Method
2.4. Parameters
3. Results
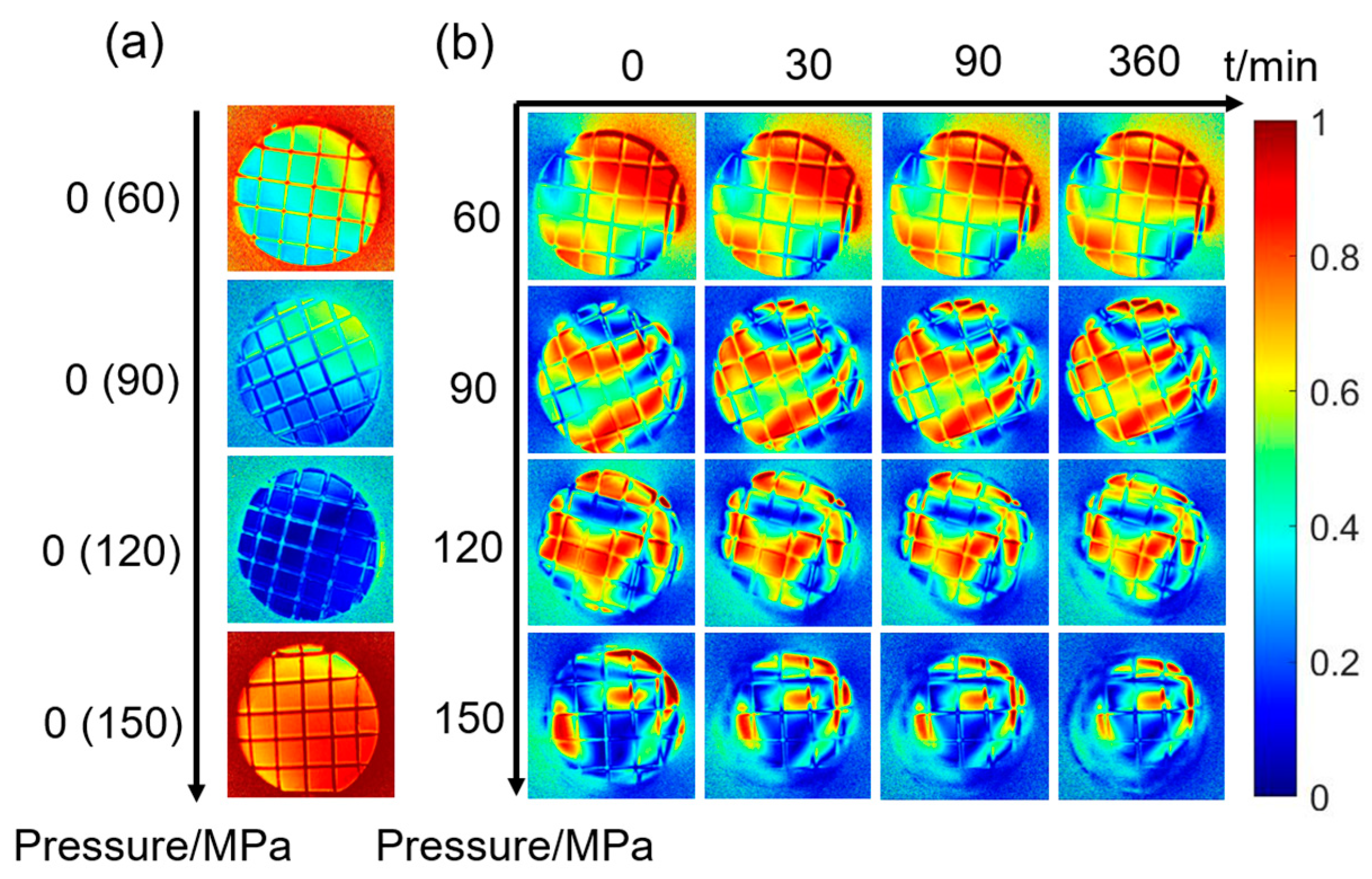
3.1. Polarization Parameter Images
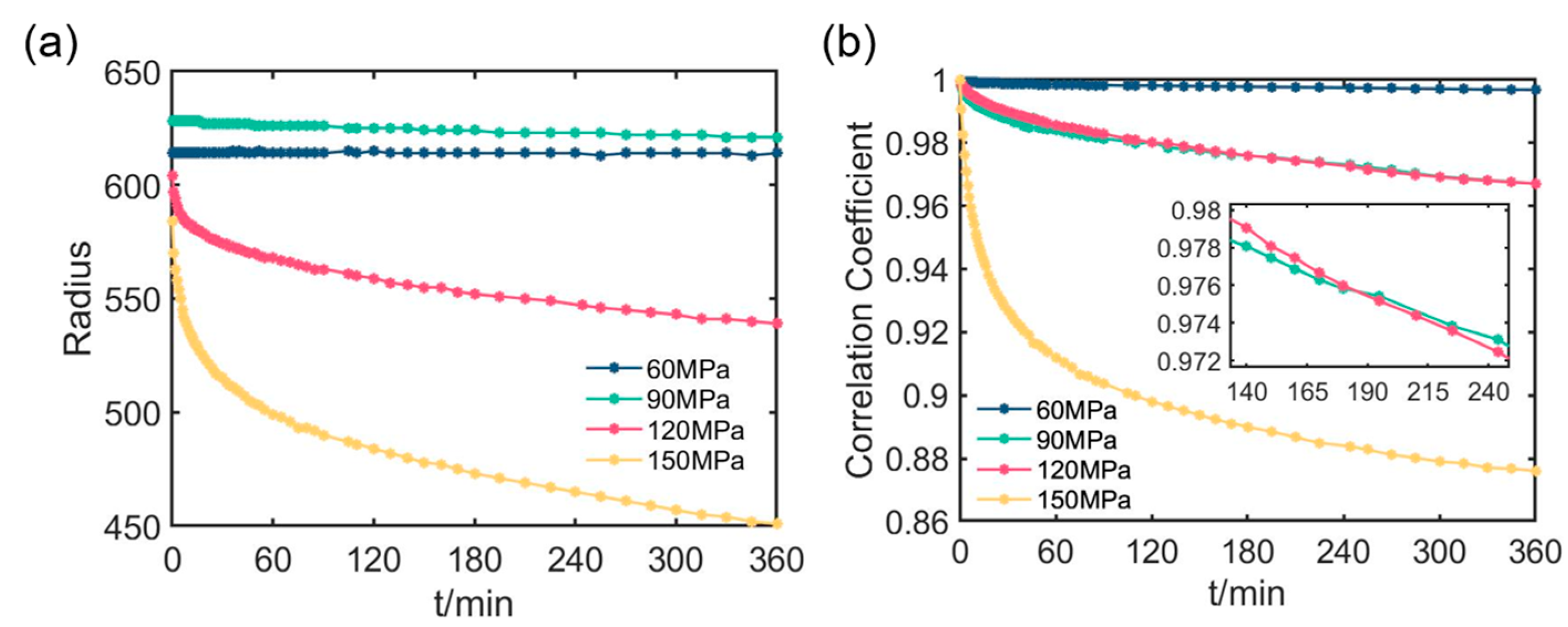
3.2. Unwrapped R Images
3.3. Correlation Coefficient of t1 Images
4. Finite Element Analysis (FEA) of Window’s Creep
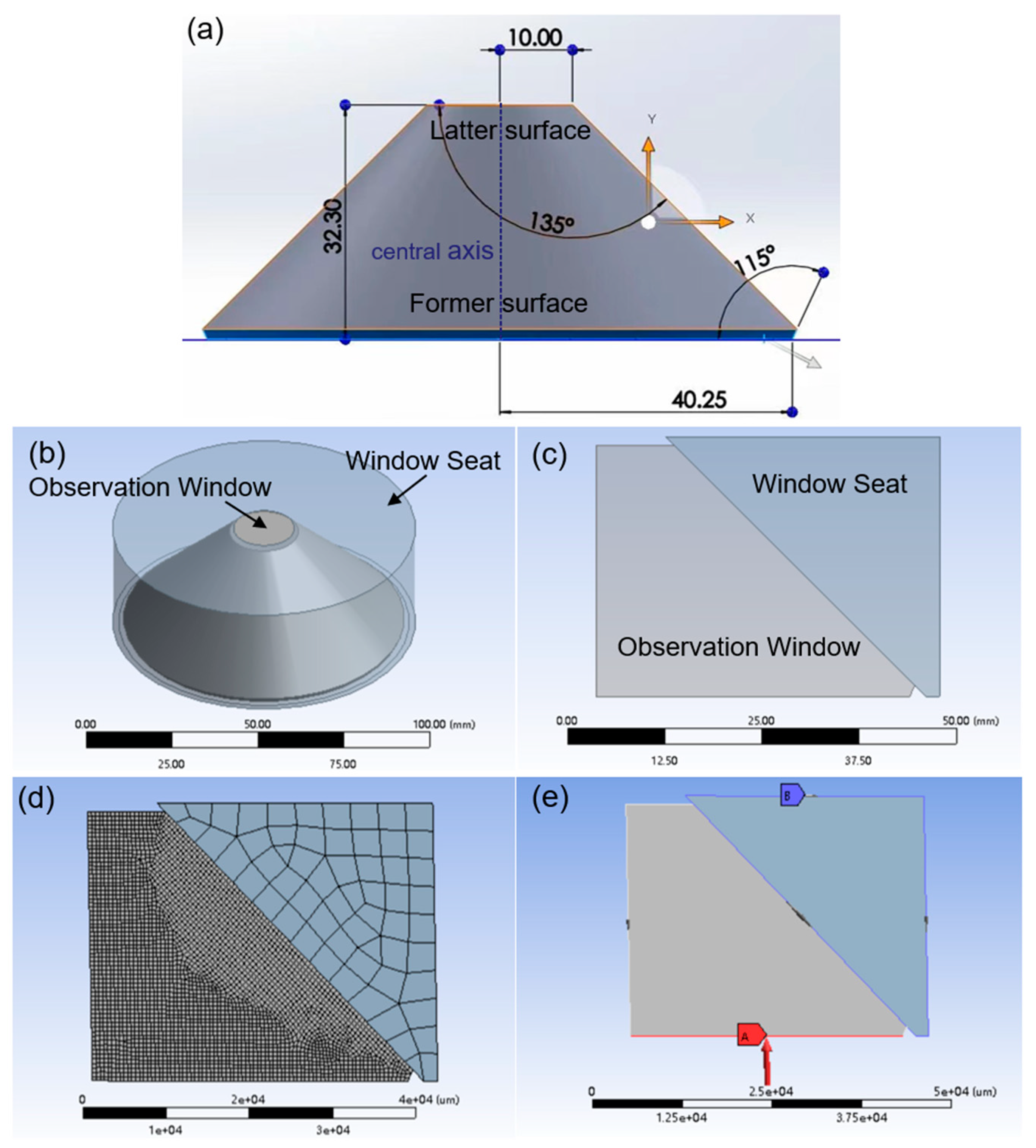
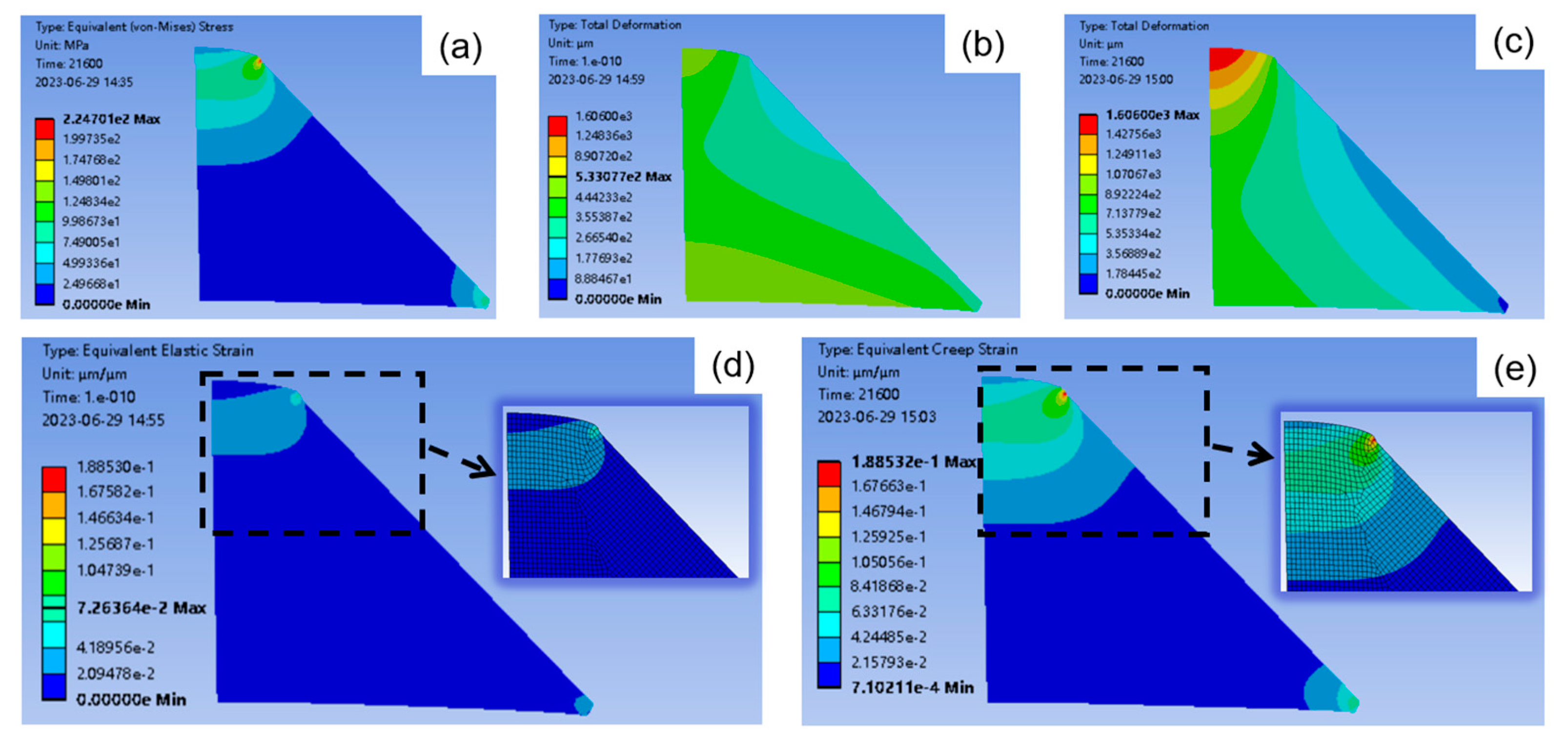
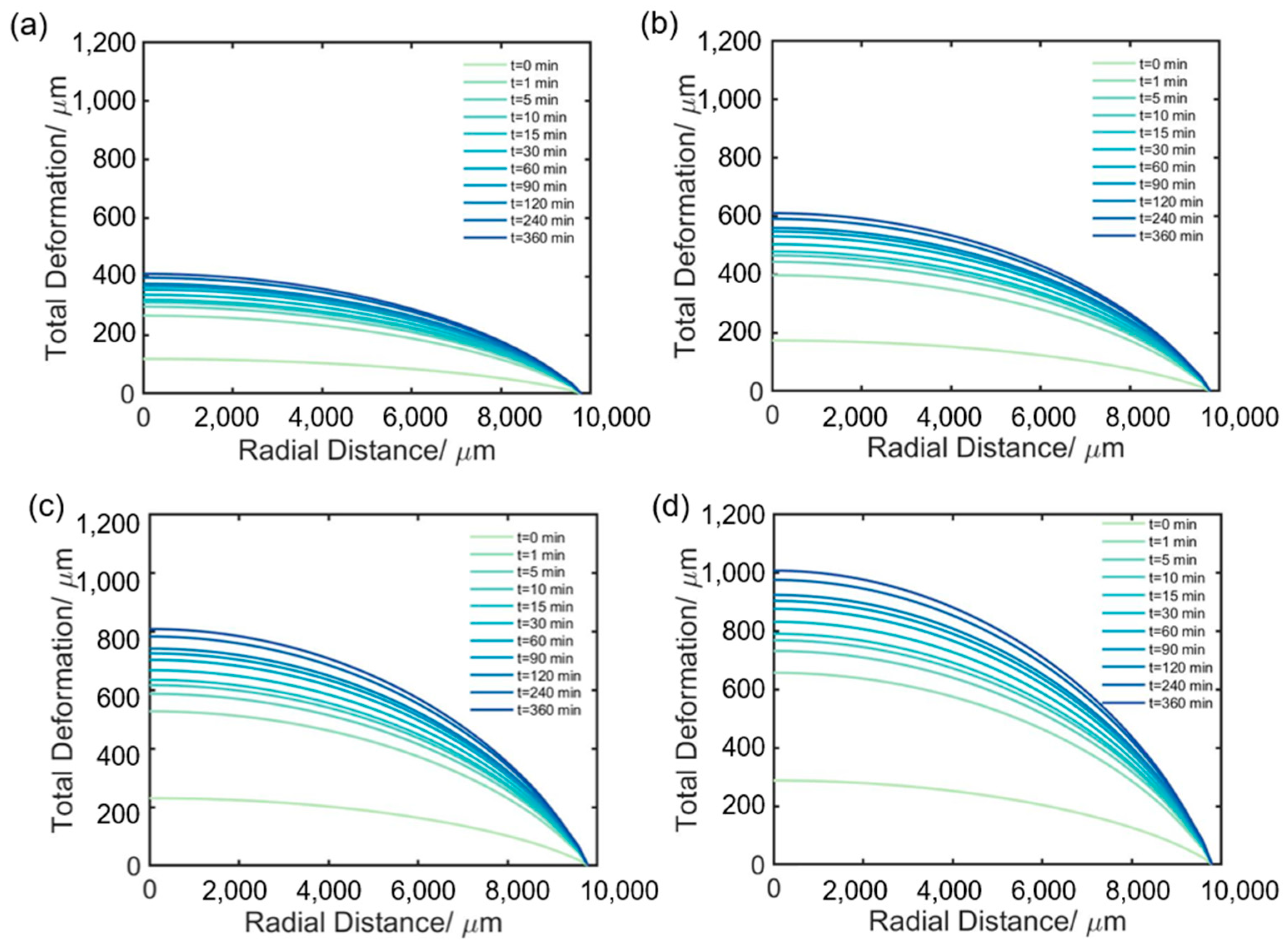
4.1. FEA Model
4.2. FEA Results
5. Discussion
5.1. More Potential Polarization Parameters
5.2. Future Work
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stachiw, J.D. Handbook of Acrylics for Submersibles, Hyperbaric Chambers, and Aquaria; Best Publishing Company: North Palm Beach, FL, USA, 2003. [Google Scholar]
- Adibeig, M.R.; Hassanifard, S.; Vakili-Tahami, F. Optimum creep lifetime of Polymethyl Methacrylate (PMMA) tube using rheological creep constitutive models based on experimental data. Polym. Test. 2019, 75, 107–116. [Google Scholar] [CrossRef]
- Sato, K.; Nakane, H.; Hideshima, T.; Iwayanagi, S. Creep of polymethyl methacrylate at low temperature. J. Phys. Soc. Jpn. 1954, 9, 413–416. [Google Scholar] [CrossRef]
- Webb, P. Introduction to Oceanography; Roger Williams University: Bristol, RI, USA, 2021. [Google Scholar]
- Boyle, J.T.; Spence, J. (Eds.) Stress Analysis for Creep; Butterworth-Heinemann: Oxford, UK, 1983; p. iv. [Google Scholar]
- Zhang, Z.; Jia, Y.; Gao, Y.; Yang, J.-L. Progress on Creep of Polymer Nanocomposites. Adv. Mech. 2010, 41, 266–278. (In Chinese) [Google Scholar]
- McCrum, N.G.; Buckley, C.P.; Buckley, C.; Bucknall, C. Principles of Polymer Engineering; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Daoqi, L.; Yong, H.; Fang, W.; Changlu, T.; Weicheng, C. Mechanics analysis on deep-sea Human Occupied Vehicle’s view-port windows. J. Ship Mech. 2010, 14, 782–788. [Google Scholar]
- Raha, S.; Bowden, P.B. Birefringence of plastically deformed poly (methyl methacrylate). Polymer 1972, 13, 174–183. [Google Scholar] [CrossRef]
- Wang, F.; Wang, W.; Zhang, Y.; Du, Q.; Jiang, Z.; Cui, W. Effect of Temperature and Nonlinearity of PMMA Material in the Design of Observation Windows for a Full Ocean Depth Manned Submersible. Mar. Technol. Soc. J. 2019, 53, 27–36. [Google Scholar] [CrossRef]
- Stachiw, J.D. Deep submergence spherical-shell window assembly with glass or transparent ceramic windows for abyssal depth service. J. Eng. Ind.-Trans. Asme 1975, 97, 1020–1034. [Google Scholar] [CrossRef]
- Li, J.X.; Liu, P.F.; Tong, X.Y. A simplified method for studying cyclic creep behaviors of deep-sea manned submersible viewport windows. Int. J. Press. Vessel. Pip. 2021, 194, 104565. [Google Scholar] [CrossRef]
- Du, Q.; Jiang, H.; Hu, X. Creep behavior analysis of conical observation window for human occupied vehicle based on ABAQUS. Chin. J. Ship Res. 2022, 17, 108–116. [Google Scholar]
- Sun, M.; He, H.; Zeng, N.; Du, E.; Guo, Y.; Liu, S.; Wu, J.; He, Y.; Ma, H. Characterizing the microstructures of biological tissues using Mueller matrix and transformed polarization parameters. Biomed. Opt. Express 2014, 5, 4223–4234. [Google Scholar] [CrossRef]
- Arteaga, O.; Baldris, M.; Anto, J.; Canillas, A.; Pascual, E.; Bertran, E. Mueller matrix microscope with a dual continuous rotating compensator setup and digital demodulation. Appl. Opt. 2014, 53, 2236–2245. [Google Scholar] [CrossRef] [PubMed]
- Ajovalasit, A.; Petrucci, G.; Scafidi, M. Measurement of edge residual stresses in glass by the phase-shifting method. Opt. Lasers Eng. 2011, 49, 652–657. [Google Scholar] [CrossRef]
- Almeida Magalhaes, P.A., Jr.; Magalhaes, C.A.; Mendonca Almeida Magalhaes, A.L. Computational methods of phase shifting to stress measurement with photoelasticity using plane polariscope. Optik 2017, 130, 213–226. [Google Scholar] [CrossRef]
- Zhang, W.; Zhu, Q.D.; Zhang, X.S. Polarization Phase-Shifting Detection Method for Central Stress in Flat Glass. Acta Opt. Sin. 2018, 38, 0426001. [Google Scholar] [CrossRef]
- Gao, Y.; Wan, X.; Xie, S. Stress measurement of transparent elements based on polarized camera. J. Appl. Opt. 2022, 43, 284–290. [Google Scholar]
- Li, H.; Liao, R.; Zhang, H.; Ma, G.; Guo, Z.; Tu, H.; Chen, Y.; Ma, H. Stress Detection of Conical Frustum Windows in Submersibles Based on Polarization Imaging. Sensors 2022, 22, 2282. [Google Scholar] [CrossRef]
- Lakes, R.; Lakes, R.S. Viscoelastic Materials; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Huang, T.; Meng, R.; Qi, J.; Liu, Y.; Wang, X.; Chen, Y.; Liao, R.; Ma, H. Fast Mueller matrix microscope based on dual DoFP polarimeters. Opt. Lett. 2021, 46, 1676–1679. [Google Scholar] [CrossRef]
- Chang, J.; He, H.; He, C.; Ma, H. DoFP polarimeter based polarization microscope for biomedical applications. In Proceedings of the Conference on Dynamics and Fluctuations in Biomedical Photonics XIII, San Francisco, CA, USA, 14–15 February 2016. [Google Scholar]
- Tyo, J.S. Design of optimal polarimeters: Maximization of signal-to-noise ratio and minimization of systematic error. Appl. Opt. 2002, 41, 619–630. [Google Scholar] [CrossRef]
- Chang, J.; He, H.; Wang, Y.; Huang, Y.; Li, X.; He, C.; Liao, R.; Zeng, N.; Liu, S.; Ma, H. Division of focal plane polarimeter-based 3 × 4 Mueller matrix microscope: A potential tool for quick diagnosis of human carcinoma tissues. J. Biomed. Opt. 2016, 21, 056002. [Google Scholar] [CrossRef]
- American National Standards Institute. Safety Standard for Pressure Vessels for Human Occupancy: ASME/ANSI PVHO-1a-1987 Addenda to ASME/ANSI PVHO-1-1987; American Society of Mechanical Engineers: New York, NY, USA, 1987. [Google Scholar]
- Cameron, B.D.; Li, Y.; Nezhuvingal, A. Determination of optical scattering properties in turbid media using Mueller matrix imaging. J. Biomed. Opt. 2006, 11, 054031. [Google Scholar] [CrossRef]
- He, H.; Zeng, N.; Liao, R.; Yun, T.; Li, W.; He, Y.; Ma, H. Application of sphere-cylinder scattering model to skeletal muscle. Opt. Express 2010, 18, 15104–15112. [Google Scholar] [CrossRef]
- He, H.; Zeng, N.; Li, D.; Liao, R.; Ma, H. Quantitative mueller matrix polarimetry techniques for biological tissues. J. Innov. Opt. Health Sci. 2012, 5, 1250017. [Google Scholar] [CrossRef]
- Sheng, W.; Li, W.; Qi, J.; Liu, T.; He, H.; Dong, Y.; Liu, S.; Wu, J.; Elson, D.S.; Ma, H. Quantitative Analysis of 4 × 4 Mueller Matrix Transformation Parameters for Biomedical Imaging. Photonics 2019, 6, 34. [Google Scholar] [CrossRef]
- Lu, S.Y.; Chipman, R.A. Interpretation of Mueller matrices based on polar decomposition. J. Opt. Soc. Am. A-Opt. Image Sci. Vis. 1996, 13, 1106–1113. [Google Scholar] [CrossRef]
- Cohen, I.; Huang, Y.; Chen, J.; Benesty, J.; Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson correlation coefficient. In Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2, pp. 1–4. [Google Scholar]
- Wang, F.; Wang, M.; Wang, W.; Yang, L.; Zhang, X. Time-dependent axial displacement of PMMA frustums designed for deep-sea manned cabin based on finite element analysis. Ships Offshore Struct. 2021, 16, 827–837. [Google Scholar] [CrossRef]
- Manjit, Y.; Limpichaipanit, A.; Ngamjarurojana, A. Isochromatic photoelasticity fringe patterns of PMMA in various shapes and stress applications. In Proceedings of the Third International Conference On Photonics Solutions (ICPS2017), Pattaya City, Thailand, 8–10 November 2017; Volume 10714. [Google Scholar]
- Manjit, Y.; Limpichaipanit, A.; Ngamjarurojana, A. Mechanical analysis of square shaped PMMA using reflection photoelasticity. Optik 2021, 240, 166943. [Google Scholar] [CrossRef]
- Song, J.; Guo, W.; Zeng, N.; Ma, H. Polarization phase unwrapping by a dual-wavelength Mueller matrix imaging system. Opt. Lett. 2023, 48, 2058–2061. [Google Scholar] [CrossRef]
- Ghiglia, D.C.; Pritt, M.D. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software, 1st ed.; Wiely-Interscience: Hoboken, NJ, USA, 1998. [Google Scholar]
- Gao, Z.; Liu, W.; Liu, Z.; Yue, Z. Experiment and simulation study on the creep behavior of PMMA at different temperatures. Polym.-Plast. Technol. Eng. 2010, 49, 1478–1482. [Google Scholar] [CrossRef]
- Ashby, M.F. Boundary defects, and atomistic aspects of boundary sliding and diffusional creep. Surf. Sci. 1972, 31, 498–542. [Google Scholar] [CrossRef]
- Arnold, J.C.; White, V.E. Predictive models for the creep behaviour of PMMA. Mater. Sci. Eng. A 1995, 197, 251–260. [Google Scholar] [CrossRef]
- Du, E.; He, H.; Zeng, N.; Sun, M.; Guo, Y.; Wu, J.; Liu, S.; Ma, H. Mueller matrix polarimetry for differentiating characteristic features of cancerous tissues. J. Biomed. Opt. 2014, 19, 076013. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Li, Q.; Wang, Y. A criterion of crazing density for the residual life assessment of PMMA during creep. Multidiscip. Model. Mater. Struct. 2015, 11, 517–526. [Google Scholar] [CrossRef]
- Li, P.; Tariq, A.; He, H.; Ma, H. Characteristic Mueller matrices for direct assessment of the breaking of symmetries. Opt. Lett. 2020, 45, 706–709. [Google Scholar] [CrossRef]
- Willson, R.G. Modeling and calibration of automated zoom lenses. In Videometrics III; SPIE: Bellingham, WA, USA, 1994; pp. 170–186. [Google Scholar]
- Booth, M.J. Adaptive optics in microscopy. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2007, 365, 2829–2843. [Google Scholar] [CrossRef] [PubMed]
- Gioux, S.; Mazhar, A.; Cuccia, D.J. Spatial frequency domain imaging in 2019: Principles, applications, and perspectives. J. Biomed. Opt. 2019, 24, 071613. [Google Scholar] [CrossRef]
- Chue-Sang, J.; Goldfain, A.M.; Hwang, J.; Germer, T.A. Spatial frequency domain Mueller matrix imaging. In Polarized Light and Optical Angular Momentum for Biomedical Diagnostics; SPIE: Bellingham, WA, USA, 2021; pp. 16–23. [Google Scholar]
- Arano-Martinez, J.A.; Martínez-González, C.L.; Salazar, M.I.; Torres-Torres, C. A Framework for Biosensors Assisted by Multiphoton Effects and Machine Learning. Biosensors 2022, 12, 710. [Google Scholar] [CrossRef]





| Properties | Value |
|---|---|
| Density/ () | 1.186 |
| Tensile Modules/ GPa | 3.13 |
| Yield Strength/ MPa | 129 |
| Poisson’s ratio | 0.37 |
| Refractive index | 1.49 |
| Properties | Value |
|---|---|
| Observation Window’s Density/ (g/cm3) | 1.186 |
| Observation Window’s Tensile Modulus/ GPa | 3.13 |
| Observation Window’s Poisson’s ratio | 0.37 |
| Window Seat’s Density/ (g/cm3) | 6.85 |
| Window Seat’s Tensile Modulus/ GPa | 200,000 |
| Window Seat’s Poisson’s ratio | 0.3 |
| Friction Coefficient | 0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, H.; Bu, X.; Liao, R.; Zhang, H.; Ma, G.; Li, H.; Wan, J.; Ma, H. Creep Monitoring of Submersible Observation Windows Using Mueller Matrix Imaging. Materials 2023, 16, 4733. https://doi.org/10.3390/ma16134733
Tu H, Bu X, Liao R, Zhang H, Ma G, Li H, Wan J, Ma H. Creep Monitoring of Submersible Observation Windows Using Mueller Matrix Imaging. Materials. 2023; 16(13):4733. https://doi.org/10.3390/ma16134733
Chicago/Turabian StyleTu, Haibo, Xingying Bu, Ran Liao, Hailong Zhang, Guoliang Ma, Hening Li, Jiachen Wan, and Hui Ma. 2023. "Creep Monitoring of Submersible Observation Windows Using Mueller Matrix Imaging" Materials 16, no. 13: 4733. https://doi.org/10.3390/ma16134733
APA StyleTu, H., Bu, X., Liao, R., Zhang, H., Ma, G., Li, H., Wan, J., & Ma, H. (2023). Creep Monitoring of Submersible Observation Windows Using Mueller Matrix Imaging. Materials, 16(13), 4733. https://doi.org/10.3390/ma16134733









