Design and Manufacturing of a Novel Trabecular Tibial Implant
Abstract
1. Introduction
2. Personalized Design of Tibial Implants
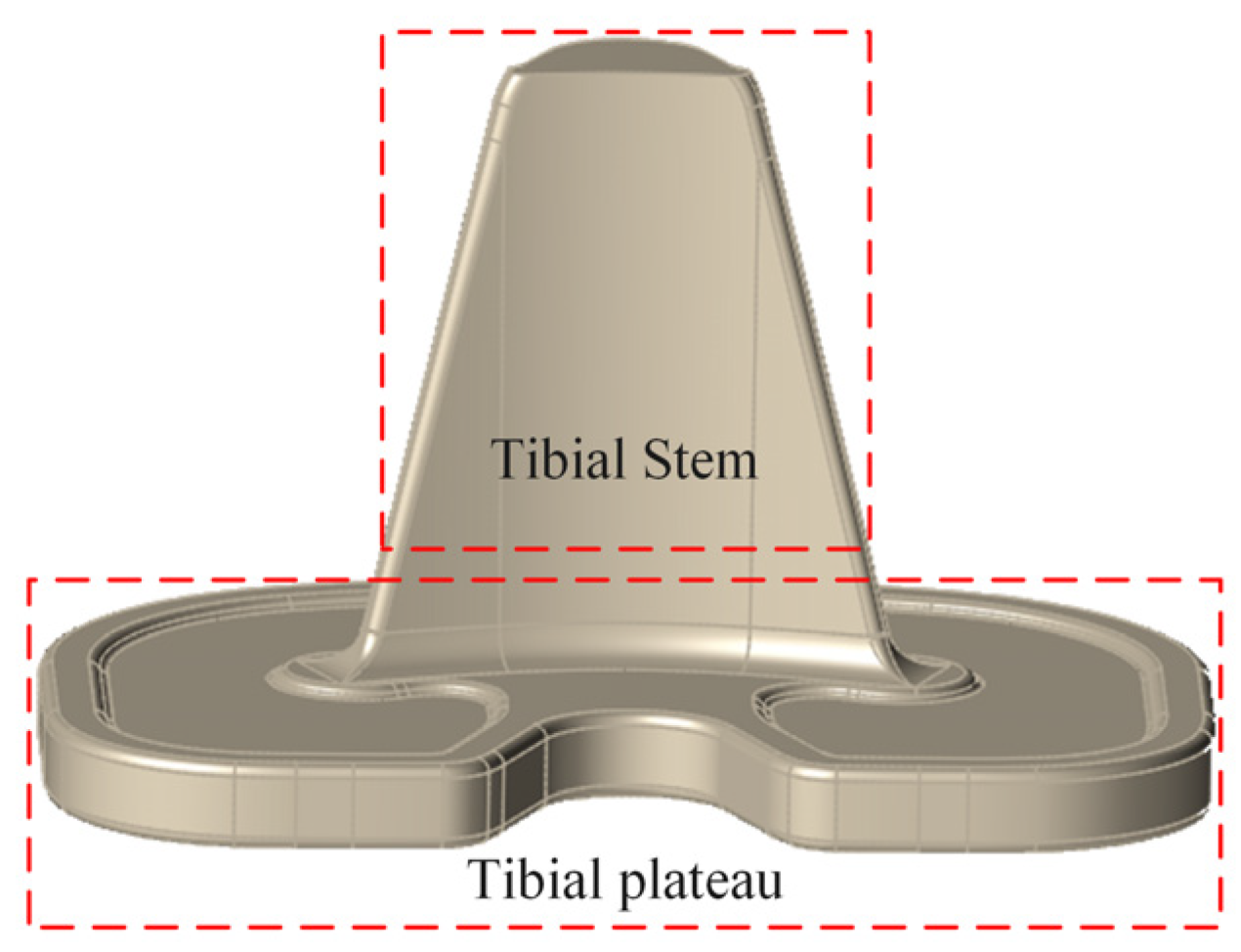
2.1. Establishment of Tibial Implant Model
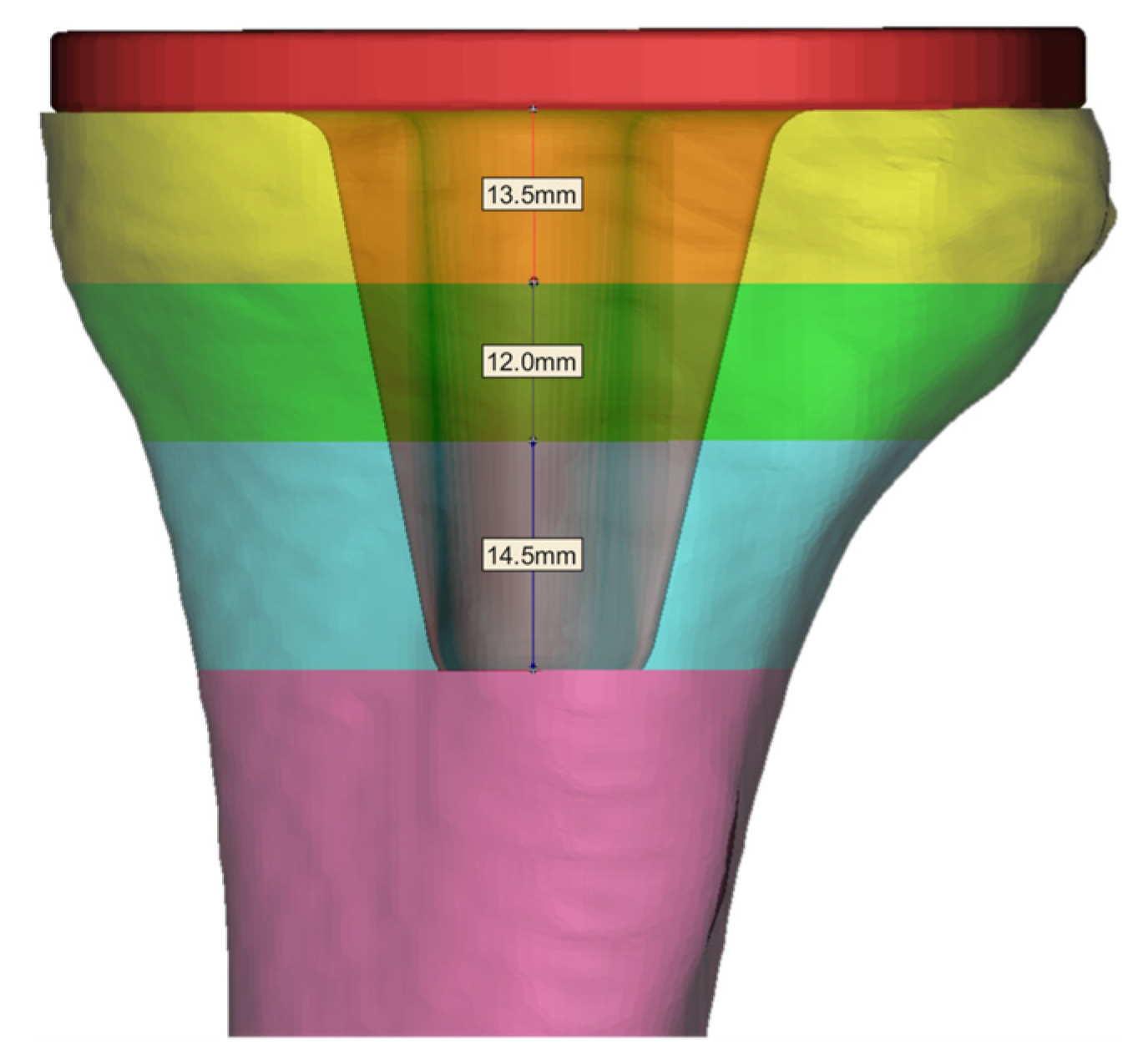
2.2. Tibia Implant Trabecular Region Segmentation
3. Topology Optimization Design and Performance Research of Unit Cell Structures
3.1. Topological Optimization Design for Unit Cells
3.2. Mechanical Performance Analysis
3.3. Permeability Analysis
4. Results and Discussion
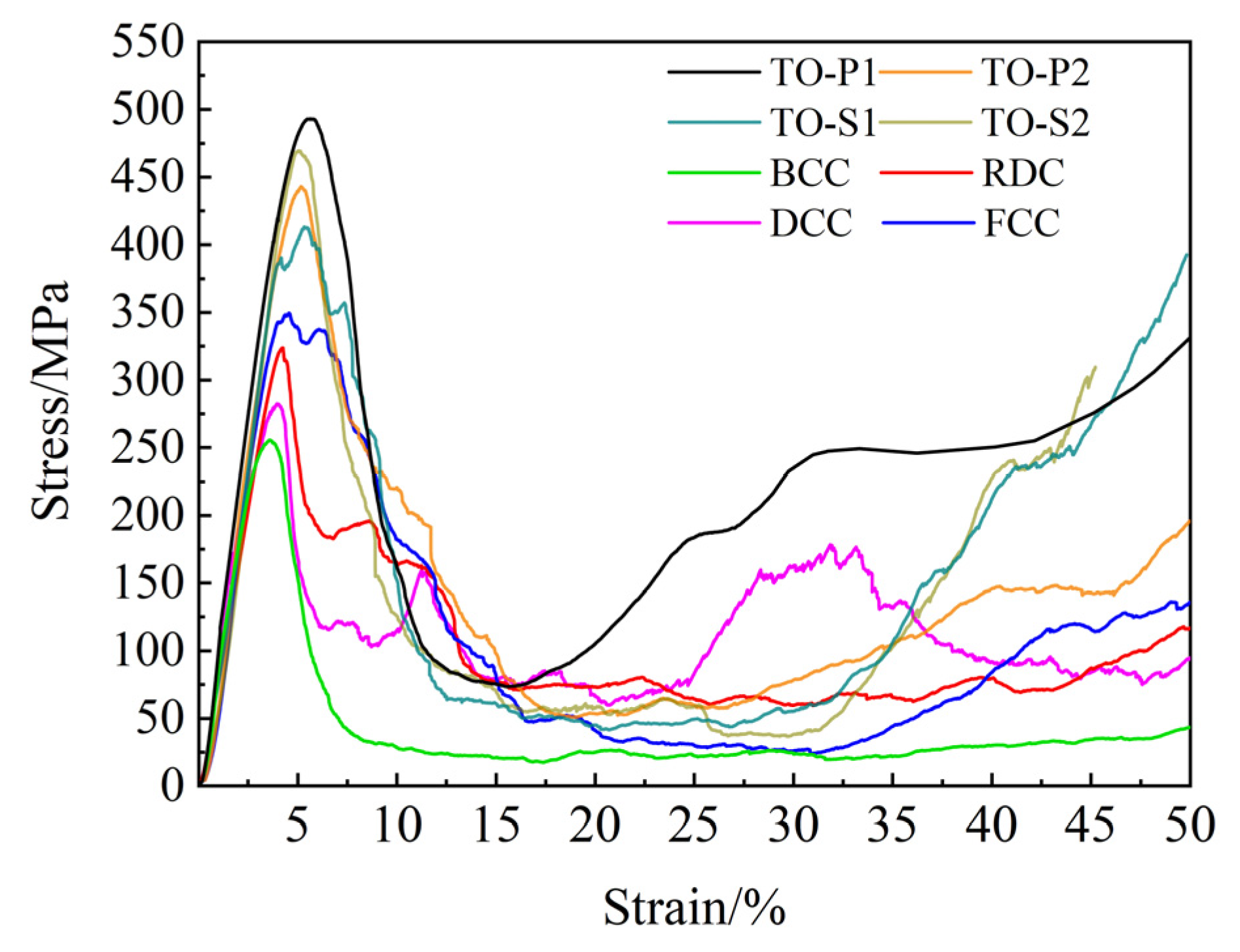
4.1. Mechanical Performance
4.2. Permeability
4.3. Establishment of a Porous Titanium Alloy Regulating Model
4.4. Printing of Trabecular Tibial Implants
5. Conclusions
- A personalized tibial implant solid model was designed based on the loading state of the tibial skeletal joint, and it was placed in the tibial resection area. The elastic modulus of the tibial stem was determined to be between 3.031 and 10.528 GPa.
- Two types of unit cell structures were designed using topology optimization for compression and shear resistance, respectively (TO-P1, TO-P2, TO-S1, TO-S2), and four common unit cell structures (BCC, FCC, RDC, DCC). A fitting model was established for the relationship between strut diameter and porosity of the unit cell structures.
- The mechanical and permeability properties of porous titanium alloys were comprehensively compared, and it was determined that the TO-S2 structure had the best overall performance and was most suitable as a trabecular structure for tibial implants.
- A model was established to regulate the mechanical properties of porous titanium alloys, and it was determined that the strut diameter of porous titanium alloy for tibial implants should be between 0.106 and 0.202 mm, and the tibial stem should be filled with porous titanium alloy. Finally, SLM technology was used to print the trabecular tibial implant with good forming results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Tan, J.; Meng, Z.D.; He, Z.Y.; Zhang, Y.Q.; Jiang, Y.H.; Zhou, R. Low elastic modulus Ti-Ag/Ti radial gradient porous composite with high strength and large plasticity prepared by spark plasma sintering. Mater. Sci. Eng. A 2017, 688, 330–337. [Google Scholar] [CrossRef]
- Tan, X.P.; Tan, Y.J.; Chow, C.S.L.; Tor, S.B.; Yeong, W.Y. Metallic powder-bed based 3D printing of cellular scaffolds for orthopaedic implants: A state-of-the-art review on manufacturing, topological design, mechanical properties and biocompatibility. Mater. Sci. Eng. C 2017, 76, 1328–1343. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.D.; Wang, C.Y.; Wang, C.W.; Yang, G. Study on Porous Ti6Al4V Alloy Formed by Selective Laser Melting and Its Heat Treatment. Rare Met. Mater. Eng. 2022, 51, 1690–1696. [Google Scholar]
- Zhang, B.Q.; Pei, X.; Zhou, C.C.; Fan, Y.J.; Jiang, Q.; Ronca, A.; D’Amora, U.; Chen, Y.; Li, H.Y.; Sun, Y.; et al. The biomimetic design and 3D printing of customized mechanical properties porous Ti6Al4V scaffold for load-bearing bone reconstruction. Mater. Design 2018, 152, 30–39. [Google Scholar] [CrossRef]
- Wu, J.Y.; Zhang, Y.W.; Lyu, Y.T.; Cheng, L.L. On the Various Numerical Techniques for the Optimization of Bone Scaffold. Materials 2023, 16, 974. [Google Scholar] [CrossRef] [PubMed]
- Lai, Y.X.; Cao, H.J.; Wang, X.L.; Chen, S.K.; Zhang, M.; Wang, N.; Yao, Z.H.; Dai, Y.; Xie, X.H.; Zhang, P.; et al. Porous composite scaffold incorporating osteogenic phytomolecule icariin for promoting skeletal regeneration in challenging osteonecrotic bone in rabbits. Biomaterials 2018, 153, 1–13. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Li, J.X.; Zhou, X.Y.; Zhou, Y.S.; Wang, A.M. Optimal Design and Processing Technology of 3D Printed Tibial Implants. Coatings 2022, 12, 561. [Google Scholar] [CrossRef]
- Ran, Q.; Yang, W.; Hu, Y.; Shen, X.; Yu, Y.; Xiang, Y.; Cai, K. Osteogenesis of 3D printed porous Ti6Al4V implants with different pore sizes. J. Mech. Behav. Biomed. 2018, 84, 1–11. [Google Scholar] [CrossRef]
- Zadpoor, A.A. Bone tissue regeneration: The role of scaffold geometry. Biomater. Sci. 2015, 3, 231–245. [Google Scholar] [CrossRef]
- Arjunan, A.; Demetriou, M.; Baroutaji, A.; Wang, C. Mechanical performance of highly permeable laser melted Ti6Al4V bone scaffolds. J. Mech. Behav. Biomed. 2020, 102, 103517. [Google Scholar] [CrossRef]
- Chakkravarthy, V.; Jose, S.P.; Lakshmanan, M.; Manojkumar, P.; Narayan, R.L.; Kumaran, M. Additive manufacturing of novel Ti-30Nb-2Zr biomimetic scaffolds for successful limb salvage. Mater. Today Proc. 2022, 64, 1711–1716. [Google Scholar] [CrossRef]
- Lv, Y.T.; Wang, B.H.; Liu, G.H.; Tang, Y.J.; Liu, E.Y.; Xie, K.J.; Lan, C.G.; Liu, G.; Qin, Z.B.; Wang, L.Q. Metal material, properties and design methods of porous biomedical scaffolds for additive manufacturing: A review. Front. Bioeng. Biotech. 2021, 9, 641130. [Google Scholar] [CrossRef]
- Alkentar, R.; Máté, F.; Mankovits, T. Investigation of the Performance of Ti6Al4V Lattice Structures Designed for Biomedical Implants Using the Finite Element Method. Materials 2022, 15, 6335. [Google Scholar] [CrossRef]
- Bazrgari, B.; Shirazi-Adl, A.; Arjmand, N. Analysis of squat and stoop dynamic liftings: Muscle forces and internal spinal loads. Eur. Spine J. 2007, 16, 687–699. [Google Scholar] [CrossRef]
- Heinert, B.L.; Collins, T.; Tehan, C.; Ragan, R.; Kernozek, T.W. Effect of hamstring-to-quadriceps ratio on knee forces in females during landing. Int. J. Sports Med. 2021, 42, 264–269. [Google Scholar] [CrossRef]
- Amis, A.A. Biomechanics of high tibial osteotomy. Knee Surg. Sport. Traumatol. Arthrosc. 2013, 21, 197–205. [Google Scholar] [CrossRef]
- Keaveny, T.M.; Kopperdahl, D.L.; Melton, L.J., III; Hoffmann, P.F.; Amin, S.; Riggs, B.L.; Khosla, S. Age-dependence of femoral strength in white women and men. J. Bone Miner. Res. 2010, 25, 994–1001. [Google Scholar] [CrossRef]
- Chernchujit, B.; Tharakulphan, S.; Prasetia, R.; Chantarapanich, N.; Jirawison, C.; Sitthiseripratip, K. Preoperative planning of medial opening wedge high tibial osteotomy using 3D computer-aided design weight-bearing simulated guidance: Technique and preliminary result. J. Orthop. Surg. 2019, 27, 2309499019831455. [Google Scholar] [CrossRef]
- Kim, T.K.; Phillips, M.; Bhandari, M.; Watson, J.; Malhotra, R. What differences in morphologic features of the knee exist among patients of various races? A systematic review. Clin. Orthop. Relat. Res. 2017, 475, 170–182. [Google Scholar] [CrossRef]
- Kamer, L.; Noser, H.; Blauth, M.; Lenz, M.; Windolf, M.; Popp, A.W. Bone mass distribution of the distal tibia in normal, osteopenic, and osteoporotic conditions: An ex vivo assessment using HR-pQCT, DXA, and computational modelling. Calcif. Tissue Int. 2016, 99, 588–597. [Google Scholar] [CrossRef]
- Lim Fat, D.; Kennedy, J.; Galvin, R.; O’Brien, F.; Mc Grath, F.; Mullett, H. The Hounsfield value for cortical bone geometry in the proximal humerus—An in vitro study. Skelet. Radiol. 2012, 41, 557–568. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Starly, B.; Nam, J.; Darling, A. Bio-CAD modeling and its applications in computer-aided tissue engineering. Comput. Aided Des. 2005, 37, 1097–1114. [Google Scholar] [CrossRef]
- Zhu, X.H. Application of subsectional relationship between elastic modulus and apparent density in the structural simulation of proximal femur. Chin. J. Biomed. Eng. 2003, 22, 250–257. [Google Scholar]
- Deng, Z.B.; Zhou, C.C.; Fan, Y.J.; Peng, J.P.; Zhu, X.D.; Pei, X.; Yin, G.F.; Zhang, X.D. Design and Charaterization of Porous Titanium Scaffold for Bone Tissue Engineering. Rare Met. Mater. Eng. 2016, 45, 2287–2292. [Google Scholar]
- Zhao, M.; Liu, F.; Fu, G.; Zhang, D.Z.; Zhang, T.; Zhou, H. Improved mechanical properties and energy absorption of BCC lattice structures with triply periodic minimal surfaces fabricated by SLM. Materials 2018, 11, 2411. [Google Scholar] [CrossRef]
- Cheng, X.F.; Liu, S.C.; Chen, C.; Chen, W.; Liu, M.; Li, R.D.; Zhang, X.Y.; Zhou, K.C. Microstructure and mechanical properties of additive manufactured porous Ti–33Nb–4Sn scaffolds for orthopaedic applications. J. Mater. Sci. Mater. Med. 2019, 30, 91. [Google Scholar] [CrossRef]
- Egan, P.F.; Gonella, V.C.; Engensperger, M.; Ferguson, S.J.; Shea, K. Computationally designed lattices with tuned properties for tissue engineering using 3D printing. PLoS ONE 2017, 12, e0182902. [Google Scholar] [CrossRef]
- Jin, N.; Yan, Z.Y.; Wang, Y.W.; Cheng, H.W.; Zhang, H.M. Effects of heat treatment on microstructure and mechanical properties of selective laser melted Ti-6Al-4V lattice materials. Int. J. Mech. Sci. 2021, 190, 106042. [Google Scholar] [CrossRef]
- Siddiqui, A.M.; Azim, Q.A. Creeping flow of a viscous fluid in a uniformly porous slit with porous medium: An application to the diseased renal tubules. Chin. J. Phys. 2020, 64, 264–277. [Google Scholar] [CrossRef]
- Ali, D.; Sen, S. Finite Element Analysis of Mechanical Behavior, Permeability and Fluid Induced Wall Shear Stress of High Porosity Scaffolds with Gyroid and Lattice-based Architectures. J. Mech. Behav. Biomed. 2017, 75, 262–270. [Google Scholar] [CrossRef]
- Ma, S.; Tang, Q.; Han, X.X.; Feng, Q.X.; Song, J.; Setchi, R.; Liu, Y.; Liu, Y.; Goulas, A.; Engstrøm, D.S.; et al. Manufacturability, Mechanical Properties, Mass-transport Properties and Biocompatibility of Triply Periodic Minimal Surface (TPMS) Porous Scaffolds Fabricated by Selective Laser Melting. Mater. Des. 2020, 195, 109034. [Google Scholar] [CrossRef]
- Baino, F.; Magnaterra, G.; Fiume, E.; Schiavi, A.; Tofan, L.P.; Schwentenwein, M.; Verné, E. Digital Light Processing Stereolithography of Hydroxyapatite Scaffolds with Bone-like Architecture, Permeability, and Mechanical Properties. J. Am. Ceram. Soc. 2022, 105, 1648–1657. [Google Scholar] [CrossRef]
- Nauman, E.A.; Fong, K.E.; Keaveny, T.M. Dependence of intertrabecular permeability on flow direction and anatomic site. Ann. Biomed. Eng. 1999, 27, 517–524. [Google Scholar] [CrossRef]
- Gibson, L.J. Biomechanics of cellular solids. J. Biomech. 2005, 38, 377–399. [Google Scholar] [CrossRef]


















| Trabecular Layer of Bone | Threshold Range/Hu | Apparent Density ρ/(g/cm3) | Elastic Modulus E/GPa |
|---|---|---|---|
| Layer 1 | 500.53–565.27 | 1.056–1.179 | 2.329–3.031 |
| Layer 2 | 565.27–682.63 | 1.179–1.402 | 3.031–5.287 |
| Layer 3 | 682.63–796.84 | 1.402–1.619 | 5.287–8.439 |
| Layer 4 | 796.84–916.78 | 1.619–1.733 | 8.439–10.528 |
| Layer 5 | 916.78–1010.40 | 1.733–1.805 | 10.528–12.017 |
| Structure Type | Abbreviation of Structure Type |
|---|---|
| Topology Optimization-Pressure-1 | TO-P1 |
| Topology Optimization-Pressure-2 | TO-P2 |
| Topology optimization-Shear-1 | TO-S2 |
| Topology optimization-Shear-2 | TO-S2 |
| P/% | 90 | 85 | 80 | 75 | 70 | 65 | 60 | |
|---|---|---|---|---|---|---|---|---|
| TO-P1 | S/mm A/mm | 0.222 0.78 | 0.276 0.73 | 0.325 0.68 | 0.37 0.63 | 0.412 0.59 | 0.452 0.55 | 0.49 0.51 |
| TO-P2 | S/mm A/mm | 0.14 0.567 | 0.168 0.539 | 0.198 0.509 | 0.225 0.482 | 0.252 0.455 | 0.279 0.428 | 0.3 0.407 |
| TO-S1 | S/mm A/mm | 0.125 0.87 | 0.157 0.843 | 0.185 0.815 | 0.21 0.79 | 0.235 0.765 | 0.257 0.743 | 0.28 0.72 |
| TO-S2 | S/mm A/mm | 0.1 0.858 | 0.123 0.826 | 0.145 0.794 | 0.165 0.766 | 0.185 0.738 | 0.202 0.714 | 0.22 0.688 |
| P/% | 90 | 85 | 80 | 75 | 70 | 65 | 60 | |
|---|---|---|---|---|---|---|---|---|
| BCC | S/mm A/mm | 0.145 0.56 | 0.182 0.52 | 0.213 0.49 | 0.242 0.46 | 0.27 0.43 | 0.296 0.41 | 0.32 0.38 |
| RDC | S/mm A/mm | 0.1 0.6 | 0.129 0.58 | 0.155 0.55 | 0.173 0.53 | 0.19 0.51 | 0.212 0.5 | 0.23 0.48 |
| DCC | S/mm A/mm | 0.13 0.57 | 0.167 0.54 | 0.2 0.5 | 0.225 0.48 | 0.25 0.45 | 0.279 0.428 | 0.3 0.4 |
| FCC | S/mm A/mm | 0.132 0.868 | 0.165 0.835 | 0.193 0.807 | 0.22 0.78 | 0.245 0.755 | 0.27 0.73 | 0.293 0.707 |
| Monoclinic Structure | Fitting Equation | Correlation Coefficient R2 |
|---|---|---|
| TO-P1 | P = 1.05271 − 0.49073S − 0.88485S2 | 0.99999 |
| TO-P2 | P = 1.09461 − 1.19359S − 1.48474S2 | 0.9993 |
| TO-S1 | P = 1.08954 − 1.21685S − 1.9013S2 | 0.99984 |
| TO-S2 | P = 1.06768 − 1.30624S − 3.73293S2 | 0.99987 |
| BCC | P = 1.04546 − 0.67328S − 2.24506S2 | 0.99992 |
| RDC | P = 1.02176 − 0.7152S − 4.88784S2 | 0.99963 |
| DCC | P = 1.02005 − 0.54815S − 2.83886S2 | 0.99945 |
| FCC | P = 1.06386 − 0.94786S − 2.17198S2 | 0.99988 |
| Elastic Modulus | Yield Strength | Density | Poisson’s Ratio |
|---|---|---|---|
| 113 GPa | 890 MPa | 4.43 g/cm3 | 0.342 |
| Porosity | TO-P1 | TO-P2 | TO-S1 | TO-S2 |
|---|---|---|---|---|
| 60% | 2.5808 | 3.824 | 4.4124 | 5.6084 |
| 70% | 2.4378 | 3.773 | 4.2336 | 5.4496 |
| 80% | 2.147 | 3.4605 | 3.7966 | 4.8854 |
| 90% | 1.5455 | 2.8233 | 3.0264 | 3.8453 |
| Porous Structures Type | Porosity (P/%) | Permeability Coefficient (K/10−9m2) | |
|---|---|---|---|
| Regular CAD | 60–90 | 1–25 | Ali [30] |
| TPMS | 75.1–88.8 | 0.29–3.91 | Ma [31] |
| Micro-CT | 78–82 | 0.75–1.74 | Baino [32] |
| Human bone | - | 0.027–20 | Nauman [33] |
| TO-P1 | 60–90 | 2.05–13.49 | This paper |
| TO-P2 | 60–90 | 1.43–7.1 | |
| TO-S1 | 60–90 | 1.45–7.2 | |
| TO-S2 | 60–90 | 1.54–7.36 |
| Structure Type | Porosity | Experimental Test Value | Mean | Gibson–Ashby Fitting Value | ||
|---|---|---|---|---|---|---|
| TO-S2 | 60% | 12.266 | 12.256 | 12.231 | 12.251 | 12.253 |
| 65% | 10.277 | 10.286 | 10.331 | 10.298 | 10.566 | |
| 70% | 9.138 | 8.809 | 8.921 | 8.956 | 8.904 | |
| 75% | 7.713 | 7.553 | 7.390 | 7.552 | 7.273 | |
| 80% | 6.158 | 5.776 | 6.015 | 5.983 | 5.678 | |
| 85% | 4.051 | 4.202 | 4.173 | 4.142 | 4.126 | |
| 90% | 2.014 | 2.135 | 2.115 | 2.088 | 2.631 | |
| Trabecular Layer | Elastic Modulus (E/GPa) | Strut Diameter (S/mm) |
|---|---|---|
| Layer 2 | 3.031–5.287 | 0.106–0.140 |
| Layer 3 | 5.287–8.439 | 0.140–0.179 |
| Layer 4 | 8.439–10.528 | 0.179–0.202 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Sun, B.; Zhao, L.; Yang, G. Design and Manufacturing of a Novel Trabecular Tibial Implant. Materials 2023, 16, 4720. https://doi.org/10.3390/ma16134720
Zhang Y, Sun B, Zhao L, Yang G. Design and Manufacturing of a Novel Trabecular Tibial Implant. Materials. 2023; 16(13):4720. https://doi.org/10.3390/ma16134720
Chicago/Turabian StyleZhang, Yongdi, Baoyu Sun, Lisong Zhao, and Guang Yang. 2023. "Design and Manufacturing of a Novel Trabecular Tibial Implant" Materials 16, no. 13: 4720. https://doi.org/10.3390/ma16134720
APA StyleZhang, Y., Sun, B., Zhao, L., & Yang, G. (2023). Design and Manufacturing of a Novel Trabecular Tibial Implant. Materials, 16(13), 4720. https://doi.org/10.3390/ma16134720






