Estimation of Stiffness of Non-Cohesive Soil in Natural State and Improved by Fiber and/or Cement Addition under Different Load Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. California Bearing Ratio Test
2.2.2. Resilient Modulus in Cyclic Triaxial Apparatus
3. Results and Discussion
4. Conclusions
- The gravelly sand, characterized by a lack of fines and compacted at the optimum water content to the maximum dry density, was sheared during the resilient modulus test after about 600 cycles of loading regardless of whether the standard or modified compaction method was used. The fiber reinforcement of the gravelly sand slightly improved cyclic resistance, but the samples were sheared after about 700 loading cycles. A resilient modulus value could not be achieved for the unbound gravelly sand.
- The 1.5% cement addition increased the resilient modulus of the gravelly sand, which was 140–324 MPa after 7 days of curing and 245–513 MPa after 28 days of curing. Therefore, the curing time also impacted the resilient modulus value. The addition of fibers to the gravelly sand stabilized with 1.5% cement increased but changed the material behavior at failure from brittle to plastic.
- The gravelly sand revealed high CBR values: 25.9–37.0% and 56.4–90.2% for the standard and modified compaction methods, respectively. An addition of 0.1% fibers doubled the CBR values of the samples compacted using the standard method; however, increasing the addition to 0.2 and 0.3% reduced the CBR value to the value found for the samples without fibers. The addition of 0.1% fibers to the modified compacted samples resulted in an approx. 10% decrease in the CBR value, and the increase in the fibers to 0.2 and 0.3% resulted in further minor drops in the CBR value. The reduction in the sand stiffness may have been caused by its plasticization upon the addition of the fibers.
- The addition of 1.5% cement improved the CBR value of the gravelly sand, with the values reaching 68.1–143.9% and 150.9–171.3% for the standard compaction and 82.7–198.7% and 183.6–281.0% for the modified compaction after 7 and 28 days of curing, respectively. The addition of 0.3% fibers to the cement-stabilized soil improved its CBR value directly after compaction and curing, which depended on the duration of the curing time and the compaction method used.
- Even though the obtained relationship of , found for all data sets, was evaluated as being statistically significant, it is not efficient from an engineering point of view. The unbound gravelly sand was non-resistant to cyclic loading regardless of the compaction method used. The above dependency of the bound samples is statistically invalid, i.e., cyclic and static material stiffnesses are quite independent. In the authors’ opinion, the CBR and resilient modulus values should not be compared due to the various ways of loading samples during tests—static and cyclic loading dependent on the stress state, especially in the case of non-cohesive materials.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brown, S.F. Soil mechanics in pavement engineering. Gėotechnique 1996, 46, 383–426. [Google Scholar] [CrossRef]
- Hveem, F.N. Pavement deflections and fatigue failures. Highw. Res. Board Bull. 1955, 55, 43–87. [Google Scholar]
- Seed, H.B.; Chan, C.K.; Lee, C.E. Resilience characteristics of subgrade soils and their relation to fatigue failures in asphalt pavements. In Proceedings of the 1st Int. Conf. on the Structural Design of Asphalt Pavements, Ann Arbor, MI, USA, 20–24 August 1962. [Google Scholar]
- Seed, H.B.; Mitry, G.; Monismith, C.L.; Chan, C.K. Factors influencing the resilient deformations of untreated aggregate base in two-layer pavements subjected to repeated loading. Highw. Res. Rec. 1967, 190, 19–57. [Google Scholar]
- AASHTO T 307-99; Standard Method of Test for Determining the Resilient Modulus of Soils and Aggregate Materials. American Association of State and Highway Transportation Officials: Washington, DC, USA, 2021.
- EN 13286-7:2004; Unbound and Hydraulically Bound Mixtures-Part 7: Cyclic Load Triaxial Test for Unbound Mixture. European Committee for Standardization: Brussels, Belgium, 2003.
- Lekarp, F.; Isacsson, U.; Dawson, A. State of the art. I: Resilient response of unbound aggregates. J. Transp. Eng. 2000, 126, 66–75. [Google Scholar] [CrossRef]
- Hicks, R.G.; Monismith, C.L. Factors influencing the resilient response of granular materials. High. Res. Rec. 1971, 345, 15–31. [Google Scholar]
- Rada, C.; Witczak, W.M. Comprehensive evaluation of laboratory resilient moduli results for granular material. Transp. Res. Rec. 1981, 810, 23–33. [Google Scholar]
- Ng, C.W.W.; Zhou, C.; Yuan, Q.; Xu, J. Resilient modulus of unsaturated subgrade soil: Experimental and theoretical investigations. Can. Geotech. J. 2013, 50, 223–232. [Google Scholar] [CrossRef]
- Samb, F.; Fall, M.; Berthaud, Y.; Bâ, M. Resilient modulus of compacted lateritic soils from Senegal at OPM conditions. Geomaterials 2013, 3, 165–171. [Google Scholar] [CrossRef]
- Tang, L.; Yan, M.H.; Ling, X.Z.; Tian, S. Dynamic behaviours of railway’s base course materials subjected to long-term low-level cyclic loading: Experimental study and empirical model. Géotechnique 2017, 67, 537–545. [Google Scholar] [CrossRef]
- Tanimoto, K.; Nishi, M. On resilient characteristics of some soils under repeated loading. Soils Found. 1970, 10, 75–92. [Google Scholar] [CrossRef][Green Version]
- Kim, D.; Kim, J.R. Resilient behavior of compacted subgrade soils under the repeated triaxial test. Constr. Build. Mat. 2007, 21, 1470–1479. [Google Scholar] [CrossRef]
- Sas, W.; Głuchowski, A.; Gabryś, K.; Soból, E.; Szymański, A. Long-term cyclic loading impact on the creep deformation mechanism in cohesive materials. Appl. Sci. 2017, 7, 370. [Google Scholar] [CrossRef]
- Jastrzębska, M.; Tokarz, K. Strength characteristics of clay–rubber waste mixtures in low-frequency cyclic triaxial tests. Minerals 2021, 11, 315. [Google Scholar] [CrossRef]
- Thakur, P.K.; Vinod, J.S.; Indraratna, B. Effect of confining pressure and frequency on the deformation of balast. Géotechnique 2013, 63, 786–790. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, J.; Liu, W.; Lu, W. Predicting resilient modulus of fine-grained subgrade soils considering relative compaction and matric suction. Road Mater. Pavement Des. 2019, 22, 702–715. [Google Scholar] [CrossRef]
- Li, J.; Qubain, B.S. Resilient modulus variations with water content. In Resilient Modulus Testing for Pavement Components, ASTM STP 1437; Durham, G.N., Marr, W.A., Eds.; ASTM International: West Conshohocken, PA, USA, 2003; pp. 59–69. [Google Scholar]
- Arshad, M. Development of a correlation between the resilient modulus and cbr value for granular blends containing natural aggregates and RAP/RCA materials. Adv. Mater. Sci. Eng. 2019, 2019, 8238904. [Google Scholar] [CrossRef]
- Zabielska-Adamska, K.; Sulewska, M.J. Dynamic CBR test to assess the soil compaction. J. Test. Eval. 2015, 53, 1028–1036. [Google Scholar] [CrossRef]
- Zabielska-Adamska, K. Characteristics of compacted fly ash as a transitional soil. Materials 2020, 13, 1387. [Google Scholar] [CrossRef]
- Heukelom, W.; Klomp, A.J.G. Dynamic testing as a means of controlling pavement during and after construction. In Proceedings of the International Conference on the Structural Design of Asphalt Pavements, Ann Arbor, MI, USA, 20–24 August 1962; pp. 667–679. [Google Scholar]
- Dione, A.; Fall, M.; Berthaud, Y.; Benboudjema, F.; Michou, A. Implementation of resilient modulus-CBR relationship in mechanistic-empirical (M-E) pavement design. Sci. Appl. l’Ingénieur 2015, 1, 65–71. [Google Scholar]
- Farrell, E.R.; Orr, T.L. Discussion: An analysis of the California bearing ratio test in saturated clays D. W. Hight and M. G. H. Stevens. Géotechnique 1984, 34, 129–130. [Google Scholar] [CrossRef]
- Razouki, S.S.; Ibrahim, A.N. Improving the resilient modulus of a gypsum sand roadbed soil by increased compaction. Int. J. Pavement Eng. 2019, 20, 432–438. [Google Scholar] [CrossRef]
- Edil, T.; Acosta, H.A.; Benson, C.H. Stabilizing soft fine-grained soils with fly ash. J. Mater. Civ. Eng. 2006, 18, 283–294. [Google Scholar] [CrossRef]
- Zabielska-Adamska, K.; Wasil, M.; Dobrzycki, P. Resilient response of cement-treated coarse post-glacial soil to cyclic load. Materials 2021, 14, 6495. [Google Scholar] [CrossRef]
- Dobrzycki, P.; Zabielska-Adamska, K.; Wasil, M. Resilient modulus as a technical parameter for evaluating the cement-stabilized soil. In Proceedings of the 5th International Conference on New Developments in Soil Mechanics and Geotechnical Engineering, Nicosia, Cyprus, 30 June–2 July 2022. [Google Scholar]
- Michalowski, R.L.; Čermák, J. Triaxial compression of sand reinforced with fibers. J. Geotech. Geoenviron. Eng. 2003, 129, 125–136. [Google Scholar] [CrossRef]
- EN 933-1:2012; Tests for Geometrical Properties of Aggregates-Part 1: Determination of Particle Size Distribution-Sieving Method. European Committee for Standardization: Brussels, Belgium, 2012.
- EN ISO 14688-1:2018; Geotechnical Investigation and Testing. Identification and Classification of Soil. Identification and Description. ISO: Geneva, Switzerland, 2018.
- EN ISO 14688-2:2018-05; Geotechnical Investigation and Testing-Identification and Classification of Soil-Part 2: Principles for a Classification. ISO: Geneva, Switzerland, 2018.
- EN 13242:2007; Aggregates for Unbound and Hydraulically Bound Materials for Use in Civil Engineering Work and Road Construction. European Committee for Standardization: Brussels, Belgium, 2007.
- ASTM D1241-15; Standard Specification for Materials for Soil-Aggregate Subbase, Base, and Surface Courses. ASTM International: West Conshohocken, PA, USA, 2020.
- Patakiewicz, M.A.; Zabielska-Adamska, K. Crushing of non-cohesive soil grains under dynamic loading. Procedia Eng. 2017, 189, 80–85. [Google Scholar] [CrossRef]
- EN 13286-2:2010; Unbound and Hydraulically Bound Mixtures-Part 2: Test Methods for Laboratory Reference Density and Water Content-Proctor Compaction. European Committee for Standardization: Brussels, Belgium, 2010.
- ASTM D1883-21; Standard Test Method for CBR (California Bearing Ratio) of Laboratory-Compacted Soils. ASTM International: West Conshohocken, PA, USA, 2021.
- EN 13286-47:2007; Unbound and Hydraulically Bound Mixtures-Part 47: Test Method for the Determination of California Bearing Ratio, Immediate Bearing Index and Linear Swelling. European Committee for Standardization: Brussels, Belgium, 2007.
- Yetimoglu, T.; Salbas, O. A study on shear strength of sands reinforced with randomly distributed discrete fibers. Geotext. Geomembr. 2003, 21, 103–110. [Google Scholar] [CrossRef]
- Hassan, H.J.A.; Rasul, J.; Samin, M. Effects of plastic waste materials on geotechnical properties of clayey soil. Transp. Infrastruct. Geotechnol. 2021, 8, 390–413. [Google Scholar] [CrossRef]
- Manasseh, J.; Ejelikwu, J. Soil modification and stabilization potential of calcium carbide waste. Adv. Mater. Res. 2013, 824, 29–36. [Google Scholar] [CrossRef]
- Tang, C.; Shi, B.; Gao, W.; Chen, F.; Cai, Y. Strength and mechanical behavior of short polypropylene fiber reinforced and cement stabilized clayey soil. Geotext. Geomembr. 2007, 25, 194–202. [Google Scholar] [CrossRef]
- Wang, W.; Lv, B.; Zhang, C.; Li, N.; Pu, S. Mechanical characteristics of lime-treated subgrade soil improved by polypropylene fiber and class F fly ash. Polymers 2022, 14, 2921. [Google Scholar] [CrossRef]
- Chen, M.; Shen, S.-L.; Arulrajah, A.; Wu, H.-N.; Hou, D.-W.; Xu, Y.-S. Laboratory evaluation on the effectiveness of polypropylene fibers on the strength of fiber-reinforced and cement-stabilized Shanghai soft clay. Geotext. Geomembr. 2015, 43, 515–523. [Google Scholar] [CrossRef]
- Ismail, A.; Baghini, M.S.; Karim, M.R.B.; Shokri, F.; Al-Mansob, R.A.; Firoozi, A.A.; Firoozi, A.A. Laboratory investigation on the strength characteristics of cement-treated base. Appl. Mech. Mater. 2014, 507, 353–360. [Google Scholar] [CrossRef]
- Hanifa, K.; Abu-Farsakh, M.Y.; Gautreau, G.P. Design Values of Resilient Modulus for Stabilized and Non-Stabilized Base; Report No. FHWA/LA.14/521; Louisiana Department of Transportation and Development: Baton Rouge, LA, USA, 2015. [Google Scholar]
- Bhuvaneshwari, S.; Robinson, R.G.; Gandhi, S.R. Resilient modulus of lime treated expansive soil. Geotech. Geol. Eng. 2019, 37, 305–315. [Google Scholar] [CrossRef]
- Robnett, Q.L.; Thompson, M.R. Effect of lime treatment on the resilient behavior of fine-grained soils. Transp. Res. Rec. 1976, 560, 11–20. [Google Scholar]
- Al-Mahbashi, A.M.; Al-Shamrani, M.A.; Moghal, A.A.B.; Vydehi, K.V. Correlation-based studies on resilient modulus values for fiber-reinforced lime-blended clay. Int. J. Geosynth. Grd. Eng. 2021, 7, 59. [Google Scholar] [CrossRef]
- ASTM D2487-17; Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System). ASTM International: West Conshohocken, PA, USA, 2017.
- Pierre, P.; Bilodeau, J.-P.; Légère, G.; Doré, G. Laboratory study on the relative performance oftreated granular materials used for unpaved roads. Can. J. Civ. Eng. 2008, 35, 624–634. [Google Scholar] [CrossRef]
- Camargoa, F.F.; Wenb, H.; Edil, T.; Son, Y.-H. Comparative assessment of crushed aggregates and bound/unbound recycled asphalt pavement as base materials. Int. J. Pavement Eng. 2013, 14, 223–230. [Google Scholar] [CrossRef]
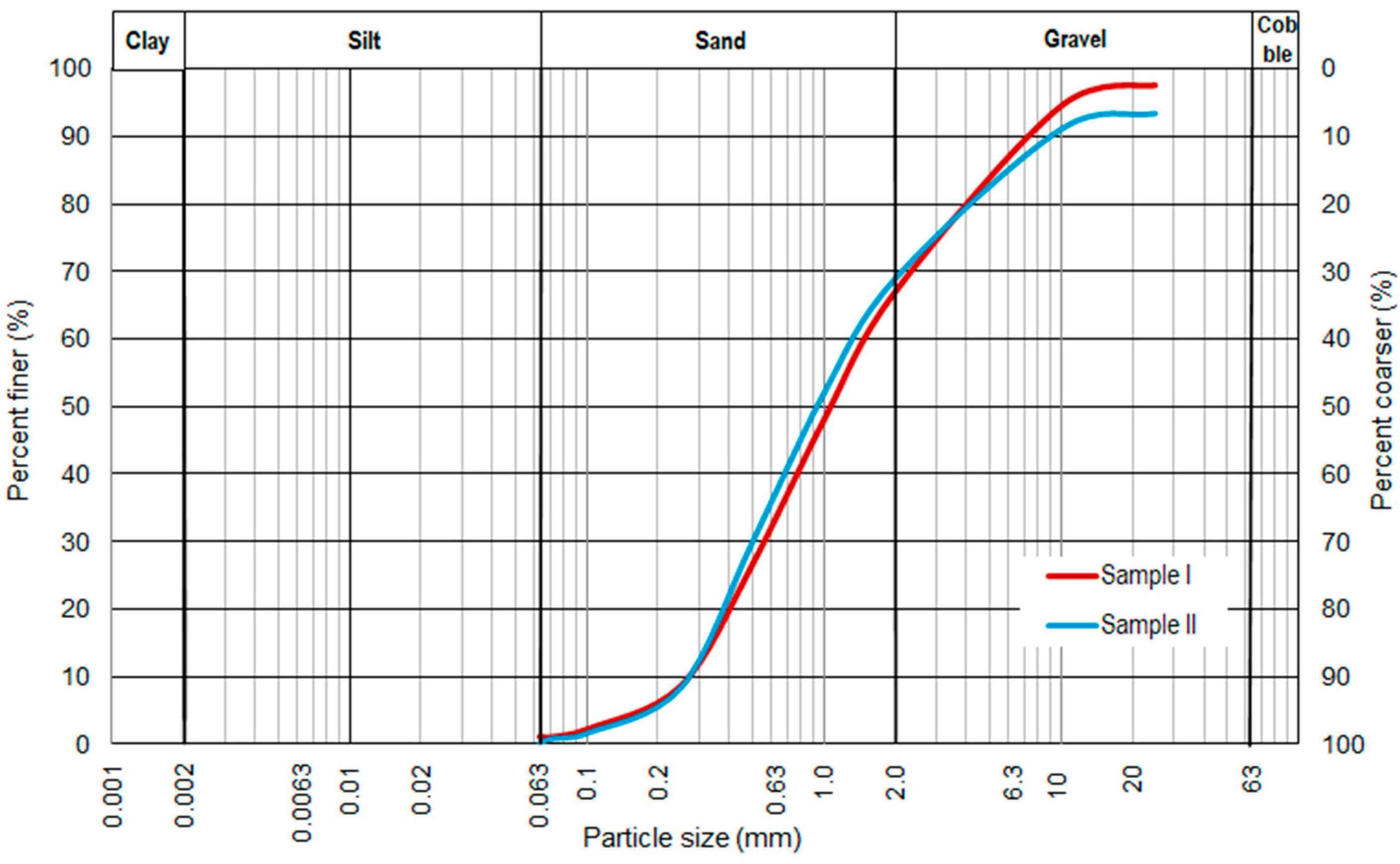




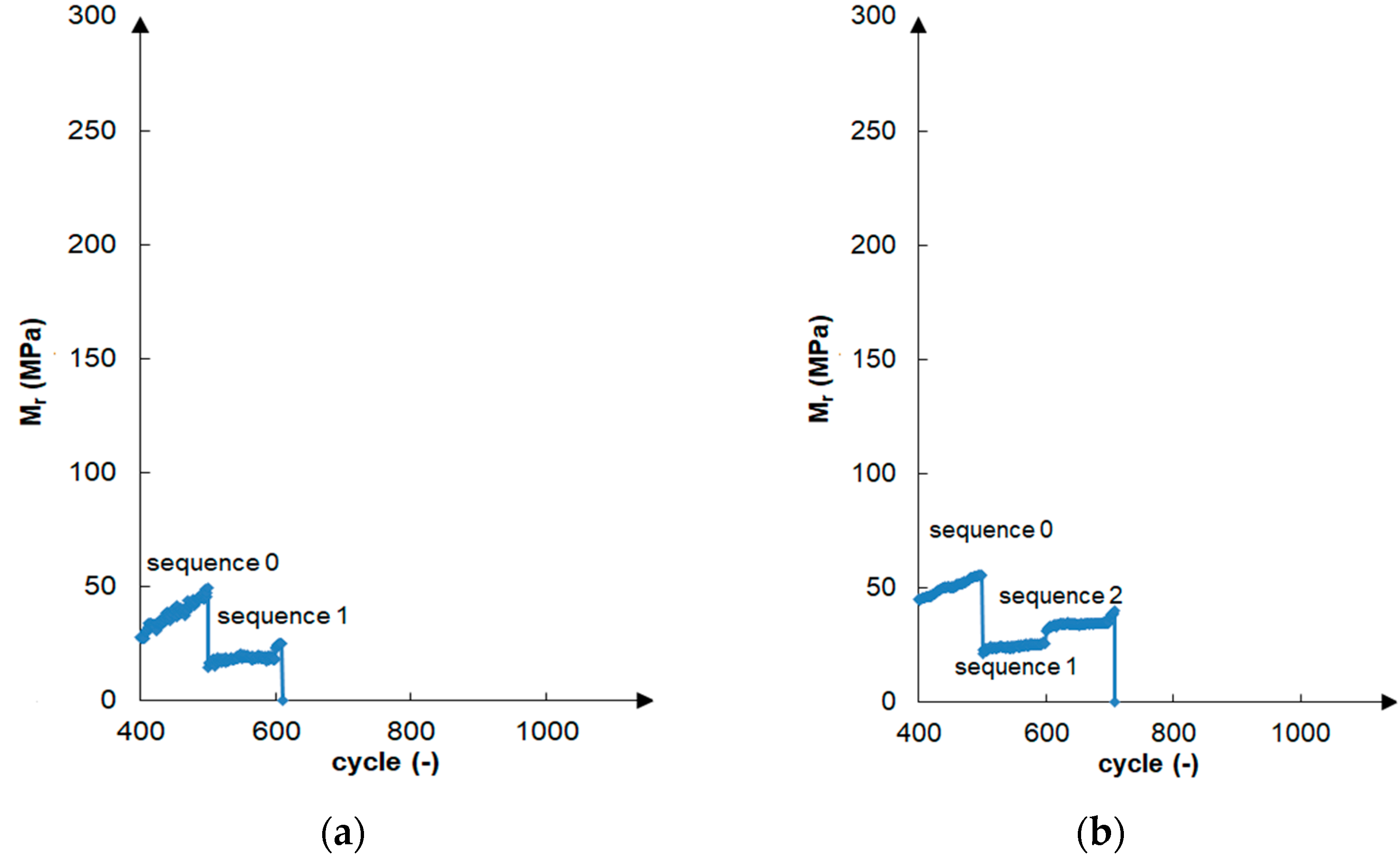
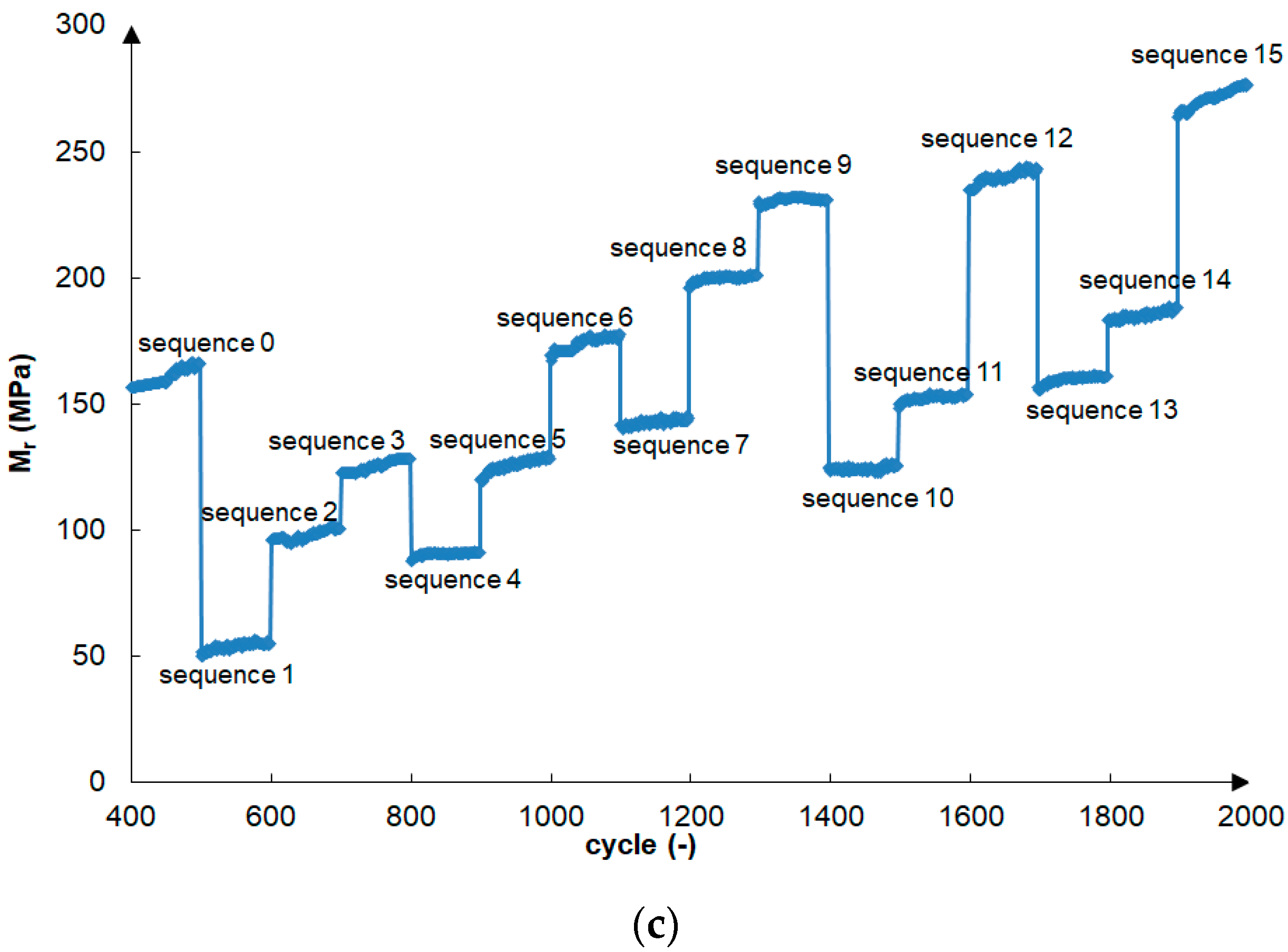

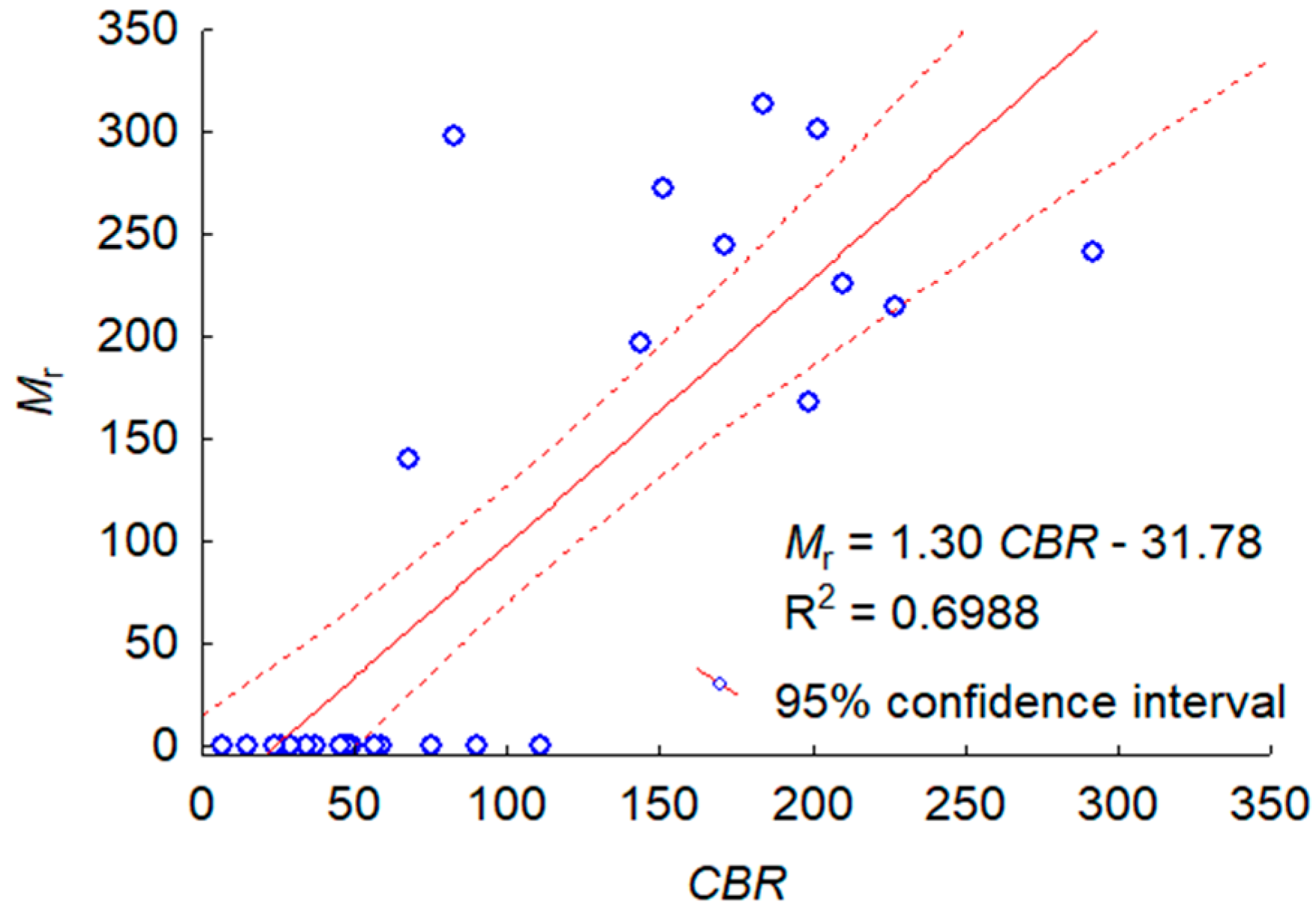
| Sample Number | Material | Compaction Method | ρs (g/cm3) | |||||
|---|---|---|---|---|---|---|---|---|
| Standard Proctor | Modified Proctor | |||||||
| wopt (%) | ρd max (g/cm3) | e (–) | wopt (%) | ρd max (g/cm3) | e (–) | |||
| I | grSa | 9.00 | 2.020 | 0.31 | 8.50 | 2.085 | 0.27 | 2.65 |
| grSa + 1.5%C | 8.90 | 2.120 | 0.25 | 8.40 | 2.130 | 0.25 | 2.66 | |
| II | grSa | 9.70 | 1.974 | 0.34 | 10.00 | 2.022 | 0.31 | 2.65 |
| grSa + 0.1%F 18 mm | 9.80 | 2.003 | 0.33 | 8.80 | 2.104 | 0.27 | 2.65 | |
| grSa + 0.2%F 18 mm | 8.00 | 2.054 | 0.30 | 7.50 | 2.158 | 0.24 | 2.65 | |
| grSa + 0.3%F 18 mm | 7.70 | 2.060 | 0.30 | 7.00 | 2.160 | 0.24 | 2.65 | |
| grSa + 1.5%C | 9.50 | 2.010 | 0.32 | 9.50 | 2.070 | 0.29 | 2.66 | |
| grSa + 1.5%C + 0.2%F 18 mm | 7.90 | 2.066 | 0.29 | 7.00 | 2.183 | 0.23 | 2.66 | |
| grSa + 1.5%C + 0.3%F 18 mm | 8.00 | 2.060 | 0.30 | 7.80 | 2.124 | 0.26 | 2.66 | |
| Sequence Number | Confining Pressure (kPa) | Max Applied Axial Stress (kPa) | Cyclic Stress (kPa) | Number of Load Applications |
|---|---|---|---|---|
| 0 | 103.4 | 103.4 | 93.1 | 500–1000 |
| 1 | 20.7 | 20.7 | 18.6 | 100 |
| 2 | 20.7 | 41.4 | 37.3 | 100 |
| 3 | 20.7 | 62.1 | 55.9 | 100 |
| 4 | 34.5 | 34.5 | 31.0 | 100 |
| 5 | 34.5 | 68.9 | 62.0 | 100 |
| 6 | 34.5 | 103.4 | 93.1 | 100 |
| 7 | 68.9 | 68.9 | 62.0 | 100 |
| 8 | 68.9 | 137.9 | 124.1 | 100 |
| 9 | 68.9 | 206.8 | 186.1 | 100 |
| 10 | 103.4 | 68.9 | 62.0 | 100 |
| 11 | 103.4 | 103.4 | 93.1 | 100 |
| 12 | 103.4 | 206.8 | 186.1 | 100 |
| 13 | 137.9 | 103.4 | 93.1 | 100 |
| 14 | 137.9 | 137.9 | 124.1 | 100 |
| 15 | 137.9 | 275.8 | 248.2 | 100 |
| Sample Number | Material | Curing Time (Days) | CBR (%) | |||
|---|---|---|---|---|---|---|
| Standard Proctor | Modified Proctor | |||||
| Unloaded | Loaded 2.44 kPa | Unloaded | Loaded 2.44 kPa | |||
| I | grSa | 0 | 29.5 | 37.0 | 71.9 | 90.2 |
| grSa + 1.5%C | 0 | − | 7.1 | − | 14.8 | |
| 7 | 68.1 | 82.7 | ||||
| 28 | 171.3 | 183.6 | ||||
| II | grSa | 0 | 19.4 | 25.9 | 52.7 | 56.4 |
| grSa + 0.1%F 18 mm | 0 | − | 46.0 | − | 49.4 | |
| grSa + 0.2%F 18 mm | 0 | − | 34.2 | − | 47.8 | |
| grSa + 0.3%F 18 mm | 0 | − | 28.7 | − | 45.8 | |
| grSa + 1.5%C | 0 | 27.9 | 24.1 | 55.5 | 75.6 | |
| 7 | 143.9 | 198.7 | ||||
| 28 | 150.9 | 281.0 | ||||
| grSa + 1.5%C + 0.3%F 18 mm | 0 | − | 59.7 | − | 111.3 | |
| 7 | 202.1 | 210.2 | ||||
| 28 | 227.3 | 290.7 | ||||
| Sample Number | Material | Curing Time (Days) | Mr (MPa) | |
|---|---|---|---|---|
| Standard Proctor | Modified Proctor | |||
| I | grSa | 0 | 0 | 0 |
| grSa + 1.5%C | 0 | 0 | 0 | |
| 7 | 324 | 217 | ||
| 28 | 349 | 513 | ||
| grSa + 1.5%C | 0 | 0 | 0 | |
| 7 | 140 | 298 | ||
| 28 | 245 | 313 | ||
| II | grSa | 0 | 0 | 0 |
| grSa + 0.1%F 18 mm | 0 | 0 | 0 | |
| grSa + 0.2%F 18 mm | 0 | 0 | 0 | |
| grSa + 0.3%F 18 mm | 0 | 0 | 0 | |
| grSa + 1.5%C | 0 | 0 | 0 | |
| 7 | 197 | 168 | ||
| 28 | 272 | 353 | ||
| grSa + 1.5%C + 0.2%F 18 mm | 0 | 0 | 0 | |
| 7 | 271 | 215 | ||
| 28 | 202 | 230 | ||
| grSa + 1.5%C + 0.3%F 18 mm | 0 | 0 | 0 | |
| 7 | 301 | 226 | ||
| 28 | 214 | 241 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zabielska-Adamska, K.; Dobrzycki, P.; Wasil, M. Estimation of Stiffness of Non-Cohesive Soil in Natural State and Improved by Fiber and/or Cement Addition under Different Load Conditions. Materials 2023, 16, 417. https://doi.org/10.3390/ma16010417
Zabielska-Adamska K, Dobrzycki P, Wasil M. Estimation of Stiffness of Non-Cohesive Soil in Natural State and Improved by Fiber and/or Cement Addition under Different Load Conditions. Materials. 2023; 16(1):417. https://doi.org/10.3390/ma16010417
Chicago/Turabian StyleZabielska-Adamska, Katarzyna, Patryk Dobrzycki, and Mariola Wasil. 2023. "Estimation of Stiffness of Non-Cohesive Soil in Natural State and Improved by Fiber and/or Cement Addition under Different Load Conditions" Materials 16, no. 1: 417. https://doi.org/10.3390/ma16010417
APA StyleZabielska-Adamska, K., Dobrzycki, P., & Wasil, M. (2023). Estimation of Stiffness of Non-Cohesive Soil in Natural State and Improved by Fiber and/or Cement Addition under Different Load Conditions. Materials, 16(1), 417. https://doi.org/10.3390/ma16010417





