Numerical Estimation of SAR and Temperature Distributions inside Differently Shaped Female Breast Tumors during Radio-Frequency Ablation
Abstract
1. Introduction
2. Materials and Methods
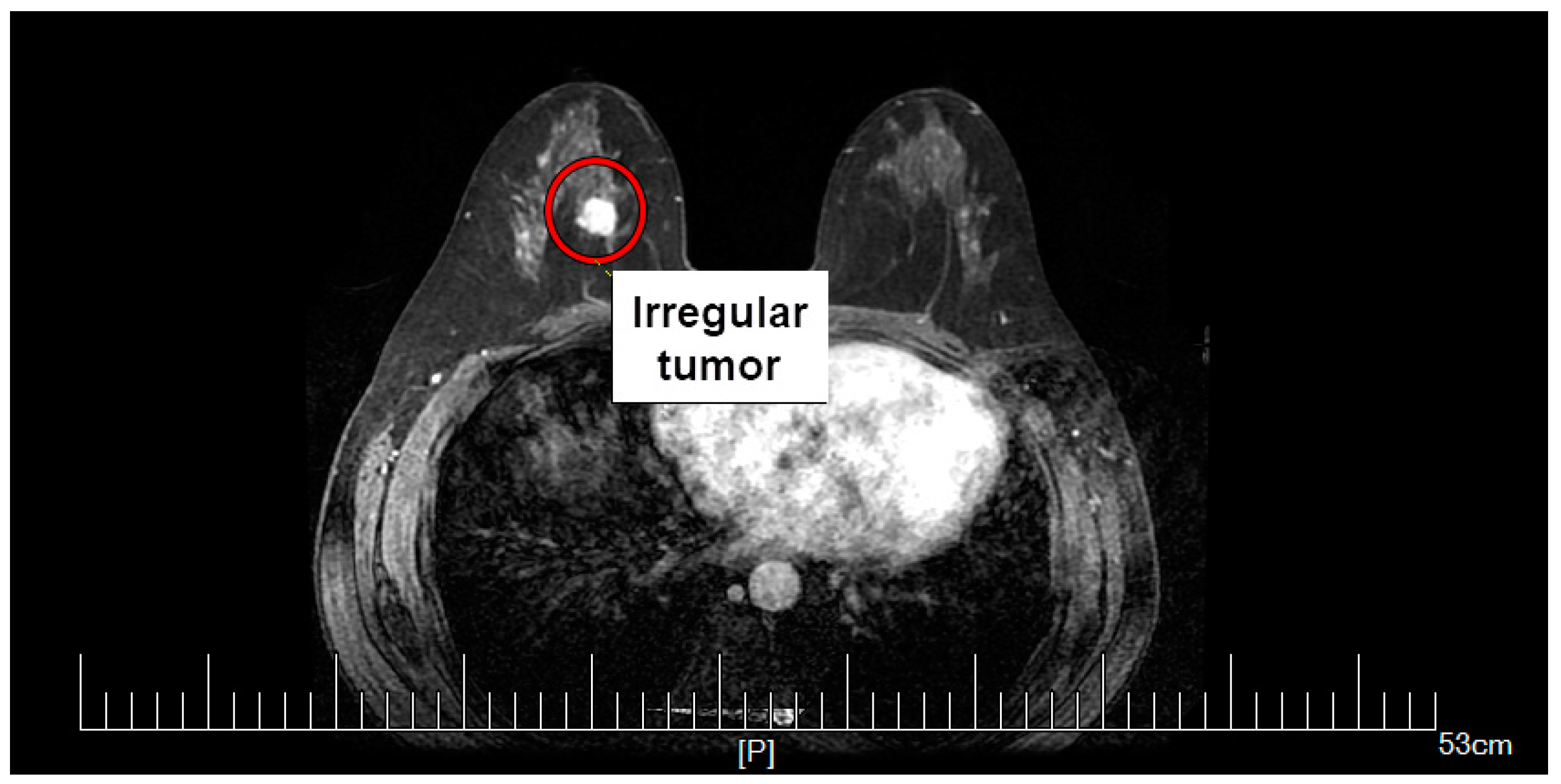
2.1. Female Breast Phantom Model
2.2. Material Properties
2.3. RF Applicator Model
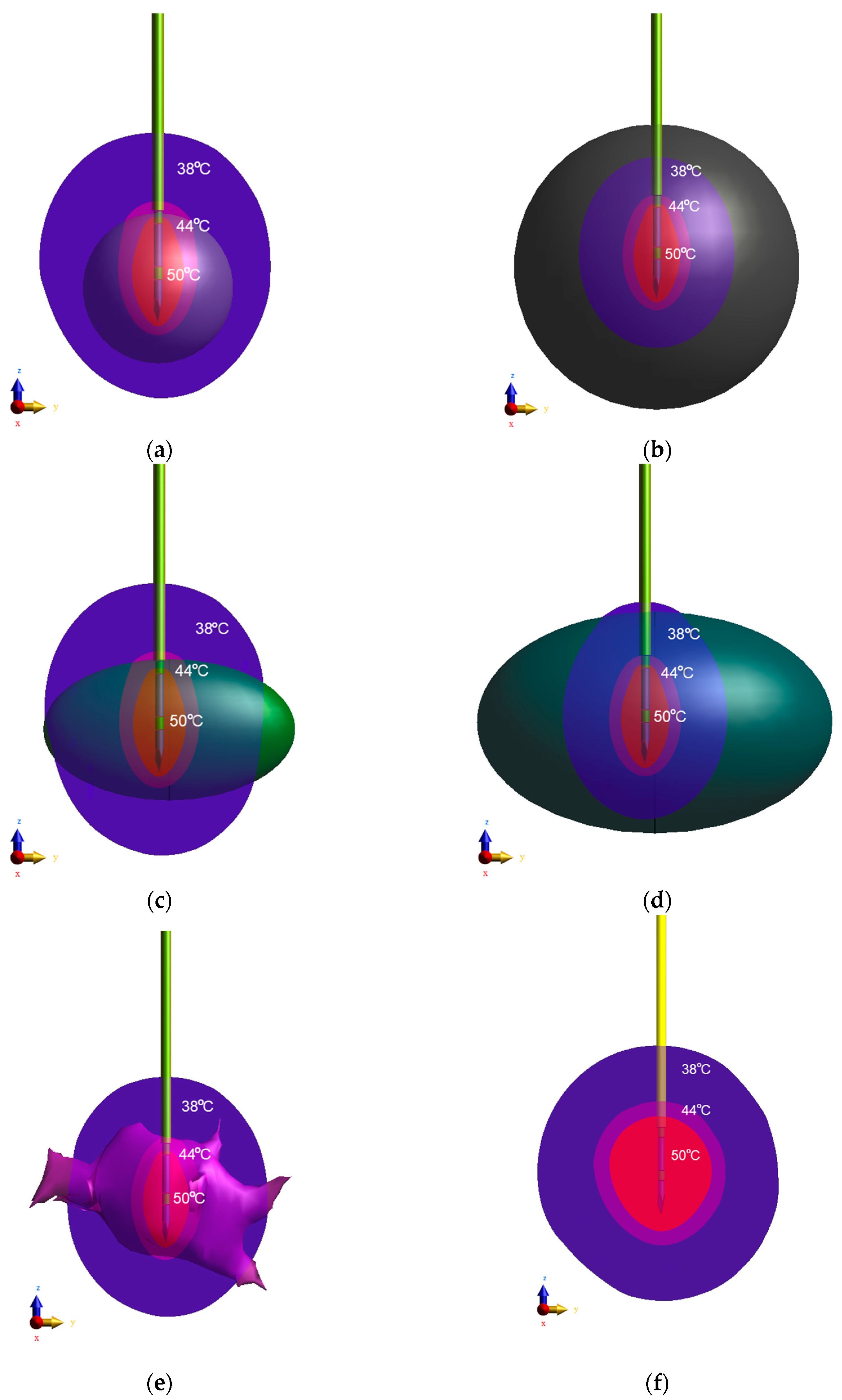
2.4. Equivalent Tumor Models
2.5. Electro-Conductive Field and Generalized Laplace Equation
2.6. Modified Pennes Bioheat Transfer Equation
2.7. SAR and Power Dissipation Values
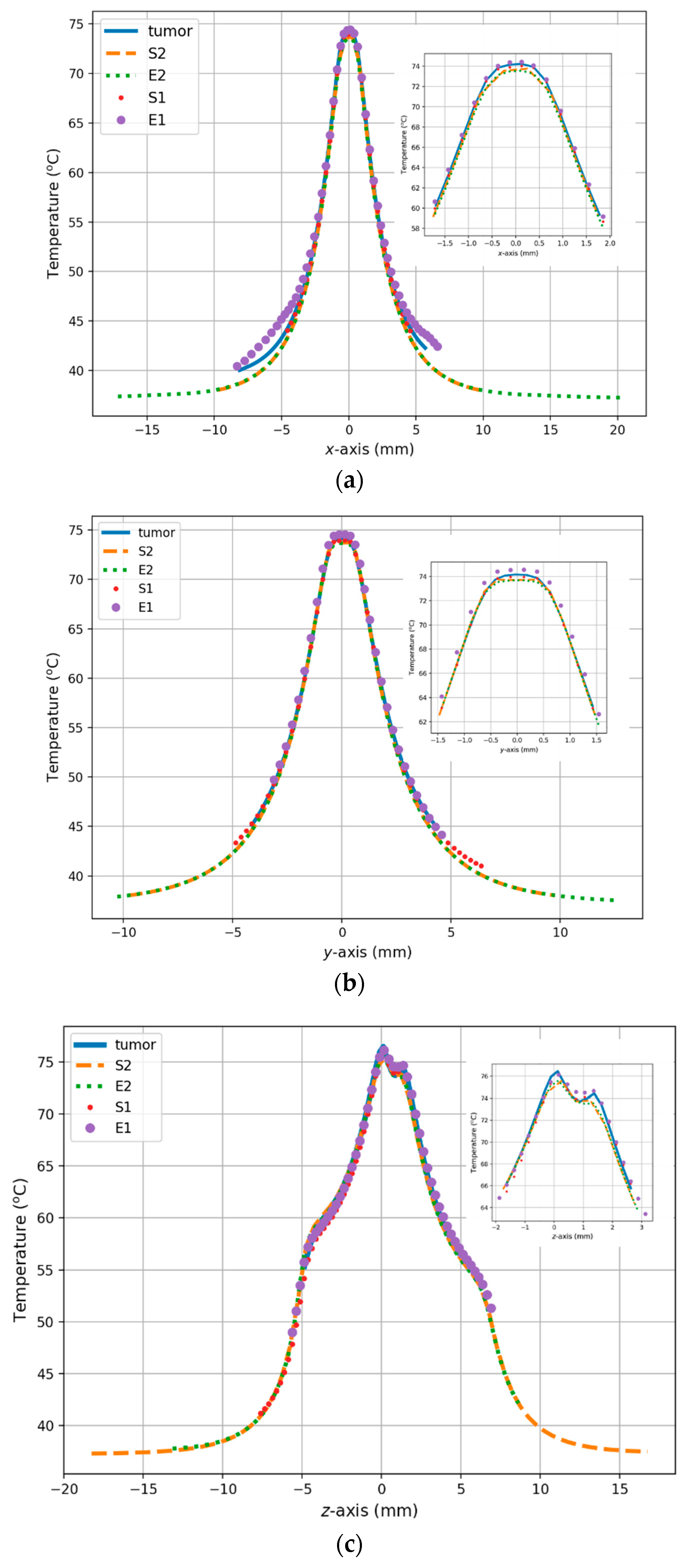
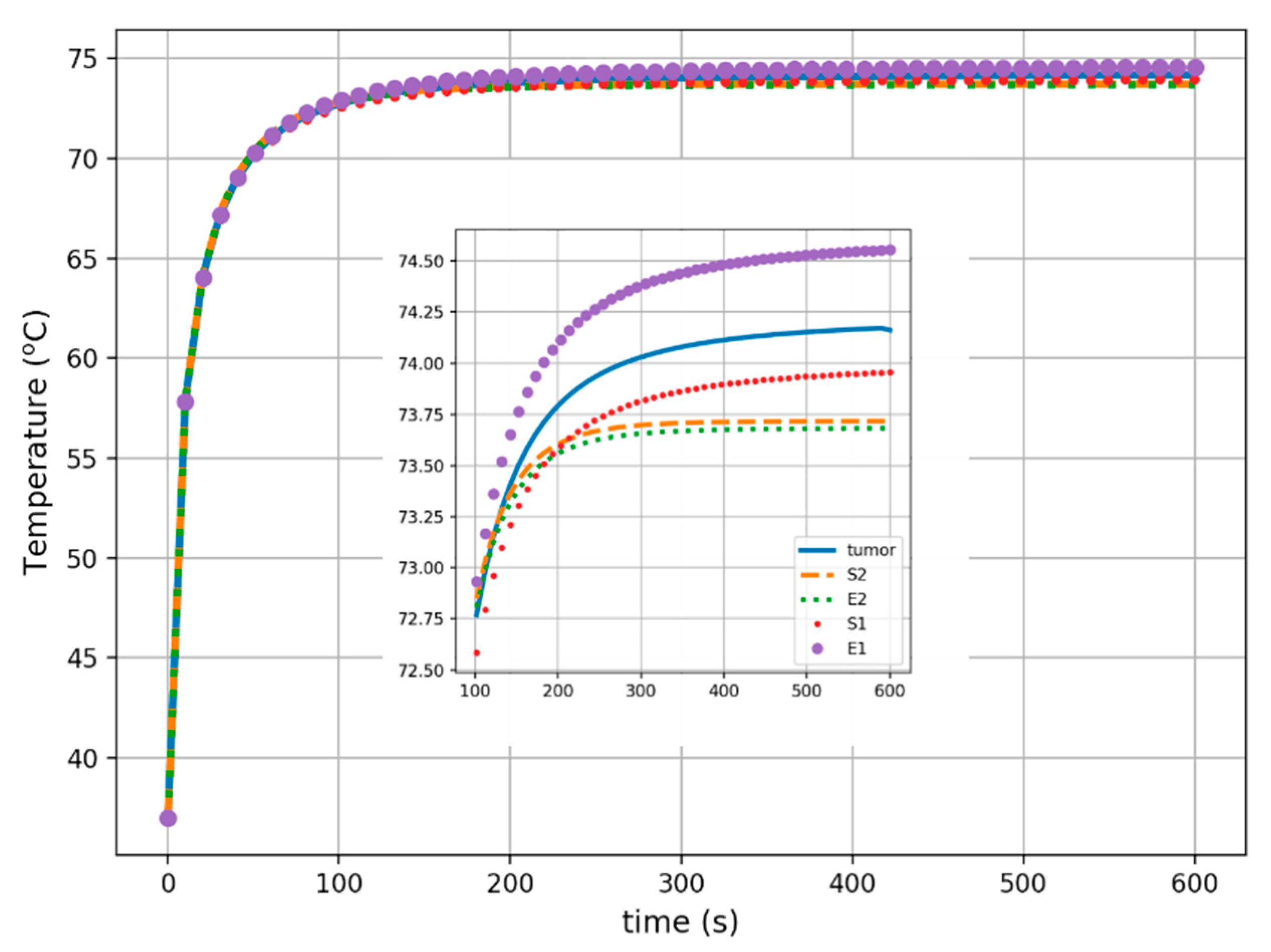
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barba, D.; Leon-Sosa, A.; Lugo, P.; Suquillo, D.; Torres, F.; Surre, F.; Trojman, L.; Caicedo, A. Breast cancer, screening and diagnostic tools: All you need to know. Crit. Rev. Oncol. Hematol. 2021, 157, 103174. [Google Scholar] [CrossRef] [PubMed]
- Pelicano, A.C.; Gonçalves, M.C.T.; Godinho, D.M.; Castela, T.; Orvalho, M.L.; Araújo, N.A.M.; Porter, E.; Conceicao, R.C. Development of 3D MRI-Based Anatomically Realistic Models of Breast Tissues and Tumours for Microwave Imaging Diagnosis. Sensors 2021, 21, 8265. [Google Scholar] [CrossRef] [PubMed]
- Korczak, I.; Romowicz, A.; Gambin, B.; Palko, T.; Kruglenko, E.; Dobruch-Sobczak, K. Numerical prediction of breast skin temperature based on thermographic and ultrasonographic data in healthy and cancerous breasts. Biocybern. Biomed. Eng. 2020, 40, 1680–1692. [Google Scholar] [CrossRef]
- Osmialowska, E.; Misiag, W.; Chabowski, M.; Jankowska-Polanska, B. Coping strategies, pain, and quality of life in patients with breast cancer. J. Clin. Med. 2021, 10, 4469. [Google Scholar] [CrossRef]
- Byrd, B.K.; Krishnaswamy, V.; Gui, J.; Rooney, T.; Zuurbier, R.; Rosenkranz, K.; Paulsen, K.; Barth, R.J. The shape of breast cancer. Breast Cancer Res. Treat. 2020, 183, 403–410. [Google Scholar] [CrossRef]
- Krekel, N.; Zonderhuis, B.; Muller, S.; Bril, H.; van Slooten, H.-J.; de Lange de Klerk, E.; van den Tol, P.; Meijer, S. Excessive Resections in Breast-Conserving Surgery: A Retrospective Multicentre Study. Breast J. 2011, 17, 602–609. [Google Scholar] [CrossRef]
- Uematsu, T.; Kasami, M.; Yuen, S. Triple-negative breast cancer: Correlation between MR imaging and pathologic findings. Radiology 2009, 250, 638–647. [Google Scholar] [CrossRef]
- Wapnir, I.L.; Wartenberg, D.E.; Greco, R.S. Three dimensional staging of breast cancer. Breast Cancer Res. Treat. 1996, 41, 15–19. [Google Scholar] [CrossRef]
- Androulakis, I.; Sumser, K.; Machielse, M.N.; Koppert, L.; Jager, A.; Nout, R.; Franckena, M.; van Rhoon, G.C.; Curto, S. Patient-derived breast model repository, a tool for hyperthermia treatment planning and applicator design. Int. J. Hyperth. 2022, 39, 1213–1221. [Google Scholar] [CrossRef]
- Burguin, A.; Diorio, C.; Durocher, F. Breast cancer treatments: Updates and new challenges. J. Pers. Med. 2021, 11, 808. [Google Scholar] [CrossRef]
- Moath, A.; Xiao, Y.X. The influence of tumour vasculature on fluid flow in solid tumours: A mathematical modelling study. Biophys. Rep. 2021, 7, 35–54. [Google Scholar] [CrossRef]
- Eltigani, F.; Ahmed, S.; Yahya, M.; Ahmed, M. Modeling of interstitial microwave hyperthermia for hepatic tumors using floating sleeve antenna. Phys. Eng. Sci. Med. 2022, 45, 569–575. [Google Scholar] [CrossRef]
- Sano, M.B.; DeWitt, M.R.; Teeter, S.D.; Xing, L. Optimization of a single insertion electrode array for the creation of clinically relevant ablations using high-frequency irreversible electroporation. Comput. Biol. Med. 2018, 95, 107–117. [Google Scholar] [CrossRef]
- de los Ríos Cardenas, L.; Bermeo, L.A.; de Albuquerque Pereira, W.C. Parameter estimation in high-intensity focused ultrasound therapy. Int. J. Numer. Methods Biomed. Eng. 2020, 38, e3591. [Google Scholar] [CrossRef] [PubMed]
- Tammam, E.; Said, A.M.; Ibrahim, A.A.; Galal, A.I. About the interstitial microwave cancer ablation: Principles, advantages and challenges. IEEE Access 2020, 8, 49685–49694. [Google Scholar] [CrossRef]
- Luyen, H.; Mohtashami, Y.; Sawicki, J.F.; Hagness, S.C.; Behdad, N. Minimally Invasive Microwave Ablation Antennas. In Antenna and Sensor Technologies in Modern Medical Applications; Rahmat-Samii, Y., Topsakal, E., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2021; pp. 345–398. [Google Scholar] [CrossRef]
- Ramirez-Guzman, T.J.; Trujillo-Romero, C.J.; Martinez-Valdez, R.; Leija-Salas, L.; Vera-Hernandez, A.; Rico-Martinez, G.; Ortega-Palacios, R.; Gutierrez-Martinez, J. Thermal Evaluation of a Micro-Coaxial Antenna Set to Treat Bone Tumors: Design, Parametric FEM Modeling and Evaluation in Multilayer Phantom and Ex Vivo Porcine Tissue. Electronics 2021, 10, 2289. [Google Scholar] [CrossRef]
- Ashour, A.S.; Guo, Y.; Mohamed, W.S. Ablation probes. In Thermal Ablation Therapy, Theory and Simulation; Elsevier: London, UK, 2021; pp. 179–220. [Google Scholar] [CrossRef]
- Preechaphonkul, W.; Rattanadecho, P. The comparative of the performance for predicted thermal models during microwave ablation process using a slot antenna. Case Stud. Therm. Eng. 2021, 25, 100908. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, L.; Moser, M.A.; Zhang, W.; Zhang, B. A review of antenna designs for percutaneous microwave ablation. Phys. Med. 2021, 84, 254–264. [Google Scholar] [CrossRef]
- Gas, P.; Szymanik, B. Shape optimization of the multi-slot coaxial antenna for local hepatic heating during microwave ablation. In Proceedings of the 2018 International Interdisciplinary PhD Workshop (IIPhDW), Swinoujscie, Poland, 9–12 May 2018; pp. 319–322. [Google Scholar] [CrossRef]
- Geoghegan, R.; Ter Haar, G.; Nightingale, K.; Marks, L.; Natarajan, S. Methods of monitoring thermal ablation of soft tissue tumors—A comprehensive review. Med. Phys. 2022, 49, 769–791. [Google Scholar] [CrossRef]
- Barnoon, P.; Ashkiyan, M. Magnetic field generation due to the microwaves by an antenna connected to a power supply to destroy damaged tissue in the liver considering heat control. J. Magn. Magn. Mater. 2020, 513, 167245. [Google Scholar] [CrossRef]
- Nizam-Uddin, N.; Abdulkawi, W.M.; Elshafiey, I.; Sheta, A.F.A. Towards an efficient system for hyperthermia treatment of breast tumors. Biomed. Signal Process. Control 2022, 71, 103084. [Google Scholar] [CrossRef]
- Gas, P.; Miaskowski, A.; Subramanian, M. In silico study on tumor-size-dependent thermal profiles inside an anthropomorphic female breast phantom subjected to multi-dipole antenna array. Int. J. Mol. Sci. 2020, 21, 8597. [Google Scholar] [CrossRef] [PubMed]
- Hassan, M.M.; Lias, K.; Buniyamin, N.; Naimullah, B.S.S.; Jobli, A.T. SAR Performance of Rectangular Microstrip Antenna for Breast Cancer Hyperthermia Treatment with Different Period of Treatment Procedure. J. Phys. Conf. Ser. 2021, 2071, 012048. [Google Scholar] [CrossRef]
- Gas, P.; Wyszkowska, J. Influence of multi-tine electrode configuration in realistic hepatic RF ablative heating. Arch. Elect. Eng. 2019, 68, 521–533. [Google Scholar] [CrossRef]
- Barnoon, P.; Bakhshandehfard, F. Thermal management in biological tissue in order to degrade tissue under local heating process. Case Stud. Therm. Eng. 2021, 26, 101105. [Google Scholar] [CrossRef]
- Rahpeima, R.; Lin, C.-A. Numerical Study of Magnetic Hyperthermia Ablation of Breast Tumor on an Anatomically Realistic Breast Phantom. PLoS ONE 2022, 17, e0274801. [Google Scholar] [CrossRef]
- Li, J.; Xu, Y.; Shen, N.; Feng, L.; Ran, Z.; Deng, Z. A practical pretreatment planning method of multiple puncturing for thermal ablation surgery. Biocybern. Biomed. Eng. 2020, 40, 1469–1485. [Google Scholar] [CrossRef]
- Liu, P.; Qin, J.; Duan, B.; Wang, Q.; Tan, X.; Zhao, B.; Peneyra Libao, J.; Chui, C.-K.; Heng, P.A. Overlapping radiofrequency ablation planning and robot-assisted needle insertion for large liver tumors. Int. J. Med. Robot. Comput. Assist. Surg. 2019, 15, e1952. [Google Scholar] [CrossRef]
- Nee Reimann, C.H.; Bazrafshan, B.; Schüßler, M.; Schmidt, S.; Schuster, C.; Hübner, F.; Vogl, T.J.; Jakoby, R. A dual-mode coaxial slot applicator for microwave ablation treatment. IEEE Trans. Microw. Theory Tech. 2018, 67, 1255–1264. [Google Scholar] [CrossRef]
- Ashour, A.S.; Asran, M.; Mohamed, W.S.; Fotiadis, D.I. Optimal Localization of a Novel Shifted 1T-Ring Based Microwave Ablation Probe in Hepatocellular Carcinoma. IEEE. Trans. Biomed. Eng. 2021, 68, 505–514. [Google Scholar] [CrossRef]
- Palandoken, M.; Murat, C.; Kaya, A.; Zhang, B. A Novel 3-D Printed Microwave Probe for ISM Band Ablation Systems of Breast Cancer Treatment Applications. IEEE Trans. Microw. Theory Tech. 2022, 70, 1943–1953. [Google Scholar] [CrossRef]
- Portosi, V.; Loconsole, A.M.; Valori, M.; Marrocco, V.; Fassi, I.; Bonelli, F.; Pascazio, G.; Lampignano, V.; Fasano, A.; Prudenzano, F. Low-Cost Mini-Invasive Microwave Needle Applicator for Cancer Thermal Ablation: Feasibility Investigation. IEEE Sens. J. 2021, 21, 14027–14034. [Google Scholar] [CrossRef]
- Wang, J.; Huang, S.; Gao, H.; Liu, J.; Zhang, Y.; Wu, S. Computer Simulations of Dual-Antenna Microwave Ablation and Comparison to Experimental Measurements. Appl. Sci. 2023, 13, 26. [Google Scholar] [CrossRef]
- Ferrero, R.; Barrera, G.; Celegato, F.; Vicentini, M.; Sozeri, H.; Yildiz, N.; Dincer, C.A.; Coisson, M.; Manzin, A.; Tiberto, P. Experimental and Modelling Analysis of the Hyperthermia Properties of Iron Oxide Nanocubes. Nanomaterials 2021, 11, 2179. [Google Scholar] [CrossRef] [PubMed]
- Raouf, I.; Gas, P.; Kim, H.S. Numerical Investigation of Ferrofluid Preparation during In-Vitro Culture of Cancer Therapy for Magnetic Nanoparticle Hyperthermia. Sensors 2021, 21, 5545. [Google Scholar] [CrossRef] [PubMed]
- Szczech, M. Magnetic fluid seal critical pressure calculation based on numerical simulations. Simulation 2020, 96, 403–413. [Google Scholar] [CrossRef]
- Yu, X.; Ding, S.; Yang, R.; Wu, C.; Zhang, W. Research progress on magnetic nanoparticles for magnetic induction hyperthermia of malignant tumor. Ceram. Int. 2021, 47, 5909–5917. [Google Scholar] [CrossRef]
- Suleman, M.; Riaz, S.; Jalil, R. A mathematical modeling approach toward magnetic fluid hyperthermia of cancer and unfolding heating mechanism. J. Therm. Anal. Calorim. 2021, 146, 1193–1219. [Google Scholar] [CrossRef]
- Tang, Y.; Su, H.; Flesch, R.C.; Jin, T. An optimization method for magnetic hyperthermia considering Nelder-Mead algorithm. J. Magn. Magn. Mater. 2022, 545, 168730. [Google Scholar] [CrossRef]
- Polychronopoulos, N.D.; Gkountas, A.A.; Sarris, I.E.; Spyrou, L.A. A Computational Study on Magnetic Nanoparticles Hyperthermia of Ellipsoidal Tumors. Appl. Sci. 2021, 11, 9526. [Google Scholar] [CrossRef]
- Tehrani, M.H.; Soltani, M.; Kashkooli, F.M.; Raahemifar, K. Use of microwave ablation for thermal treatment of solid tumors with different shapes and sizes—A computational approach. PLoS ONE 2020, 15, e0233219. [Google Scholar] [CrossRef] [PubMed]
- Segura Felix, K.; Lopez, G.; Geshel, D.; Cepeda Rubio, M.F.; Hernandez Jacquez, J.I.; Flores Garcia, F.G.; Vera Hernandez, A.; Leija Salas, L.; Orozco Ruiz de la Pena, E.C. Computational FEM Model and Phantom Validation of Microwave Ablation for Segmental Microcalcifications in Breasts Using a Coaxial Double-Slot Antenna. BioMed Res. Int. 2021, 2021, 8858822. [Google Scholar] [CrossRef] [PubMed]
- Lim, S.; Yoon, Y.J. Phase Compensation Technique for Effective Heat Focusing in Microwave Hyperthermia Systems. Appl. Sci. 2021, 11, 5972. [Google Scholar] [CrossRef]
- Kalogeropoulos, A.; Tsitsas, N.L. Analysis of Interaction Scattering Cross Sections and Their Physical Bounds for Multiple-Dipole Stimulation of a Three-Dimensional Layered Medium. IEEE Trans. Antennas Propag. 2021, 2, 506–520. [Google Scholar] [CrossRef]
- Prokhorova, A.; Ley, S.; Helbig, M. Quantitative Interpretation of UWB Radar Images for Non-Invasive Tissue Temperature Estimation during Hyperthermia. Diagnostics 2021, 11, 818. [Google Scholar] [CrossRef]
- Paruch, M. Mathematical Modeling of Breast Tumor Destruction using Fast Heating during Radiofrequency Ablation. Materials 2020, 13, 136. [Google Scholar] [CrossRef]
- Rajput, J.L.; Nandgaonkar, A.B.; Nalbalwar, S.L.; Wagh, A.E. Heat Flow Modeling for Controlled Focusing of Microwave Hyperthermia of Breast Cancer: A Computational Feasibility Study. Int. J. Adv. Sci. Eng. Inf. Technol. 2021, 11, 1281–1287. [Google Scholar] [CrossRef]
- Michalowska-Samonek, J.; Miaskowski, A.; Wac-Wlodarczyk, A. Numerical analysis of high frequency electromagnetic field distribution and specific absorption rate in realistic breast models. Prz. Elektrotechniczny 2012, 88, 97–99. [Google Scholar]
- Sawicki, B.; Miaskowski, A. Nonlinear higher-order transient solver for magnetic fluid hyperthermia. J. Comput. Appl. Math. 2014, 270, 143–151. [Google Scholar] [CrossRef]
- Cao, T.L.; Le, T.A.; Hadadian, Y.; Yoon, J. Theoretical Analysis for Using Pulsed Heating Power in Magnetic Hyperthermia Therapy of Breast Cancer. Int. J. Mol. Sci. 2021, 22, 8895. [Google Scholar] [CrossRef]
- Radjenovic, B.; Sabo, M.; Soltes, L.; Prnova, M.; Cicak, P.; Radmilovic-Radjenovic, M. On Efficacy of Microwave Ablation in the Thermal Treatment of an Early-Stage Hepatocellular Carcinoma. Cancers 2021, 13, 5784. [Google Scholar] [CrossRef] [PubMed]
- Phantom Repository. University of Wisconsin Cross-Disciplinary Electromagnetics Laboratory. Available online: https://uwcem.ece.wisc.edu/phantomRepository.html (accessed on 10 September 2022).
- Zastrow, E.; Davis, S.K.; Lazebnik, M.; Kelcz, F.; Van Veen, B.D.; Hagness, S.C. Development of anatomically realistic numerical breast phantoms with accurate dielectric properties for modeling microwave interactions with the human breast. IEEE Trans. Biomed. Eng. 2008, 55, 2792–2800. [Google Scholar] [CrossRef] [PubMed]
- Gas, P.; Miaskowski, A.; Dobrowolski, D. Modelling the tumor temperature distribution in anatomically correct female breast phantom. Prz. Elektrotechniczny 2020, 96, 146–149. [Google Scholar] [CrossRef]
- Koh, J.; Kim, M.J. Introduction of a New Staging System of Breast Cancer for Radiologists: An 614 Emphasis on the Prognostic Stage. Korean J. Radiol. 2019, 20, 69–82. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The dielectric properties of biological tissues: III. Parametric models for the dielectric spectrum of tissues. Phys. Med. Biol. 1996, 41, 2271–2293. [Google Scholar] [CrossRef]
- Hasgall, P.A.; Di Gennaro, F.; Baumgartner, C.; Neufeld, E.; Lloyd, B.; Gosselin, M.C.; Payne, D.; Klingenbock, A.; Kuster, N. IT’IS Database for Thermal and Electromagnetic Parameters of Biological Tissues, Version 4.1, 22 February 2022. Available online: https://itis.swiss/database (accessed on 10 September 2022). [CrossRef]
- Pennes, H.H. Analysis of Tissue and Arterial Blood Temperatures in the Resting Human Forearm. J. Appl. Physiol. 1998, 85, 5–34. [Google Scholar] [CrossRef]
- Szasz, O.; Szasz, A. Approaching Complexity: Hyperthermia Dose and its Possible Measurement in Oncology. Open J. Biophys. 2021, 11, 68–132. [Google Scholar] [CrossRef]
- Michalowska, J.; Wac-Wlodarczyk, A.; Koziel, J. Monitoring of the Specific Absorption Rate in Terms of Electromagnetic Hazards. J. Ecol. Eng. 2020, 21, 224–230. [Google Scholar] [CrossRef]
- Wainwright, P.R. The relationship of temperature rise to specific absorption rate and current in the human leg for exposure to electromagnetic radiation in the high frequency band. Phys. Med. Biol. 2003, 48, 3143–3155. [Google Scholar] [CrossRef]
- IEC/IEEE 62704-1:2017, Determining the Peak Spatial-Average Specific Absorption Rate (SAR) in the Human Body from Wireless Communications Devices, 30 MHz to 6 GHz—Part 1: General Requirements for Using the Finite Difference Time-Domain (FDTD) Method for SAR Calculations. Available online: https://standards.ieee.org/ieee/62704-1/5747/ (accessed on 10 September 2022).
- Kurazumi, Y.; Tsuchikawa, T.; Ishii, J.; Fukagawa, K.; Yamato, Y.; Matsubara, N. Radiative and convective heat transfer coefficients of the human body in natural convection. Build Environ. 2008, 43, 2142–2153. [Google Scholar] [CrossRef]
- Prasad, B.; Ha, Y.H.; Lee, S.K.; Kim, J.K. Patient-specific simulation for selective liver tumor treatment with noninvasive radiofrequency hyperthermia. J. Mech. Sci. Technol. 2016, 30, 5837–5845. [Google Scholar] [CrossRef]






| Tissue | σ (S/m) | ρ (kg/m3) | C (J/kg/K) | k (W/m/K) | HTR * (mL/min/kg) | HTR * (W/m3) | HGR ** (W/kg) |
|---|---|---|---|---|---|---|---|
| Blood | 0.7030 | 1050 | 3617 | 0.517 | 10,000 | 6.646 × 105 | 0 |
| Breast fat | 0.0250 | 911 | 2348 | 0.209 | 47 | 2710 | 0.728 |
| Breast gland | 0.5370 | 1041 | 2960 | 0.334 | 150 | 9884 | 2.323 |
| Fat | 0.0434 | 911 | 2348 | 0.211 | 33 | 1903 | 0.507 |
| Muscle | 0.3618 | 1090 | 3421 | 0.495 | 37 | 2553 | 0.906 |
| Skin | 0.0005 | 1109 | 3391 | 0.372 | 106 | 7441 | 1.648 |
| Tumor | 0.3618 | 1090 | 3437 | 0.563 | Equation (9) | Equation (9) | 12 |
| Breast Tumor Tissues | x-axis Length a (mm) | y-axis Length b (mm) | z-axis Length c (mm) | Total Surface Area Acalc (cm2) | Total Surface Area Ameas (cm2) | Total Volume Vcalc (cm3) | Total Volume Vmeas (cm3) | Total Mass mcalc (g) | Total Mass mmeas (g) |
|---|---|---|---|---|---|---|---|---|---|
| Ellipsoid E1 | 16.412 | 29.354 | 10.866 | 13.153 | 12.716 * | 2.740 | 2.749 * | 2.989 | 2.998 * |
| Sphere S1 | 17.474 | 17.474 | 17.474 | 9.593 | 9.538 * | 2.794 | 2.771 * | 3.046 | 3.021 * |
| Ellipsoid E2 | 26.574 | 42.588 | 27.675 | 31.498 | 32.153 * | 16.395 | 16.310 * | 17.882 | 17.790 * |
| Sphere S2 | 36.000 | 36.000 | 36.000 | 40.715 | 40.484 * | 24.429 | 24.270 * | 26.637 | 26.460 * |
| Tumor T | 38.630 | 24.269 | 24.269 | 12.320 ** | 12.722 * | 2.844 ** | 2.791 * | 3.101 ** | 3.043 * |
| Breast Tissues | Total Mass m (g) | Total Volume V (cm3) | Maximum Local SAR SARmax (W/kg) | Mass-Average Local SAR SARmass (W/kg) | Total Loss Power Density p = SARvol (W/m3) | Spatial-Average Local SAR ** psSAR1g (W/kg) | Total Loss Power P (W) |
|---|---|---|---|---|---|---|---|
| Breast fat * | 4766.2 | 5232.1 | 9560 | 4.95 × 10−3 | 13.525 | 650.82 | 0.0254 |
| Breast gland * | 814.8 | 783.0 | 2,7440 | 7.099 | 7388.65 | 699.33 | 1.1485 |
| Fat * | 441.3 | 484.4 | 11,430 | 4.41 × 10−2 | 40.153 | 1050.0 | 0.0195 |
| Muscle * | 731.3 | 670.6 | 1.61 × 10−6 | 8.24 × 10−7 | 8.99 × 10−4 | 1.58 × 10−6 | 6.0 × 10−7 |
| Skin * | 495.6 | 446.9 | 4.10 × 10−4 | 8.31 × 10−7 | 9.22 × 10−4 | 0.142 | 19.524 |
| Ellipsoid E1 | 2.998 | 2.749 | 152,700 | 326.435 | 355 984 | 823.41 | 0.9786 |
| Sphere S1 | 3.021 | 2.771 | 151,900 | 327.576 | 357,163 | 825.05 | 0.9897 |
| Ellipsoid E2 | 17.79 | 16.31 | 155,600 | 58.844 | 64,175 | 833.98 | 1.0467 |
| Sphere S2 | 26.46 | 24.27 | 155,800 | 39.733 | 43,325 | 835.40 | 1.0515 |
| Tumor T | 3.043 | 2.791 | 167,200 | 327.894 | 357,506 | 824.83 | 0.9978 |
| Breast Tissues | Ablation Volume VISO-50 (mm3) | Relative Error δ (%) |
|---|---|---|
| Ellipsoid E1 | 242.536 | 8.656 |
| Sphere S1 | 226.064 | 1.276 |
| Ellipsoid E2 | 201.253 | 9.839 |
| Sphere S2 | 204.365 | 8.445 |
| Tumor T | 223.215 | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miaskowski, A.; Gas, P. Numerical Estimation of SAR and Temperature Distributions inside Differently Shaped Female Breast Tumors during Radio-Frequency Ablation. Materials 2023, 16, 223. https://doi.org/10.3390/ma16010223
Miaskowski A, Gas P. Numerical Estimation of SAR and Temperature Distributions inside Differently Shaped Female Breast Tumors during Radio-Frequency Ablation. Materials. 2023; 16(1):223. https://doi.org/10.3390/ma16010223
Chicago/Turabian StyleMiaskowski, Arkadiusz, and Piotr Gas. 2023. "Numerical Estimation of SAR and Temperature Distributions inside Differently Shaped Female Breast Tumors during Radio-Frequency Ablation" Materials 16, no. 1: 223. https://doi.org/10.3390/ma16010223
APA StyleMiaskowski, A., & Gas, P. (2023). Numerical Estimation of SAR and Temperature Distributions inside Differently Shaped Female Breast Tumors during Radio-Frequency Ablation. Materials, 16(1), 223. https://doi.org/10.3390/ma16010223









