A Model of Stress-Damage-Permeability Relationship of Weakly Cemented Rocks under Triaxial Compressive Conditions
Abstract
1. Introduction
2. Materials
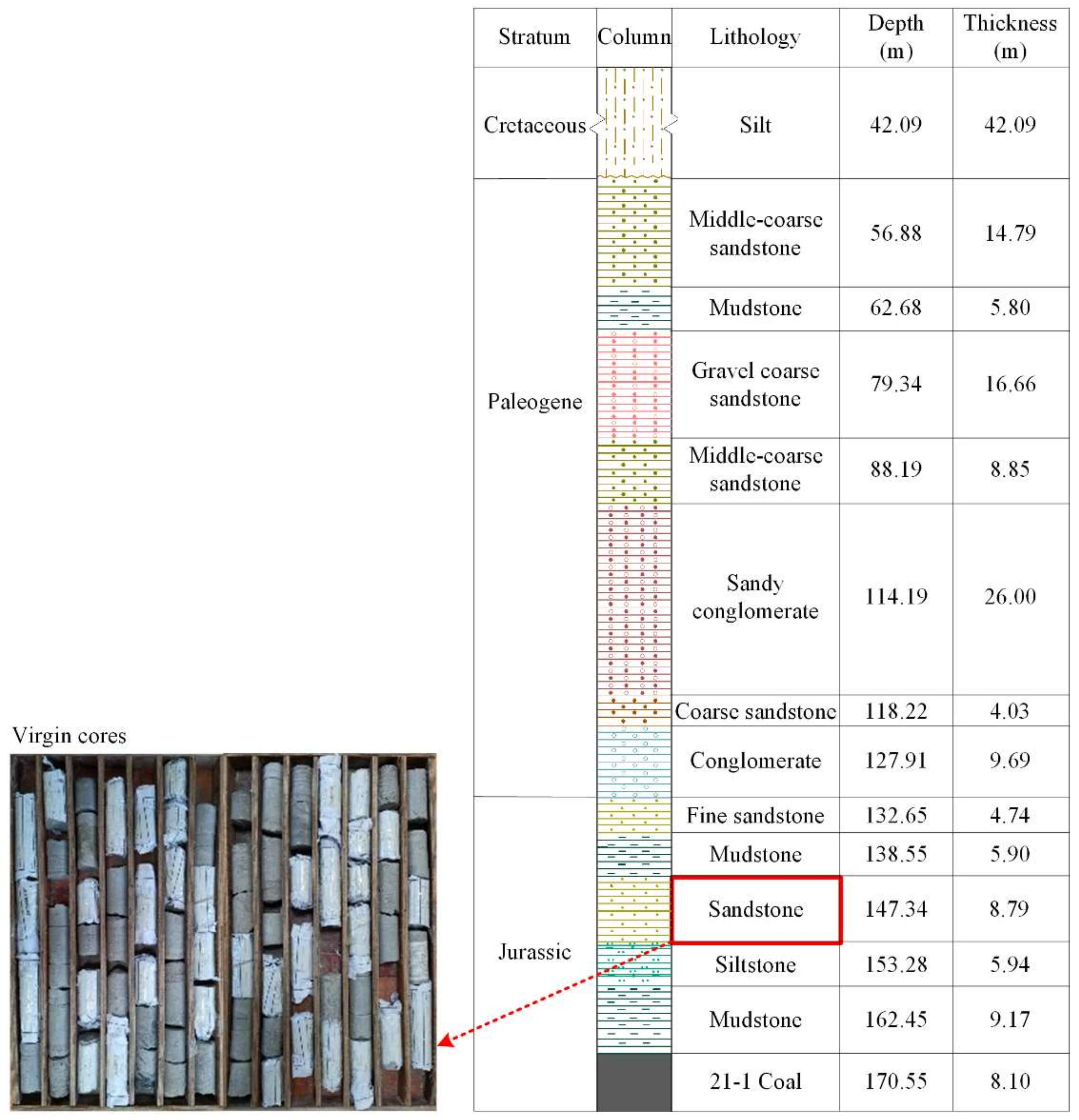
2.1. Sampling
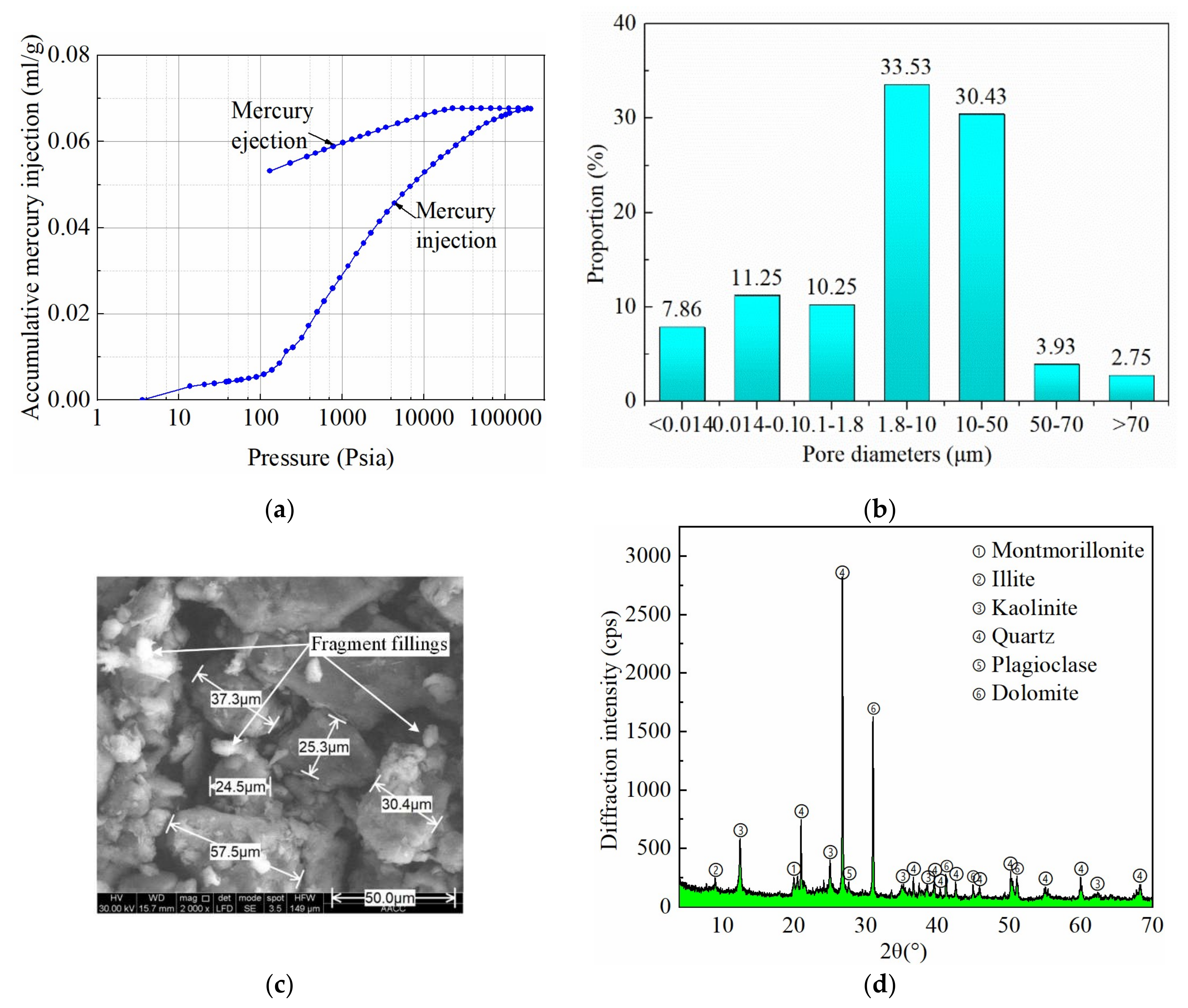
2.2. Rock Physics
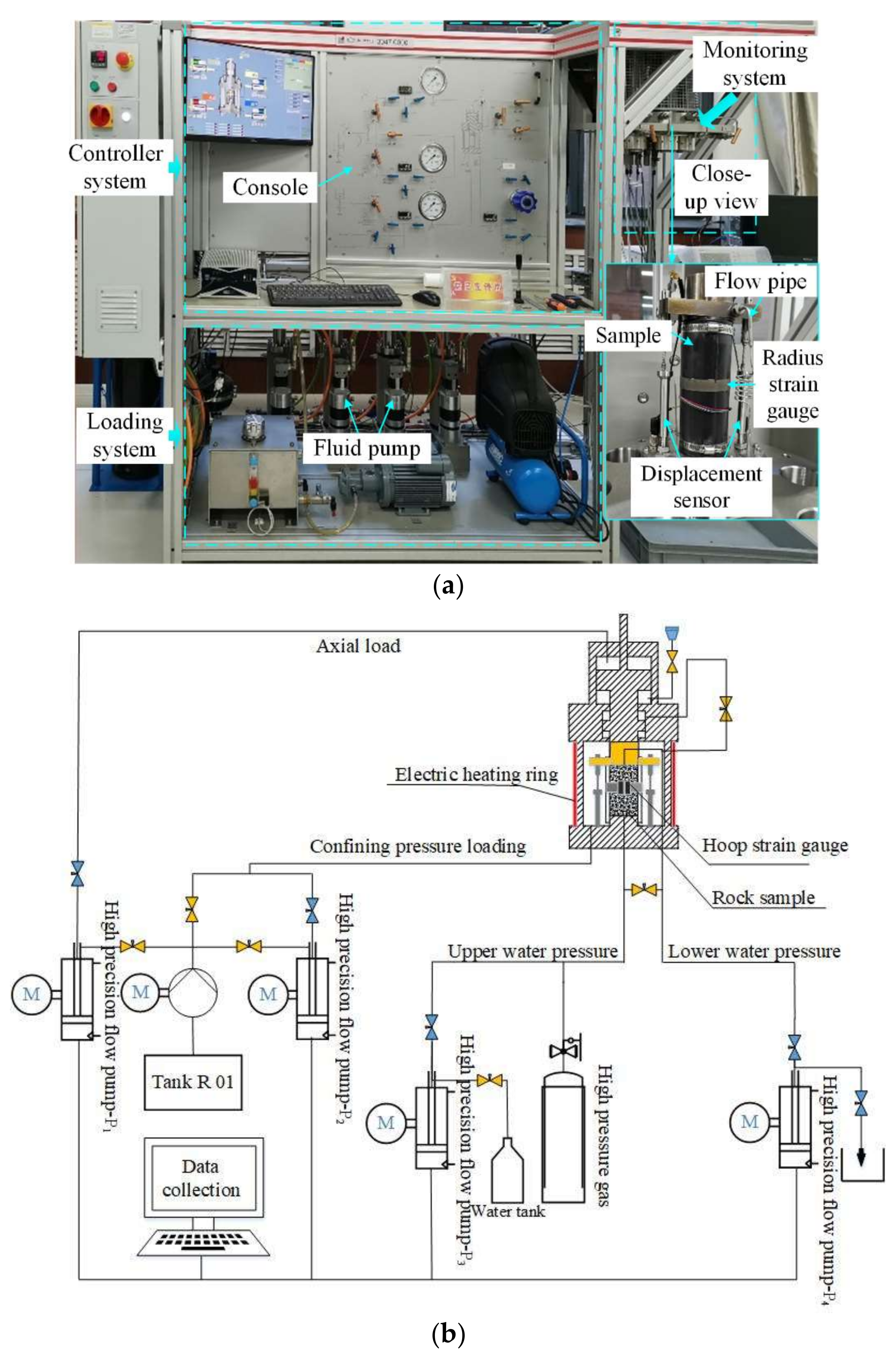
3. Complete Stress–Strain Permeability Tests
3.1. Methods
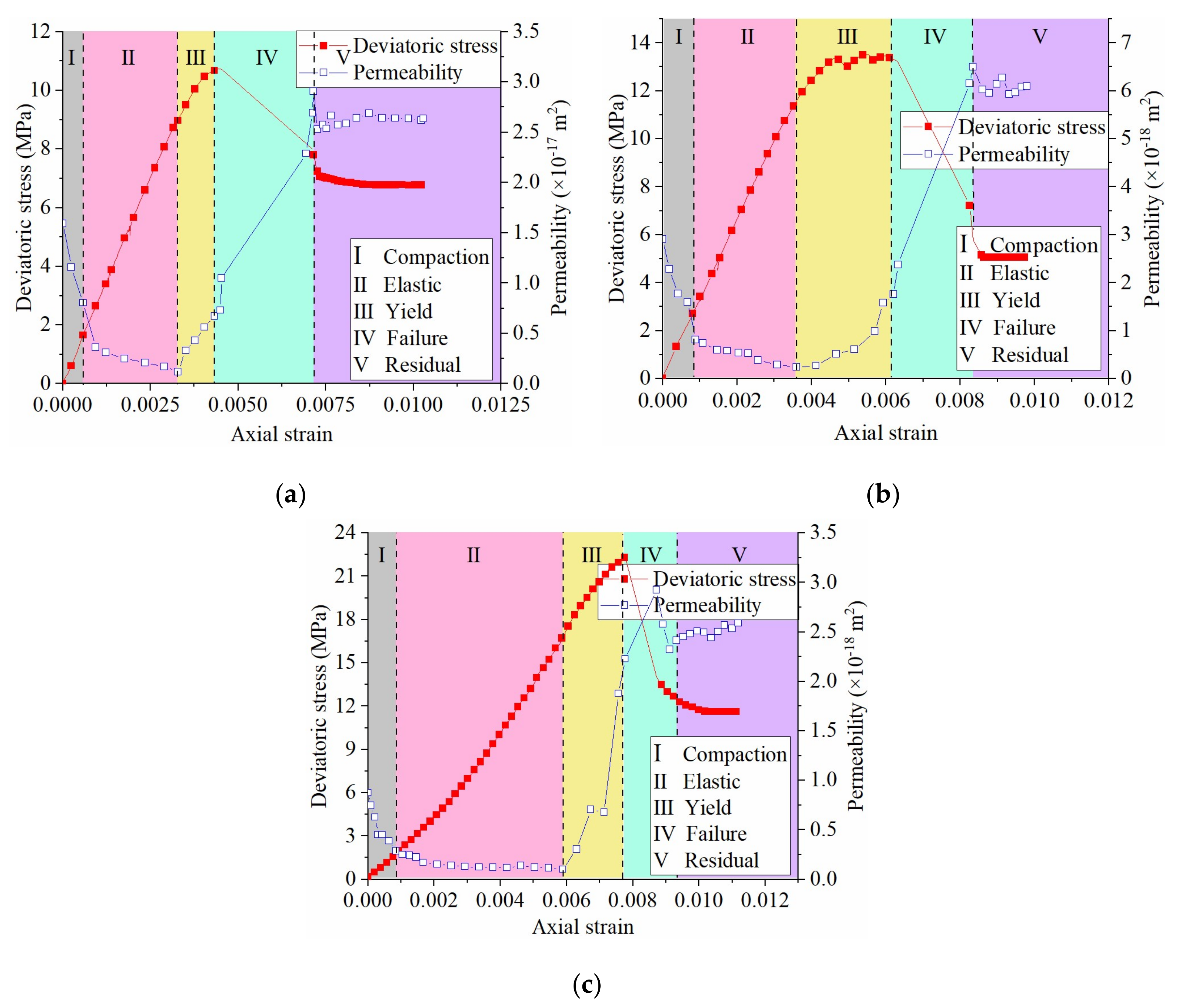
3.2. Results
3.3. Relationship between WCR Permeability and Physical Properties
4. Stress–Damage–Permeability Relationship Model
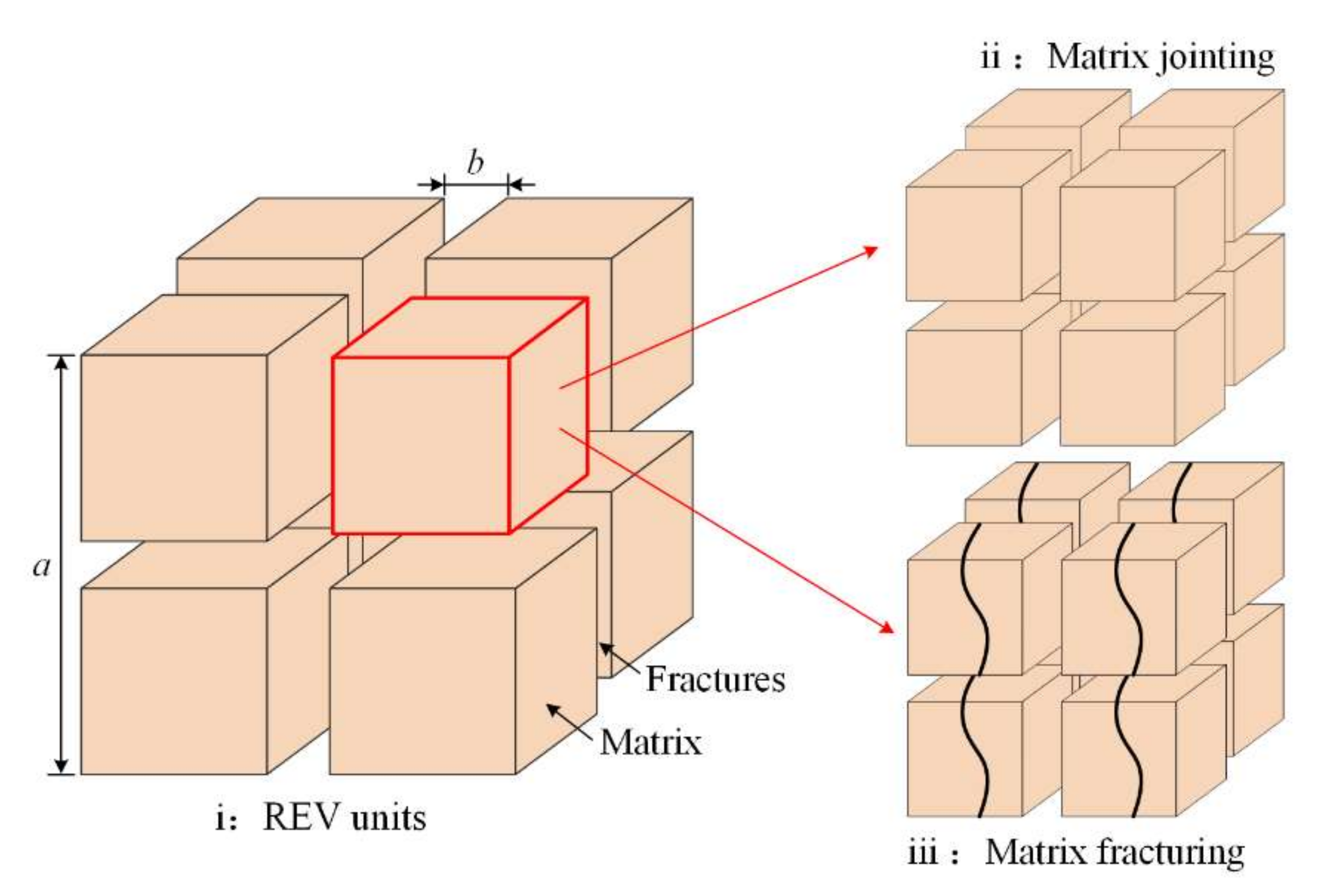
4.1. Model Construction
- (1)
- Weakly cemented rocks were composed of matrix and fractures; the matrix contained natural pores that can be squeezed and closed in the compaction stage and allow matrix materials to be jointed.
- (2)
- The matrix can fracture in response to triaxial compression, further affecting the effective aperture of fractures and thus permeabilities.
4.2. Damage Variable Determination
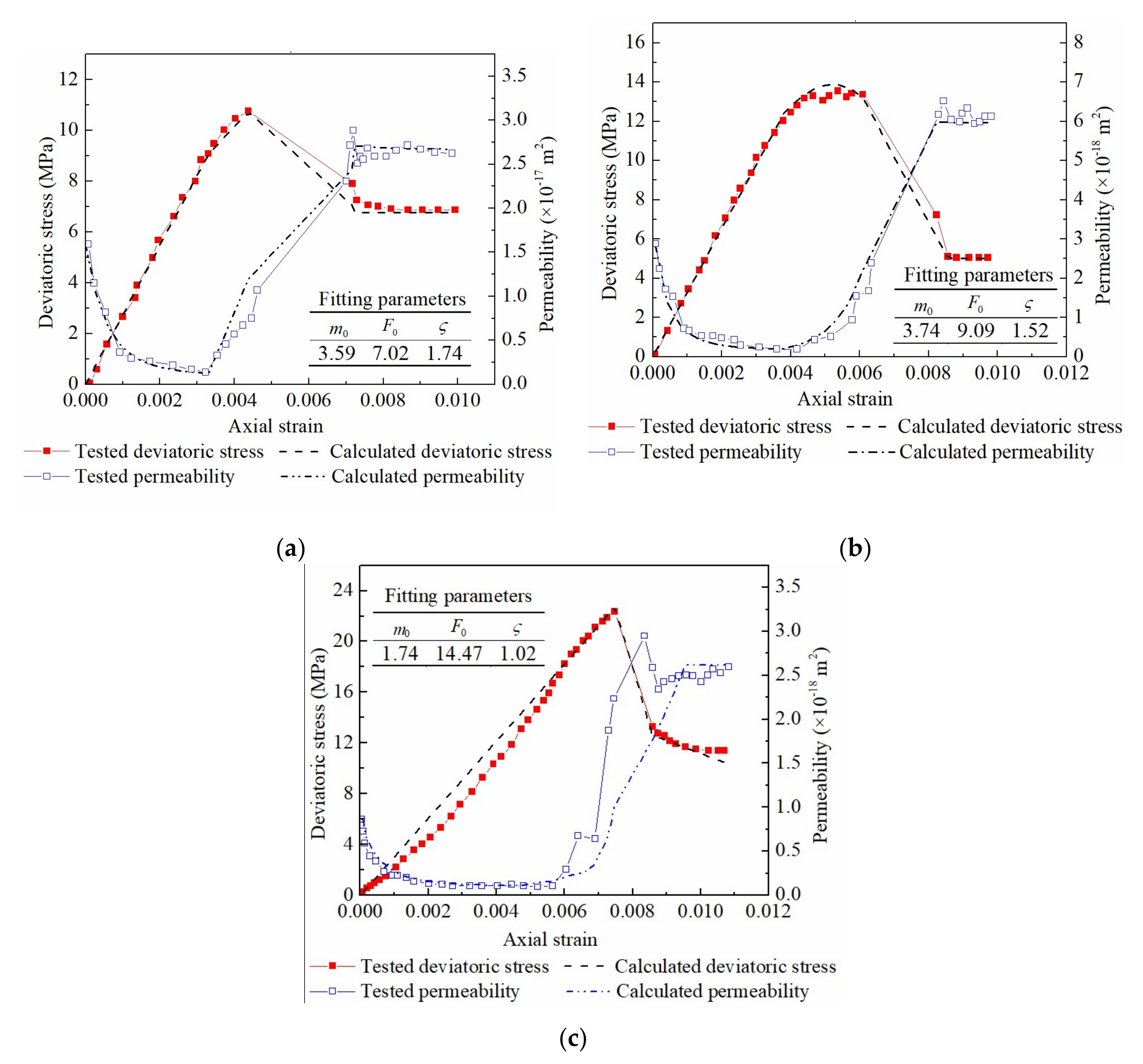
4.3. Model Verification
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grgic, D.; Al Sahyouni, F.; Golfier, F.; Moumni, M.; Schoumacker, L. Evolution of gas permeability of rock salt under different loading conditions and implications on the underground hydrogen storage in salt caverns. Rock Mech. Rock Eng. 2021, 55, 691–714. [Google Scholar] [CrossRef]
- Rutqvist, J.; Borgesson, L.; Chijimatsu, M.; Hernelind, J.; Jing, L.; Kobayashi, A.; Nguyen, S. Modeling of damage, permeability changes and pressure responses during excavation of the TSX tunnel in granitic rock at URL, Canada. Environ. Geol. 2009, 57, 1263–1274. [Google Scholar] [CrossRef]
- Akbarimehr, D.; Aflaki, E. Site investigation and use of artificial neural networks to predict rock permeability at the Siazakh Dam, Iran. Q. J. Eng. Geol. Hydrogeol. 2019, 52, 230–239. [Google Scholar] [CrossRef]
- Khanal, M.; Guo, H.; Adhikary, D. 3D Numerical Study of Underground Coal Mining Induced Strata Deformation and Subsequent Permeability Change. Geotech. Geol. Eng. 2019, 37, 235–249. [Google Scholar] [CrossRef]
- Zhao, Z.; Lv, X.; Wang, W.; Tan, Y. Damage evolution of bi-body model composed of weakly cemented soft rock and coal considering different interface effect. Springerplus 2016, 5, 292. [Google Scholar] [CrossRef]
- Zhang, S.; Fan, G.; Zhang, D.; Li, Q. Physical simulation research on evolution laws of clay aquifuge stability during slice mining. Environ. Earth Sci. 2018, 77, 278. [Google Scholar] [CrossRef]
- Fan, G.; Chen, M.; Zhang, D.; Wang, Z.; Zhang, S.; Zhang, C.; Li, Q.; Cao, B. Experimental study on the permeability of weakly cemented rock under different stress states in triaxial compression tests. Geofluids 2018, 2018, 9035654. [Google Scholar] [CrossRef]
- Zhang, S.; Fan, G.; Zhang, D.; Li, S.; Fan, Y.; Luo, T. Impacts of longwall mining speeds on permeability of weakly cemented strata and subsurface watertable: A case study. Geomat. Nat. Hazards Risk 2021, 12, 3063–3088. [Google Scholar] [CrossRef]
- Dong, J.; Tu, C.; Lee, W.; Jheng, Y. Effects of hydraulic conductivity/strength anisotropy on the stability of stratified, poorly cemented rock slopes. Comput. Geotech. 2012, 40, 147–159. [Google Scholar] [CrossRef]
- Holtzman, R. Micromechanical model of weakly-cemented sediments. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 944–958. [Google Scholar] [CrossRef]
- Yeh, P.; Lee, K.Z.; Chang, K. 3D Effects of permeability and strength anisotropy on the stability of weakly cemented rock slopes subjected to rainfall infiltration. Eng. Geol. 2020, 266, 105459. [Google Scholar] [CrossRef]
- Wang, Z.; Li, W.; Wang, Q.; Liu, S.; Hu, Y.; Fan, K. Relationships between the petrographic, physical and mechanical characteristics of sedimentary rocks in Jurassic weakly cemented strata. Environ. Earth Sci. 2019, 78, 131. [Google Scholar] [CrossRef]
- Sharma, M.S.R.; O’Regan, M.; Baxter, C.D.P.; Moran, K.; Vaziri, H.; Narayanasamy, R. Empirical relationship between strength and geophysical properties for weakly cemented formations. J. Pet. Sci. Eng. 2010, 72, 134–142. [Google Scholar] [CrossRef]
- Konstantinou, C.; Biscontin, G.; Logothetis, F. Tensile strength of artificially cemented sandstone generated via microbially induced carbonate precipitation. Materials 2021, 14, 4735. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, B. Deformation field and acoustic emission characteristics of weakly cemented rock under brazilian splitting test. Nat. Resour. Res. 2021, 30, 1925–1939. [Google Scholar] [CrossRef]
- Li, P.; Li, Z.; Liu, B.; Teng, T.; Guo, J. Experimental investigation on the tensile properties of weakly cemented sandstone in China Shendong mining area. Therm. Sci. 2020, 24, 3987–3994. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, D.; Zhao, H.; Chi, M.; Yu, W. Behavior of weakly cemented rock with different moisture contents under various tri-axial loading stats. Energies 2019, 12, 1563. [Google Scholar] [CrossRef]
- Yu, W.; Li, K.; Liu, Z.; An, B.; Wang, P.; Wu, H. Mechanical characteristics and deformation control of surrounding rock in weakly cemented siltstone. Environ. Earth Sci. 2021, 80, 337. [Google Scholar] [CrossRef]
- Tommasi, P.; Verrucci, L.; Rotonda, T. Mechanical properties of a weak pyroclastic rock and their relationship with microstructure. Can. Geotech. J. 2015, 52, 211–223. [Google Scholar] [CrossRef]
- Ruistuen, H.; Teufel, L.W.; Rhett, D. Influence of reservoir stress path on deformation and permeability of weakly cemented sandstone reservoirs. SPE Reserv. Eval. Eng. 1999, 2, 266–272. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Gland, N.; Dautriat, J.; David, C.; Wassermann, J.; Guélard, J. Compaction, permeability evolution and stress path effects in unconsolidated sand and weakly consolidated sandstone. Int. J. Rock Mech. Min. Sci. 2014, 67, 226–239. [Google Scholar] [CrossRef]
- You, S.; Ji, H.; Wang, T.; Song, Z. Thermal and mechanical coupling effects on permeability of weakly cemented sandstone. Emerg. Mater. Res. 2018, 7, 100–108. [Google Scholar] [CrossRef]
- Liu, J.; Jiang, H.; Meng, B.; Wang, L.; Yang, J.; Zhang, X. A four-element fractional creep model of weakly cemented soft rock. Bull. Eng. Geol. Environ. 2020, 79, 5569–5584. [Google Scholar] [CrossRef]
- Liu, Q.; Sun, Y.; Li, J. Experimental study on seepage characteristics of Jurassic weakly cemented sandstone under water-rock interaction. Geofluids 2020, 2020, 854368. [Google Scholar] [CrossRef]
- Lyu, X.; Zhao, Z.; Wang, X.; Wang, W. Study on the Permeability of Weakly Cemented Sandstones. Geofluids 2019, 2019, 8310128. [Google Scholar] [CrossRef]
- Han, T.; Best, A.I.; Sothcott, J.; North, L.J.; Macgregor, L.M. Relationships among low frequency (2 Hz) electrical resistivity, porosity, clay content and permeability in reservoir sandstones. J. Appl. Geophys. 2015, 112, 279–289. [Google Scholar] [CrossRef]
- Chao, Z.; Ma, G.; He, K.; Wang, M. Investigating low-permeability sandstone based on physical experiments and predictive modeling. Undergr. Space 2021, 6, 364–378. [Google Scholar] [CrossRef]
- Singh, V.K.; Kumar, D.; Kashyap, P.S.; Singh, P.K.; Kumar, A.; Singh, S.K. Modelling of soil permeability using different data driven algorithms based on physical properties of soil. J. Hydrol. 2020, 580, 124223. [Google Scholar] [CrossRef]
- Liu, X.; Xu, M.; Wang, K. Mechanism of permeability evolution for reservoir sandstone with different physical properties. Geofluids 2018, 2018, 5327895. [Google Scholar] [CrossRef]
- Saki, M.; Siahpoush, S.; Khaz’ali, A.R. A new generalized equation for estimation of sandstone and carbonate permeability from mercury intrusion porosimetry data. J. Pet. Explor. Prod. Technol. 2020, 10, 2637–2644. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, D.; Zhang, W.; Guo, J.; Yao, N.; Fan, G.; Zhang, S.; Wang, X.; Wu, P. Experimental Investigation on Post-Peak Permeability Evolution Law of Saturated Sandstone under Various Cyclic Loading-Unloading and Confining Pressure. Water 2022, 14, 1773. [Google Scholar] [CrossRef]
- Greco, O.D.; Ferrero, A.M.; Oggeri, C. Experimental and analytical interpretation of the behaviour of laboratory tests on composite specimens. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1993, 30, 1539–1543. [Google Scholar] [CrossRef]
- Fan, Z.; Fan, G.; Zhang, D. Permeability and energy evolution characteristics of heterogeneous coal and rock mass. Nat. Resour. Res. 2021, 30, 4493–4514. [Google Scholar] [CrossRef]
- Li, L.; Tu, W.; Zhou, Z.; Shi, S.; Zhang, M.; Chen, Y. Dynamic unloading instability mechanism of underground cavern based on seepage-damage coupling. KSCE J. Civ. Eng. 2020, 24, 1620–1631. [Google Scholar] [CrossRef]
- Jiang, A.; Yang, X.; Xu, M.; Jiang, T. Coupled hydrologic-mechanical-damage analysis and its application to diversion tunnels of hydropower station. Adv. Civ. Eng. 2021, 2021, 8341528. [Google Scholar] [CrossRef]
- Wang, S.; Yang, T.; Zhang, Z.; Sun, Z. Unsaturated seepage-stress-damage coupling and dynamic analysis of stability on discrete fractured rock slope. Environ. Earth Sci. 2021, 80, 660. [Google Scholar] [CrossRef]
- Fan, Z.; Fan, G.; Zhang, D.; Zhang, L.; Zhang, S.; Liang, S.; Yu, W. Optimal injection timing and gas mixture proportion for enhancing coalbed methane recovery. Energy 2021, 222, 119880. [Google Scholar] [CrossRef]
- Qiao, T.; Zhang, G.; Hu, S.; Zhao, S. Research on constitutive model of microcrack compaction section in brittle rock. J. Saf. Sci. Technol. 2017, 13, 128–135. [Google Scholar] [CrossRef]
- Pan, X.; Guo, W.; Wu, S.; Chu, J. An experimental approach for determination of the Weibull homogeneity index of rock or rock-like materials. Acta Geotech. 2020, 15, 375–391. [Google Scholar] [CrossRef]
- Xiao, W.; Zhang, D.; Wang, X.; Yang, H.; Wang, X.; Wang, C. Research on Microscopic Fracture Morphology and Damage Constitutive Model of Red Sandstone Under Seepage Pressure. Nat. Resour. Res. 2020, 29, 3335–3350. [Google Scholar] [CrossRef]

| Projects | Confining Pressure (MPa) | Osmotic Pressure by Both Ends (MPa) | Hydraulic Difference (MPa) | Loading Controlled by | Loading Rate (mm/min) |
|---|---|---|---|---|---|
| 1 | 2.0 | Top: 0.5 Bottom: 1.5 | 1.0 | Displacement | 0.03 |
| 2 | 3.5 | ||||
| 3 | 5.0 |
| Lithology | Confining Pressure (MPa) | k0 (m2) | kmax (m2) | kres (m2) | Ratio | ||
|---|---|---|---|---|---|---|---|
| kmax/k0 | kres/k0 | kmax/kres | |||||
| Sandstone | 2.0 | 1.59 × 10−17 | 2.91 × 10−17 | 2.61 × 10−17 | 1.83 | 1.64 | 1.11 |
| 3.5 | 2.91 × 10−18 | 6.50 × 10−18 | 6.06 × 10−18 | 2.23 | 2.08 | 1.07 | |
| 5.0 | 8.75 × 10−19 | 2.92 × 10−18 | 2.49 × 10−18 | 3.34 | 2.85 | 1.17 | |
| Lithology | Confining Pressure (MPa) | Statistical Parameters | ||
|---|---|---|---|---|
| m0 | F0 | ζ | ||
| Sandstone | 2.0 | 3.59 | 7.02 | 1.74 |
| 3.5 | 3.74 | 9.09 | 1.52 | |
| 5.0 | 1.74 | 14.47 | 1.02 | |
| Lithology | Confining Pressure (MPa) | Mean Relative Error (%) | |
| Deviatoric Stress | Permeability | ||
| Sandstone | 2.0 | 7.24 | 7.13 |
| 3.5 | 5.59 | 6.32 | |
| 5.0 | 11.39 | 14.79 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Fan, G.; Zhang, D.; Li, W.; Luo, T.; Liang, S.; Fan, Z. A Model of Stress-Damage-Permeability Relationship of Weakly Cemented Rocks under Triaxial Compressive Conditions. Materials 2023, 16, 210. https://doi.org/10.3390/ma16010210
Zhang S, Fan G, Zhang D, Li W, Luo T, Liang S, Fan Z. A Model of Stress-Damage-Permeability Relationship of Weakly Cemented Rocks under Triaxial Compressive Conditions. Materials. 2023; 16(1):210. https://doi.org/10.3390/ma16010210
Chicago/Turabian StyleZhang, Shizhong, Gangwei Fan, Dongsheng Zhang, Wenping Li, Tao Luo, Shuaishuai Liang, and Zhanglei Fan. 2023. "A Model of Stress-Damage-Permeability Relationship of Weakly Cemented Rocks under Triaxial Compressive Conditions" Materials 16, no. 1: 210. https://doi.org/10.3390/ma16010210
APA StyleZhang, S., Fan, G., Zhang, D., Li, W., Luo, T., Liang, S., & Fan, Z. (2023). A Model of Stress-Damage-Permeability Relationship of Weakly Cemented Rocks under Triaxial Compressive Conditions. Materials, 16(1), 210. https://doi.org/10.3390/ma16010210







