Measurements of Surface Impedance in MgB2 in DC Magnetic Fields: Insights in Flux-Flow Resistivity
Abstract
1. Introduction
2. Surface Resistance in the Mixed State
3. Measurement Technique
4. Experimental Section
4.1. Sample Preparation
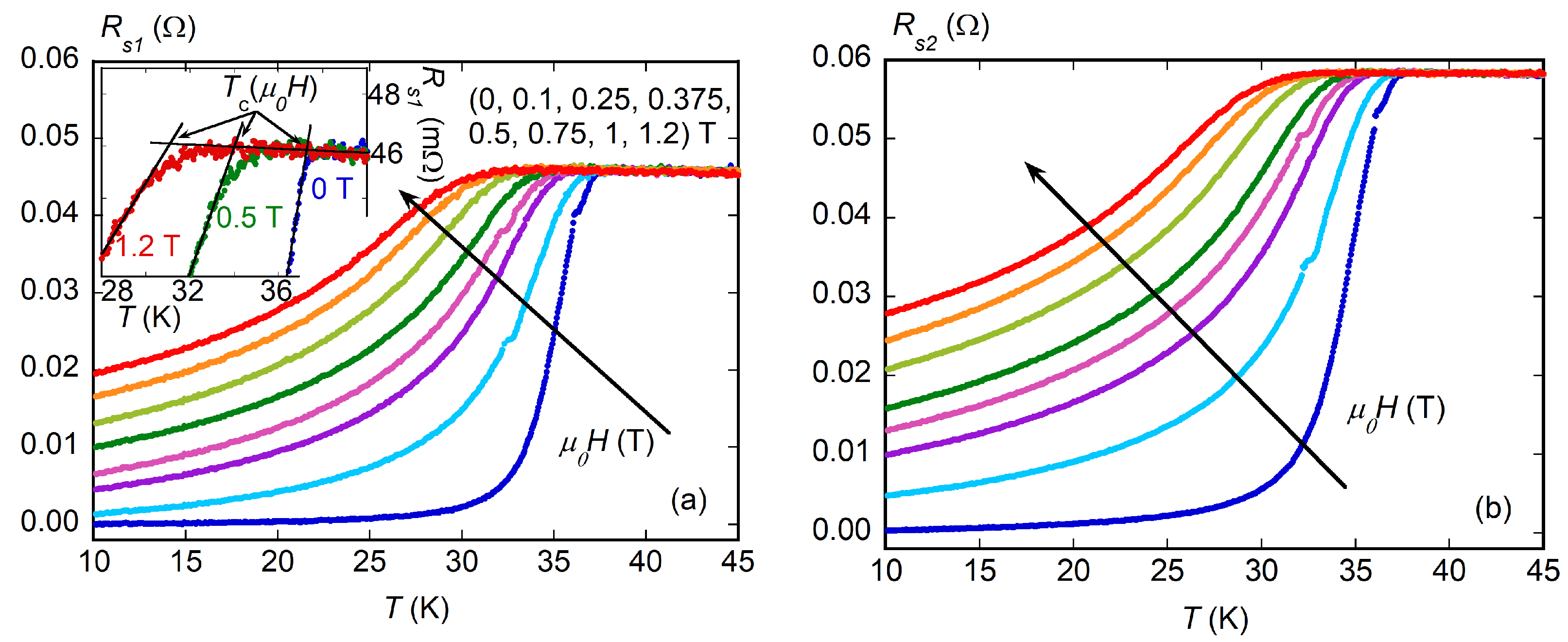
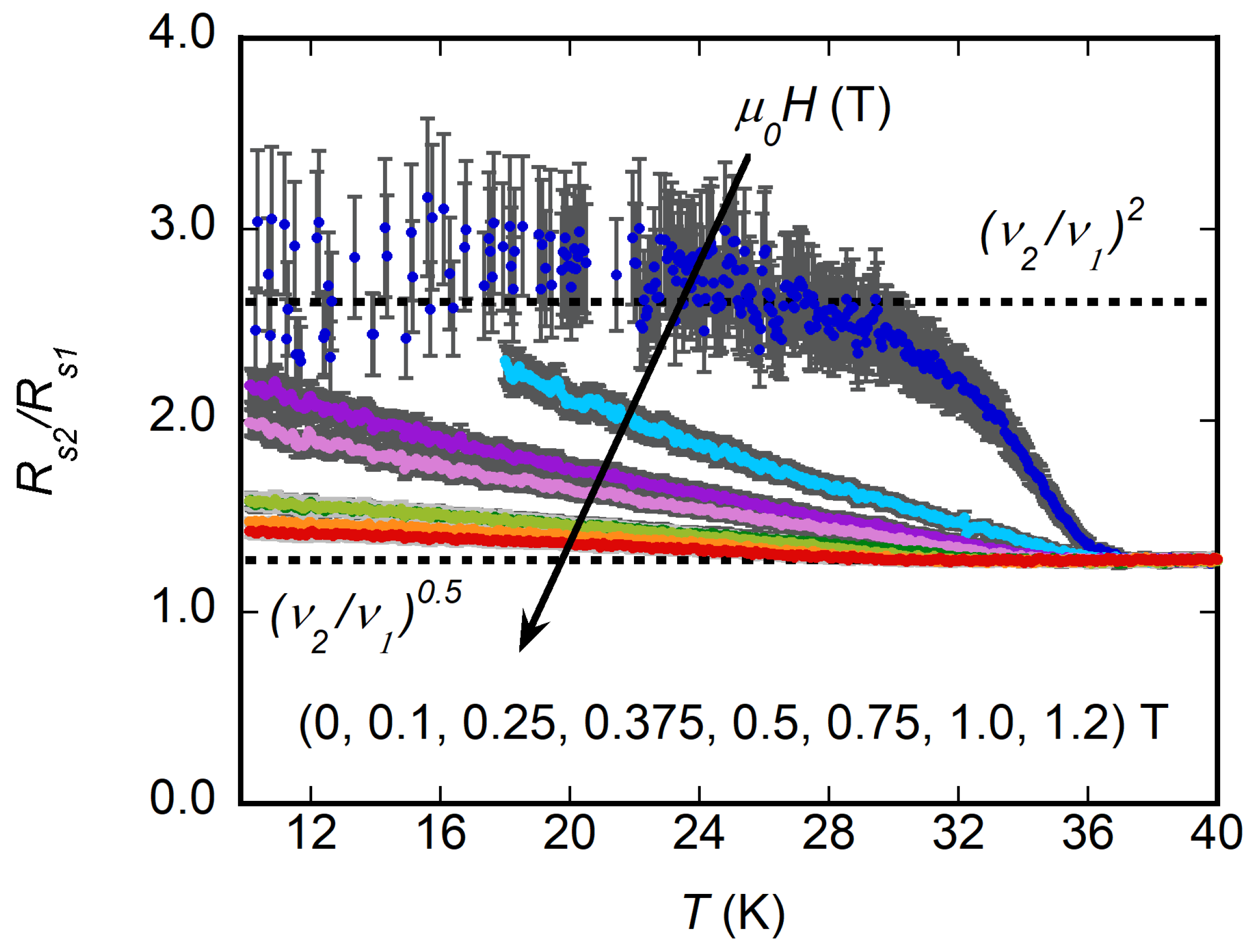
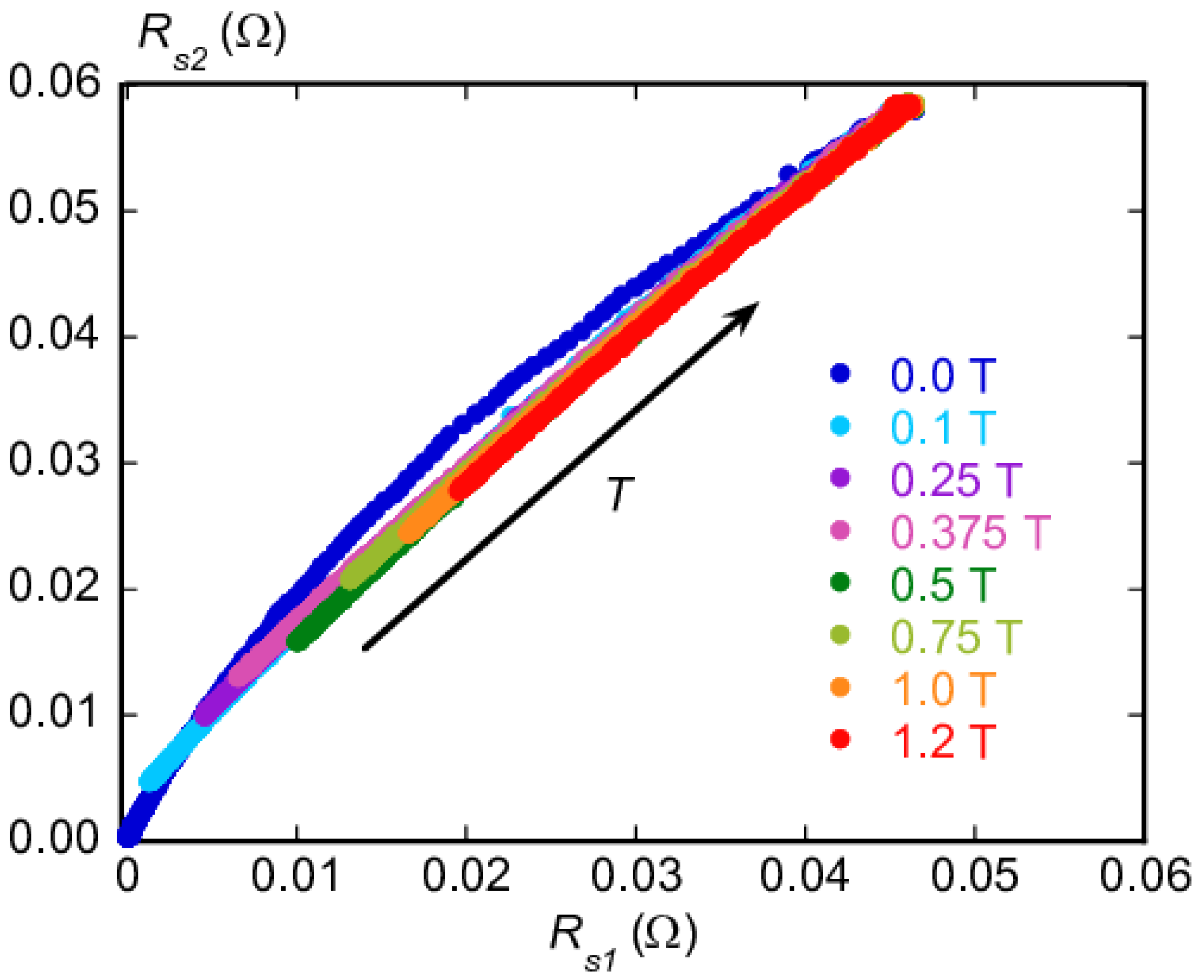
4.2. Surface Resistance
4.3. Vortex Parameters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Buzea, C.; Yamashita, T. Review of the Superconducting Properties of MgB2. Supercond. Sci. Technol. 2001, 14, R115–R146. [Google Scholar] [CrossRef]
- Choi, H.J.; Roundy, D.; Sun, H.; Cohen, M.L.; Louie, S.G. The Origin of the Anomalous Superconducting Properties of MgB2. Nature 2002, 418, 758–760. [Google Scholar] [CrossRef] [PubMed]
- Szabó, P.; Samuely, P.; Kačmarčík, J.; Klein, T.; Marcus, J.; Fruchart, D.; Miraglia, S.; Marcenat, C.; Jansen, A.G.M. Evidence for Two Superconducting Energy Gaps in MgB2 by Point-Contact Spectroscopy. Phys. Rev. Lett. 2001, 87, 137005. [Google Scholar] [CrossRef] [PubMed]
- Sarti, S.; Amabile, C.; Silva, E.; Giura, M.; Fastampa, R.; Ferdeghini, C.; Ferrando, V.; Tarantini, C. Dynamic Regimes in MgB2 Probed by Swept Frequency Microwave Measurements. Phys. Rev. B 2005, 72, 024542. [Google Scholar] [CrossRef]
- Babaev, E. Vortices with Fractional Flux in Two-Gap Superconductors and in Extended Faddeev Model. Phys. Rev. Lett. 2002, 89, 067001. [Google Scholar] [CrossRef]
- Moshchalkov, V.; Menghini, M.; Nishio, T.; Chen, Q.; Silhanek, A.; Dao, V.; Chibotaru, L.; Zhigadlo, N.; Karpinski, J. Type-1.5 Superconductivity. Phys. Rev. Lett. 2009, 102, 117001. [Google Scholar] [CrossRef]
- Dao, V.H.; Chibotaru, L.F.; Nishio, T.; Moshchalkov, V.V. Giant Vortices, Rings of Vortices, and Reentrant Behavior in Type-1.5 Superconductors. Phys. Rev. B 2011, 83, 020503. [Google Scholar] [CrossRef]
- Silaev, M.; Babaev, E. Microscopic Theory of Type-1.5 Superconductivity in Multiband Systems. Phys. Rev. B 2011, 84, 094515. [Google Scholar] [CrossRef]
- Gutierrez, J.; Raes, B.; Silhanek, A.V.; Li, L.J.; Zhigadlo, N.D.; Karpinski, J.; Tempere, J.; Moshchalkov, V.V. Scanning Hall Probe Microscopy of Unconventional Vortex Patterns in the Two-Gap MgB2 Superconductor. Phys. Rev. B 2012, 85, 094511. [Google Scholar] [CrossRef]
- Lin, S.Z.; Bulaevskii, L.N. Dissociation Transition of a Composite Lattice of Magnetic Vortices in the Flux-Flow Regime of Two-Band Superconductors. Phys. Rev. Lett. 2013, 110, 087003. [Google Scholar] [CrossRef]
- Aguirre, C.; Martins, Q.; Barba-Ortega, J. Vortices in a superconducting two-band disk: Role of the Josephson and bi-quadratic coupling. Phys. C Supercond. Its Appl. 2021, 581, 1353818. [Google Scholar] [CrossRef]
- Jorge, T.N.; Aguirre, C.; de Arruda, A.; Barba-Ortega, J. Two-band superconducting square with a central defect: Role of the deGennes extrapolation length. Eur. Phys. J. B 2020, 93, 1–7. [Google Scholar] [CrossRef]
- Aguirre, C.; Joya, M.; Barba-Ortega, J. On the vortex matter in a two-band superconducting meso-prism. Phys. C Supercond. Its Appl. 2021, 585, 1353867. [Google Scholar] [CrossRef]
- Flükiger, R. MgB2 Superconducting Wires: Basics and Applications; World Scientific Series in Applications of Superconductivity and Related Phenomena; World Scientific Publishing Company Pte. Limited: Singpore, 2016. [Google Scholar]
- Ballarino, A.; Flükiger, R. Status of MgB2 Wire and Cable Applications in Europe. J. Phys. Conf. Ser. 2017, 871, 012098. [Google Scholar] [CrossRef]
- Gozzelino, L.; Gerbaldo, R.; Ghigo, G.; Torsello, D.; Bonino, V.; Truccato, M.; Grigoroscuta, M.A.; Burdusel, M.; Aldica, G.V.; Sandu, V.; et al. High Magnetic Shielding Properties of an MgB2 Cup Obtained by Machining a Spark-Plasma-Sintered Bulk Cylinder. Supercond. Sci. Technol. 2020, 33, 044018. [Google Scholar] [CrossRef]
- Fracasso, M.; Gömöry, F.; Solovyov, M.; Gerbaldo, R.; Ghigo, G.; Laviano, F.; Napolitano, A.; Torsello, D.; Gozzelino, L. Modelling and Performance Analysis of MgB2 and Hybrid Magnetic Shields. Materials 2022, 15, 667. [Google Scholar] [CrossRef]
- Iwasa, Y. Towards Liquid-Helium-Free, Persistent-Mode MgB2 MRI Magnets: FBML Experience. Supercond. Sci. Technol. 2017, 30, 053001. [Google Scholar] [CrossRef]
- Yamamoto, A. Advances in MgB2 Superconductor Applications for Particle Accelerators. arXiv 2022. [Google Scholar] [CrossRef]
- Takano, Y.; Takeya, H.; Fujii, H.; Kumakura, H.; Hatano, T.; Togano, K.; Kito, H.; Ihara, H. Superconducting Properties of MgB2 Bulk Materials Prepared by High-Pressure Sintering. Appl. Phys. Lett. 2001, 78, 2914–2916. [Google Scholar] [CrossRef]
- Tampieri, A.; Celotti, G.; Sprio, S.; Caciuffo, R.; Rinaldi, D. Study of the Sintering Behaviour of MgB2 Superconductor during Hot-Pressing. Phys. C Supercond. 2004, 400, 97–104. [Google Scholar] [CrossRef]
- Schmidt, J.; Schnelle, W.; Grin, Y.; Kniep, R. Pulse Plasma Synthesis and Chemical Bonding in Magnesium Diboride. Solid State Sci. 2003, 5, 535–539. [Google Scholar] [CrossRef]
- Aldica, G.; Batalu, D.; Popa, S.; Ivan, I.; Nita, P.; Sakka, Y.; Vasylkiv, O.; Miu, L.; Pasuk, I.; Badica, P. Spark Plasma Sintering of MgB2 in the Two-Temperature Route. Phys. C Supercond. 2012, 477, 43–50. [Google Scholar] [CrossRef]
- Badica, P.; Aldica, G.; Ionescu, A.; Burdusel, M.; Batalu, D. The influence of different additives on MgB2 superconductor obtained by ex situ spark plasma sintering: Pinning force aspects. In Correlated Functional Oxides; Springer: Berlin, Germany, 2017; pp. 75–116. [Google Scholar] [CrossRef]
- Sandu, V.; Aldica, G.; Grigoroscuta, M.; Burdusel, M.; Pasuk, I.; Ching, Y.; Ionescu, A.; Badica, P. Effect of polysilane addition on spark plasma sintering and superconducting properties of MgB2 bulks. Ceram. Int. 2022, 48, 31914–31922. [Google Scholar] [CrossRef]
- Maeda, A.; Kitano, H.; Inoue, R. Microwave Conductivities of High-Tc Oxide Superconductors and Related Materials. J. Phys. Condens. Matter 2005, 17, R143–R185. [Google Scholar] [CrossRef]
- Grigoroscuta, M.; Aldica, G.; Burdusel, M.; Sandu, V.; Kuncser, A.; Pasuk, I.; Ionescu, A.; Suzuki, T.; Vasylkiv, O.; Badica, P. Towards high degree of c-axis orientation in MgB2 bulks. J. Magnes. Alloys 2022, 10, 2173–2184. [Google Scholar] [CrossRef]
- Sandu, V.; Aldica, G.; Popa, S.; Enculescu, M.; Badica, P. Tellurium Addition as a Solution to Improve Compactness of Ex-Situ Processed MgB2-SiC Superconducting Tapes. Supercond. Sci. Technol. 2016, 29, 065012. [Google Scholar] [CrossRef]
- Jin, B.; Klein, N.; Kang, W.; Kim, H.J.; Choi, E.M.; Lee, S.I.; Dahm, T.; Maki, K. Energy Gap, Penetration Depth, and Surface Resistance of MgB2 Thin Films Determined by Microwave Resonator Measurements. Phys. Rev. B 2002, 66, 104521–1/104521–6. [Google Scholar] [CrossRef]
- Ghigo, G.; Botta, D.; Chiodoni, A.; Gozzelino, L.; Gerbaldo, R.; Laviano, F.; Mezzetti, E. Effective Gap at Microwave Frequencies in MgB2 Thin Films with Strong Interband Scattering. Phys. Rev. B 2005, 71, 214522. [Google Scholar] [CrossRef]
- Lee, S.Y.; Lee, J.H.; Han, J.H.; Moon, S.H.; Lee, H.N.; Booth, J.C.; Claassen, J.H. Effects of the Two-Gap Nature on the Microwave Conductivity of Polycrystalline MgB2 Films with a Critical Temperature of 39 K. Phys. Rev. B 2005, 71, 104514. [Google Scholar] [CrossRef]
- Ghigo, G.; Ummarino, G.A.; Gerbaldo, R.; Gozzelino, L.; Laviano, F.; Mezzetti, E. Effects of Disorder on the Microwave Properties of MgB2 Polycrystalline Films. Phys. Rev. B 2006, 74, 184518. [Google Scholar] [CrossRef]
- Oates, D.E.; Agassi, Y.D.; Moeckly, B.H. Microwave Measurements of MgB2: Implications for Applications and Order-Parameter Symmetry. Supercond. Sci. Technol. 2010, 23, 034011. [Google Scholar] [CrossRef]
- Gallitto, A.A.; Camarda, P.; Vigni, M.L.; Albisetti, A.F.; Saglietti, L.; Giunchi, G. Microwave Response of Coaxial Cavities Made of Bulk Magnesium Diboride. IEEE Trans. Appl. Supercond. 2014, 24, 1500109. [Google Scholar] [CrossRef]
- Pompeo, N.; Alimenti, A.; Torokhtii, K.; Silva, E. Physics of Vortex Motion by Means of Microwave Surface Impedance Measurements (Review Article). Low Temp. Phys. 2020, 46, 343–347. [Google Scholar] [CrossRef]
- Shibata, A.; Matsumoto, M.; Izawa, K.; Matsuda, Y.; Lee, S.; Tajima, S. Anomalous Flux Flow Resistivity in the Two-Gap Superconductor MgB2. Phys. Rev. B 2003, 68, 060501. [Google Scholar] [CrossRef]
- Dulčić, A.; Paar, D.; Požek, M.; Williams, G.; Krämer, S.; Jung, C.; Park, M.s.; Lee, S.i. Magnetization and Microwave Study of Superconducting MgB2. Phys. Rev. B 2002, 66, 014505. [Google Scholar] [CrossRef]
- Sarti, S.; Amabile, C.; Fastampa, R.; Giura, M.; Pompeo, N.; Silva, E. Vortex Motion and Quasiparticle Resistivity in MgB2 at Microwave Frequencies. J. Supercond. Nov. Magn. 2007, 20, 51–57. [Google Scholar] [CrossRef]
- Zaitsev, A.; Schneider, R.; Hott, R.; Schwarz, T.; Geerk, J. Effect of a Dc Magnetic Field on the Microwave Losses in MgB2 Thin Films. Phys. Rev. B 2007, 75, 212505. [Google Scholar] [CrossRef]
- Bardeen, J.; Stephen, M. Theory of the Motion of Vortices in Superconductors. Phys. Rev. 1965, 140, 1197–1207. [Google Scholar] [CrossRef]
- Goryo, J.; Matsukawa, H. Flux Flow Resistivity in Two-Gap Superconductor. J. Phys. Soc. Jpn. 2005, 74, 1394–1396. [Google Scholar] [CrossRef]
- Tinkham, M. Introduction to Superconductivity, 2nd ed.; McGraw-Hill, Inc.: New York, NY, USA, 1996. [Google Scholar]
- Coffey, M.W.; Clem, J.R. Unified Theory of Effects of Vortex Pinning and Flux Creep upon the Rf Surface Impedance of Type-II Superconductors. Phys. Rev. Lett. 1991, 67, 386–389. [Google Scholar] [CrossRef]
- Brandt, E. Linear a.c. Response of High-Tc Superconductors and the Irreversibility Line. Phys. Scr. 1992, T45, 63–68. [Google Scholar] [CrossRef]
- Pompeo, N.; Silva, E. Reliable Determination of Vortex Parameters from Measurements of the Microwave Complex Resistivity. Phys. Rev. B 2008, 78, 094503. [Google Scholar] [CrossRef]
- Goryo, J.; Saito, T.; Matsukawa, H. Vortex Pinning in Two-Gap Superconductors. J. Phys. Conf. Ser. 2007, 89, 012022. [Google Scholar] [CrossRef]
- Alimenti, A.; Torokhtii, K.; Silva, E.; Pompeo, N. Challenging Microwave Resonant Measurement Techniques for Conducting Material Characterization. Meas. Sci. Technol. 2019, 30, 065601. [Google Scholar] [CrossRef]
- Torokhtii, K.; Pompeo, N.; Silva, E.; Alimenti, A. Optimization of Q-factor and Resonance Frequency Measurements in Partially Calibrated Resonant Systems. Meas. Sens. 2021, 18, 100314. [Google Scholar] [CrossRef]
- Torokhtii, K.; Alimenti, A.; Pompeo, N.; Silva, E. Estimation of Microwave Resonant Measurements Uncertainty from Uncalibrated Data. Acta IMEKO 2020, 9, 47–52. [Google Scholar] [CrossRef]
- Torokhtii, K.; Alimenti, A.; Pompeo, N.; Leccese, F.; Orsini, F.; Scorza, A.; Sciuto, S.A.; Silva, E. Q-Factor of Microwave Resonators: Calibrated vs. Uncalibrated Measurements. J. Phys. Conf. Ser. 2018, 1065, 052027. [Google Scholar] [CrossRef]
- Pompeo, N.; Torokhtii, K.; Alimenti, A.; Silva, E. A Method Based on a Dual Frequency Resonator to Estimate Physical Parameters of Superconductors from Surface Impedance Measurements in a Magnetic Field. Measurement 2021, 184, 109937. [Google Scholar] [CrossRef]
- Pompeo, N.; Alimenti, A.; Torokhtii, K.; Bartolomé, E.; Palau, A.; Puig, T.; Augieri, A.; Galluzzi, V.; Mancini, A.; Celentano, G.; et al. Intrinsic Anisotropy and Pinning Anisotropy in Nanostructured YBa2Cu3O7-δ from Microwave Measurements. Supercond. Sci. Technol. 2020, 33, 044017. [Google Scholar] [CrossRef]
- Fuchs, G.; Müller, K.H.; Handstein, A.; Nenkov, K.; Narozhnyi, V.N.; Eckert, D.; Wolf, M.; Schultz, L. Upper Critical Field and Irreversibility Line in Superconducting MgB2. Solid State Commun. 2001, 118, 497–501. [Google Scholar] [CrossRef]
- Handstein, A.; Hinz, D.; Fuchs, G.; Müller, K.H.; Nenkov, K.; Gutfleisch, O.; Narozhnyi, V.N.; Schultz, L. Fully Dense MgB2 Superconductor Textured by Hot Deformation. J. Alloys Compd. 2001, 329, 285–289. [Google Scholar] [CrossRef]
- Alimenti, A.; Torokhtii, K.; Grigoroscuta, M.; Badica, P.; Crisan, A.; Silva, E.; Pompeo, N. Microwave Investigation of Pinning in Te- and Cubic-BN- Added MgB2. J. Phys. Conf. Ser. 2020, 1559, 12039. [Google Scholar] [CrossRef]
- Mazin, I.I.; Andersen, O.K.; Jepsen, O.; Dolgov, O.V.; Kortus, J.; Golubov, A.A.; Kuz’menko, A.B.; van der Marel, D. Superconductivity in MgB2: Clean or Dirty? Phys. Rev. Lett. 2002, 89, 107002. [Google Scholar] [CrossRef] [PubMed]
- Bonura, M.; Gallitto, A.A.; Vigni, M.L.; Ummarino, G.A. Field-Induced Suppression of the π-Band Superconductivity and Magnetic Hysteresis in the Microwave Surface Resistance of MgB2 at Temperatures near Tc. Supercond. Sci. Technol. 2009, 22, 055010. [Google Scholar] [CrossRef]
- Alimenti, A.; Pompeo, N.; Torokhtii, K.; Spina, T.; Muzzi, L.; Silva, E. Surface Impedance Measurements on Nb3Sn in High Magnetic Fields. IEEE Trans. Appl. Supercond. 2019, 29, 3500104. [Google Scholar] [CrossRef]
- Alimenti, A.; Pompeo, N.; Torokhtii, K.; Spina, T.; Flükiger, R.; Muzzi, L.; Silva, E. Microwave Measurements of the High Magnetic Field Vortex Motion Pinning Parameters in Nb3Sn. Supercond. Sci. Technol. 2021, 34, 014003. [Google Scholar] [CrossRef]
- Silaev, M.; Vargunin, A. Vortex Motion and Flux-Flow Resistivity in Dirty Multiband Superconductors. Phys. Rev. B 2016, 94, 224506. [Google Scholar] [CrossRef]
- Takahashi, H.; Okada, T.; Imai, Y.; Kitagawa, K.; Matsubayashi, K.; Uwatoko, Y.; Maeda, A. Investigation of the Superconducting Gap Structure in SrFe2(As0.7P0.3)2 by Magnetic Penetration Depth and Flux Flow Resistivity Analysis. Phys. Rev. B 2012, 86, 144525. [Google Scholar] [CrossRef]
- Okada, T.; Imai, Y.; Takahashi, H.; Nakajima, M.; Iyo, A.; Eisaki, H.; Maeda, A. Penetration Depth and Flux-Flow Resistivity Measurements of BaFe2(As0.55P0.45)2 Single Crystals. Phys. C Supercond. 2014, 504, 24–27. [Google Scholar] [CrossRef]
- Okada, T.; Nabeshima, F.; Takahashi, H.; Imai, Y.; Maeda, A. Exceptional Suppression of Flux-Flow Resistivity in FeSe0.4Te0.6 by Back-Flow from Excess Fe Atoms and Se/Te Substitutions. Phys. Rev. B 2015, 91, 054510. [Google Scholar] [CrossRef]
- Pompeo, N.; Torokhtii, K.; Alimenti, A.; Sylva, G.; Braccini, V.; Silva, E. Pinning Properties of FeSeTe Thin Film through Multifrequency Measurements of the Surface Impedance. Supercond. Sci. Technol. 2020, 33, 114006. [Google Scholar] [CrossRef]
- Pompeo, N.; Alimenti, A.; Torokhtii, K.; Sylva, G.; Braccini, V.; Silva, E. Microwave Properties of Fe(Se, Te) Thin Films in a Magnetic Field: Pinning and Flux Flow. J. Phys. Conf. Ser. 2020, 1559, 012055. [Google Scholar] [CrossRef]
- Xu, M.; Kitazawa, H.; Takano, Y.; Ye, J.; Nishida, K.; Abe, H.; Matsushita, A.; Kido, G. Single crystal MgB2 with anisotropic superconducting properties. arXiv1 2001, arXiv:cond-mat/0105271. [Google Scholar]
- Lee, S.; Mori, H.; Masui, T.; Eltsev, Y.; Yamamoto, A.; Tajima, S. Growth, structure analysis and anisotropic superconducting properties of MgB2 single crystals. J. Phys. Soc. Jpn. 2001, 70, 2255–2258. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alimenti, A.; Torokhtii, K.; Vidal García, P.; Silva, E.; Grigoroscuta, M.A.; Badica, P.; Crisan, A.; Pompeo, N. Measurements of Surface Impedance in MgB2 in DC Magnetic Fields: Insights in Flux-Flow Resistivity. Materials 2023, 16, 205. https://doi.org/10.3390/ma16010205
Alimenti A, Torokhtii K, Vidal García P, Silva E, Grigoroscuta MA, Badica P, Crisan A, Pompeo N. Measurements of Surface Impedance in MgB2 in DC Magnetic Fields: Insights in Flux-Flow Resistivity. Materials. 2023; 16(1):205. https://doi.org/10.3390/ma16010205
Chicago/Turabian StyleAlimenti, Andrea, Kostiantyn Torokhtii, Pablo Vidal García, Enrico Silva, Mihai Alexandru Grigoroscuta, Petre Badica, Adrian Crisan, and Nicola Pompeo. 2023. "Measurements of Surface Impedance in MgB2 in DC Magnetic Fields: Insights in Flux-Flow Resistivity" Materials 16, no. 1: 205. https://doi.org/10.3390/ma16010205
APA StyleAlimenti, A., Torokhtii, K., Vidal García, P., Silva, E., Grigoroscuta, M. A., Badica, P., Crisan, A., & Pompeo, N. (2023). Measurements of Surface Impedance in MgB2 in DC Magnetic Fields: Insights in Flux-Flow Resistivity. Materials, 16(1), 205. https://doi.org/10.3390/ma16010205






