Excitonic Enhancement and Excited Excitonic States in CsPbBr3 Halide Perovskite Single Crystals
Abstract
1. Introduction
2. Materials and Methods
2.1. Crystal Growth
2.2. Reflectivity Measurements
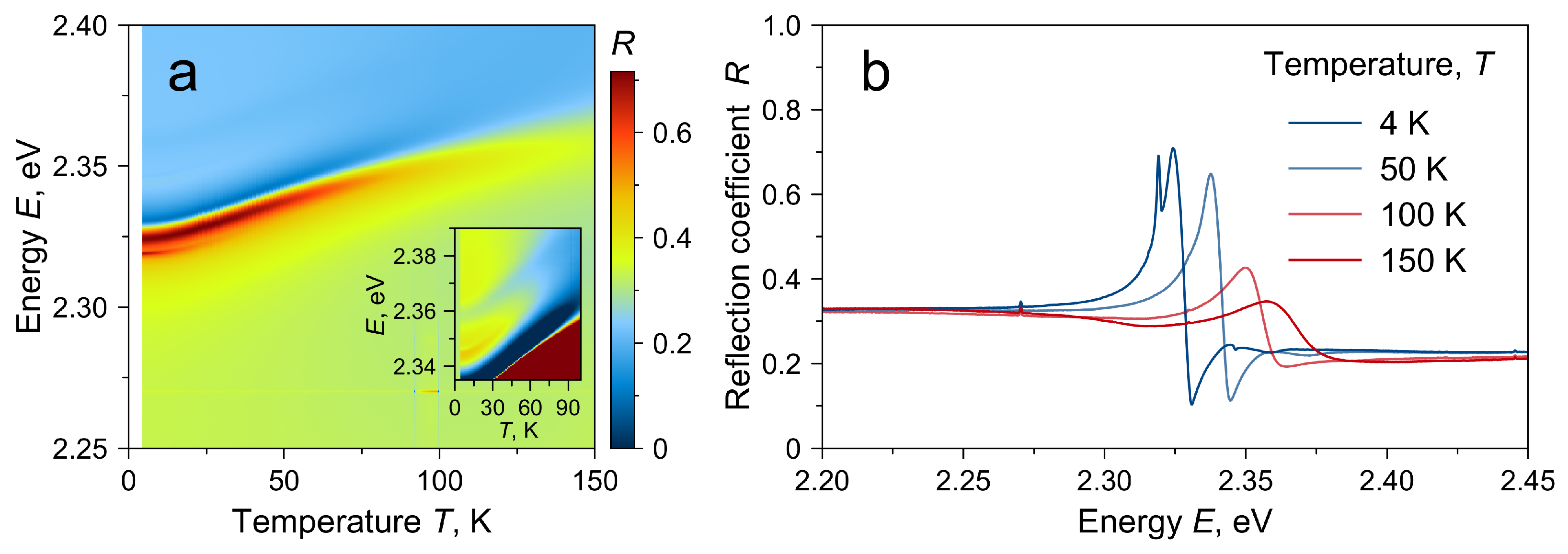
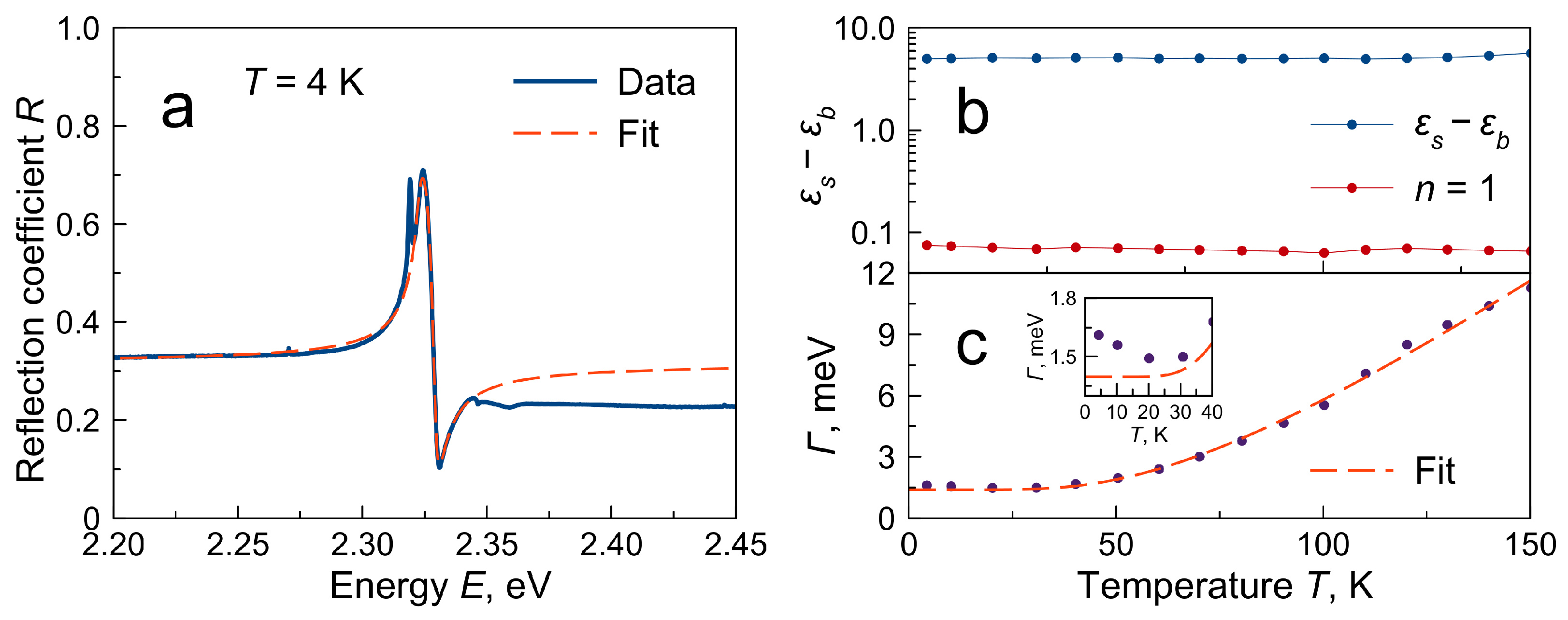
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PL | Photoluminescence |
References
- Fakharuddin, A.; Gangishetty, M.K.; Abdi-Jalebi, M.; Chin, S.; Yusoff, A.R.B.M.; Congreve, D.N.; Tress, W.; Deschler, F.; Vasilopoulou, M.; Bolink, H.J. Perovskite light-emitting diodes. Nat. Electron. 2022, 5, 203–216. [Google Scholar] [CrossRef]
- Dong, H.; Zhang, C.; Liu, X.; Yao, J.; Zhao, Y.S. Materials chemistry and engineering in metal halide perovskite lasers. Chem. Soc. Rev. 2020, 49, 951–982. [Google Scholar] [CrossRef] [PubMed]
- Wei, H.; Huang, J. Halide lead perovskites for ionizing radiation detection. Nat. Commun. 2019, 10, 1066. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Sun, Y.; Chen, J.; Wang, F.; Han, R.; Zhang, C.; Kong, J.; Li, L.; Yang, J. A Review of Perovskite-Based Photodetectors and Their Applications. Nanomaterials 2022, 12, 4390. [Google Scholar] [CrossRef]
- Goldschmidt, V.M. Die Gesetze der Krystallochemie. Naturwissenschaften 1926, 14, 477–485. [Google Scholar] [CrossRef]
- Tilchin, J.; Dirin, D.N.; Maikov, G.I.; Sashchiuk, A.; Kovalenko, M.V.; Lifshitz, E. Hydrogen-like Wannier–Mott Excitons in Single Crystal of Methylammonium Lead Bromide Perovskite. ACS Nano 2016, 10, 6363–6371. [Google Scholar] [CrossRef]
- Diab, H.; Trippé-Allard, G.; Lédée, F.; Jemli, K.; Vilar, C.; Bouchez, G.; Jacques, V.; Tejeda, A.; Even, J.; Lauret, J.; et al. Narrow Linewidth Excitonic Emission in Organic–Inorganic Lead Iodide Perovskite Single Crystals. J. Phys. Chem. Lett. 2016, 7, 5093–5100. [Google Scholar] [CrossRef]
- Galkowski, K.; Mitioglu, A.; Miyata, A.; Plochocka, P.; Portugall, O.; Eperon, G.E.; Wang, J.T.; Stergiopoulos, T.; Stranks, S.D.; Snaith, H.J.; et al. Determination of the exciton binding energy and effective masses for methylammonium and formamidinium lead tri-halide perovskite semiconductors. Energy Environ. Sci. 2016, 9, 962–970. [Google Scholar] [CrossRef]
- Yang, Z.; Surrente, A.; Galkowski, K.; Bruyant, N.; Maude, D.K.; Haghighirad, A.A.; Snaith, H.J.; Plochocka, P.; Nicholas, R.J. Unraveling the Exciton Binding Energy and the Dielectric Constant in Single-Crystal Methylammonium Lead Triiodide Perovskite. J. Phys. Chem. Lett. 2017, 8, 1851–1855. [Google Scholar] [CrossRef]
- Yang, Z.; Surrente, A.; Galkowski, K.; Miyata, A.; Portugall, O.; Sutton, R.J.; Haghighirad, A.A.; Snaith, H.J.; Maude, D.K.; Plochocka, P.; et al. Impact of the Halide Cage on the Electronic Properties of Fully Inorganic Cesium Lead Halide Perovskites. ACS Energy Lett. 2017, 2, 1621–1627. [Google Scholar] [CrossRef]
- March, S.A.; Clegg, C.; Riley, D.B.; Webber, D.; Hill, I.G.; Hall, K.C. Simultaneous observation of free and defect-bound excitons in CH3NH3PbI3 using four-wave mixing spectroscopy. Sci. Rep. 2016, 6, 39139. [Google Scholar] [CrossRef] [PubMed]
- March, S.A.; Riley, D.B.; Clegg, C.; Webber, D.; Liu, X.; Dobrowolska, M.; Furdyna, J.K.; Hill, I.G.; Hall, K.C. Four-Wave Mixing in Perovskite Photovoltaic Materials Reveals Long Dephasing Times and Weaker Many-Body Interactions than GaAs. ACS Photonics 2017, 4, 1515–1521. [Google Scholar] [CrossRef]
- March, S.A.; Riley, D.B.; Clegg, C.; Webber, D.; Hill, I.G.; Yu, Z.; Hall, K.C. Ultrafast acoustic phonon scattering in CH3NH3PbI3 revealed by femtosecond four-wave mixing. J. Chem. Phys. 2019, 151, 144702. [Google Scholar] [CrossRef]
- Trifonov, A.V.; Grisard, S.; Kosarev, A.N.; Akimov, I.A.; Yakovlev, D.R.; Höcker, J.; Dyakonov, V.; Bayer, M. Photon Echo Polarimetry of Excitons and Biexcitons in a CH3NH3PbI3 Perovskite Single Crystal. ACS Photonics 2022, 9, 621–629. [Google Scholar] [CrossRef]
- Nazarov, R.S.; Solovev, I.A.; Murzin, A.O.; Selivanov, N.I.; Even, J.; Emeline, A.V.; Kapitonov, Y.V. Photon echo from free excitons in a CH3NH3PbI3 halide perovskite single crystal. Phys. Rev. B 2022, 105, 621–629. [Google Scholar] [CrossRef]
- Lozhkina, O.A.; Yudin, V.I.; Murashkina, A.A.; Shilovskikh, V.V.; Davydov, V.G.; Kevorkyants, R.; Emeline, A.V.; Kapitonov, Y.V.; Bahnemann, D.W. Low Inhomogeneous Broadening of Excitonic Resonance in MAPbBr3 Single Crystals. J. Phys. Chem. Lett. 2018, 9, 302–305. [Google Scholar] [CrossRef] [PubMed]
- Selivanov, N.I.; Murzin, A.O.; Yudin, V.I.; Kapitonov, Y.V.; Emeline, A.V. Counterdiffusion-in-gel growth of high optical and crystal quality MAPbX3 (MA = CH3, X = I−, Br−) lead-halide perovskite single crystals. CrystEngComm 2022, 24, 2976–2981. [Google Scholar] [CrossRef]
- Yudin, V.I.; Lozhkin, M.S.; Shurukhina, A.V.; Emeline, A.V.; Kapitonov, Y.V. Photoluminescence Manipulation by Ion Beam Irradiation in CsPbBr3 Halide Perovskite Single Crystals. J. Phys. Chem. C 2019, 123, 21130–21134. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, F.; Mi, Q. Preferential Facet Growth of Methylammonium Lead Halide Single Crystals Promoted by Halide Coordination. Chem. Lett. 2016, 45, 1030–1032. [Google Scholar] [CrossRef]
- Murzin, A.O.; Selivanov, N.I.; Kozlov, V.O.; Ryzhov, I.I.; Miyasaka, T.; Emeline, A.V.; Kapitonov, Y.V. Photoluminescence Excitation Spectroscopy of Defect-Related States in MAPbI3 Perovskite Single Crystals. Adv. Opt. Mater. 2021, 9, 1030–1032. [Google Scholar] [CrossRef]
- Mamaeva, M.P.; Samsonova, A.Y.; Murzin, A.O.; Lozhkina, O.A.; Murashkina, A.A.; Selivanov, N.I.; Kapitonov, Y.V. Ultrafast Random Lasing in MAPbI3 Halide Perovskite Single Crystals. J. Phys. Chem. C 2022, 126, 19816–19821. [Google Scholar] [CrossRef]
- Harbeke, G.; Tosatti, E. Band-Edge Excitons in PbI2: A Puzzle? Phys. Rev. Lett. 1972, 28, 1567–1570. [Google Scholar] [CrossRef]
- Thanh, L.C.; Depeursinge, C.; Levy, F.; Mooser, E. The band gap excitons in PbI2. J. Phys. Chem. Solids 1975, 36, 699–702. [Google Scholar] [CrossRef]
- Bréhault, A.; Cozic, S.; Boidin, R.; Calvez, L.; Bychkov, E.; Masselin, P.; Zhang, X.; Le Coq, D. Influence of NaX (X = I or Cl) additions on GeS2–Ga2S3 based glasses. J. Solid State Chem. 2014, 220, 238–244. [Google Scholar] [CrossRef]
- Shapochkin, P.Y.; Eliseev, S.A.; Lovtcius, V.A.; Efimov, Y.P.; Grigoryev, P.S.; Khramtsov, E.S.; Ignatiev, I.V. Excitonic Probe for Characterization of High-Quality Quantum-Well Heterostructures. Phys. Rev. Appl. 2019, 12, 034034. [Google Scholar] [CrossRef]
- Solovev, I.A.; Davydov, V.G.; Kapitonov, Y.V.; Shapochkin, P.Y.; Efimov, Y.P.; Lovcjus, V.A.; Eliseev, S.A.; Petrov, V.V.; Ovsyankin, V.V. Increasing of AlGaAs/GaAs quantum well robustness to resonant excitation by lowering Al concentration in barriers. J. Phys. Conf. Ser. 2015, 643, 012085. [Google Scholar] [CrossRef]
- Kapitonov, Y.V.; Shapochkin, P.Y.; Petrov, Y.V.; Efimov, Y.P.; Eliseev, S.A.; Dolgikh, Y.K.; Petrov, V.V.; Ovsyankin, V.V. Effect of irradiation by He+ and Ga+ ions on the 2D-exciton susceptibility of InGaAs/GaAs quantum-well structures. Phys. Status Solidi B 2015, 252, 1950–1954. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Y.; Song, J.; Li, X.; Xu, J.; Zeng, H.; Sun, H. Temperature Dependent Reflectance and Ellipsometry Studies on a CsPbBr3 Single Crystal. J. Phys. Chem. C 2019, 123, 10564–10570. [Google Scholar] [CrossRef]
- Klingshirn, C.F. Semiconductor Optics; Springer: Berlin/Heidelberg, Germany, 2005; pp. 73–90. [Google Scholar]
- Elliott, R.J. Intensity of Optical Absorption by Excitons. Phys. Rev. 1957, 108, 1384. [Google Scholar] [CrossRef]
- Tanguy, C. Optical Dispersion by Wannier Excitons. Phys. Rev. Lett. 1995, 75, 4090. [Google Scholar] [CrossRef]
- Tanguy, C. Refractive index of direct bandgap semiconductors near the absorption threshold: Influence of excitonic effects. IEEE J. Quantum Electron. 1996, 32, 1746–1751. [Google Scholar] [CrossRef]
- O’Neill, M.; Oestreich, M.; Rühle, W.W.; Ashenford, D.E. Exciton radiative decay and homogeneous broadening in CdTe/Cd0.85Mn0.15Te multiple quantum wells. Phys. Rev. B 1993, 48, 8980. [Google Scholar] [CrossRef] [PubMed]
- Sebastian, M.; Peters, J.A.; Stoumpos, C.C.; Im, J.; Kostina, S.S.; Liu, Z.; Kanatzidis, M.G.; Freeman, A.J.; Wessels, B.W. Excitonic emissions and above-band-gap luminescence in the single-crystal perovskite semiconductors CsPbBr3 and CsPbCl3. Phys. Rev. B 2015, 92, 235210. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samsonova, A.Y.; Yudin, V.I.; Shurukhina, A.V.; Kapitonov, Y.V. Excitonic Enhancement and Excited Excitonic States in CsPbBr3 Halide Perovskite Single Crystals. Materials 2023, 16, 185. https://doi.org/10.3390/ma16010185
Samsonova AY, Yudin VI, Shurukhina AV, Kapitonov YV. Excitonic Enhancement and Excited Excitonic States in CsPbBr3 Halide Perovskite Single Crystals. Materials. 2023; 16(1):185. https://doi.org/10.3390/ma16010185
Chicago/Turabian StyleSamsonova, Anna Yu., Vsevolod I. Yudin, Anna V. Shurukhina, and Yury V. Kapitonov. 2023. "Excitonic Enhancement and Excited Excitonic States in CsPbBr3 Halide Perovskite Single Crystals" Materials 16, no. 1: 185. https://doi.org/10.3390/ma16010185
APA StyleSamsonova, A. Y., Yudin, V. I., Shurukhina, A. V., & Kapitonov, Y. V. (2023). Excitonic Enhancement and Excited Excitonic States in CsPbBr3 Halide Perovskite Single Crystals. Materials, 16(1), 185. https://doi.org/10.3390/ma16010185





