Numerical Study on the Tensile Performance of Headed Stud Shear Connectors with Head-Sectional Damage
Abstract
:1. Introduction
2. Pull-Out Tests
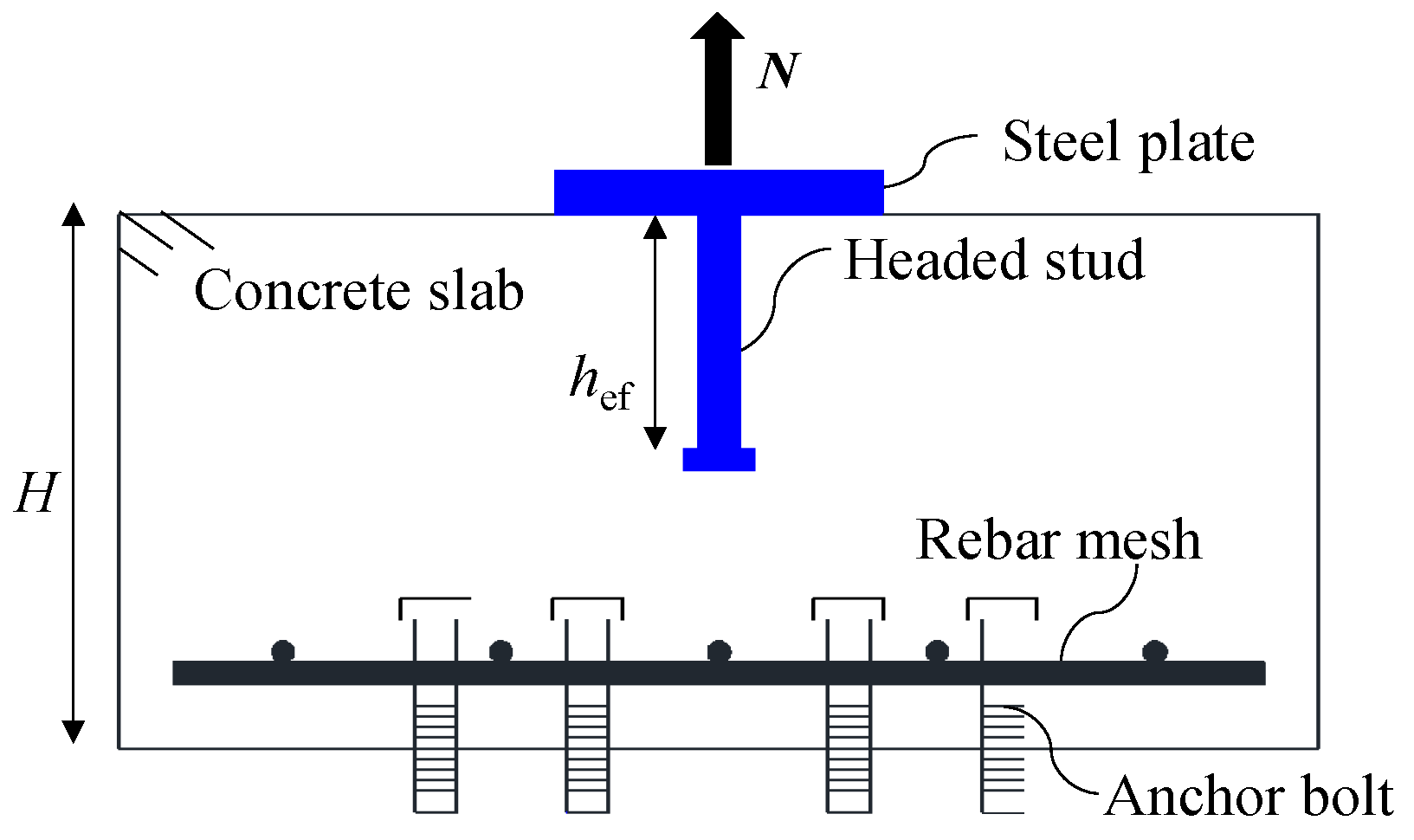
2.1. Specimens
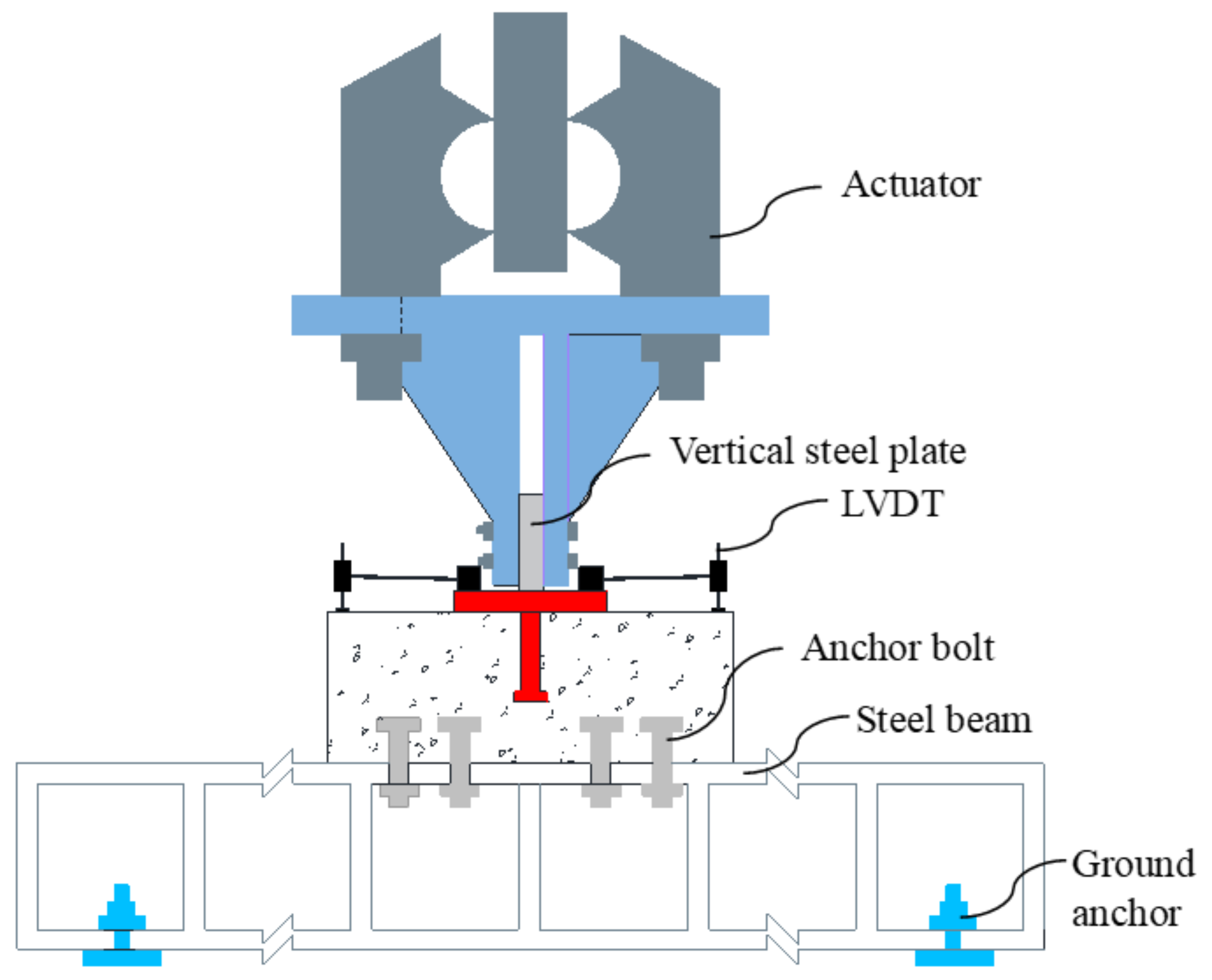
2.2. Test Setup
2.3. Material Properties
3. Experimental Results
4. Numerical Investigation
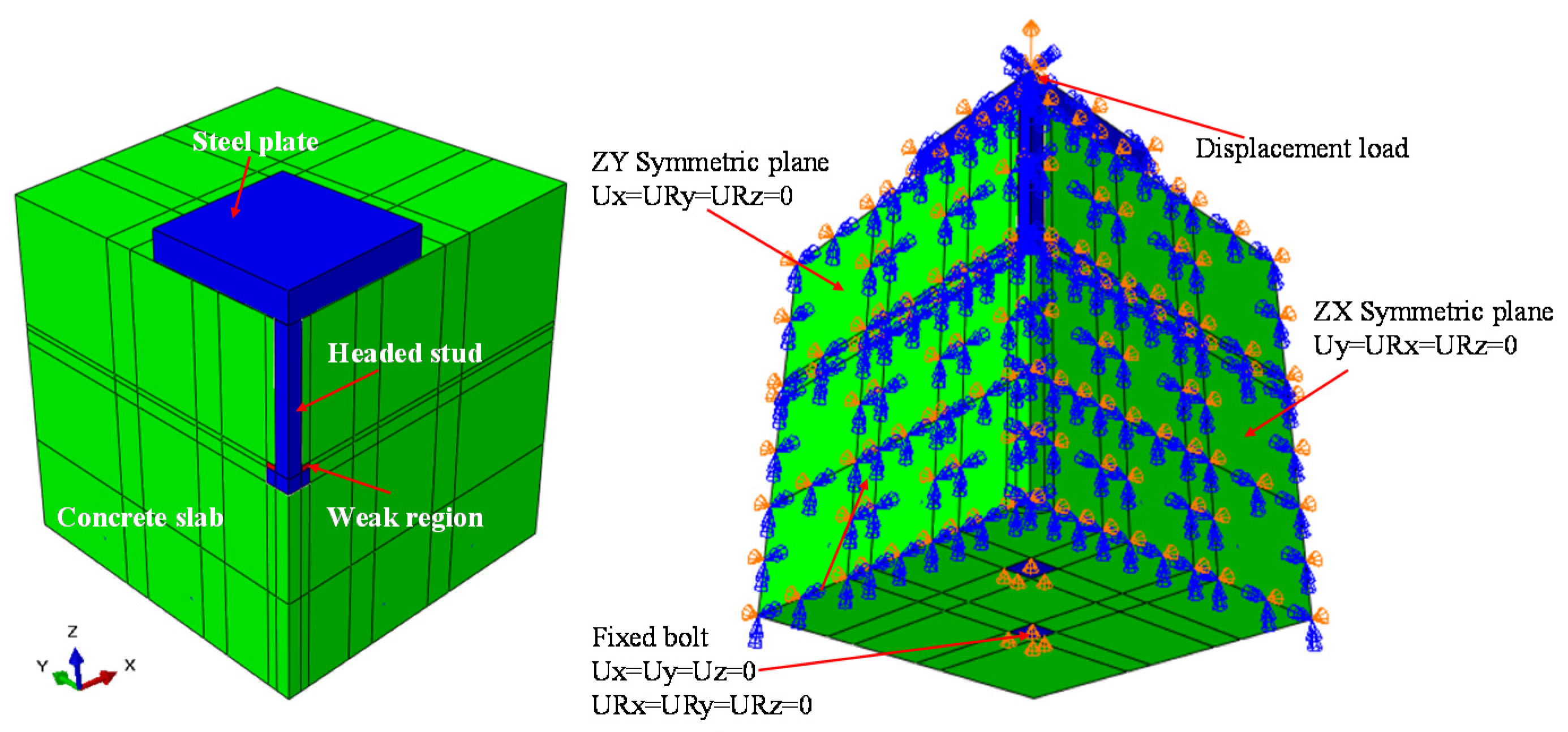
4.1. Establishment of Finite Element Models
4.1.1. General
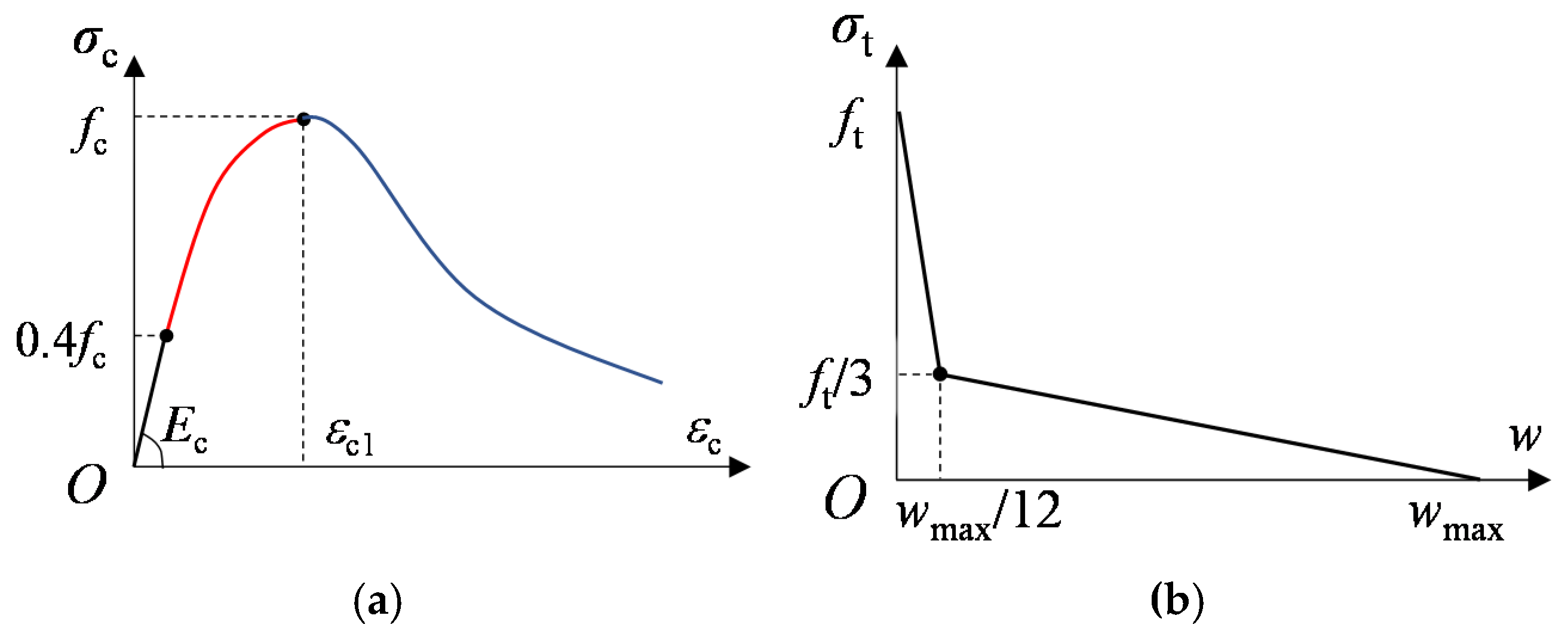
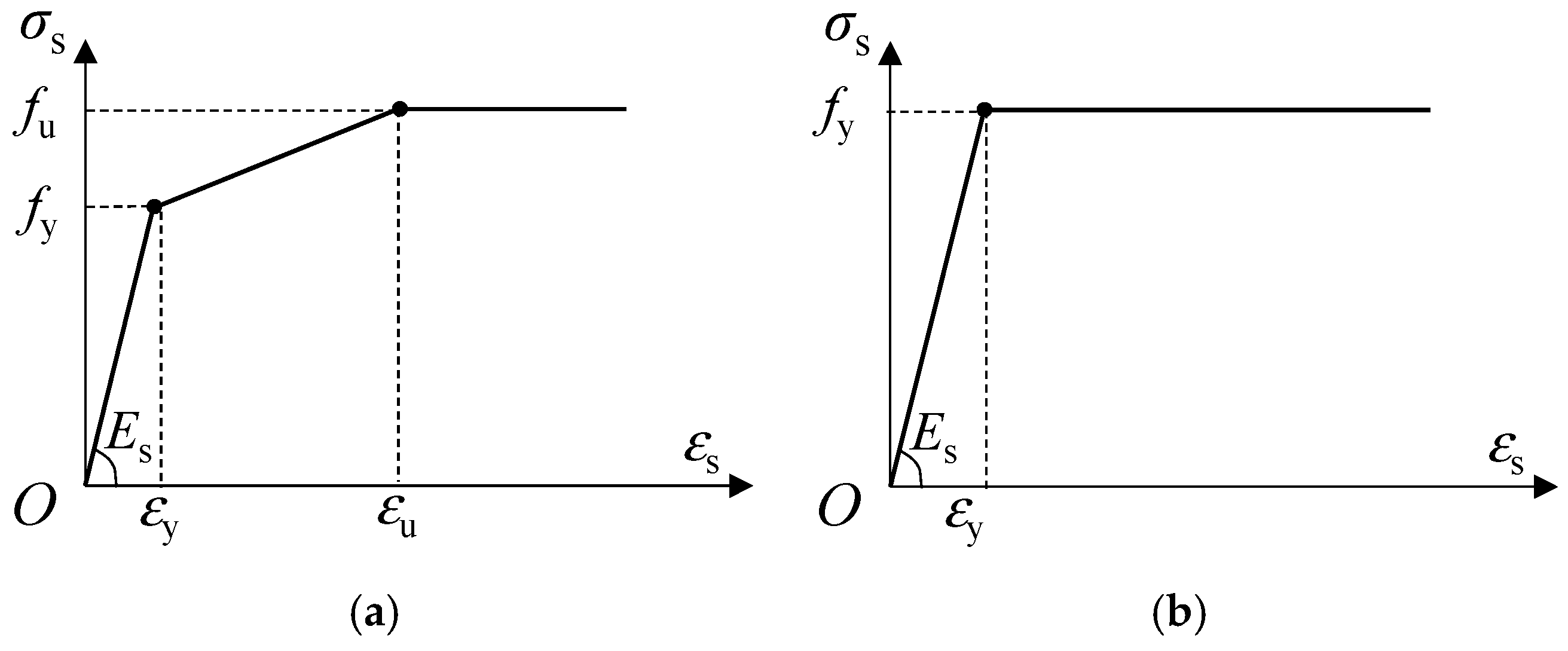
4.1.2. Material Modeling
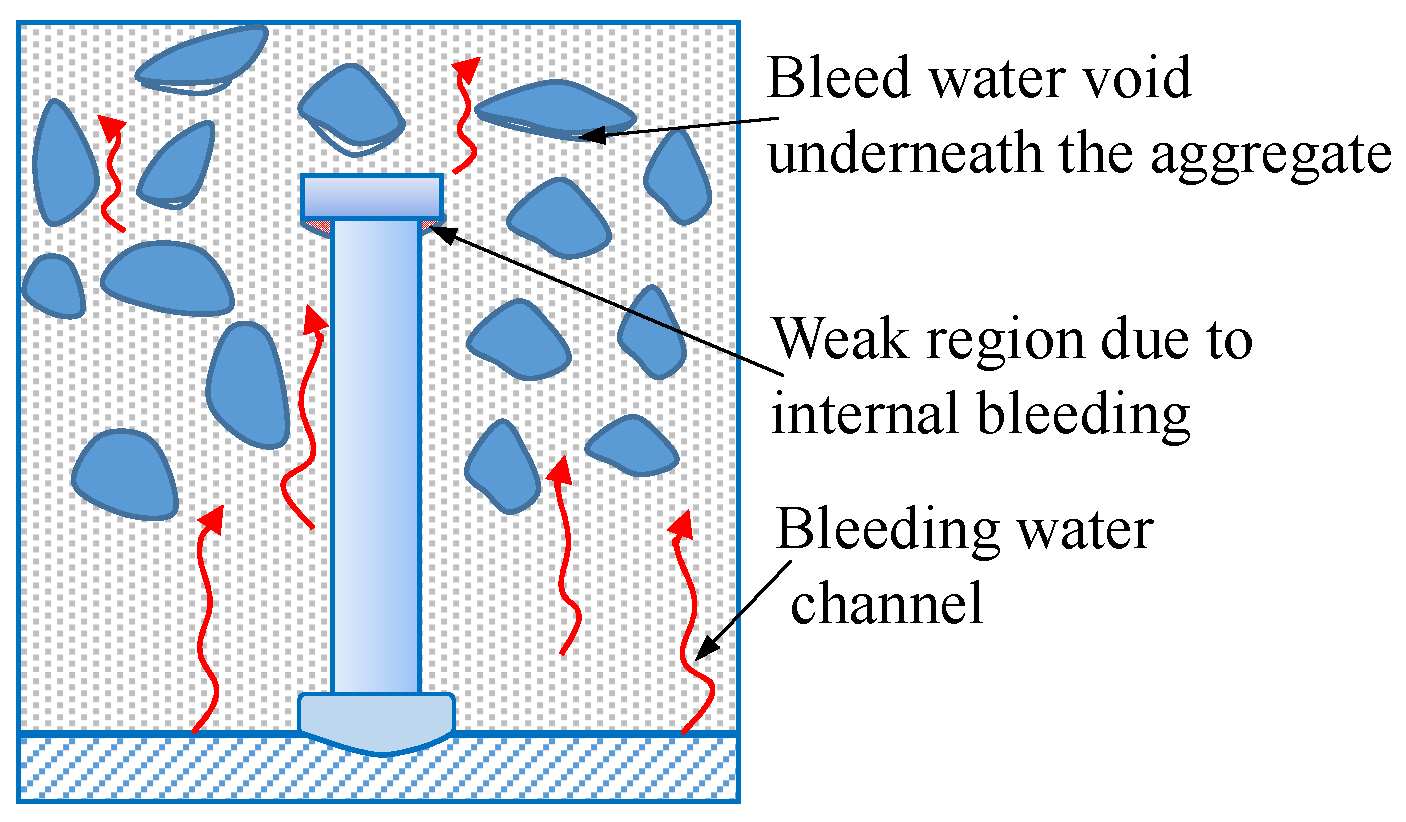
4.1.3. Modeling the Concrete Weak Region Due to Bleeding
4.1.4. Mesh
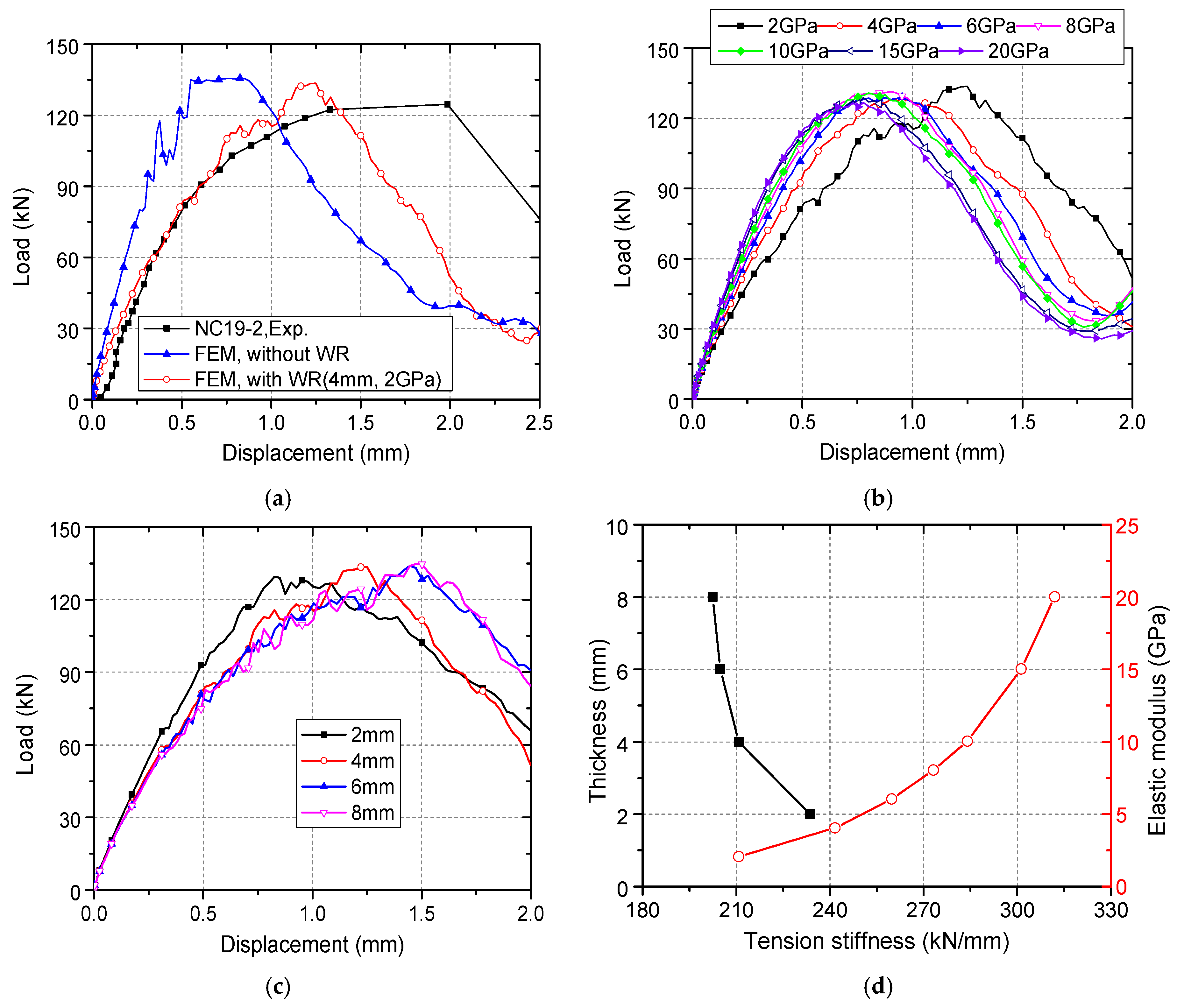
4.2. Validation Studies
5. Parametrical Analysis and Proposed Reduction Factors
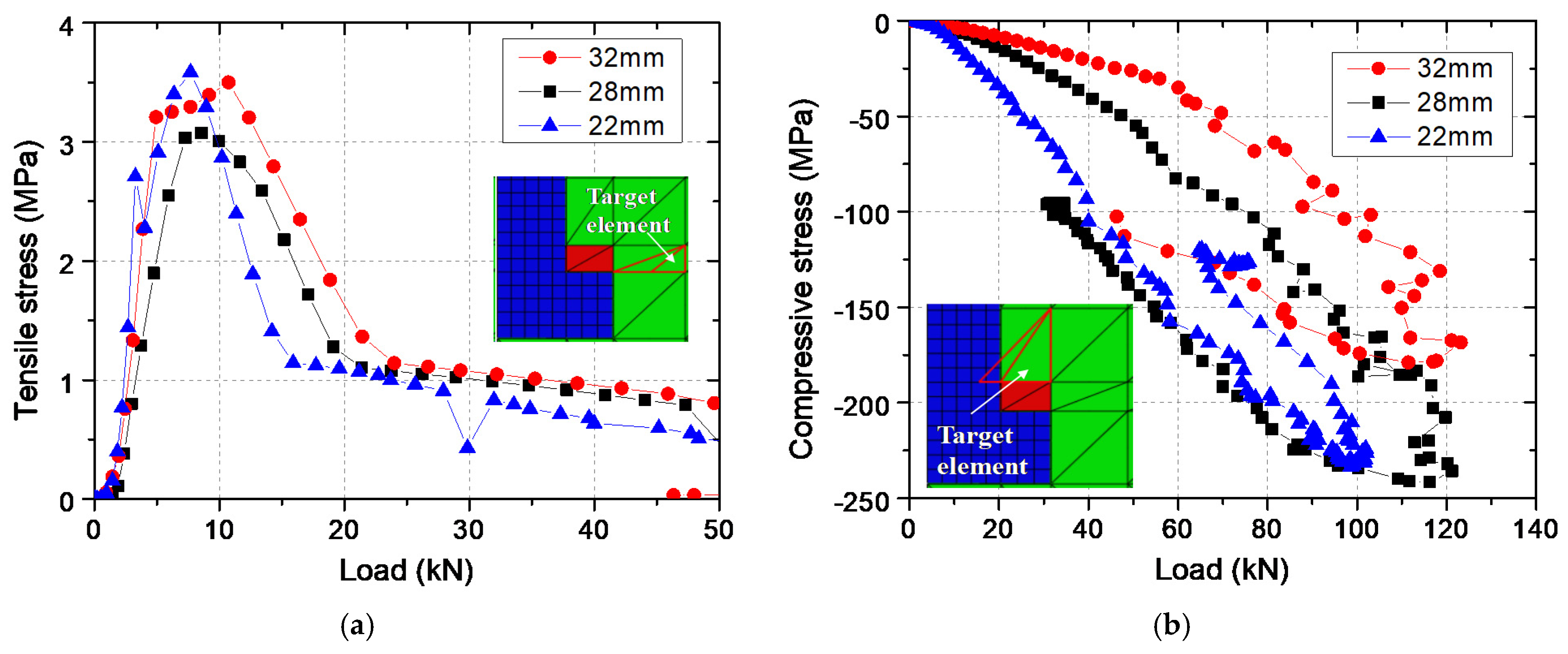
5.1. Failure Mechanism
5.2. Tensile Capacity
5.3. Tensile Stiffness
6. Conclusions
- (1)
- Concrete weak region due to bleeding should be considered in the finite element models, and it was found that its elastic modulus significantly affected the stiffness of connectors, while the influence of its thickness on the capacity and stiffness was minor. After modeling a weak region with an elastic modulus of 2 GPa and a thickness of 4mm, the simulation results demonstrated good agreement with the test results in terms of the initial stiffness and the ultimate load.
- (2)
- When the head-sectional damage degree was 38%, the failure mode changed from concrete cone breakout to pull-out failure, resulting in a decrease in loading capacity and ductility. The numerical results show that the load, when concrete, near the stud head cracked decreased with the damage degree, while the crack width increased with the damage degree. The cracking load was found to be less than 10% of the connector’s tensile capacity, which was much smaller than the 30% reported by Eligehausen and Sawade [24]. Meanwhile, when the head diameter reduced from 32 mm to 22 mm, the bearing stress of the concrete above the stud head and shear stress of concrete in the vicinity of the stud head had more than doubled. These differences in stress state and failure process were causes for the change from concrete cone breakout failure to pull-out failure when the damage degree increased.
- (3)
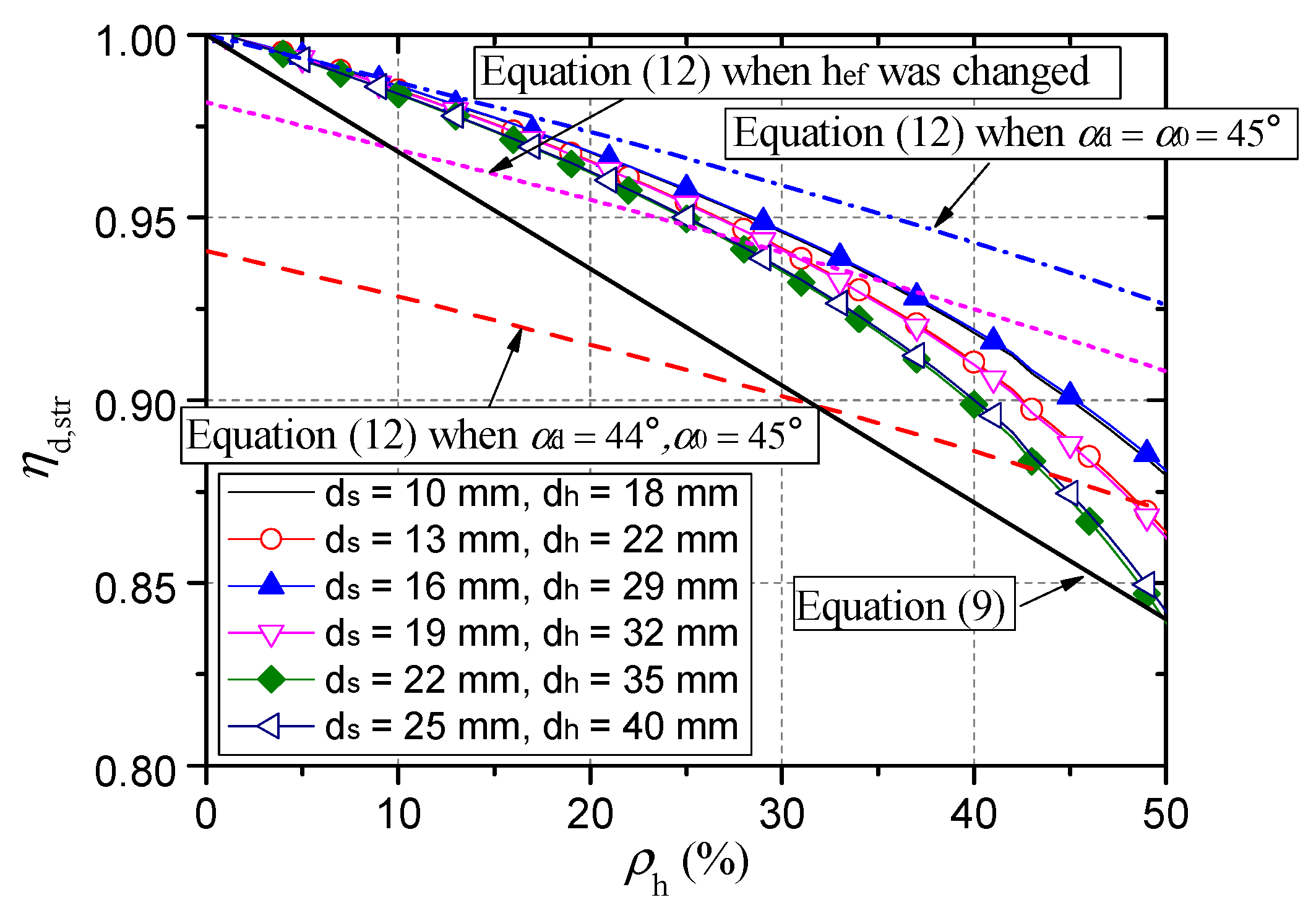
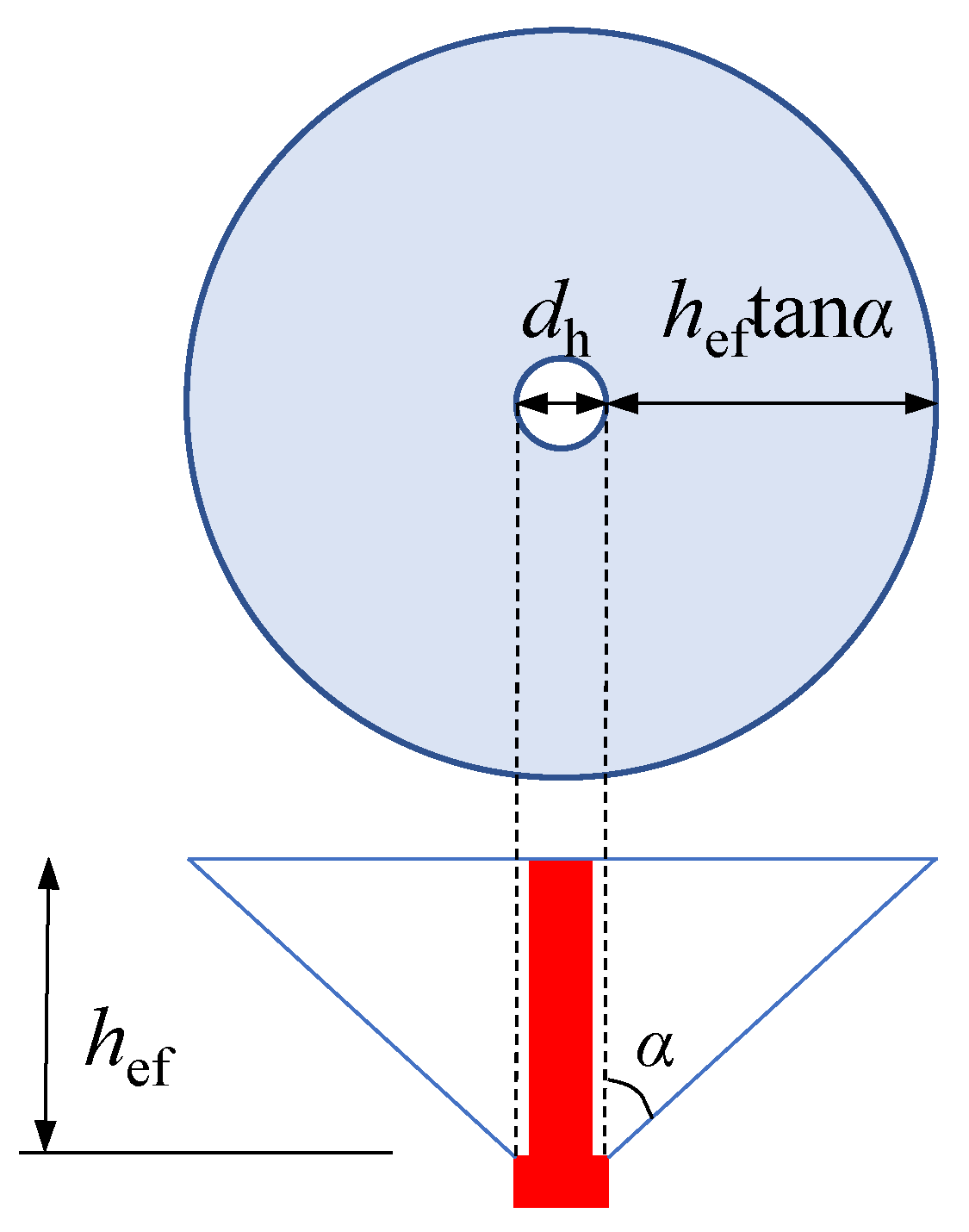
- An equation of capacity reduction factor with the bearing area and damage degree as parameters (Equation (8)) was proposed and verified by numerical results. Furthermore, a concise formula, Equation (9), was suggested to calculate the reduction factor of different types of headed stud shear connectors easily and on the safe side. With reference to the Concrete Capacity method, the decrease in head diameter, concrete cone angle, and embedment depth was found to be the reason for the reduction in tensile capacity of connectors with head-sectional damage.
- (4)
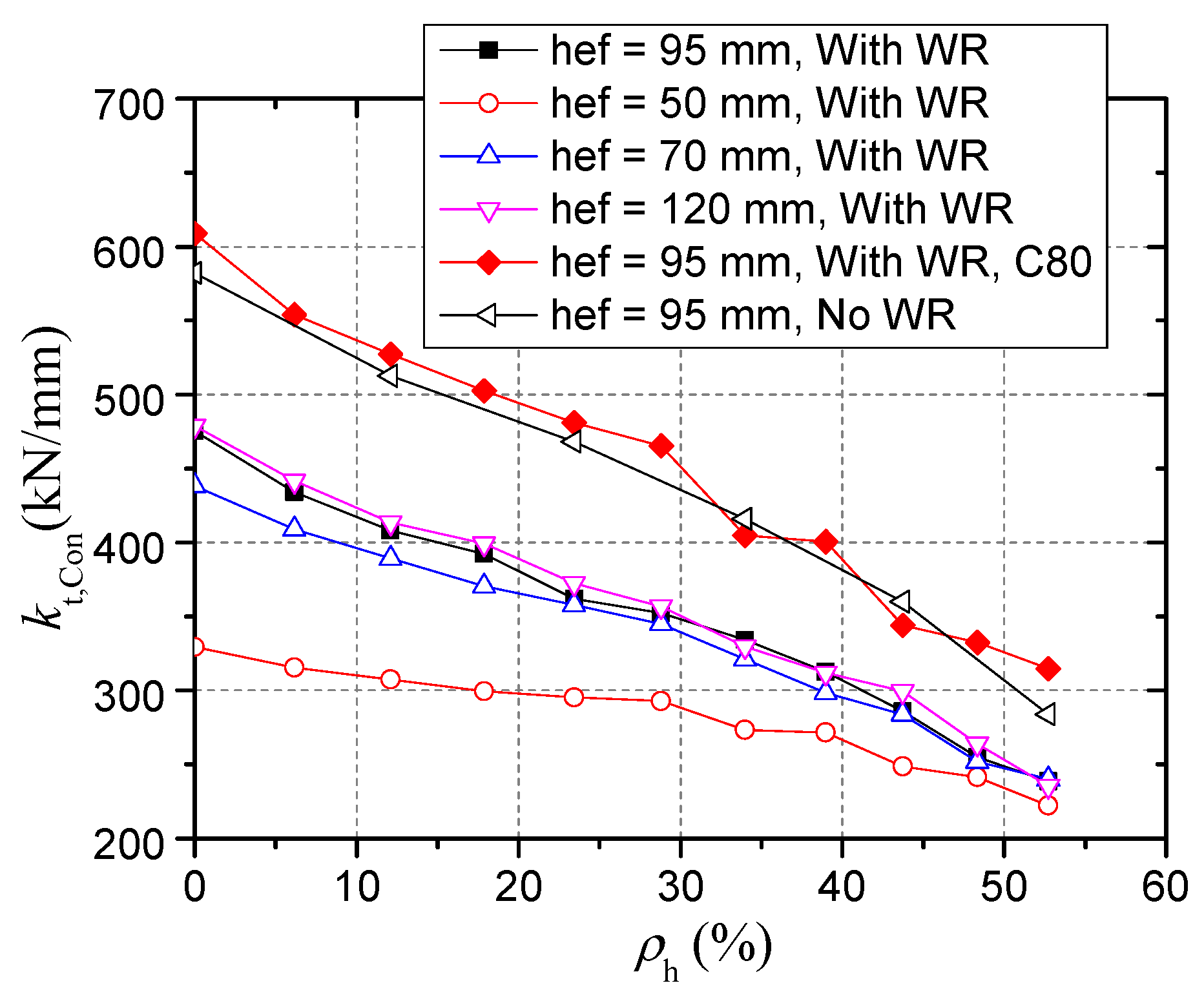
- Tensile stiffness was observed to decrease with the decrease in the stud’s head size, which has not been considered by Yang et al. [26]. A linear relationship between the stiffness reduction factor and head-sectional damage degree was found, and a formula for the stiffness reduction factor (Equation (16)) was obtained by linear regression on the numerical results. The numerical results also showed that the stiffness of a connector at a high embedment depth or in high strength concrete was more sensitive to head-sectional damage. Compared with the capacity reduction factor, the stiffness reduction factor decreased faster with an increase in the damage degree.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sharma, A.; Hofmann, J. Preface. In Proceedings of the 3rd International Symposium on Connections between Steel and Concrete, Stuttgart, Germany, 27–29 September 2017; Institute of Construction Materials, University of Stuttgart: Stuttgart, Germany, 2017. [Google Scholar]
- De Normalisation, C.E. Eurocode 4: Design of Composite Steel and Concrete Structures, Part 1-1: General Rules and Rules for Buildings; CEN: Brussels, Belgium, 2010. [Google Scholar]
- Qi, J.; Wang, J.; Li, M.; Chen, L. Shear capacity of stud shear connectors with initial damage: Experiment, FEM model and theoretical formulation. Steel Compos. Struct. 2017, 25, 79–92. [Google Scholar]
- Oehlers, D.; Bradford, M. Elementary Behaviour of Composite Steel and Concrete Structural Members; Butterworth-Heinemann: Oxford, UK, 1999. [Google Scholar]
- Hanswille, G.; Porsch, M.; Ustundag, C. Resistance of headed studs subjected to fatigue loading: Part I: Experimental study. J. Constr. Steel Res. 2007, 63, 475–484. [Google Scholar] [CrossRef]
- Hanswille, G.; Porsch, M.; Ustundag, C. Resistance of headed studs subjected to fatigue loading: Part II: Analytical study. J. Constr. Steel Res. 2007, 63, 485–493. [Google Scholar] [CrossRef]
- Rong, X.L.; Huang, Q.; Ren, Y. Experimental study on static and fatigue behaviors of stud connectors for composite beams after corrosion. China Civil Eng. J. 2013, 46, 10–18. [Google Scholar]
- Chen, J.; Zhao, Y.X.; Wu, L.; Jin, W.L. Experimental investigation and design of corroded stud shear connectors. Adv. Struct. Eng. 2016, 19, 218–226. [Google Scholar] [CrossRef]
- Wang, W.L.; Chen, J.; Jin, W.L. Experimental investigation of corroded stud shear connectors subjected to fatigue loading. J. Mater. Civil Eng. 2017, 29, 04016175. [Google Scholar] [CrossRef]
- Xue, W.; Chen, J.; Zhu, J.H. Behaviour of corroded single stud shear connectors. Materials 2017, 10, 276. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, Q.; Wang, Y.; Xu, J.; Xing, Y. Static behavior of stud shear connectors in elastic concrete-steel composite beams. J. Constr. Steel Res. 2015, 113, 115–126. [Google Scholar] [CrossRef]
- Xu, X.; He, D.; Zeng, S.; He, W.; Tan, H.; Yu, Z. Effect of concrete cracks on the corrosion of headed studs in steel and concrete composite structures. Constr. Build. Mater. 2021, 293, 123440. [Google Scholar] [CrossRef]
- Nilforoush, R.; Nilsson, M.; Elfgren, L.; Ožbolt, J.; Hofmann, J.; Eligehausen, R. Tensile capacity of anchor bolts in uncracked concrete: Influence of member thickness and anchor’s head size. ACI Struct. J. 2017, 114, 1519–1530. [Google Scholar] [CrossRef]
- Nilforoush, R.; Nilsson, M.; Elfgren, L. Experimental evaluation of influence of member thickness, anchor-head size, and orthogonal surface reinforcement on the tensile capacity of headed anchors in uncracked concrete. J. Struct. Eng. 2018, 144, 04018012. [Google Scholar] [CrossRef]
- GB/T 0433-2002; Cheese Head Suds for Arc Stud Welding. China Standardization Press: Beijing, China, 2003. (In Chinese)
- GB/T 6478-2001; Steels for Cold Heading and Cold Extruding. China Standardization Press: Beijing, China, 2001. (In Chinese)
- ABAQUS/Explicit User’s Manual, Version 6.10; Hibbitt, Karlsson & Sorensen, Inc.: Pawtucket, RI, USA, 2010.
- Xu, X.; Zhou, X.; Liu, Y. Fatigue life prediction of rubber-sleeved stud shear connectors under shear load based on finite element simulation. Eng. Struct. 2021, 227, 111449. [Google Scholar] [CrossRef]
- Krätzig, W.B.; Pölling, R. An elasto-plastic damage model for reinforced concrete with minimum number of material parameters. Comput. Struct. 2004, 82, 1201–1215. [Google Scholar] [CrossRef]
- Birtel, V.; Mark, P. Parameterised finite element modelling of RC beam shear failure. In Proceedings of the 19th Annual International ABAQUS Users’ Conference, Boston, MA, USA, 23–25 May 2006; pp. 95–108. [Google Scholar]
- Reinhardt, H.; Cornelissen, H.; Hordijk, D. Tensile tests and failure analysis of concrete. J. Struct. Eng. 1986, 112, 2462–2477. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, Z.; Hu, Y.; Wang, X. Bearing strength of crumb rubber concrete under partial area loading. Materials 2020, 13, 2446. [Google Scholar] [CrossRef] [PubMed]
- Han, J.; Wang, K. Influence of bleeding on properties and microstructure of fresh and hydrated Portland cement paste. Constr. Build. Mater. 2016, 115, 240–246. [Google Scholar] [CrossRef]
- Eligehausen, R.; Sawade, G. A fracture mechanics based description of the pull-out behaviour of headed studs embedded in concrete. In Fracture Mechanics of Concrete Structures, from Theory to Applications; Elfgren, L., Ed.; Chapman and Hall: London, UK; New York, NY, USA, 1989; pp. 281–298. [Google Scholar]
- Fuchs, W.; Eligehausen, R.; Breen, J.E. Concrete capacity design (CCD) approach for fastening to concrete. ACI Struct. J. 1995, 92, 73–94. [Google Scholar]
- Yang, F.; Liu, Y.; Liang, C. Analytical study on the tensile stiffness of headed stud connectors. Adv. Struct. Eng. 2019, 22, 1149–1160. [Google Scholar] [CrossRef]







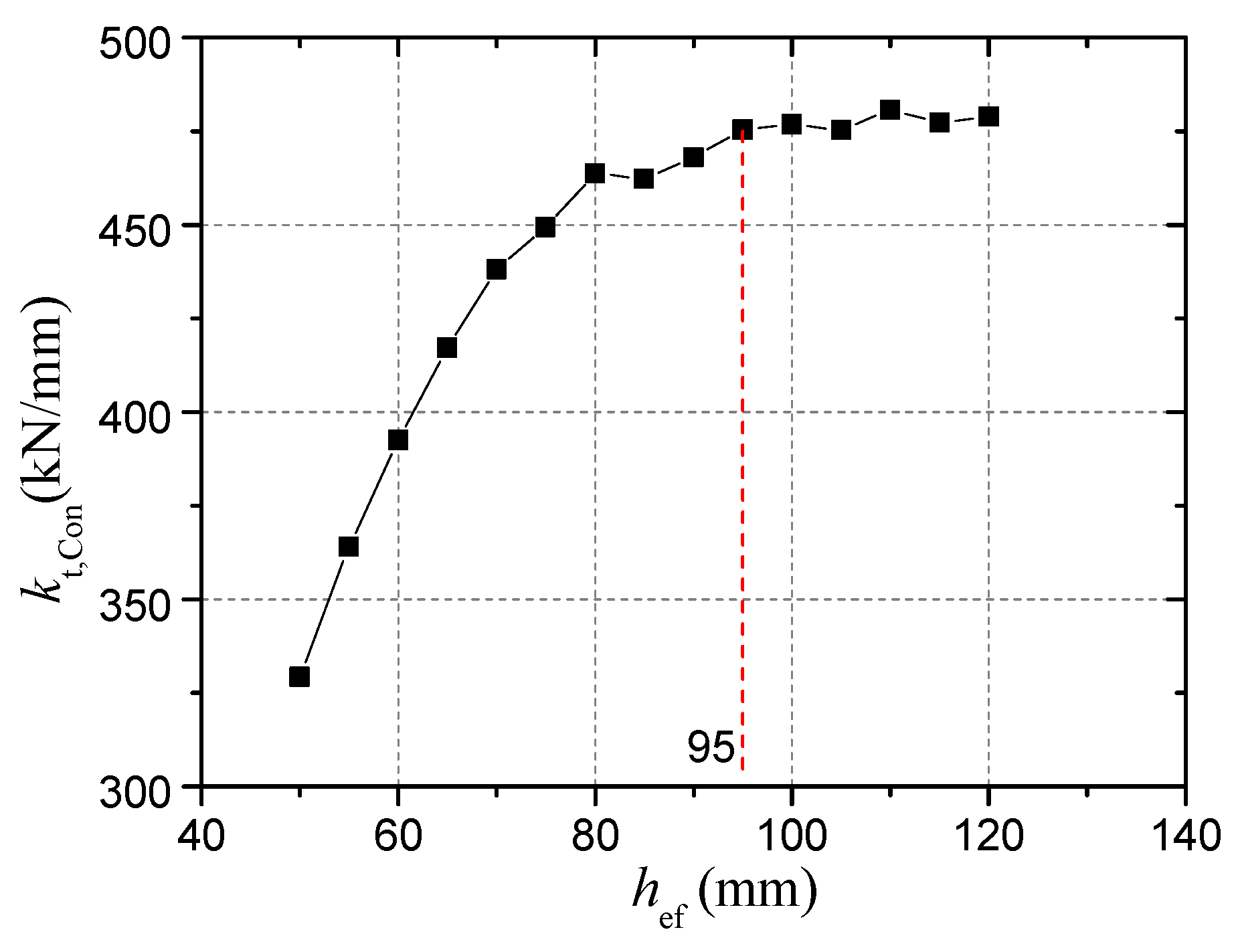
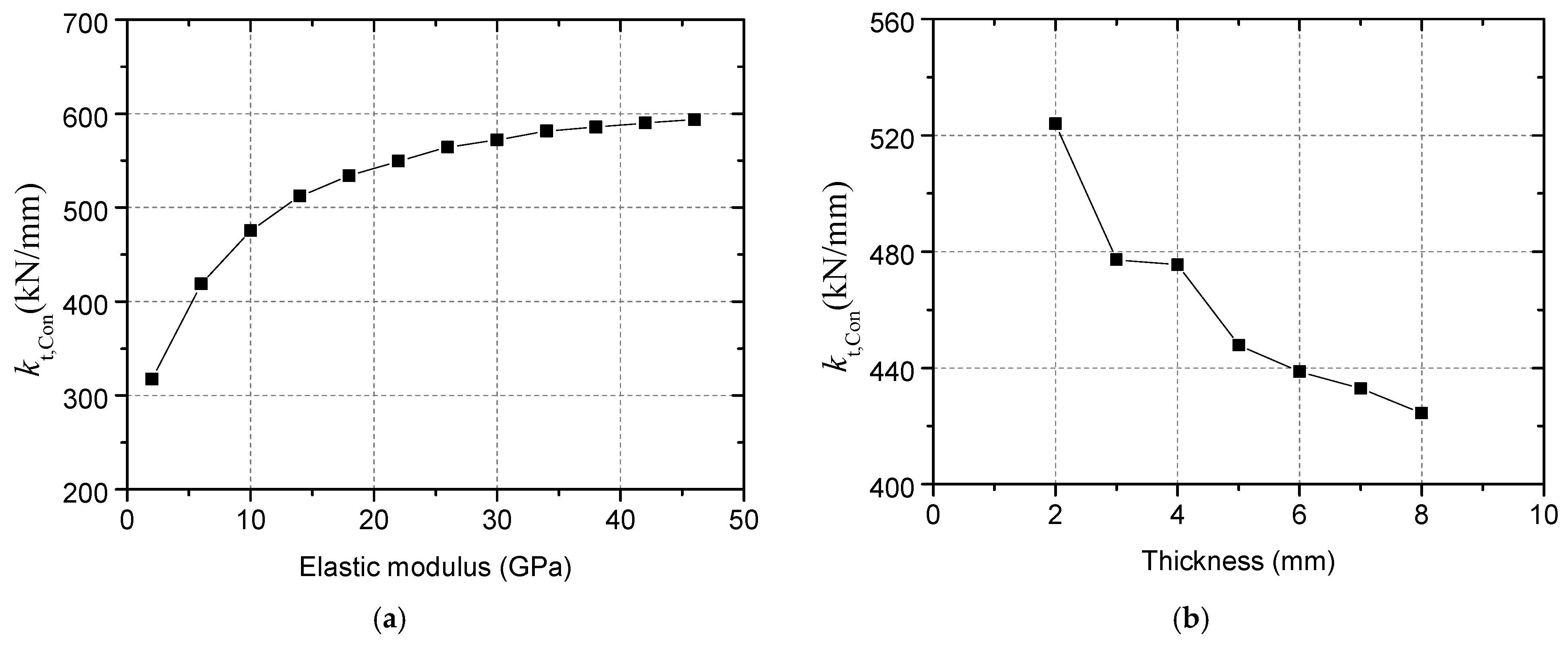

| Labels | ds (mm) | dh (mm) | hef (mm) | Ah,d (mm2) | ρh | Concrete Slab Geometry (mm × mm × mm) |
|---|---|---|---|---|---|---|
| NC19-2 | 19 | 32 | 95 | 783.66 | 2.6% | 550 × 550 × 250 |
| NC19-38 | 19 | 32 | 95 | 498.76 | 38.0% | 550 × 550 × 250 |
| Labels | Nu (kN) | δu (mm) | Failure Mode |
|---|---|---|---|
| NC19-2 | 124.7 | 1.99 | Concrete cone failure |
| NC19-38 | 119.2 | 1.70 | Pull-out failure |
| Poisson’s Ratio | Dilation Angle | Eccentricity Factor | Biaxial-to-Uniaxial Strength Ratio | Shape Factor | Viscosity Parameter |
|---|---|---|---|---|---|
| 0.16 | 32 | 0.1 | 1.16 | 0.667 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Zeng, S.; He, W.; Hou, Z.; He, D.; Yang, T. Numerical Study on the Tensile Performance of Headed Stud Shear Connectors with Head-Sectional Damage. Materials 2022, 15, 2802. https://doi.org/10.3390/ma15082802
Xu X, Zeng S, He W, Hou Z, He D, Yang T. Numerical Study on the Tensile Performance of Headed Stud Shear Connectors with Head-Sectional Damage. Materials. 2022; 15(8):2802. https://doi.org/10.3390/ma15082802
Chicago/Turabian StyleXu, Xiaoqing, Shanwen Zeng, Wei He, Zhujian Hou, Dongyang He, and Tao Yang. 2022. "Numerical Study on the Tensile Performance of Headed Stud Shear Connectors with Head-Sectional Damage" Materials 15, no. 8: 2802. https://doi.org/10.3390/ma15082802
APA StyleXu, X., Zeng, S., He, W., Hou, Z., He, D., & Yang, T. (2022). Numerical Study on the Tensile Performance of Headed Stud Shear Connectors with Head-Sectional Damage. Materials, 15(8), 2802. https://doi.org/10.3390/ma15082802








