The Effects of the Mechanical Properties of Vascular Grafts and an Anisotropic Hyperelastic Aortic Model on Local Hemodynamics during Modified Blalock–Taussig Shunt Operation, Assessed Using FSI Simulation
Abstract
:1. Introduction
2. Materials and Methods
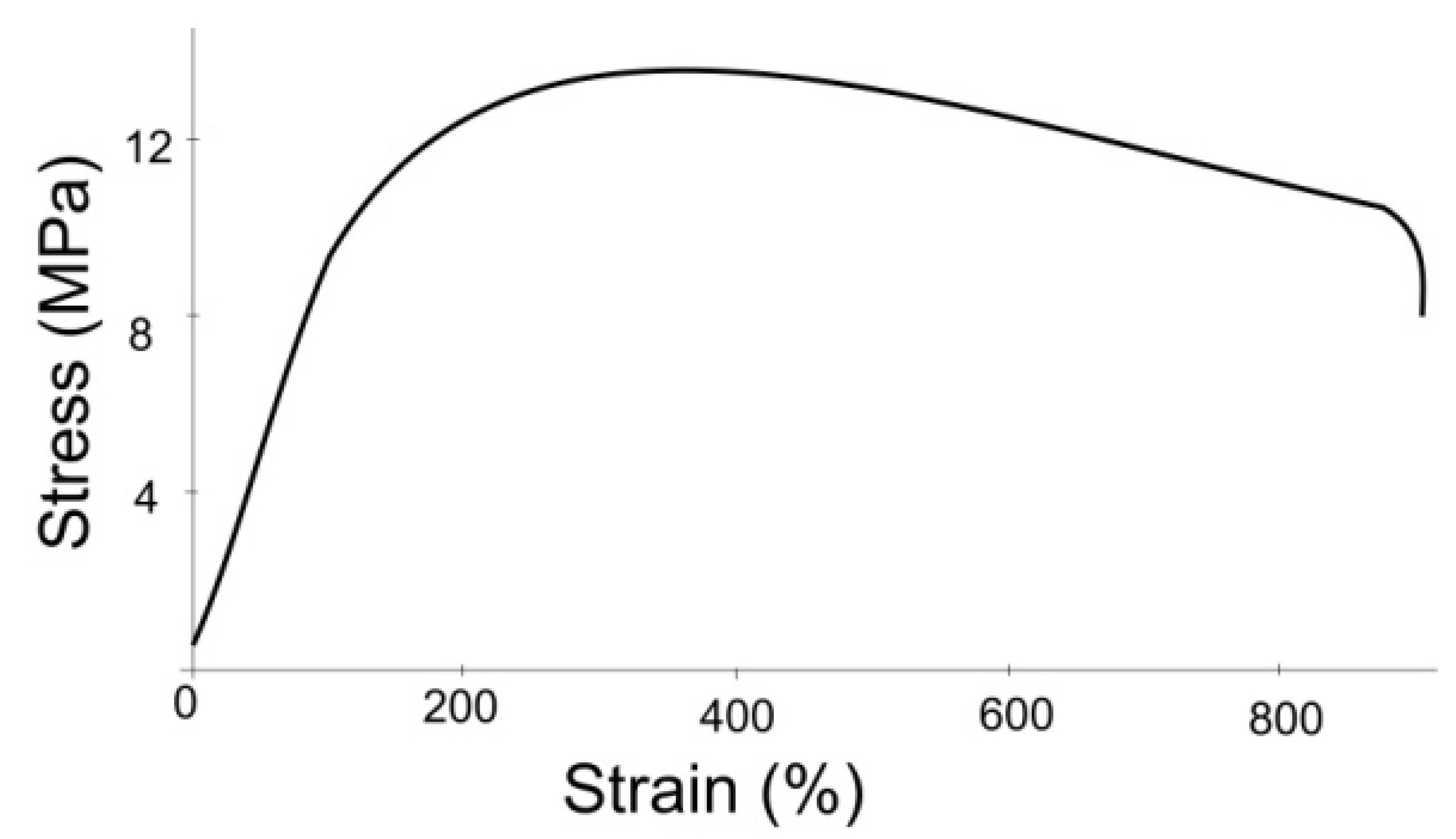
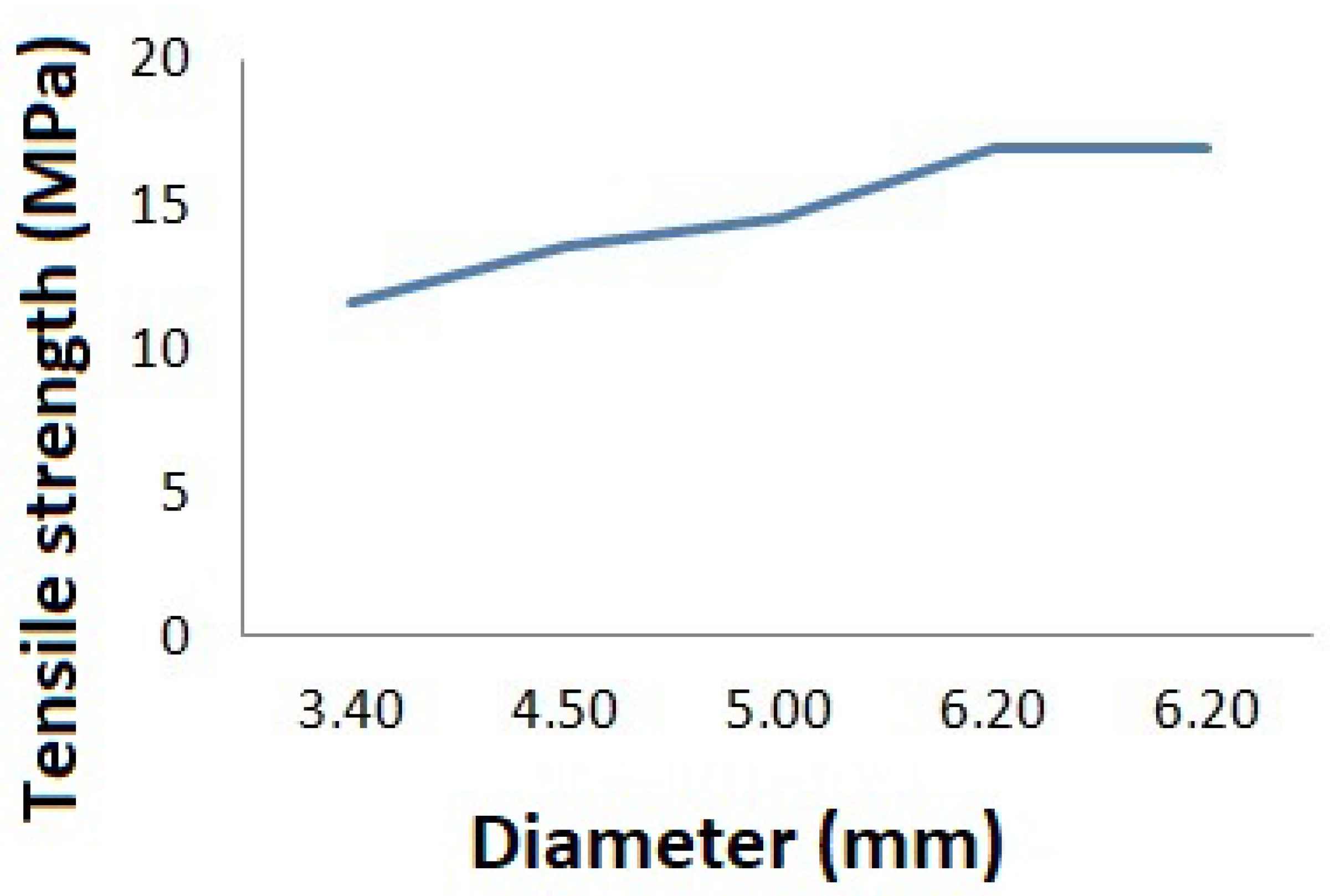
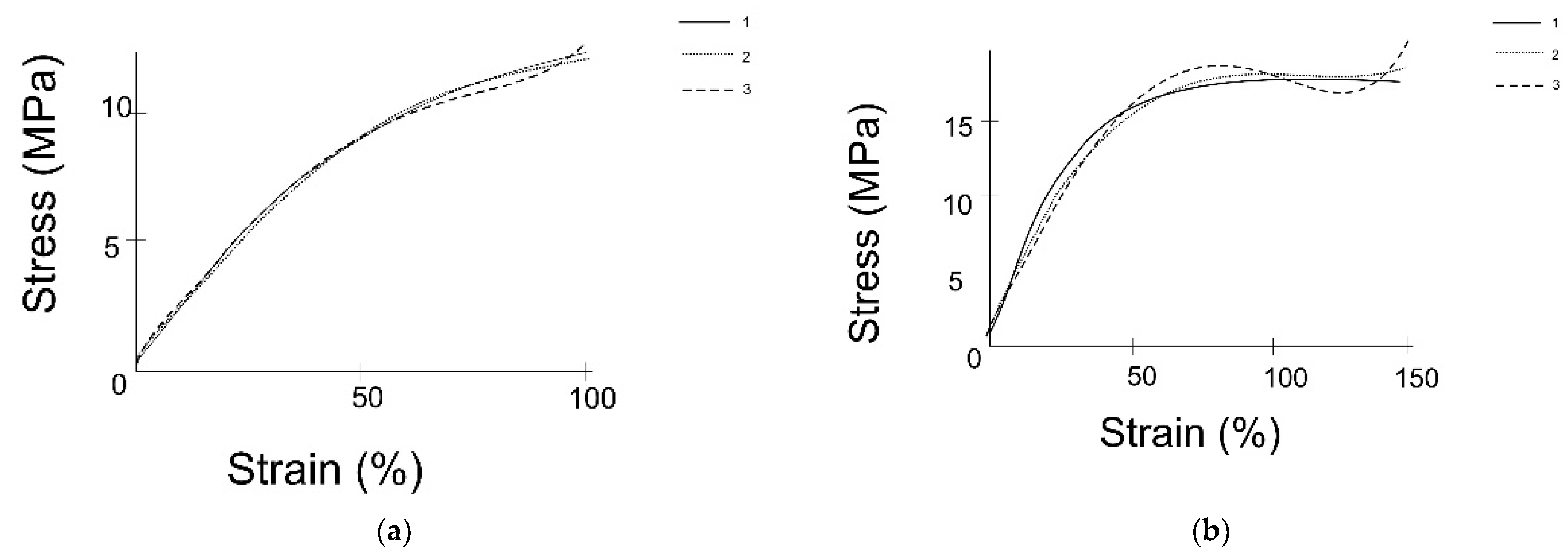
2.1. Experimental Study on Mechanical Properties of Grafts
2.2. Mechanical Properties of Aorta
2.2.1. Ogden Model for Description of Isotropic Hyperelastic Behavior of Aorta
2.2.2. Holzapfel–Gasser–Ogden Model for Description of Anisotropic Hyperelastic Behavior of Aorta
2.3. FSI Simulations of Blood Flow in the Aorta–Pulmonary Artery–Shunt System
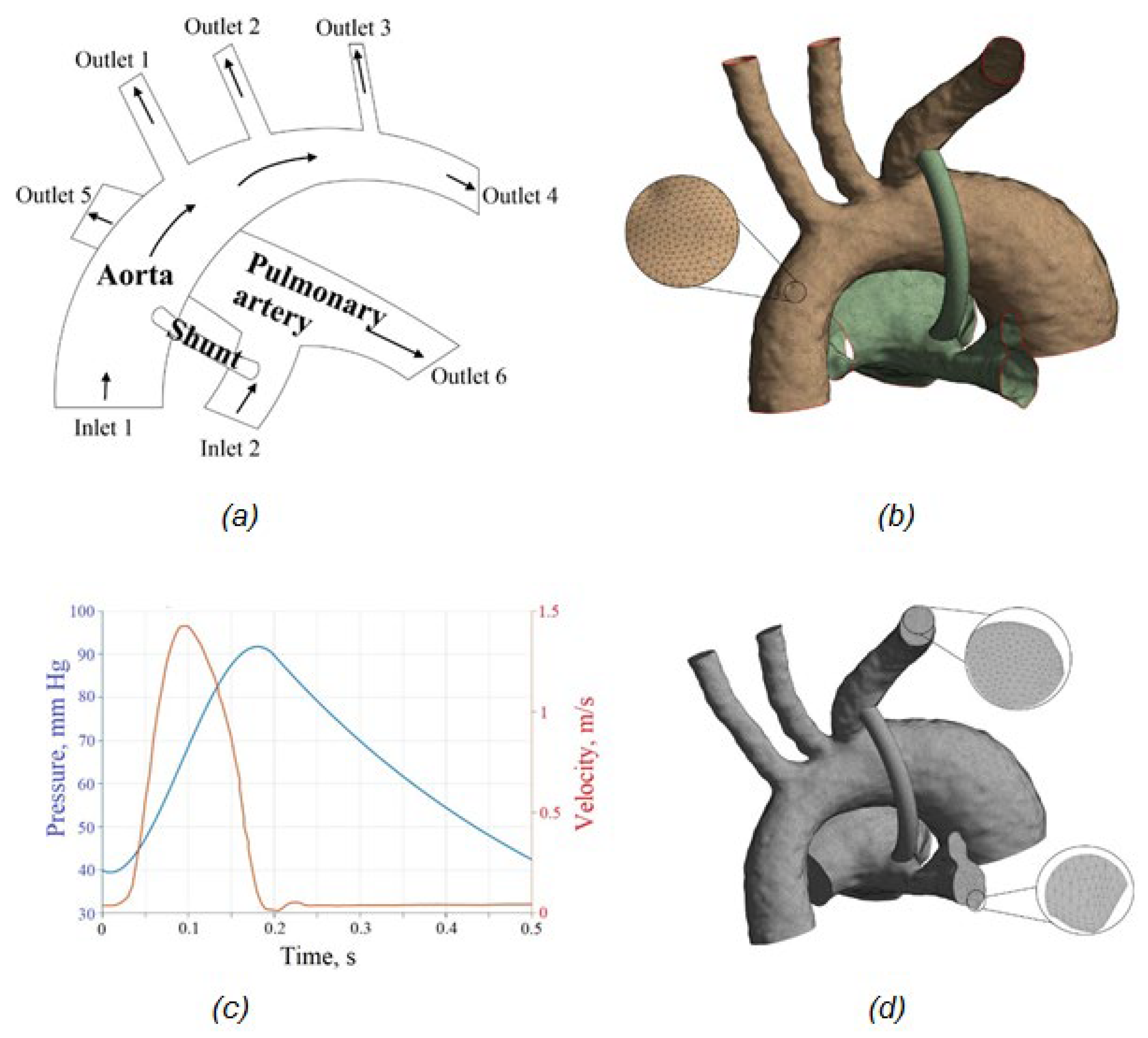
2.3.1. Problem Formulation
2.3.2. Mathematical Problem Statement
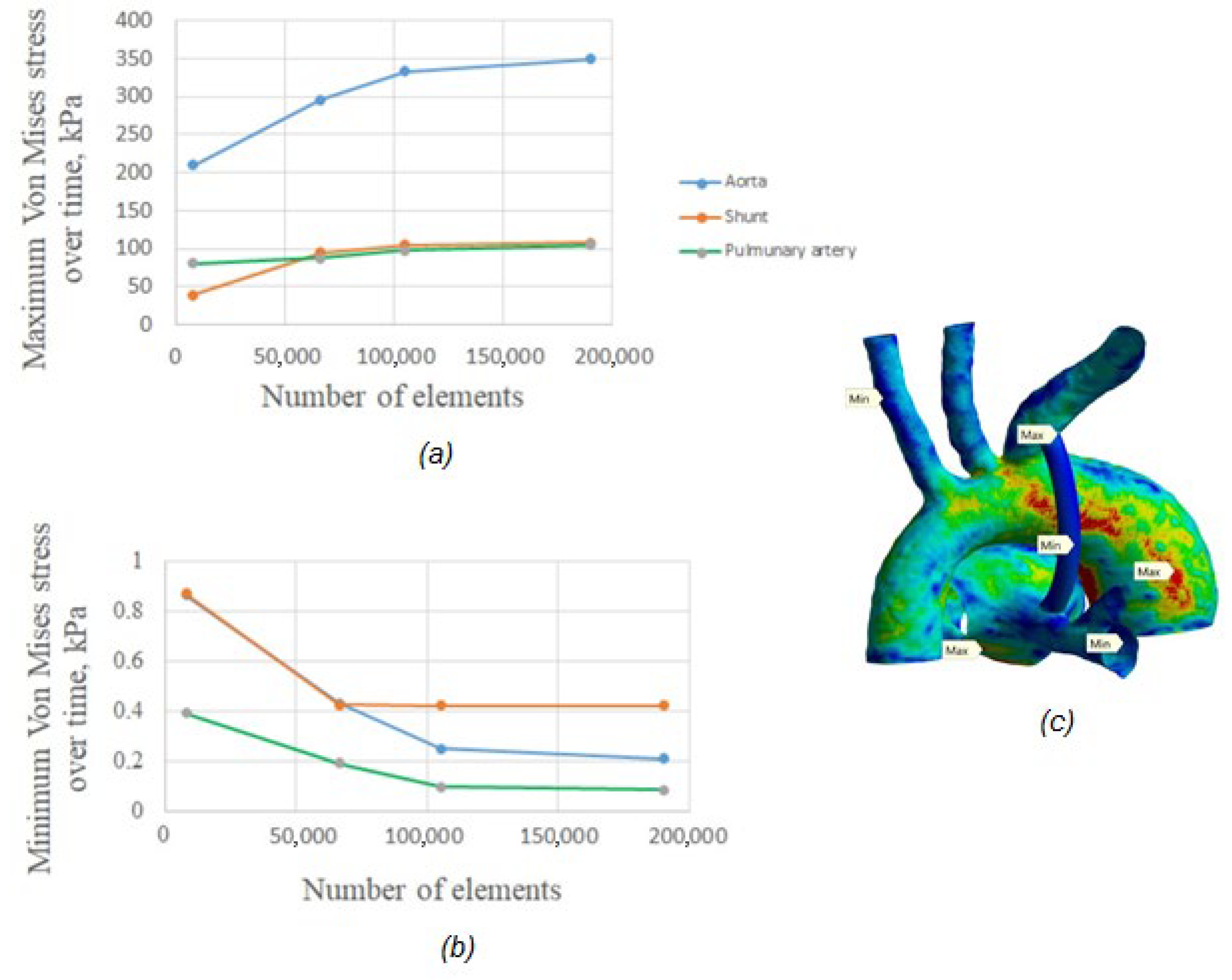
2.3.3. Mesh and Convergence
3. Results
3.1. Results of the Experimental Study
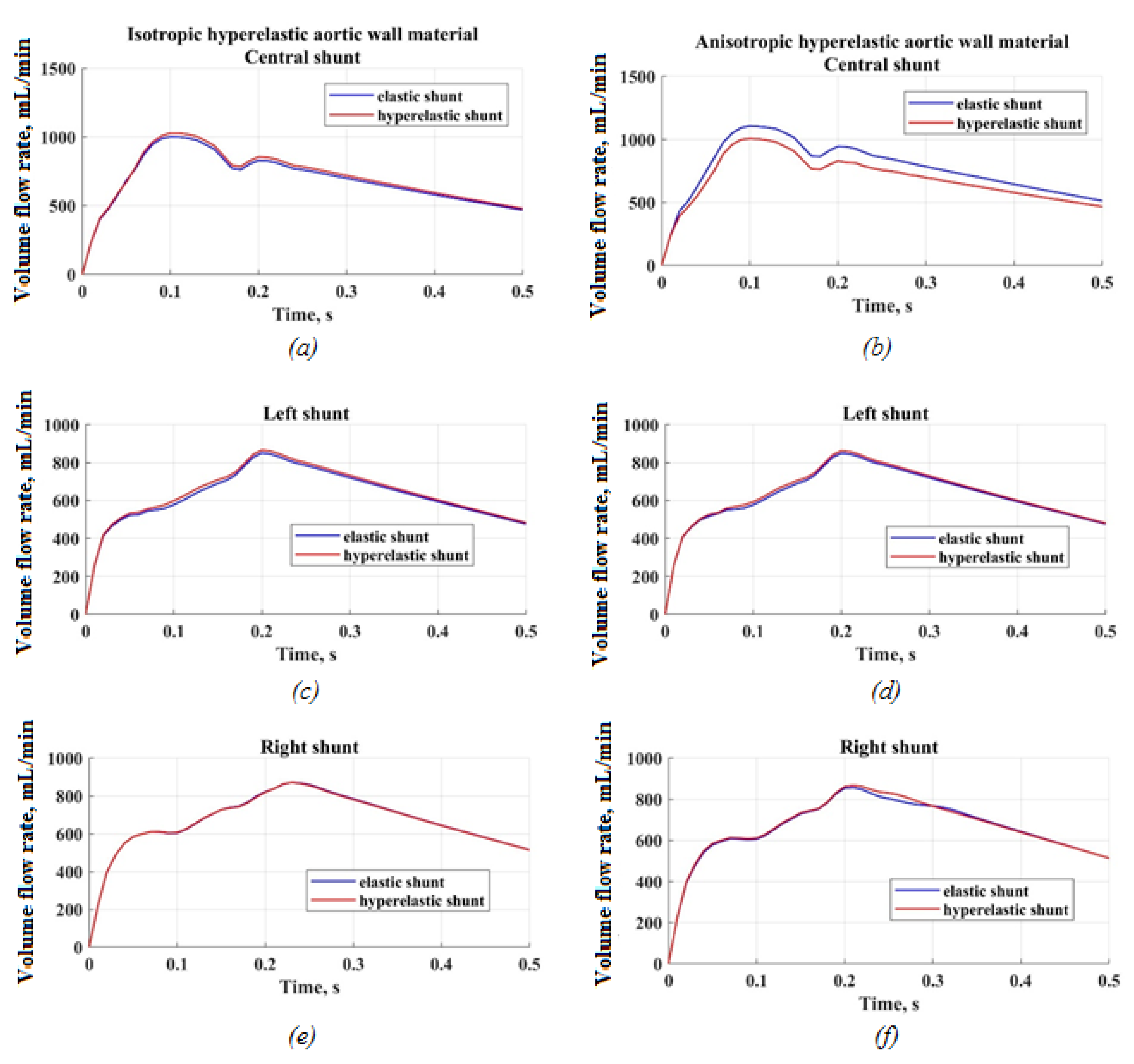
3.2. Results of FSI Simulation of the Blood Flow
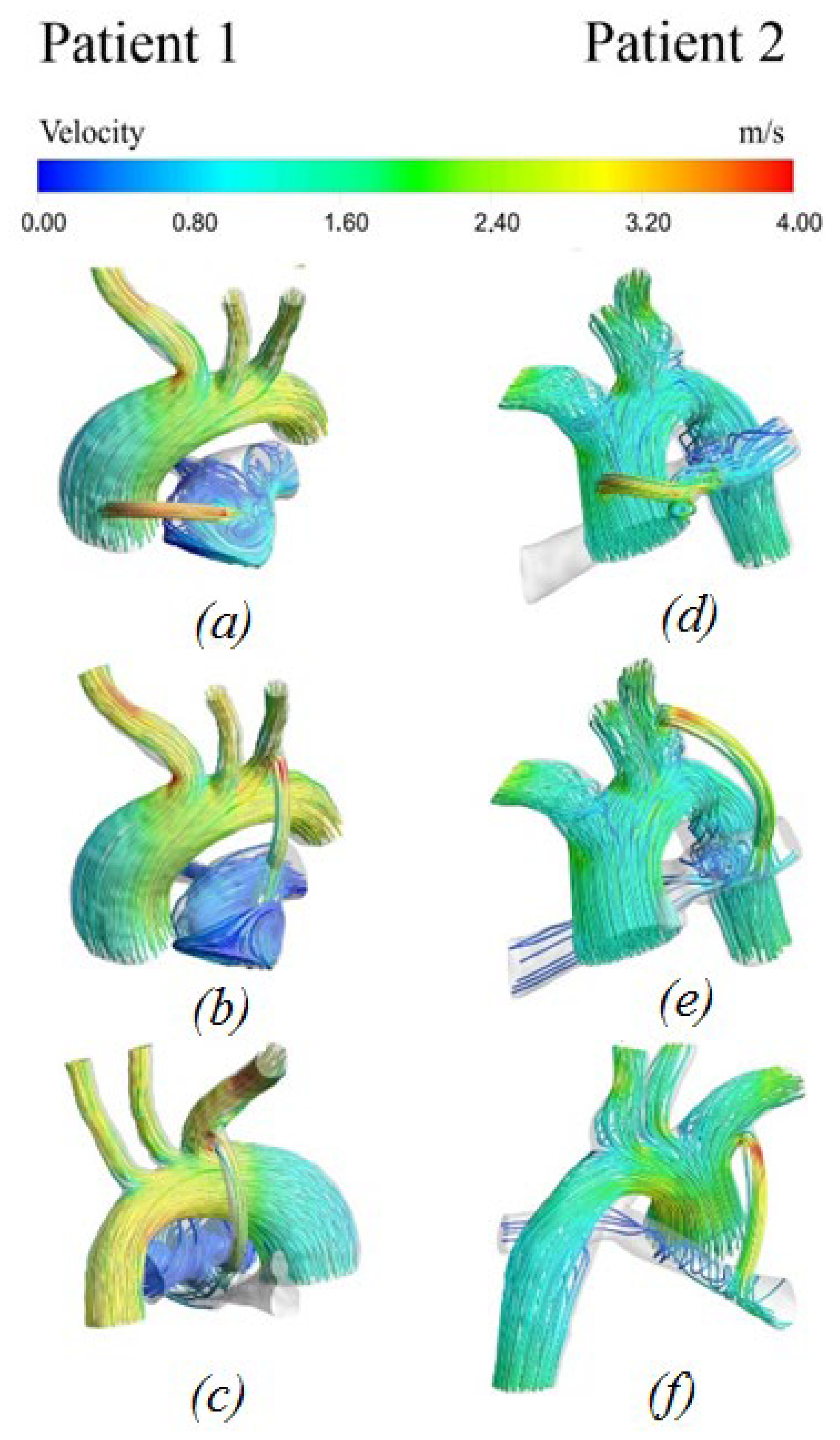
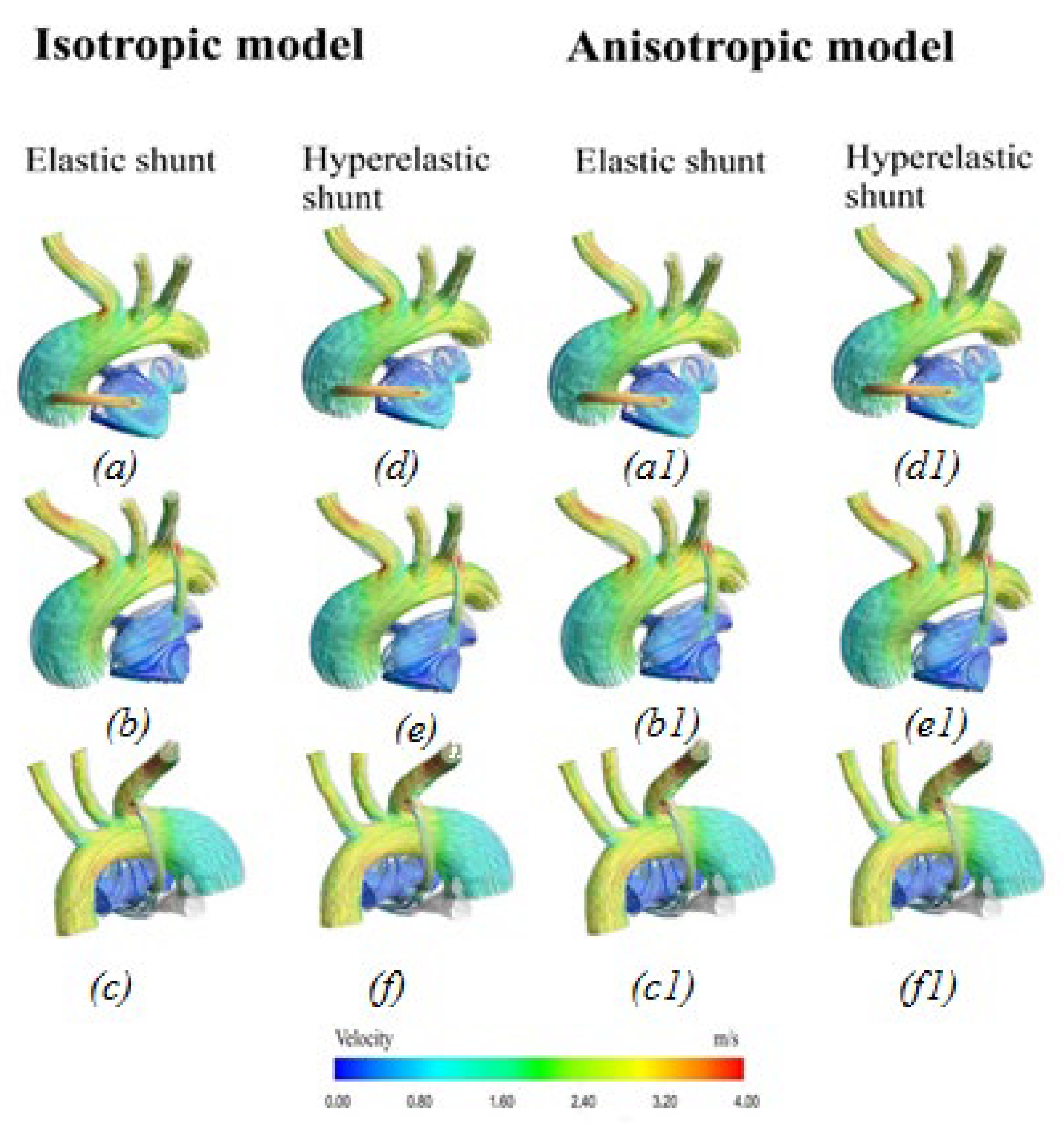
3.2.1. Velocity Distribution
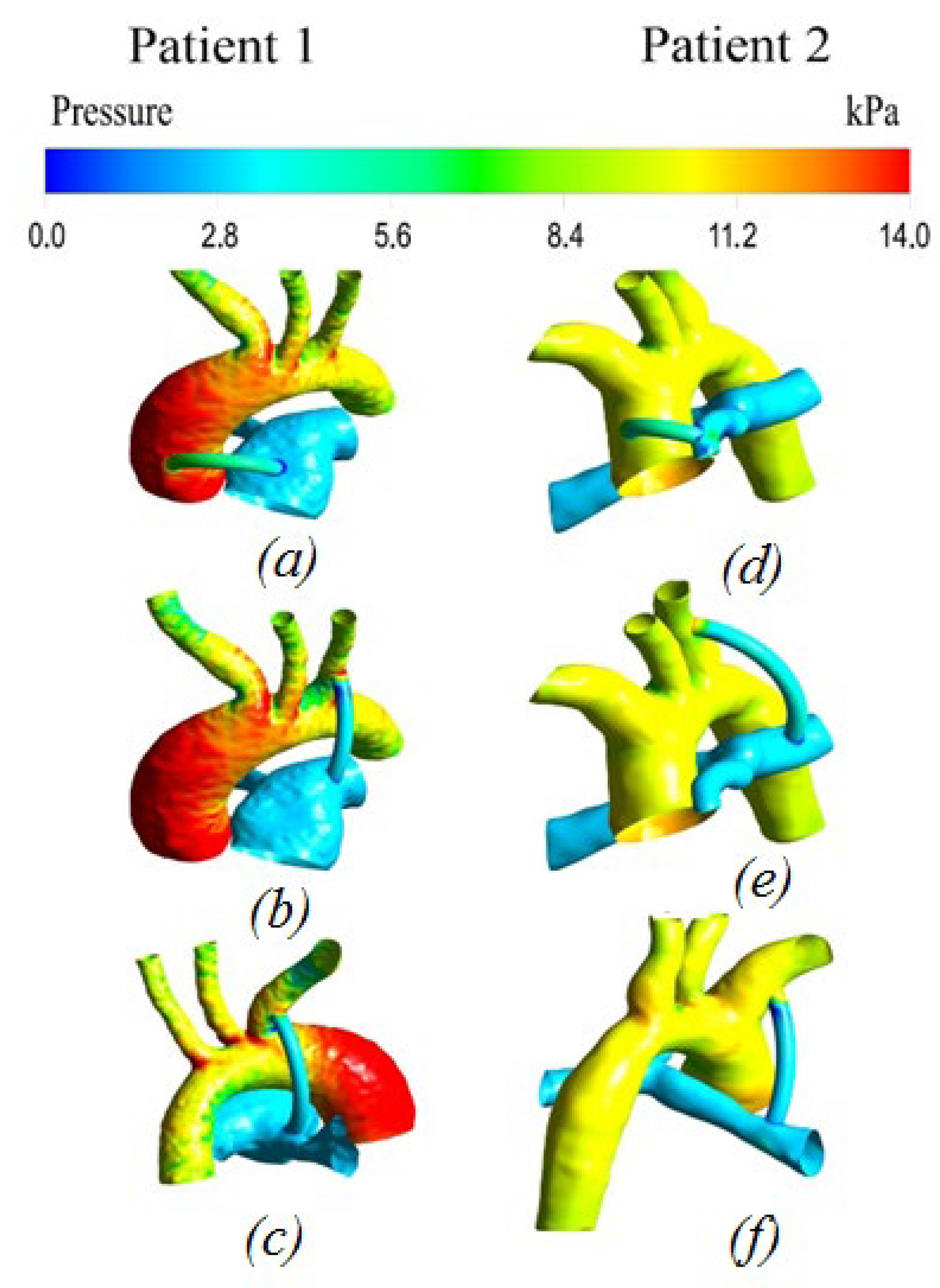
3.2.2. Pressure distribution
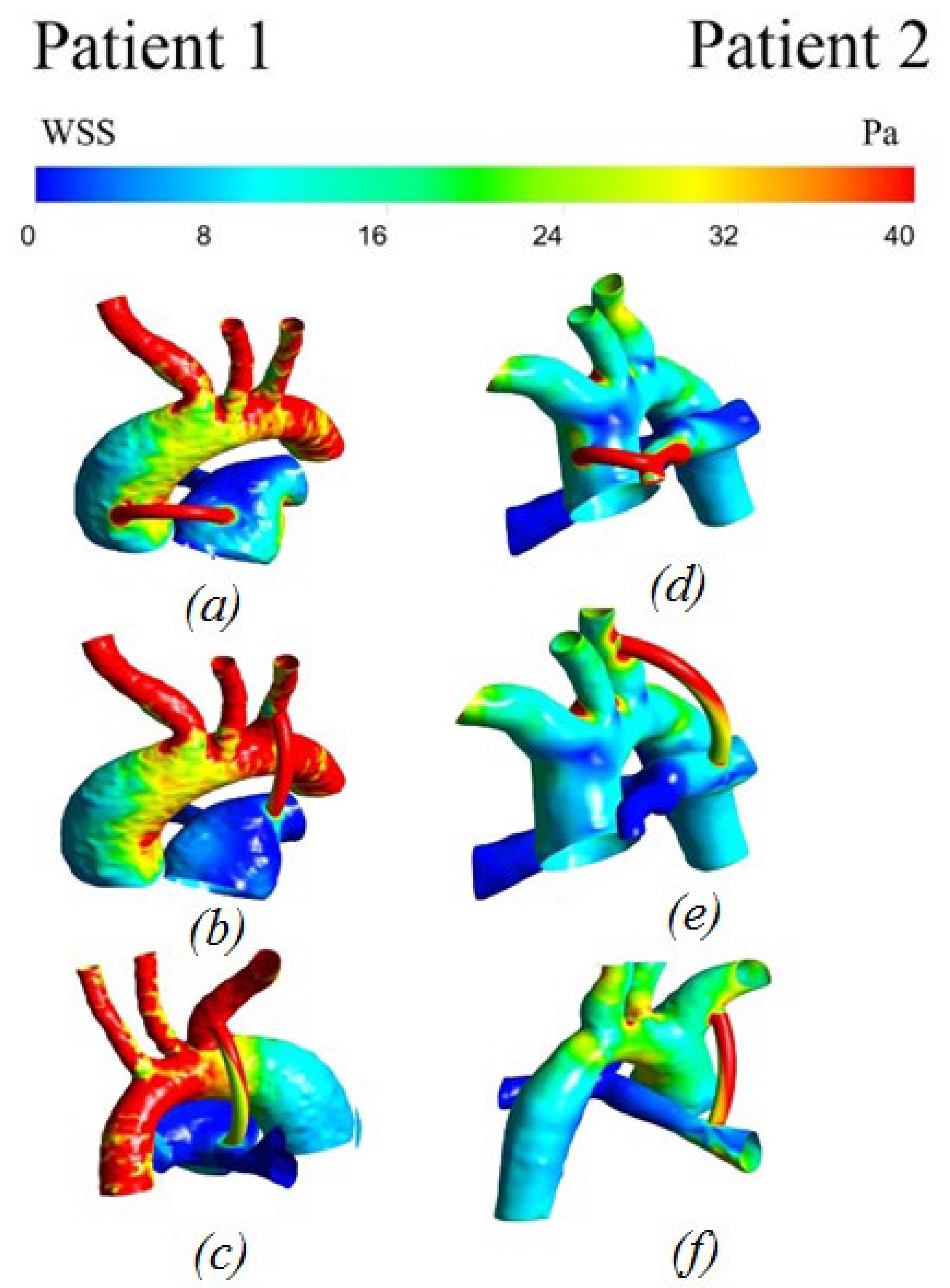
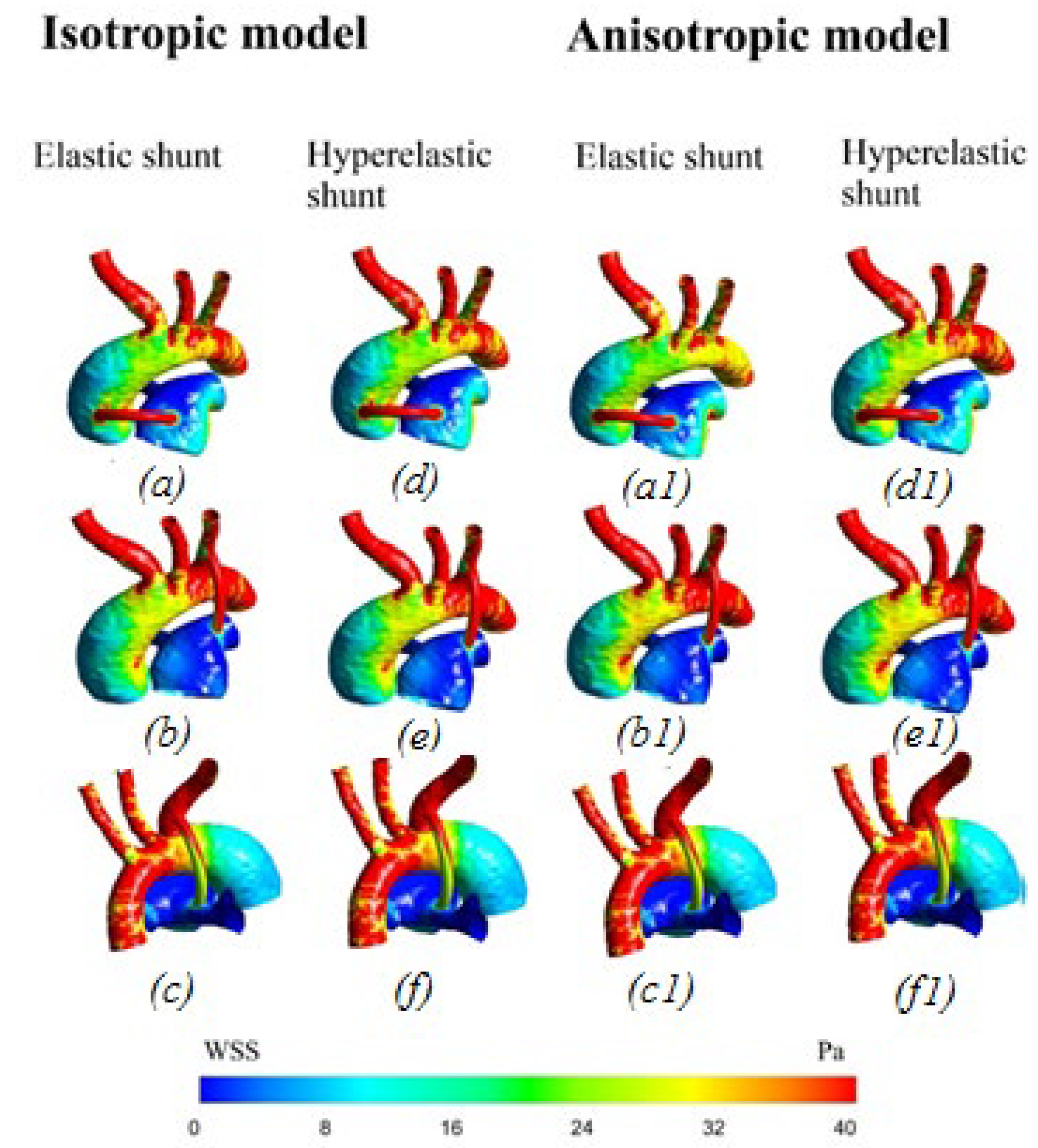
3.2.3. Wall Shear Stress
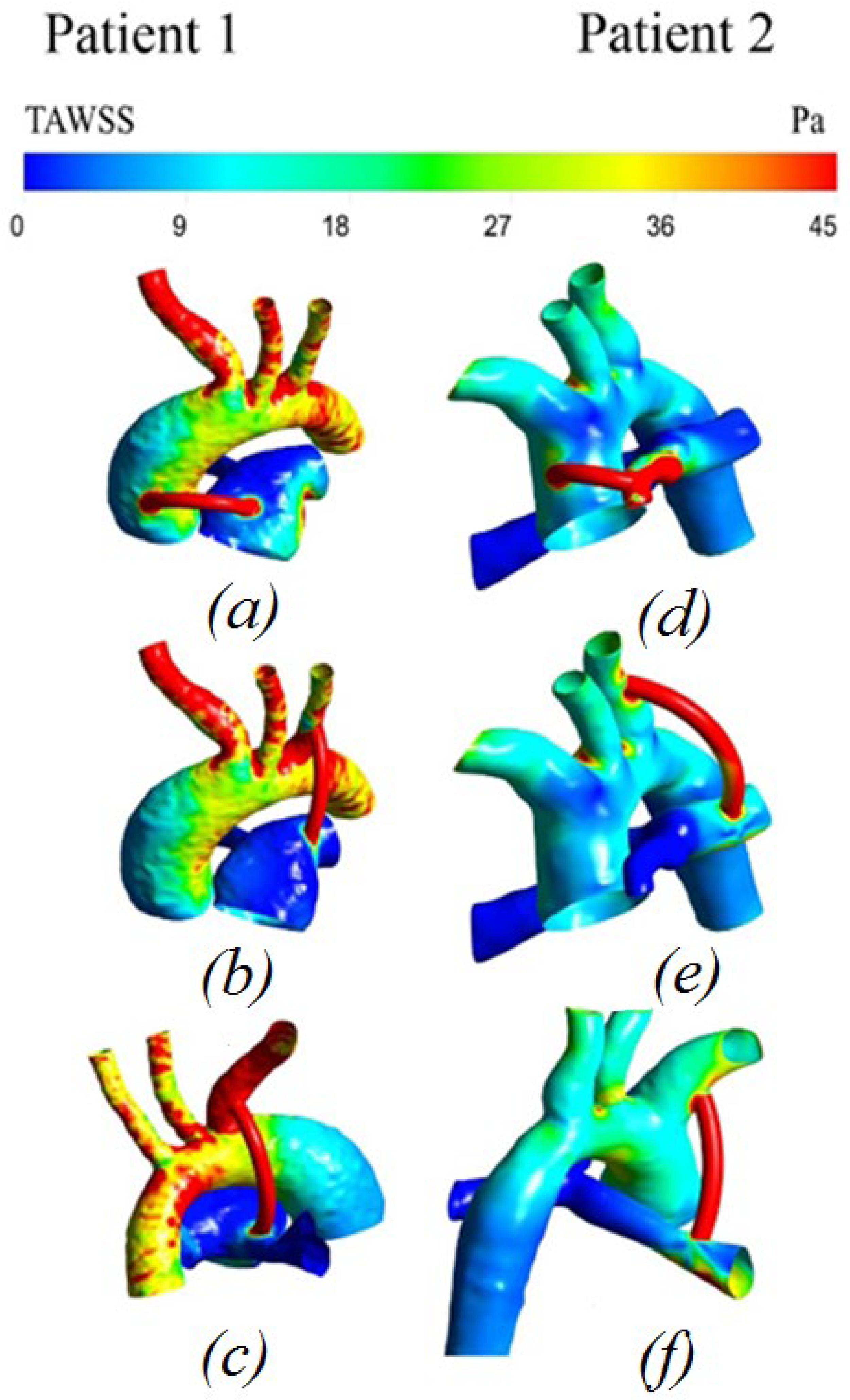
3.2.4. Distribution of Time-Averaged Shear Stress
3.2.5. Displacement Distribution
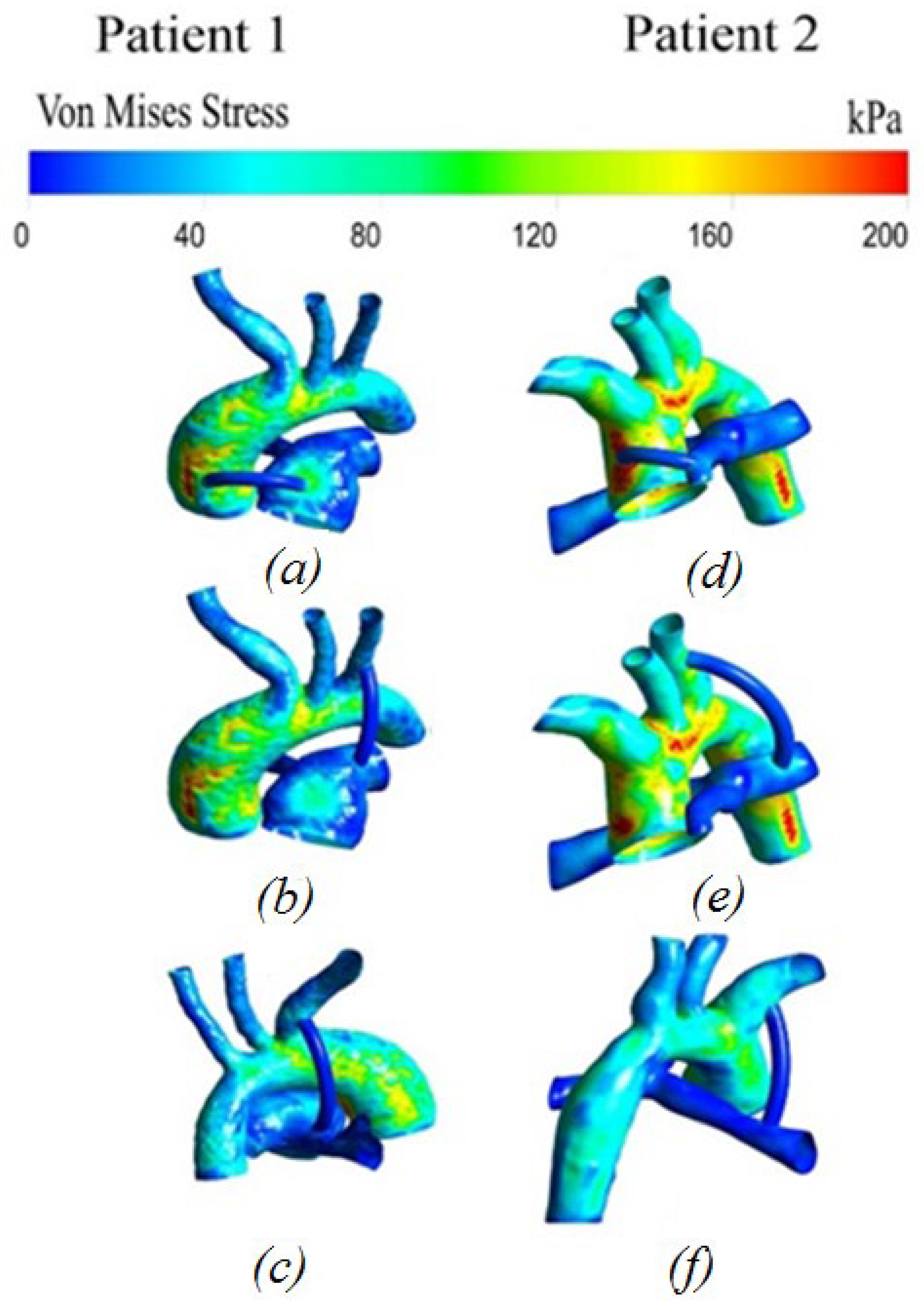
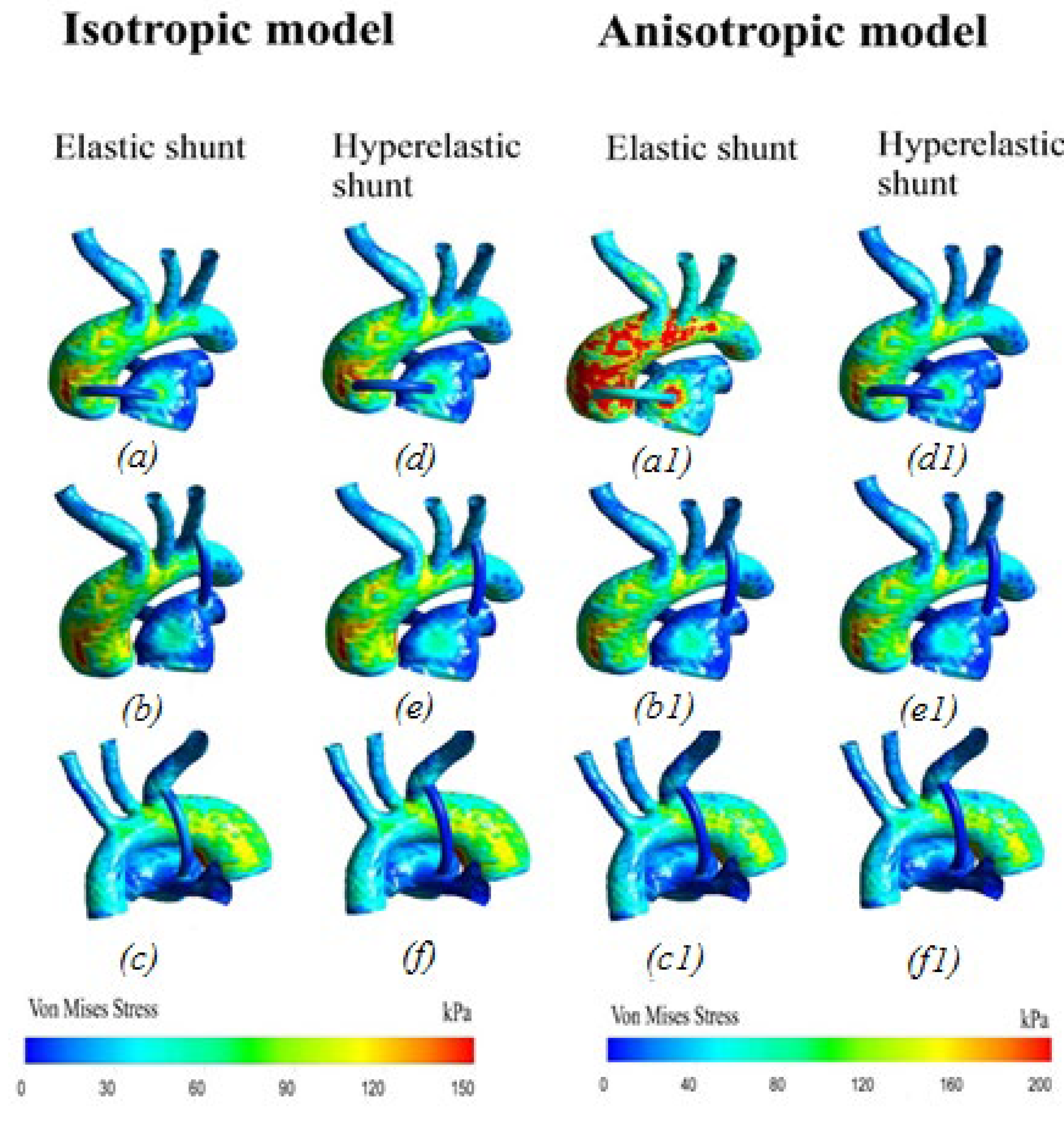
3.2.6. Von Mises Stress Distribution
4. Discussion
4.1. Difference between Isotropic and Anisotropic Models
4.2. Concluding Remarks
4.3. Limitations
4.4. Possible Future Clinical Application
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alsoufi, B.; Gillespie, S.; Kogon, B.; Schlosser, B.; Sachdeva, R.; Kim, D.; Clabby, M.; Kanter, K. Results of palliation with an initial modified blalock-taussig shunt in neonates with single ventricle anomalies associated with restrictive pulmonary blood flow. Ann. Thorac. Surg. 2015, 99, 1639–1647. [Google Scholar] [CrossRef] [PubMed]
- Sant’Anna, J.R.M.; Pereira, D.C.; Kalil, R.A.K.; Prates, P.R.; Horowitz, E.; Sant’Anna, R.T.; Prates, P.R.L.; Nesralla, I.A. Computer dynamics to evaluate blood flow through the modified Blalock-Taussig shunt. Rev. Bras. Cir. Cardiovasc. 2003, 18, 253–260. [Google Scholar] [CrossRef] [Green Version]
- Laganà, K.; Balossino, R.; Migliavacca, F.; Pennati, G.; Bove, E.L.; De Leval, M.R.; Dubini, G. Multiscale modeling of the cardiovascular system: Application to the study of pulmonary and coronary perfusions in the univentricular circulation. J. Biomech. 2005, 38, 1129–1141. [Google Scholar] [CrossRef] [PubMed]
- Arnaz, A.; Pişkin, Ş.; Oğuz, G.N.; Yalçınbaş, Y.; Pekkan, K.; Sarıoğlu, T. Effect of modified Blalock-Taussig shunt anastomosis angle and pulmonary artery diameter on pulmonary flow. Anatol. J. Cardiol. 2018, 20, 2–8. [Google Scholar] [CrossRef]
- Zhang, N.; Yuan, H.; Chen, X.; Liu, J.; Zhou, C.; Huang, M.; Jian, Q.; Zhuang, J. Hemodynamic of the patent ductus arteriosus in neonates with modified Blalock-Taussig shunts. Comput. Methods Programs Biomed. 2020, 186, 105223. [Google Scholar] [CrossRef]
- Arthurs, C.J.; Agarwal, P.; John, A.V.; Dorfman, A.L.; Grifka, R.G.; Figueroa, C.A. Reproducing patient-specific hemodynamics in the Blalock-Taussig circulation using a flexible multi-domain simulation framework: Applications for optimal shunt design. Front. Pediatr. 2017, 5, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Bove, E.L.; Migliavacca, F.; de Leval, M.R.; Balossino, R.; Pennati, G.; Lloyd, T.R.; Khambadkone, S.; Hsia, T.Y.; Dubini, G. Use of mathematic modeling to compare and predict hemodynamic effects of the modified Blalock-Taussig and right ventricle-pulmonary artery shunts for hypoplastic left heart syndrome. J. Thorac. Cardiovasc. Surg. 2008, 136, 312–320.e2. [Google Scholar] [CrossRef] [Green Version]
- Hsia, T.Y.; Cosentino, D.; Corsini, C.; Pennati, G.; Dubini, G.; Migliavacca, F. Use of mathematical modeling to compare and predict hemodynamic effects between hybrid and surgical norwood palliations for hypoplastic left heart syndrome. Circulation 2011, 124, 204–210. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Sun, Q.; Hong, H.; Sun, Y.; Liu, J.; Qian, Y.; Wang, Q.; Umezu, M. Medical image-based hemodynamic analysis for modified blalock-taussig shunt. J. Mech. Med. Biol. 2015, 15, 1–17. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, Y.; Ding, J.; Ren, X.; Bai, F.; Zhang, M.; Ma, L.; Wang, W.; Xie, J.; Qiao, A. Hemodynamic effects of the anastomoses in the modified blalock-taussig shunt: A numerical study using a 0D/3D coupling method. J. Mech. Med. Biol. 2015, 15, 1–19. [Google Scholar] [CrossRef]
- Liiu, J.; Sun, Q.; Qian, Y.; Hong, H.; Liu, J. Numerical Simulation and Hemodynamic Analysis of the Modified Blalock-Taussig Shunt. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Osaka, Japan, 3–7 July 2013; pp. 707–710. [Google Scholar]
- Zhou, T.; Wang, Y.; Liu, J.; Wang, Y.; Wang, Y.; Chen, S.; Zhou, C.; Dong, N. Pulmonary artery growth after Modified Blalock-Taussig shunt: A single center experience. Asian J. Surg. 2020, 43, 428–437. [Google Scholar] [CrossRef] [PubMed]
- Piskin, S.; Altin, H.F.; Yildiz, O.; Bakir, I.; Pekkan, K. Hemodynamics of patient-specific aorta-pulmonary shunt configurations. J. Biomech. 2017, 50, 166–171. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, N.; Yuan, H.; Chen, X.; Liu, J.; Jian, Q.; Huang, M.; Zhang, K. Computational Fluid Dynamics Characterization of Two Patient-Specific Systemic-to-Pulmonary Shunts before and after Operation. Comput. Math. Methods Med. 2019, 2019, 1502318. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luo, K.; Jiang, W.; Yu, C.; Tian, X.; Zhou, Z.; Ding, Y. Fluid-Solid Interaction Analysis on Iliac Bifurcation Artery: A Numerical Study. Int. J. Comput. Methods 2019, 16, 1850112. [Google Scholar] [CrossRef]
- Stergiou, Y.G.; Kanaris, A.G.; Mouza, A.A.; Paras, S.V. Fluid-structure interaction in abdominal aortic aneurysms: Effect of haematocrit. Fluids 2019, 4, 11. [Google Scholar] [CrossRef] [Green Version]
- Sousa, L.C.; Castro, C.F.; António, C.C.; Azevedo, E. Fluid-Structure Interaction Modeling of Blood Flow in a Non-Stenosed Common Carotid Artery Bifurcation. In Proceedings of the 7th International Conference on Mechanics and Materials in Design, Albufeira, Portugal, 11–15 June 2017; pp. 1559–1564. [Google Scholar]
- Holzapfel, G.A.; Gasser, T.C.; Ogden, R.W. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. 2000, 61, 1–48. [Google Scholar] [CrossRef]
- Vassilevski, Y.V.; Salamatova, V.Y.; Simakov, S.S. On the elasticity of blood vessels in one-dimensional problems of hemodynamics. Comput. Math. Math. Phys. 2015, 55, 1567–1578. [Google Scholar] [CrossRef]
- Amabili, M.; Balasubramanian, P.; Bozzo, I.; Breslavsky, I.D.; Ferrari, G.; Franchini, G.; Giovanniello, F.; Pogue, C. Nonlinear Dynamics of Human Aortas for Material Characterization. Phys. Rev. X 2020, 10, 011015. [Google Scholar] [CrossRef] [Green Version]
- Malek, A.M.; Alper, S.L.; Izumo, S. Hemodynamic shear stress and its role in atherosclerosis. JAMA 2013, 282, 2035–2042. [Google Scholar] [CrossRef]
- Lin, S.; Han, X.; Bi, Y.; Ju, S.; Gu, L. Fluid-structure interaction in abdominal aortic aneurysm: Effect of modeling techniques. Biomed. Res. Int. 2017, 2017, 7023078. [Google Scholar] [CrossRef]
- Kuchumov, A.G.; Khairulin, A.R.; Biyanov, A.N.; Porodikov, A.A.; Arutyunyan, V.B.; Sinelnikov, Y.S. Effectiveness of blalock-taussig shunt performance in the congenital heart disease children. Russ. J. Biomech. 2020, 24, 65–83. [Google Scholar] [CrossRef]
- Han, D.; Starikov, A.; Hartaigh, B.; Gransar, H.; Kolli, K.K.; Lee, J.H.; Rizvi, A.; Baskaran, L.; Schulman-Marcus, J.; Lin, F.Y.; et al. Relationship between endothelial wall shear stress and high-risk atherosclerotic plaque characteristics for identification of coronary lesions that cause ischemia: A direct comparison with fractional flow reserve. J. Am. Heart Assoc. 2016, 5, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Samady, H.; Eshtehardi, P.; McDaniel, M.C.; Suo, J.; Dhawan, S.S.; Maynard, C.; Timmins, L.H.; Quyyumi, A.A.; Giddens, D.P. Coronary artery wall shear stress is associated with progression and transformation of atherosclerotic plaque and arterial remodeling in patients with coronary artery disease. Circulation 2011, 124, 779–788. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Campobasso, R.; Condemi, F.; Viallon, M.; Croisille, P.; Campisi, S.; Avril, S. Evaluation of Peak Wall Stress in an Ascending Thoracic Aortic Aneurysm Using FSI Simulations: Effects of Aortic Stiffness and Peripheral Resistance. Cardiovasc. Eng. Technol. 2018, 9, 707–722. [Google Scholar] [CrossRef] [Green Version]
- Traub, O.; Berk, B.C. Laminar shear stress: Mechanisms by which endothelial cells transduce an atheroprotective force. Arterioscler. Thromb. Vasc. Biol. 1998, 18, 677–685. [Google Scholar] [CrossRef] [Green Version]
- Badimon, L.; Vilahur, G. Thrombosis formation on atherosclerotic lesions and plaque rupture. J. Intern. Med. 2014, 276, 618–632. [Google Scholar] [CrossRef]
- Küçük, M.; Özdemir, R.; Karaçelik, M.; Doksöz, Ö.; Karadeniz, C.; Yozgat, Y.; Meşe, T.; Sarıosmanoǧlu, O.N. Risk factors for thrombosis, overshunting and death in infants after modified blalock-Taussig shunt. Acta Cardiol. Sin. 2016, 32, 337–342. [Google Scholar] [CrossRef]

| No. | Body Sizing, mm | Inflation | Number of Elements | Maximum Pressure, Pa | Maximum Velocity, m/s | ||
|---|---|---|---|---|---|---|---|
| Transition Ratio | Maximum Layers | Growth Ratio | |||||
| 1 | 0.95 | 0.5 | 3 | 1.2 | 80,353 | 17,634 | 3.85 |
| 2 | 0.8 | 0.4 | 5 | 1.4 | 159,379 | 17,952 | 4.38 |
| 3 | 0.63 | 0.3 | 7 | 1.3 | 349,926 | 17,892 | 4.47 |
| 4 | 0.5 | 0.35 | 8 | 1.6 | 709,578 | 18,470 | 4.71 |
| 5 | 0.38 | 0.32 | 10 | 1.3 | 1,544,745 | 18,509 | 4.75 |
| Sample Number | E (MPa) | Diameter, d (mm) | Wall Thickness (mm) |
|---|---|---|---|
| 1 | 7.41 | 4.32 | 0.34 |
| 2 | 9.8 | 3.4 | 0.4 |
| 3 | 10.3 | 4.5 | 0.35 |
| 4 | 11.1 | 5.5 | 0.48 |
| 5 | 43.5 | 5 | 0.53 |
| Sample Number | σY (MPa) | Diameter, d (mm) | Wall Thickness, (mm) | Loading Rate, (mm/min) |
|---|---|---|---|---|
| 1 | 11.6 | 3.4 | 0.4 | 30 |
| 2 | 13.6 | 4.5 | 0.35 | 30 |
| 3 | 14.5 | 5 | 0.53 | 30 |
| 4 | 17.0 | 6.2 | 0.85 | 50 |
| 5 | 16.9 | 6.2 | 0.85 | 250 |
| Strain Density Function | Constants, Specimen No. 1 (MPa) | Constants, Specimen No. 2 (MPa) |
|---|---|---|
| The five-parameter Mooney–Rivlin model | , , , , | , , , , |
| The three-parameter Yeoh model | , |
| The Aorta | The Shunt | ||
|---|---|---|---|
| Isotropic Hyperelastic Material | Anisotropic Hyperelastic Material) | Isotropic Elastic Material | Isotropic Hyperelastic Material |
| Ogden model: MPa MPa | Holzapfel–Gasser–Ogden model: MPa MPa MPa−1 | E = 10.3 MPa | Experimental data (Table 3) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuchumov, A.G.; Khairulin, A.; Shmurak, M.; Porodikov, A.; Merzlyakov, A. The Effects of the Mechanical Properties of Vascular Grafts and an Anisotropic Hyperelastic Aortic Model on Local Hemodynamics during Modified Blalock–Taussig Shunt Operation, Assessed Using FSI Simulation. Materials 2022, 15, 2719. https://doi.org/10.3390/ma15082719
Kuchumov AG, Khairulin A, Shmurak M, Porodikov A, Merzlyakov A. The Effects of the Mechanical Properties of Vascular Grafts and an Anisotropic Hyperelastic Aortic Model on Local Hemodynamics during Modified Blalock–Taussig Shunt Operation, Assessed Using FSI Simulation. Materials. 2022; 15(8):2719. https://doi.org/10.3390/ma15082719
Chicago/Turabian StyleKuchumov, Alex G., Aleksandr Khairulin, Marina Shmurak, Artem Porodikov, and Andrey Merzlyakov. 2022. "The Effects of the Mechanical Properties of Vascular Grafts and an Anisotropic Hyperelastic Aortic Model on Local Hemodynamics during Modified Blalock–Taussig Shunt Operation, Assessed Using FSI Simulation" Materials 15, no. 8: 2719. https://doi.org/10.3390/ma15082719
APA StyleKuchumov, A. G., Khairulin, A., Shmurak, M., Porodikov, A., & Merzlyakov, A. (2022). The Effects of the Mechanical Properties of Vascular Grafts and an Anisotropic Hyperelastic Aortic Model on Local Hemodynamics during Modified Blalock–Taussig Shunt Operation, Assessed Using FSI Simulation. Materials, 15(8), 2719. https://doi.org/10.3390/ma15082719








