Experimental Study of Flexural Performance of UHPC–NC Laminated Beams Exposed to Fire
Abstract
:1. Introduction
2. Experimental Program
2.1. Material Properties
2.2. Specimen Design
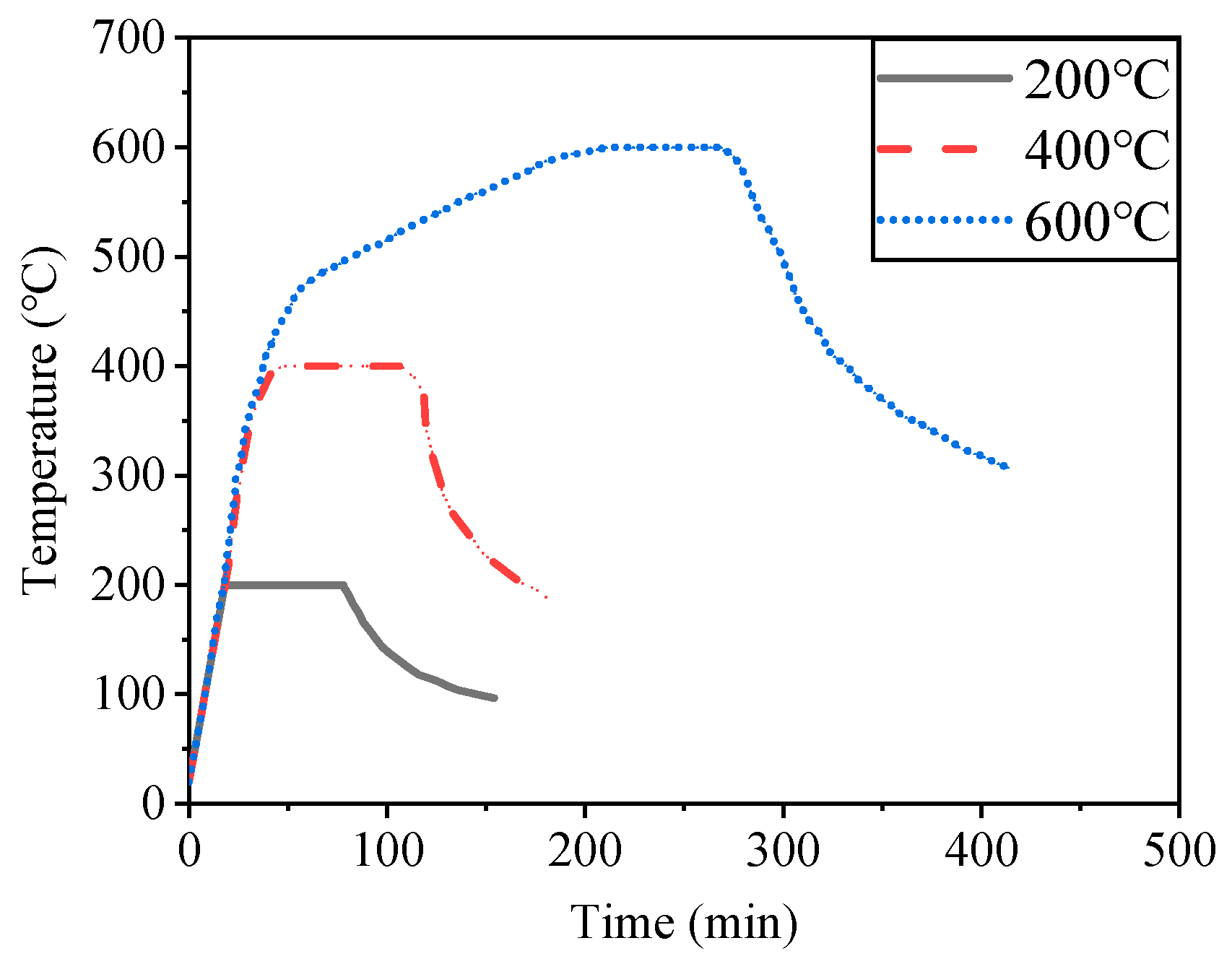
2.3. Heating and Cooling Treatment
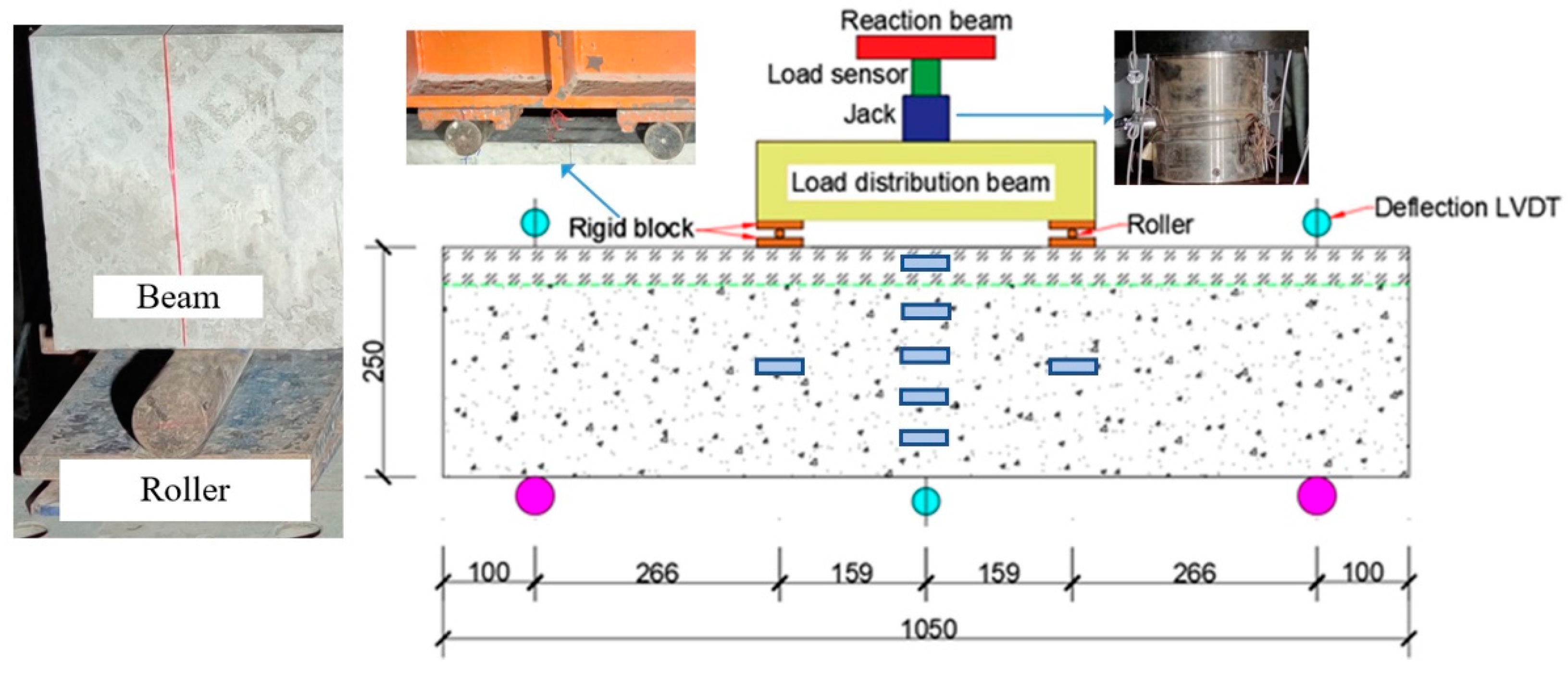
2.4. Loading Setup and Measurements System
3. Experimental Results and Discussion
3.1. Apparent Characteristics after Heating and Cooling
3.2. Cracking Patterns and Failure Modes
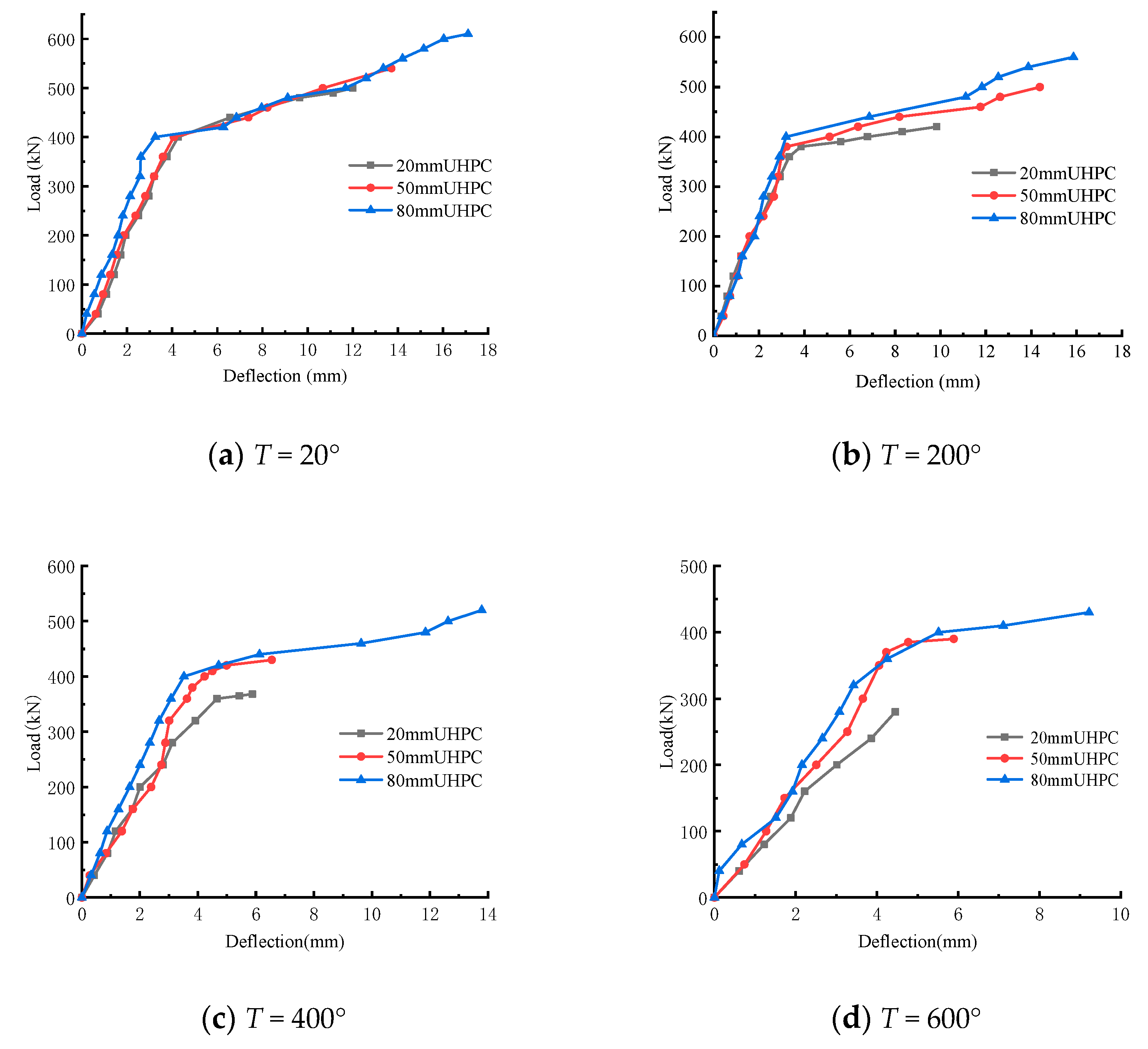
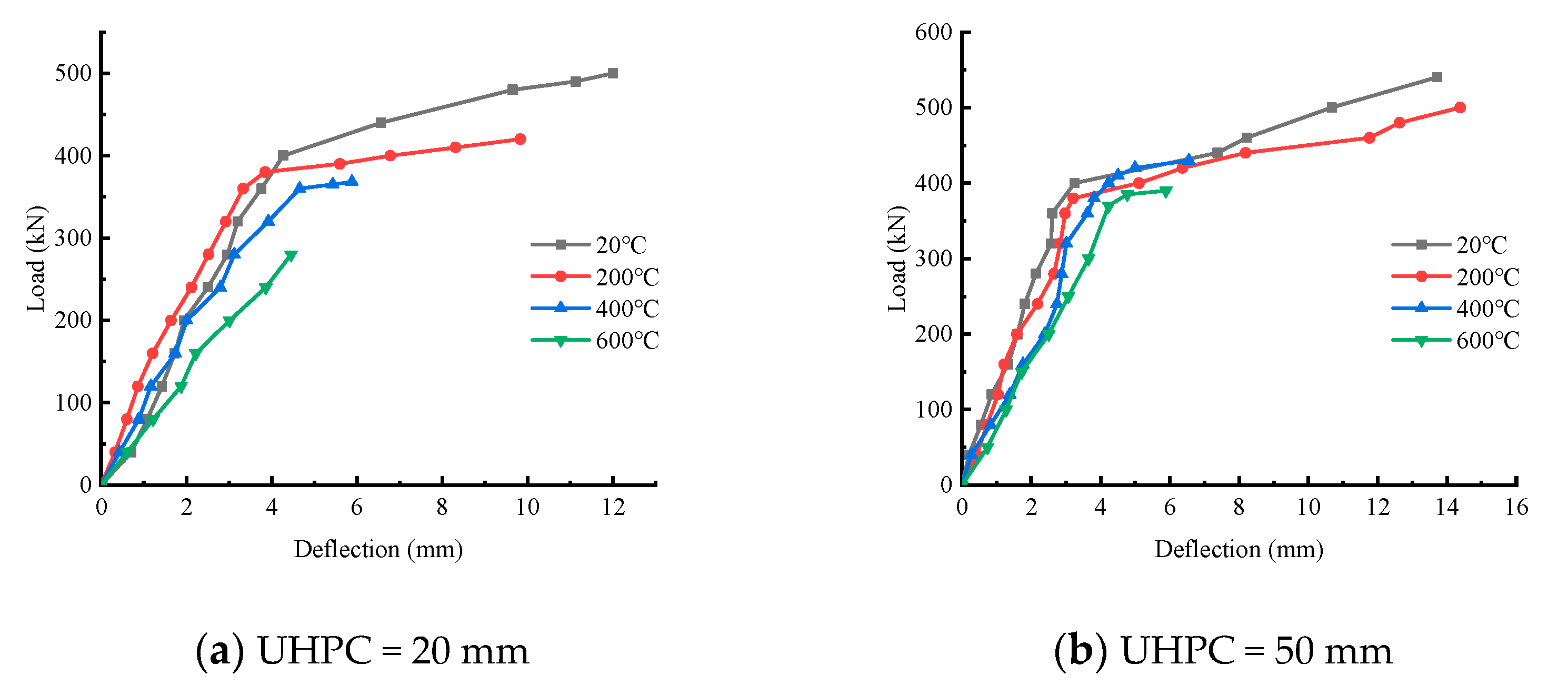
3.3. Load-Versus-Deflection Curves at Mid-Span
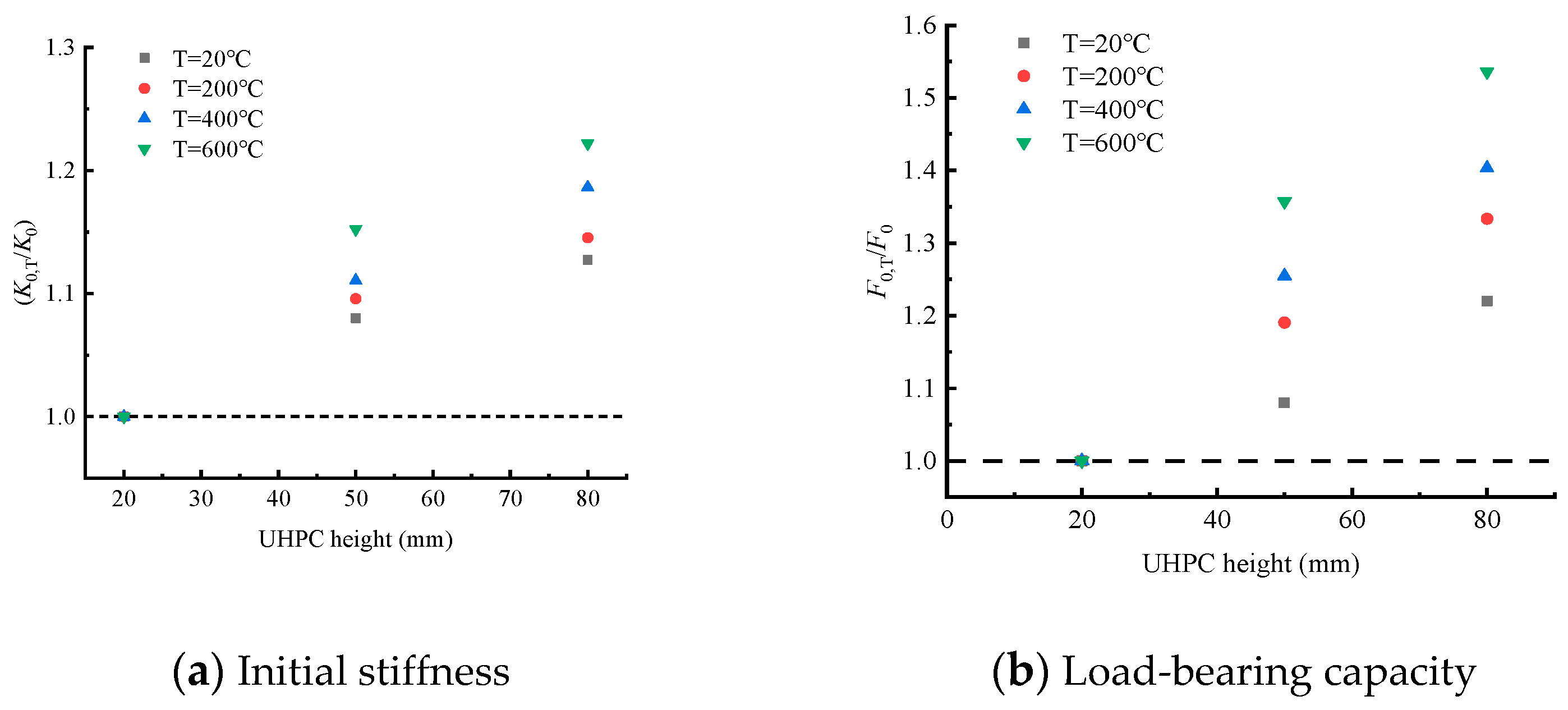
3.4. Initial Stiffness and Load-Bearing Capacity
3.5. Strain Distribution
4. Flexural Load Capacity of UHPC–RC Composite Beam after Fire
5. Conclusions
- (1)
- The results demonstrate that the exposure of the laminated-beam structures to high temperature causes a significant loss of stiffness as well as load-bearing capacity. The increase in the height of the UHPC layer, on the other hand, has an enhancing effect on the laminated beam.
- (2)
- The damage mode of the laminated beam changes under the combined effect of the UHPC height and temperature change, and the effect of the two factors on the damage mode of the laminated beam is not a simple linear relationship.
- (3)
- The test-strain distribution shows that the strain in the top of the beam exceeds the crushing strain limit of the compressive strain of the UHPC, and the crushing of the UHPC can be observed during the damage process.
- (4)
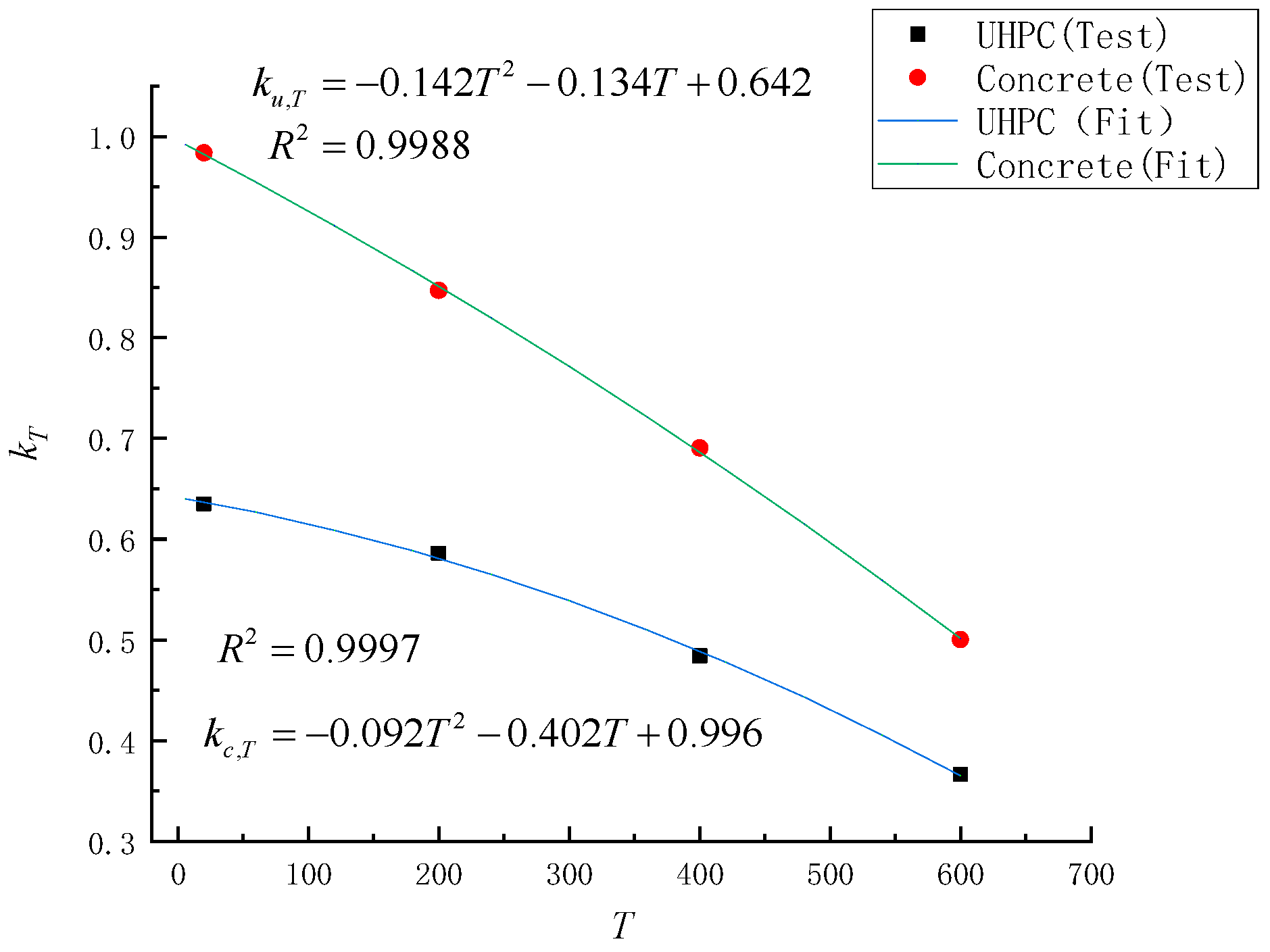
- The quadratic relationship between UHPC and concrete strength and fire temperature was established by introducing the strength-degradation factor and compared with the experimental results with good fitting results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nasser, H.; Vandewalle, L.; Verstrynge, E. Effect of pre-existing longitudinal and transverse corrosion cracks on the flexural behaviour of corroded RC beams. Constr. Build. Mater. 2021, 319, 126141. [Google Scholar] [CrossRef]
- Wu, J.; Xu, J.; Diao, B.; Jin, L.; Du, X. Fatigue life prediction for the reinforced concrete (RC) beams under the actions of chloride attack and fatigue. Eng. Struct. 2021, 242, 112543. [Google Scholar] [CrossRef]
- Ahmed, A.; Kodur, V. The experimental behavior of FRP-strengthened RC beams subjected to design fire exposure. Eng. Struct. 2011, 33, 2201–2211. [Google Scholar] [CrossRef]
- Lu, L.; Yuan, Y.; Caspeele, R.; Taerwe, L. Influencing factors for fire performance of simply supported RC beams with implicit and explicit transient creep strain material models. Fire Saf. J. 2015, 73, 29–36. [Google Scholar] [CrossRef]
- Fan, S.; Zhang, Y.; Tan, K. Fire behaviour of deep beams under unsymmetrical loading. Eng. Struct. 2022, 250, 113419. [Google Scholar] [CrossRef]
- Tariq, R.; Gaikwad, M.; Bhargava, P. Analysis of behaviour of corroded RC beams exposed to elevated temperatures. J. Build. Eng. 2021, 42, 102508. [Google Scholar] [CrossRef]
- Hao, H.; Tran, T.; Li, H.; Pham, T.; Chen, W. On the accuracy, reliability and controllability of impact tests of RC beams. Int. J. Impact Eng. 2021, 157, 103979. [Google Scholar] [CrossRef]
- Marzec, I.; Tejchman, J. Experimental and numerical investigations on RC beams with stirrups scaled along height or length. Eng. Struct. 2022, 252, 113621. [Google Scholar] [CrossRef]
- Poon, C.; Azhar, S.; Anson, M.; Wong, Y. Comparison of the strength and durability performance of normal- and high-strength pozzolanic concretes at elevated temperatures. Cem. Concr. Res. 2001, 31, 1291–1300. [Google Scholar] [CrossRef]
- Elleithy, W.; Amoudi, O.; Sharif, A.; Maslehuddin, M. Effect of thermal variations on bond strength of fusion-bonded epoxy-coated bars. Cem. Concr. Aggreg. 1998, 20, 163–168. [Google Scholar]
- Diederichs, U.; Schneider, U. Bond strength at high temperatures. Mag. Concr. Res. 1981, 33, 75–84. [Google Scholar] [CrossRef]
- Morley, P.; Royles, R. Response of the bond in reinforced concrete to high temperatures. Mag. Concr. Res. 1983, 35, 67–74. [Google Scholar] [CrossRef]
- Kodur, V.; Dwaikat, M. Effect of fire induced spalling on the response of reinforced concrete beams. Int. J. Concr. Struct. Mater. 2008, 2, 71–81. [Google Scholar]
- Kodur, V.; Wang, T.; Cheng, F. Predicting the fire resistance behaviour of high strength concrete columns. Cem. Concr. Compos. 2004, 26, 141–153. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.; Royles, R. Post heat exposure behaviour of reinforced concrete beams. Mag. Concr. Res. 1986, 38, 59–66. [Google Scholar] [CrossRef]
- Banerji, S.; Kodur, V.; Solhmirzaei, R. Experimental behavior of ultra high performance fiber reinforced concrete beams under fire conditions. Eng. Struct. 2020, 208, 110316. [Google Scholar] [CrossRef]
- Li, Y.; Yang, E.; Tan, K. Flexural behavior of ultra-high performance hybrid fiber reinforced concrete at the ambient and elevated temperature. Constr. Build. Mater. 2018, 105, 64–71. [Google Scholar] [CrossRef]
- Kahanji, C.; Ali, F.; Nadjai, A.; Alam, N. Effect of curing temperature on the behaviour of UHPFRC at elevated temperatures. Constr. Build. Mater. 2018, 182, 670. [Google Scholar] [CrossRef]
- Wu, F.; Liu, S.; Xue, C.; Yang, K.; Zhang, H. Experimental study on the mechanical properties of perfobond rib shear connectors with steel fiber high strength concrete. Materials 2021, 14, 3345. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Guo, T.; Li, A. Experimental investigation on long-term behavior of prestressed concrete beams under coupled effect of sustained load and corrosion. Adv. Struct. Eng. 2020, 23, 2587–2596. [Google Scholar] [CrossRef]
- Bonopera, M.; Chang, K. Novel method for identifying residual prestress force in simply supported concrete girder-bridges. Adv. Struct. Eng. 2021, 24, 3238–3251. [Google Scholar] [CrossRef]
- Ahmad, S.; Rasul, M.; Adekunle, S.K.; Al-Dulaijan, S.U.; Maslehuddin, M.; Ali, S.I. Mechanical properties of steel fiber-reinforced UHPC mixtures exposed to elevated temperature: Effects of exposure duration and fiber content. Compos. B Eng. 2019, 168, 291–301. [Google Scholar] [CrossRef]
- Shi, C.; Wu, Z.; Xiao, J.; Wang, D.; Huang, Z.; Fang, Z. A review on ultra high performance concrete: Part I. Raw materials and mixture design. Constr. Build. Mater. 2015, 101, 741–751. [Google Scholar] [CrossRef]
- Kadhim, M.; Jawdhari, A.; Peiris, A. Development of hybrid UHPC-NC beams: A numerical study. Eng. Struct. 2021, 233, 111893. [Google Scholar] [CrossRef]
- GB/T 50081-2019; Standard for Test Methods of Concrete Physical and Mechanical Properties. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2019.
- Zheng, W.; Pan, Z.; Chen, Z.; Xu, J.; Xiao, J.; Chen, W. Shear behavior of reinforced recycled aggregate concrete beams after exposure to temperatures up to 600 °C. Eng. Struct. 2021, 244, 112756. [Google Scholar] [CrossRef]
- Hou, X.; Ren, P.; Rong, Q.; Zheng, W.; Zhan, Y. Comparative fire behavior of reinforced RPC and NSC simply supported beams. Eng. Struct. 2019, 185, 122–140. [Google Scholar] [CrossRef]
- Zhu, Y.; Hussein, H.; Kumar, A.; Chen, G. A review: Material and structural properties of UHPC at elevated temperatures or fire conditions. Cem. Concr. Compos. 2021, 123, 104212. [Google Scholar] [CrossRef]
- Tong, T.; Yuan, S.; Wang, J.; Liu, Z. The Role of Bond Strength in Structural Behaviors of UHPC-NC Composite Beams: Experimental Investigation and Finite Element Modeling. Compos. Struct. 2020, 255, 112914. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Zhu, Y.; Shao, X. Experimental study on flexural behavior of damaged reinforced concrete (RC) beam strengthened by toughness-improved ultra-high performance concrete (UHPC) layer. Compos. Part B 2020, 186, 107834. [Google Scholar] [CrossRef]








| Type | Cement | Sand | Silica Fume | Powder | Steel Fiber | Superplasticizer | |
|---|---|---|---|---|---|---|---|
| Glass | Limestone | ||||||
| NC | 450 | 992 | 60 | 36.3 | 36.3 | 110 | 12.5 |
| UHPC | 1026.3 | 1282.3 | 128.3 | 64.1 | 64.1 | 156 | 25.6 |
| Grade | fy (MPa) | fst (MPa) | Es (MPa) |
|---|---|---|---|
| HRB400 | 441 | 636 | 2.0 × 105 |
| HRB500 | 522 | 677 | 2.1 × 105 |
| Type | Temperature (℃) | fc (MPa) | Ec (GPa) | Decrease Factor |
|---|---|---|---|---|
| NC | 20 | 51.2 | 34.6 | - |
| 200 | 39.8 | 26.7 | 0.85 | |
| 400 | 27.3 | 15.9 | 0.63 | |
| 600 | 11.1 | 6.8 | 0.38 | |
| UHPC | 20 | 120.1 | 24.3 | - |
| 200 | 100.9 | 17.8 | 0.88 | |
| 400 | 85.2 | 10.5 | 0.67 | |
| 600 | 61.3 | 5.4 | 0.40 |
| Test Group | Specimen Label | Temperature (°C) | UHPC Thickness (mm) |
|---|---|---|---|
| TB-NT | T20-H20 | 20 | 20 |
| T20-H50 | 50 | ||
| T20-H80 | 80 | ||
| TB-200 | T200-H20 | 200 | 20 |
| T200-H50 | 50 | ||
| T200-H80 | 80 | ||
| TB-400 | T400-H20 | 400 | 20 |
| T400-H50 | 50 | ||
| T400-H80 | 80 | ||
| TB-600 | T600-H20 | 600 | 20 |
| T600-H50 | 50 | ||
| T600-H80 | 80 |
| UHPC Height hu (mm) Fire Temperature T (°C) | 20 | 50 | 80 |
|---|---|---|---|
| 20 | 80 | 73 | 60 |
| 200 | 85 | 80 | 73 |
| 400 | 93 | 86 | 76 |
| 600 | 100 | 90 | 79 |
| Fire Temperature T (°C) | Verification Error (%) | ||
|---|---|---|---|
| 20 | 0.6352 | 0.5860 | −4.97 |
| 200 | 0.9837 | 0.8471 | −3.60 |
| 400 | 0.6352 | 0.5860 | −3.15 |
| 600 | 0.9837 | 0.8471 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, T.; Sheng, X. Experimental Study of Flexural Performance of UHPC–NC Laminated Beams Exposed to Fire. Materials 2022, 15, 2605. https://doi.org/10.3390/ma15072605
Zhou T, Sheng X. Experimental Study of Flexural Performance of UHPC–NC Laminated Beams Exposed to Fire. Materials. 2022; 15(7):2605. https://doi.org/10.3390/ma15072605
Chicago/Turabian StyleZhou, Tieming, and Xingwang Sheng. 2022. "Experimental Study of Flexural Performance of UHPC–NC Laminated Beams Exposed to Fire" Materials 15, no. 7: 2605. https://doi.org/10.3390/ma15072605
APA StyleZhou, T., & Sheng, X. (2022). Experimental Study of Flexural Performance of UHPC–NC Laminated Beams Exposed to Fire. Materials, 15(7), 2605. https://doi.org/10.3390/ma15072605





