Secondary Creep Analysis of FG Rotating Cylinder with Exponential, Linear and Quadratic Volume Reinforcement
Abstract
1. Introduction
2. Secondary Creep Phenomenon in Engineering Applications
2.1. Problem Description of Functionally Graded Cylinder in Engineering
2.2. Mathematical Modeling for Secondary Creep Analysis of FG Cylinder
3. Results and Discussion
3.1. Effect of Exponential Volume Reinforcement
3.2. Effect of Linear Volume Reinforcement
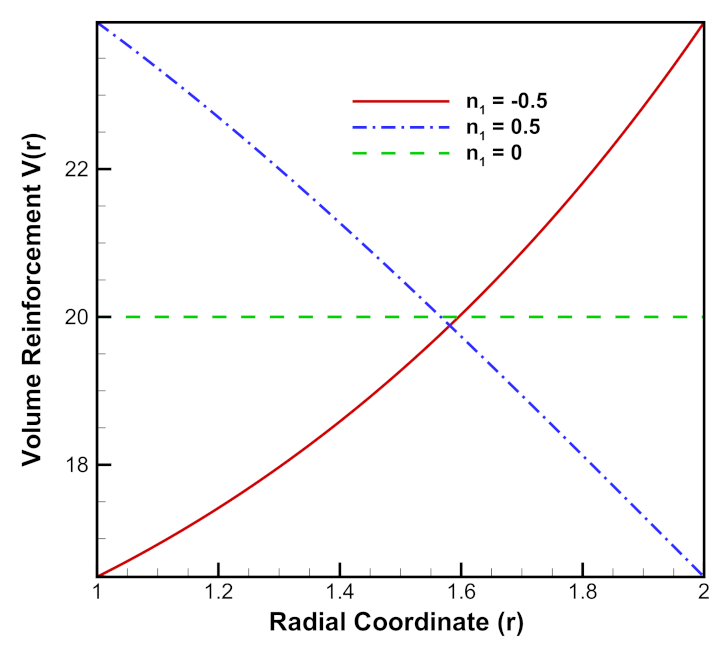
3.3. Effect of Quadratic Volume Reinforcement
4. Conclusions
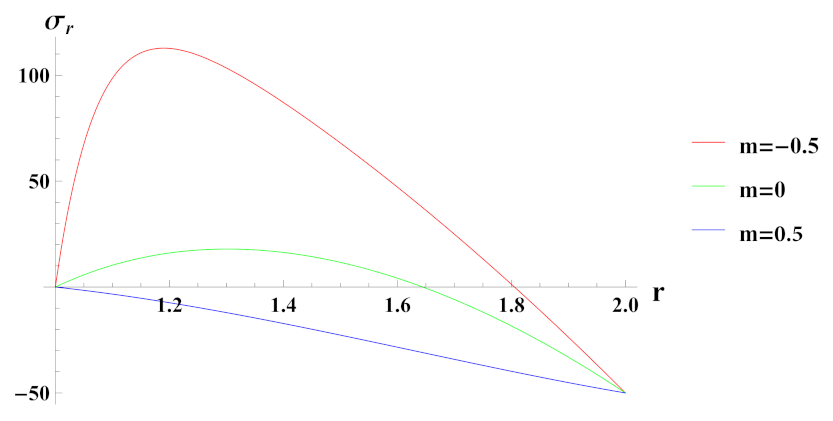
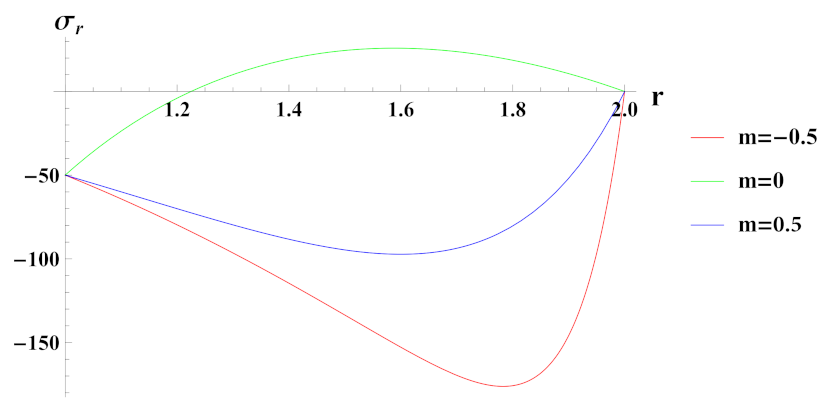
- Radial stress in a rotating cylinder with an increasing exponential volume reinforcement gradation has higher magnitude and compressiveness as compared to increasing linear volume reinforcement gradation.
- Radial stress in a rotating cylinder with decreasing exponential volume reinforcement gradation has lower magnitude as compared to decreasing linear volume reinforcement gradation.
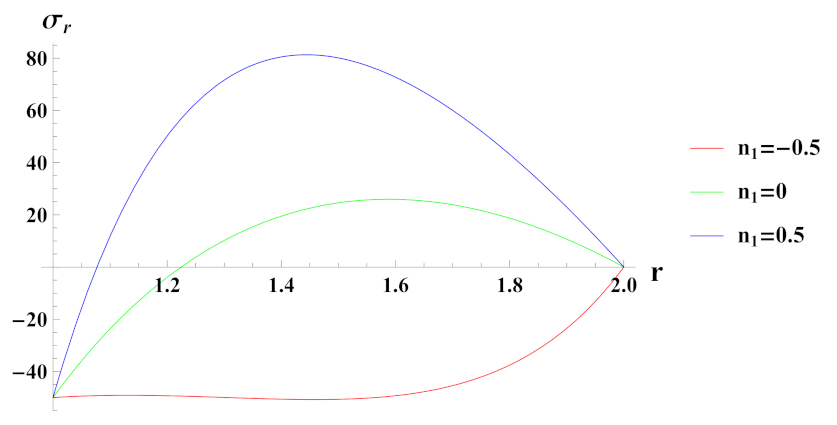
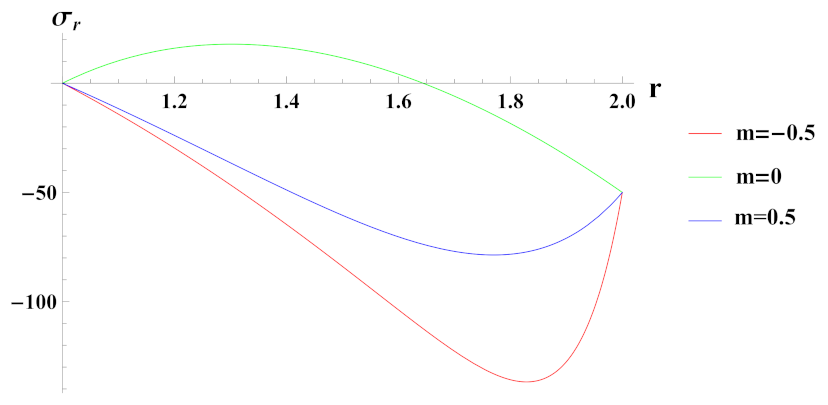
- Radial stresses in cylinder with quadratic volume reinforcement profile are found to be compressive throughout the radius. Its compressiveness increases towards the outer radial points of the cylinder as we increase the volume reinforcement. Further, the compressiveness at the outer radial points is higher in the case of internal pressure as compared to external pressure.
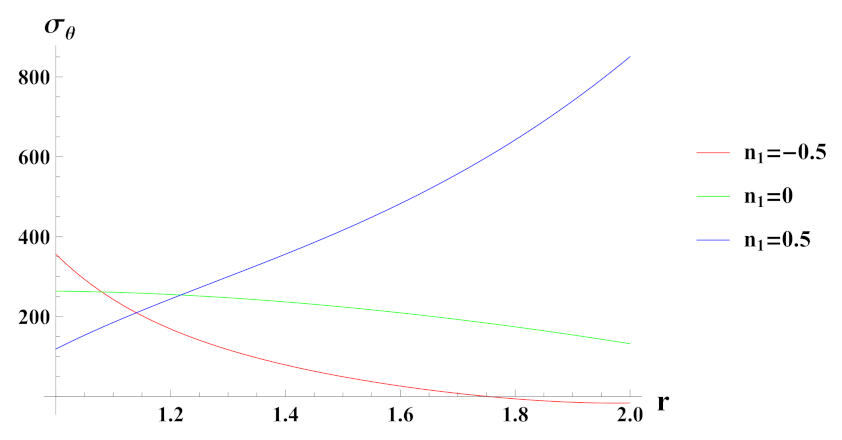
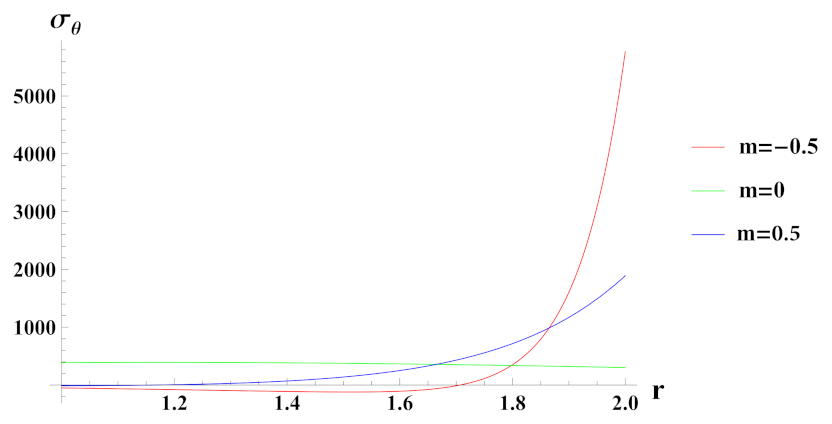
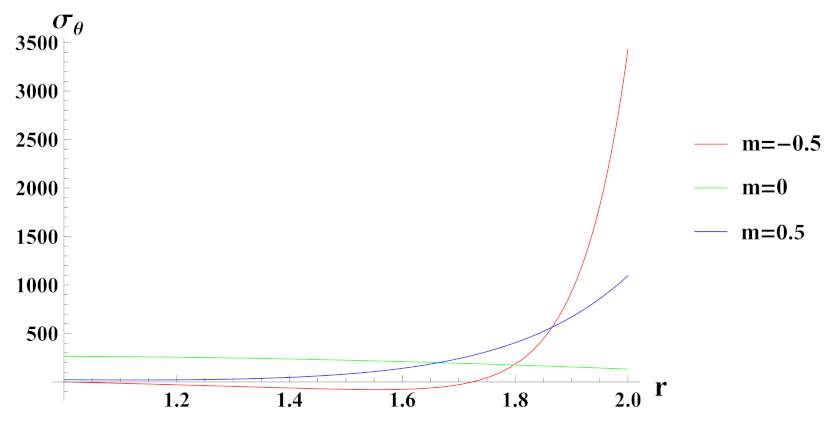
- Tangential stresses in a rotating cylinder with increasing exponential volume reinforcement profile decreases from inner to outer radius of the cylinder whereas under increasing linear volume reinforcement profile it increases from inner to outer radius of the cylinder.
- In a rotating cylinder with decreasing exponential volume reinforcement profile, tangential stress increases from inner to outer radius of the cylinder whereas under linear volume reinforcement profile, it decreases from inner to outer radius of the cylinder.
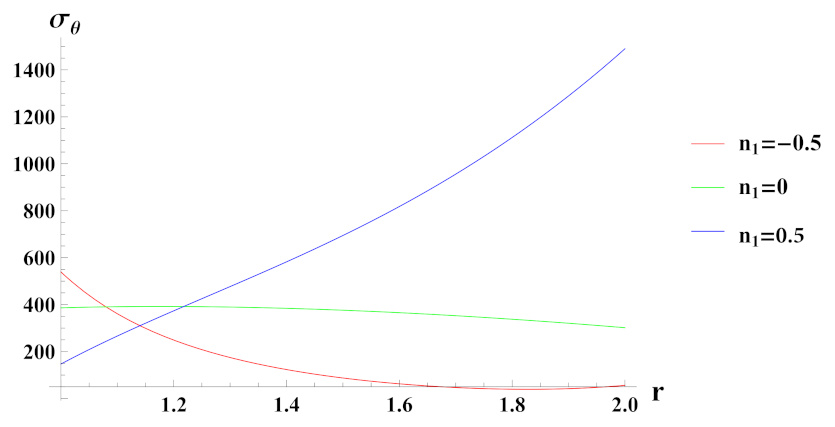
- In case of quadratic volume reinforcement profile, tangential stress increase from inner to outer radius of the cylinder and their magnitude also increase with increase in volume reinforcement in cylinder.
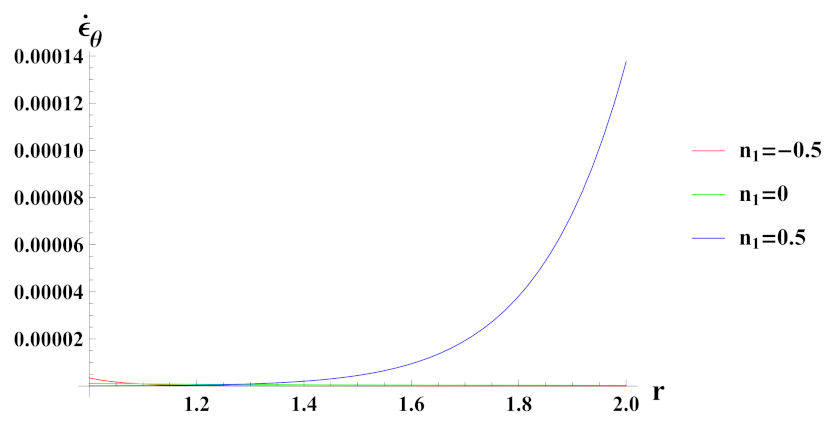
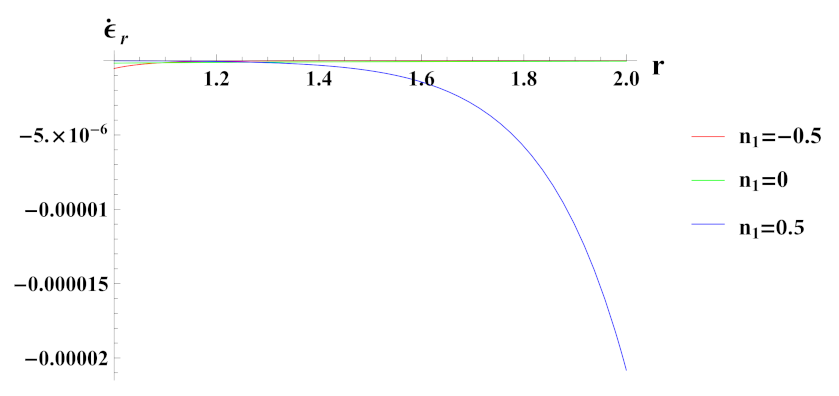
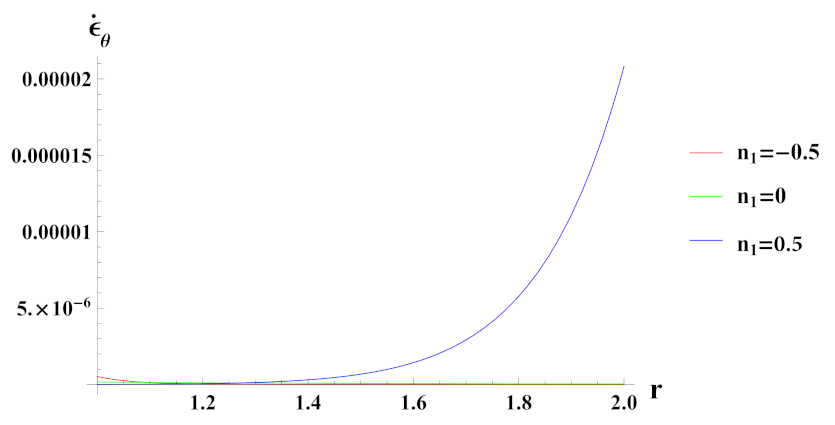
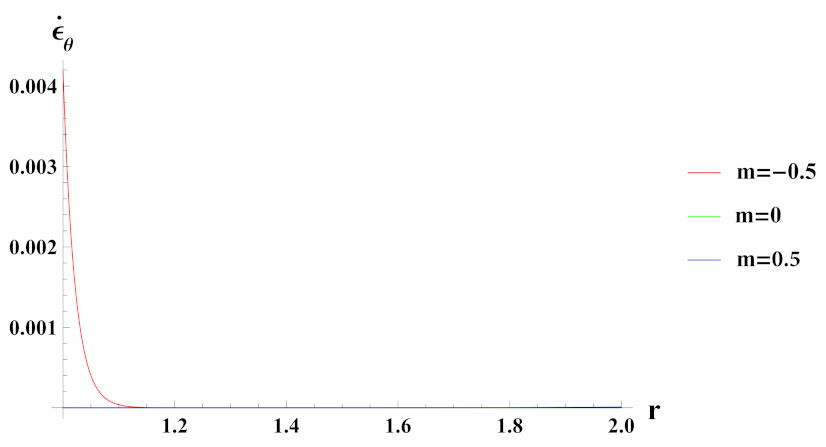
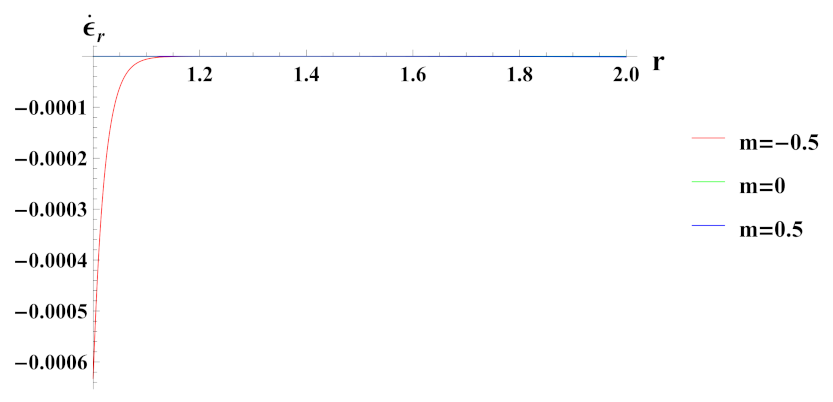
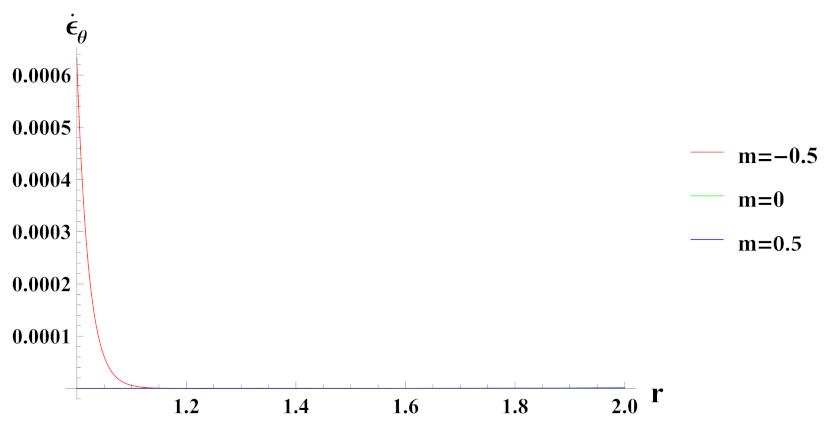
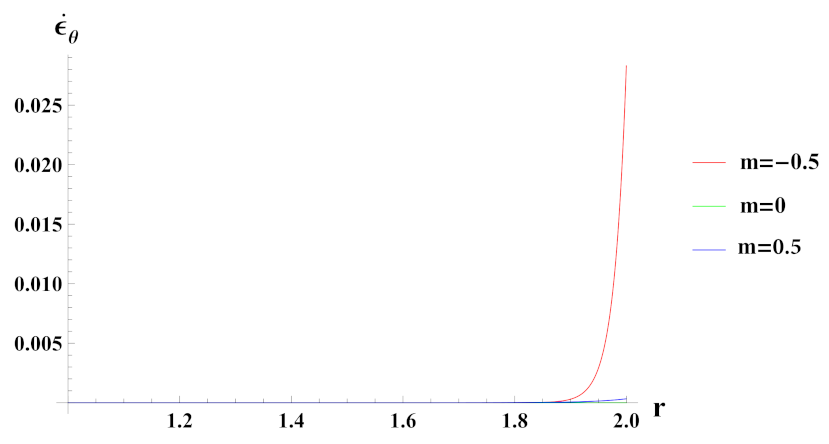
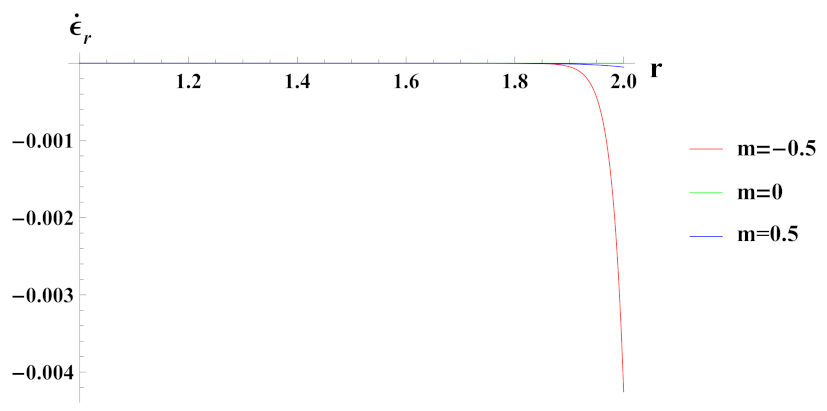
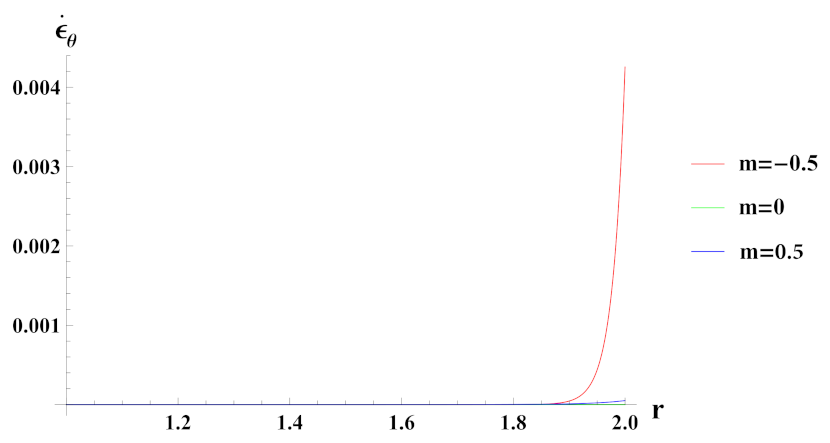
- Strain rates in radial and tangential directions of cylinder under decreasing exponential volume reinforcement profile are of higher magnitude under internal pressure as compared to external pressure. In the case of linear volume reinforcement, it has higher magnitude under internal pressure as compared to external pressure. Further, under decreasing exponential volume reinforcement profile, their magnitude increases from the inner to outer radius whereas in the linear volume reinforcement profile, their magnitude decreases from the inner to outer radius.
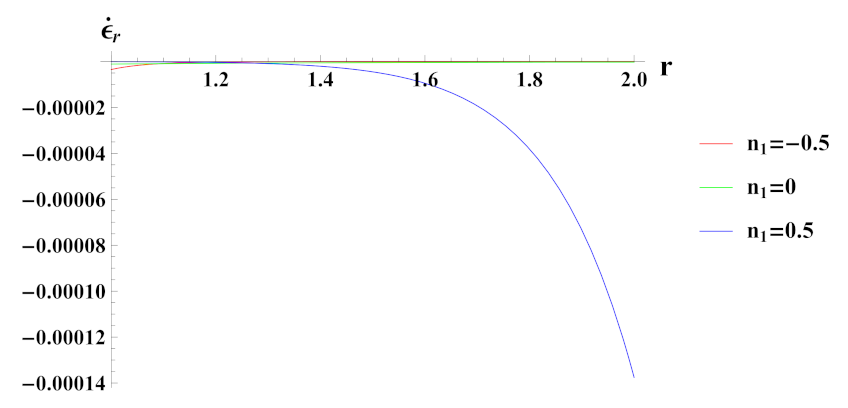
- Strain rates in radial and tangential directions of a cylinder with quadratic reinforcement are higher in magnitude under internal pressure as compared to external pressure. Further, with an increase in volume reinforcement, their magnitude increases from the inner to outer radius of the cylinder.
- Thus, based on the obtained results, a comparison of creep stresses and strain rates among rotating cylinders with linearly and non-linearly varying volume reinforcement profile is presented. It can be observed from the above study outcomes that the nature of reinforcement function of in metal matrix at inner and outer radial surfaces causes a significant effect on the magnitude of creep stresses and strain rates at inner and outer radial surfaces, under internal/external pressure conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FGM | Functionally Graded Material |
| SiCp | Silicon Carbide Particulates |
Appendix A
References
- You, L.H.; Ou, H.; Zheng, Z.Y. Creep deformations and stresses in thick-walled cylindrical vessels of functionally graded materials subjected to internal pressure. Compos. Struct. 2007, 78, 285–291. [Google Scholar] [CrossRef]
- Chen, J.J.; Tu, S.T.; Xuan, F.Z.; Wang, Z.D. Creep analysis for a functionally graded cylinder subjected to internal and external pressure. J. Strain Anal. Eng. Des. 2007, 42, 69–77. [Google Scholar] [CrossRef]
- Sharma, S.; Sahni, M.; Kumar, R. Elastic-plastic transition of transversely isotropic thick-walled rotating cylinder under internal pressure. Def. Sci. J. 2009, 59, 260–264. [Google Scholar] [CrossRef][Green Version]
- Atabakhshian, V.; Loghman, A. Semi-analytical solution for time-dependent creep analysis of rotating cylinders made of anisotropic exponentially graded material (EGM). J. Solid Mech. 2012, 4, 313–326. [Google Scholar]
- Nejad, M.Z.; Abedi, M.; Lotfian, M.H.; Ghannad, M. An exact solution for stresses and displacements of pressurized FGM thick-walled spherical shells with exponential-varying properties. J. Mech. Sci. Technol. 2012, 26, 4081–4087. [Google Scholar] [CrossRef]
- Sharma, S.; Aggarwal, A.K.; Sharma, R. Safety analysis of thermal creep non-homogeneous thick-walled circular cylinder under internal and external pressure using Lebesgue strain measure. Multidiscip. Model. Mater. Struct. 2013, 26, 499–513. [Google Scholar] [CrossRef]
- Sahni, M.; Sharma, S. Analysis of safety measure in creep transversely isotropic thick-walled rotating cylinder by finitesimal deformation under external pressure. In Proceedings of the 3rd International Conference on Reliability, Infocom Technologies and Optimization (ICRITO), Noida, India, 8–10 October 2014; pp. 1–5. [Google Scholar]
- Kashkoli, M.D.; Nejad, M.Z. Effect of heat flux on creep stresses of thick-walled cylindrical pressure vessels. J. Appl. Res. Technol. 2014, 12, 585–597. [Google Scholar] [CrossRef][Green Version]
- Vedeld, K.; Sollund, H.A.; Hellesland, J. Closed analytical expressions for stress distributions in two-layer cylinders and their application to offshore lined and clad pipes. J. Offshore Mech. Arct. Eng. 2015, 137, 021702. [Google Scholar] [CrossRef]
- Loghman, A.; Shayestemoghadam, H. Magneto-thermo-mechanical creep behavior of nano-composite rotating cylinder made of polypropylene reinforced by MWCNTs. J. Theor. Appl. Mech. 2016, 54, 239–249. [Google Scholar] [CrossRef]
- Kalai, A.T.; Moud, S.H.; Hassani, B. Elasto-plastic stress analysis in rotating disks and pressure vessels made of functionally graded materials. Lat. Am. J. Solids Struct. 2016, 13, 819–834. [Google Scholar] [CrossRef]
- Sharma, S.; Yadav, S. Thermo creep analysis of thick-walled functionally graded cylinder under internal and external pressure. In Proceedings of the AIP Conference Proceedings, Mathematical Sciences and its Applications, Uttar Pradesh, India, 8–10 December 2016; p. 020014. [Google Scholar]
- Celebi, K.; Yarimpabu, D.; Keles, I. A novel approach to thermal and mechanical stresses in a FGM cylinder with exponentially-varying properties. J. Theor. Appl. Mech. 2017, 55, 343–351. [Google Scholar] [CrossRef]
- Bakhshizadeh, A.; Nejad, M.; Kashkoli, M.D. Time-dependent hygro-thermal creep analysis of pressurized FGM rotating thick cylindrical shells subjected to uniform magnetic field. J. Solid Mech.1 2017, 9, 663–679. [Google Scholar]
- Sahni, M.; Sahni, R.; Mehta, P. Creep Behaviour under SiCp Exponential Volume Reinforcement in FGM Composite Rotating Cylinders. In Proceedings of the International Conference on Recent Trends in Engineering and Material Sciences (ICEMS-2016), Jaipur, India, 17–19 March 2016; pp. 9529–9533. [Google Scholar]
- Habib, E.S.; El-Hadak, M.A.; El-Megharbel, A. Stress analysis for cylinder made of FGM and subjected to thermo-mechanical loadings. Metals 2018, 9, 4. [Google Scholar] [CrossRef]
- Kashkoli, M.D.; Tahan, K.N.; Nejad, M.Z. Thermo-mechanical creep analysis of FGM thick cylindrical pressure vessels with variable thickness. Int. J. Appl. Mech. 2018, 10, 1850008. [Google Scholar] [CrossRef]
- Çallioğlu, H.; Sayer, M.; Demir, E. Elastic-plastic stress analysis of rotating functionally graded discs. Thin-Walled Struct. 2015, 94, 38–44. [Google Scholar] [CrossRef]
- Mehta, P.D.; Sahni, M. Thermo-Mechanical Analysis for an Axisymmetric Functionally Graded Rotating Disc under Linear and Quadratic Thermal Loading. Int. J. Math. Eng. Manag. Sci. 2020, 5, 744–757. [Google Scholar] [CrossRef]
- Mehta, P.D.; Mishra, L.; Sahni, M. Thermomechanical Stress Analysis of Thick-Walled Cylinder with Inner FGM Layer. Struct. Integr. Life 2019, 19, 211–233. [Google Scholar]
- Hajisadeghian, A.; Masoumi, A.; Parvizi, A. Investigating the magnetic field effects on thermomechanical stress behavior of thick-walled cylinder with inner FGM layer. J. Therm. Stresses 2018, 41, 286–301. [Google Scholar] [CrossRef]
- Dini, A.; Nematollahi, M.A.; Hosseini, M. Analytical solution for magneto-thermo-elastic responses of an annular functionally graded sandwich disk by considering internal heat generation and convective boundary condition. J. Sandw. Struct. Mater 2021, 23, 542–567. [Google Scholar] [CrossRef]
- Singh, T.; Gupta, V.K. Modeling steady state creep in functionally graded thick cylinder subjected to internal pressure. J. Compos. Mater 2010, 44, 1317–1333. [Google Scholar] [CrossRef]
- Garg, M.; Deepak, D.; Gupta, V.K. FE modeling of creep in linear and non-linear FGM cylinder under internal pressure. Multidiscip. Model. Mater. Struct. 2014, 10, 94–105. [Google Scholar] [CrossRef]
- Aggarwal, A.K.; Sharma, R.; Sharma, S. Collapse pressure analysis of transversely isotropic thick-walled cylinder using Lebesgue strain measure and transition theory. Sci. World J. 2014, 2014, 2240954. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Nie, G.J.; Batra, R.C. Material tailoring and analysis of functionally graded isotropic and incompressible linear elastic hollow cylinders. Compos. Struct. 2010, 92, 265–274. [Google Scholar] [CrossRef]
- Murata, A.; Karwowski, W. On the Root Causes of the Fukushima Daiichi Disaster from the Perspective of High Complexity and Tight Coupling in Large-Scale Systems. Symmetry 2021, 13, 414. [Google Scholar] [CrossRef]
- Mao, J.F.; Zhu, J.W.; Bao, S.Y.; Luo, L.J.; Gao, Z.L. Creep and damage analysis of reactor pressure vessel considering core meltdown Scenario. Procedia Eng. 2015, 130, 1148–1161. [Google Scholar] [CrossRef][Green Version]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sahni, M.; Mehta, P.D.; Sahni, R.; León-Castro, E.; Espinoza-Audelo, L.F. Secondary Creep Analysis of FG Rotating Cylinder with Exponential, Linear and Quadratic Volume Reinforcement. Materials 2022, 15, 1803. https://doi.org/10.3390/ma15051803
Sahni M, Mehta PD, Sahni R, León-Castro E, Espinoza-Audelo LF. Secondary Creep Analysis of FG Rotating Cylinder with Exponential, Linear and Quadratic Volume Reinforcement. Materials. 2022; 15(5):1803. https://doi.org/10.3390/ma15051803
Chicago/Turabian StyleSahni, Manoj, Parth Dinesh Mehta, Ritu Sahni, Ernesto León-Castro, and Luis F. Espinoza-Audelo. 2022. "Secondary Creep Analysis of FG Rotating Cylinder with Exponential, Linear and Quadratic Volume Reinforcement" Materials 15, no. 5: 1803. https://doi.org/10.3390/ma15051803
APA StyleSahni, M., Mehta, P. D., Sahni, R., León-Castro, E., & Espinoza-Audelo, L. F. (2022). Secondary Creep Analysis of FG Rotating Cylinder with Exponential, Linear and Quadratic Volume Reinforcement. Materials, 15(5), 1803. https://doi.org/10.3390/ma15051803







