Thermal Mass Effect on the Solution Cooling Rate and on HIPped Astroloy Component Properties
Abstract
:1. Introduction
2. Material and Methods
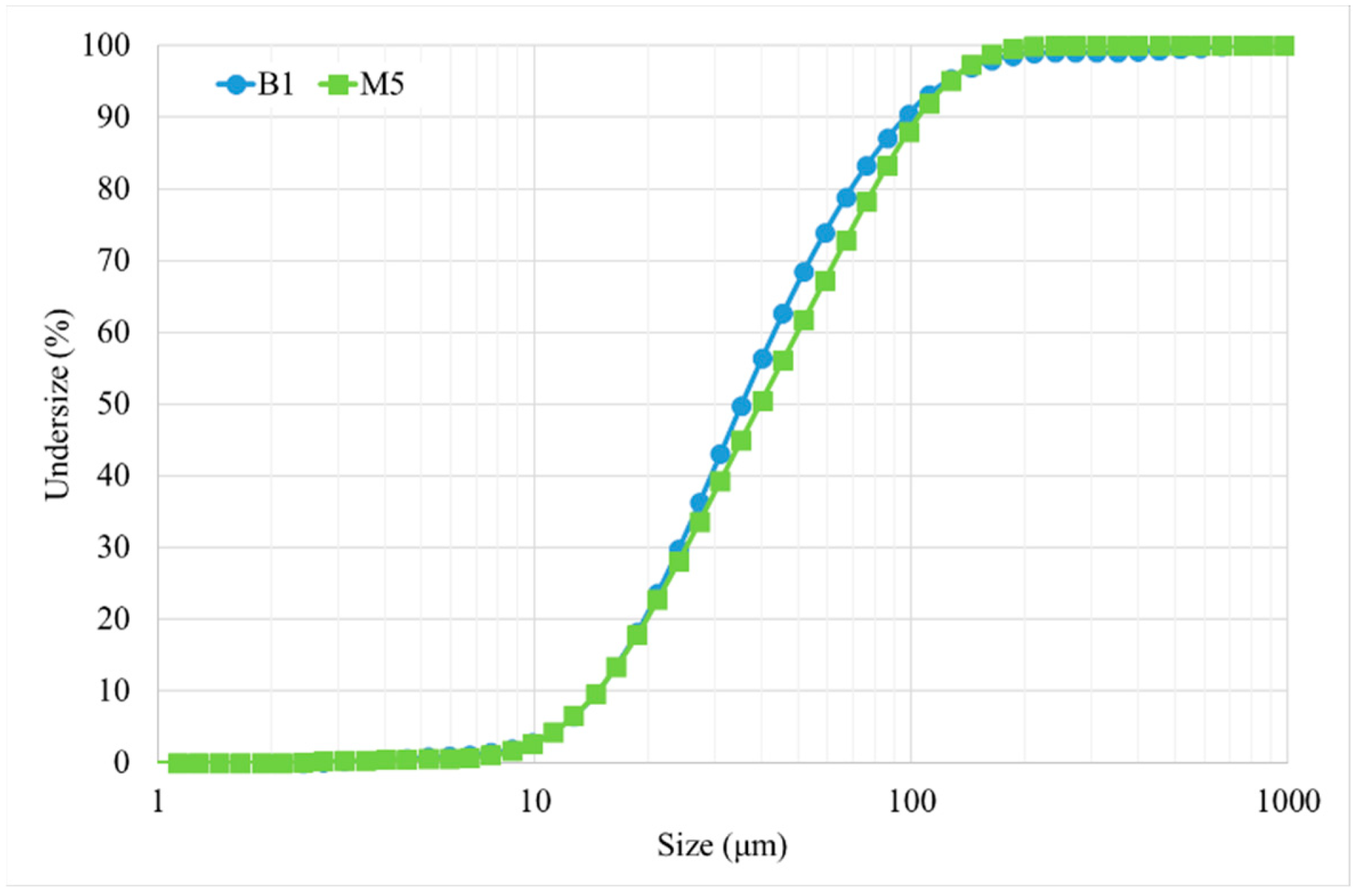
2.1. As-Received Powder
2.2. HIP + HT and Samples Preparation
2.3. Microstructural Assessment
2.4. Hardness Evaluation
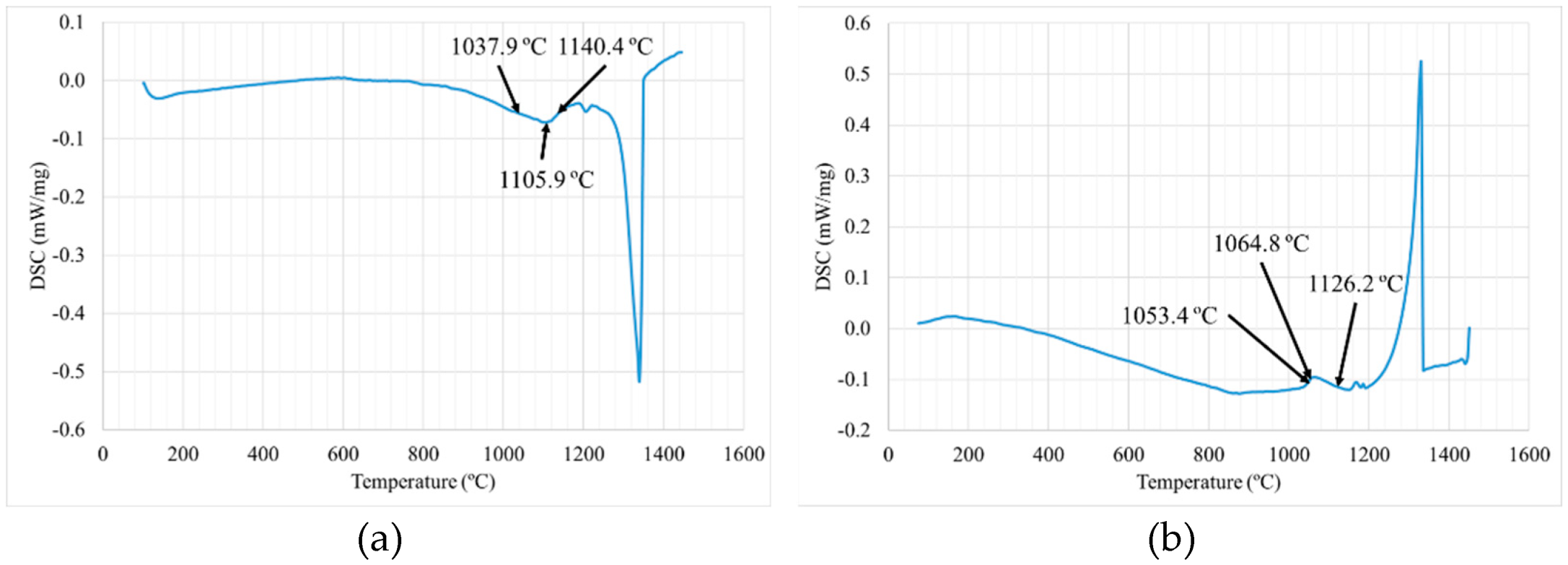
2.5. DSC Measurements
2.6. Simulations of Cooling Rates
3. Results
3.1. Study A, Simulation Model
3.1.1. DSC Analysis
3.1.2. Solutioning Cooling Process for Simulation
3.1.3. Hardness Measurements after Solutioning
3.1.4. γ′. Quantification and Classification after Solutioning
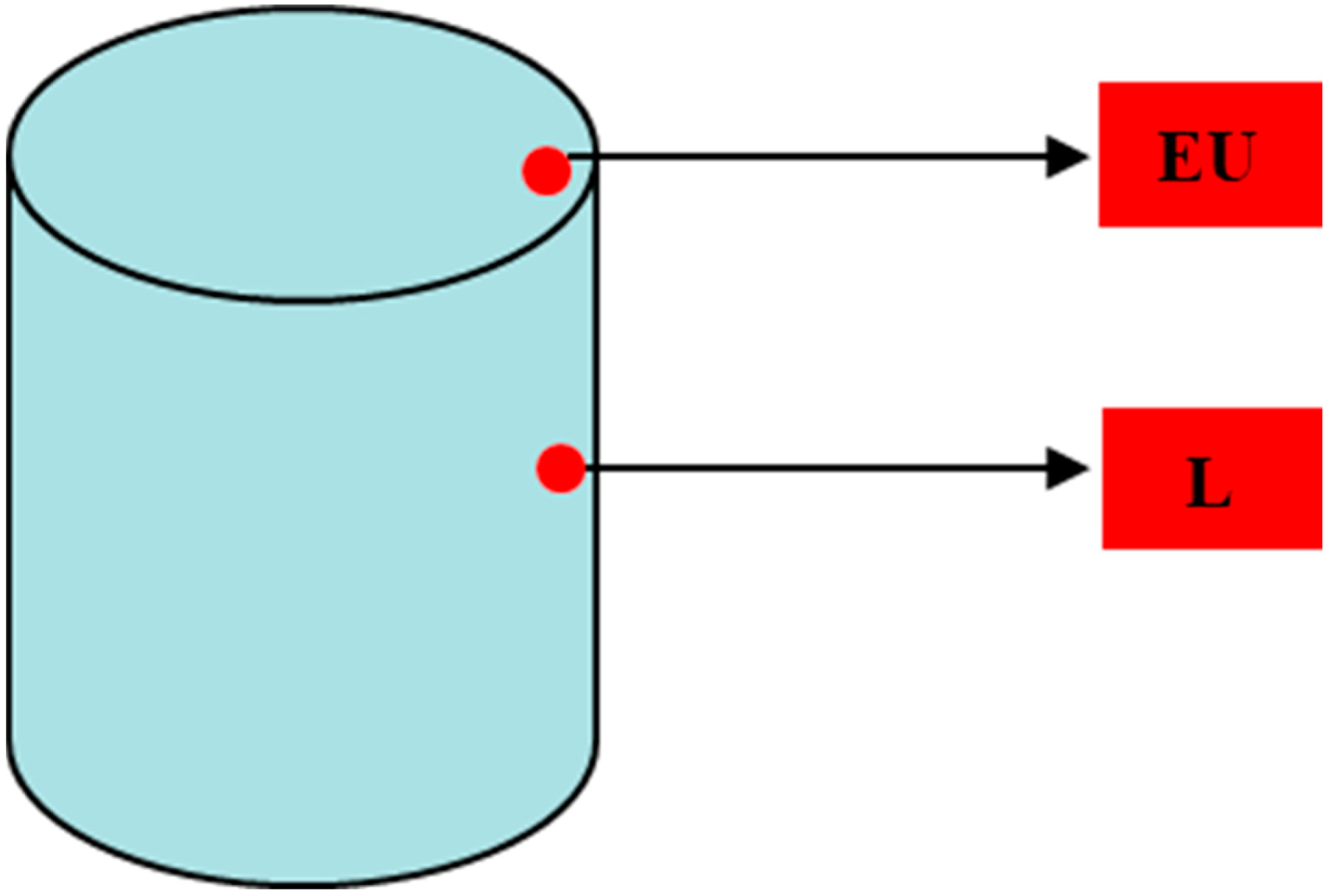
3.1.5. Hardness Mapping after HT-A
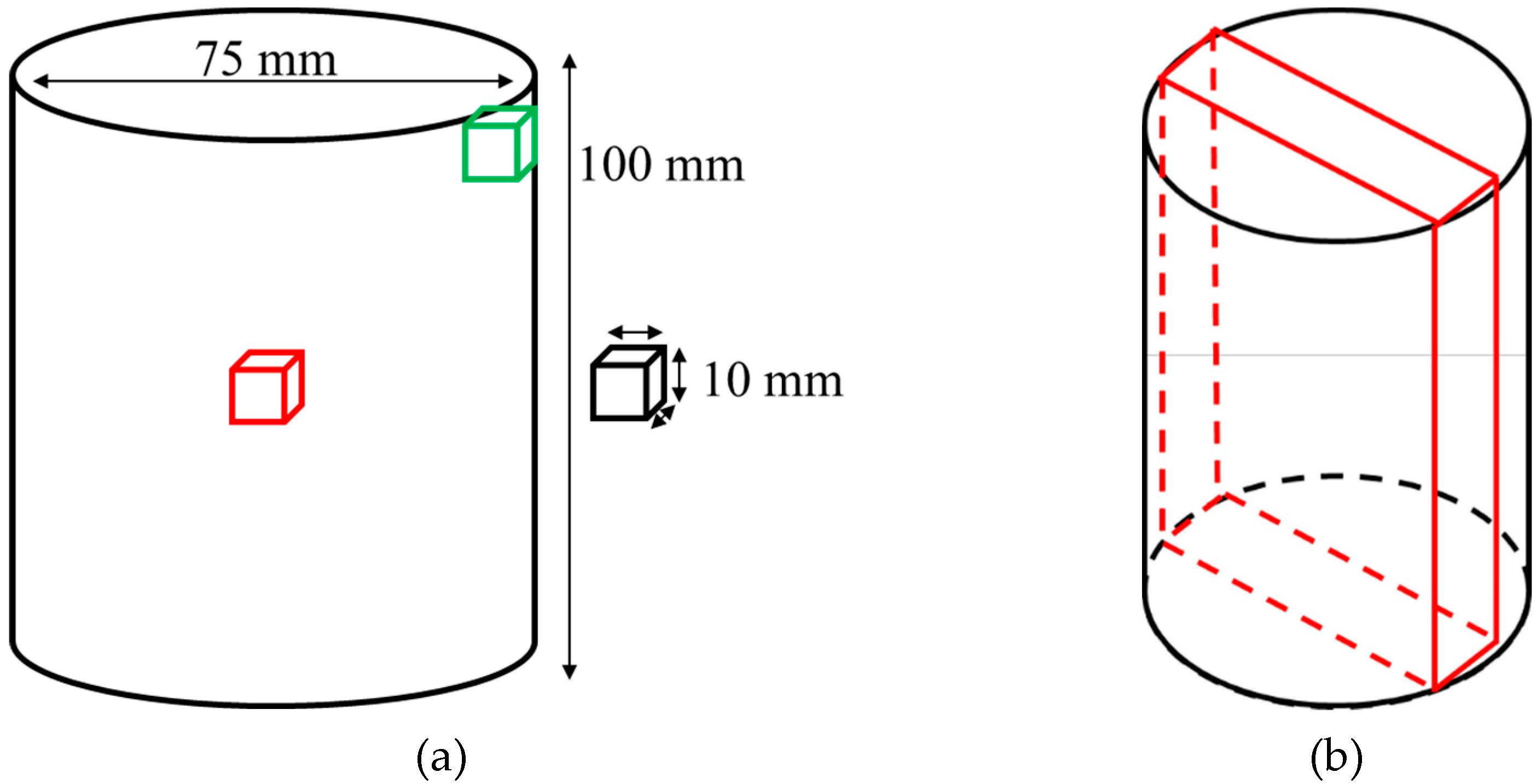
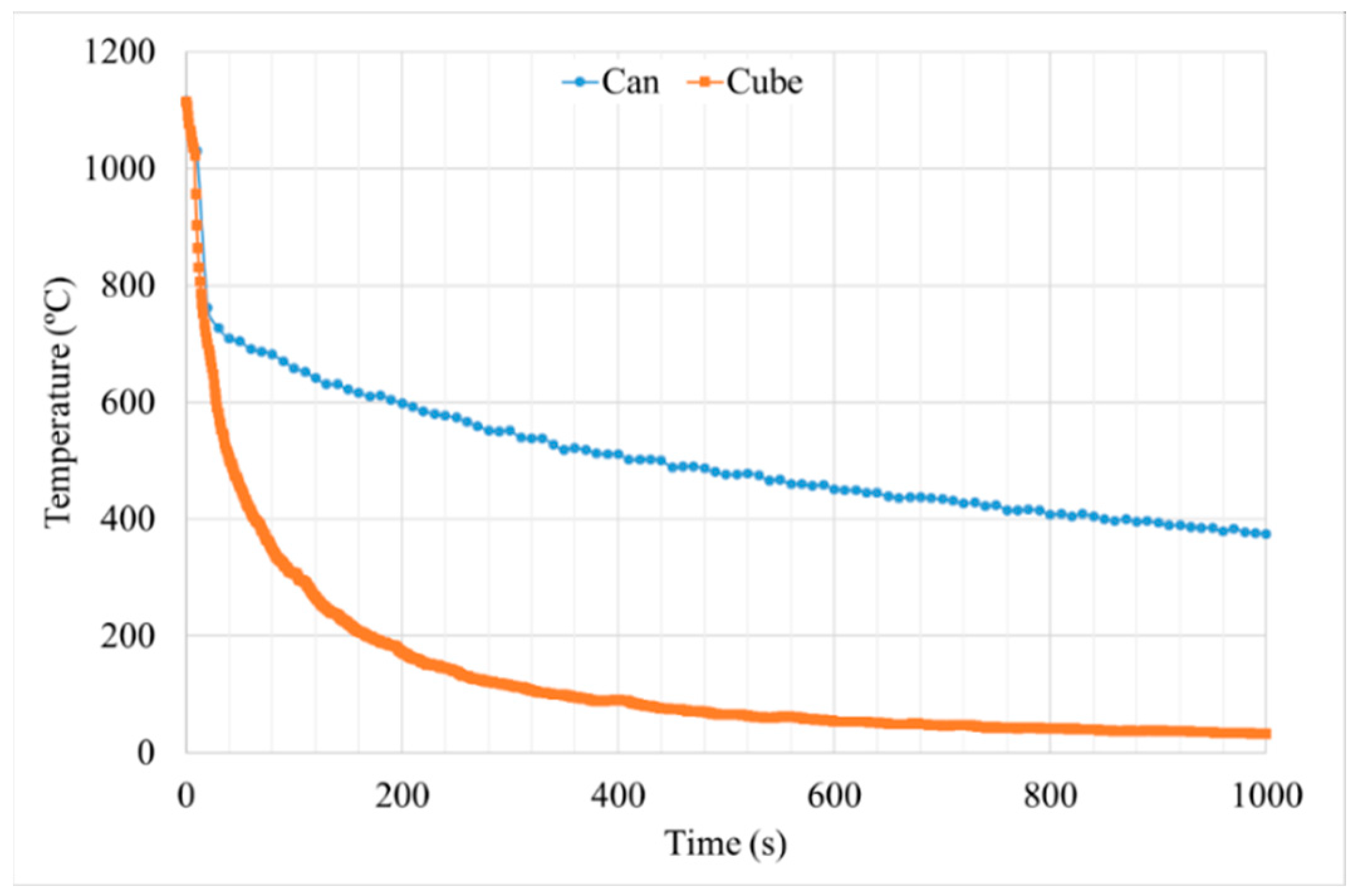
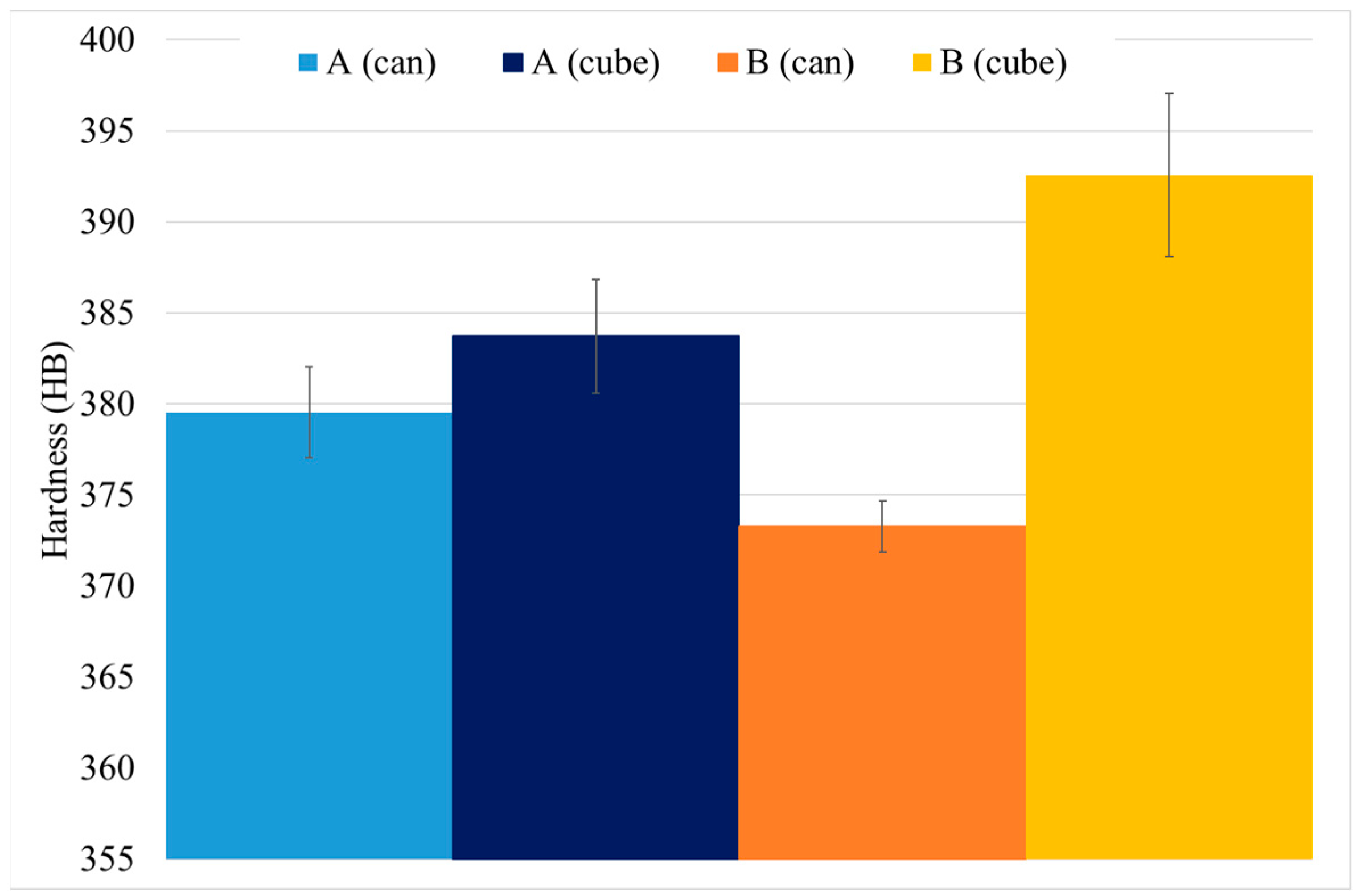
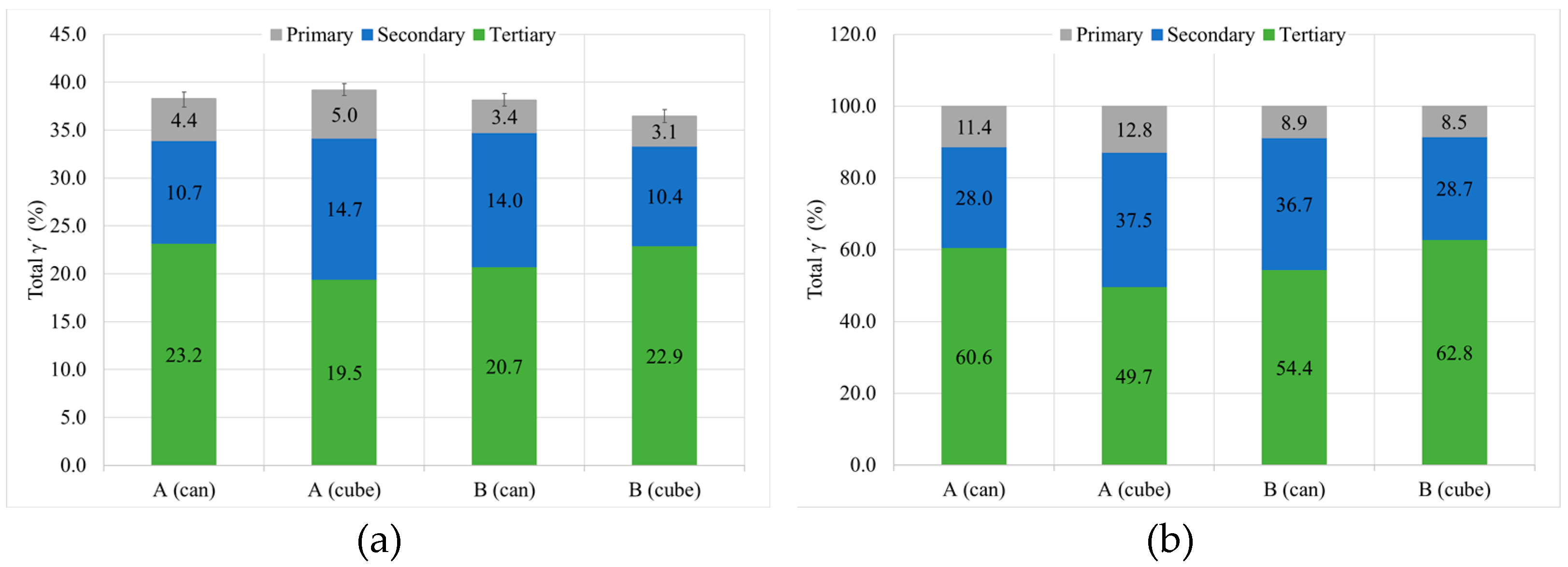
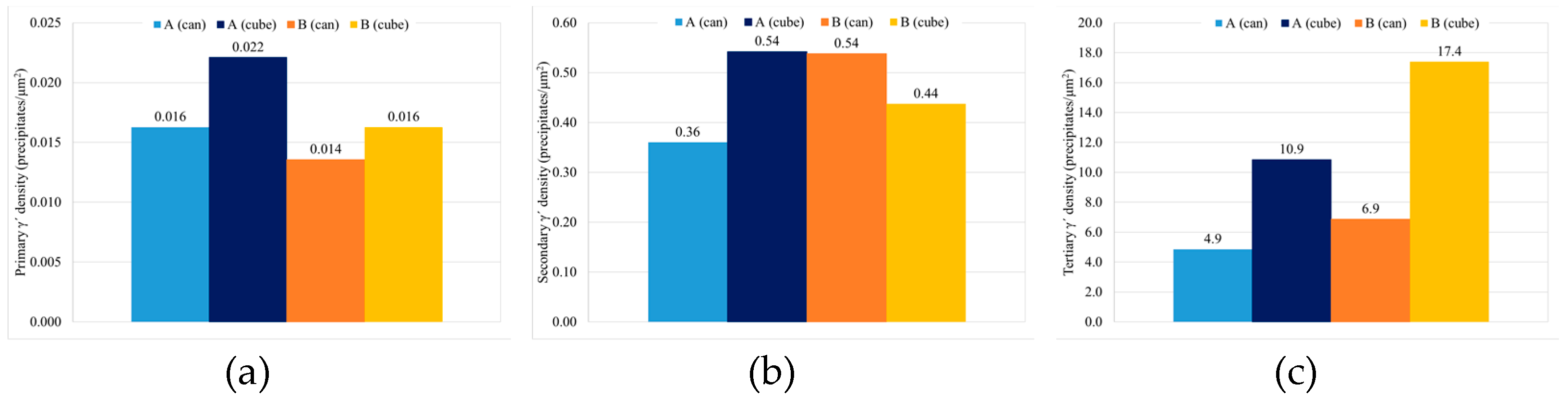
3.2. Study B, Can and Cube Samples
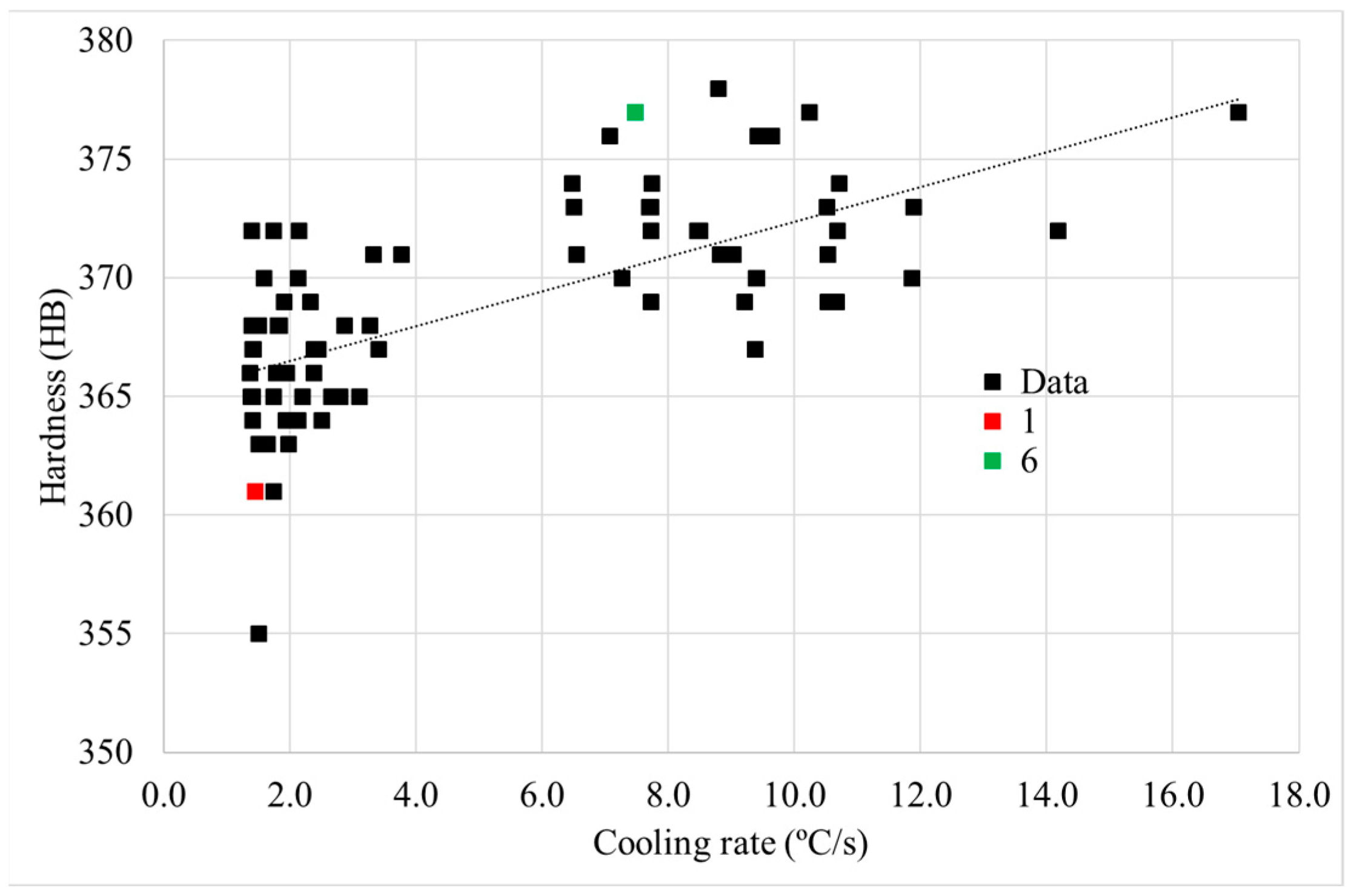
3.2.1. Cooling Rate
3.2.2. Hardness Determination
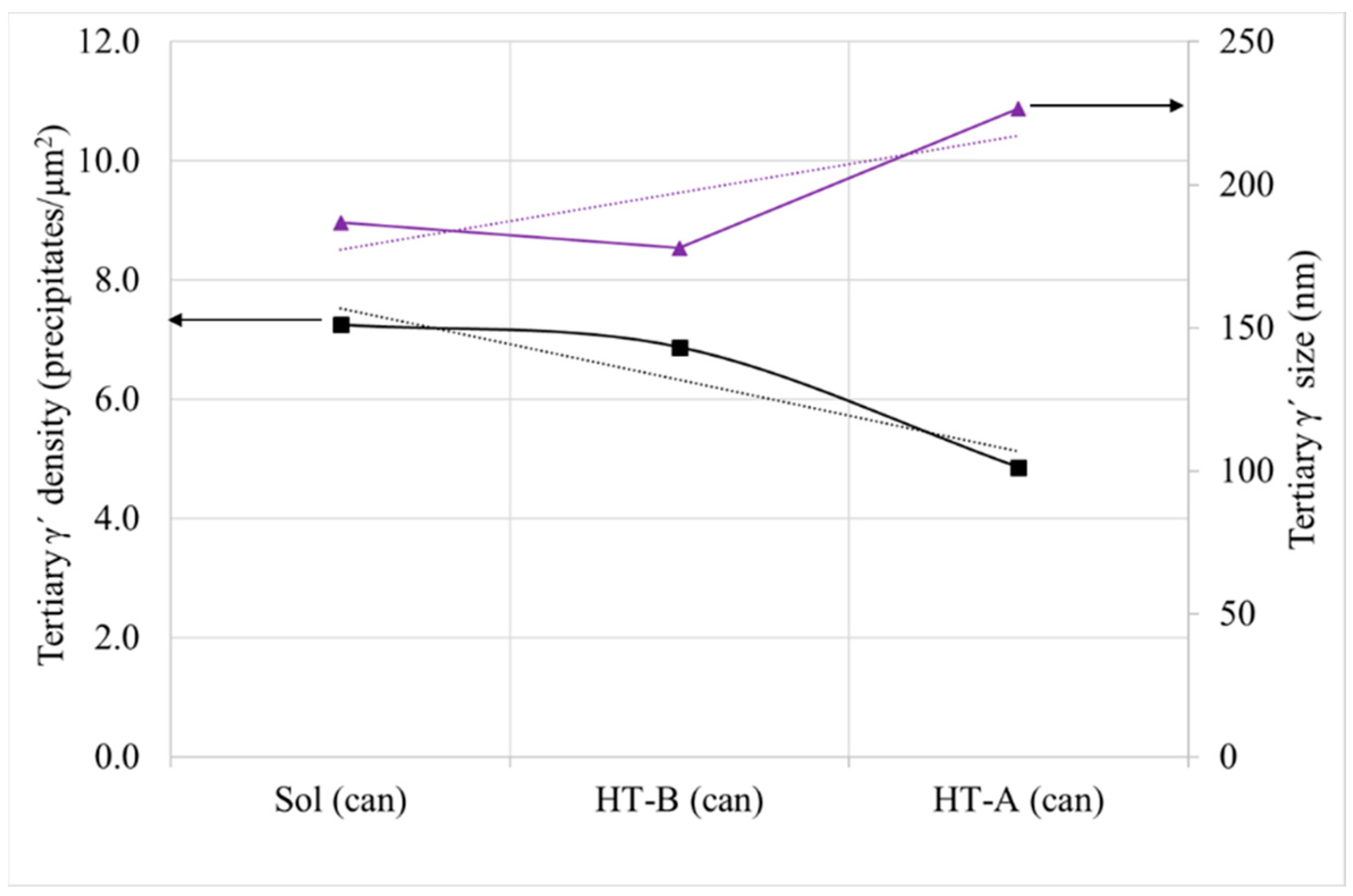
3.2.3. γ′. Determination
4. Discussion
4.1. Study A
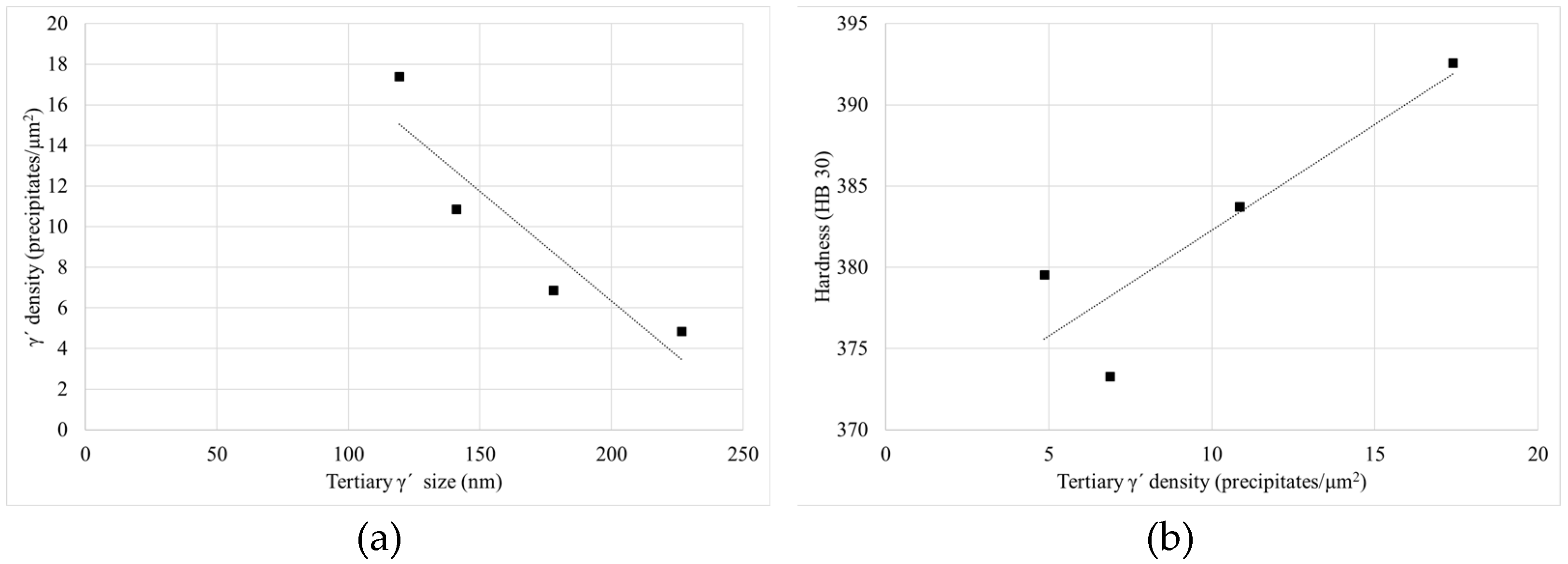
4.1.1. Relationship between Cooling Rate, Hardness and γ′ Microstructure after Solutioning
4.1.2. Solutioning Cooling Rate Effect on the Final Hardness of a Full HTed Component
4.2. Study B
5. Conclusions
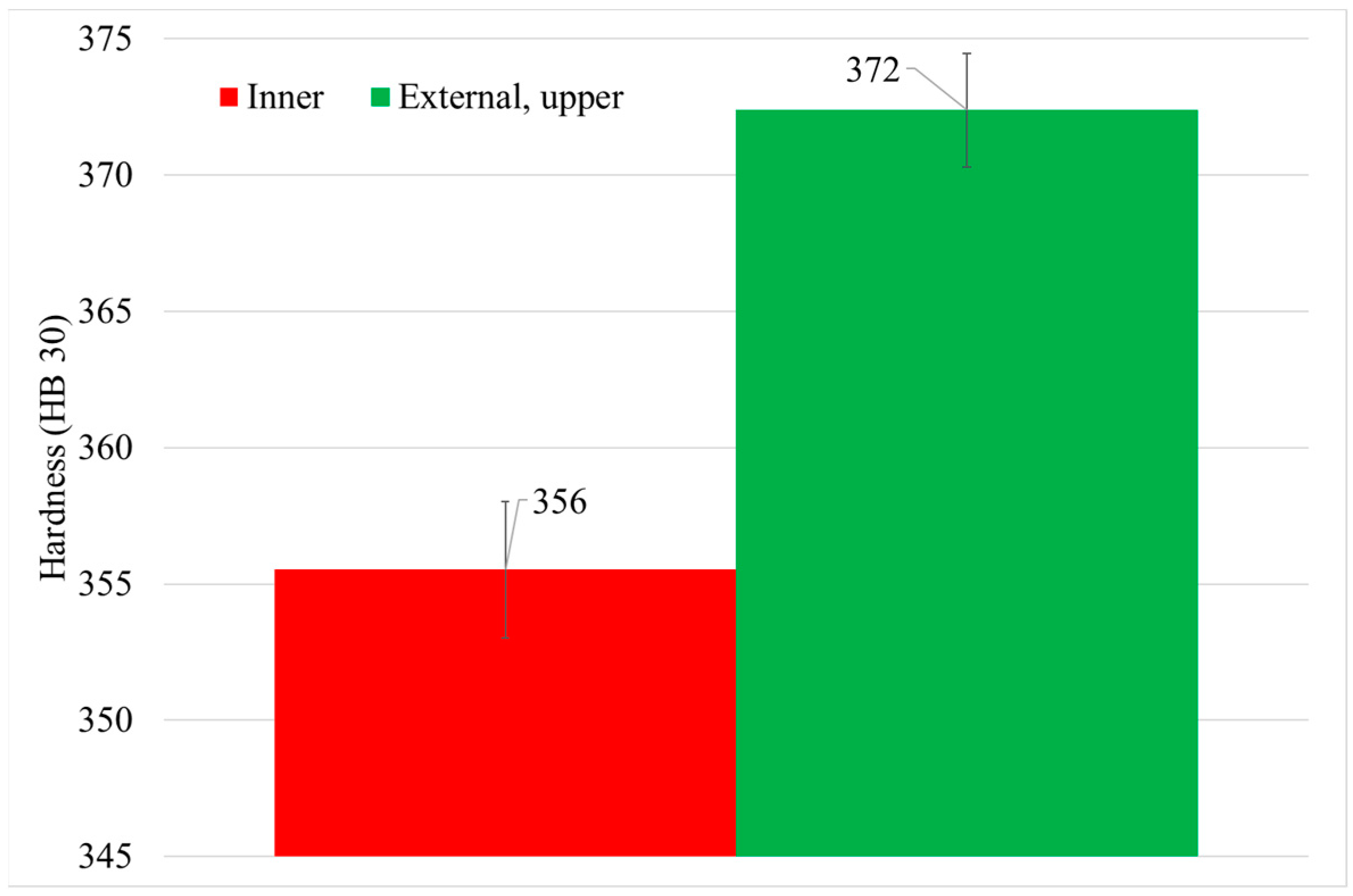
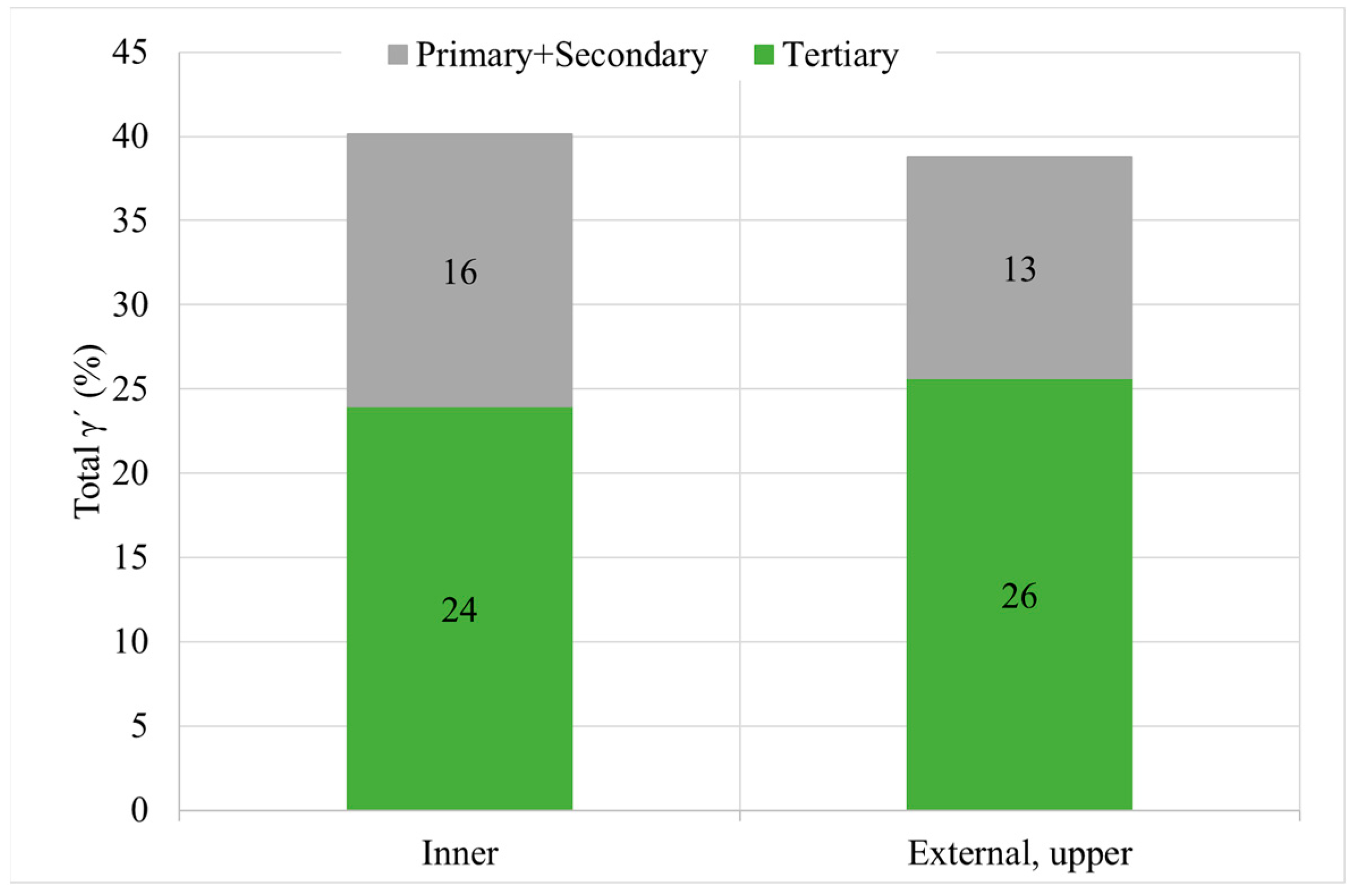
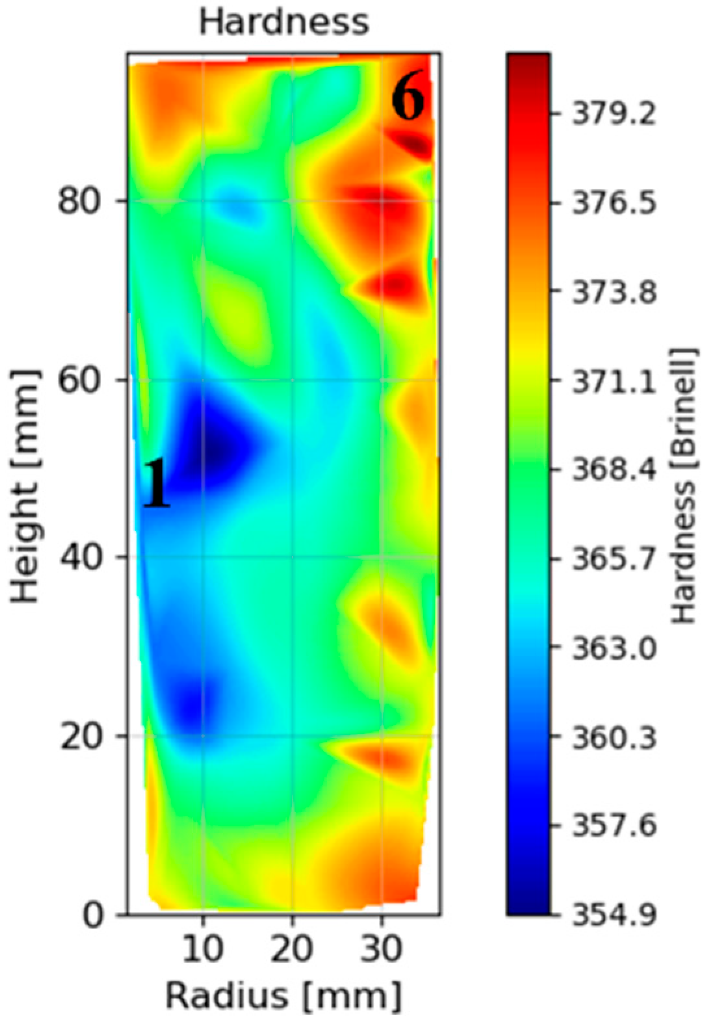
- First, after solutioning, a correlation between cooling rate and hardness inside big components has been confirmed. Moreover, this has been proved to be related to the variation in γ′ system. Higher cooling rate leads to a higher density of tertiary γ′ precipitates with a lower size. The external area of the can has an 85% more of tertiary γ′ precipitates with a 22% lower size than the inner part, which leads to an increase of 16 HB 30. However, the external part of the component that suffers this high cooling rate is small.
- After a full HT, the hardness differences in the component tend to reduce, but a small difference is maintained. The hardness differences between the external and the inner part of the can are reduced from 16 to 6 HB 30. Therefore, it would be recommendable to have a track of the place that samples are extracted inside big components. This effect could be much higher in gigantic parts, and could be the subject of a future work.
- HTs after solutioning provokes the increase in the volume fraction of γ′, mainly through coarsening and coalescence of the previous existent precipitates, as can be seen in the decreasing population density of tertiary γ′. In the case of cans, from solutioning to a full standard HT (HT-A), the density of tertiary γ′ precipitates decreases by 33%, whereas their size increases by 21%. These means of precipitation are related to the obtention of the lower energy state in the material, reducing the interface energy between γ and γ′.
- Cube samples have much higher cooling rates than cans due to their much lower thermal mass, which produces a much finer microstructure. As a result, cube samples have double the number tertiary γ′ precipitates with a reduction in size of at least 33%, which increases cube sample hardness by a minimum of 4 HB 30.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gessinger, G.H. Introduction. In Powder Metallurgy of Superalloys; Butterworth-Heinemann: Oxford, UK, 1984. [Google Scholar] [CrossRef]
- Reed, R.C. The Superalloys: Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Bassini, E.; Galech, U.; Soria, T.; Aristizabal, M.; Iturriza, I.; Biamino, S.; Ugues, D. Effect of the particle size distribution on physical properties, composition, and quality of gas atomized Astroloy powders for HIP application. J. Alloys Compd. 2021, 890, 161631. [Google Scholar] [CrossRef]
- Fernsler, E. Nickel-Base Alloys. In CRC Handbook of Materials Science; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar] [CrossRef]
- Gewin, V. The Jet Engine. Nature 2019, 574, 590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Long, H.; Mao, S.; Liu, Y.; Zhang, Z.; Han, X. Microstructural and compositional design of Ni-based single crystalline superalloys—A review. J. Alloys Compd. 2018, 743, 203–220. [Google Scholar] [CrossRef]
- Gogia, A.K. High-temperature titanium alloys. Def. Sci. J. 2005, 55, 149–173. [Google Scholar] [CrossRef]
- Blavette, D.; Cadel, E.; Pareige, C.; Deconihout, B.; Caron, P. Phase Transformation and Segregation to Lattice Defects in Ni-Base Superalloys. Microsc. Microanal. 2007, 13, 464–483. [Google Scholar] [CrossRef] [PubMed]
- Bassini, E.; Cattano, G.; Marchese, G.; Biamino, S.; Ugues, D.; Lombardi, M.; Vallillo, G.; Picqué, B. Study of the Effects of Aging Treatment on Astroloy Processed via Hot Isostatic Pressing. Materials 2019, 12, 1517. [Google Scholar] [CrossRef] [Green Version]
- Masoumi, F.; Jahazi, M.; Shahriari, D.; Cormier, J. Coarsening and dissolution of γ′ precipitates during solution treatment of AD730™ Ni-based superalloy: Mechanisms and kinetics models. J. Alloys Compd. 2016, 658, 981–995. [Google Scholar] [CrossRef]
- McLean, D. Predicting growth of γ′ in nickel alloys. Met. Sci. 1984, 18, 249–256. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, H.; He, X.; Din, R.U.; Qu, X.; Qin, M.; Li, Z.; Zhang, G. Thermal evolution behavior of carbides and γ′ precipitates in FGH96 superalloy powder. Mater. Charact. 2012, 67, 52–64. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, X.; Du, K.; Zhou, Y.; Jin, T.; Ye, H. Microstructure of Carbides at Grain Boundaries in Nickel Based Superalloys. J. Mater. Sci. Technol. 2012, 28, 1031–1038. [Google Scholar] [CrossRef]
- Bassini, E.; Vola, V.; Lorusso, M.; Ghisleni, R.; Lombardi, M.; Biamino, S.; Ugues, D.; Vallillo, G.; Picqué, B. Net shape HIPping of Ni-superalloy: Study of the interface between the capsule and the alloy. Mater. Sci. Eng. A 2017, 695, 55–65. [Google Scholar] [CrossRef]
- Bassini, E.; Basile, G.; Marchese, G.; Lorusso, M.; Lombardi, M.; Picqué, B.; Biamino, S.; Ugues, D. Assessment of the reinforcing system and carbides evolution in hot isostatically pressed astroloy after prolonged exposure at 820 °C. Mater. Sci. Eng. A 2020, 773, 138879. [Google Scholar] [CrossRef]
- Huron, E.S.; Bain, K.R.; Mourer, D.P.; Schirra, J.J.; Reynolds, P.L.; Montero, E.E. The influence of grain boundary elements on properties and microstructures of P/M nickel base superalloys. Superalloys 2004, 73–81. [Google Scholar] [CrossRef]
- Bampton, C.; Goodin, W.; Van Daam, T.; Creeger, G.; James, S. Net-Shape HIP Powder Metallurgy Components for Rocket Engines, (n.d.). Available online: https://ntrs.nasa.gov/api/citations/20050181957/downloads/20050181957.pdf (accessed on 21 September 2021).
- Ezugwu, E.O.; Wang, Z.M.; Machado, A.R. The machinability of nickel-based alloys: A review. J. Mater. Process. Technol. 1999, 86, 1–16. [Google Scholar] [CrossRef]
- Raisson, G.; Guédou, J.Y.; Guichard, D.; Rongvaux, J.M. Production of Net-Shape Static Parts by Direct HIPing of Nickel Base Superalloy Prealloyed Powders. Adv. Mater. Res. 2011, 278, 277–282. [Google Scholar] [CrossRef] [Green Version]
- Kissinger, R.D.; Nair, S.; Tien, J. Influence of Powder Particle Size Distribution and Pressure on the Kinetics of Hot Isostatic Pressing (HIP) Consolidation of P/M Superalloy Rene 95. Superalloys 1984, 285–294. [Google Scholar] [CrossRef]
- Rao, G.A.; Srinivas, M.; Sarma, D. Influence of modified processing on structure and properties of hot isostatically pressed superalloy Inconel 718. Mater. Sci. Eng. A 2006, 418, 282–291. [Google Scholar] [CrossRef]
- Rao, G.; Kumar, M.; Srinivas, M.; Sarma, D. Effect of standard heat treatment on the microstructure and mechanical properties of hot isostatically pressed superalloy inconel 718. Mater. Sci. Eng. A 2003, 355, 114–125. [Google Scholar] [CrossRef]
- Ning, Y.; Fu, M.; Yao, W. Recrystallization of the hot isostatic pressed nickel-base superalloy FGH4096. II: Characterization and application. Mater. Sci. Eng. A 2012, 539, 101–106. [Google Scholar] [CrossRef]
- Wang, X.; Carter, L.N.; Adkins, N.J.E.; Essa, K.; Attallah, M.M. Novel Hybrid Manufacturing Process of CM247LC and Multi-Material Blisks. Micromachines 2020, 11, 492. [Google Scholar] [CrossRef]
- Bassini, E.; Marchese, G.; Cattano, G.; Lombardi, M.; Biamino, S.; Ugues, D.; Vallillo, G.; Picqué, B. Influence of solutioning on microstructure and hardness of hot isostatically pressed Astroloy. J. Alloys Compd. 2017, 723, 1082–1090. [Google Scholar] [CrossRef]
- Kim, M.; Chang, S.; Won, J. Effect of HIP process on the micro-structural evolution of a nickel-based superalloy. Mater. Sci. Eng. A 2006, 441, 126–134. [Google Scholar] [CrossRef]
- Sczerzenie, F.; Maurer, G. Development of Udimet 720 for High Strength Disk Applications. Superalloys 1984, 573–580. [Google Scholar] [CrossRef]
- Baldan, R.; Da Rocha, R.L.P.; Tomasiello, R.B.; Nunes, C.A.; da Silva Costa, A.M.; Barboza, M.J.R.; Coelho, G.C.; Rosenthal, R. Solutioning and Aging of MAR-M247 Nickel-Based Superalloy. J. Mater. Eng. Perform. 2013, 22, 2574–2579. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, Y.; Zhao, Z.; Zhang, Z. Effects of Solutioning on the Dissolution and Coarsening of γ′ Precipitates in a Nickel-Based Superalloy. J. Mater. Eng. Perform. 2015, 24, 1492–1504. [Google Scholar] [CrossRef]
- Masoumi, F.; Shahriari, D.; Jahazi, M.; Cormier, J.; Devaux, A. Kinetics and Mechanisms of γ′ Reprecipitation in a Ni-based Superalloy. Sci. Rep. 2016, 6, 28650. [Google Scholar] [CrossRef] [Green Version]
- Ardell, A.J. The effect of volume fraction on particle coarsening: Theoretical considerations. Acta Metall. 1972, 20, 61–71. [Google Scholar] [CrossRef]
- Davies, C.K.L.; Nash, P.; Stevens, R.N. The effect of volume fraction of precipitate on ostwald ripening. Acta Metall. 1980, 28, 179–189. [Google Scholar] [CrossRef]
- Footner, P.K.; Richards, B.P. Long—Term growth of superalloy γ′ particles. J. Mater. Sci. 1982, 17, 2141–2153. [Google Scholar] [CrossRef]
- Vaunois, J.R.; Cormier, J.; Villechaise, P.; Devaux, A.; Flageolet, B. Influence of both γ′ distribution and grain size on the tensile properties of UDIMET 720Li at room temperature. In Superalloy 718 and Derivatives; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010; pp. 199–213. [Google Scholar] [CrossRef]
- Wangyao, P.; Polsilapa, S.; Chaishom, P.; Zrnik, J.; Homkrajai, W.; Panich, N. Gamma Prime Particle Coarsening Behavior at Elevated Temperatures in Cast Nickel-Based Superalloy, GTD-111 EA. High Temp. Mater. Process. 2008, 27, 41–49. [Google Scholar] [CrossRef] [Green Version]
- Maciejewski, K.; Ghonem, H. Isotropic and kinematic hardening as functions of gamma prime precipitates in a nickel-based superalloy. Int. J. Fatigue 2014, 68, 123–135. [Google Scholar] [CrossRef]







| Powders | Ni | Co | Cr | Mo | Al | Ti | Fe | B | C | O |
|---|---|---|---|---|---|---|---|---|---|---|
| B1 | 55.3 | 17.0 | 15.3 | 4.8 | 3.9 | 3.6 | 0.05 | 0.026 | 0.015 | 0.015 |
| M5 | 55.3 | 16.8 | 15.1 | 5.0 | 3.9 | 3.8 | 0.06 | 0.026 | 0.020 | 0.009 |
| HT | Solution | S1 | S2 | P1 | P2 |
|---|---|---|---|---|---|
| A | X | X | X | X | X |
| B | X | X |
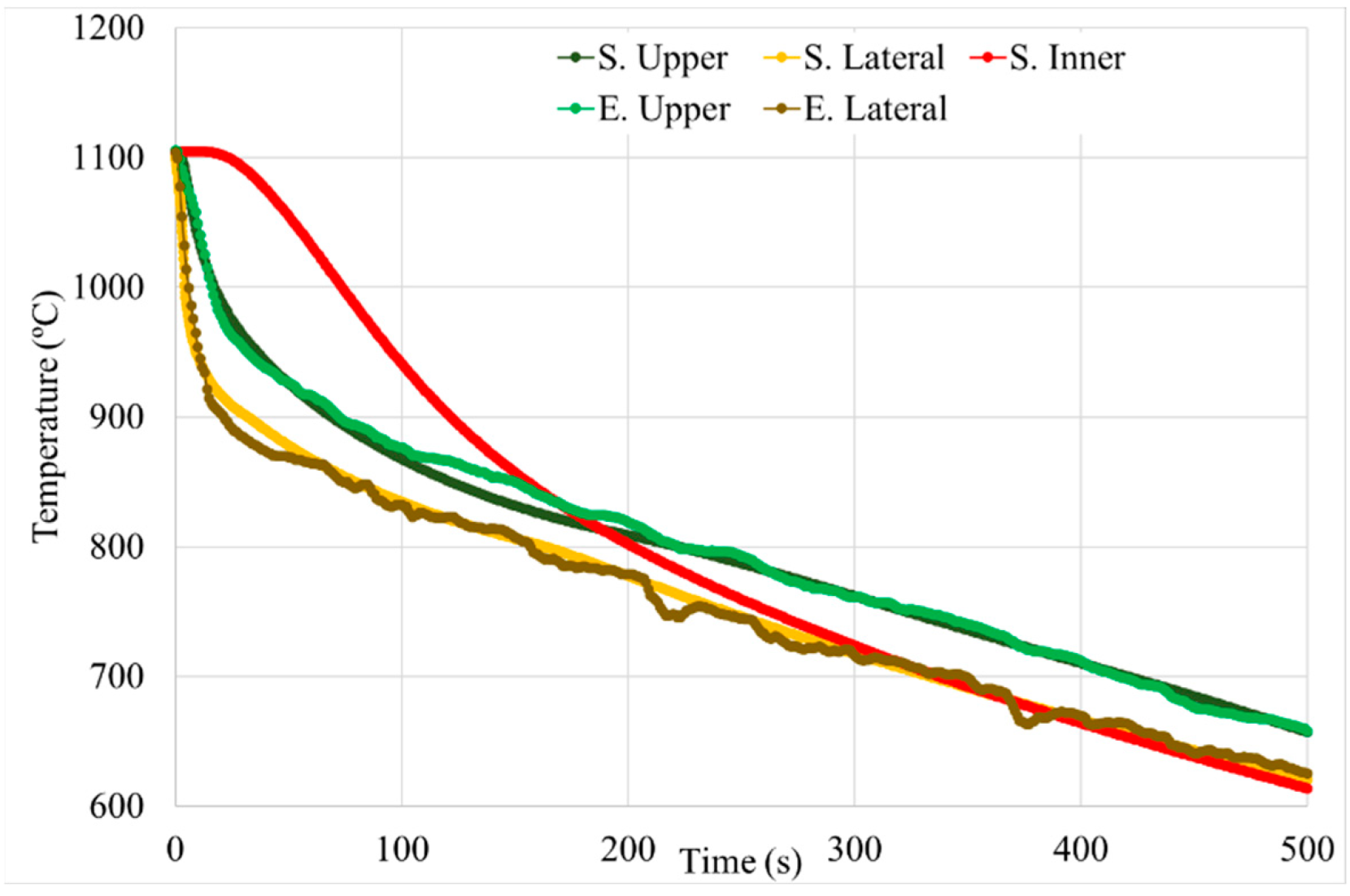
| Area | Data | Cooling Rate (°C/s) |
|---|---|---|
| Upper | Experimental | 5.3 |
| Simulation | 6.4 | |
| Lateral | Experimental | 16.6 |
| Simulation | 19.0 | |
| Inner | Simulation | 1.3 |
| Sample | Cooling Rate (°C/s) |
|---|---|
| Can | 0.8 |
| Cube | 11.2 |
| Location | Cooling Rate (°C/s) | Hardness (HB 30) | Tertiary γ′ Density (Precipitates/μm2) | Tertiary γ′ Size (nm) |
|---|---|---|---|---|
| Inner (1) | 1.3 | 356 ± 3 | 7.3 | 187 ± 66 |
| External upper (6) | 6.4 | 372 ± 2 | 13.5 | 145 ± 44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Napal, U.G.; Segarra, M.A.; Lazcano, B.E.; Sivo, A.; Zubillaga, I.I. Thermal Mass Effect on the Solution Cooling Rate and on HIPped Astroloy Component Properties. Materials 2022, 15, 1434. https://doi.org/10.3390/ma15041434
Napal UG, Segarra MA, Lazcano BE, Sivo A, Zubillaga II. Thermal Mass Effect on the Solution Cooling Rate and on HIPped Astroloy Component Properties. Materials. 2022; 15(4):1434. https://doi.org/10.3390/ma15041434
Chicago/Turabian StyleNapal, Unai Galech, Miren Aristizabal Segarra, Borja Elguezabal Lazcano, Antonio Sivo, and Iñigo Iturriza Zubillaga. 2022. "Thermal Mass Effect on the Solution Cooling Rate and on HIPped Astroloy Component Properties" Materials 15, no. 4: 1434. https://doi.org/10.3390/ma15041434
APA StyleNapal, U. G., Segarra, M. A., Lazcano, B. E., Sivo, A., & Zubillaga, I. I. (2022). Thermal Mass Effect on the Solution Cooling Rate and on HIPped Astroloy Component Properties. Materials, 15(4), 1434. https://doi.org/10.3390/ma15041434








