Rotating Directional Solidification of Ternary Eutectic Microstructures in Bi-In-Sn: A Phase-Field Study
Abstract
:1. Introduction
2. Methods
- (i)
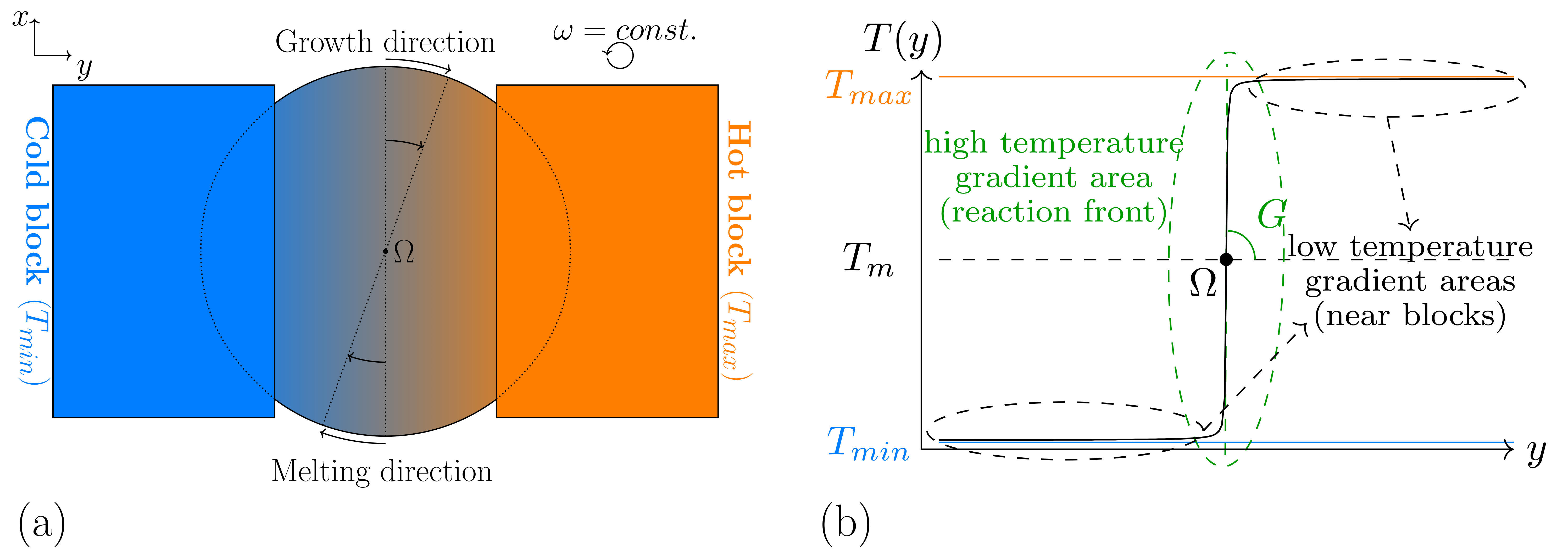
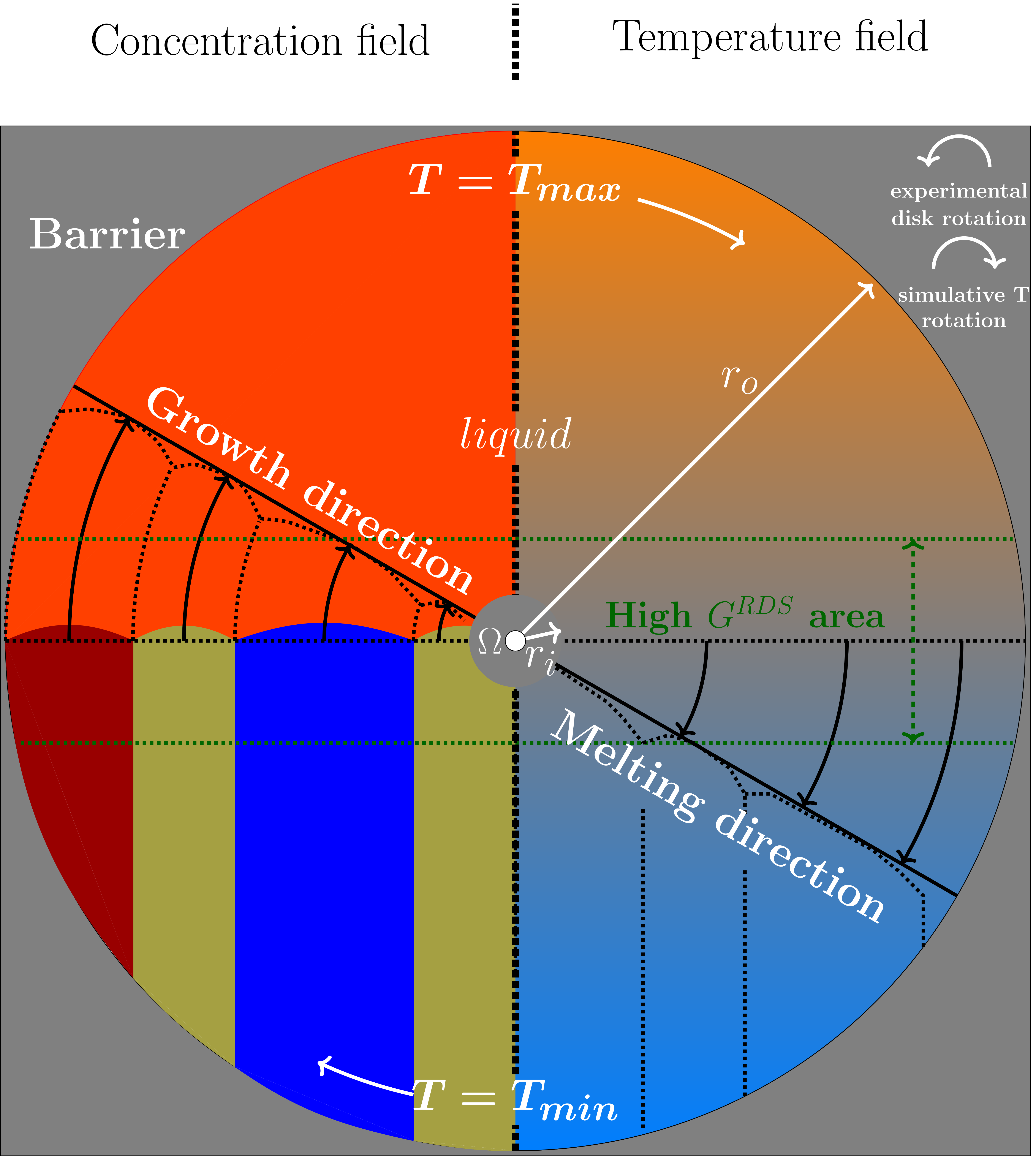
- The sought formulation for the temperature has to represent the effects of the hot and cold isothermal blocks, the effects of the temperature profile in between, and the caused variations of the temperature, due to the rotation. To resemble the near uniform distribution of the heat in the vicinity of the blocks, a low temperature gradient is required in these segments, whereas in the segments nearer to the disk center, containing the solidification front, a sharper temperature change is necessary. Hence, a linear function for the whole simulation domain with a constant temperature gradient amount, as described in Equation (5), is not favored. By using such a function, the system temperature can rise dramatically with increasing distance from the rotation center, which can lead to a destabilization of the modeled material system, specially in large domain simulations.
- (ii)
- To ensure a correct calculation of the evolution equations (Equations (1) and (2)), a continuously differentiable function is needed for the temperature, with respect to the space, in which differing amounts of the derivatives can exist in different space points. Based on this constraint, a piecewise function, composed of three linear functions with different temperature gradients can not be considered due to non-continuity of the first derivatives in the connection points.
3. Simulations and Results
3.1. Modeling the System Bi-In-Sn
3.2. Simulation Setup and Parameters
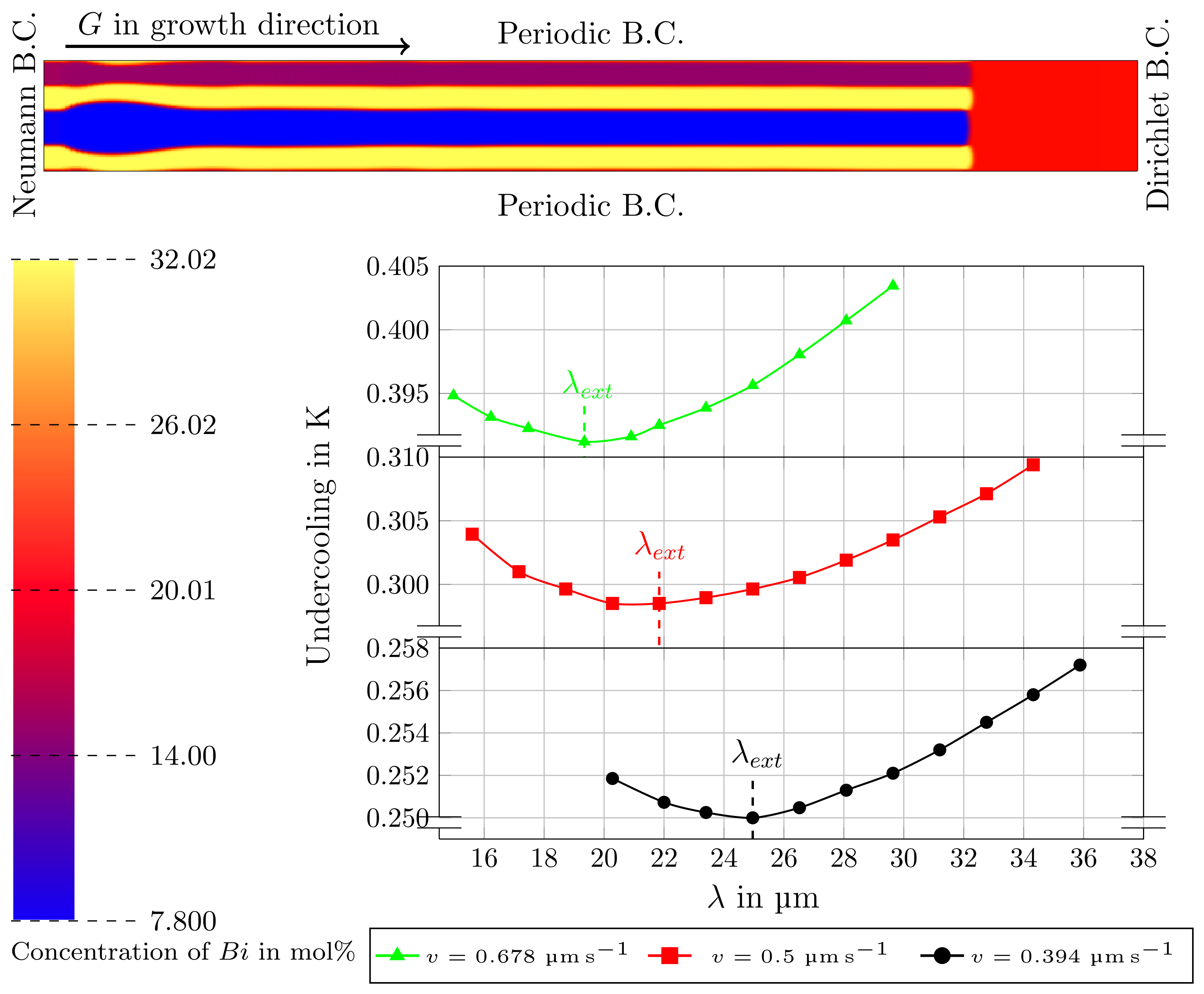
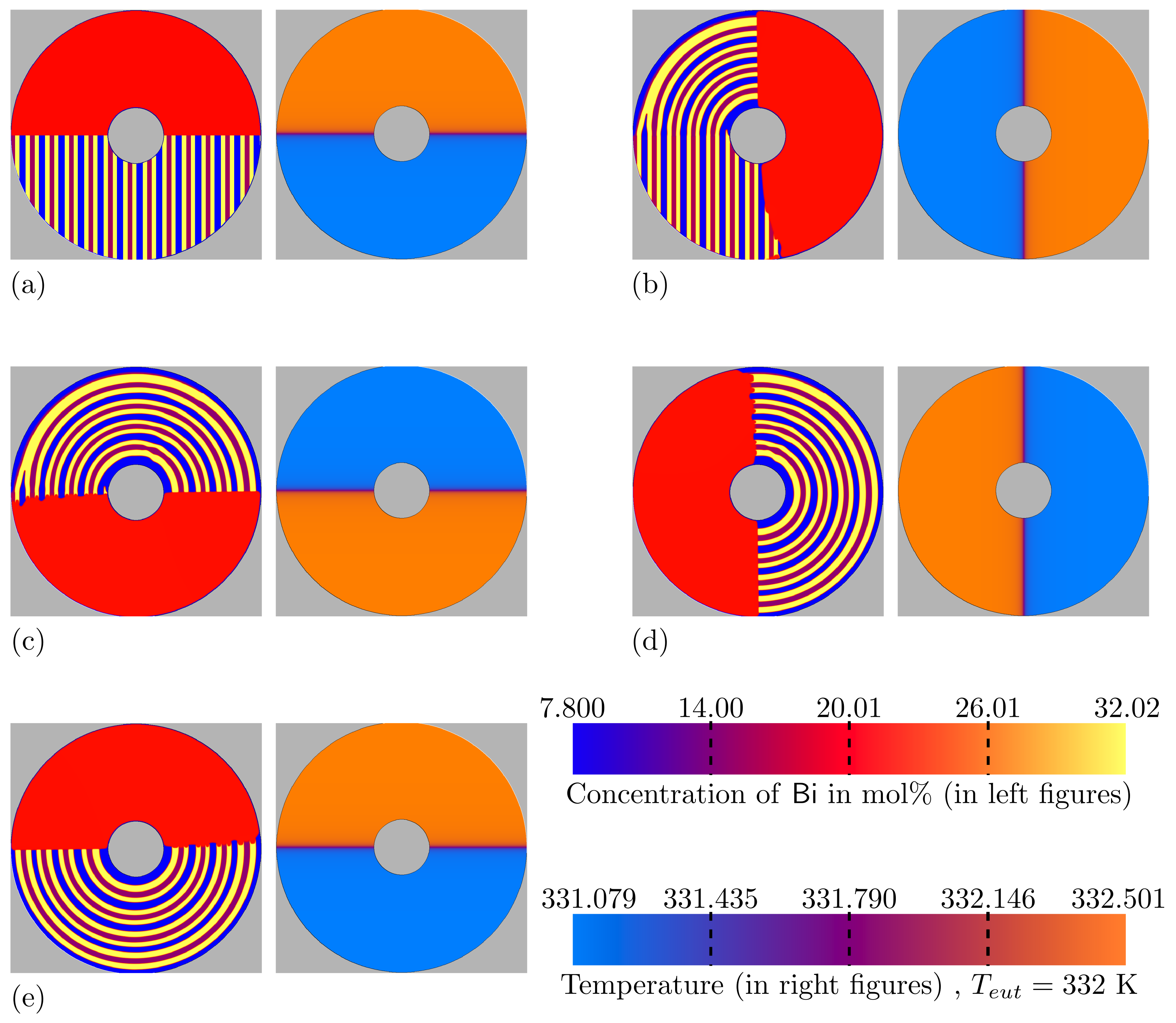
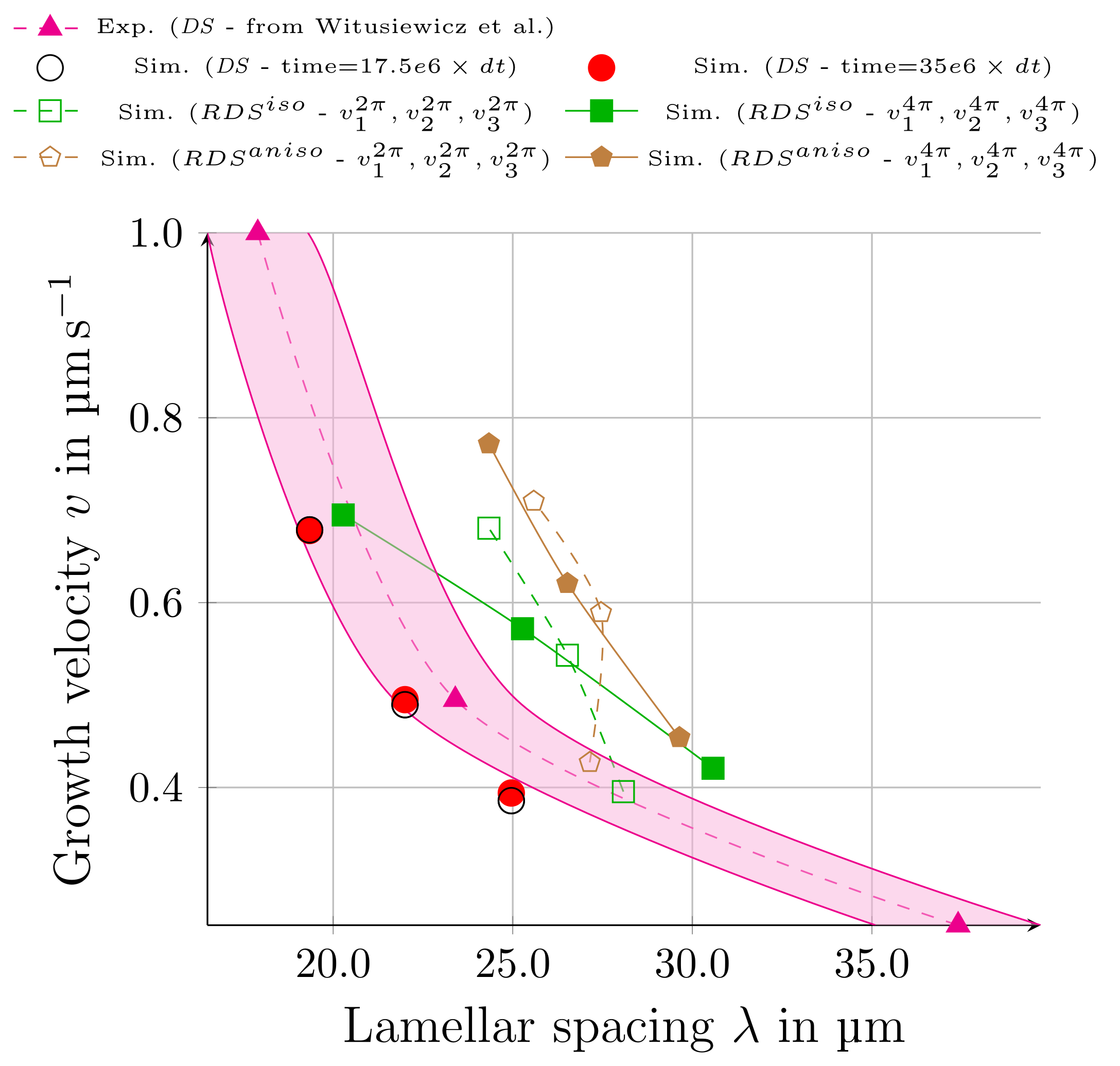
3.3. Directional Solidification (DS) Results
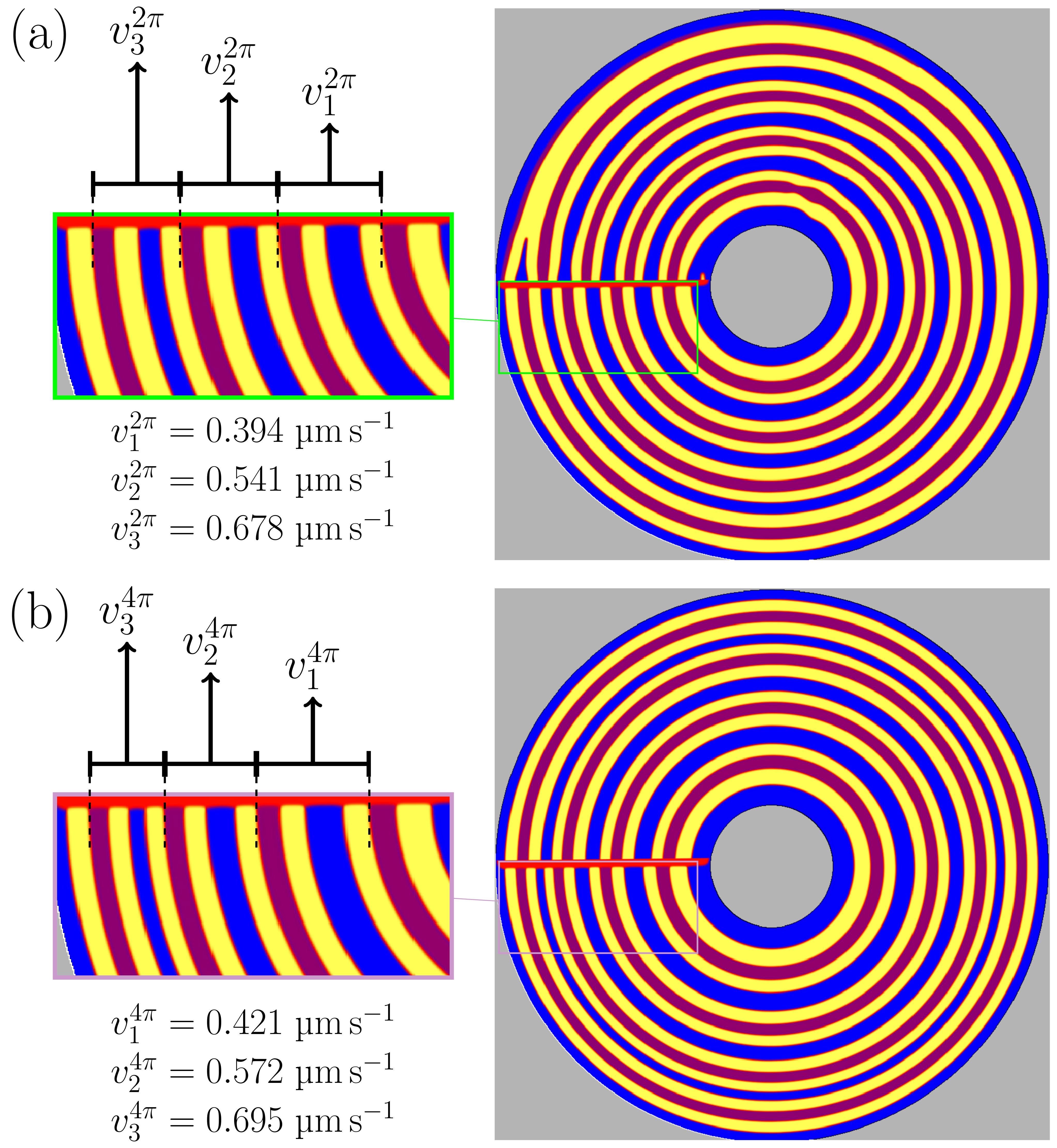
3.4. Rotating Directional Solidification (RDS) Results
4. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DS | Directional Solidification |
| RDS | Rotating Directional Solidification |
| Pace3D | Parallel Algorithms for Crystal Evolution in 3D |
Appendix A
| Parameters for the Gibbs Energy Function | ||
|---|---|---|
| Comparison of Calculated Values from Gibbs Energy Functions | ||||
|---|---|---|---|---|
| and the Calphad Database in J mol. | ||||
| Parameter | Simulation Value | Physical Value | |
|---|---|---|---|
| ,, | J m | ||
| , | J m | ||
| , | J m | [59] | |
| 15 | - | ||
| K | |||
| K | |||
| 1 | 332 K | [29] | |
| m s | [60] | ||
| 0 | 0 m s | ||
| 8 K mm | |||
| 0.786–240 K mm | |||
| °s | |||
| 1 | 332 K | ||
| µm | |||
| s | |||
| , | |||
| , | |||
| , | |||
| 0 | - | ||
| 0.15 | - |
| Property | Amount | Unit |
|---|---|---|
| Thermal expansion coefficient | °C | |
| Average density | g/cm |
References
- Hötzer, J.; Kellner, M.; Steinmetz, P.; Nestler, B. Applications of the Phase-Field Method for the Solidification of Microstructures in Multi-Component Systems. J. Indian Inst. Sci. 2016, 96, 235–256. [Google Scholar]
- Chen, L.Q. Phase-field models for microstructure evolution. Annu. Rev. Mater. Res. 2002, 32, 113–140. [Google Scholar] [CrossRef] [Green Version]
- Steinbach, I. Phase-field models in materials science. Model. Simul. Mater. Sci. Eng. 2009, 17, 073001. [Google Scholar] [CrossRef]
- Wesner, E.; Choudhury, A.; August, A.; Berghoff, M.; Nestler, B. A phase-field study of large-scale dendrite fragmentation in Al-Cu. J. Cryst. Growth 2012, 359, 107–121. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, B.; Hou, H.; Chen, W.; Wang, M. Phase-field simulation for the evolution of solid/liquid interface front in directional solidification process. J. Mater. Sci. Technol. 2019, 35, 1044–1052. [Google Scholar] [CrossRef]
- Galenko, P.; Reutzel, S.; Herlach, D.; Fries, S.; Steinbach, I.; Apel, M. Dendritic solidification in undercooled Ni-Zr-Al melts: Experiments and modeling. Acta Mater. 2009, 57, 6166–6175. [Google Scholar] [CrossRef]
- Choudhury, A.; Kellner, M.; Nestler, B. A method for coupling the phase-field model based on a grand-potential formalism to thermodynamic databases. Curr. Opin. Solid State Mater. Sci. 2015, 19, 287–300. [Google Scholar] [CrossRef]
- Enugala, S.N.; Kellner, M.; Kobold, R.; Hötzer, J.; Kolbe, M.; Nestler, B.; Herlach, D. Theoretical and numerical investigations of rod growth of an Ni–Zr eutectic alloy. J. Mater. Sci. 2019, 54, 12605–12622. [Google Scholar] [CrossRef]
- Hinrichs, F.; Kellner, M.; Hötzer, J.; Nestler, B. Calibration of a concentration-driven nucleation mechanism for phase-field simulations of eutectic and off-eutectic compositions in AlCu-5Ag. Scr. Mater. 2020, 186, 89–94. [Google Scholar] [CrossRef]
- Lo, T.S.; Karma, A.; Plapp, M. Phase-field modeling of microstructural pattern formation during directional solidification of peritectic alloys without morphological instability. Phys. Rev. E 2001, 63, 031504. [Google Scholar]
- Phelan, D.; Reid, M.; Dippenaar, R. Kinetics of the peritectic phase transformation: In-situ measurements and phase field modeling. Metall. Mater. Trans. A 2006, 37, 985–994. [Google Scholar] [CrossRef]
- Moelans, N.; Blanpain, B.; Wollants, P. An introduction to phase-field modeling of microstructure evolution. CALPHAD 2008, 32, 268–294. [Google Scholar] [CrossRef]
- Noubary, K.D.; Kellner, M.; Steinmetz, P.; Hötzer, J.; Nestler, B. Phase-field study on the effects of process and material parameters on the tilt angle during directional solidification of ternary eutectics. Comput. Mater. Sci. 2017, 138, 403–411. [Google Scholar] [CrossRef]
- Akamatsu, S.; Faivre, G. Anisotropy-driven dynamics of cellular fronts in directional solidification in thin samples. Phys. Rev. E 1998, 58, 3302. [Google Scholar] [CrossRef]
- Akamatsu, S.; Plapp, M. Eutectic and peritectic solidification patterns. Curr. Opin. Solid State Mater. Sci. 2016, 20, 46–54. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.; Choudhury, A.; Plapp, M.; Bottin-Rousseau, S.; Faivre, G.; Akamatsu, S. Interphase anisotropy effects on lamellar eutectics: A numerical study. Phys. Rev. E 2015, 91, 022407. [Google Scholar] [CrossRef] [Green Version]
- Hötzer, J.; Steinmetz, P.; Jainta, M.; Schulz, S.; Kellner, M.; Nestler, B.; Genau, A.; Dennstedt, A.; Bauer, M.; Köstler, H.; et al. Phase-field simulations of spiral growth during directional ternary eutectic solidification. Acta Mater. 2016, 106, 249–259. [Google Scholar] [CrossRef]
- Apel, M.; Boettger, B.; Diepers, H.J.; Steinbach, I. 2D and 3D phase-field simulations of lamella and fibrous eutectic growth. J. Cryst. Growth 2002, 237, 154–158. [Google Scholar] [CrossRef]
- Hunt, J.; Jackson, K. Lamellar and rod eutectic growth. Trans. Metall. Soc. AIME 1966, 236, 1129–1142. [Google Scholar]
- Oswald, P.; Moulin, M.; Metz, P.; Géminard, J.C.; Sotta, P.; Sallen, L. An improved directional growth apparatus for liquid crystals: Applications to thermotropic and lyotropic systems. J. Phys. III 1993, 3, 1891–1907. [Google Scholar] [CrossRef] [Green Version]
- Akamatsu, S.; Bottin-Rousseau, S.; Şerefoğlu, M.; Faivre, G. Lamellar eutectic growth with anisotropic interphase boundaries: Experimental study using the rotating directional solidification method. Acta Mater. 2012, 60, 3206–3214. [Google Scholar] [CrossRef] [Green Version]
- Mohagheghi, S.; Şerefoğlu, M. Quasi-isotropic and locked grain growth dynamics in a three-phase eutectic system. Acta Mater. 2018, 151, 432–442. [Google Scholar] [CrossRef]
- Bottin-Rousseau, S.; Şerefoğlu, M.; Yücetürk, S.; Faivre, G.; Akamatsu, S. Stability of three-phase ternary-eutectic growth patterns in thin sample. Acta Mater. 2016, 109, 259–266. [Google Scholar] [CrossRef] [Green Version]
- Luan, Y.; Song, N.; Bai, Y.; Kang, X.; Li, D. Effect of solidification rate on the morphology and distribution of eutectic carbides in centrifugal casting high-speed steel rolls. J. Mater. Process. Technol. 2010, 210, 536–541. [Google Scholar] [CrossRef]
- Hötzer, J.; Steinmetz, P.; Dennstedt, A.; Genau, A.; Kellner, M.; Sargin, I.; Nestler, B. Influence of growth velocity variations on the pattern formation during the directional solidification of ternary eutectic Al-Ag-Cu. Acta Mater. 2017, 136, 335–346. [Google Scholar] [CrossRef]
- Kellner, M.; Kunz, W.; Steinmetz, P.; Hötzer, J.; Nestler, B. Phase-field study of dynamic velocity variations during directional solidification of eutectic NiAl-34Cr. Comput. Mater. Sci. 2018, 145, 291–305. [Google Scholar] [CrossRef]
- Rátkai, L.; Tóth, G.I.; Környei, L.; Pusztai, T.; Gránásy, L. Phase-field modeling of eutectic structures on the nanoscale: The effect of anisotropy. J. Mater. Sci. 2017, 52, 5544–5558. [Google Scholar] [CrossRef] [Green Version]
- Mohagheghi, S.; Şerefoğlu, M. Dynamics of spacing adjustment and recovery mechanisms of ABAC-type growth pattern in ternary eutectic systems. J. Cryst. Growth 2017, 470, 66–74. [Google Scholar] [CrossRef]
- Witusiewicz, V.; Hecht, U.; Böttger, B.; Rex, S. Thermodynamic re-optimisation of the Bi–In–Sn system based on new experimental data. J. Alloy. Compd. 2007, 428, 115–124. [Google Scholar] [CrossRef]
- Witusiewicz, V.; Hecht, U.; Rex, S.; Apel, M. In situ observation of microstructure evolution in low-melting Bi–In–Sn alloys by light microscopy. Acta Mater. 2005, 53, 3663–3669. [Google Scholar] [CrossRef]
- Ruggiero, M.; Rutter, J. Origin of microstructure in the 332 K eutectic of the Bi-In-Sn system. Mater. Sci. Technol. 1997, 13, 5–11. [Google Scholar] [CrossRef]
- Rex, S.; Böttger, B.; Witusiewicz, V.; Hecht, U. Transient eutectic solidification in In–Bi–Sn: Two-dimensional experiments and numerical simulation. Mater. Sci. Eng. A 2005, 413, 249–254. [Google Scholar] [CrossRef]
- Dargahi Noubary, K.; Kellner, M.; Hötzer, J.; Seiz, M.; Seifert, H.J.; Nestler, B. Data workflow to incorporate thermodynamic energies from Calphad databases into grand-potential-based phase-field models. J. Mater. Sci. 2021, 56, 11932–11952. [Google Scholar] [CrossRef]
- Plapp, M. Unified derivation of phase-field models for alloy solidification from a grand-potential functional. Phys. Rev. E 2011, 84, 031601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Choudhury, A.; Nestler, B. Grand-potential formulation for multicomponent phase transformations combined with thin-interface asymptotics of the double-obstacle potential. Phys. Rev. E 2012, 85, 021602. [Google Scholar] [CrossRef]
- Bauer, M.; Hötzer, J.; Jainta, M.; Steinmetz, P.; Berghoff, M.; Schornbaum, F.; Godenschwager, C.; Köstler, H.; Nestler, B.; Rüde, U. Massively Parallel Phase-Field Simulations for Ternary Eutectic Directional Solidification. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, Austin, TX, USA, 15–20 November 2015; p. 8. [Google Scholar]
- Hötzer, J.; Tschukin, O.; Said, M.B.; Berghoff, M.; Jainta, M.; Barthelemy, G.; Smorchkov, N.; Schneider, D.; Selzer, M.; Nestler, B. Calibration of a multi-phase field model with quantitative angle measurement. J. Mater. Sci. 2016, 51, 1788–1797. [Google Scholar] [CrossRef]
- Hötzer, J.; Jainta, M.; Steinmetz, P.; Nestler, B.; Dennstedt, A.; Genau, A.; Bauer, M.; Köstler, H.; Rüde, U. Large scale phase-field simulations of directional ternary eutectic solidification. Acta Mater. 2015, 93, 194–204. [Google Scholar] [CrossRef]
- Steinmetz, P.; Yabansu, Y.; Hötzer, J.; Jainta, M.; Nestler, B.; Kalidindi, S. Analytics for microstructure datasets produced by phase-field simulations. Acta Mater. 2016, 103, 192–203. [Google Scholar] [CrossRef]
- Hötzer, J.; Reiter, A.; Hierl, H.; Steinmetz, P.; Selzer, M.; Nestler, B. The parallel multi-physics phase-field framework Pace3D. J. Comput. Sci. 2018, 26, 1–12. [Google Scholar] [CrossRef]
- Software Package Parallel Algorithms for Crystal Evolution in 3D – Pace3D. Available online: https://www.h-ka.de/en/idm/profile/pace3d-software (accessed on 28 November 2021).
- Nestler, B.; Garcke, H.; Stinner, B. Multicomponent alloy solidification: Phase-field modeling and simulations. Phys. Rev. E 2005, 71, 041609. [Google Scholar] [CrossRef] [Green Version]
- Moelans, N. A quantitative and thermodynamically consistent phase-field interpolation function for multi-phase systems. Acta Mater. 2011, 59, 1077–1086. [Google Scholar] [CrossRef] [Green Version]
- Karma, A. Phase-field formulation for quantitative modeling of alloy solidification. Phys. Rev. Lett. 2001, 87, 115701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Echebarria, B.; Folch, R.; Karma, A.; Plapp, M. Quantitative phase-field model of alloy solidification. Phys. Rev. E 2004, 70, 061604. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Steinmetz, P.; Hötzer, J.; Kellner, M.; Dennstedt, A.; Nestler, B. Large-scale phase-field simulations of ternary eutectic microstructure evolution. Comput. Mater. Sci. 2016, 117, 205–214. [Google Scholar] [CrossRef]
- Kellner, M.; Hötzer, J.; Steinmetz, P.; Dargahi Noubary, K.; Kunz, W.; Nestler, B. Phase-field study of microstructure evolution in directionally solidified NiAl-34Cr during dynamic velocity changes. In Proceedings of the Solidification Processing 2017: Proceedings of the 6th Decennial International Conference on Solidification Processing, Beaumont Estate, Old Windsor, UK, 25–28 July 2017; pp. 372–375.
- Kellner, M.; Hötzer, J.; Schoof, E.; Nestler, B. Phase-field study of eutectic colony formation in NiAl-34Cr. Acta Mater. 2020, 182, 267–277. [Google Scholar] [CrossRef]
- Kellner, M.; Sprenger, I.; Steinmetz, P.; Hötzer, J.; Nestler, B.; Heilmaier, M. Phase-field simulation of the microstructure evolution in the eutectic NiAl-34Cr system. Comput. Mater. Sci. 2017, 128, 379–387. [Google Scholar] [CrossRef]
- Andersson, J.O.; Helander, T.; Höglund, L.; Shi, P.; Sundman, B. Thermo-Calc & DICTRA, computational tools for materials science. Calphad 2002, 26, 273–312. [Google Scholar]
- Yang, C.; Wang, X.; Wang, J.; Huang, H. Multiphase-field approach with parabolic approximation scheme. Comput. Mater. Sci. 2020, 172, 109322. [Google Scholar] [CrossRef]
- Kellner, M.; Enugala, S.N.; Nestler, B. Modeling of stoichiometric phases in off-eutectic compositions of directional solidifying NbSi-10Ti for phase-field simulations. Comput. Mater. Sci. 2022, 203, 111046. [Google Scholar] [CrossRef]
- Vondrous, A.; Selzer, M.; Hötzer, J.; Nestler, B. Parallel computing for phase-field models. Int. J. High Perform. Comput. Appl. 2014, 28, 61–72. [Google Scholar] [CrossRef]
- Ben Said, M.; Selzer, M.; Nestler, B.; Braun, D.; Greiner, C.; Garcke, H. A phase-field approach for wetting phenomena of multiphase droplets on solid surfaces. Langmuir 2014, 30, 4033–4039. [Google Scholar] [CrossRef] [PubMed]
- Prajapati, N.; Selzer, M.; Nestler, B.; Busch, B.; Hilgers, C. Modeling fracture cementation processes in calcite limestone: A phase-field study. Geotherm. Energy 2018, 6, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Nestler, B. Wetting transition and phase separation on flat substrates and in porous structures. J. Chem. Phys. 2021, 154, 094704. [Google Scholar] [CrossRef]
- Şerefoğlu, M.; Napolitano, R. On the role of initial conditions in the selection of eutectic onset mechanisms in directional growth. Acta Mater. 2011, 59, 1048–1057. [Google Scholar] [CrossRef]
- Napolitano, R.; Şerefoğlu, M. Control and interpretation of finite-size effects and initial morphology in directional solidification of a rod-type eutectic transparent metal-analog. JOM 2012, 64, 68–75. [Google Scholar] [CrossRef]
- Akbulut, S.; Ocak, Y.; Maraşlı, N.; Keşlioğlu, K.; Kaya, H.; Çadırlı, E. Determination of interfacial energies of solid Sn solution in the In–Bi–Sn ternary alloy. Mater. Charact. 2009, 60, 183–192. [Google Scholar] [CrossRef]
- Yao, W.; Han, X.; Wei, B. Microstructural evolution during containerless rapid solidification of Ni-Mo eutectic alloys. J. Alloy Compd. 2003, 348, 88–99. [Google Scholar] [CrossRef]
- Noor, E.E.M.; Ismail, A.B.; Sharif, N.M.; Ariga, T.; Hussain, Z. Characteristic of low temperature of Bi-In-Sn solder alloy. In Proceedings of the 2008 33rd IEEE/CPMT International Electronics Manufacturing Technology Conference (IEMT), Penang, Malaysia, 4–6 November 2008; pp. 1–4. [Google Scholar]
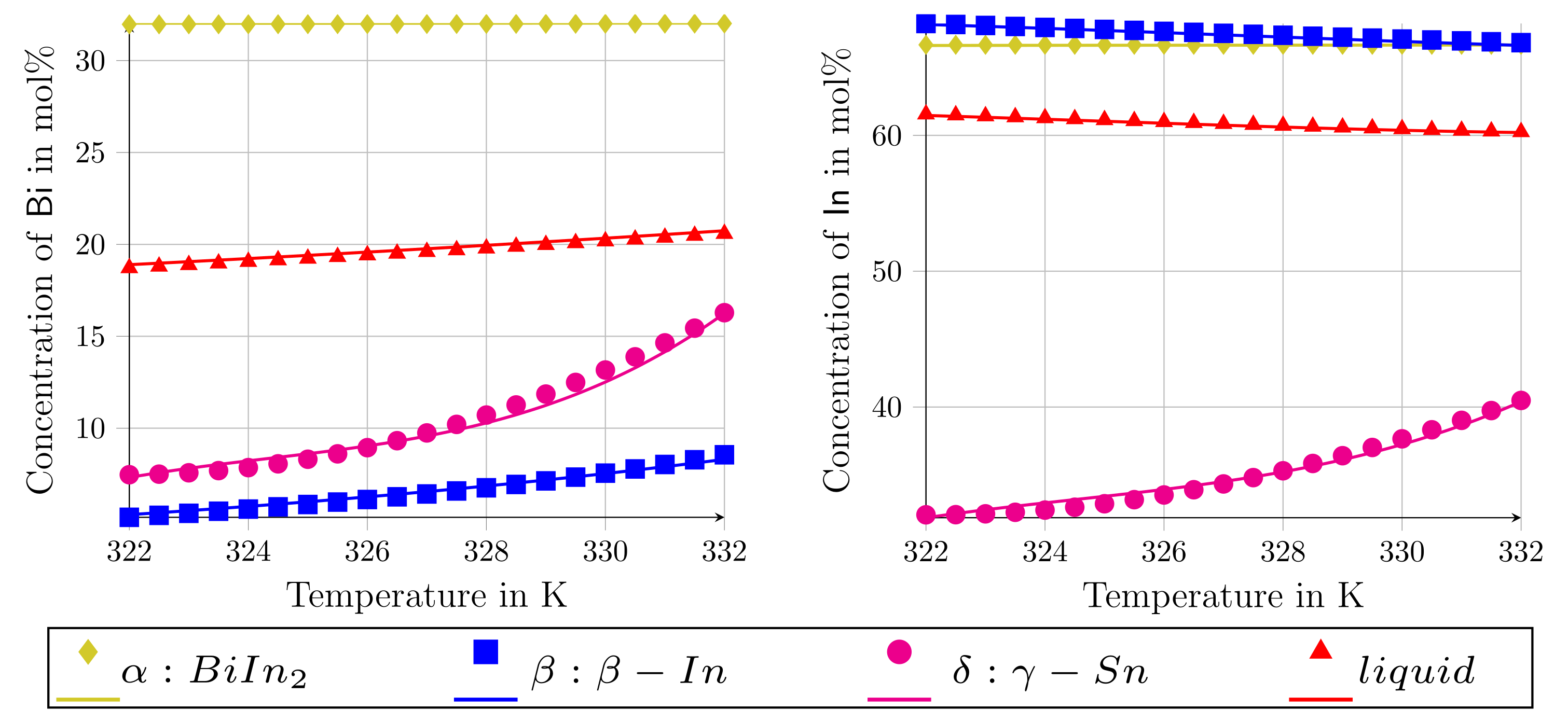

| Phase | in mol-% | in mol-% | in mol-% |
|---|---|---|---|
| 14.84 | 39.21 | 45.95 | |
| 32.01 | 66.67 | 1.32 | |
| 8.02 | 66.96 | 25.02 | |
| 20.37 | 60.36 | 19.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dargahi Noubary, K.; Kellner, M.; Nestler, B. Rotating Directional Solidification of Ternary Eutectic Microstructures in Bi-In-Sn: A Phase-Field Study. Materials 2022, 15, 1160. https://doi.org/10.3390/ma15031160
Dargahi Noubary K, Kellner M, Nestler B. Rotating Directional Solidification of Ternary Eutectic Microstructures in Bi-In-Sn: A Phase-Field Study. Materials. 2022; 15(3):1160. https://doi.org/10.3390/ma15031160
Chicago/Turabian StyleDargahi Noubary, Kaveh, Michael Kellner, and Britta Nestler. 2022. "Rotating Directional Solidification of Ternary Eutectic Microstructures in Bi-In-Sn: A Phase-Field Study" Materials 15, no. 3: 1160. https://doi.org/10.3390/ma15031160
APA StyleDargahi Noubary, K., Kellner, M., & Nestler, B. (2022). Rotating Directional Solidification of Ternary Eutectic Microstructures in Bi-In-Sn: A Phase-Field Study. Materials, 15(3), 1160. https://doi.org/10.3390/ma15031160







