Hot Deformation Behavior and Microstructural Evolution Based on the Processing Map of Dual-Phase Mg-Li Based Alloy

Abstract

The deformation behavior of the as-extruded Mg-Li-Al-Zn-Si alloy was studied by conducting a hot compression test, with a temperature range of 180–330 °C and a strain rate range of 0.01–10 s⁻¹. The constitutive relationship of flow stress, temperature, and strain rate was expressed by the Zener–Hollomon parameter and included the Arrhenius term. By considering the effect of strain on the material constants, the flow stress at 240–330 °C could be precisely predicted with the constitutive equation (incorporating the influence of strain). A processing map was established at the strain of 0.7. The unsafe domains that are characterized by uneven microstructures were detected at low temperatures (<230 °C) or high temperatures (>280 °C), with high strain rates (>1 s⁻¹). The optimum hot deformation region was obtained at a medium temperature (270–300 °C), with a peak power dissipation efficiency of 0.44. The microstructural evolution in different domains is investigated. The unstable domains are characterized by a non-uniform flow behavior and uneven microstructure. The observation showed that the dynamic recrystallization (DRX) process could easily occur at the safe domain with high power dissipation efficiency. For the α-phase, some features of continuous dynamic recrystallization can be found. The triple points serve as prominent nucleation sites for the β-phase DRX grains and the growth in the grains was carried out by subgrain boundary migration. The microstructure exhibits characteristics of discontinuous dynamic recrystallization.

1. Introduction

Mg-Li alloy, usually referred to as ultra-light Mg alloy, is currently considered to be the lightest metal structural material. The density of Mg-Li alloy is 1/4–1/3 lower than that of the Mg alloy, and is only about 1.30–1.65 g/cm³ [1]. Additionally, owing to properties such as superior specific strength, high specific stiffness, and high damping capacity, the Mg-Li alloy is widely used in aerospace, the military, and the 3C industry [2]. Traditional Mg alloys have poor formability due to their hexagonal, close-packed (HCP) structure, which leads to poor ductility and limits their applications. Below 22 °C, the plastic deformation of polycrystalline magnesium relies on basal slip and twinning. With the addition of the Li element, not only the density of the alloy but also the c/a axial ratio decreases. The decrease in c/a could cause non-basal slip (pyramidal <c + a> slip) to occur at the initial stage of deformation [3]. Based on the Mg-Li phase diagram, the crystal structure of the alloy that consists of less than 5.5% Li content has an HCP structure, like traditional Mg alloys. The alloy containing 5.5–11.5% Li content is composed of an HCP a-Mg phase and a BCC β-Li phase, which have a great advantage with regard to ductility. Once the content of Li is over 11.5 wt.%, there will be a single BCC β-Li phase [4]. Among various Mg-Li alloys, the dual-phase alloys keep a superior balance of strength and ductility [5]. However, the relatively low strength and poor thermal stability become obstacles when it comes to their application.

Plenty of studies have shown that alloying and plastic deformation strengthening can significantly improve the mechanical properties and corrosion resistance of Mg-Li alloys. Research has shown that Al reinforces the mechanical strength of the Mg-Li matrix [6]. Li et al. studied the solid solution treatment of Mg-10.1Li-4.8Al. The results indicated that the tensile strength of a sample was increased from 127 MPa (as-cast sample) to 250 MPa (T4 sample) by adjusting the solution parameters, and the corrosion resistance of the T4 sample was also improved simultaneously [7]. With the addition of Zn, the corrosion resistance of the alloy is further enhanced. Anna et al. have investigated the influence of bimodal grain size distribution on the corrosion resistance of Mg-4Li-3Al-1Zn. The study of extruded and annealed alloy showed the major corrosion mechanism that occurred between high-angle grain boundaries and grain interiors [8]. A further addition of elemental Si can produce particle reinforcement, which can improve the thermal stability of the Mg-Li alloy. Shao et al. have researched the microstructural evolution and mechanical properties of Mg-10Li-3Al-3Zn-0.25Si during the thermal cycling process. After the thermal cycling process, the strength of the alloy was decreased by 6–8%, while the elongation was enhanced by about 65% [9].

There are quite a few studies on the hot deformation behavior of the Mg-Li alloys [10,11]. Due to their low stacking fault energy, dynamic recrystallization (DRX) is the main softening mechanism of Mg alloys during the hot deformation process [12]. Yang et al. have discussed the microstructural evolution of the LA93-xSr alloy during extrusion. To account for the differences in structure between α-Mg and β-Li, the dominant mechanism of the DRX in the α-Mg phase is continuous dynamic recrystallization (CDRX) process. The existence of α-Mg and Al₄Sr phases promote the discontinuous dynamic recrystallization (DDRX) of the β-Li phase [13]. The DRX process achieves refinement of the grains and the well-distribution of phases in the microstructure. Therefore, studying the influence of the DRX process on deformation parameters is beneficial to the understanding of the microstructural evolution of duplex phase Mg-Li alloys.

In this study, hot compression tests were conducted at various temperatures and strain rates. The hot deformation behavior and microstructural evolution were studied. One purpose of this study is to construct the constitutive relation and the processing map of the as-extruded Mg-Li-Al-Zn-Si alloy to optimize conditions for hot working, and the other is to improve the understanding of nucleation mechanisms of the DRX process in two phases.

2. Materials and Methods

The material used in the experiment was an as-extruded rod from an industrial company (Sifang ULW Co., Ltd., Xi’an, China), and the chemical composition of Mg-Li-Al-Zn-Si alloy is given in

Table 1. The element contents of the Mg-Li-Al-Zn-Si alloy (wt.%).

Li	Al	Zn	Si	Mg
10.10	2.98	3.12	0.22	Bal.

.

The cylindrical specimens for hot compression tests, which were 10 mm in diameter and 15 mm in height, were machined from the extruded rod along the extrusion direction. Isothermal hot compression tests were performed on a thermo-mechanical simulator (Gleeble-3500) (DATA SCIENCES INTERNATIONAL, INC, St. Paul, MN, USA). The compression tests were performed at temperatures that ranged from 180 to 330 °C, with strain rates that ranged from 0.01 to 10 s⁻¹. Both ends of the specimen were padded with graphite sheets to reduce the effect of friction. The specimens were heated to the predetermined temperature at a heating rate of 10 K/s and held for 1 min to eliminate thermal gradients. Subsequently, the specimens were compressed to a true strain of about 0.7 and immediately followed by water quenching to maintain the deformed microstructure.

For microstructural observation, the deformed specimens were cut along the direction of compression. The surfaces were mechanically polished and boiled in the solution of 1 mL HNO₃ + 1 mL CH₃COOH + 3 g C₂H₂O₄ + 100 mL H₂O for the observation by an optical metallographic technique and a scanning electron microscope (SEM, JSM-7001F-JOEL, Tokyo, Japan) equipped with an Oxford energy-dispersive X-ray spectroscope (EDS, Aztec, Oxford Instruments, Oxford, UK). To confirm the phase composition of the alloy, X-ray diffraction (XRD) was performed using a Bruker D8 Advance diffractometer (Bruker, Karlsruhe, Germany) operating at 40 kV and 40 mA with Cu Ka radiation. Transmission Electron Microscope (TEM) characterization was carried out with a Tecnai-G2-F20-FEI transmission electron microscope (FEI, Hillsboro, OR, USA) operated at 200 kV. The samples with a 3 mm diameter for TEM investigation were prepared by mechanical grinding to a thickness of 50 μm, and then thinned using twin-jet electropolishing with a solution of HClO₄ (10%) + C₂H₅OH (90%) at the temperature of −30 °C. The voltage and current used were 80 V and 90 mA, respectively.

3. Results and Discussion

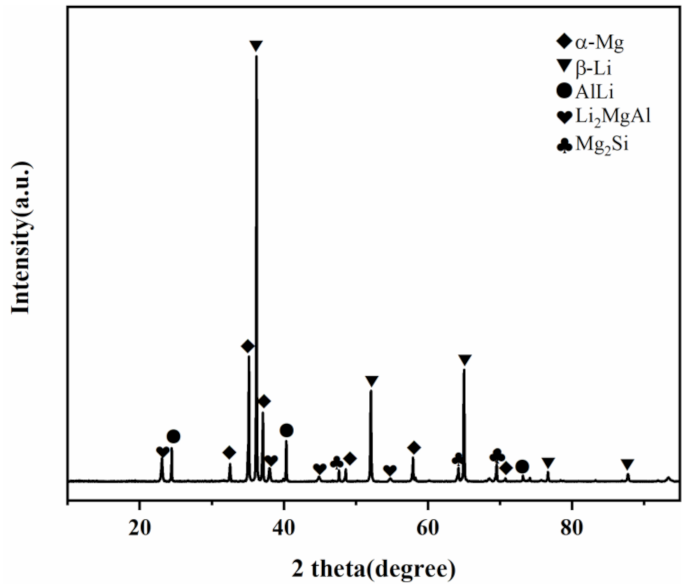
3.1. Microstructure of As-Extruded Mg-Li-Al-Zn-Si Alloy

The optical micrograph of the as-extruded Mg-Li-Al-Zn-Si alloy is shown in Figure 1. The typical duplex phase consists of α-Mg with an HCP structure and β-Li with a BCC structure. The dark areas are the β-Li matrix phases with equiaxed grains, and the bright areas are the α-Mg phases, which are lath-shaped and run parallel to the extrusion direction (ED, as the arrow shown in Figure 1). The average grain size of the β-phase is about 10.71 μm.

Figure 2 shows the XRD pattern measurements of the as-extruded Mg-Li-Al-Zn-Si alloy. Due to the addition of alloying elements, there are several extra phases. The α-Mg and β-Li are the major phases of the alloy. With the addition of Al, AlLi and Li₂MgAl despites in the matrix [14,15]. After the introduction of Si, the Mg₂Si phase remains and is stable during the thermal cycling process. Furthermore, its existence is beneficial to the thermal stability of the alloy [9].

Figure 3 shows the element distribution maps. With the high solid solubility in Mg-Li alloy, Al and Zn elements mostly exist in the matrix, inducing the increase in lattice distortion energy, which results in the obvious inhibitory effect of dislocation movement to improve the strength of materials [16]. The AlLi and Li₂MgAl phases are dispersed in the matrix as granular bright phases. The Mg₂Si phases are spread in grain boundaries and phase boundaries.

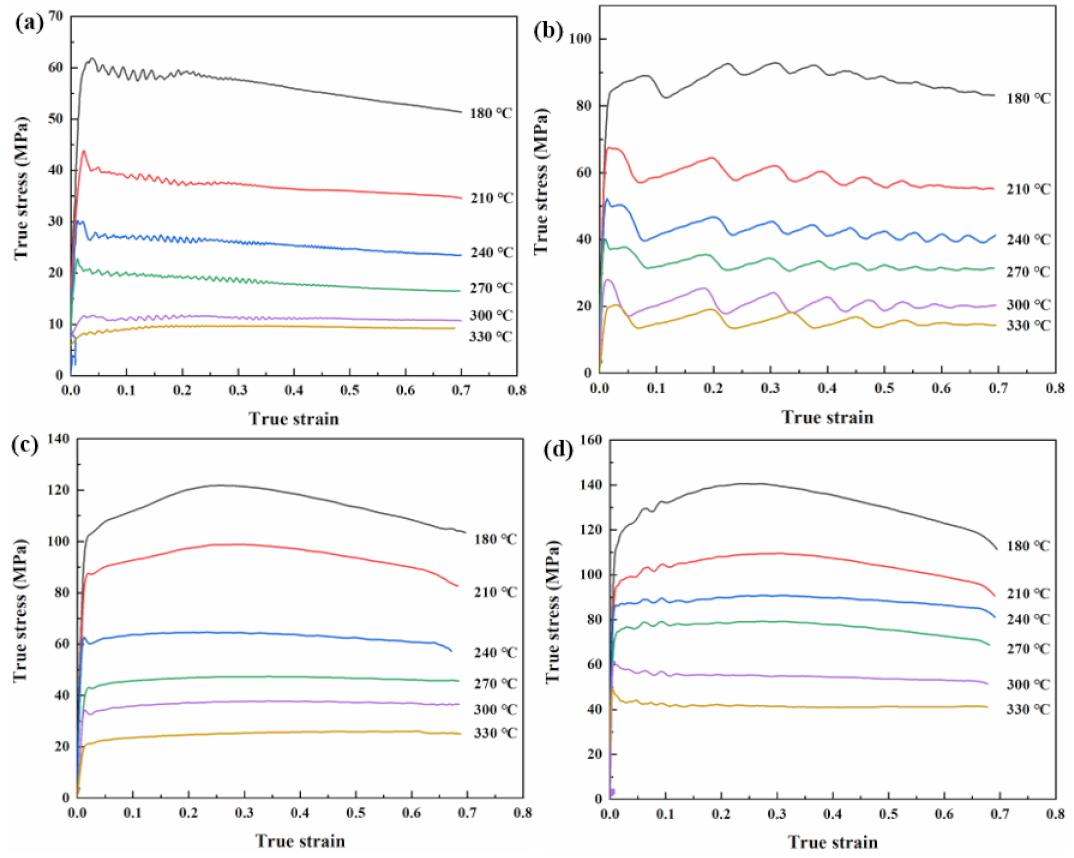
3.2. True Stress–Strain Curves

Figure 4 shows the smoothed true stress–strain curves of the Mg-Li-Al-Zn-Si alloy, deformed under temperatures ranging from 180 to 330 °C withstrain of 0.7, and at strain rates from 0.01 s⁻¹ to 10 s⁻¹. It is revealed that the flow stress is obviously affected by the deformation temperature during hot compression deformation [17,18]. With an increased deformation temperature or decreased strain rate, the flow stress decreased. Notably, the flow stress was increased rapidly at a very early stage of the deformation, and can be related to the work hardening caused by dislocation multiplication and tangle. With an increased strain, the flow stress slowly reaches a peak value. The internal distortion energy of the metal accumulates to a certain extent with an increased dislocation density. Furthermore, the softening mechanisms, such as dynamic recovery (DRV) and dynamic recrystallization (DRX), play an important role. It is worth noting that a dynamic equilibrium mode between work hardening and dynamic softening is established at the strain rate of 0.01 and 0.1 s⁻¹. The multiple peaks caused by the DRX cycle occurred before a steady-state arrived. The DRX cycle phenomenon has been described by a multi-phase-field model [19,20] and has been observed in other research projects [21,22].

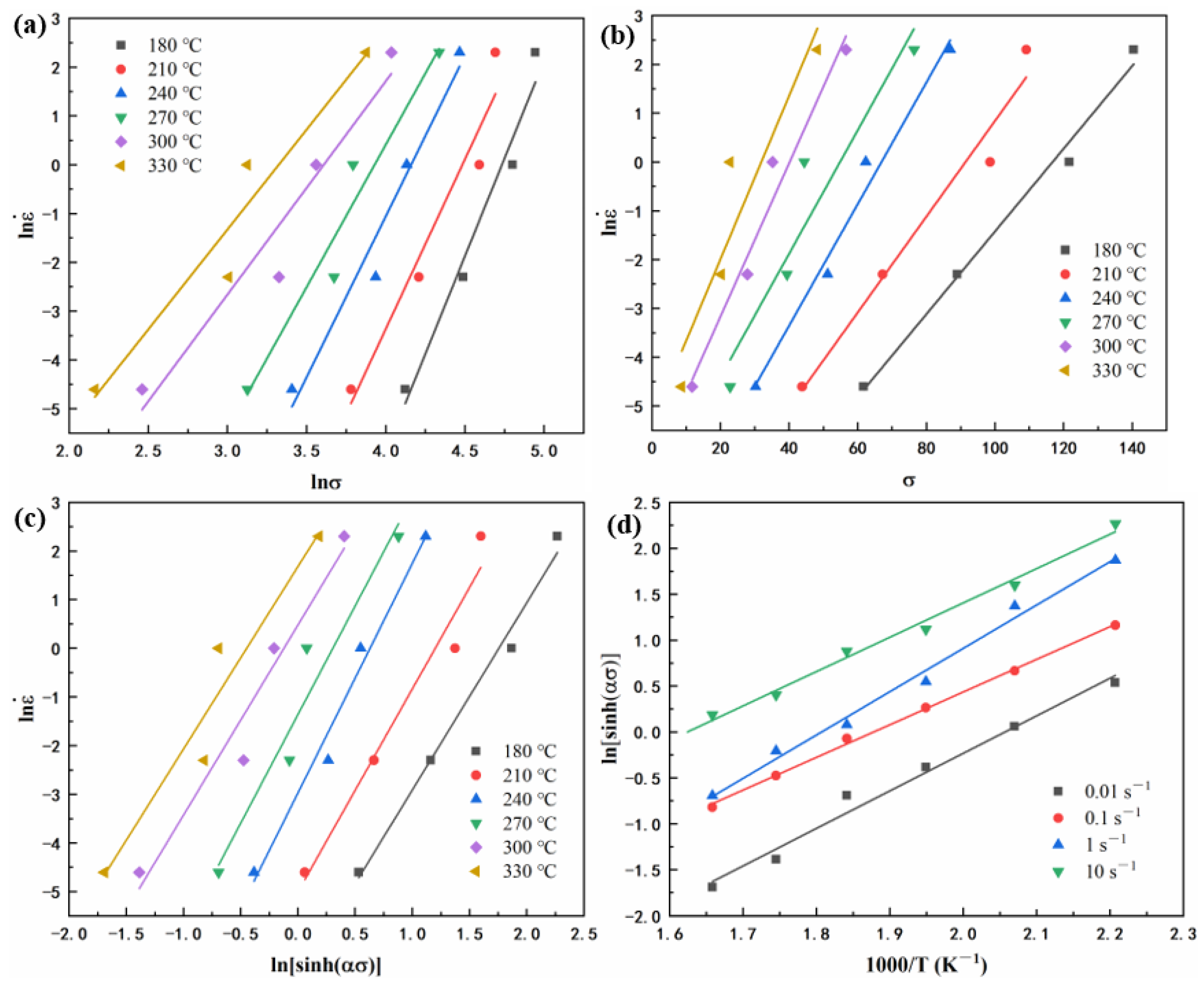
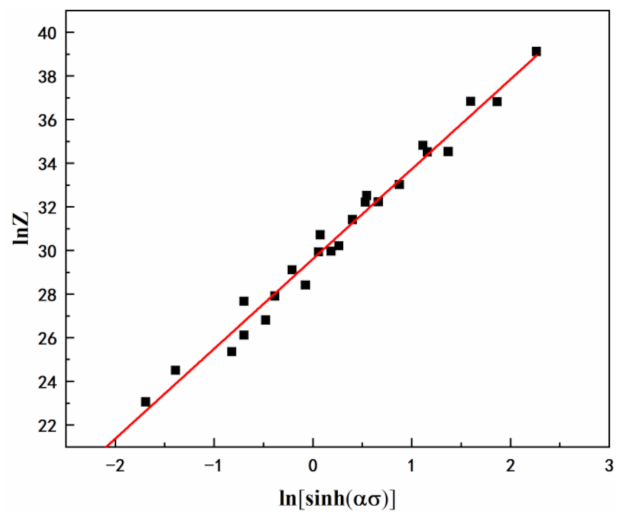
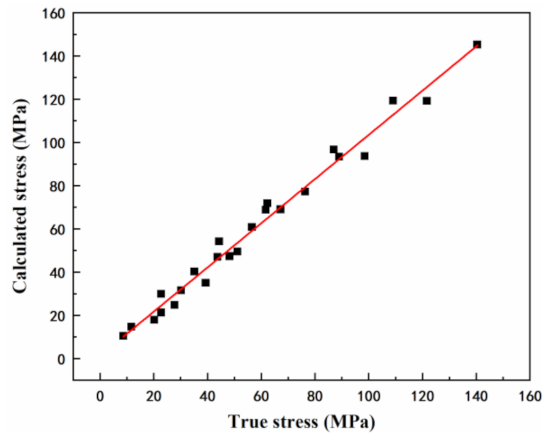
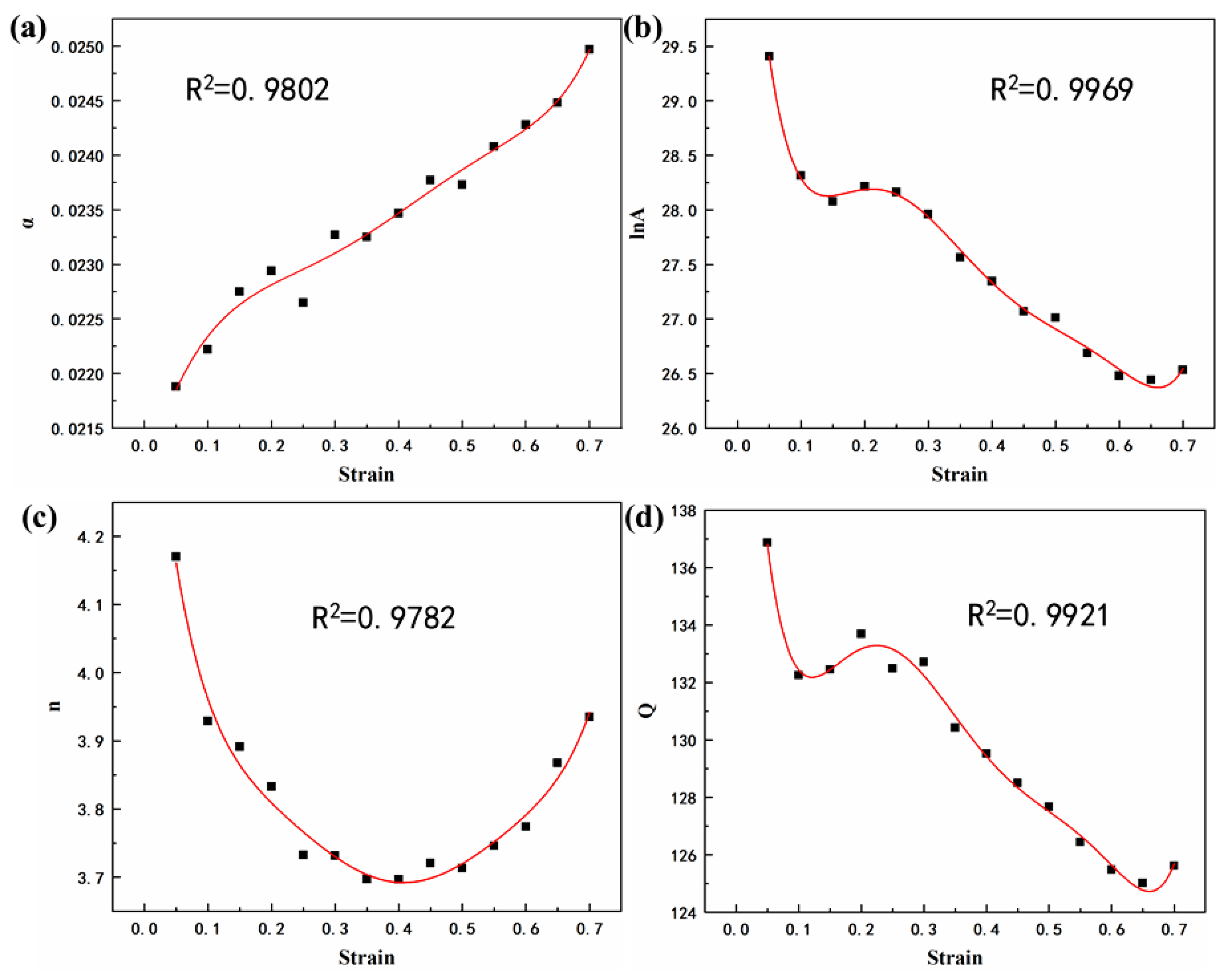
3.3. Constitutive Equation

There is an interactive relationship among the flow stress (σ), deformation temperature (T), and strain rate ($\dot{\epsilon }$) during the hot deformation process. The study of Sellars suggests that σ is determined by T and $\dot{\epsilon }$, which can be expressed as [23]:

$$Z=\dot{\epsilon }\exp \left(\frac{Q}{RT}\right)=A{\left[\sinh \left(\alpha \sigma \right)\right]}^n$$

(1)

Equation (1) is also known as the Arrhenius equation, where Z is the Zener–Holloman parameter, and its physical meaning is the deformation rate factor of temperature compensation: $\dot{\epsilon }$ is the strain rate (s⁻¹), Q is the deformation activation energy (kJ·mol⁻¹), R is the universal gas constant (R = 8.314 J·mol⁻¹·K⁻¹), T is the deformation temperature (K), σ is the true stress (MPa), A, α, and n are the temperature-independent material constants. Equation (2) is based on the Taylor expansion [24]:

$$Z=\dot{\epsilon }\exp \left(\frac{Q}{RT}\right)=\left\{\begin{array}{l}{A}_1{\sigma }^{n_1},\alpha \sigma <0.8\\ A_2\exp \left(\beta \sigma \right),\alpha \sigma >1.2\end{array}\right.$$

(2)

where α = β/n₁. Taking the natural logarithm of Equations (1) and (2), respectively, Equations (3) and (4) were then obtained:

$$\ln Z=\ln \dot{\epsilon }+\frac{Q}{RT}=\ln A+n\ln \left[\sinh \left(\alpha \sigma \right)\right]$$

(3)

$$\ln Z=\ln \dot{\epsilon }+\frac{Q}{RT}=\left\{\begin{array}{l}\ln A_1+n_1\ln \sigma ,\alpha \sigma <0.8\\ \ln A_2+\beta \sigma ,\alpha \sigma >1.2\end{array}\right.$$

(4)

Take the derivative of 1/T on both sides of Equation (3):

$$\frac{Q}{R}=n\cdot {\left.\frac{\partial \ln \left[\sinh \left(\alpha \sigma \right)\right]}{\partial \left(\frac{1}{T}\right)}\right|}_{\dot{\epsilon }},$$

(5)

The discrete flow stress data at strains ranging from 0.01 to 0.69, with an interval of 0.0004, are used to calculate the parameters mentioned above. The lnσ-ln$\dot{\epsilon }$, σ-ln$\dot{\epsilon }$, ln[sinh(ασ)]-ln$\dot{\epsilon }$, and 1000/T-ln[sinh(ασ)] curves shown in Figure 5 were processed and linearly fitted according to the experimental data based on Equations (3)–(5).

The slopes of the corresponding lines shown in Figure 4 represent n₁, β, n, Q/Rn, respectively. The mean values of the slopes are taken to evaluate the values of n₁, β, n, Q/Rn, which are 5.981, 0.126, 4.143, 4.0251. The values of α and Q can be calculated as 0.0211 and 138.643 kJ·mol⁻¹, respectively.

Substitute values of n, α, Q into Equation (3):

$$\ln Z=\ln A+4.143\ln \left[\sinh \left(0.0211\sigma \right)\right],$$

(6)

Figure 6 shows a linear relationship between lnZ-ln[sinhασ] based on Equation (6). lnA is the intercept of Figure 6, which can be obtained as lnA = 29.6. Therefore, the value of A could be obtained as A = e^29.6.

According to the above values, the hyperbolic sine equations of the peak stress for the as-extruded Mg-Li-Al-Zn-Si alloy can be expressed as follows:

$$\dot{\epsilon }\exp \left(\frac{138,643}{RT}\right)=e^{29.6}{\left[\sinh \left(0.0211\sigma \right)\right]}^{4.143},$$

(7)

Figure 7 shows the comparison of the peak stress between the experimental and predicted results by the developed constitutive equations of the as-extruded Mg-Li-Al-Zn-Si alloy at different temperatures under strain rates of 0.01, 0.1, 1, 10 s⁻¹. The correlation coefficient was used to quantify the predictability of the peak stress and was calculated as 0.992.

As Figure 4 shows, the effect of strain is significant in regimes with a lower working temperature. To improve the applicability of the constitutive equation, compensation of strain should be taken into account [25,26]. Assuming that the material constants are a polynomial function of the strains, as shown in Equation (8), then the values of material constants (α, A, n, Q) of the constitutive equation were computed under different strains in the range of 0.05-0.7, with the interval of 0.05. The polynomial fit results of α, lnA, n, Q of the Mg-Li-Al-Zn-Si alloy are provided in

Table 2. Polynomial fit results of α, n, Q, and lnA of Mg-Li-Al-Zn-Si alloy.

α	Value	N	Value	Q	Value/(kJ/mol)	lnA	Value
α0	0.021	n0	4.580	Q0	152.508	A0	32.906
α1	0.020	n1	−11.689	Q1	−495.219	A1	−107.133
α2	−0.088	n2	80.028	Q2	4475.528	A2	914.041
α3	0.173	n3	−308.404	Q3	−18,940.418	A3	−3753.913
α4	−0.019	n4	644.671	Q4	40,466.631	A4	7862.544
α5	−0.311	n5	−677.602	Q5	−42,731.404	A5	−8179.457
α6	0.258	n6	282.294	Q6	17,758.101	A6	3359.740

and the relationships between α, lnA, n, Q, and the true strain are shown in Figure 8. The fitted curves are strongly correlative to the values of the constants.

$$\left\{\begin{array}{l}\alpha ={\alpha }_0+{\alpha }_1\epsilon +{\alpha }_2{\epsilon }^2+{\alpha }_3{\epsilon }^3+{\alpha }_4{\epsilon }^4+{\alpha }_5{\epsilon }^5+{\alpha }_6{\epsilon }^6\\ \ln A=A_0+A_1\epsilon +A_2{\epsilon }^2+A_3{\epsilon }^3+A_4{\epsilon }^4+A_5{\epsilon }^5+A_6{\epsilon }^6\\ n=n_0+n_1\epsilon +n_2{\epsilon }^2+n_3{\epsilon }^3+n_4{\epsilon }^4+n_5{\epsilon }^5+n_6{\epsilon }^6\\ Q=Q_0+Q_1\epsilon +Q_2{\epsilon }^2+Q_3{\epsilon }^3+Q_4{\epsilon }^4+Q_5{\epsilon }^5+Q_6{\epsilon }^6\end{array}\right.$$

(8)

To confirm the accuracy of the constitutive equation with relation to the compensation of strain, a comparison between the calculated and the experimental stresses was performed. The flow stress values, which deformed at 180–330 °C/0.01–10 s⁻¹ under different strains, in the range of 0.05–0.7 with the interval of 0.05 were calculated from the above strain-compensation constitutive equation. Figure 9 shows the distribution of the calculated datapoints. One can determine that the calculated and experimental values are in good agreement above 240 °C, and there are significant errors between the datapoints and curves below 240 °C.

3.4. Processing Map

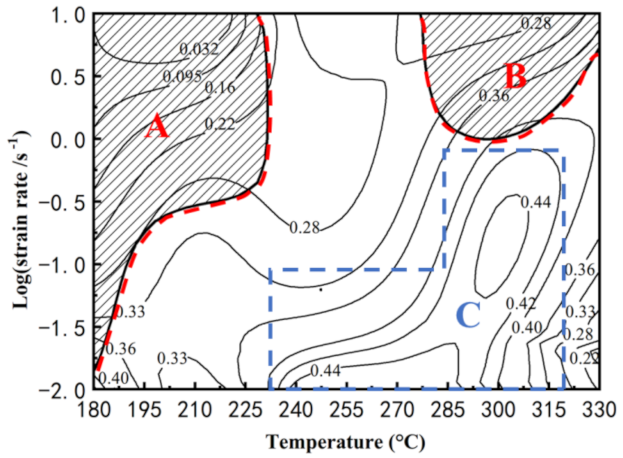
3.4.1. Establishment of Processing Map

The workability of a material is determined by chemical composition, microstructural characteristic, deformation path, and thermal processing parameters. Therefore, the processing map can be used to analyze the thermoformabilities and the deformation mechanism, under different deformation conditions, and to optimize the thermal processing parameters to avoid the occurrence of defects. The processing maps are established based on the dynamic materials model (DMM), which was presented by Prasad and Gegel [27]. The dynamic materials model regards the thermal deformed material as a nonlinear power dissipator and the material processing of the material as an energy dissipation system. The input power (represented by P) is consumed in two ways: the plastic deformation heat (represented by G) and the microstructural evolution (represented by J). This can be defined as [28]:

$$P=\sigma \dot{\epsilon }=G+J={\displaystyle {\int }_0^{\dot{\epsilon }}\sigma d\dot{\epsilon }+{\displaystyle {\int }_0^{\sigma }\dot{\epsilon }}d\sigma },$$

(9)

the ratio of G and J is determined by the strain rate sensitivity (m), m is material constant and can be described as [29]:

$$m=\frac{\partial J}{\partial G}=\frac{\dot{\epsilon }\partial \sigma }{\sigma \partial \dot{\epsilon }}=\frac{\partial \left(\ln \sigma \right)}{\partial \left(\ln \dot{\epsilon }\right)},$$

(10)

assuming the flow behavior of the material follows a power-law equation:

$$\sigma =k\cdot {\dot{\epsilon }}^m,$$

(11)

then J can be expressed by:

$$J={\displaystyle {\int }_0^{\dot{\epsilon }}\sigma d\dot{\epsilon }}=\frac{m}{m+1}\sigma \dot{\epsilon }$$

(12)

The proportion between the energy dissipated in microstructure evolution and the linear energy dissipated (m = 1) is defined as efficiency of power dissipation (η):

$$\eta =\frac{J}{J_{\max }}=\frac{2m}{2m+1}$$

(13)

According to the extremum principle of irreversible thermodynamics, several instability criteria were established. Based on the maximum entropy production principle, the criterion presented by Prasad is expressed as follows [30]:

$$\xi \left(\dot{\epsilon }\right)=\frac{\partial \ln \left[m/\left(m+1\right)\right]}{\partial \ln \dot{\epsilon }}+m<0,$$

(14)

where ξ is the instability parameter. Figure 10 shows the processing map of the Mg-Li-Al-Zn-Si alloy at the strain of 0.7 in the temperature range of 180–330 °C and strain rate range of 0.01–10 s⁻¹, which is developed by the supposition of the power dissipation map and the instability map. The shadows represent the flow instability domain and the contour numbers represent the efficiency of power dissipation. The peak power dissipation efficiency is 0.44 under the processing parameters of 0.1 s⁻¹/300 °C and 0.01 s⁻¹/270 °C. The instability domains lie in the temperature range of 180–230 °C and 280–330 °C with high strain rates.

3.4.2. Microstructural Analysis Based on the Processing Map

The domains marked in Figure 10 can be interpreted based on the power dissipation efficiency and the relationship with microstructural evolution. Domain A and B are unstable regions that lie within the low-temperature range (180–230 °C) and the high-temperature range (280–330 °C), respectively. Conversely, domain A covers a larger range of strain rates. Domain A and B are unsuitable as deformation regions that prevent deformation defects. Domain C spreads over the temperature and strain rate range of 240–320 °C and 0.01–1 s⁻¹ with high power dissipation efficiency. For the low stacking fault energy alloys, there is evidence that domains with a power dissipation efficiency of 30–50% are liable for DRX processes [31]. The dominant mechanism in each region is investigated by microstructural evolution.

Domain A is an instability region at a low temperature. The typical microstructure of the alloy deformed at 180 °C, with a strain rate of 0.01 s⁻¹ and 0.1 s⁻¹, is shown in Figure 11. Strong strip structure, which has a certain angle to the axis of compression leading to the formation of shear bands, is shown in Figure 11a. As Figure 11b shows, the microstructure deformed at 180 °C and 0.1 s⁻¹ exhibits a flow localization, which may cause microcracking and a feasible deformation zone [32]. In many cases, due to the differences between the ductility of the two phases, the strain/stress-bearing of the phases reflects a synergistic interaction of their properties [33,34]. The contribution of strain hardening and high local stress concentrations, caused by the plastic incompatibility between the phases, lead to the local instability. The TEM image of the specimen deformed at 180 °C with a strain rate of 10 s⁻¹ is shown in Figure 12. Compared with the β-phase, the dislocation density in the α-phase is high. Due to the HCP structure, the dislocation glide and climb is particularly difficult, resulting in a dislocation pile-up in α-phase grains.

Domain B lies in the temperature range of 280–330 °C and the strain rate range of 1–10 s⁻¹. With a power dissipation efficiency of around 0.3, the microstructure deformed at the condition of 330 °C/10 s⁻¹ is shown in Figure 13. As Figure 13a shows, a considerable amount of refined α-phase DRX grains are surrounded by growth β-phase DRX grains. Part of α-phases transform into the approximately globular grains. The grain boundaries of the untransformed α-phase grains remain as a uniform vector in the radial direction owing to the weak recovery of grain boundary torsion [35]. Meanwhile, the glomeration morphology of the α-phase occurred during the deformation, which is considered responsible for the flow softening [36]. The mechanism of softening of Mg-Li duplex phase alloys is not only attributed to DRX but also to the glomeration of α-phase [37]. An inhomogeneous microstructure of β-phase is shown in Figure 13, which is composed of large grains (17.85 μm) and a few relatively fine grains (3.05 μm). Due to the high deformation temperature and the strain rate, the process of DRX in β-phase seems to be complete. It can be concluded that the formation of some excessively coarse grains, surrounded by DRXed finer grains, is the result of an abnormal grain growth. Similar phenomena have been observed in the investigation of an extruded LZ121 alloy [38,39]. This type of microstructure is undesirable in the hot working process and should be avoided.

Domain C is the high value of the power dissipation efficiency region. With the peak power dissipation efficiency of 0.44, the microstructure obtained at the deformation condition of 270 °C/0.01 s⁻¹ and 300 °C/0.1 s⁻¹ is shown in Figure 14a,b, respectively. With the exception of newly formed DRX grains from the α-phase, the grain boundaries of the microstructure deformed at 270 °C/0.01 s⁻¹ are formed via dislocation rearrangement. Therefore, the grain boundaries of the α-phase are deformed and curved. Typically, CDRX occurs in the deformed region, with a high dislocation density and is favored at low temperatures. The increase in temperature will enhance dislocation recovery, slowing down the CDRX [40]. However, in related studies, strain is an important factor that affects CDRX, acting as an enabler [41,42]. As the deformation condition changes to 300 °C/0.1 s⁻¹, most α-phases maintain the elongated microstructure without shear bands. Due to the relatively low strength of the α-phase, plastic deformation occurs first in the β-phase. The stored energy in the β-phase will increase. Therefore, DRX preferentially occurs in the β-phase. The same phenomenon has been detected in the Mg-8Li-3Al-2Zn-0.2Zr alloy [43]. One can observe that the β-phase developed many equiaxed grains, together with some finer grains. The average grain sizes of the β-phase in Figure 14a,b are about 15.37 μm and 9.16 μm, respectively. The formation of a considerable amount of equiaxed grains proves that DRX has comprehensively occurred [44].

To further investigate the microstructure evolution of the DRX process, the TEM micrographs of specimens deformed at 270 °C/0.01 s⁻¹ are shown in Figure 15. Figure 15a shows that the grain boundaries of the α-phase grains are irregular. The dislocation density in the grain interior is lower than that of the specimen deformed at 180 °C/10 s⁻¹. The original grain is subdivided by some developing subgrain boundaries. Through deformation-induced dislocation accumulation and recombination, the dislocation cells start to generate in the original grains. During the deformation process, the dislocation cell boundaries are transformed into low-angle subgrain boundaries. The appearance of transformation from the low-angle boundaries to the high-angle boundaries occurs with the increased strain [45]. Such a morphology of the subgrain boundaries confirms that the mechanism of the DRX belongs to the CDRX process [46]. As Figure 15b illustrates, the grain boundaries of the β-phase are sharp and there are few dislocations inside the grains, which are typical attributes of grains generated by DDRX [47]. The triple point serves as a prominent nucleation site for a DRX grain and there are few dislocations in grains. At the early stage, the entire DRX nucleus represents a grain boundary region. During the process of deformation, the DRX grain boundary region progressively travels outwards [48]. With the strain rate of 0.1 s⁻¹, the time for the DRX process is relatively short. As a result, the DRX nuclei could not entirely grow.

4. Conclusions

The hot deformation behavior of the Mg-Li-Al-Zn-Si alloy was studied through constitutive equations and processing maps through a hot compression test and further observation of microstructural characteristics. The main conclusions, based on the experiments and analyses, are summarized below.

(1)

At the temperature range of 180–330 °C and strain rate range of 0.01–10 s⁻¹, the flow-stress–true-strain curves for the Mg-Li-Al-Zn-Si alloy are sensitive to the deformation temperature and strain rate. The shape transformation from the multiple to single peak of the flow-stress–true-strain curves with the increasing strain rate was caused by the DRX cycle.

(2)

The constitutive equation was found to precisely predict flow stress at high temperatures (>240 °C) but showed significant deviation at low temperatures.

(3)

The processing map based on DMM at the strain of 0.7 was established for the Mg-Li-Al-Zn-Si alloy. The peak power dissipation efficiency is 0.44 when the deformation conditions are 300 °C/0.1 s⁻¹ and 270 °C/0.01 s⁻¹. The unsafe domains are detected at low temperatures (<230 °C) and high temperatures (>280 °C) with high strain rates (>1 s⁻¹) that should be avoided.

(4)

The dominant nucleation mechanism of DRX in the safe region of the Mg-Li-Al-Zn-Si alloy is different in two phases. In the α-phase, CDRX occurs with the accumulation of dislocations in subgrain boundaries, leading to the increase in their orientation. The microstructure of the β-phase exhibits a DDRX character.