Probabilistic Analysis of Composite Materials with Hyper-Elastic Components
Abstract
1. Introductory Remarks
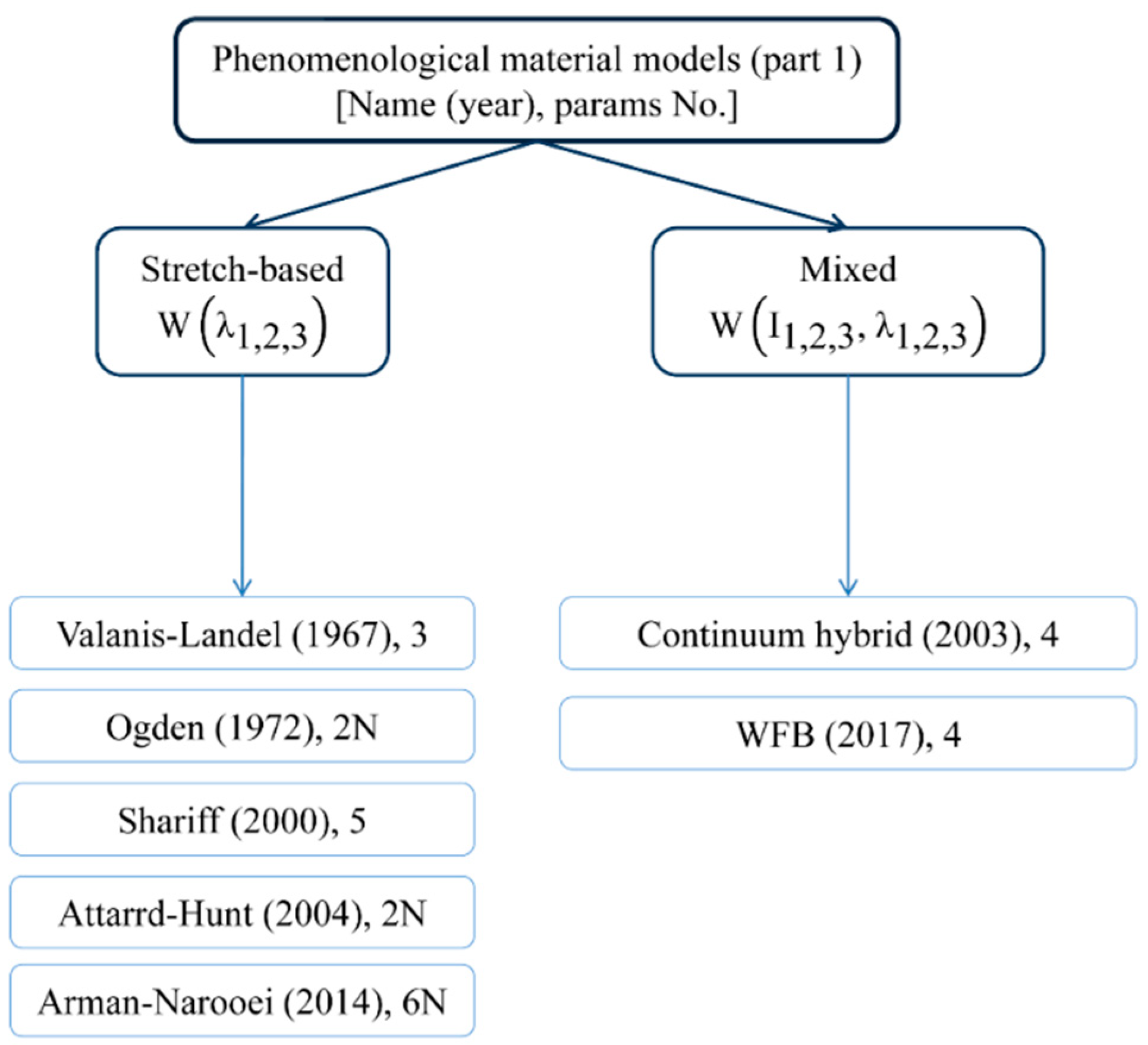
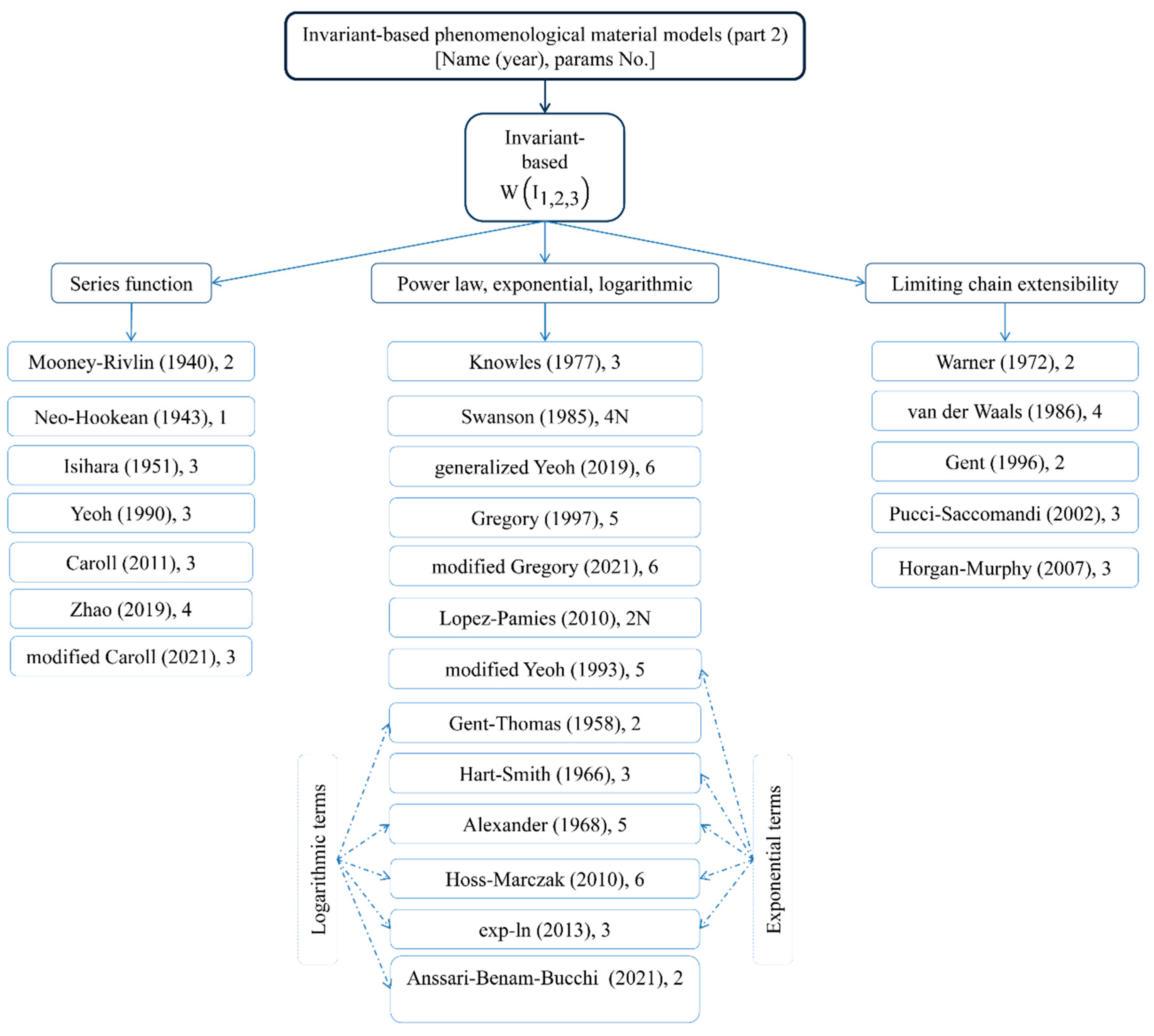
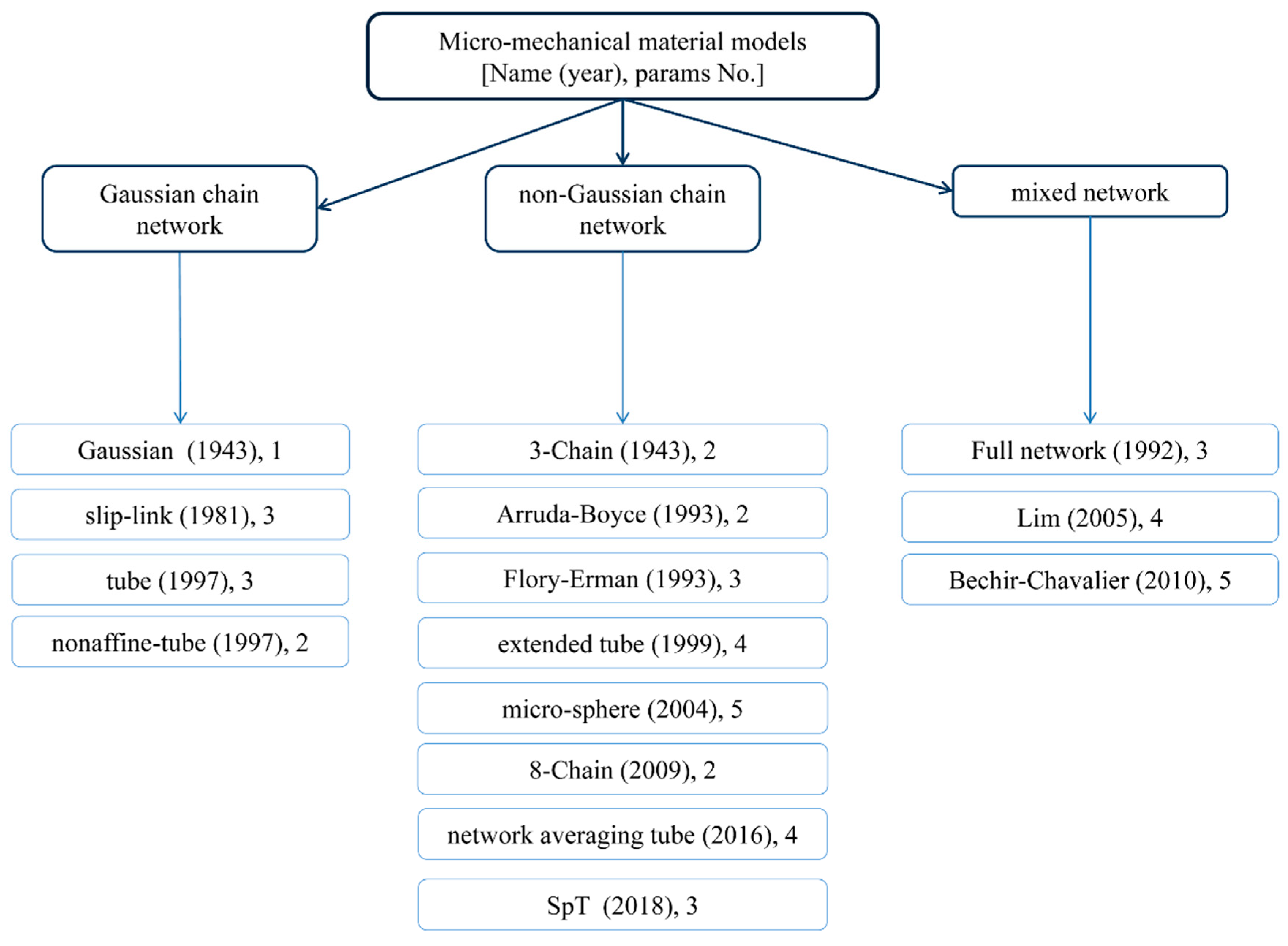
2. Hyper-Elastic Materials
3. Probabilistic Methods
4. Interphase and Interface Defects
5. Multiscale Models and Numerical Simulation
6. Homogenization Method and Effective Medium Response
7. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mark, J.E. Physical Properties of Polymers Handbook, 2nd ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Heinrich, G.; Klűppel, M.; Vilgis, T.A. Reinforcement of elastomers. Curr. Opin. Solid State Mat. Sci. 2002, 6, 195–203. [Google Scholar] [CrossRef]
- Vilgis, T.A.; Heinrich, G.; Klüppel, M. Reinforcement of Polymer Nanocomposites: Theory, Experiment and Applications; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Khalifa, M.; Anandhan, S.; Wuzella, G.; Lammer, H.; Mahendran, A.R. Thermoplastic polyurethane composites reinforced with renewable and sustainable fillers—A review. Polym. Technol. Mater. 2020, 59, 1751–1769. [Google Scholar] [CrossRef]
- Máša, B.; Náhlík, L.; Hutař, P. Particulate Composite Materials: Numerical Modeling of a Cross-Linked Polymer Reinforced With Alumina-Based Particles. Polym. Mech. 2013, 49, 421–428. [Google Scholar] [CrossRef]
- Delfani, M.; Bagherpour, V. Overall properties of particulate composites with periodic microstructure in second strain gradient theory of elasticity. Mech. Mater. 2017, 113, 89–101. [Google Scholar] [CrossRef]
- Fukahori, Y. The mechanics and mechanism of the carbon black reinforcement of elastomers. Rubber Chem. Technol. 2003, 76, 548–566. [Google Scholar] [CrossRef]
- Kamiński, M. Sensitivity analysis of homogenized charactersitics for random elastic composites. Comput. Methods Appl. Mech. Eng. 2003, 192, 1973–2005. [Google Scholar] [CrossRef]
- Kamiński, M.; Sokołowski, D. Dual probabilistic homogenization of the rubber-based composite with random carbon black particle reinforcement. Comp. Struct. 2016, 140, 783–797. [Google Scholar] [CrossRef]
- Fish, J.; Shek, K.; Pandheeradi, M.; Shephard, M.S. Computational plasticity for composite structures based on mathematical homogenization: Theory and practice. Comput. Methods Appl. Mech. Eng. 1997, 148, 53–73. [Google Scholar] [CrossRef]
- Sokołowski, D.; Kamiński, M. Homogenization of carbon/polymer composites with anisotropic distribution of particles and stochastic interface defects. Acta Mech. 2018, 229, 3727–3765. [Google Scholar] [CrossRef]
- Le, T.T.; Guilleminot, J.; Soize, C. Stochastic continuum modelling of random interphases from atomistic simulations. Application to a polymer nanocomposite. Comput. Methods Appl. Mech. Eng. 2016, 303, 430–449. [Google Scholar] [CrossRef]
- Clement, A.; Soize, C.; Yvonnet, J. Computational nonlinear stochastic homogenization using a non-concurrent multiscale approach for hyperelastic heterogeneous microstructures analysis. Int. J. Numer. Methods Eng. 2012, 91, 799–824. [Google Scholar] [CrossRef]
- Melchers, R.E. Structural Reliability Analysis and Prediction, 3rd ed.; Wiley: Chichester, UK, 2002. [Google Scholar] [CrossRef]
- Wang, X.; Xu, X.; Choi, S.U.S. Thermal conductivity of nanoparticle-fluid mixture. J. Thermophys. Heat Transf. 1999, 13, 474–480. [Google Scholar] [CrossRef]
- López-Pernía, C.; Muñoz-Ferreiro, C.; González-Orellana, C.; Morales-Rodríguez, A.; Gallardo-López, Á.; Poyato, R. Optimizing the homogenization technique for graphene nanoplatelet/yttria tetragonal zirconia composites: Influence on the microstructure and the electrical conductivity. J. Alloy. Compd. 2018, 767, 994–1002. [Google Scholar] [CrossRef]
- Miehe, C.; Diez, J.; Goktepe, S.; Schanzel, L. Coupled thermovisco-elastoplasticity of glassy polymers in the logarithmic strain space based on the free volume theory. Int. J. Sol. Struct. 2011, 48, 1799–1817. [Google Scholar] [CrossRef]
- Christensen, R.M. Mechanics of Composite Materials; Wiley: New York, NY, USA, 1979. [Google Scholar]
- Timoshenko, S.; Goodier, J.N. Elasticity Theory; McGraw-Hill: New York, NY, USA, 1951. [Google Scholar]
- Zener, C. Elasticity and Anelasticity of Metals; University of Chicago: Chicago, IL, USA, 1948. [Google Scholar]
- Humphrey, J.D. Cardiovascular Solid Mechanics: Cells, Tissues and Organs; Springer: New York, NY, USA, 2002. [Google Scholar]
- Glotzer, S.C.; Paul, W. Molecular and Mesoscale Simulation Methods for Polymer Materials. Annu. Rev. Mater. Sci. 2002, 32, 401–436. [Google Scholar] [CrossRef]
- Bhowmick, A. Current Topics in Elastomers Research; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Christensen, R.M. Theory of Viscoelasticity; Dover Publications: Dover, UK, 2010. [Google Scholar]
- Attard, M.M.; Hunt, G.W. Hyperelastic constitutive modeling under finite strain. Int. J. Solids Struct. 2004, 41, 5327–5350. [Google Scholar] [CrossRef]
- Yang, B.; Kim, B.; Lee, H. Predictions of viscoelastic strain rate dependent behavior of fiber-reinforced polymeric composites. Compos. Struct. 2012, 94, 1420–1429. [Google Scholar] [CrossRef]
- Zhang, J.; Ostoja-Starzewski, M. Mesoscale bounds in viscoelasticity of random composites. Mech. Res. Commun. 2015, 68, 98–104. [Google Scholar] [CrossRef]
- Heinrich, G.; Struve, J.; Gerber, G. Mesoscopic simulation of dynamic crack propagation in rubber materials. Polymer 2002, 43, 395–401. [Google Scholar] [CrossRef]
- Harth, T.; Schwan, S.; Lehn, J.; Kollmann, F. Identification of material parameters for inelastic constitutive models: Statistical analysis and design of experiments. Int. J. Plast. 2004, 20, 1403–1440. [Google Scholar] [CrossRef]
- Mandel, J.; Roth, F.L.; Steel, M.N.; Stiehler, R.D. Measurement of the aging of rubber vulcanizates. J. Res. Natl. Bur. Stand. Sect.—C. Eng. Instr. 1959, 63, 141–145. [Google Scholar] [CrossRef]
- Mott, P.H.; Roland, C.M. Aging of natural rubber in air and seawater. Rubber Chem. Technol. 2001, 74, 79–88. [Google Scholar] [CrossRef]
- Mullins, L. Softening of rubber by deformation. Rubber Chem. Technol. 1969, 42, 339–362. [Google Scholar] [CrossRef]
- Ogden, R.; Roxburgh, D.G. A pseudo–elastic model for the Mullins effect in filled rubber. Proc. R. Soc. A Math. Phys. Eng. Sci. 1999, 455, 2861–2877. [Google Scholar] [CrossRef]
- Dorfmann, A.; Ogden, R. A constitutive model for the Mullins effect with permanent set in particle-reinforced rubber. Int. J. Solids Struct. 2004, 41, 1855–1878. [Google Scholar] [CrossRef]
- Lorenz, H.; Klüppel, M.; Heinrich, G. Microstructure-based modelling and FE implementation of filler-induced stress softening and hysteresis of reinforced rubbers. ZAMM-J. Appl. Math. Mech. 2012, 92, 608–631. [Google Scholar] [CrossRef]
- Volokh, K. On modeling failure of rubber-like materials. Mech. Res. Commun. 2010, 37, 684–689. [Google Scholar] [CrossRef]
- Volokh, K.Y. Review of the energy limiters approach to modeling failure of rubber. Rubber Chem. Technol. 2013, 86, 470–487. [Google Scholar] [CrossRef]
- Treloar, L.R. The Physics of Rubber Elasticity; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Heinrich, G.; Straube, E.; Helmis, G. Rubber elasticity of polymer networks: Theories. Adv. Polymer Sci. 1988, 85, 33–87. [Google Scholar]
- Holzapfel, G.A. Nonlinear Solid Mechanics: A Continuum Approach for Engineering; Wiley: Chichester, UK, 2000. [Google Scholar]
- Truesdell, C.; Noll, W. The Non-Linear Field Theories of Mechanics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Sussman, T.; Bathe, K.-J. A finite element formulation for nonlinear incompressible elastic and inelastic analysis. Comput. Struct. 1987, 26, 357–409. [Google Scholar] [CrossRef]
- Heinrich, G.; Kaliske, M. Theoretical and numerical formulation of a molecular based constitutive tube-model of rubber elasticity. Comput. Theor. Polym. Sci. 1997, 7, 227–241. [Google Scholar] [CrossRef]
- Kaliske, M.; Rothert, H. On the finite element implementation of rubber-like materials at finite strains. Eng. Comput. 1997, 14, 216–232. [Google Scholar] [CrossRef]
- Jin, T.; Yu, L.; Yin, Z.; Xiao, H. Bounded elastic potentials for rubberlike materials with strain-stiffening effects. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. 2014, 95, 1230–1242. [Google Scholar] [CrossRef]
- Hossain, M.; Steinmann, P. More hyperelastic models for rubber-like materials: Consistent tangent operators and comparative study. J. Mech. Behav. Mater. 2013, 22, 27–50. [Google Scholar] [CrossRef]
- He, H.; Zhang, Q.; Chen, J.; Zhang, L.; Li, F. A comparative study of 85 hyperelastic constitutive models for both unfilled rubber and highly filled rubber nanocomposite material. Nano Mater. Sci. 2022, 4, 64–82. [Google Scholar] [CrossRef]
- Zopf, C.; Kaliske, M. Numerical characterisation of uncured elastomers by a neural network based approach. Comput. Struct. 2017, 182, 504–525. [Google Scholar] [CrossRef]
- Shen, Y.; Chandrashekhara, K.; Breig, W.F.; Oliver, L.R. Neural Network Based Constitutive Model for Rubber Material. Rubber Chem. Technol. 2004, 77, 257–277. [Google Scholar] [CrossRef]
- Klein, D.K.; Fernández, M.; Martin, R.J.; Neff, P.; Weeger, O. Polyconvex anisotropic hyperelasticity with neural networks. J. Mech. Phys. Solids 2022, 159, 104703. [Google Scholar] [CrossRef]
- Chung, I.; Im, S.; Cho, M. A neural network constitutive model for hyperelasticity based on molecular dynamics simulations. Int. J. Numer. Methods Eng. 2021, 122, 5–24. [Google Scholar] [CrossRef]
- Le, B.A.; Yvonnet, J.; He, Q.-C. Computational homogenization of nonlinear elastic materials using neural networks: Neural networks-based computational homogenization. Int. J. Numer. Methods Eng. 2015, 104, 1061–1084. [Google Scholar] [CrossRef]
- Mooney, M. A theory of large elastic deformation. J. Appl. Phys. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Rivlin, R.S. Large elastic deformations of isotropic materials. IV. Further developments of the general theory. Phil. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1948, 241, 379–397. [Google Scholar]
- Ogden, R. On the overall moduli of non-linear elastic composite materials. J. Mech. Phys. Solids 1974, 22, 541–553. [Google Scholar] [CrossRef]
- Ogden, R.W. Non-Linear Elastic Deformations; Dover Publishers: Dover, UK, 1984. [Google Scholar]
- Treloar, L. The elasticity of a network of long-chain molecules II. Trans. Faraday Soc. 1943, 39, 241–246. [Google Scholar] [CrossRef]
- Isihara, A.; Hashitsume, N.; Tatibana, M. Statistical theory of rubber-like elasticity. IV. (two-dimensional stretching). J. Chem. Phys. 1951, 19, 1508–1512. [Google Scholar] [CrossRef]
- Yeoh, O.H. Characterization of elastic properties of carbon-black-filled rubber vulcanizates. Rubber Chem. Technol. 1990, 63, 792–805. [Google Scholar] [CrossRef]
- Carroll, M.M. A strain energy function for vulcanized rubbers. J. Elast. 2010, 103, 173–187. [Google Scholar] [CrossRef]
- Melly, S.K.; Liu, L.; Liu, Y.; Leng, J. Improved Carroll’s hyperelastic model considering compressibility and its finite element implementation. Acta Mech. Sin. 2021, 37, 785–796. [Google Scholar] [CrossRef]
- Zhao, Z.; Mu, X.; Du, F. Modeling and verification of a new hyperelastic model for rubber-like materials. Math. Probl. Eng. 2019, 2019, 2832059. [Google Scholar] [CrossRef]
- Knowles, J.K. The finite anti-plane shear field near the tip of a crack for a class of incompressible elastic solids. Int. J. Fract. 1977, 13, 611–639. [Google Scholar] [CrossRef]
- Swanson, S.R. A Constitutive Model for High Elongation Elastic Materials. ASME J. Eng. Mater. Technol. 1985, 107, 110–114. [Google Scholar] [CrossRef]
- Gregory, I.H.; Muhr, A.H.; Stephens, I.J. Engineering applications of rubber in simple extension. Plast. Rubber Compos. Process. Appl. 1997, 26, 118–122. [Google Scholar]
- Lopez-Pamies, O. A new I1-based hyperelastic model for rubber elastic materials. Comptes Rendus Mec. 2010, 338, 3–11. [Google Scholar] [CrossRef]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Hohenberger, T.W.; Windslow, R.J.; Pugno, N.M.; Busfield, J.J.C. A constitutive model for both low and high strain nonlinearities in highly filled elastomers and implementation with user-defined material soubrutines in ABAQUS. Rubber Chem. Technol. 2019, 92, 653–686. [Google Scholar] [CrossRef]
- Gent, A.N.; Thomas, A. Forms for the stored (strain) energy function for vulcanized rubber. J. Polym. Sci. 1958, 28, 625–628. [Google Scholar] [CrossRef]
- Hart-Smith, L.J. Elasticity parameters for finite deformations of rubber-like materials. Z. Angew. Math. Phys. 1966, 17, 608–626. [Google Scholar] [CrossRef]
- Alexander, H. A constitutive relation for rubber-like materials. Int, J. Eng. Sci. 1968, 6, 549–563. [Google Scholar] [CrossRef]
- Hoss, L.; Marczak, R.J. A New Constitutive Model for Rubber-Like Materials. Mecánica Comput. 2010, 29, 2759–2773. [Google Scholar]
- Khajehsaeid, H.; Arghavani, J.; Naghdabadi, R. A hyperelastic constitutive model for rubber-like materials. Eur. J. Mech. A/Solids 2013, 38, 144–151. [Google Scholar] [CrossRef]
- Anssari-Benam, A.; Bucchi, A. A generalised neo-Hookean strain energy function for application to the finite deformation of elastomers. Int. J. Non-Linear Mech. 2020, 128, 103626. [Google Scholar] [CrossRef]
- Warner, H.R., Jr. Kinetic theory and rheology of dilute suspensions of finitely extendible dumbbells. Ind. Eng. Chem. Fundam. 1972, 11, 379–387. [Google Scholar] [CrossRef]
- Kilian, H.-G. A molecular interpretation of the parameters of the van der Waals equation of state for real networks. Polym. Bull. 1980, 3, 151–158. [Google Scholar] [CrossRef]
- Gent, A.N. A new constitutive relation for rubber. Rubber Chem. Technol. 1996, 69, 59–61. [Google Scholar] [CrossRef]
- Pucci, E.; Saccomandi, G. A note on the Gent model for rubber-like materials. Rubber Chem. Technol. 2002, 75, 839–852. [Google Scholar] [CrossRef]
- Horgan, C.O.; Murphy, J.G. Limiting chain extensibility constitutive models of Valanis–Landel type. J. Elast. 2007, 86, 101–111. [Google Scholar] [CrossRef]
- Valanis, K.C.; Landel, R.F. The strain-energy function of a hyperelastic material in terms of the extension ratios. J. Appl. Phys. 1967, 38, 2997–3002. [Google Scholar] [CrossRef]
- Valanis, K.C. The Valanis–Landel strain energy function Elasticity of incompressible and compressible rubber-like materials. Int. J. Solids Struct. 2021, 238, 111271. [Google Scholar] [CrossRef]
- Narooei, K.; Arman, M. Modification of exponential based hyperelastic strain energy to consider free stress initial configuration and Constitutive modeling. J. Comput. Appl. Mech. 2018, 49, 189–196. [Google Scholar]
- Beda, T.; Chevalier, Y. Hybrid continuum model for large elastic deformation of rubber. J. Appl. Phys. 2003, 94, 2701–2706. [Google Scholar] [CrossRef]
- Korba, A.G.; Barkey, M.E. New model for hyper-elastic materials behavior with an application on natural rubber. In Proceedings of the ASME 2017 12th International Manufacturing Science and Engineering Conference Collocated with the JSME/ASME 2017 6th International Conference on Materials and Processing, American Society of Mechanical Engineers Digital Collection, Los Angeles, CA, USA, 4–8 June 2017; pp. 1–10. [Google Scholar]
- Treloar, L. The elasticity of a network of long-chain molecules. I. Trans. Faraday Soc. 1943, 39, 36–41. [Google Scholar] [CrossRef]
- Ball, R.; Doi, M.; Edwards, S.; Warner, M. Elasticity of entangled networks. Polymer 1981, 22, 1010–1018. [Google Scholar] [CrossRef]
- Rubinstein, M.; Panyukov, S. Nonaffine deformation and elasticity of polymer networks. Macromolecules 1997, 30, 8036–8044. [Google Scholar] [CrossRef]
- James, H.M.; Guth, E. Theory of the elastic properties of rubber. J. Chem. Phys. 1943, 11, 455–481. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Boehler, J.-P.; Khan, A.S. (Eds.) Anisotropy and Localization of Plastic Deformation; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Song, D.; Oberai, A.A.; Janmey, P.A. Hyperelastic continuum models for isotropic athermal fibrous networks. Interface Focus 2022, 12, 20220043. [Google Scholar] [CrossRef]
- Flory, P.J. Thermodynamic relations for high elastic materials. Trans. Faraday Soc. 1961, 57, 829–838. [Google Scholar] [CrossRef]
- Miehe, C.; Göktepe, S.; Lulei, F. A micro-macro approach to rubber-like materials—Part I: The non-affine micro-sphere model of rubber elasticity. J. Mech. Phys. Solids 2004, 52, 2617–2660. [Google Scholar] [CrossRef]
- Kaliske, M.; Heinrich, G. An extended tube-model for rubber elasticity: Statistical-mechanical theory and finite element implementation. Rubber Chem. Technol. 2010, 72, 602–632. [Google Scholar] [CrossRef]
- Khiêm, V.N.; Itskov, M. Analytical network-averaging of the tube model: Rubber elasticity. J. Mech. Phys. Solid. 2016, 95, 254–269. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhong, D.; Wang, P.; Mao, G.; Yu, H.; Qu, S. A general constitutive model of soft elastomers. J. Mech. Phys. Solids 2018, 117, 110–122. [Google Scholar] [CrossRef]
- Wu, P.; van der Giessen, E. On improved 3-D non-Gaussian network models for rubber elasticity. Mech. Res. Commun. 1992, 19, 427–433. [Google Scholar] [CrossRef]
- Lim, G.T. Scratch Behavior of Polymers; Texas A&M University: College Station, TX, USA, 2005. [Google Scholar]
- Bechir, H.; Chevalier, L.; Idjeri, M. A three-dimensional network model for rubber elasticity: The effect of local entanglements constraints. Int. J. Eng. Sci. 2010, 48, 265–274. [Google Scholar] [CrossRef]
- Elhaouzi, F.; Nourdine, A.; Brosseau, C.; Mdarhri, A.; El Aboudi, I.; Zaghrioui, M. Hyperelastic behavior and dynamic mechanical relaxation in carbon black-polymer composites. Polym. Compos. 2018, 40, 3005–3011. [Google Scholar] [CrossRef]
- Fritzen, F.; Kunc, O. Two-stage data-driven homogenization for nonlinear solids using a reduced order model. Eur. J. Mech. A/Solids 2018, 69, 201–220. [Google Scholar] [CrossRef]
- Li, X.; Xia, Y.; Li, Z.; Xia, Y. Three-dimensional numerical simulations on the hyperelastic behavior of carbon-black particle filled rubbers under moderate finite deformation. Comput. Mater. Sci. 2012, 55, 157–165. [Google Scholar] [CrossRef]
- Shahabodini, A.; Ansari, R.; Darvizeh, M. Multiscale modeling of embedded graphene sheets based on the higher-order Cauchy-Born rule: Nonlinear static analysis. Compos. Struct. 2017, 165, 25–43. [Google Scholar] [CrossRef]
- Temizer, I.; Zohdi, T.I. A numerical method for homogenization in non-linear elasticity. Comput. Mech. 2007, 40, 281–298. [Google Scholar] [CrossRef]
- Sokołowski, D.; Kamiński, M. Hysteretic behavior of random particulate composites by the Stochastic Finite Element Method. Materials 2019, 12, 2909. [Google Scholar] [CrossRef]
- Leonard, M.; Wang, N.; Lopez-Pamies, O.; Nakamura, T. The nonlinear elastic response of filled elastomers: Experiments vs. theory for the basic case of particulate fillers of micrometer size. J. Mech. Phys. Solids 2019, 135, 103781. [Google Scholar] [CrossRef]
- Jiménez, F.L. Variations in the distribution of local strain energy within different realizations of a representative volume element. Compos. Part B Eng. 2019, 176, 107111. [Google Scholar] [CrossRef]
- Ban, Y.; Mi, C. On spherical nanoinhomogeneity embedded in a half-space analyzedwith Steigmann–Ogden surface and interface models. Int. J. Solids Struct. 2021, 216, 123–135. [Google Scholar] [CrossRef]
- Pallicity, T.D.; Böhlke, T. Effective viscoelastic behavior of polymer composites with regularperiodic microstructures. Int. J. Solids Struct. 2021, 216, 167–181. [Google Scholar] [CrossRef]
- Avril, S.; Badel, P.; Duprey, A. Anisotropic and hyperelastic identification of in vitro human arteries from full-field optical measurements. J. Biomech. 2010, 43, 2978–2985. [Google Scholar] [CrossRef] [PubMed]
- Sakata, S.; Ashida, F.; Kojima, T.; Zako, M. Three-dimensional stochastic analysis using a perturbation based homogenization metod for elastic properties of composite material considering microscopic uncertainty. Int. J. Solids Struct. 2007, 45, 894–907. [Google Scholar] [CrossRef]
- Kalamkarov, A.L.; Kolpakov, A.G. Analysis, Design and Optimization of Composite Structures; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Guedri, M.; Lima, A.; Bouhaddi, N.; Rade, D. Robust design of viscoelastic structures based on stochastic finite element models. Mech. Syst. Signal Process. 2010, 24, 59–77. [Google Scholar] [CrossRef]
- Nezamabadi, S.; Zahrouni, H.; Yvonnet, J. Solving hyperelastic material problems by asymptotic numerical method. Comput. Mech. 2010, 47, 77–92. [Google Scholar] [CrossRef]
- Kamiński, M.; Sokołowski, D. An introduction to stochastic finite element method analysis of hyper-elastic structures. In Proceedings of the 7th European Congress on Computational Methods in Applied Sciences and Engineering, Crete, Greece, 5–10 June 2016; Volume 3, pp. 6078–6090. [Google Scholar]
- Zeraatpisheh, M.; Bordas, S.P.; Beex, L.A. Bayesian model uncertainty quantification for hyperelastic soft tissue models. Data-Cent. Eng. 2021, 2, e9. [Google Scholar] [CrossRef]
- Liu, Z.; Bessa, M.; Liu, W.K. Self-consistent clustering analysis: An efficient multi-scale scheme for inelastic heterogeneous materials. Comput. Methods Appl. Mech. Eng. 2016, 306, 319–341. [Google Scholar] [CrossRef]
- Staber, B.; Guilleminot, J. Stochastic hyperelastic constitutive laws and identification procedure for soft biological tissues with intrinsic variability. J. Mech. Behav. Biomed. Mater. 2017, 65, 743–752. [Google Scholar] [CrossRef][Green Version]
- Staber, B.; Guilleminot, J. Stochastic modeling of the Ogden class of stored energy functions for hyperelastic materials: The compressible case. Z. Angew. Math. Mech. 2017, 97, 273–295. [Google Scholar] [CrossRef]
- Lopez-Pamies, O.; Idiart, M.I. Fiber-reinforced hyperelastic solids: A realizable homogenization constitutive theory. J. Eng. Math. 2010, 68, 57–83. [Google Scholar] [CrossRef]
- López Jiménez, F. Modeling of soft composites under three-dimensional loading. Compos. Part B Eng. 2014, 59, 173–180. [Google Scholar] [CrossRef]
- Staber, B.; Guilleminot, J. Functional approximation and projection of stored energy functions in computational homogenization of hyperelastic materials: A probabilistic perspective. Comput. Method. Appl. Mech. 2017, 313, 1–27. [Google Scholar] [CrossRef]
- Ghaboussi, J.; Garrett, J.H.; Wu, X. Knowledge-Based Modeling of Material Behavior with Neural Networks. J. Eng. Mech. 1991, 117, 132–153. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- As’ad, F.; Avery, P.; Farhat, C. A mechanics-informed artificial neural network approach in data-driven constitutive modeling. Intenat. J. Numer. Methods Eng. 2022, 123, 2738–2759. [Google Scholar] [CrossRef]
- Mahnken, R. Strain mode-dependent weighting functions in hyperelasticity accounting for verification, validation, and stability of material parameters. Arch. Appl. Mech. 2022, 92, 713–754. [Google Scholar] [CrossRef]
- Linka, K.; Kuhl, E. A new family of Constitutive Artificial Neural Networks towards automated model discovery. Comput. Methods Appl. Mech. Eng. 2023, 403, 115731. [Google Scholar] [CrossRef]
- Kalina, K.A.; Linden, L.; Brummund, J.; Metsch, P.; Kästner, M. Automated constitutive modeling of isotropic hyperelasticity based on artificial neural networks. Comput. Mech. 2021, 69, 213–232. [Google Scholar] [CrossRef]
- Hien, T.D.; Kleiber, M. On solving nonlinear transient heat transfer problems with random parameters. Comput. Methods Appl. Mech. Eng. 1998, 151, 287–299. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. A new stochastic approach to transient heat conduction modeling with uncertainty. Int. J. Heat Mass Transf. 2003, 46, 4681–4693. [Google Scholar] [CrossRef]
- Figiel, Ł.; Kamiński, M. Numerical probabilistic approach to sensitivity analysis in a fatigue delamination problem of a two-layer composite. Appl. Math. Comput. 2009, 209, 75–90. [Google Scholar] [CrossRef]
- Kamiski, M. On probabilistic fatigue models for composite materials. Int. J. Fatigue 2002, 24, 477–495. [Google Scholar] [CrossRef]
- Mustafa, G.; Suleman, A.; Crawford, C. Probabilistic micromechanical analysis of composite material stiffness properties for a wind turbine blade. Compos. Struct. 2015, 131, 905–916. [Google Scholar] [CrossRef]
- Vořehovský, M. Incorporation of statistical length scale into Weibull strength theory for composites. Compos. Struct. 2010, 92, 2027–2034. [Google Scholar] [CrossRef]
- Karakoç, A.; Freud, J. A statistical failure initiation model for honeycomb materials. Compos. Struct. 2013, 95, 154–162. [Google Scholar] [CrossRef]
- Ghaderi, A.; Morovati, V.; Dargazany, R. A Bayesian surrogate constitutive model to estimate failure probability of elastomers. Mech. Mater. 2021, 162, 104044. [Google Scholar] [CrossRef]
- Martínez-Frutos, J.; Ortigosa, R.; Pedregal, P.; Periago, F. Robust optimal control of stochastic hyperelastic materials. Appl. Math. Model. 2020, 88, 888–904. [Google Scholar] [CrossRef]
- Kamiński, M.M. The Stochastic Perturbation Method for Computational Mechanics; Wiley: Chichester, UK, 2013; ISBN 9780470770825. [Google Scholar]
- Kamiński, M. On semi-analytical probabilistic finite element method for homogenization of the periodic fiber-reinforced composites. Int. J. Numer. Methods Eng. 2011, 86, 1144–1162. [Google Scholar] [CrossRef]
- Cruz, M.E.; Patera, A.T. A parallel Monte-Carlo finite-element procedure for the analysis of multicomponent random media. Int. J. Numer. Methods Eng. 1995, 38, 1087–1121. [Google Scholar] [CrossRef]
- Hurtado, J.E. Reanalysis of linear and nonlinear structures using iterated Shanks transformation. Comput. Methods Appl. Mech. Eng. 2002, 191, 4215–4229. [Google Scholar] [CrossRef]
- Hurtado, J.E.; Barbat, A.H. Monte Carlo techniques in computational stochastic mechanics. Arch. Comput. Methods Eng. 1998, 5, 3–29. [Google Scholar] [CrossRef]
- Hamada, M.; Wilson, A.; Reese, C.; Martz, H. Bayesian Reliability; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Lunn, D.J.; Thomas, A.; Best, N.; Spiegelhalter, D. WinBUGS—A Bayesian modelling framework: Concepts, structure, and extensibility. Stat. & Comput. 2000, 10, 325–337. [Google Scholar]
- Zimmermann, H. Fuzzy set theory. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 317–332. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Hastings, W.K. Monte-Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Bendat, J.S.; Piersol, A.G. Random Data: Analysis and Measurement Procedures; Wiley: New York, NY, USA, 1971. [Google Scholar]
- Doucet, A.; Godsill, S.; Andrieu, C. On sequential Monte Carlo sampling methods for Bayesian filtering. Stat. Comput. 2000, 10, 197–208. [Google Scholar] [CrossRef]
- Wilkinson, S.N.; Olley, J.M.; Furuichi, T.; Burton, J.; Kinsey-Henderson, A.E. Sediment source tracing with stratified sampling and weightings based on spatial gradients in soil erosion. J. Soils Sediments 2015, 15, 2038–2051. [Google Scholar] [CrossRef]
- Helton, J.C.; Davis, F.J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab. Eng. Syst. Saf. 2003, 81, 23–69. [Google Scholar] [CrossRef]
- Chung, D.B.; Gutiérrez, M.A.; Graham-Brady, L.L.; Lingen, F.-J. Efficient numerical strategies for spectral stochastic finite element models. Int. J. Numer. Methods Eng. 2005, 64, 1334–1349. [Google Scholar] [CrossRef]
- Ghanem, R.G.; Spanos, P.D. Stochastic Finite Elements: A Spectral Approach; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Ghanem, R.G.; Spanos, P.D. Spectral techniques for stochastic finite elements. Arch. Comput. Methods Eng. 1997, 4, 63–100. [Google Scholar] [CrossRef]
- Sasikumar, P.; Venketeswaran, A.; Suresh, R.; Gupta, S. A data driven polynomial chaos based approach for stochastic analysis of CFRP laminated composite plates. Compos. Struct. 2015, 125, 212–227. [Google Scholar] [CrossRef]
- Blatman, G.; Sudret, B. An adaptive algorithm to build up sparse polynomial chaos expansions for stochastic finite element analysis. Probabilistic Eng. Mech. 2010, 25, 183–197. [Google Scholar] [CrossRef]
- Tootkaboni, M.; Graham-Brady, L. A multi-scale spectral stochastic method for homogenization of multi-phase periodic composites with random material properties. Int. J. Numer. Methods Eng. 2010, 83, 59–90. [Google Scholar] [CrossRef]
- Xu, X.; Graham-Brady, L. A stochastic computational method for evaluation of global and local behavior of random elastic media. Comput. Methods Appl. Mech. Eng. 2005, 194, 4362–4385. [Google Scholar] [CrossRef]
- Kleiber, M.; Hien, T.D. The Stochastic Finite Element Method; Wiley: Chichester, UK, 1992. [Google Scholar]
- Liu, W.K.; Belytschko, T.; Mani, A. Random field finite elements. Int. J. Numer. Methods Eng. 1986, 23, 1831–1845. [Google Scholar] [CrossRef]
- Matthies, H.G.; Brenner, C.E.; Bucher, C.G.; Soares, C.G. Uncertainties in probabilistic numerical analysis of structures and solids-Stochastic finite elements. Struct. Saf. 1997, 19, 283–336. [Google Scholar] [CrossRef]
- Stefanou, G.; Papadrakakis, M. Stochastic finite element analysis of shells with combined random material and geometric properties. Comput. Methods Appl. Mech. Eng. 2004, 193, 139–160. [Google Scholar] [CrossRef]
- Stefanou, G.; Savvas, D.; Papadrakakis, M. Stochastic finite element analysis of composite structures based on material microstructure. Compos. Struct. 2015, 132, 384–392. [Google Scholar] [CrossRef]
- Sasikumar, P.; Suresh, R.; Gupta, S. Analysis of CFRP laminated plates with spatially varying non-Gaussian inhomogeneities using SFEM. Compos. Struct. 2014, 112, 308–326. [Google Scholar] [CrossRef]
- Honda, R. Stochastic BEM with spectral approach in elastostatic and elastodynamic problems with geometrical uncertainty. Eng. Anal. Bound. Elements 2005, 29, 415–427. [Google Scholar] [CrossRef]
- Kaminski, M. Iterative scheme in determination of the probabilistic moments of the structural response in the Stochastic perturbation-based Boundary Element Method. Comput. Struct. 2015, 151, 86–95. [Google Scholar] [CrossRef]
- Wang, C.; Qiu, Z.; Wu, D. Numerical analysis of uncertain temperature field by stochastic finite difference method. Sci. China Ser. G Phys. Mech. Astron. 2014, 57, 698–707. [Google Scholar] [CrossRef]
- Zienkiewicz, O.; Taylor, R.; Zhu, J. The Finite Element Method Set. Its Basis and Fundamentals, 6th ed.; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Ho, H.; Drzal, L.T. Evaluation of interfacial mechanical properties of fiber reinforced composites using the micro-indentation method. Comp. Part A 1996, 27, 961–971. [Google Scholar] [CrossRef]
- Zavarise, G.; Wriggers, P.; Stein, E.; Schrefler, B. A numerical model for thermomechanical contact based on microscopic interface laws. Mech. Res. Commun. 1992, 19, 173–182. [Google Scholar] [CrossRef]
- Khurshudyan, A.Z. The meso-scale behavior of anisotropic particle-reinforcedthermo-elastic composites. Contin. Mech. Thermodyn. 2021, 33, 1363–1374. [Google Scholar] [CrossRef]
- Chang, C.S.; Chao, S.J.; Chang, Y. Estimates of elastic moduli for granular material with anisotropic random packing structure. Int. J. Solids Struct. 1995, 32, 1989–2008. [Google Scholar] [CrossRef]
- Benveniste, Y. The effective mechanical behavior of composite material with imperfect contact between the constituents. Mech. Mater. 1985, 4, 197–208. [Google Scholar] [CrossRef]
- Firooz, S.; Javili, A. Understanding the role of general interfaces in the overall behavior of composites and size effects. Comput. Mater. Sci. 2019, 162, 245–254. [Google Scholar] [CrossRef]
- Lamon, J. Interfaces and Interphases. In Ceramic Matrix Composites: Fiber Reinforced Ceramics and Their Applications; Krenkel, W., Weinheim, E., Eds.; Wiley: Hoboken, NJ, USA, 2008; pp. 169–179. [Google Scholar]
- Soize, C. Tensor-valued random fields for meso-scale stochastic model of anisotropic elastic microstructure and probabilistic analysis of representative volume element size. Probabilistic Eng. Mech. 2008, 23, 307–323. [Google Scholar] [CrossRef]
- Yang, B.; Hwang, Y.; Lee, H. Elastoplastic modeling of polymeric composites containing randomly located nanoparticles with an interface effect. Compos. Struct. 2013, 99, 123–130. [Google Scholar] [CrossRef]
- Choi, H.; Achenbach, J. Stress states at neighboring fibers induced by single-fiber interphase defects. Int. J. Solids Struct. 1995, 32, 1555–1570. [Google Scholar] [CrossRef]
- Goudarzi, T.; Spring, D.W.; Paulino, G.H.; Lopez-Pamies, O. Filled elastomers: A theory of filler reinforcement based on hydrodynamic and interphasial effects. J. Mech. and Phys. Solids 2015, 80, 37–67. [Google Scholar] [CrossRef]
- Meddeb, A.B.; Tighe, T.; Ounaies, Z.; Lopez-Pamies, O. Extreme enhancement of the nonlinear elastic response of elastomer nanoparticulate composites via interphases. Compos. Part B Eng. 2018, 156, 166–173. [Google Scholar] [CrossRef]
- Paran, S.M.R.; Saeb, M.R.; Formela, K.; Goodarzi, V.; Vijayan, P.P.; Puglia, D.; Khonakdar, H.A.; Thomas, S. To what extent can hyperelastic models make sense the effect of clay surface treatment on the mechanical properties of elastomeric nanocomposites? Macromol. Mater. Eng. 2017, 302, 1700036. [Google Scholar] [CrossRef]
- Qu, M.; Deng, F.; Kalkhoran, S.M.; Gouldstone, A.; Robisson, A.; Van Vliet, K.J. Nanoscale visualisation and multiscale mechanical implications of bound rubber interphases in rubber-carbon black nanocomposites. J. Soft Matter 2011, 7, 1066–1077. [Google Scholar] [CrossRef]
- Bismarck, A.; Blaker, J.; Anthony, D.; Qian, H.; Maples, H.; Robinson, P.; Shaffer, M.; Greenhalgh, E.; Anthony, D. Development of novel composites through fibre and interface/interphase modification. IOP Conf. Ser. Mater. Sci. Eng. 2016, 139, 012001. [Google Scholar] [CrossRef]
- Livanov, K.; Yang, L.; Nissenbaum, A.; Wagner, H.D. Interphase tuning for stronger and tougher composites. Sci. Rep. 2016, 6, 26305. [Google Scholar] [CrossRef]
- Shang-Lin, G.; Mäder, E. Characterization of interphase nanoscale property variation in glass fiber reinforced polypropylene and epoxy resin composites. Comp. Part A Appl. Sci. Manuf. 2002, 33, 559–576. [Google Scholar]
- Kamiński, M.; Kleiber, M. Stochastic structural interface defects in fiber composites. Int. J. Solids Struct. 1996, 33, 3035–3056. [Google Scholar] [CrossRef]
- Le Duigou, A.; Davies, P.; Baley, C. Exploring durability of interfaces in flax fibre/epoxy micro-composites. Compos. Part Ad Appl. Sci. Manuf. 2013, 48, 121–128. [Google Scholar] [CrossRef]
- Beckmann, C.; Hohe, J. Effects of material uncertainty in the structural response of metal foam core sandwich beams. Compos. Struct. 2014, 113, 382–395. [Google Scholar] [CrossRef]
- Koutsawa, Y.; Karatrantos, A.; Yu, W.; Ruch, D. A micromechanics approach for the effective thermal conductivity of composite materials with general linear imperfect interfaces. Compos. Struct. 2018, 200, 747–756. [Google Scholar] [CrossRef]
- Whitehouse, A.F.; Clyne, T.W. Effects of reinforcement contact and shape on cavitation and failure in metal-matrix composites. Composites 1993, 24, 256–261. [Google Scholar] [CrossRef]
- Nazarenko, L.; Stolarski, H.; Altenbach, H. A statistical interphase damage model of random particulate composites. Int. J. Plast. 2019, 116, 118–142. [Google Scholar] [CrossRef]
- Reincke, K.; Grellmann, W.; Heinrich, G. Investigation of mechanical and fracture mechanical properties of elastomers filled with precipitated silica and nanofillers based upon layered silicates. Rubber Chem. Technol. 2004, 77, 662–677. [Google Scholar] [CrossRef]
- Golanski, D.; Terada, K.; Kikuchi, N. Macro and micro scale modeling of thermal residual stresses in metal matrix composite surface layers by the homogenization method. Comput. Mech. 1997, 19, 188–202. [Google Scholar] [CrossRef]
- Mura, T. Micromechanics of Defects in Solids; Springer Science & Business Media: Dordrecht, The Netherlands, 1987; ISBN 978-90-247-3256-2. [Google Scholar]
- Hashin, Z. Thermoelastic properties of fiber composites with imperfect interface. Mech. Mater. 1990, 8, 333–348. [Google Scholar] [CrossRef]
- Theocaris, P.S. Definition of interphase in composites. In The Role of the Polymeric Matrix in the Processing and Structural Properties of Composite Materials; Seferis, J.C., Nicolais, L., Eds.; Springer Science & Business Media: New York, NY, USA, 1983. [Google Scholar]
- Yanase, K.; Ju, J.W. Effective elastic moduli of spherical particle reinforced composites containing imperfect interfaces. Int. J. Damage Mech. 2011, 21, 97–127. [Google Scholar] [CrossRef]
- Wu-Gui, J.; Ren-Zhi, Z.; Quing, H.; Yong-Gang, T. Homogenized finite element analysis on effective elastoplastic mechanical behaviors of composite with imperfect interfaces. Int. J. Mol. Sci. 2014, 15, 23389–23407. [Google Scholar]
- Yanase, K.; Ju, J. Overall elastoplastic damage responses of spherical particle-reinforced composites containing imperfect interfaces. Int. J. Damage Mech. 2013, 23, 411–429. [Google Scholar] [CrossRef]
- Hashin, Z. The spherical inclusion with imperfect interface conditions. J. Appl. Mech. 1991, 58, 444–449. [Google Scholar] [CrossRef]
- Hashin, Z. Thin interphase/imperfect interface in elasticity with application to coated fiber composites. J. Mech. Phys. Solids 2002, 50, 2509–2537. [Google Scholar] [CrossRef]
- Jesson, A.D.; Watts, J.F. The interface and interphase in polymer matrix composites: Effect on mechanical properties and methods for identification. Polym. Rev. 2012, 52, 321–354. [Google Scholar] [CrossRef]
- Ručevskis, S.; Čate, A.; Reichhold, J.; Błędzki, A. Effective elastic constants of fiber-reinforced polymer-matrix composites with the concept of interphase. Int. J. Appl. Mech. Engrg. 2003, 8, 109–115. [Google Scholar]
- Sokołowski, D.; Kamiński, M. Computational homogenization of carbon/polymer composites with stochastic interface defects. Compos. Struct. 2018, 183, 434. [Google Scholar] [CrossRef]
- Barulich, N.D.; Godoy, L.A.; Dardati, P.M. A computational micromechanics approach to evaluate elastic properties of composites with fiber-matrix interface damage. Compos. Struct. 2016, 154, 309–318. [Google Scholar] [CrossRef]
- Schellekens, J.C.; de Borst, R. The application of interface elements and enriched or rate-dependent continua to micro-mechanical analyses of fracture in composites. Comput. Mech. 1994, 14, 68–83. [Google Scholar] [CrossRef]
- Gutiérrez, M.A.; de Borst, R. Numerical analysis of localization using a viscoplastic regularization: Influence of stochastic material defects. Int. J. Numer. Methods Eng. 1999, 44, 1823–1841. [Google Scholar] [CrossRef]
- Géhant, S.; Fond, C.; Schirrer, R. Criteria for cavitation of rubber particles: Influence of plastic yielding in the matrix. Int. J. Fract. 2003, 122, 161–175. [Google Scholar] [CrossRef]
- Gurtin, M.E. An Introduction to Continuum Mechanics; Academic Press: Pittsburgh, PE, USA, 1982. [Google Scholar]
- Kevrekidis, I.G.; Gear, C.W.; Hyman, J.M.; Kevrekidis, P.G.; Runborg, O.; Theodoropoulos, C. Equation-free, coarse-grained multiscale computation: Enabling microscopic simulators to perform system-level analysis. Commun. Math. Sci. 2003, 1, 715–762. [Google Scholar]
- Jeulin, D.; Ostoja-Starzewski, M. (Eds.) Mechanics of Random and Multiscale Structures; CISM Courses and Lectures No. 430; Springer: New York, NY, USA, 2001. [Google Scholar]
- Flores, E.S.; DiazDelaO, F.; Friswell, M.; Sienz, J. A computational multi-scale approach for the stochastic mechanical response of foam-filled honeycomb cores. Compos. Struct. 2011, 94, 1861–1870. [Google Scholar] [CrossRef]
- Bungartz, H.J.; Griebel, M. Sparse grids. Acta Numer. 2004, 13, 147–269. [Google Scholar] [CrossRef]
- Garcia-Cervera, C.; Ren, W.; Lu, J. Sequential multiscale modeling using sparse representation. Commun. Comput. Phys. 2008, 4, 1025–1033. [Google Scholar]
- Tasan, C.C.; Hoefnagels, J.P.; Diehl, M.; Yan, D.; Roters, F.; Raabe, D. Strain localization and damage in dual phase steels investigated by coupledin-situde formation experiments and crystalplasticity simulations. Int. J. Plast. 2014, 63, 198–221. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mat. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Cusatis, G.; Rezakhani, R.; Alnaggar, M.; Zhou, Z.; Pelessone, D. Multiscale computational models for the simulation of concrete materials and structures. In Proceedings of the EURO-C 2014, Computational Modelling of Concrete and Concrete Structures, St. Anton am Arlberg, Austria, 24–27 March 2014; Bicanic, N., Mang, H., Meschke, G., de Borst, R., Eds.; CRC Press/Taylor & Francis Group, 2014; pp. 23–38. [Google Scholar]
- Kanouté, P.; Boso, D.P.; Chaboche, J.L.; Schrefler, B.A. Multiscale methods for composites: A review. Arch. Comput. Methods Eng. 2009, 16, 31–75. [Google Scholar] [CrossRef]
- Brandt, A. Scientific Computation: Review. In Multiscale and Multiresolution Methods: Theory and Applications, Yosemite Educational Symposium Conf. Proc.; Barth, T.J., Ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Weinan, E.; Engquist, B. The heterogeneous multi-scale methods. Commun. Math. Sci. 2003, 1, 87–133. [Google Scholar]
- Ruban, A.I. Fluid Dynamics Part 2: Asymptotic Problems of Fluid Dynamics; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Kevorkian, J.; Cole, J.D. Perturbation Methods in Applied Mathematics; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Zhao, J.; Li, H.; Cheng, G.; Cai, Y. On predicting the effective elastic properties of polymer nanocomposites by novel numerical implementation of asymptotic homogenization method. Compos. Struct. 2016, 135, 297–305. [Google Scholar] [CrossRef]
- Arnold, V.I. Geometrical Methods in the Theory of Ordinary Differential Equations; Springer: New York, NY, USA, 1983. [Google Scholar]
- Kushnevsky, V.; Morachkovsky, O.; Altenbach, H. Identification of effective properties of particle reinforced composite materials. Comput. Mech. 1988, 22, 317–325. [Google Scholar] [CrossRef]
- Spohn, H. Large Scale Dynamics of Interacting Particles; Springer: New York, NY, USA, 1991. [Google Scholar]
- Zwanzig, R.W. Collision of a Gas Atom with a Cold Surface. J. Chem. Phys. 1960, 32, 1173–1177. [Google Scholar] [CrossRef]
- Wilson, K.G.; Kogut, J. The renormalization group and the ε expansion. Phys. Rep. 1974, 12, 75–200. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Bensoussan, A.; Lions, J.L.; Papanicolaou, G. Asymptotic Analysis for Periodic Structures; North-Holland: Amsterdam, The Netherland, 1978. [Google Scholar]
- Fish, J.; Chen, W. Higher-Order Homogenization of Initial/Boundary-Value Problem. J. Eng. Mech. 2001, 127, 1223–1230. [Google Scholar] [CrossRef]
- Ghosh, S.; Lee, K.; Moorthy, S. Multiple scale analysis of heterogeneous elastic structures using homogenization theory and voronoi cell finite element method. Int. J. Solids Struct. 1995, 32, 27–62. [Google Scholar] [CrossRef]
- Kamiński, M. Computational Mechanics of Composite Materials; Springer: London, UK; New York, NY, USA, 2005. [Google Scholar]
- Wang, M.; Zhang, K.; Chen, C. A mixed FFT-Galerkin approach for incompressible or slightly compressible hyperelastic solids under finite deformation. Comput. Methods Appl. Mech. Eng. 2022, 396, 115092. [Google Scholar] [CrossRef]
- Zhang, G.; Feng, N.; Khandelwal, K. A computational framework for homogenization and multiscale stability analyses of nonlinear periodic materials. Int. J. Numer. Methods Eng. 2021, 122, 6527–6575. [Google Scholar] [CrossRef]
- Fernández, M.; Jamshidian, M.; Böhlke, T.; Kersting, K.; Weeger, O. Anisotropic hyperelastic constitutive models for finite deformations combining material theory and data-driven approaches with application to cubic lattice metamaterials. Comput. Mech. 2020, 67, 653–677. [Google Scholar] [CrossRef]
- Brändel, M.; Brands, D.; Maike, S.; Rheinbach, O.; Schröder, J.; Schwarz, A.; Stoyan, D. Effective hyperelastic material parameters from microstructures constructed using the planar Boolean model. Comput. Mech. 2022, 69, 1295–1321. [Google Scholar] [CrossRef]
- Somoh, G.K.; Ben Toumi, R.; Renard, J.; Monin, M. Statistical approach of elastic properties of continuous fiber composite. Compos. Struct. 2015, 119, 287–297. [Google Scholar] [CrossRef]
- Milton, G.W. The Theory of Composites; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Fu, S.-Y.; Lauke, B.; Mai, Y.-W. Science and Engineering of Short Fibre Reinforced Polymer Composites; CRC Press: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Sanchez-Palencia, E. Non-Homogeneous Media and Vibration Theory; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. Math. Phys. Eng. Sci. 1957, 241, 376–396. [Google Scholar]
- Shin, H.; Choi, J.; Cho, M. An efficient multiscale homogenization modeling approach to describe hyperelastic behavior of polymer nanocomposites. Compos. Sci. Technol. 2019, 175, 128–134. [Google Scholar] [CrossRef]
- Mei, C.C.; Vernescu, B. Homogenization Methods for Multiscale Mechanics; World Scientific Publishers: Hackensack, NJ, USA, 2010. [Google Scholar]
- Segurado, J.; Llorca, J. A numerical approximation to the elastic properties of sphere-reinforced composites. J. Mech. Phys. Solids 2002, 50, 2107–2121. [Google Scholar] [CrossRef]
- Fritzen, F.; Böhlke, T. Periodic three-dimensional mesh generation for particle reinforced composites with application to metal matrix composites. Int. J. Solids Struct. 2011, 48, 706–718. [Google Scholar] [CrossRef]
- Chen, G.; Bezold, A.; Broeckmann, C. Influence of the size and boundary conditions on the predicted effective strengths of particulate reinforced metal matrix composites (PRMMCs). Compos. Struct. 2018, 189, 330–339. [Google Scholar] [CrossRef]
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: Statistical and numerical approach. Int. J. Solids Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
- Savvas, D.; Stefanou, G.; Papadrakakis, M. Determination of RVE size for random composites with local volume fraction variation. Comput. Methods Appl. Mech. Eng. 2016, 305, 340–358. [Google Scholar] [CrossRef]
- Majewski, M.; Kursa, M.; Holobut, P.; Kowalczyk-Gajewska, K. Micromechanical and numerical analysis of packing and size effects in elastic particulate composites. Compos. Part B Eng. 2017, 124, 158–174. [Google Scholar] [CrossRef]
- Ostoja-Starzewski, M. Scale effects in plasticity of random media: Status and challenges. Int. J. Plast. 2005, 21, 1119–1160. [Google Scholar] [CrossRef]
- Kuang, C.L.; Anindya, G. Validity of random microstructures simulation in fiber-reinforced composite materials. Compos. Part B-Eng. 2014, 57, 56–70. [Google Scholar]
- Pivovarov, D.; Zabihyan, R.; Mergheim, J.; Willner, K.; Steinmann, P. On periodic boundary conditions and ergodicity in computational homogenization of heterogeneous materials with random microstructure. Comput. Methods Appl. Mech. Eng. 2019, 357, 112563. [Google Scholar] [CrossRef]
- Betsch, P.; Gruttmann, F.; Stein, E. A 4-node finite shell element for the implementation of general hyperelastic 3D-elasticity at finite strains. Comput. Methods Appl. Mech. Eng. 1996, 130, 57–79. [Google Scholar] [CrossRef]
- Bessa, M.A.; Bostanabad, R.; Liu, Z.; Hu, A.; Apley, D.W.; Brinson, C.; Chen, W.; Liu, W.K. A framework for data-driven analysis of materials under uncertainty: Countering the curse of dimensionality. Comput. Methods Appl. Mech. Eng. 2017, 320, 633–667. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, C. Exploring the 3D architectures of deep material network in data-driven multiscale mechanics. J. Mech. Phys. Solids 2019, 127, 20–46. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, C.; Koishi, M. A deep material network for multiscale topology learning and accelerated nonlinear modeling of heterogeneous materials. Comput. Methods Appl. Mech. Eng. 2019, 345, 1138–1168. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Matous, K. A nonlinear manifold-based reduced order model for multiscale analysis of heterogeneous hyperelastic materials. J. Comput. Phys. 2016, 313, 635–653. [Google Scholar] [CrossRef]
- Yvonnet, J.; He, Q.-C. The reduced model multiscale method (R3M) for the non-linear homogenization of hyperelastic media at finite strains. J. Comput. Phys. 2007, 223, 341–368. [Google Scholar] [CrossRef]
- Yvonnet, J.; Monteiro, E.; He, Q.-C. Computational homogenization method and reduced database model for hyperelastic heterogeneous structures. Int. J. Multiscale Comput. 2013, 11, 201–225. [Google Scholar] [CrossRef]
- Wu, C.; Koishi, M. Three-dimensional meshfree-enriched finite element formulation for micromechanical hyperelastic modeling of particulate rubber composites. Int. J. Numer. Methods Eng. 2012, 91, 1137–1157. [Google Scholar] [CrossRef]
- Triantafyllidis, N.; Aifantis, E.C. A gradient approach to localization of deformation. I. Hyperelastic materials. J. Elast. 1986, 16, 225–237. [Google Scholar] [CrossRef]
- de Geus, T.; Vondřejc, J.; Zeman, J.; Peerlings, R.; Geers, M. Finite strain FFT-based non-linear solvers made simple. Comput. Methods Appl. Mech. Eng. 2017, 318, 412–430. [Google Scholar] [CrossRef]
- Michel, J.C.; Suquet, P. Computational analysis of nonlinear composite structure using the non-uniform transformation 3field analysis. Comput. Methods Appl. Mech. Eng. 2004, 193, 5477–5502. [Google Scholar] [CrossRef]
- Ehlers, W.; Bidier, S. From particle mechanics to micromorphic media. Part I: Homogenisation of discrete interactions towards stress quantities. Int. J. Solids Struct. 2018, 187, 23–37. [Google Scholar] [CrossRef]
- Huang, Z.P.; Wang, J. A theory of hyperelasticity of multi-phase media with surface/interface energy effect. Acta Mech. 2006, 182, 195–210. [Google Scholar] [CrossRef]
- Jahanshahi, M.; Ahmadi, H.; Khoei, A. A hierarchical hyperelastic-based approach for multi-scale analysis of defective nano-materials. Mech. Mater. 2019, 140, 103206. [Google Scholar] [CrossRef]
- Masud, A.; Truster, T.J. A framework for residual-based stabilization of incompressible finite elasticity: Stabilized formulations and F methods for linear triangles and tetrahedra. Comput. Methods Appl. Mech. Eng. 2013, 267, 359–399. [Google Scholar] [CrossRef]
- Bisegna, P.; Luciano, R. Bounds on the overall properties of composites with debonded frictionless interfaces. Mech. Mater. 1998, 28, 23–32. [Google Scholar] [CrossRef]
- Dai, M.; Schiavone, P.; Gao, C.-F. Neutral nano-inhomogeneities in hyperelastic materials with a hyperelastic interface model. Int. J. Non-Linear Mech. 2016, 87, 38–42. [Google Scholar] [CrossRef]
- Wang, X.; Schiavone, P. Harmonic three-phase circular inclusions in finite elasticity. Contin. Mech. Thermodyn. 2015, 27, 739–747. [Google Scholar] [CrossRef]
- Wang, X.; Schiavone, P. Neutral coated circular inclusions in finite plane elasticity of harmonic materials. Eur. J. Mech. A/Solids 2012, 33, 75–81. [Google Scholar] [CrossRef]
- Ma, J.; Sahraeem, S.; Wriggers, P.; de Lorenzis, L. Stochastic multiscale homogenization analysis of heterogeneous materials under finite deformations with full uncertainty in the microstructure. Comput. Mech. 2015, 55, 819–835. [Google Scholar] [CrossRef]
- Sasikumar, P.; Suresh, R.; Gupta, S. Stochastic model order reduction in uncertainty quantification of composite structures. Compos. Struct. 2015, 128, 21–34. [Google Scholar] [CrossRef]
- Kamiński, M. Sensitivity and randomness in homogenization of periodic fiber-reinforced composites via the response function method. Int. J. Solids Struct. 2009, 46, 923–937. [Google Scholar] [CrossRef]
- Ma, J.; Temizer, I.; Wriggers, P. Random homogenization analysis in linear elasticity based on analytical bounds and estimates. Int. J. Solids Struct. 2011, 48, 280–291. [Google Scholar] [CrossRef]
- Kamiński, M. Gaussian uncertainty in homogenization of rubber–carbon black nanocomposites. Compos. Struct. 2014, 113, 225–235. [Google Scholar] [CrossRef]
- Kamiński, M.; Lauke, B. Parameter sensitivity and probabilistic analysis of the elastic homogenized properties for rubber filled polymers. CMES Comput. Model. Eng. Sci. 2013, 93, 411–440. [Google Scholar]
- Kamiński, M.; Lauke, B. Probabilistic homogenization of polymers filled with rubber particles. Comput. Mater. Sci. 2014, 82, 483–496. [Google Scholar] [CrossRef]
- Kamiński, M. Multiscale homogenization of n-component composites with semi-elliptical random interface defects. Int. J. Solids Struct. 2005, 42, 3571–3590. [Google Scholar] [CrossRef]
- Sokołowski, D.; Kamiński, M. Probabilistic homogenization of hyper-elastic particulate composites with random interface. Compos. Struct. 2020, 241, 112118. [Google Scholar] [CrossRef]
- Sokołowski, D.; Kamiński, M.; Wirowski, A. Energy fluctuations in the homogenized hyper-elastic particulate composites with stochastic interface defects. Energies 2020, 13, 20112020. [Google Scholar] [CrossRef]
- Allaix, D.; Carbone, V. An improvement of the response surface method. Struct. Saf. 2011, 33, 165–172. [Google Scholar] [CrossRef]
- Rajashekhar, M.R.; Ellingwood, B.R. A new look at the response surface approach for reliability analysis. Struct. Saf. 1993, 12, 205–220. [Google Scholar] [CrossRef]
- Jurecka, F.; Ganser, M.; Bletzinger, K.U. Update scheme for sequential spatial correlation approximations in robust design optimization. Comp. Struct. 2007, 85, 606–614. [Google Scholar] [CrossRef]
- Simpson, T.W.; Poplinski, J.D.; Koch, P.N.; Allen, J.K. Metamodels for Computer-based Engineering Design: Survey and recommendations. Eng. Comput. 2001, 17, 129–150. [Google Scholar] [CrossRef]
- Draper, N.; Smith, H. Applied Regression Analysis; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Myers, R.H.; Montgomery, D.C. Response Surface Methodology, Process and Product Optimization Using Designed Experiments, 2nd ed.; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Alibrandi, U.; Impollonia, N.; Ricciardi, G. Probabilistic eigenvalue buckling analysis solved through the ratio of polynomial response surface. Comput. Methods Appl. Mech. Eng. 2010, 199, 450–464. [Google Scholar] [CrossRef]
- Settineri, D.; Falsone, G. An APDM-based method for the analysis of systems with uncertainties. Comput. Methods Appl. Mech. Eng. 2014, 278, 828–852. [Google Scholar] [CrossRef]
- Dantzig, G.B. Linear Programming and Extensions; Princeton University Press: Princeton, NJ, USA, 1963. [Google Scholar]
- Lemke, C.E. The dual method of solving the linear programming problem. Nav. Res. Logist. Q. 1954, 1, 36–47. [Google Scholar] [CrossRef]
- Forrest, J.J.H.; Tomlin, J.A. Vector processing in simplex and interior methods for linear programming. Ann. Oper. Res. 1990, 22, 71–100. [Google Scholar] [CrossRef]
- Boland, N. A dual-active-set algorithm for positive semi-definite quadratic programming. Math. Program. 1996, 78, 1–27. [Google Scholar] [CrossRef]
- Gould, N.I.M.; Toint, P.L. An iterative working-set method for large-scale non-convex quadratic programming. Appl. Numer. Math. 2002, 43, 109–128. [Google Scholar] [CrossRef][Green Version]
- Monteiro, R.D.C.; Adler, I. Interior path following primal-dual algorithms, Part II: Convex quadratic programming. Math. Program. 1989, 44, 43–66. [Google Scholar] [CrossRef]
- Vanderbei, R.J. LOQO:an interior point code for quadratic programming. Optim. Methods Softw. 1999, 11, 451–484. [Google Scholar] [CrossRef]
- Wright, M.H. Interior methods for constrained optimization. Acta Numer. 1992, 1, 341–407. [Google Scholar] [CrossRef]
- Gill, P.E.; Murray, W.; Ponceleón, D.B.; Saunders, M.A. Solving Reduced KKT Systems in Barrier Methods for Linear and Quadratic Programming; Report SOL 91-7; Department of Operations Research, Stanford University: Stanford, CA, USA, 1991. [Google Scholar]
- Gill, P.E.; Murray, W.; Saunders, M.A.; Tomlin, J.A.; Wright, M.H. Wright, On projected Newton barrier methods for linear programming and an equivalence to Karmarkar’s projective method. Math. Program. 1986, 36, 183–209. [Google Scholar] [CrossRef]
- AFiacco, V. Barrier methods for nonlinear programming. In Operations Research Support Methodology; Marcel Dekker: New York, NY, USA, 1979; pp. 377–440. [Google Scholar]
- Murray, W. Analytical expressions for the eigenvalues and eigenvectors of the Hessian matrices of barrier and penalty functions. J. Optim. Theory Appl. 1971, 7, 189–196. [Google Scholar] [CrossRef]
- Vavasis, S.A. Nonlinear Optimization: Complexity Issues; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Wu, C.; Tau, X.C. Augmented lagrangian method, dual methods, and split Bregman iteration for ROF, Vectorial TV, and High Order Models. SIAM J. Imaging Sci. 2010, 3, 330–339. [Google Scholar] [CrossRef]
- Forsgren, A.; Gill, P.E.; Wright, M.H. Interior Methods for Nonlinear Optimization. SIAM Rev. 2002, 44, 525–597. [Google Scholar] [CrossRef]
- Diehl, M.; Ferreau, H.J.; Haverbeke, N. Efficient Numerical Methods for Nonlinear MPC and Moving Horizon Estimation; Springer: Berlin/Heidelberg, Germany, 2009; pp. 391–417. [Google Scholar]
- Lasdon, L.S.; Waren, A.D.; Jain, A.; Ratner, M. Design and testing of a generalized reduced gradient code for nonlinear programming. ACM Trans. Math. Soft. 1978, 4, 34–50. [Google Scholar] [CrossRef]
- Gabriele, G.A.; Ragsdell, K.M. The generalized reduced gradient method: A reliable tool for optimal design. J. Eng. Ind. 1977, 99, 394–400. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamiński, M.; Sokołowski, D. Probabilistic Analysis of Composite Materials with Hyper-Elastic Components. Materials 2022, 15, 8878. https://doi.org/10.3390/ma15248878
Kamiński M, Sokołowski D. Probabilistic Analysis of Composite Materials with Hyper-Elastic Components. Materials. 2022; 15(24):8878. https://doi.org/10.3390/ma15248878
Chicago/Turabian StyleKamiński, Marcin, and Damian Sokołowski. 2022. "Probabilistic Analysis of Composite Materials with Hyper-Elastic Components" Materials 15, no. 24: 8878. https://doi.org/10.3390/ma15248878
APA StyleKamiński, M., & Sokołowski, D. (2022). Probabilistic Analysis of Composite Materials with Hyper-Elastic Components. Materials, 15(24), 8878. https://doi.org/10.3390/ma15248878






