Recrystallization of Si Nanoparticles in Presence of Chalcogens: Improved Electrical and Optical Properties
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Annealing of Nanosilicon with Sulfur
3.2. Annealing of Nanosilicon with Selenium and Tellurium
3.3. Electron Diffraction
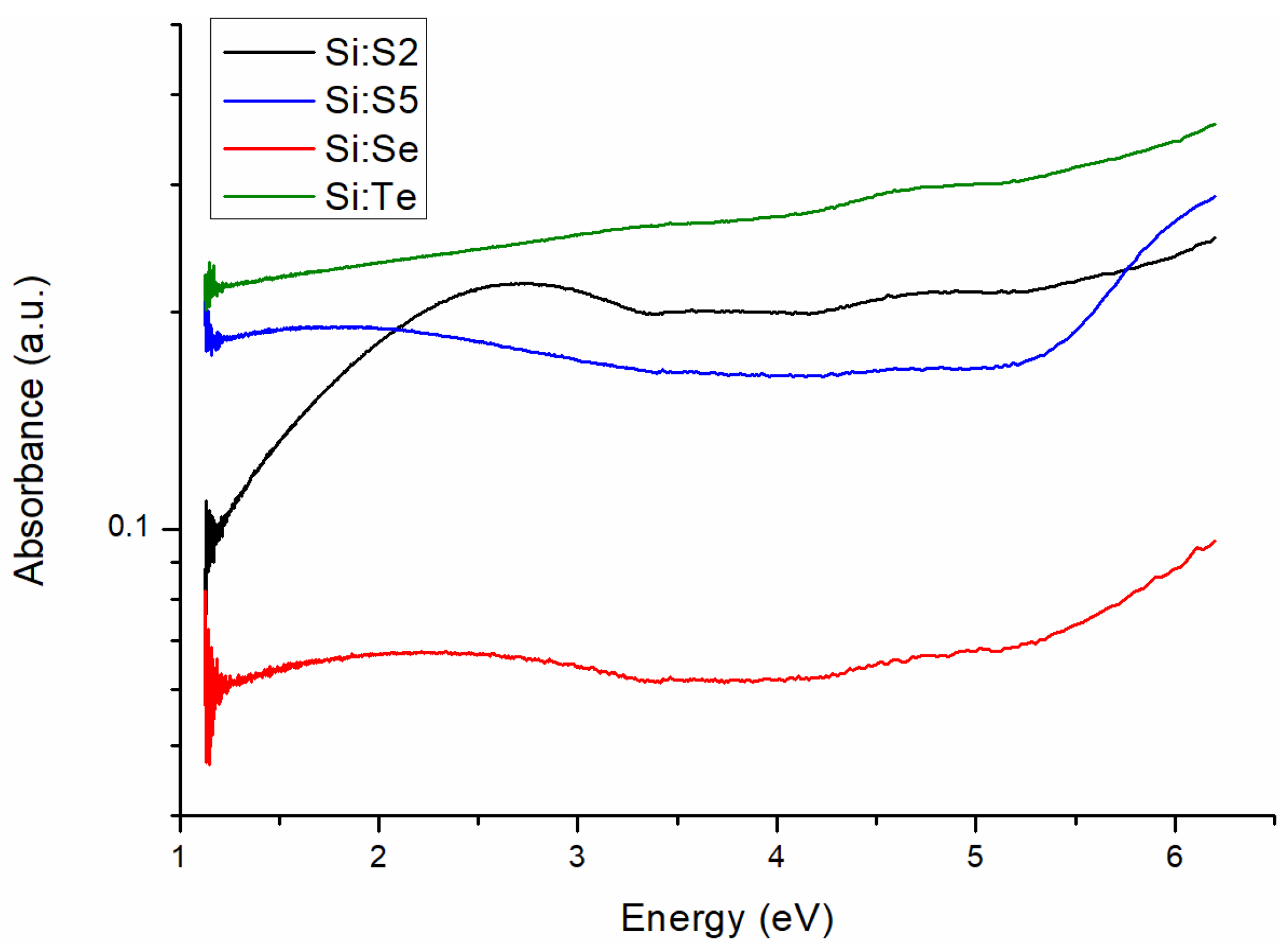
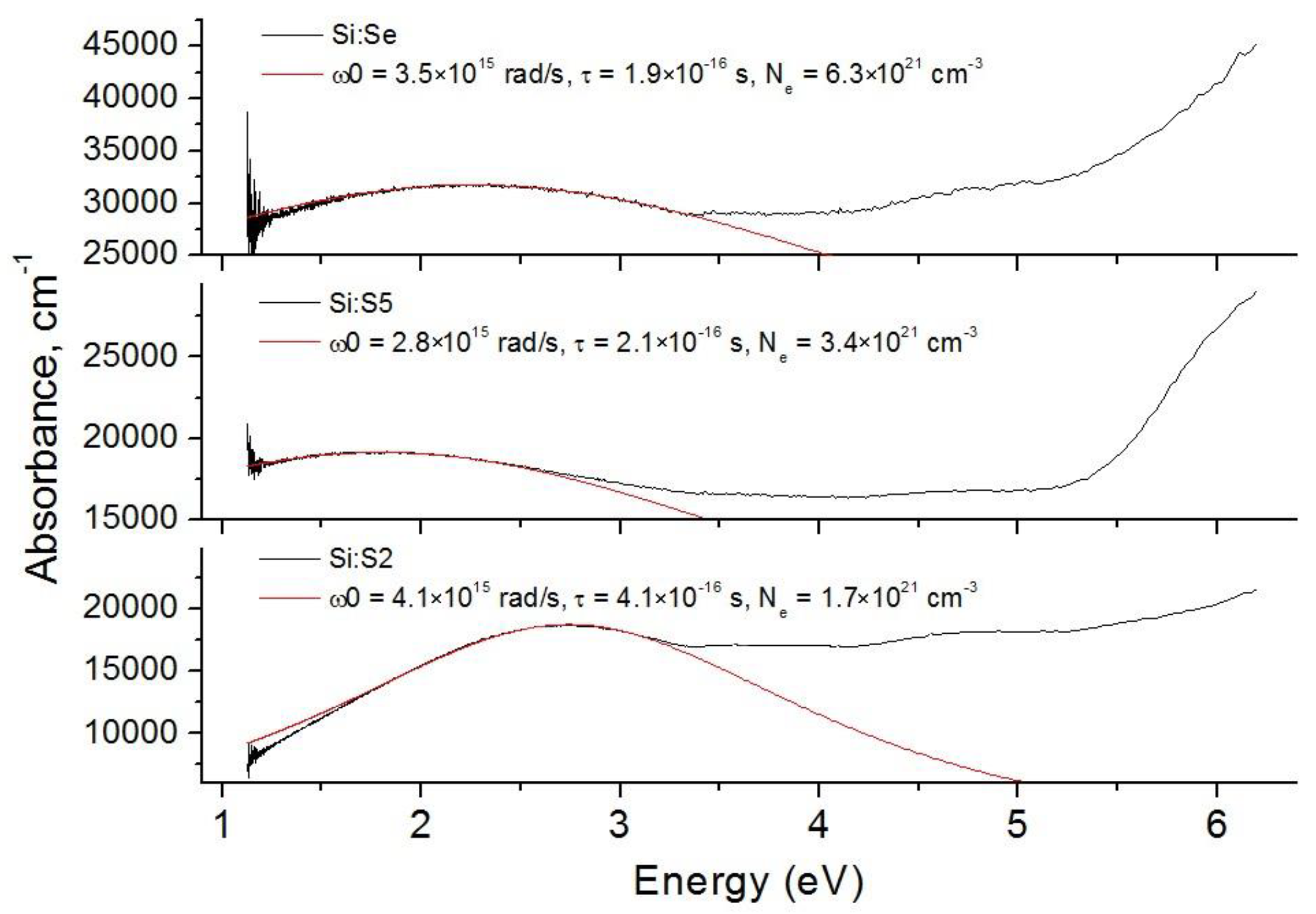
3.4. Optical Absorption
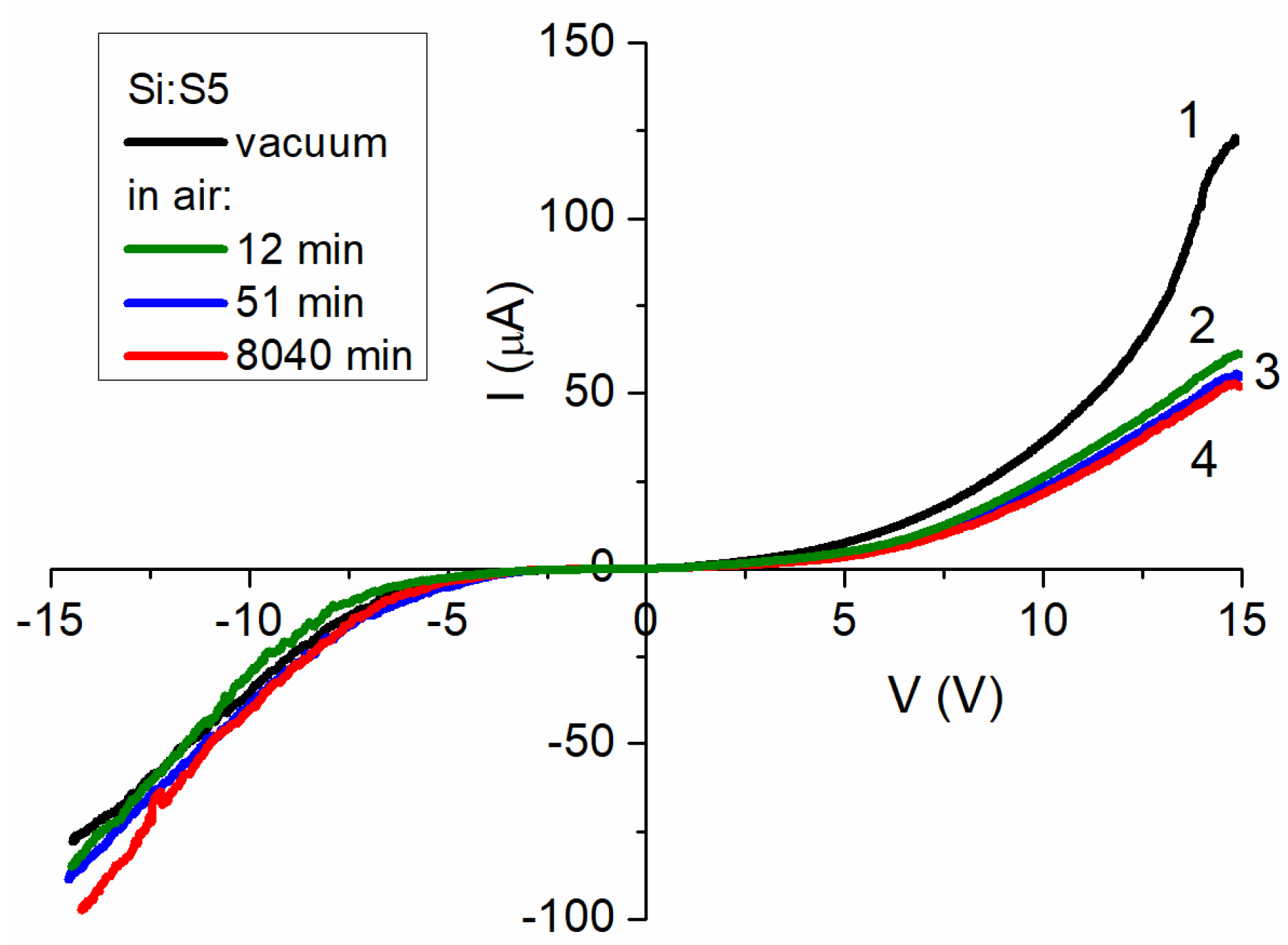
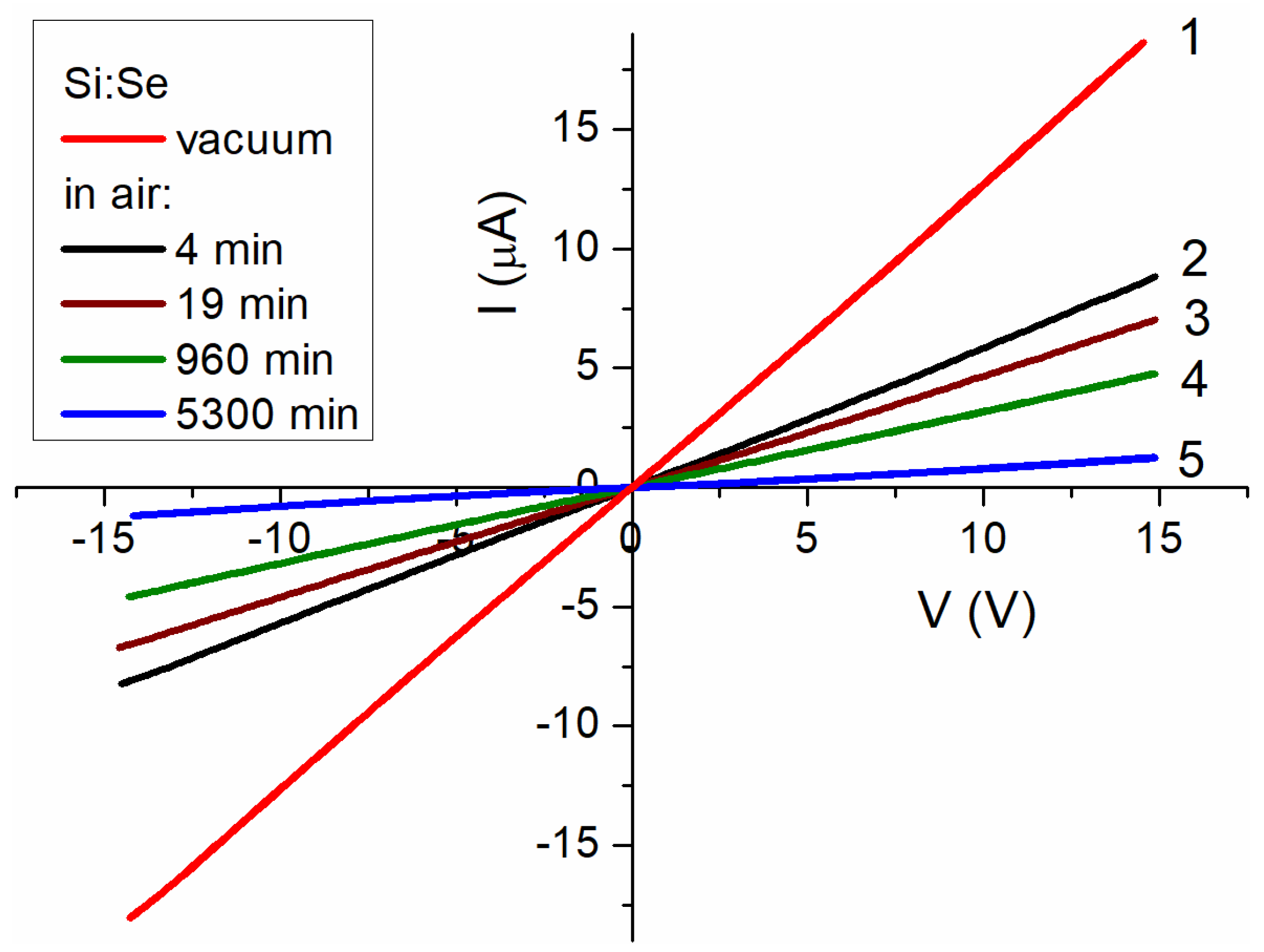
3.5. Electrical Properties of Films
3.5.1. Si:S5 Film
3.5.2. Si:Se Film
3.5.3. Si:Te Film
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hull, R. Properties of Crystalline Silicon; INSPEC: London, UK, 1999. [Google Scholar]
- Fan, L.; Yang, D.; Li, D. A Review on Metastable Silicon Allotropes. Materials 2021, 14, 3964. [Google Scholar] [CrossRef]
- Barth, S.; Seifner, M.S.; Maldonado, S. Metastable Group IV Allotropes and Solid Solutions: Nanoparticles and Nanowires. Chem. Mater. 2020, 32, 2703–2741. [Google Scholar] [CrossRef]
- Fan, Q.; Chai, C.; Wei, Q.; Yan, H.; Zhao, Y.; Yang, Y.; Yu, X.; Liu, Y.; Xing, M.; Zhang, J.; et al. Novel silicon allotropes: Stability, mechanical, and electronic properties. J. Appl. Phys. 2015, 118, 185704. [Google Scholar] [CrossRef]
- Ahn, H.S.; Kim, S.W.; Lee, G.S.; Kim, H.K.; Lee, J.H.; Ha, D.H.; Chun, Y.T.; Ryu, S. Optical property of hexagonal (2H) silicon crystal. Semicond. Sci. Technol. 2021, 36, 095023. [Google Scholar] [CrossRef]
- Wang, Q.; Xu, B.; Sun, J.; Liu, H.; Zhao, Z.; Yu, D.; Fan, C.; He, J. Direct Band Gap Silicon Allotropes. J. Am. Chem. Soc. 2014, 136, 9826–9829. [Google Scholar] [CrossRef]
- Joannopoulos, J.D.; Cohen, M.L. Electronic Properties of Complex Crystalline and Amorphous Phases of Ge and Si. I. Density of States and Band Structures. Phys. Rev. B 1973, 7, 2644–2657. [Google Scholar] [CrossRef]
- Beekman, M.; Kauzlarich, S.; Doherty, L.; Nolas, G. Zintl Phases as Reactive Precursors for Synthesis of Novel Silicon and Germanium-Based Materials. Materials 2019, 12, 1139. [Google Scholar] [CrossRef]
- Raffy, C.; Furthmüller, J.; Bechstedt, F. Properties of hexagonal polytypes of group-IV elements from first-principles calculations. Phys. Rev. B 2002, 66, 075201. [Google Scholar] [CrossRef]
- Dixit, S.; Shukla, A.K. Optical Properties of Lonsdaleite Silicon Nanowires: A Promising Material for Optoelectronic Applications. J. Appl. Phys. 2018, 123, 224301. [Google Scholar] [CrossRef]
- Jamieson, J.C. Crystal Structures at High Pressures of Metallic Modifications of Silicon and Germanium. Science 1963, 139, 762–764. [Google Scholar] [CrossRef]
- Olijnyk, H.; Sikka, S.K.; Holzapfel, W.B. Structural Phase Transitions in Si and Ge under Pressures up to 50 GPa. Phys. Lett. A 1984, 103, 137–140. [Google Scholar] [CrossRef]
- Besson, J.M.; Mokhtari, E.H.; Gonzalez, J.; Weill, G. Electrical Properties of Semimetallic Silicon III and Semiconductive Silicon IV at Ambient Pressure. Phys. Rev. Lett. 1987, 59, 473–476. [Google Scholar] [CrossRef] [PubMed]
- Persson, C.; Janzén, E. Electronic Band Structure in Hexagonal Close-Packed Si Polytypes. J. Phys. Condens. Matter 1998, 10, 10549–10555. [Google Scholar] [CrossRef]
- Shiell, T.B.; Zhu, L.; Cook, B.A.; Bradby, J.E.; McCulloch, D.G.; Strobel, T.A. Bulk Crystalline 4H-Silicon through a Metastable Allotropic Transition. Phys. Rev. Lett. 2021, 126, 215701. [Google Scholar] [CrossRef]
- Kurakevych, O.O.; Le Godec, Y.; Strobel, T.A.; Kim, D.Y.; Crichton, W.A.; Guidnard, J. Exploring silicon allotropy and chemistry by high pressure—High temperature conditions. J. Phys. Conf. Ser. 2017, 950, 042049. [Google Scholar] [CrossRef]
- Pandolfi, S.; Renero-Lecuna, c.; Le Godec, Y.; Baptiste, B.; Menguy, N.; Lazerri, M.; Gervais, C.; Spektor, K.; Crichton, W.A.; Kurakevych, O.O. Nature of Hexagonal Silicon Forming via High-Pressure Synthesis: Nanostructured Hexagonal 4H Polytype. Nano Lett. 2018, 18, 5989–5995. [Google Scholar] [CrossRef]
- Xuan, Y.; Tan, L.; Cheng, B.; Zhang, F.; Chen, X.; Ge, M.; Zeng, Q.; Zeng, Z. Pressure-Induced Phase Transitions in Nanostructured Silicon. J. Phys. Chem. C 2020, 124, 27089–27096. [Google Scholar] [CrossRef]
- Kurakevych, O.O.; Le Godec, Y.; Crichton, W.A.; Strobel, T.A. Silicon allotropy and chemistry at extreme conditions. Energy Procedia 2016, 92, 839–844. [Google Scholar] [CrossRef][Green Version]
- Huston, L.Q.; Lugstein, A.; Shen, G.; Cullen, D.A.; Haberl, B.; Williams, J.S.; Bradby, J.E. Synthesis of Novel Phases in Si Nanowires Using Diamond Anvil Cells at High Pressures and Temperatures. Nano Lett. 2021, 21, 1427–1433. [Google Scholar] [CrossRef]
- Ren, Y.; Leubner, P.; Verheijen, M.A.; Haverkort, J.E.M.; Bakkers, E.P.A.M. Hexagonal Silicon grown from higher order Silanes. Nanotechnology 2019, 30, 295602. [Google Scholar] [CrossRef]
- Hauge, H.I.T.; Verheijen, M.A.; Conesa-Boj, S.; Etzelstorfer, T.; Watzinger, M.; Krieger, D.; Zardo, I.; Fasolato, C.; Capitani, F.; Postorino, P.; et al. Hexagonal Silicon Realized. Nano Lett. 2015, 15, 5855–5860. [Google Scholar] [CrossRef] [PubMed]
- Haberl, B.; Strobel, T.A.; Bradby, J.E. Pathways to exotic metastable silicon allotropes. Appl. Phys. Rev. 2016, 3, 040808. [Google Scholar] [CrossRef]
- Rodichkina, S.P.; Lysenko, V.; Belarouci, A.; Bezverkhyy, I.; Chassagnon, R.; Isaiev, M.; Nychyporuk, T.; Timoshenko, V.Y. Photo-induced cubic-to-hexagonal polytype transition in silicon nanowires. CrystEngComm 2019, 21, 4747–4752. [Google Scholar] [CrossRef]
- He, Z.; Maurice, J.; Li, Q.; Pribat, D. Direct evidence of 2H hexagonal Si in Si nanowires. Nanoscale 2019, 11, 4846–4853. [Google Scholar] [CrossRef] [PubMed]
- Fontcuberta i Morral, A.; Arbiol, J.; Prades, J.D.; Cirera, A.; Morante, J.R. Synthesis of Silicon Nanowires with Wurtzite Crystalline Structure by Using Standard Chemical Vapor Deposition. Adv. Mater. 2007, 19, 1347–1351. [Google Scholar] [CrossRef]
- Liu, X.; Wang, D. Kinetically-Induced Hexagonality in Chemically Grown Silicon Nanowires. Nano Res. 2009, 2, 575–582. [Google Scholar] [CrossRef]
- Fabbri, F.; Rotunno, E.; Lazzarini, L.; Fukata, N.; Salviati, G. Visible and Infra-red Light Emission in Boron-Doped Wurtzite Silicon Nanowires. Sci. Rep. 2014, 4, 3603. [Google Scholar] [CrossRef]
- Koren, E.; Rosenwaks, Y.; Allen, J.E.; Hemesath, E.R.; Lauhon, L.J. Nonuniform doping distribution along silicon nanowires measured by Kelvin probe force microscopy and scanning photocurrent microscopy. Appl. Phys. Lett. 2009, 95, 092105. [Google Scholar] [CrossRef]
- Popelensky, V.M.; Dorofeev, S.G.; Chernysheva, G.S.; Kononov, N.N.; Bubenov, S.S.; Vinokurov, A.A. Doping of nanocrystalline silicon with sulfur by gas-phase diffusion. Inorg. Chem. Comm. 2022, 141, 109602. [Google Scholar] [CrossRef]
- Hayzelden, C.; Batstone, J.L. Silicide formation and silicide-mediated crystallization of nickel-implanted amorphous silicon thin films. J. Appl. Phys. 1993, 73, 8279. [Google Scholar] [CrossRef]
- Odin, I.N.; Ivanov, V.A.; Petrovskii, A.Y.; Kozlovskii, V.F.; Rezvanov, R.R. The ptot-T-x Diagram of the Si-S System. Russ. J. Inorg. Chem. 2000, 45, 479–481. [Google Scholar]
- Du, L.; Wu, Z.; Li, S.; Hu, Z.; Jiang, Y. First-principles calculations of properties for chalcogen (S, Se, Te) doped silicon. Solid State Commun. 2016, 226, 1–4. [Google Scholar] [CrossRef]
- Odin, I.N.; Ivanov, V.A. ptot-T-x Diagram of the Si-Se System and Homogeneity Ranges of Silicon Chalcogenides from Tensimetric Data. Russ. J. Inorg. Chem. 2000, 45, 98–102. [Google Scholar]
- Mishra, R.; Mishra, P.K.; Phapale, S.; Babu, P.D.; Sastry, P.U.; Ravikumar, G.; Yadav, A.K. Evidences of the existence of SiTe2 crystalline phase and a proposed new Si–Te phase diagram. J. Solid State Chem. 2016, 237, 234–241. [Google Scholar] [CrossRef]
- Kuzmin, G.P.; Kononov, N.N.; Rozhanskii, N.V.; Surkov, A.A.; Tikhonevich, O.V. The formation of nanoparticles in laser-induced SiH4 gas reactions. Mater. Lett. 2012, 68, 504. [Google Scholar] [CrossRef]
- Shuman, V.B.; Makhova, A.A.; Yu, A.; Ivanov, A.M.; Lodygin, A.N. Solubility of sulfur in silicon. Semiconductors 2012, 46, 993. [Google Scholar] [CrossRef]
- Holm, C.; Sirtl, E. Crystallization of silicon from the silicon-chalcogen vapor phase. J. Cryst. Growth. 1981, 54, 253–266. [Google Scholar] [CrossRef]
- Vydyanath, H.R.; Lorenzo, J.S.; Kroger, F.A. Defect pairing diffusion, and solubility studies in selenium-doped silicon. J. Appl. Phys. 1978, 49, 5928. [Google Scholar] [CrossRef]
- Komarov, F.F.; Lastovsky, S.B.; Romanov, I.A.; Parkhomenko, I.N.; Vlasukova, L.A.; Ivlev, G.D.; Berencen, Y.; Tsivako, A.A.; Kovalchuk, N.S.; Wendler, E. Tellurium hypersaturated silicon layers for visible and infrared photodiodes. J. Tech. Phys. 2021, 91, 2026–2037. [Google Scholar] [CrossRef]
- Kim, T.G.; Warrender, J.M.; Aziz, M.J. Strong sub-band-gap infrared absorption in silicon supersaturated with sulfur. Appl. Phys. Lett. 2006, 88, 241902. [Google Scholar] [CrossRef]
- Tull, B.R.; Winkler, M.T.; Mazur, E. The role of diffusion in broadband infrared absorption in chalcogen-doped silicon. Appl. Phys. A 2009, 96, 327–334. [Google Scholar] [CrossRef]
- Pan, S.H.; Recht, D.; Charnvanichborikarn, S.; Williams, J.S.; Aziz, M.J. Enhanced visible and near-infrared optical absorption in silicon supersaturated with chalcogens. Appl. Phys. Lett. 2011, 98, 121913. [Google Scholar] [CrossRef]
- Janzén, E.; Stedman, R.; Grossmann, G.; Grimmeiss, H.G. High-resolution studies of sulfur- and selenium-related donor centers in silicon. Phys. Rev. B 1984, 29, 1907–1918. [Google Scholar] [CrossRef]
- Ertekin, E.; Winkler, M.T.; Recht, D.; Said, A.J.; Aziz, M.J.; Buonassisi, T.; Grossman, J.C. Insulator-to-Metal Transition in Selenium-Hyperdoped Silicon: Observation and Origin. Phys. Rev. Lett. 2012, 108, 026401. [Google Scholar] [CrossRef]
- Winkler, M.T.; Recht, D.; Sher, M.-J.; Said, A.J.; Mazur, E.; Aziz, M.J. Insulator-to-Metal Transition in Sulfur-Doped Silicon. Phys. Rev. Lett. 2011, 106, 178701. [Google Scholar] [CrossRef]
- Sze, S.M. Physics of Semiconductor Devices, 2nd ed.; Wiley: New York, NY, USA, 1981; Volume 2, p. 112. [Google Scholar]
- Chen, T.; Reich, K.V.; Kramer, N.J.; Fu, H.; Kortshagen, U.R.; Shklovskii, B.I. Metal-insulator transition in films of doped semiconductor nanocrystals. Nat. Mater. 2016, 15, 299–303. [Google Scholar] [CrossRef]






| Sample | Initial. S conc., at.% | T, °C | t, h | Presence of Rods * | S conc., at.% before Etching | S conc., at.% after Etching |
|---|---|---|---|---|---|---|
| Si:S500 | 10 | 500 | 1 | - | 1.54 | 0.60 |
| Si:S700 | 10 | 700 | 1 | - | 1.56 | 0.50 |
| Si:S900 | 10 | 900 | 1 | + | 0.94 | 0.24 |
| Si:S1 | 20 | 800 | 1 | - | 2.31 | 0.21 |
| Si:S2 | 20 | 825 | 3 | + | 1.33 | 0.12 |
| Si:S3 | 20 | 850 | 1 | + | 2.28 | 0.19 |
| Si:S4 | 20 | 850 | 3 | ++ | 5.04 | 0.23 |
| Si:S5 | 20 | 850 | 5 | +++ | 1.90 | 0.38 |
| Sample | Morphology | X, at.% before Etching | X, at.% after Etching |
|---|---|---|---|
| Si:S5 | Hexahedral rods | 1.90 | 0.38 |
| Si:Se | Faceted crystallites | 1.06 | 0.64 |
| Si:Te | Faceted crystallites and tetrahedral rods | 0.60 | 0.59 |
| Sample | ω0, rad/s | τ, s | Ne, cm−3 |
|---|---|---|---|
| Si:S2 | 4.1 × 1015 | 4.1 × 10−16 | 1.7 × 1021 |
| Si:S5 | 2.8 × 1015 | 2.1 × 10−16 | 3.4 × 1021 |
| Si:Se | 3.5 × 1015 | 1.9 × 10−16 | 6.3 × 1021 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vinokurov, A.; Popelensky, V.; Bubenov, S.; Kononov, N.; Cherednichenko, K.; Kuznetsova, T.; Dorofeev, S. Recrystallization of Si Nanoparticles in Presence of Chalcogens: Improved Electrical and Optical Properties. Materials 2022, 15, 8842. https://doi.org/10.3390/ma15248842
Vinokurov A, Popelensky V, Bubenov S, Kononov N, Cherednichenko K, Kuznetsova T, Dorofeev S. Recrystallization of Si Nanoparticles in Presence of Chalcogens: Improved Electrical and Optical Properties. Materials. 2022; 15(24):8842. https://doi.org/10.3390/ma15248842
Chicago/Turabian StyleVinokurov, Alexander, Vadim Popelensky, Sergei Bubenov, Nikolay Kononov, Kirill Cherednichenko, Tatyana Kuznetsova, and Sergey Dorofeev. 2022. "Recrystallization of Si Nanoparticles in Presence of Chalcogens: Improved Electrical and Optical Properties" Materials 15, no. 24: 8842. https://doi.org/10.3390/ma15248842
APA StyleVinokurov, A., Popelensky, V., Bubenov, S., Kononov, N., Cherednichenko, K., Kuznetsova, T., & Dorofeev, S. (2022). Recrystallization of Si Nanoparticles in Presence of Chalcogens: Improved Electrical and Optical Properties. Materials, 15(24), 8842. https://doi.org/10.3390/ma15248842








