Non-Isothermal Dynamic Mechanical Analysis of Ribbon Metallic Glasses and Its Thermodynamic Description
Abstract
1. Introduction
2. Materials and Methods
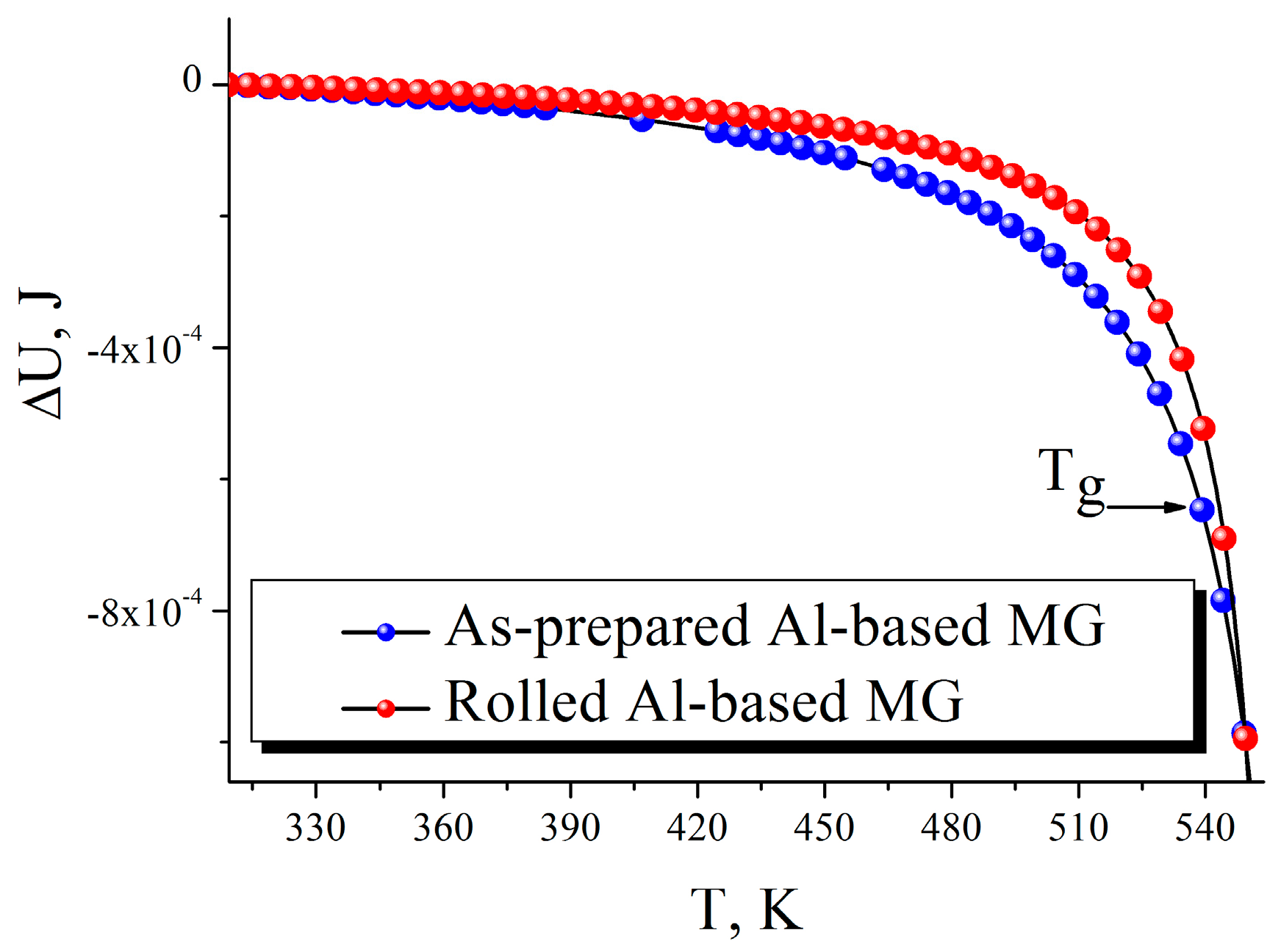
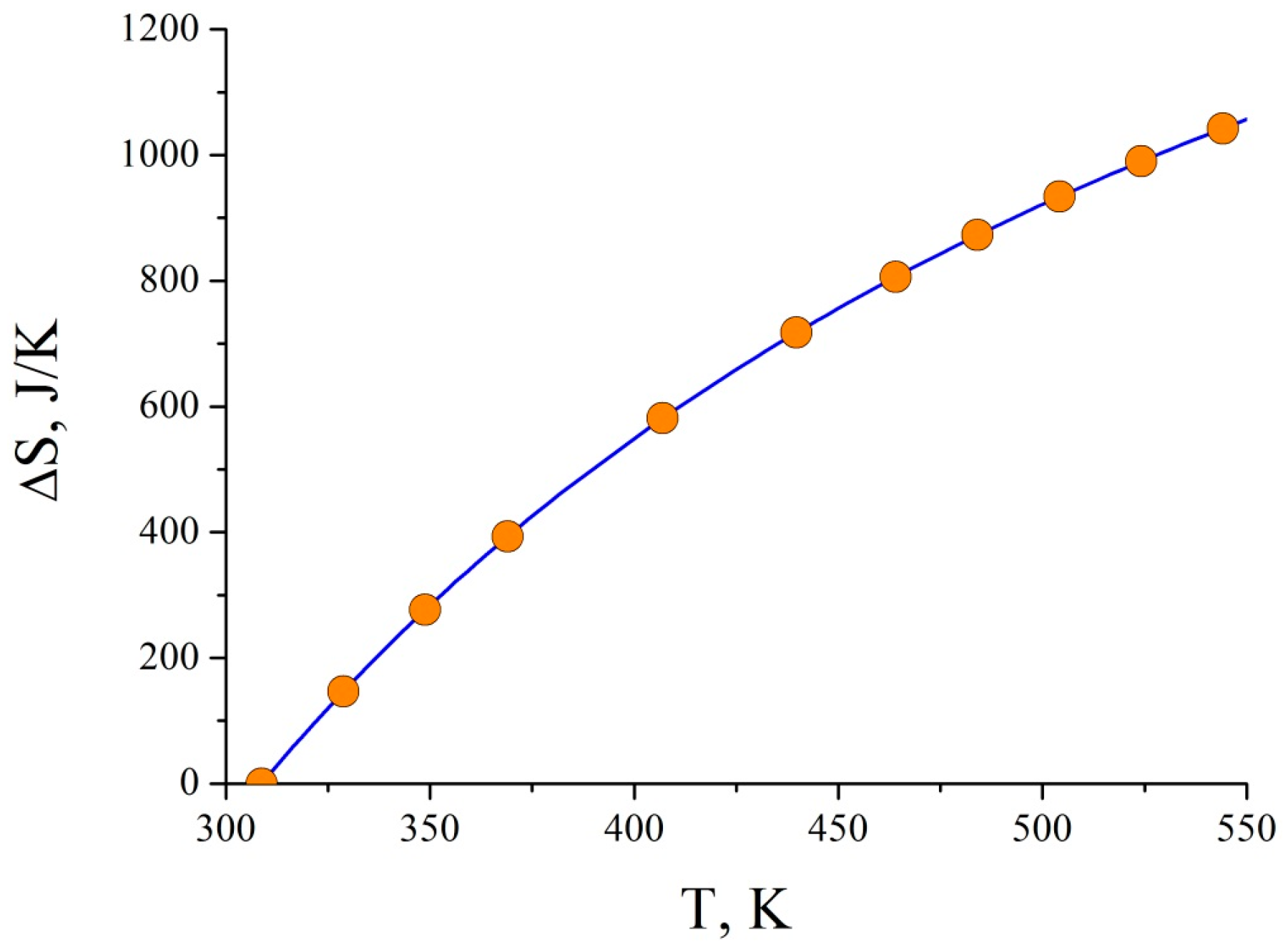
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Meyers, M.; Chawla, K. Mechanical Behavior of Materials, 2nd ed.; Cambridge University Press: Cambridge, UK, 2008; pp. 1–882. [Google Scholar]
- Rees, D.W.A. Basic Engineering Plasticity; Butterworth-Heinemann: Oxford, UK, 2006; pp. 1–528. [Google Scholar]
- Da Costa Andrade, E.N. On the viscous flow in metals, and allied phenomena. Proc. R. Soc. Lond. A 1910, 84, 1–12. [Google Scholar]
- Khonik, V.A.; Mikhailov, V.A.; Safonov, I.A. Non-isothermal creep of metallic glasses. Scr. Mater. 1997, 37, 921–928. [Google Scholar] [CrossRef]
- De Batist, R. Internal Friction of Structural Defects in Crystalline Solids; North-Holland Publishing Company: Amsterdam, The Netherlands, 1973; pp. 1–477. [Google Scholar]
- Liu, C.; Liu, P.; Zhao, Z.; Northwood, D.O. Room temperature creep of a high strength steel. Mater. Des. 2001, 22, 325–328. [Google Scholar] [CrossRef]
- Cannon, W.R.; Langdon, T.G. Creep of ceramics. J. Mater. Sci. 1988, 18, 1–20. [Google Scholar] [CrossRef]
- Raghavan, J.; Meshii, M. Creep of polymer composites. Compos. Sci. Technol. 1998, 57, 1673–1688. [Google Scholar] [CrossRef]
- Lomer, W.M. The yield phenomenon in polycrystalline mild steel. J. Mech. Phys. Solids 1952, 1, 64–73. [Google Scholar] [CrossRef]
- Wagner, M.H. Analysis of time-dependent non-linear stress-growth data for shear and elongational flow of a low-density branched polyethylene melt. Rheol. Acta 1976, 15, 136–142. [Google Scholar] [CrossRef]
- Wilkinson, W. Non-Newtonian Fluids; Pergamon Press: Oxford, UK, 1960; pp. 1–138. [Google Scholar]
- Menard, K.P. Dynamic Mechanical Analysis: A practical Introduction; CRC Press: Boca Raton, FL, USA, 1999; pp. 1–205. [Google Scholar]
- Pluzhnikova, T.N.; Fedorov, V.A.; Balybin, D.V.; Berezner, A.D.; Mikhlin, Y.L.; Fedotov, D.Y. Solid-Phase Hydrogen Diffusion through a Fe92Si6B6 Amorphous Membrane and its Effect on the Mechanical Properties of a Non-Crystalline Environment. Prot. Met. Phys. Chem. Surf. 2021, 57, 1235–1241. [Google Scholar] [CrossRef]
- Berezner, A.D.; Fedorov, V.A.; Perov, N.S.; Pluzhnikova, T.N.; Fedotov, D.Y.; Shlikova, A.A. Magnetic properties of Co-based and Fe-based tape amorphous alloys. J. Phys. Condens. Matter 2020, 32, 1–9. [Google Scholar] [CrossRef]
- Louzguine-Luzgin, D.V.; Zadorozhnyy, M.Y.; Ketov, S.V.; Jiang, J.; Golovin, I.S.; Aronin, A.S. Influence of cyclic loading on the structure and double-stage structure relaxation behavior of a Zr-Cu-Fe-Al metallic glass. Mater. Sci. Eng. A 2019, 742, 526–531. [Google Scholar] [CrossRef]
- Duwez, P. Structure and Properties of Alloys Rapidly Quenched from the Liquid State. Trans. Am. Soc. Metals. 1967, 60, 607–633. [Google Scholar]
- Lenel, F.V.; Ansell, G.S. Creep Mechanisms and Their Role in the Sintering of Metal Powders. In Modern Developments in Powder Metallurgy; Hausner, H.H., Ed.; Springer: Berlin/Heidelberg, Germany, 1966; pp. 281–296. [Google Scholar]
- Ketov, S.V.; Inoue, A.; Kato, H.; Louzguine-Luzgin, D.V. Viscous flow of Cu55Zr30Ti10Co5 bulk metallic glass in glass-transition and semi-solid regions. Scr. Mater. 2013, 68, 219–222. [Google Scholar] [CrossRef]
- Zadorozhnyy, V.Y.; Zadorozhnyy, M.Y.; Churyumov, A.Y.; Ketov, S.V.; Golovin, I.S.; Louzguine-Luzgin, D.V. Room-temperature dynamic quasi-elastic mechanical behavior of a Zr–Cu–Fe–Al bulk metallic glass. Phys. Status Solidi A 2016, 213, 450–456. [Google Scholar] [CrossRef]
- Bazlov, A.I.; Igrevskaya, A.G.; Tabachkova, N.Y.; Chen, C.; Cheverikin, V.V.; Pozdniakov, A.V.; Jiang, J.; Louzguine-Luzgin, D.V. Thermo-mechanical processing of a Zr62.5Cu22.5Fe5Al10 glassy alloy as a way to obtain tensile ductility. J. Alloy. Compd. 2021, 853, 1–10. [Google Scholar] [CrossRef]
- Louzguine-Luzgin, D.V.; Inoue, A. Comparative study of the effect of cold rolling on the structure of Al–RE–Ni–Co (RE = rare-earth metals) amorphous and glassy alloys. J. Non-Cryst. Solids 2006, 352, 3903–3909. [Google Scholar] [CrossRef]
- Inoue, A.; Wang, X.M.; Zhang, W. Developments and applications of bulk metallic glasses. Rev. Adv. Mater. Sci. 2008, 18, 1–9. [Google Scholar]
- Anderson, P.W. Through the Glass Lightly. Science 1995, 267, 1615–1616. [Google Scholar] [CrossRef]
- Kauzmann, W. The Nature of the Glassy State and the Behavior of Liquids at Low Temperatures. Chem. Rev. 1948, 43, 219–256. [Google Scholar] [CrossRef]
- Mitrofanov, Y.P.; Khonik, V.A.; Granato, A.V.; Joncich, D.M.; Khonik, S.V.; Khoviv, A.M. On the nature of enthalpy relaxation below and above the glass transition of metallic glasses. Appl. Phys. Lett. 2012, 100, 131903. [Google Scholar] [CrossRef]
- Berezner, A.D.; Fedorov, V.A.; Zadorozhnyy, M.Y.; Golovin, I.S.; Louzguine-Luzgin, D.V. Deformation of Al85Y8Ni5Co2 Metallic Glasses under Cyclic Mechanical Load and Uniform Heating. Metals 2021, 11, 908. [Google Scholar] [CrossRef]
- Berezner, A.D.; Fedorov, V.A.; Zadorozhnyy, M.Y.; Golovin, I.S.; Louzguine-Luzgin, D.V. Deformation of Cu-Pd-P metallic glass under cyclic mechanical load on continous heating. Theor. Appl. Fract. Mech. 2022, 118, 103262. [Google Scholar] [CrossRef]
- Berezner, A.D.; Fedorov, V.A.; Zadorozhnyy, M.Y. Relaxation behavior of an Al-Y-Ni-Co metallic glass in as-prepared and cold-rolled state. J. Alloy. Compd. 2022, 923, 166313. [Google Scholar] [CrossRef]
- Wang, G.Y.; Liaw, P.; Peter, W.H.; Yang, B.X.; Freels, M.; Yokoyama, Y.; Benson, M.L.; Green, B.A.; Saleh, T.A.; Mcdaniels, R.; et al. Fatigue behavior and fracture morphology of Zr50Al10Cu40 and Zr50Al10Cu30Ni10 bulk-metallic glasses. Intermetallics 2004, 12, 1219. [Google Scholar] [CrossRef]
- Whitman, A.M. Thermodynamics: Basic Principles and Engineering Applications; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–320. [Google Scholar]
- Zorich, V.A. Mathematical Analysis I (Universitext), 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1–616. [Google Scholar]
- Wang, W.H. Dynamic relaxations and relaxation-property relationships in metallic glasses. Prog. Mater. Sci. 2019, 106, 100561. [Google Scholar] [CrossRef]
- McQuarrie, A. Statistical Mechanics; Harper & Row: New York, NY, USA, 1976; pp. 1–641. [Google Scholar]
- Dyre, J.C. Colloquium: The glass transition and elastic models of glass-forming liquids. Rev. Mod. Phys. 2006, 78, 953. [Google Scholar] [CrossRef]
- Van der Waals, J.D. Over de Continuiteit van den Gasen Vloeistoftoestand; Sijthoff: Leiden, The Netherlands, 1873. [Google Scholar]
- Berezner, A.; Fedorov, V.; Grigoriev, G. A few fracture features of Al-based and Cu-based ribbon metallic glasses under non-isothermal and oscillating loading. Lect. Notes Mech. Eng. 2023, 1–8. [Google Scholar]
- Podgornykh, S.M.; Kazantsev, V.A. Relationship between the heat capacity, thermal expansion coefficient, and spontaneous magnetization in the invarlike compound YFe10Mo2. Phys. Met. Metallogr. 2010, 109, 247–254. [Google Scholar] [CrossRef]
- González, S.; Pellicer, E.; Suriñach, S.; Baró, M.D.; Sort, J. Mechanical and corrosion behaviour of as-cast and annealed Zr60Cu20Al10Fe5Ti5 bulk metallic glass. Intermetallics 2012, 28, 149–155. [Google Scholar] [CrossRef]
- Barsoum, M.W.; Rawn, C.J.; Ei-Raghy, T.; Procopio, A.; Porter, W.D.; Wang, H.; Hubbard, C. Thermal properties of Ti4AlN3. J. Appl. Phys. 2000, 87, 8407. [Google Scholar] [CrossRef]
- Calvin, J.J.; Asplund, M.; Zhang, Y.; Huang, B.; Woodfield, B.F. Heat capacity and thermodynamic functions of γ-Al2O3. J. Chem. Thermodyn. 2017, 112, 77–85. [Google Scholar] [CrossRef]
- Suryanarayana, C.; Inoue, A. Bulk Metallic Glasses, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2020; pp. 1–542. [Google Scholar]
- Gromov, V.E.; Ivanov, Y.F.; Stolboushkina, O.A.; Konovalov, S.V. Dislocation substructure evolution on Al creep under the action of the weak electric potential. Mater. Sci. Eng. A 2010, 527, 858–861. [Google Scholar] [CrossRef]
- Konovalov, S.V.; Komissarova, I.A.; Kosinov, D.A.; Ivanov, Y.F.; Ivanova, O.V.; Gromov, V.E. The structure of the titanium alloy, modified by electron beams and destroyed during fatigue. Lett. Mater. 2017, 7, 266–271. [Google Scholar] [CrossRef][Green Version]
| Alloy (at.%) | C, [m·s] | B, [s] | m, [kg] | Fload, [N] | A, [N] |
|---|---|---|---|---|---|
| Al85Y8Ni5Co2 | 0.078 | 3157 | 10−4 | 3.6 | 0.0036 |
| Cu54Pd28P18 | 0.0492 | 2827 | 10−4 | 0.9 | 0.0063 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berezner, A.; Fedorov, V. Non-Isothermal Dynamic Mechanical Analysis of Ribbon Metallic Glasses and Its Thermodynamic Description. Materials 2022, 15, 8659. https://doi.org/10.3390/ma15238659
Berezner A, Fedorov V. Non-Isothermal Dynamic Mechanical Analysis of Ribbon Metallic Glasses and Its Thermodynamic Description. Materials. 2022; 15(23):8659. https://doi.org/10.3390/ma15238659
Chicago/Turabian StyleBerezner, Arseniy, and Victor Fedorov. 2022. "Non-Isothermal Dynamic Mechanical Analysis of Ribbon Metallic Glasses and Its Thermodynamic Description" Materials 15, no. 23: 8659. https://doi.org/10.3390/ma15238659
APA StyleBerezner, A., & Fedorov, V. (2022). Non-Isothermal Dynamic Mechanical Analysis of Ribbon Metallic Glasses and Its Thermodynamic Description. Materials, 15(23), 8659. https://doi.org/10.3390/ma15238659






