Viscoelasticity in Large Deformation Analysis of Hyperelastic Structures
Abstract
1. Introduction
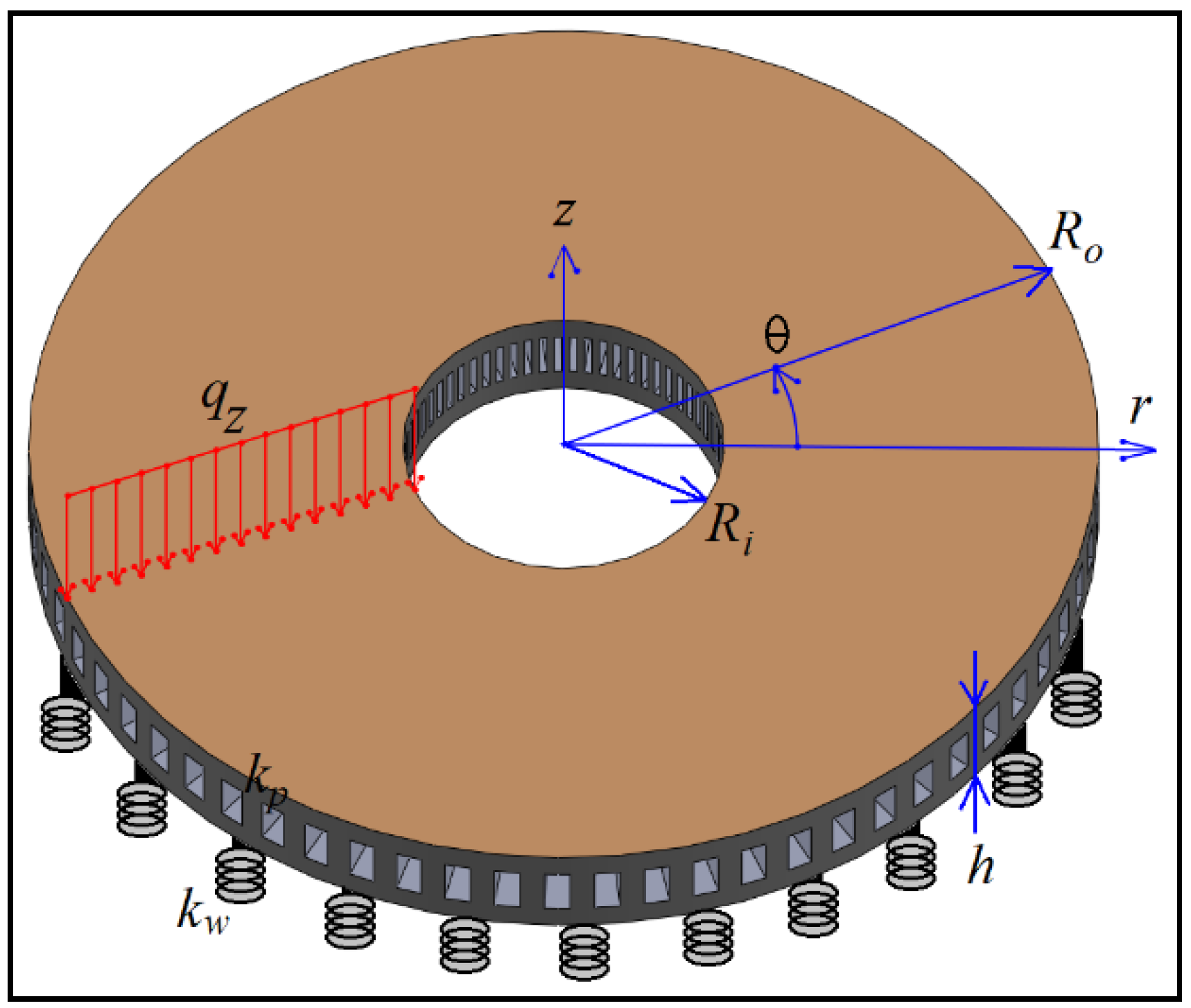
2. Geometry of the Structure
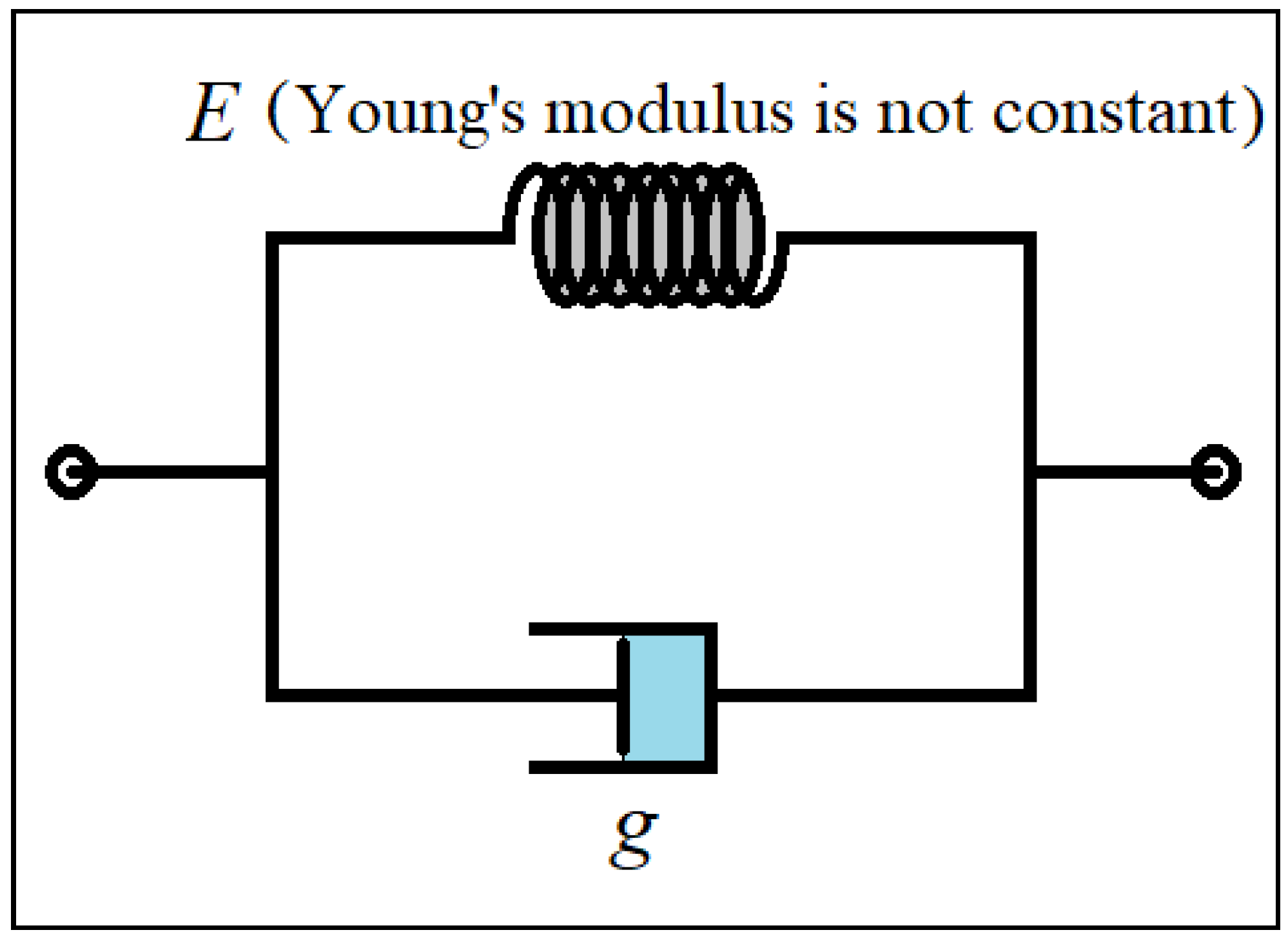
3. Viscoelastic Property
4. Nonlinear Elastic Material and Governing Equations
5. Solution Method
6. Discussion
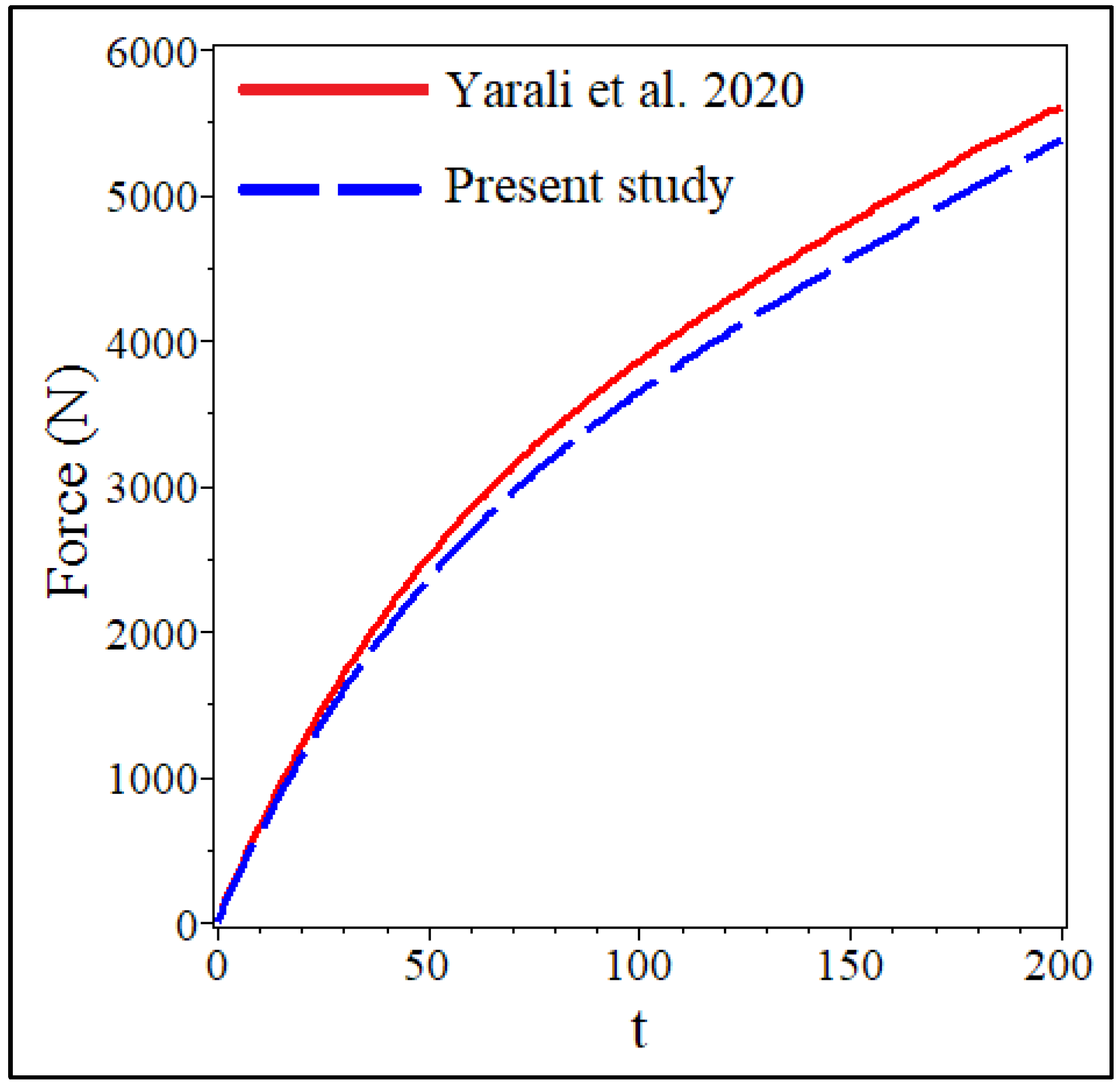
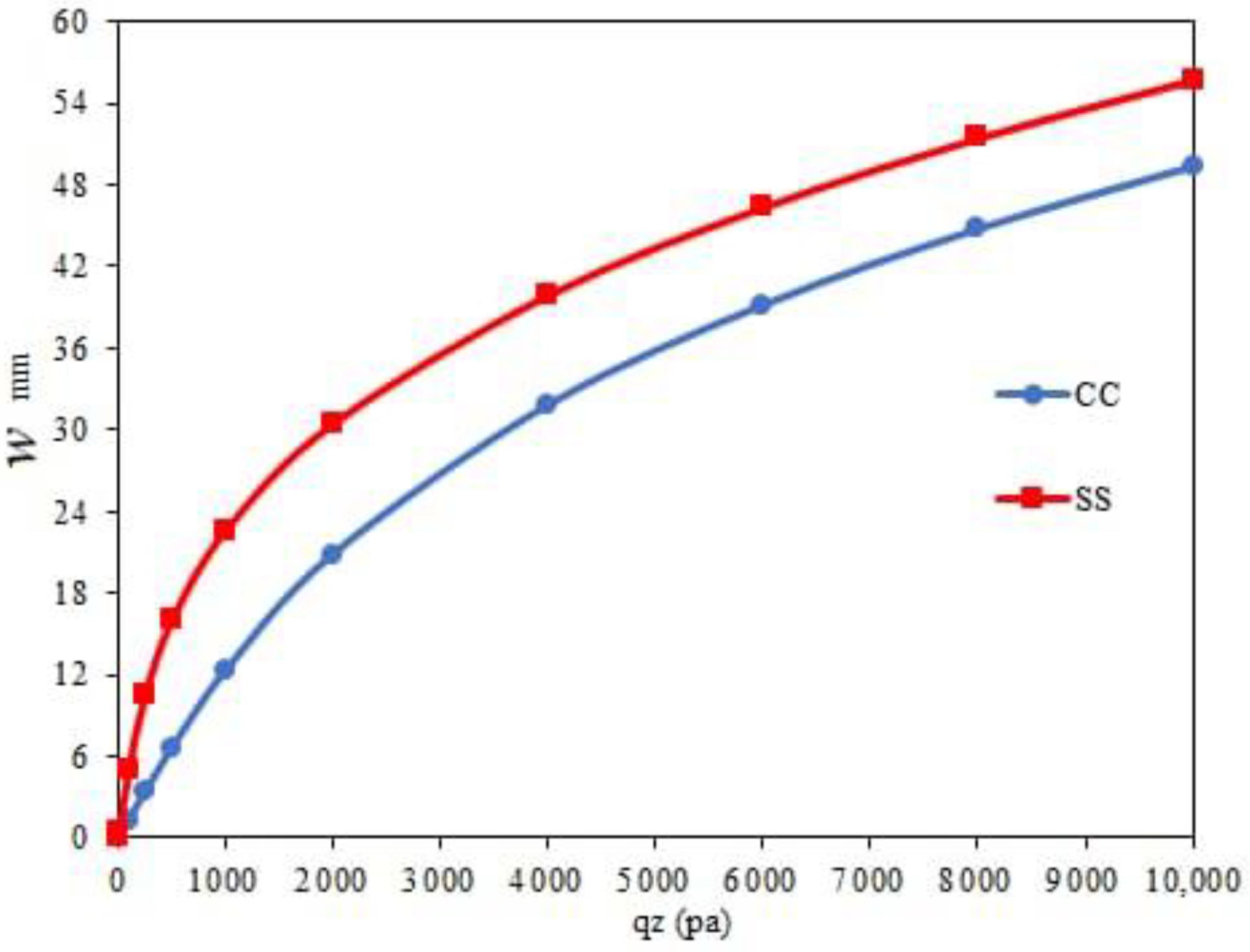
6.1. Validation
6.1.1. The Solving Method (SAPM)
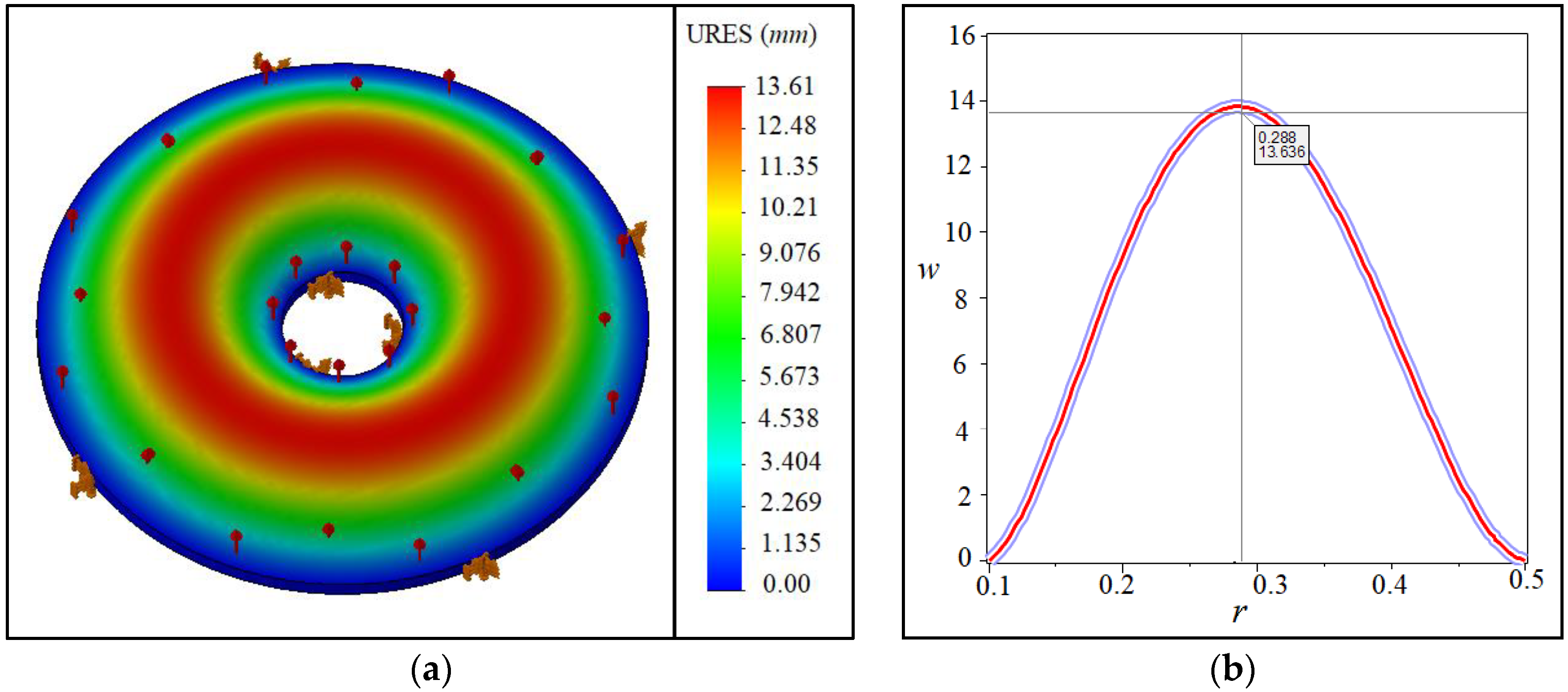
6.1.2. Comparisons
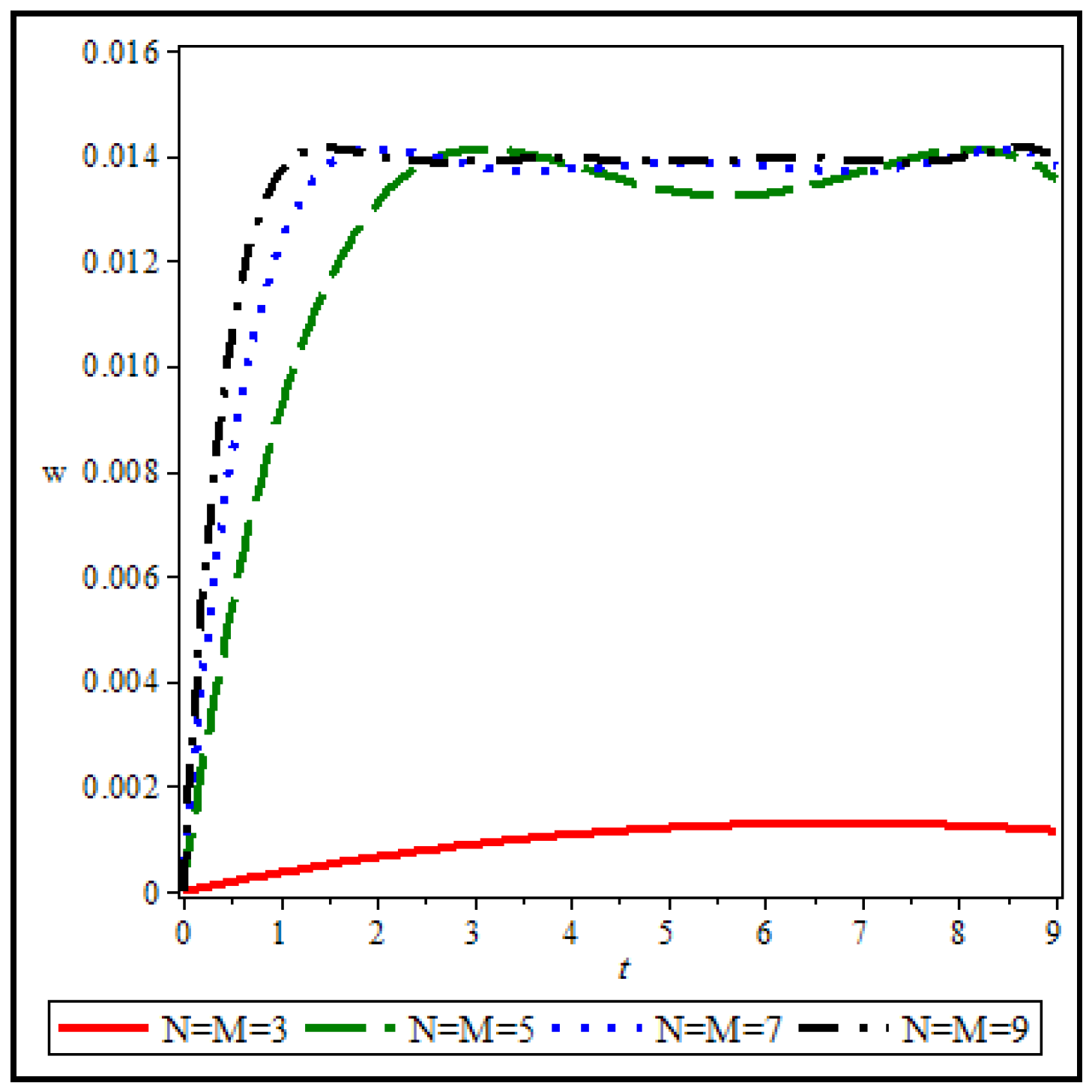
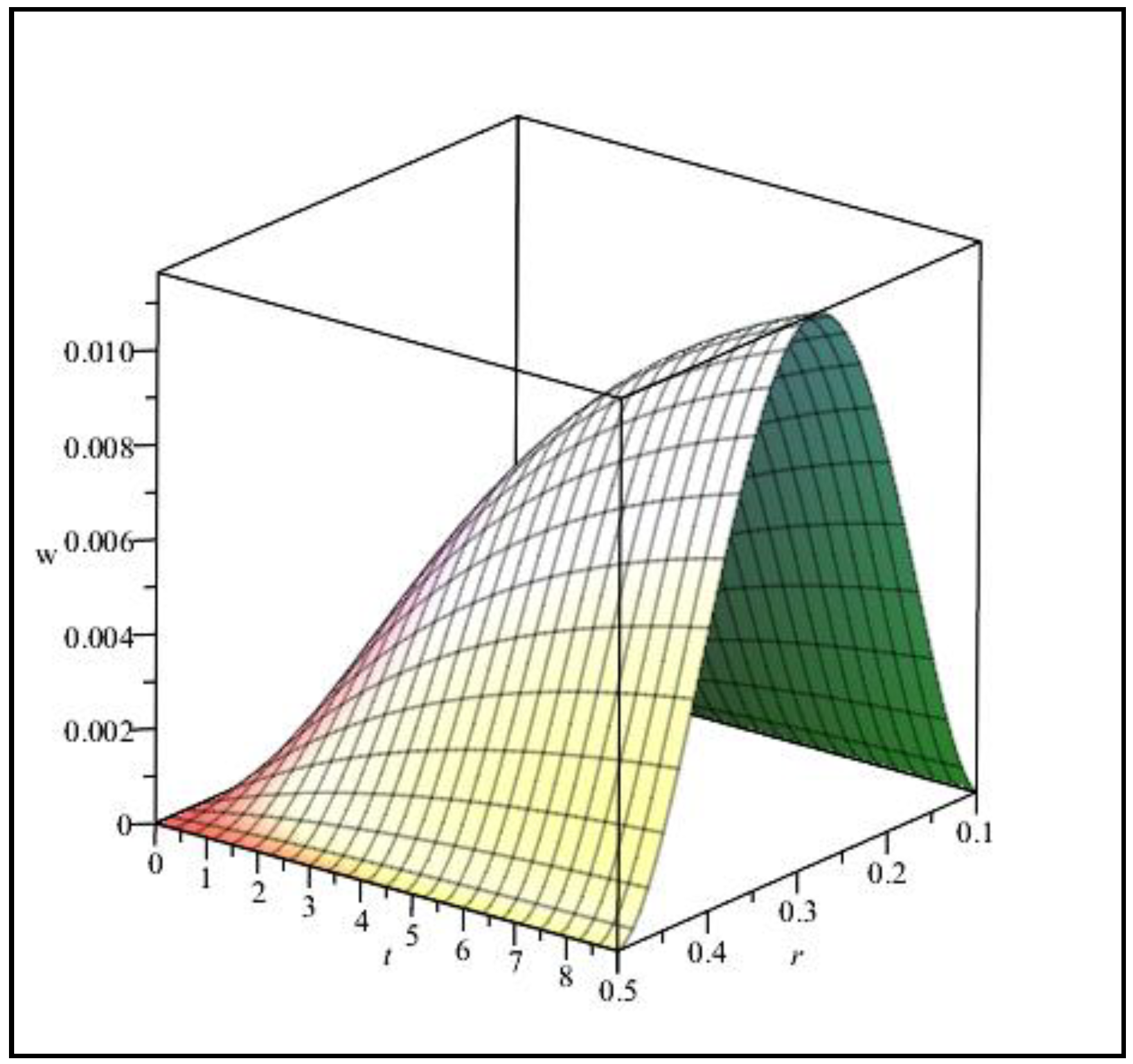
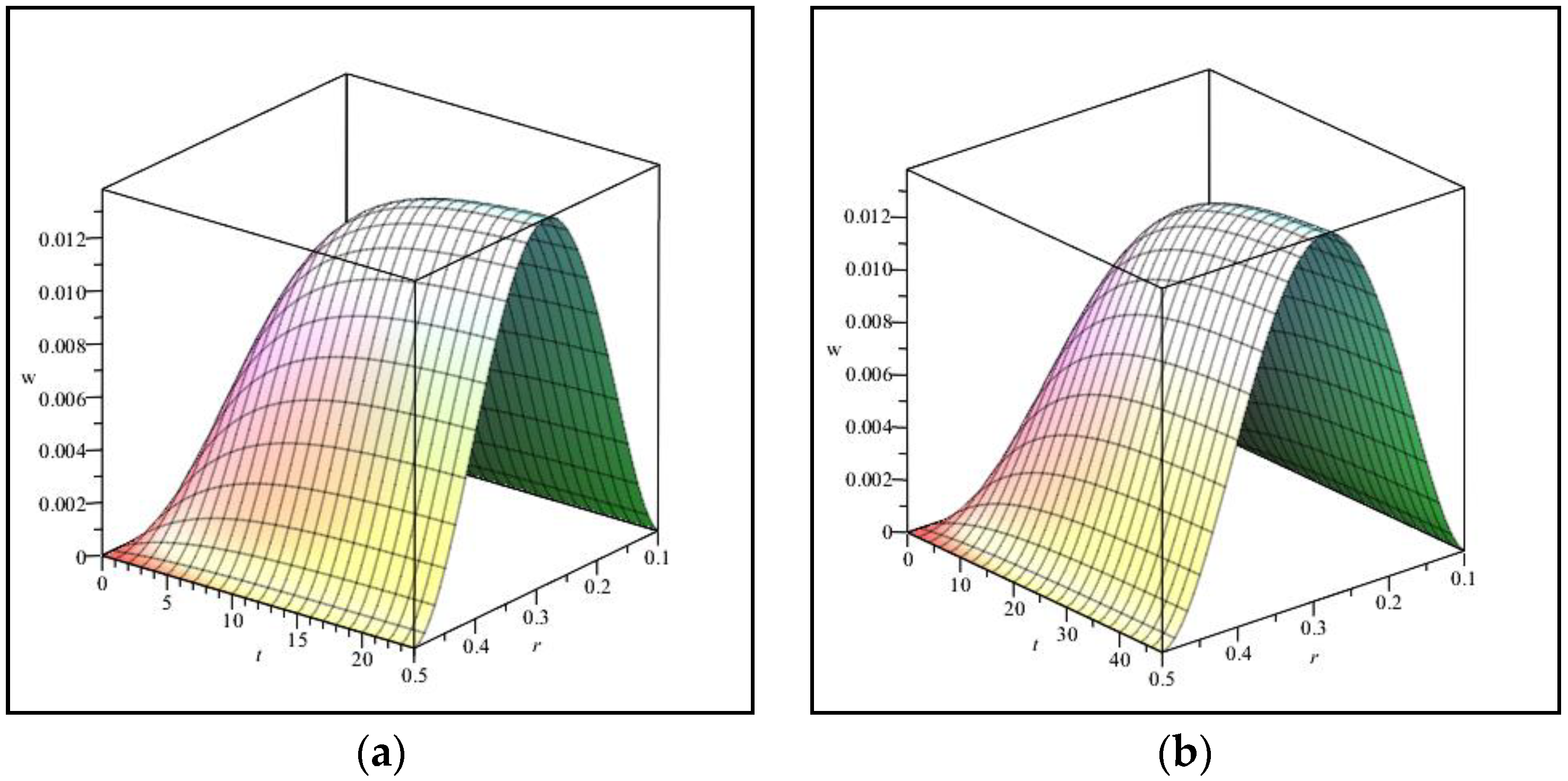
6.2. Numerical Results
7. Conclusions
- The new theory of hyperelastic structures can be used with appropriate confidence for viscoelastic properties.
- Structures made of nonlinear elastic material are sensitive to changes in applied transverse loads, and the changes are entirely nonlinear, even with the low-load application.
- For low loads, it has a significant impact on the deformation by the boundary conditions. However, as the load increases, these effects decrease.
- As the viscosity increases, the duration of the final deformation increases, which has a direct relationship with the viscosity of the material.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Boyce, M.C.; Arruda, E.M. Constitutive models of rubber elasticity: A review. Rubber Chem. Technol. 2000, 73, 504–523. [Google Scholar] [CrossRef]
- Gent, A.N. A new constitutive relation for rubber. Rubber Chem. Technol. 1996, 69, 59–61. [Google Scholar] [CrossRef]
- Anssari-Benam, A.; Bucchi, A. A generalised neo-Hookean strain energy function for application to the finite deformation of elastomers. Int. J. Non-Linear Mech. 2021, 128, 103626. [Google Scholar] [CrossRef]
- Yeoh, O.H. Characterization of Elastic Properties of Carbon-Black-Filled Rubber Vulcanizates. Rubber Chem. Technol. 1990, 63, 792–805. [Google Scholar] [CrossRef]
- Erchiqui, F.; Gakwaya, A.; Rachik, M. Dynamic finite element analysis of nonlinear isotropic hyperelastic and viscoelastic materials for thermoforming applications. Polym. Eng. Sci. 2005, 45, 125–134. [Google Scholar] [CrossRef]
- Kocaturk, T.; Akbas, S.D. Geometrically nonlinear static analysis of a simply supported beam made of hyperelastic material. Struct. Eng. Mech. 2010, 35, 677–697. [Google Scholar] [CrossRef]
- Li, Y.L.; Oh, I.; Chen, J.H.; Zhang, H.H.; Hu, Y.H. Nonlinear dynamic analysis and active control of visco-hyperelastic dielectric elastomer membrane. Int. J. Solids Struct. 2018, 152, 28–38. [Google Scholar] [CrossRef]
- Alibakhshi, A.; Dastjerdi, S.; Akgoz, B.; Civalek, O. Parametric vibration of a dielectric elastomer microbeam resonator based on a hyperelastic cosserat continuum model. Compos. Struct. 2022, 287, 115386. [Google Scholar] [CrossRef]
- Almasi, A.; Baghani, M.; Moallemi, A. Thermomechanical analysis of hyperelastic thick-walled cylindrical pressure vessels, analytical solutions and FEM. Int. J. Mech. Sci. 2017, 130, 426–436. [Google Scholar] [CrossRef]
- Asgari, M.; Hashemi, S.S. Dynamic visco-hyperelastic behavior of elastomeric hollow cylinder by developing a constitutive equation. Struct. Eng. Mech. 2016, 59, 601–619. [Google Scholar] [CrossRef]
- Pascon, J.P. Finite element analysis of functionally graded hyperelastic beams under plane stress. Eng. Comput. 2020, 36, 1265–1288. [Google Scholar] [CrossRef]
- Pascon, J.P. Large deformation analysis of functionally graded visco-hyperelastic materials. Comput. Struct. 2018, 206, 90–108. [Google Scholar] [CrossRef]
- Gharooni, H.; Ghannad, M. Nonlinear analysis of radially functionally graded hyperelastic cylindrical shells with axially-varying thickness and non-uniform pressure loads based on perturbation theory. J. Comput. Appl. Mech. 2019, 50, 324–340. [Google Scholar]
- Hosseini, S.; Rahimi, G. Nonlinear Bending Analysis of Hyperelastic Plates Using FSDT and Meshless Collocation Method Based on Radial Basis Function. Int J Appl Mech 2021, 13, 2150007. [Google Scholar] [CrossRef]
- Xu, Q.P.; Liu, J.Y.; Qu, L.Z. A Higher-Order Plate Element Formulation for Dynamic Analysis of Hyperelastic Silicone Plate. J. Mech. 2019, 35, 795–808. [Google Scholar] [CrossRef]
- Dadgar-Rad, F.; Firouzi, N. Large deformation analysis of two-dimensional visco-hyperelastic beams and frames. Arch. Appl. Mech. 2021, 91, 4279–4301. [Google Scholar] [CrossRef]
- Ansari, R.; Hassani, R.; Oskouie, M.F.; Rouhi, H. Nonlinear bending analysis of hyperelastic Mindlin plates: A numerical approach. Acta Mech. 2021, 232, 741–760. [Google Scholar] [CrossRef]
- Tashiro, K.; Shobayashi, Y.; Ota, I.; Hotta, A. Finite element analysis of blood clots based on the nonlinear visco-hyperelastic model. Biophys. J. 2021, 120, 4547–4556. [Google Scholar] [CrossRef] [PubMed]
- Shariyat, M.; Abedi, S. An accurate hyperelasticity-based plate theory and nonlinear energy-based micromechanics for impact and shock analyses of compliant particle-reinforced FG hyperelastic plates. Zamm-Z. Angew. Math. Mech. 2022, 102, e202100099. [Google Scholar] [CrossRef]
- Karimi, S.; Ahmadi, H.; Foroutan, K. Nonlinear vibration and resonance analysis of a rectangular hyperelastic membrane resting on a Winkler-Pasternak elastic medium under hydrostatic pressure. J. Vib. Control 2022. [Google Scholar] [CrossRef]
- Alibakhshi, A.; Heidari, H. Nonlinear dynamics of dielectric elastomer balloons based on the Gent-Gent hyperelastic model. Eur. J. Mech. A-Solid 2020, 82, 103986. [Google Scholar] [CrossRef]
- Alibakhshi, A.; Rahmanian, S.; Dastjerdi, S.; Malikan, M.; Karami, B.; Akgoz, B.; Civalek, O. Hyperelastic Microcantilever AFM: Efficient Detection Mechanism Based on Principal Parametric Resonance. Nanomaterials 2022, 12, 2598. [Google Scholar] [CrossRef] [PubMed]
- Falope, F.O.; Lanzoni, L.; Tarantino, A.M. FE Analyses of Hyperelastic Solids under Large Bending: The Role of the Searle Parameter and Eulerian Slenderness. Materials 2020, 13, 1597. [Google Scholar] [CrossRef] [PubMed]
- Hosseini, S.; Rahimi, G.; Shahgholian-Ghahfarokhi, D. A meshless collocation method on nonlinear analysis of functionally graded hyperelastic plates using radial basis function. Zamm-Z. Angew. Math. Mech. 2022, 102, e202100216. [Google Scholar] [CrossRef]
- Coda, H.B.; Bernardo, C.C.L.G.; Paccola, R.R. A FEM formulation for the analysis of laminated and functionally graded hyperelastic beams with continuous transverse shear stresses. Compos. Struct. 2022, 292, 115606. [Google Scholar] [CrossRef]
- Dastjerdi, S.; Alibakhshi, A.; Akgoz, B.; Civalek, O. A Novel Nonlinear Elasticity Approach for Analysis of Nonlinear and Hyperelastic Structures. Eng. Anal. Bound. Elem. 2022, 143, 219–236. [Google Scholar] [CrossRef]
- Zhao, Z.T.; Niu, D.T.; Zhang, H.W.; Yuan, X.G. Nonlinear dynamics of loaded visco-hyperelastic spherical shells. Nonlinear Dyn. 2020, 101, 911–933. [Google Scholar] [CrossRef]
- Zhao, Z.T.; Yuan, X.G.; Zhang, W.Z.; Niu, D.T.; Zhang, H.W. Dynamical modeling and analysis of hyperelastic spherical shells under dynamic loads and structural damping. Appl. Math. Model. 2021, 95, 468–483. [Google Scholar] [CrossRef]
- Bacciocchi, M.; Tarantino, A.M. Bending of hyperelastic beams made of transversely isotropic material in finite elasticity. Appl. Math. Model. 2021, 100, 55–76. [Google Scholar] [CrossRef]
- Khaniki, H.B.; Ghayesh, M.H.; Chin, R.; Amabili, M. A review on the nonlinear dynamics of hyperelastic structures. Nonlinear Dyn. 2022, 110, 963–994. [Google Scholar] [CrossRef]
- Zenkour, A.M. Nonlocal thermal vibrations of embedded nanoplates in a viscoelastic medium. Struct. Eng. Mech. 2022, 82, 701–711. [Google Scholar]
- Yuan, Y.; Niu, Z.Q.; Smitt, J. Magneto-hygro-thermal vibration analysis of the viscoelastic nanobeams reinforcedwith carbon nanotubes resting on Kerr’s elastic foundation based on NSGT. Adv. Compos. Mater. 2022. [Google Scholar] [CrossRef]
- Soleimani-Javid, Z.; Arshid, E.; Amir, S.; Bodaghi, M. On the higher-order thermal vibrations of FG saturated porous cylindrical micro-shells integrated with nanocomposite skins in viscoelastic medium. Def. Technol. 2022, 18, 1416–1434. [Google Scholar] [CrossRef]
- Moayeri, M.; Darabi, B.; Sianaki, A.H.; Adamian, A. Third order nonlinear vibration of viscoelastic circular microplate based on softening and hardening nonlinear viscoelastic foundation under thermal loading. Eur. J. Mech. A-Solid 2022, 95, 104644. [Google Scholar] [CrossRef]
- Li, Y.; Liu, B. Thermal buckling and free vibration of viscoelastic functionally graded sandwich shells with tunable auxetic honeycomb core. Appl. Math. Model. 2022, 108, 685–700. [Google Scholar] [CrossRef]
- Dang, R.Q.; Yang, A.M.; Chen, Y.M.; Wei, Y.Q.; Yu, C.X. Vibration analysis of variable fractional viscoelastic plate based on shifted Chebyshev wavelets algorithm. Comput. Math. Appl. 2022, 119, 149–158. [Google Scholar] [CrossRef]
- Alizadeh, A.; Shishehsaz, M.; Shahrooi, S.; Reza, A. Free vibration characteristics of viscoelastic nano-disks based on modified couple stress theory. J. Strain Anal. Eng. 2022. [Google Scholar] [CrossRef]
- Ghobadi, E.; Shutov, A.; Steeb, H. Parameter Identification and Validation of Shape-Memory Polymers within the Framework of Finite Strain Viscoelasticity. Materials 2021, 14, 2049. [Google Scholar] [CrossRef]
- Dacol, V.; Caetano, E.; Correia, J.R. A New Viscoelasticity Dynamic Fitting Method Applied for Polymeric and Polymer-Based Composite Materials. Materials 2020, 13, 5213. [Google Scholar] [CrossRef]
- Chang, J.J.; Li, Y.Y.; Zeng, X.F.; Zhong, H.Y.; Wan, T.L.; Lu, C. Study on the Viscoelasticity Measurement of Materials Based on Surface Reflected Waves. Materials 2019, 12, 1875. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.Z.; de Boer, G.; Ghanbarzadeh, A. A Numerical Model for Investigating the Effect of Viscoelasticity on the Partial Slip Solution. Materials 2022, 15, 5182. [Google Scholar] [CrossRef] [PubMed]
- Itou, H.; Kovtunenko, V.A.; Rajagopal, K.R. The Boussinesq flat-punch indentation problem within the context of linearized viscoelasticity. Int. J. Eng. Sci. 2020, 151, 103272. [Google Scholar] [CrossRef]
- Dastjerdi, S.; Akgoz, B.; Civalek, O. On the effect of viscoelasticity on behavior of gyroscopes. Int. J. Eng. Sci. 2020, 149, 103236. [Google Scholar] [CrossRef]
- Dastjerdi, S.; Akgoz, B.; Civalek, O. On the shell model for human eye in Glaucoma disease. Int. J. Eng. Sci. 2021, 158, 103414. [Google Scholar] [CrossRef]
- Dastjerdi, S.; Malikan, M.; Akgoz, B.; Civalek, O.; Wiczenbach, T.; Eremeyev, V.A. On the deformation and frequency analyses of SARS-CoV-2 at nanoscale. Int. J. Eng. Sci. 2022, 170, 103604. [Google Scholar] [CrossRef]
- Li, C.; Zhu, C.; Sui, S.; Yan, J. A Perturbation Approach for Lateral Excited Vibrations of a Beam-like Viscoelastic Microstructure Using the Nonlocal Theory. Appl. Sci. 2022, 12, 40. [Google Scholar] [CrossRef]
- Hu, W.; Xu, M.; Song, J.; Gao, Q.; Deng, Z. Coupling dynamic behaviors of flexible stretching hub-beam system. Mech. Syst. Signal Process. 2021, 151, 107389. [Google Scholar] [CrossRef]
- Yan, J.W.; Lai, S.K.; He, L.H. Nonlinear dynamic behavior of single-layer graphene under uniformly distributed loads. Compos. B Eng. 2019, 165, 473–490. [Google Scholar] [CrossRef]
- Pascon, J.P.; Coda, H.B. Finite deformation analysis of visco-hyperelastic materials via solid tetrahedral finite elements. Finite Elem. Anal. Des. 2017, 133, 25–41. [Google Scholar] [CrossRef]
- López-Campos, J.A.; Segade, A.; Fernández, J.R.; Casarejos, E.; Vilán, J.A. Behavior characterization of visco-hyperelastic models for rubber-like materials using genetic algorithms. Appl. Math. Model. 2019, 66, 241–255. [Google Scholar] [CrossRef]
- Yarali, E.; Baniasadi, M.; Bodaghi, M.; Bodaghi, M. 3D constitutive modeling of electro-magneto-viscohyperelastic elastomers: A semi-analytical solution for cylinders under large torsion–extension deformation. Smart Mater. Struct. 2020, 29, 085031. [Google Scholar] [CrossRef]
- Dastjerdi, S.; Tadi Beni, Y.; Malikan, M. A comprehensive study on nonlinear hygro-thermo-mechanical analysis of thick functionally graded porous rotating disk based on two quasi-three-dimensional theories. Mech Based Des Struct 2022, 50, 3596–3625. [Google Scholar] [CrossRef]
- Zhang, D.G.; Zhou, H.M. Nonlinear bending analysis of FGM circular plates based on physical neutral surface and higher-order shear deformation theory. Aerosp. Sci. Technol. 2015, 41, 90–98. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dastjerdi, S.; Akgöz, B.; Civalek, Ö. Viscoelasticity in Large Deformation Analysis of Hyperelastic Structures. Materials 2022, 15, 8425. https://doi.org/10.3390/ma15238425
Dastjerdi S, Akgöz B, Civalek Ö. Viscoelasticity in Large Deformation Analysis of Hyperelastic Structures. Materials. 2022; 15(23):8425. https://doi.org/10.3390/ma15238425
Chicago/Turabian StyleDastjerdi, Shahriar, Bekir Akgöz, and Ömer Civalek. 2022. "Viscoelasticity in Large Deformation Analysis of Hyperelastic Structures" Materials 15, no. 23: 8425. https://doi.org/10.3390/ma15238425
APA StyleDastjerdi, S., Akgöz, B., & Civalek, Ö. (2022). Viscoelasticity in Large Deformation Analysis of Hyperelastic Structures. Materials, 15(23), 8425. https://doi.org/10.3390/ma15238425








