Elastic Moduli of Non-Chiral Singe-Walled Silicon Carbide Nanotubes: Numerical Simulation Study
Abstract
1. Introduction
2. Materials and Methods
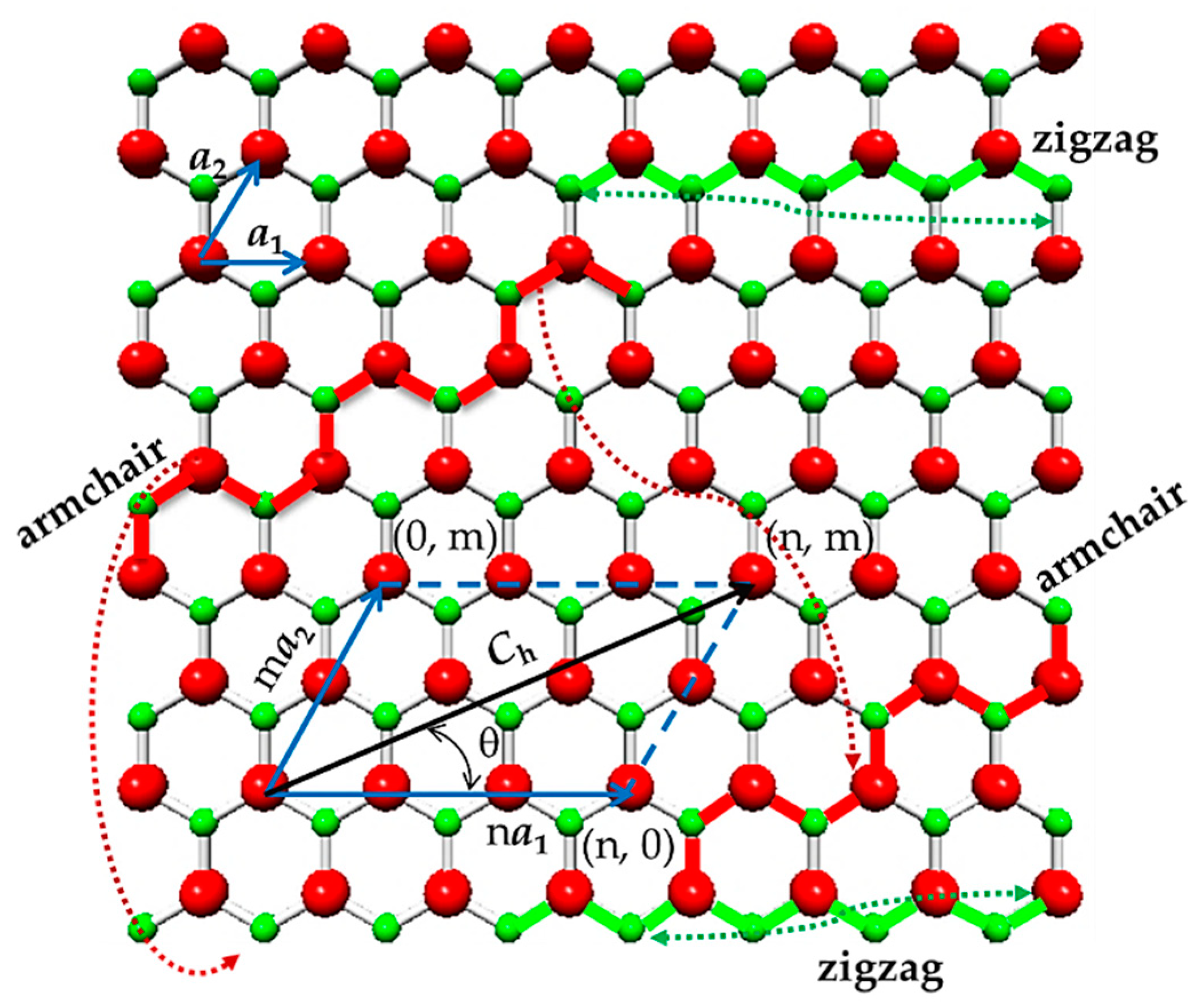
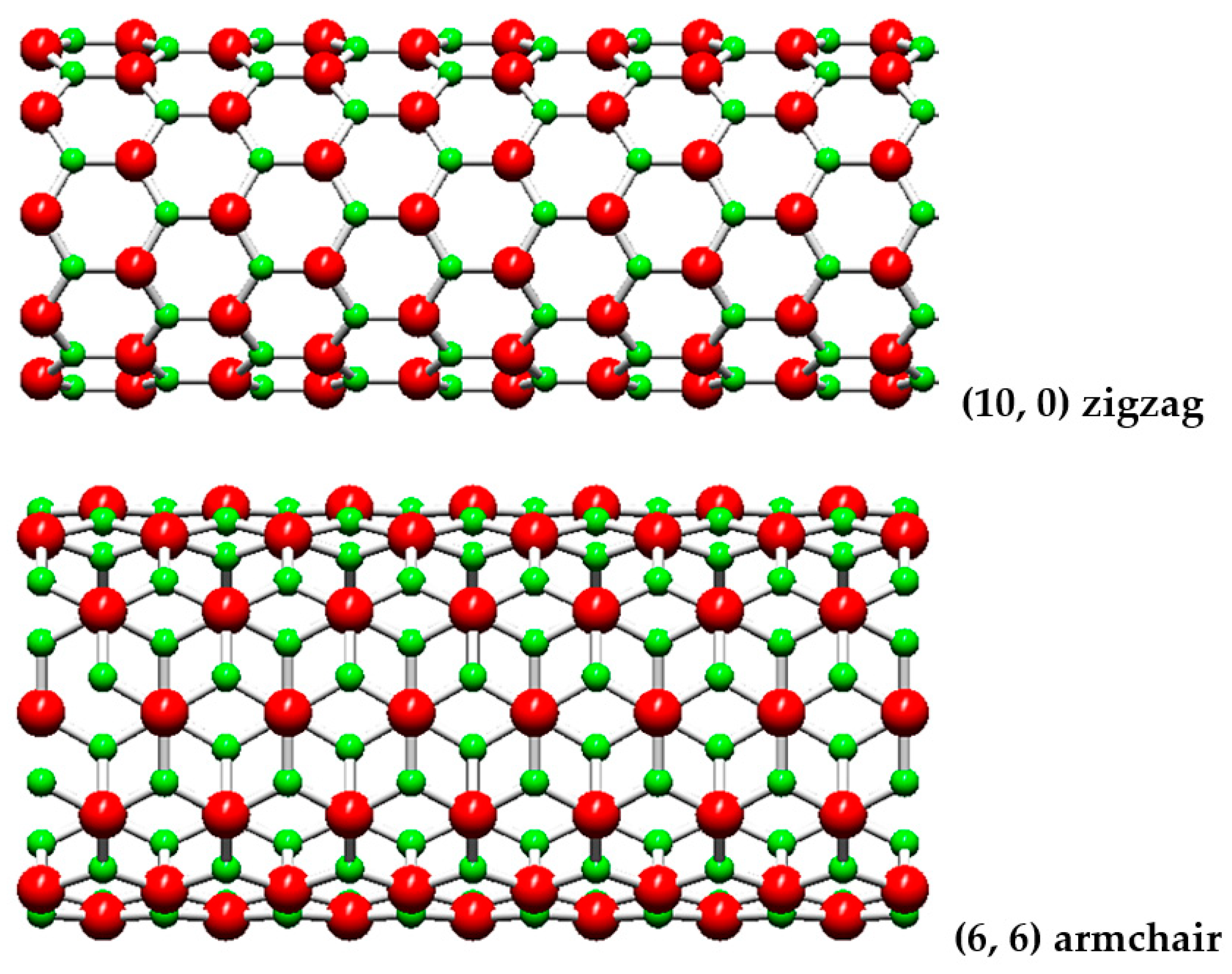
2.1. Atomic Structure of SWSiCNTs
2.2. Geometric Characteristics of the SWSiCNTs and FE Modelling
2.3. Young’s and Shear Moduli of SWSiCNTs
3. Results and Discussion
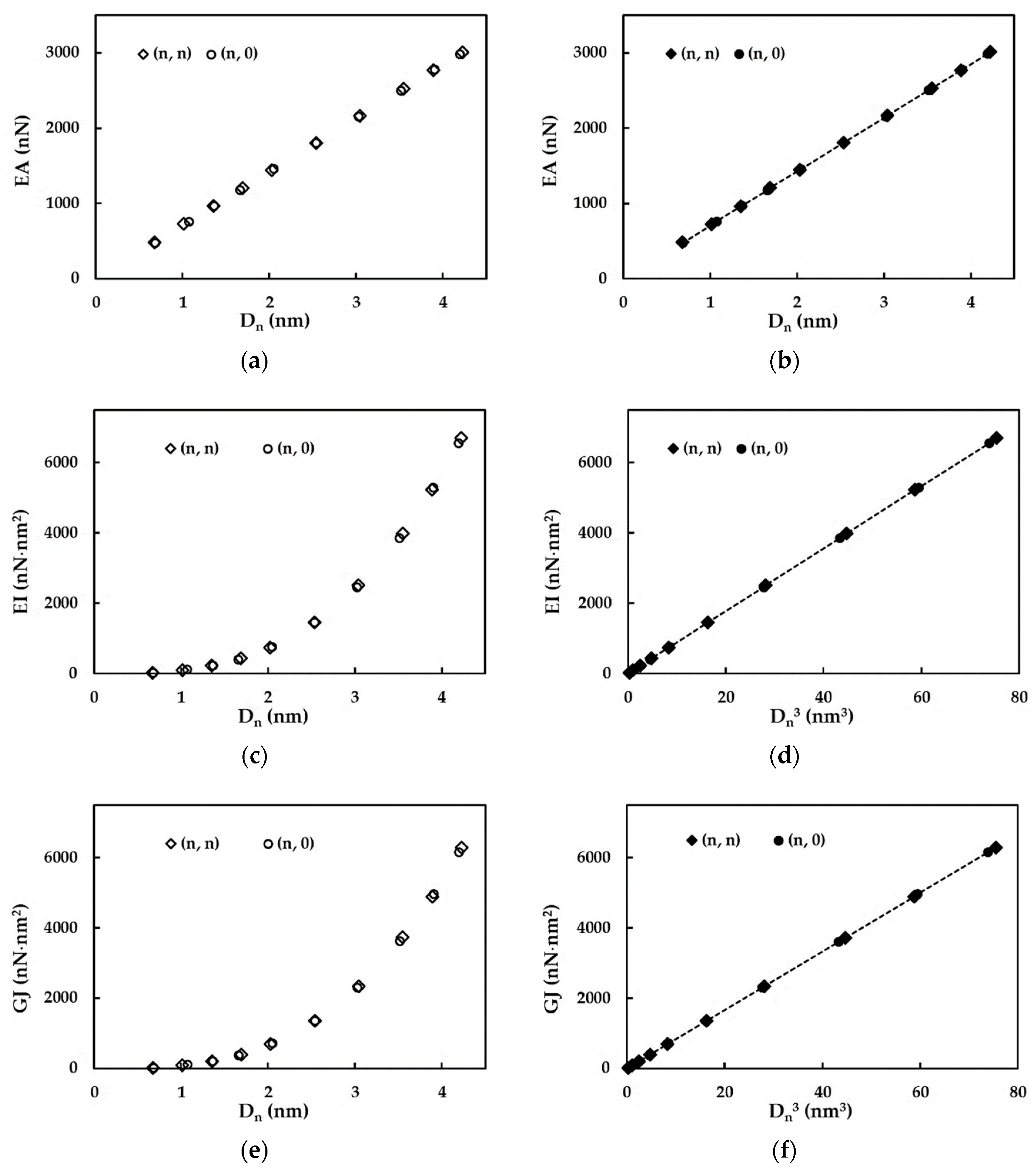
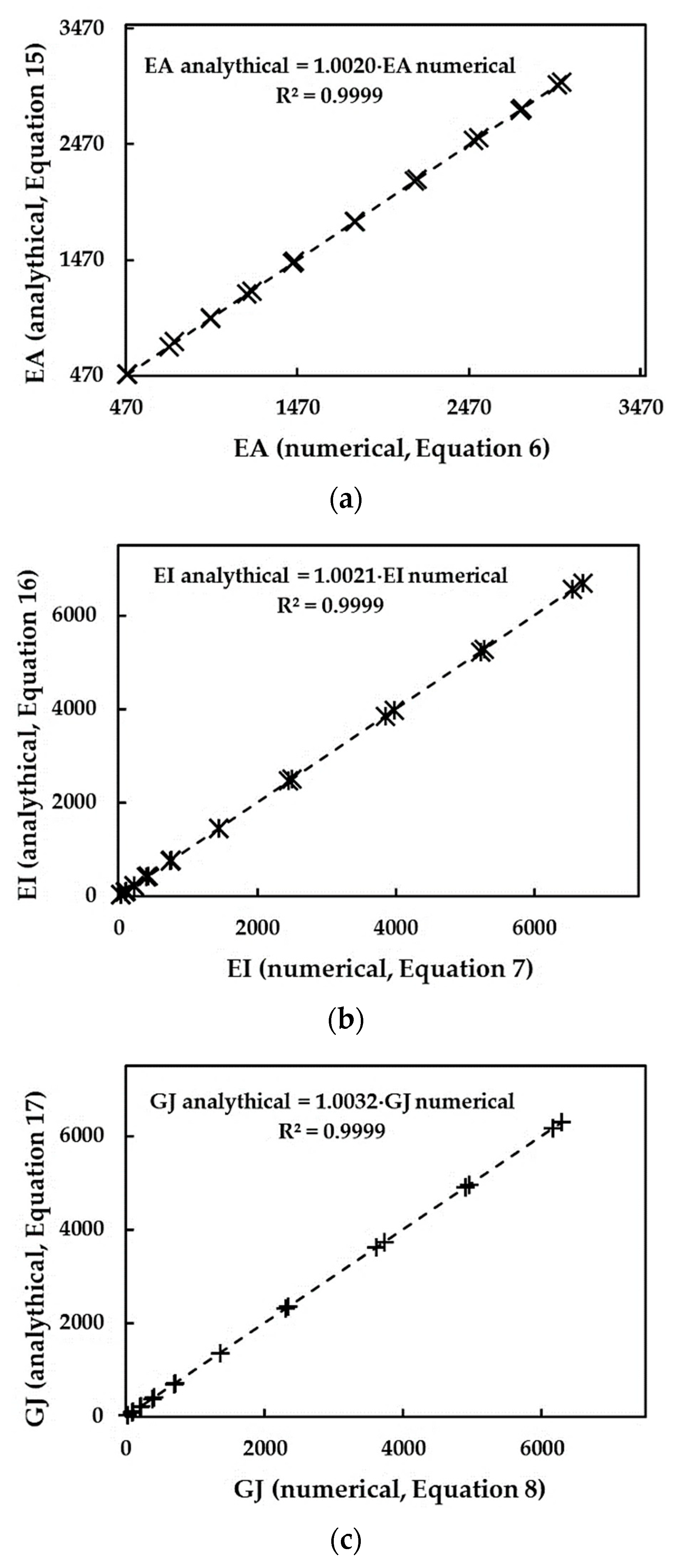
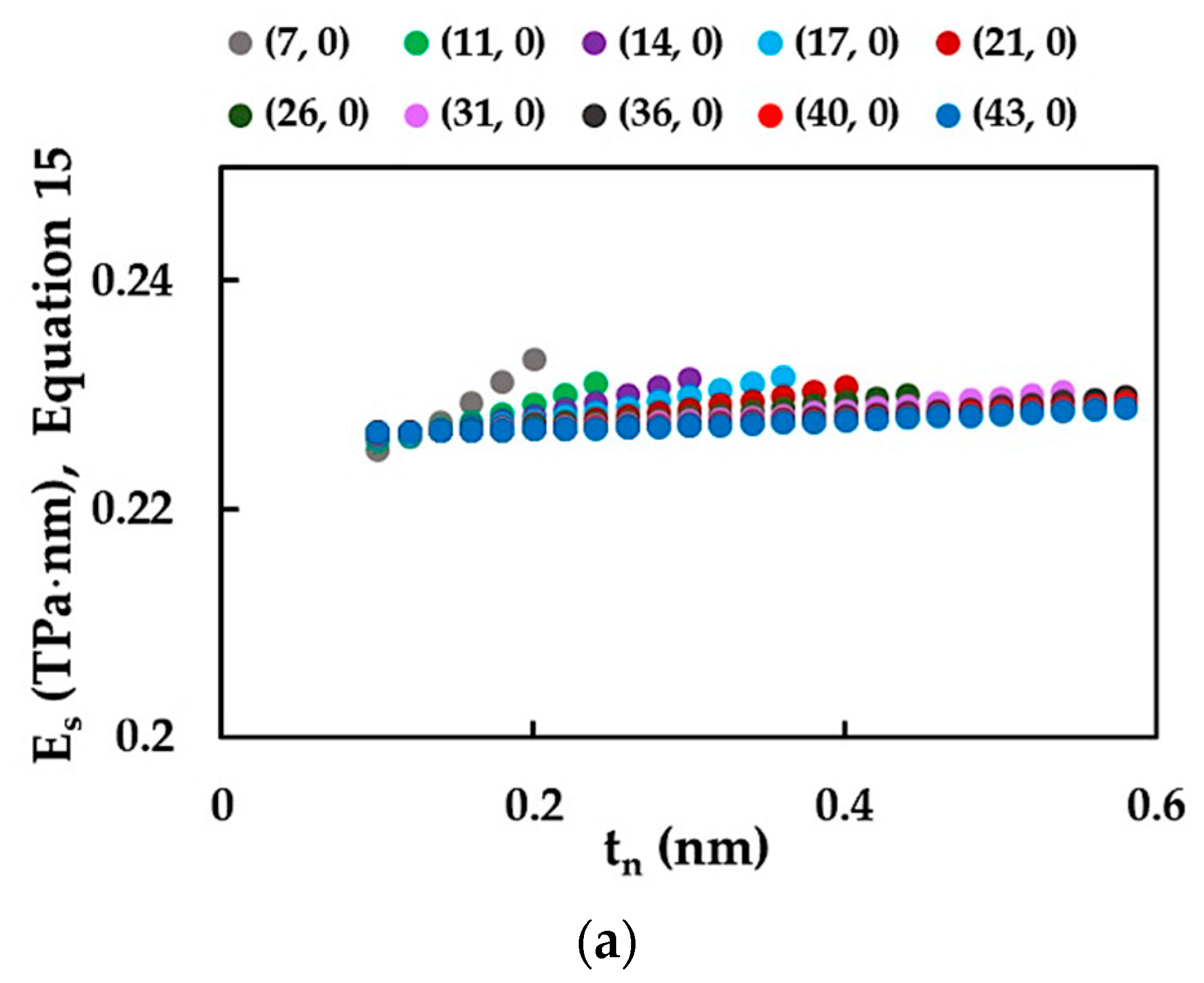
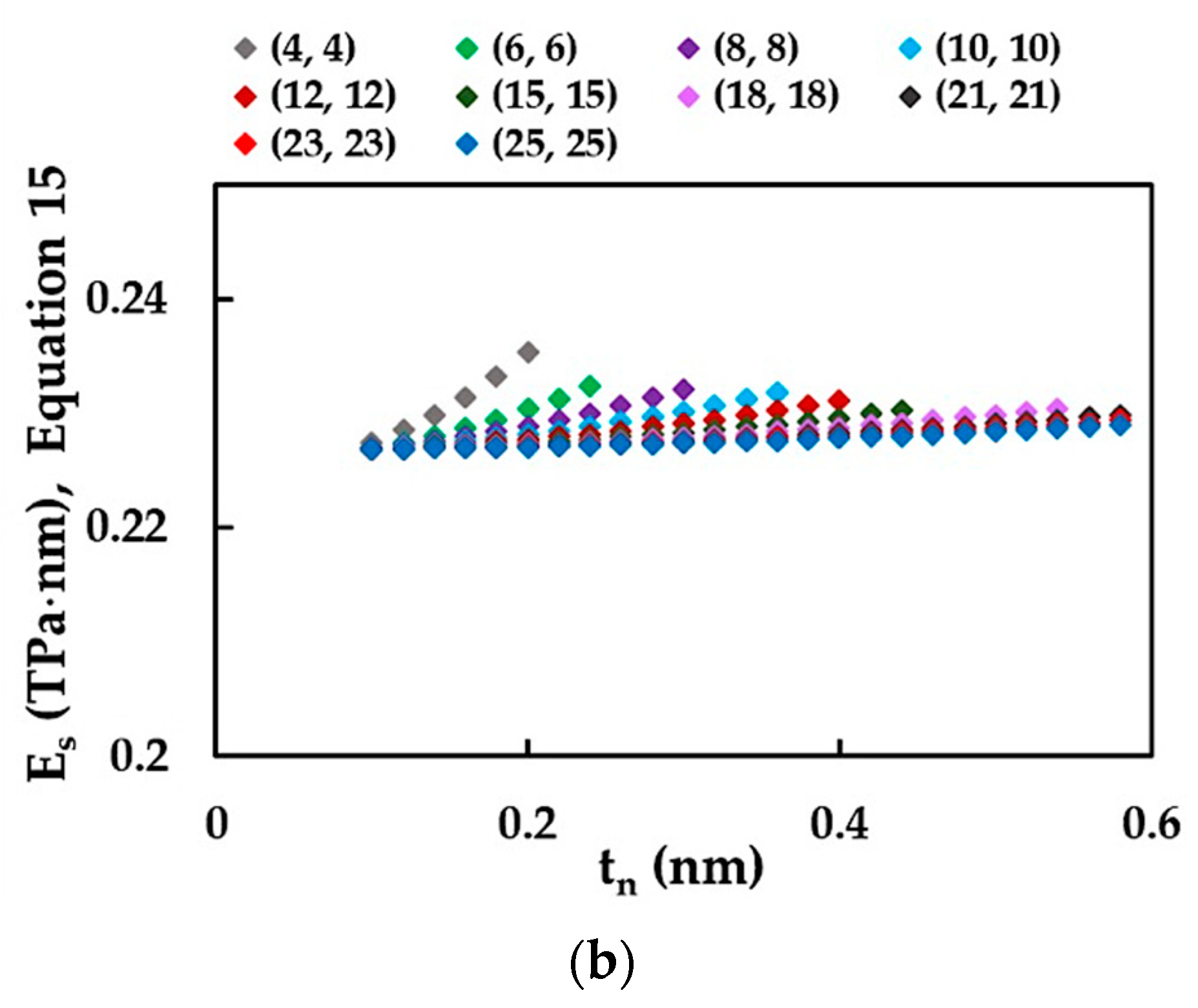
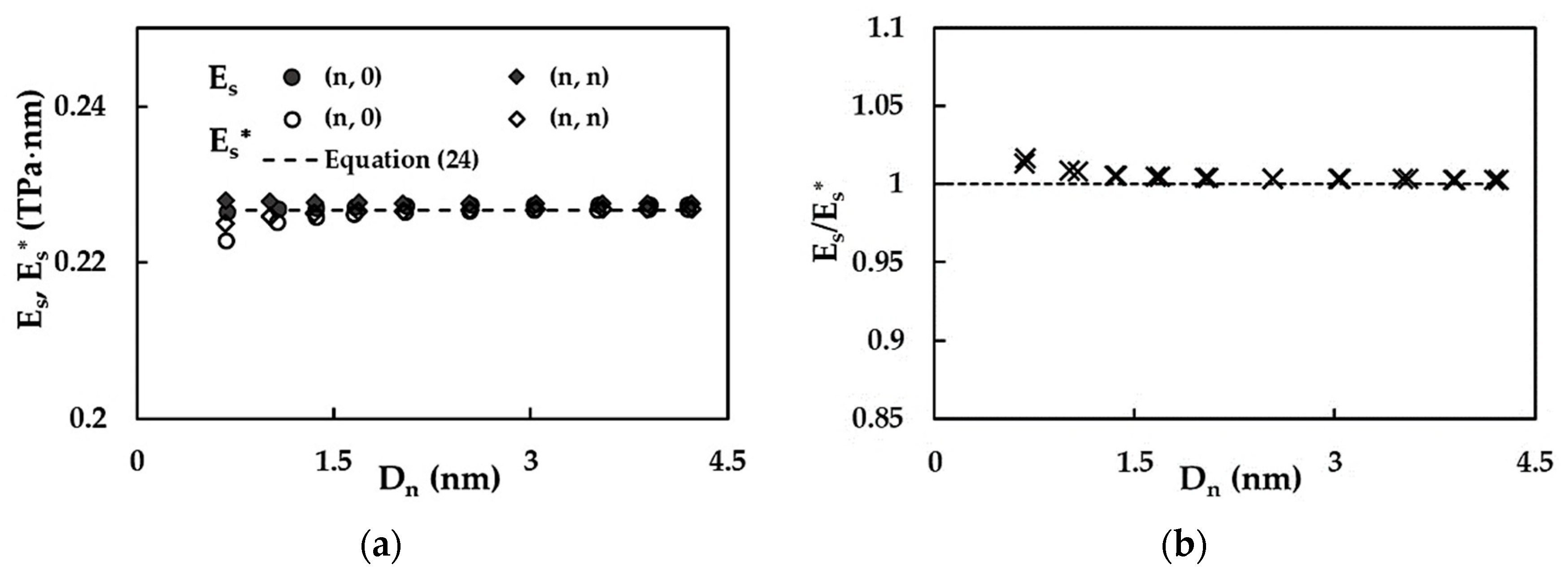
3.1. Rigidities of SWSiCNTs
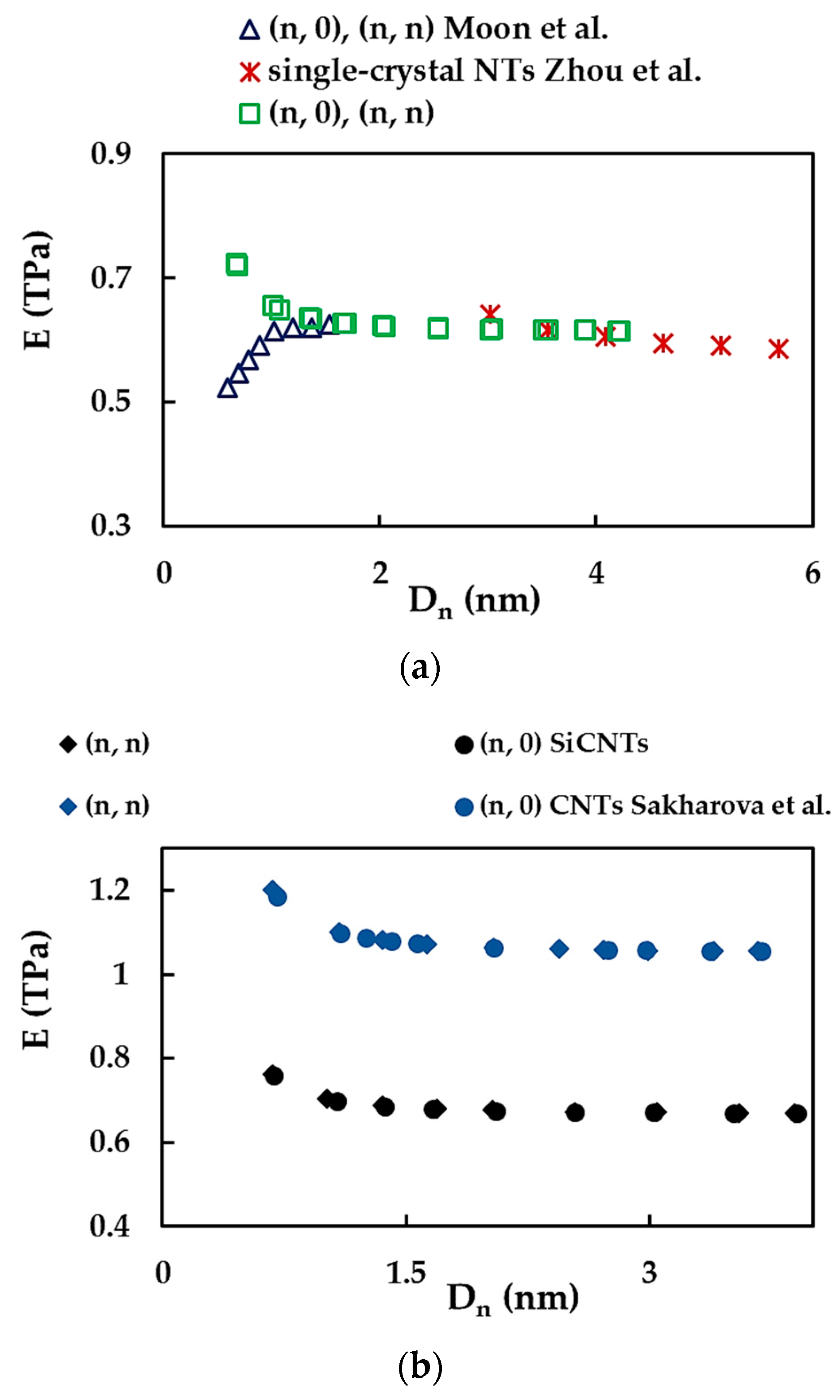
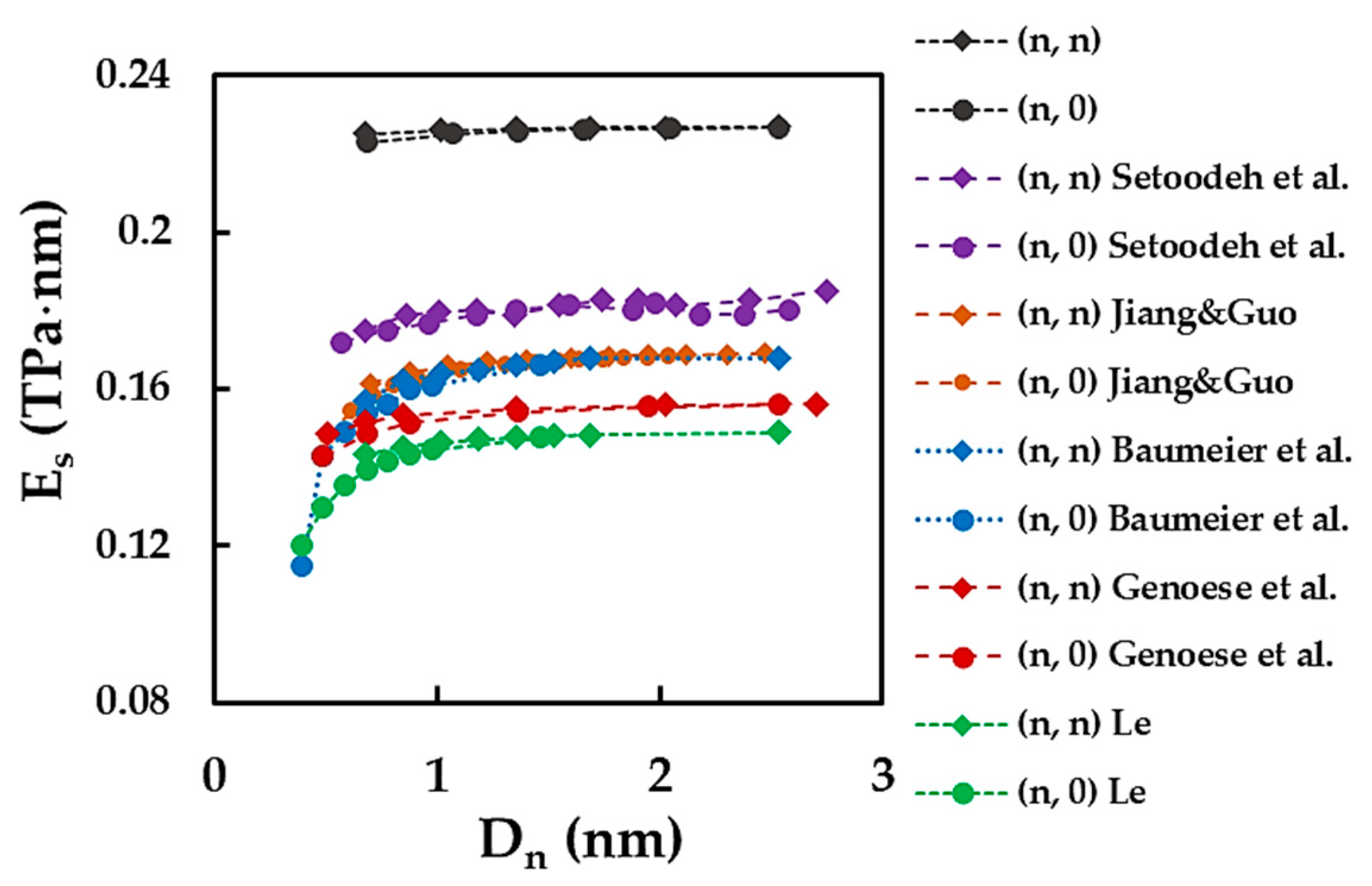
3.2. Young’s Modulus of SWSiCNTs
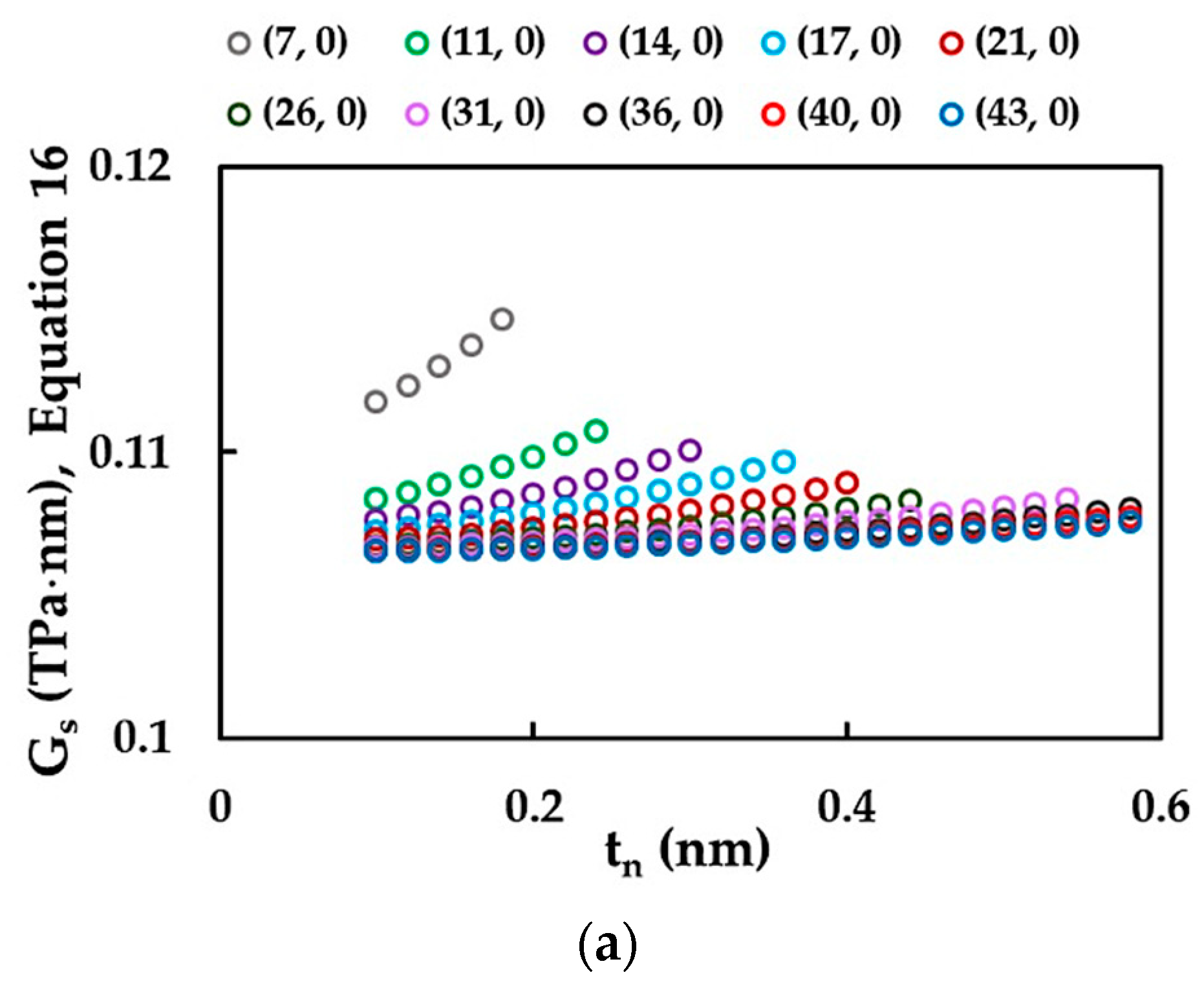
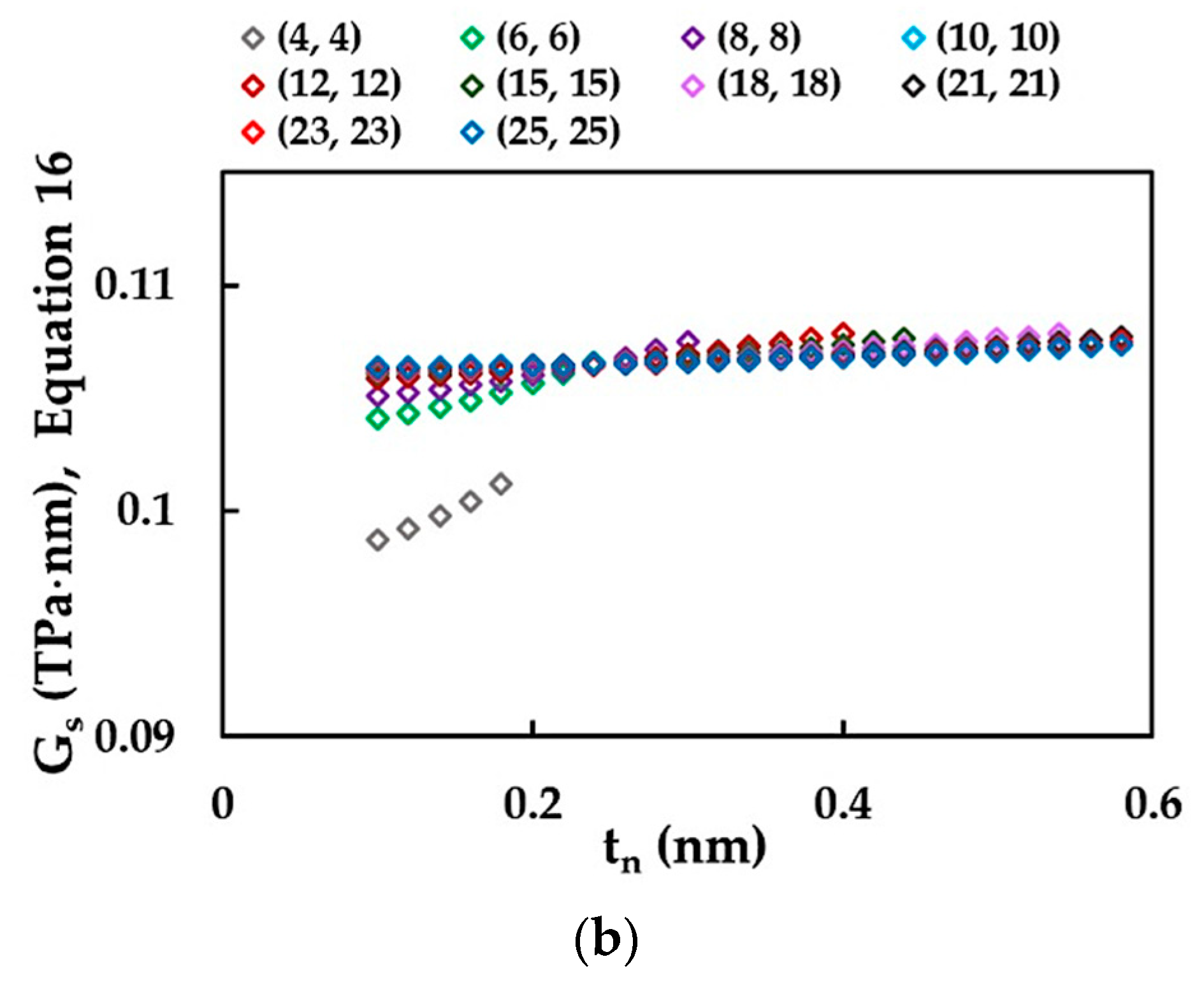
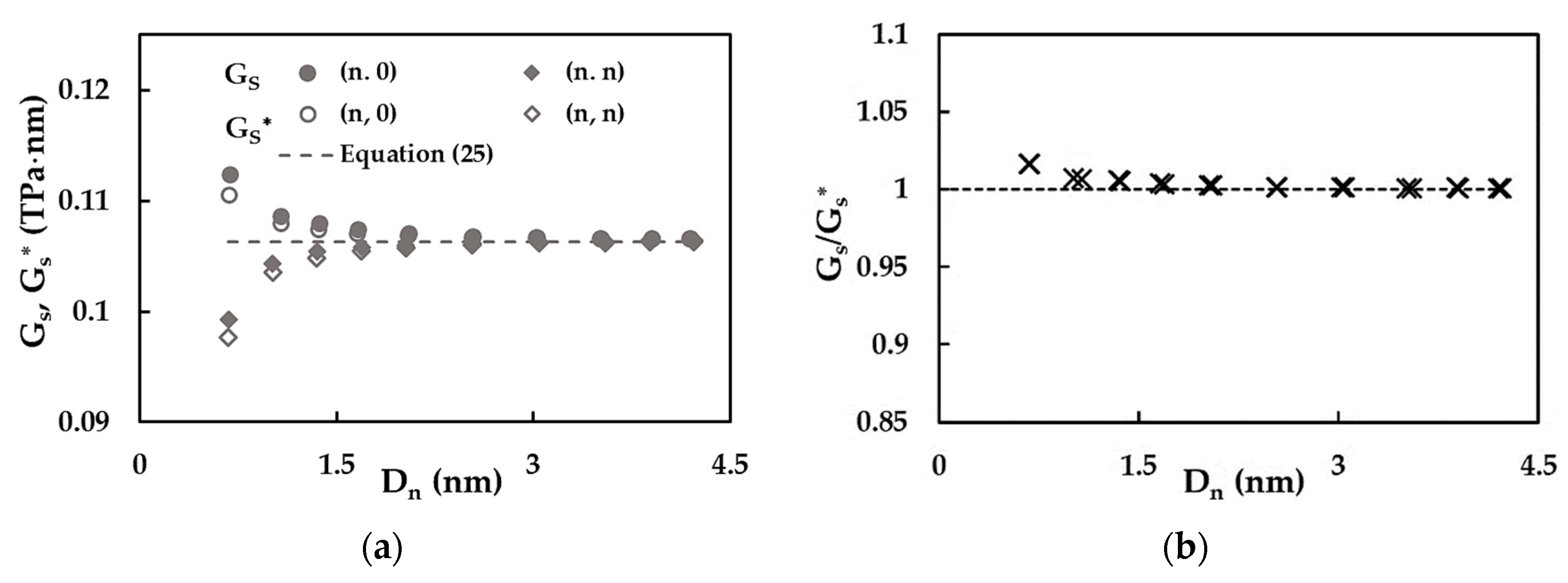
3.3. Shear Modulus of SWSiCNTs
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hurst, J. Boron nitride nanotubes, silicon carbide nanotubes, and carbon nanotubes—A comparison of properties and applications. In Nanotube Superfiber Materials: Changing Engineering Design, 1st ed.; Schulz, M.J., Shanov, V.N., Yin, Z., Eds.; Elsevier: Oxford, UK, 2014; pp. 267–287. [Google Scholar]
- Zhang, R.; Zhang, Y.; Wei., F. Synthesis and properties of ultralong carbon nanotubes. In Nanotube Superfiber Materials: Changing Engineering Design, 1st ed.; Schulz, M.J., Shanov, V.N., Yin, Z., Eds.; Elsevier: Oxford, UK, 2014; pp. 87–136. [Google Scholar]
- Oliveros, A.; Guiseppi-Elie, A.; Saddow, S.E. Silicon carbide: A versatile material for biosensor applications. Biomed. Microdevices 2013, 15, 353–368. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, M.D.; Abdullah, H.Y.; Bhowmick, S.; Biskos, G. Silicon carbide based nanotubes as a sensing material for gaseous H2SiCl2. Silicon 2022. [Google Scholar] [CrossRef]
- Sun, X.H.; Li, C.P.; Wong, W.K.; Wong, N.B.; Lee, C.S.; Lee, S.T.; Teo, B.K. Formation of silicon carbide nanotubes and nanowires via reaction of silicon (from disproportionation of silicon monoxide) with carbon nanotubes. J. Am. Chem. Soc. 2002, 124, 14464–14471. [Google Scholar] [CrossRef] [PubMed]
- Borowiak-Palena, E.; Ruemmeli, M.H.; Gemming, T.; Knupfer, M.; Biedermann, K.; Leonhardt, A.; Pichler, T.; Kalenczuk, R.J. Bulk synthesis of carbon-filled silicon carbide nanotubes with a narrow diameter distribution. J. Appl. Phys. 2005, 97, 056102. [Google Scholar] [CrossRef]
- Hu, J.Q.; Bando, Y.; Zhan, J.H.; Golberg, D. Fabrication of ZnS∕SiC nanocables, SiC-shelled ZnS nanoribbons (and sheets), and SiC nanotubes (and tubes). J. Appl. Phys. Lett. 2004, 85, 2932–2934. [Google Scholar] [CrossRef]
- Pei, L.Z.; Tang, Y.H.; Chen, Y.W.; Guo, C.; Li, X.X.; Yuan, Y.; Zhang, Y. Preparation of silicon carbide nanotubes by hydrothermal method. J. Appl. Phys. 2006, 99, 114306. [Google Scholar] [CrossRef]
- Tony, V.C.S.; Voon, C.H.; Lee, C.C.; Lim, B.Y.; Gopinatha, S.C.B.; Foo, K.L.; Arshad, M.K.M.; Ruslinda, A.R.; Hashim, U.; Nashaain, M.N.; et al. Effective synthesis of silicon carbide nanotubes by microwave heating of blended silicon dioxide and multi-walled carbon nanotube. Mater. Res. 2017, 20, 1658–1668. [Google Scholar]
- Teo, B.K.; Huang, S.P.; Zhang, R.Q.; Li, W.K. Theoretical calculations of structures and properties of one-dimensional silicon-based nanomaterials: Particularities and peculiarities of silicon and silicon-containing nanowires and nanotubes. Coord. Chem. Rev. 2009, 253, 2935–2958. [Google Scholar] [CrossRef]
- Sakharova, N.A.; Antunes, J.M.; Pereira, A.F.G.; Fernandes, J.V. Developments in the evaluation of elastic properties of carbon nanotubes and their heterojunctions by numerical simulation. AIMS Mater. Sci. 2017, 4, 706–737. [Google Scholar] [CrossRef]
- Baumeier, B.; Kruger, P.; Pollmann, J. Structural, elastic, and electronic properties of SiC, BN, and BeO nanotubes. Phys. Rev. B 2007, 76, 085407. [Google Scholar] [CrossRef]
- Moon, W.H.; Ham, J.K.; Hwang, H.J. Mechanical properties of SiC nanotubes. In Proceedings of the Technical Proceedings of the 2003 Nanotechnology Conference and Trade Show, San Francisco, CA, USA, 23–27 February 2003. [Google Scholar]
- Setoodeh, A.R.; Jahanshahi, M.; Attariani, H. Atomistic simulations of the buckling behavior of perfect and defective silicon carbide nanotubes. Comput. Mater. Sci. 2009, 47, 388–397. [Google Scholar] [CrossRef]
- Pan, H.; Si, X. Molecular dynamics simulations of diameter dependence tensile behavior of silicon carbide nanotubes. Physica B 2009, 404, 1809–1812. [Google Scholar] [CrossRef]
- Zhou, R.L.; Wang, L.; Pan, B.C. Elastic and Melting Properties of Crystalline SiC Nanotubes. J. Phys. Chem. C 2010, 114, 8199–8205. [Google Scholar] [CrossRef]
- Le, M.-Q. Young’s modulus prediction of hexagonal nanosheets and nanotubes based on dimensional analysis and atomistic simulations. Meccanica 2014, 49, 1709–1719. [Google Scholar] [CrossRef]
- Mercan, K.; Civalek, O. Buckling analysis of Silicon carbide nanotubes (SiCNTs) with surface effect and nonlocal elasticity using the method of HDQ. Comp. Part B Eng. 2017, 114, 34–45. [Google Scholar] [CrossRef]
- Genoese, A.; Genoese, A.; Salerno, G. On the nanoscale behaviour of single-wall C, BN and SiC nanotubes. Acta Mech. 2019, 230, 1105–1128. [Google Scholar] [CrossRef]
- Jiang, L.; Guo, W. Analytical solutions for elastic binary nanotubes of arbitrary chirality. Acta Mech. Sin. 2016, 32, 1046–1057. [Google Scholar] [CrossRef]
- Ansari, R.; Rouhi, S.; Aryayi, M.; Mirnezhad, M. On the buckling behavior of single-walled silicon carbide nanotubes. Sci. Iran. 2012, 19, 1984–1990. [Google Scholar] [CrossRef][Green Version]
- Şahin, H.; Cahangirov, S.; Topsakal, M.; Bekaroglu, E.; Akturk, E.; Senger, R.T.; Ciraci, S. Monolayer honeycomb structures of group-IV elements and III-V binary compounds: First-principles calculations. Phys. Rev. B 2009, 80, 155453. [Google Scholar] [CrossRef]
- Huber, K.P.; Hertzberg, G. Molecular Spectra and Molecular Siructure: IV. Constants of Diatomic Molecules, 1st ed.; Van Nostrand Reinhold Company: New York, NY, USA, 1979. [Google Scholar]
- Li, C.; Chou, T.W. A structural mechanics approach for the analysis of carbon nanotubes. Int. J. Solids Struct. 2003, 40, 2487–2499. [Google Scholar] [CrossRef]
- Sakharova, N.A.; Antunes, J.M.; Pereira, A.F.G.; Chaparro, B.M.; Fernandes, J.V. On the determination of elastic properties of single-walled boron nitride nanotubes by numerical simulation. Materials 2021, 14, 3183. [Google Scholar] [CrossRef] [PubMed]
- Sakharova, N.A.; Pereira, A.F.G.; Antunes, J.M.; Brett, C.M.A.; Fernandes, J.V. Mechanical characterization of single-walled carbon nanotubes. Numerical simulation study. Compos. B-Eng. 2015, 75, 73–85. [Google Scholar] [CrossRef]
- Pereira, A.F.G.; Antunes, J.M.; Fernandes, J.V.; Sakharova, N.A. Shear modulus and Poisson’s ratio of single-walled carbon nanotubes: Numerical evaluation. Phys. Status Solidi B 2016, 253, 366–376. [Google Scholar] [CrossRef]
- Sakharova, N.A.; Antunes, J.M.; Pereira, A.F.G.; Chaparro, B.M.; Fernandes, J.V. Elastic Properties of Single-Walled Phosphide Nanotubes: Numerical Simulation Study. Nanomaterials 2022, 12, 2360. [Google Scholar] [CrossRef] [PubMed]
- Antunes, J.M.; Pereira, A.F.G.; Sakharova, N.A. Overview on the Evaluation of the Elastic Properties of Non-Carbon Nanotubes by Theoretical Approaches. Materials 2022, 15, 3325. [Google Scholar] [CrossRef]




| Parameter | Value | Formulation |
|---|---|---|
| 1 bond stretching force constant, kr [21] | 417 nN/nm | – |
| 1 bond bending force constant, kθ [21] | 0.842 nN⋅nm/rad2 | – |
| 1 torsional resistance force constant, kτ [21] | 1.505 nN⋅nm/rad2 | – |
| Si–C bond/beam lengths [22] | 0.177 nm | l = |
| diameter, d | 0.1797 nm | |
| Young’s modulus, | 2937 GPa | |
| shear modulus, | 2625 GPa | |
| Poisson’s ratio, | 0.29 | |
| tensile rigidity, | 74.5 nN | |
| bending rigidity, | 0.1504 nN⋅nm2 | |
| torsional rigidity, | 0.2688 nN⋅nm2 |
| NT Type | (n, m) | θ° | |
|---|---|---|---|
| zigzag | (7, 0) | 0 | 0.683 |
| (11, 0) | 1.073 | ||
| (14, 0) | 1.366 | ||
| (17, 0) | 1.659 | ||
| (21, 0) | 2.049 | ||
| (26, 0) | 2.537 | ||
| (31, 0) | 3.025 | ||
| (36, 0) | 3.513 | ||
| (40, 0) | 3.903 | ||
| (43, 0) | 4.196 | ||
| armchair | (4, 4) | 30 | 0.676 |
| (6, 6) | 1.014 | ||
| (8, 8) | 1.352 | ||
| (10, 10) | 1.690 | ||
| (12, 12) | 2.028 | ||
| (15, 15) | 2.535 | ||
| (18, 18) | 3.042 | ||
| (21, 21) | 3.549 | ||
| (23, 23) | 3.888 | ||
| (25, 25) | 4.226 |
| Reference | Method | NT Type | |
|---|---|---|---|
| Baumeier et al. [12] | ab initio | (n, n) | 0.167 |
| (n, 0) | 0.162 | ||
| Setoodeh et al. [14] | MD: Tersoff potential | (n, n) | 0.182 |
| (n, 0) | 0.180 | ||
| Le [17] | MD: harmonic force fields | (n, n) | 0.148 |
| (n, 0) | 0.145 | ||
| Genoese et al. [19] | NCM/MSM + CM: “stick-and-spring” + thin shell models | (n, n) | 0.152 |
| (n, 0) | 0.149 | ||
| Jiang and Guo [20] | NCM/MSM: “stick-and-spring” model + analytical | (n, n) | 0.169 |
| (n, 0) | 0.168 | ||
| Present study | NCM/MSM: beams | (n, n) | 0.227 |
| (n, 0) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakharova, N.A.; Pereira, A.F.G.; Antunes, J.M. Elastic Moduli of Non-Chiral Singe-Walled Silicon Carbide Nanotubes: Numerical Simulation Study. Materials 2022, 15, 8153. https://doi.org/10.3390/ma15228153
Sakharova NA, Pereira AFG, Antunes JM. Elastic Moduli of Non-Chiral Singe-Walled Silicon Carbide Nanotubes: Numerical Simulation Study. Materials. 2022; 15(22):8153. https://doi.org/10.3390/ma15228153
Chicago/Turabian StyleSakharova, Nataliya A., André F. G. Pereira, and Jorge M. Antunes. 2022. "Elastic Moduli of Non-Chiral Singe-Walled Silicon Carbide Nanotubes: Numerical Simulation Study" Materials 15, no. 22: 8153. https://doi.org/10.3390/ma15228153
APA StyleSakharova, N. A., Pereira, A. F. G., & Antunes, J. M. (2022). Elastic Moduli of Non-Chiral Singe-Walled Silicon Carbide Nanotubes: Numerical Simulation Study. Materials, 15(22), 8153. https://doi.org/10.3390/ma15228153







