Heuristic Optimization of a New Type of Prestressed Arched Truss
Abstract
1. Introduction
2. Problem Formulation
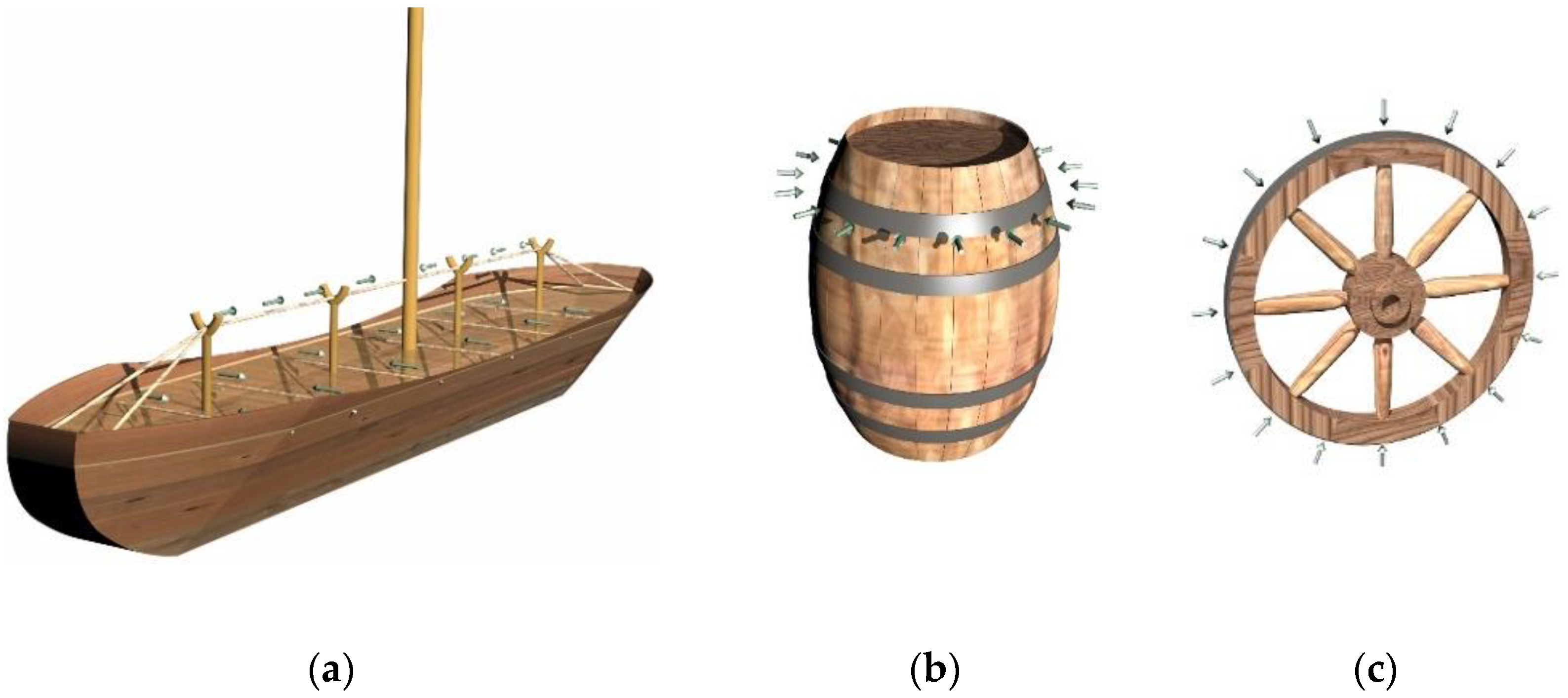
2.1. General Aspects of Understanding the Prestressing Method
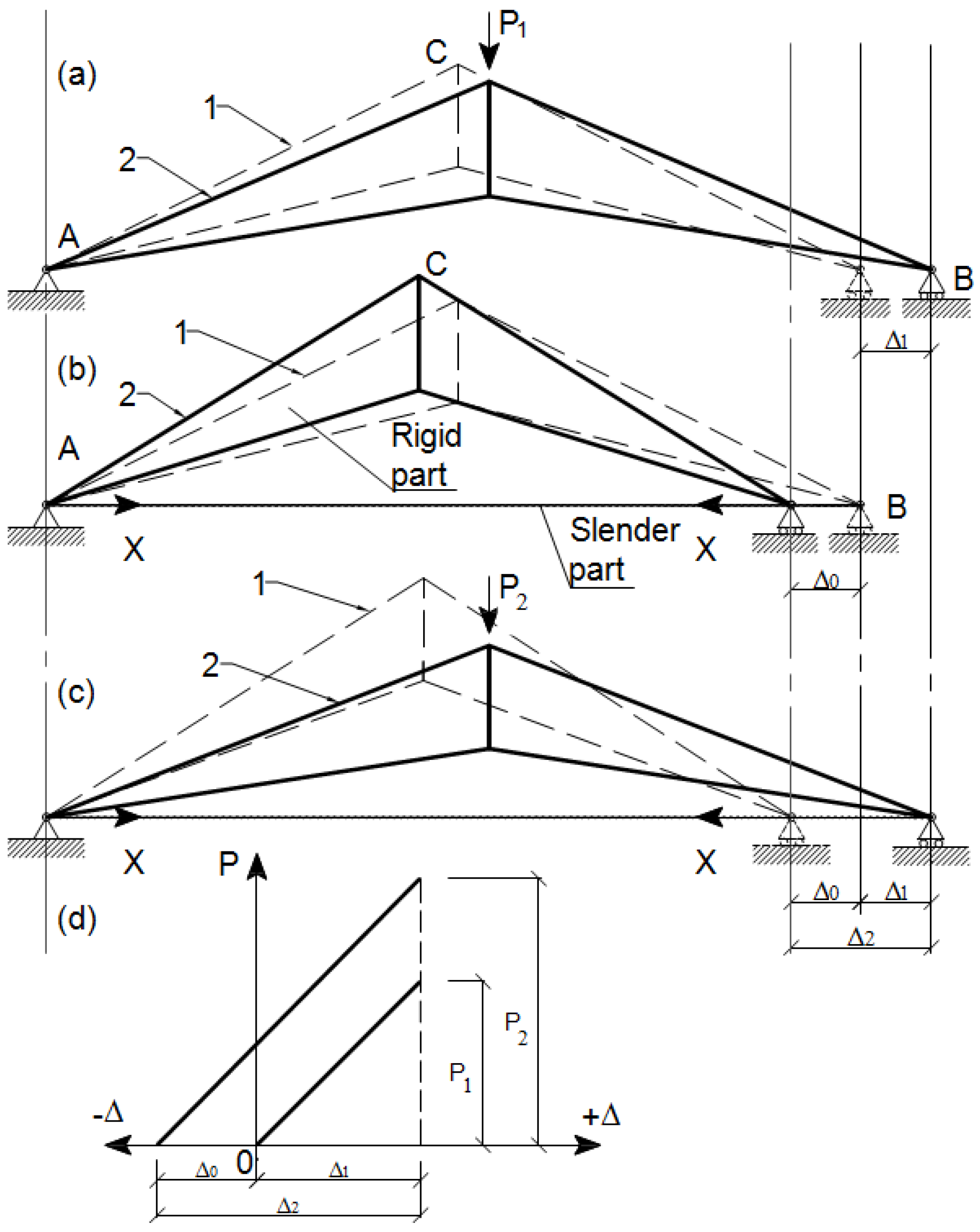
2.2. Static Analysis of the Arched Trusses with a Cable
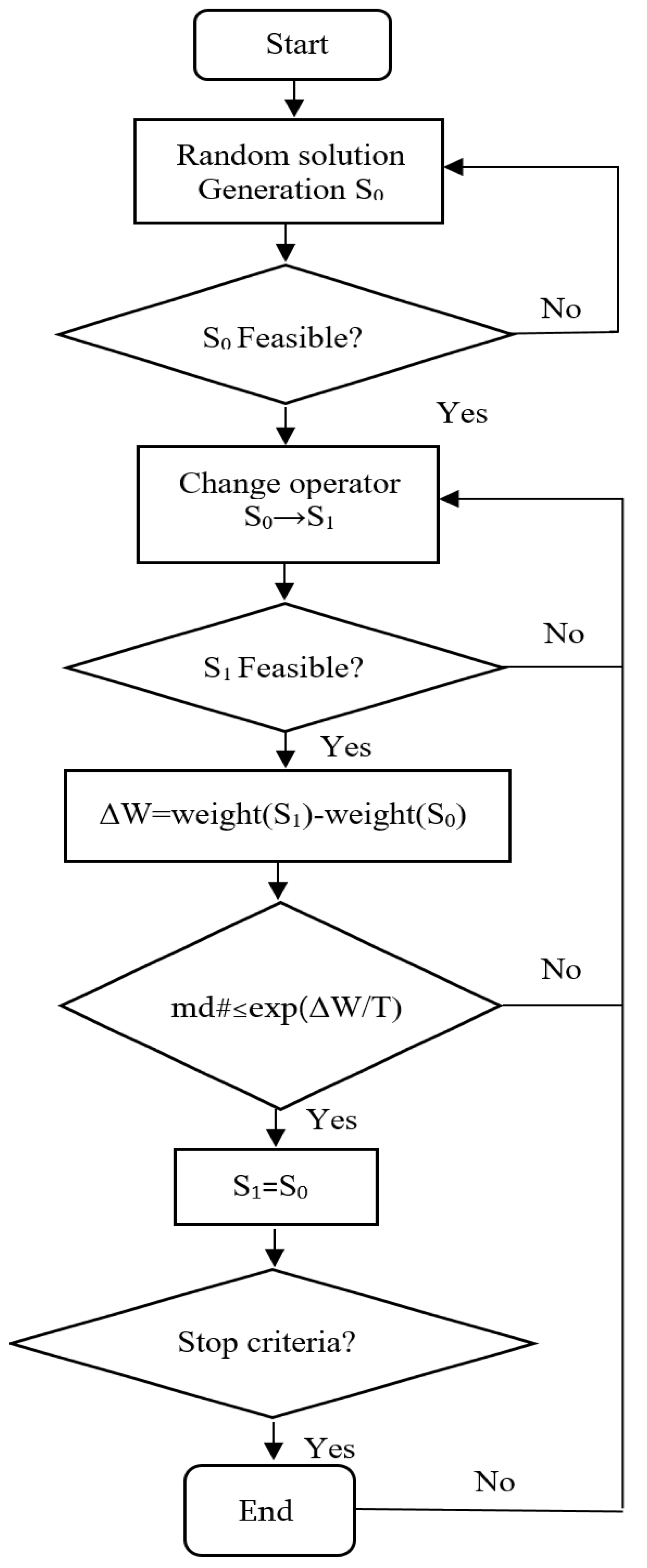
2.3. Algorithm for the Calculation of Prestressed Trusses
2.4. Disadvantages in the Calculation Method
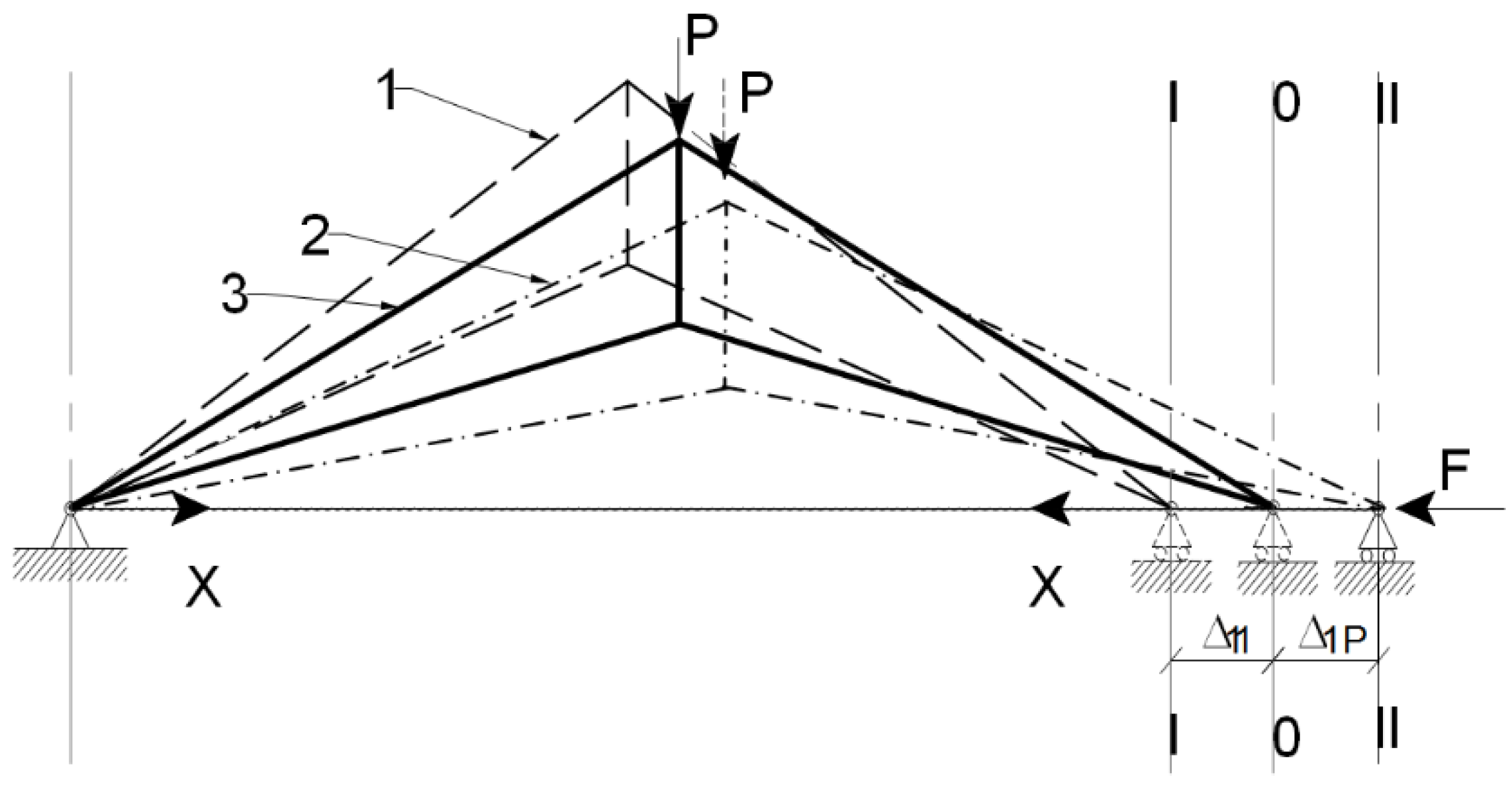
2.5. Disadvantages in the Structural Design Process of the Arched Truss with Tie Members (Cable)
3. Problem Solution
3.1. Geometric, Physical and Mechanical Characteristics of a New Type of Prestressed Arched Truss
3.2. Problem Solution in the Structural Design Process Method
3.3. Problem Solution in the Calculation Method
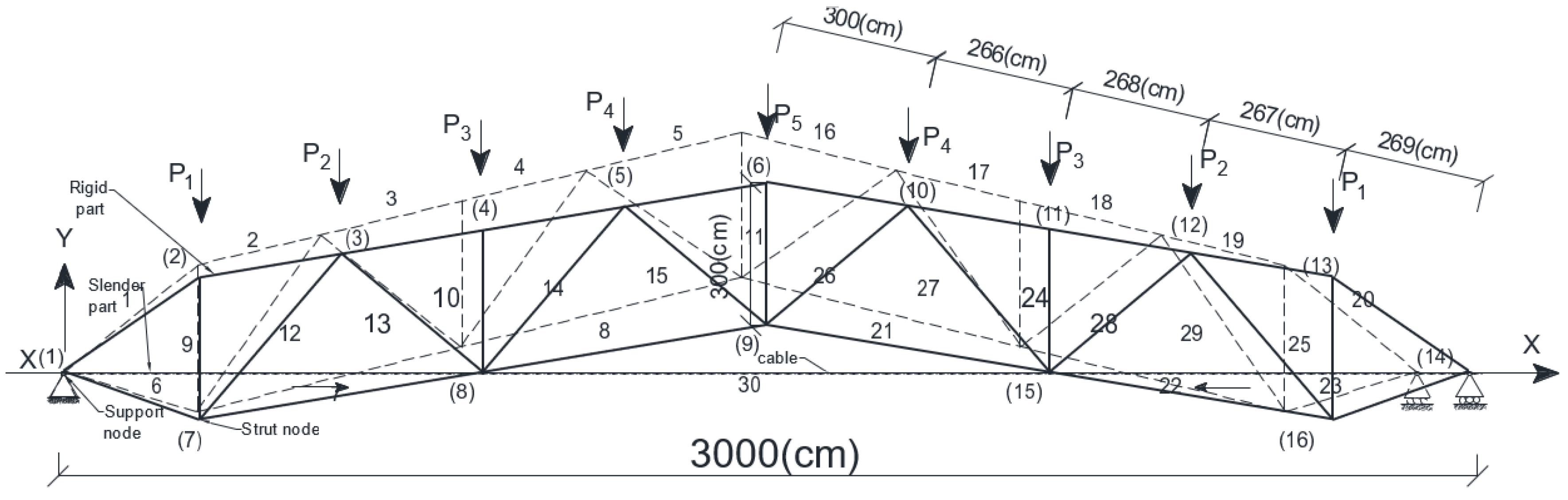
3.4. Calculation of the New Model of the Prestressed Arched Truss Using the Matrix Stiffness Method and a Numerical Example
3.5. Optimization of Prestressed Truss
3.6. Sizing of the Cross-Section of the Truss Elements
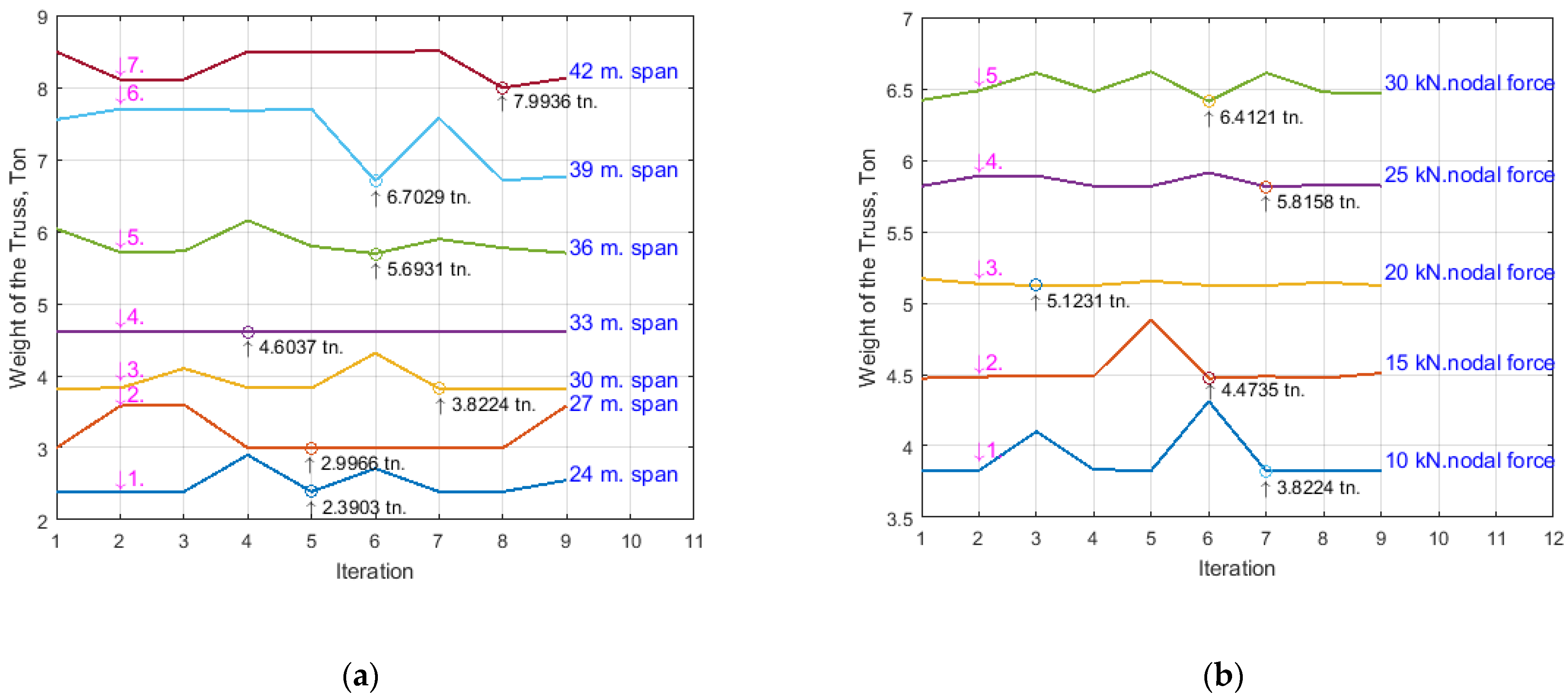
4. Results and Analyses
- (1)
- A new geometric and innovative form was discerned for a prestressed arched truss that allows the development of higher values of prestressing force;
- (2)
- A new geometric and innovative truss was discerned that does not have unloading elements in the bottom chord, and the materials consumption exceeding problem was solved;
- (3)
- A new approach to the calculation (metaheuristic optimization) of a prestressed arched truss has been developed, resulting in the determination of the highest values of prestressing force with high accuracy in the tie member.
- (4)
- (5)
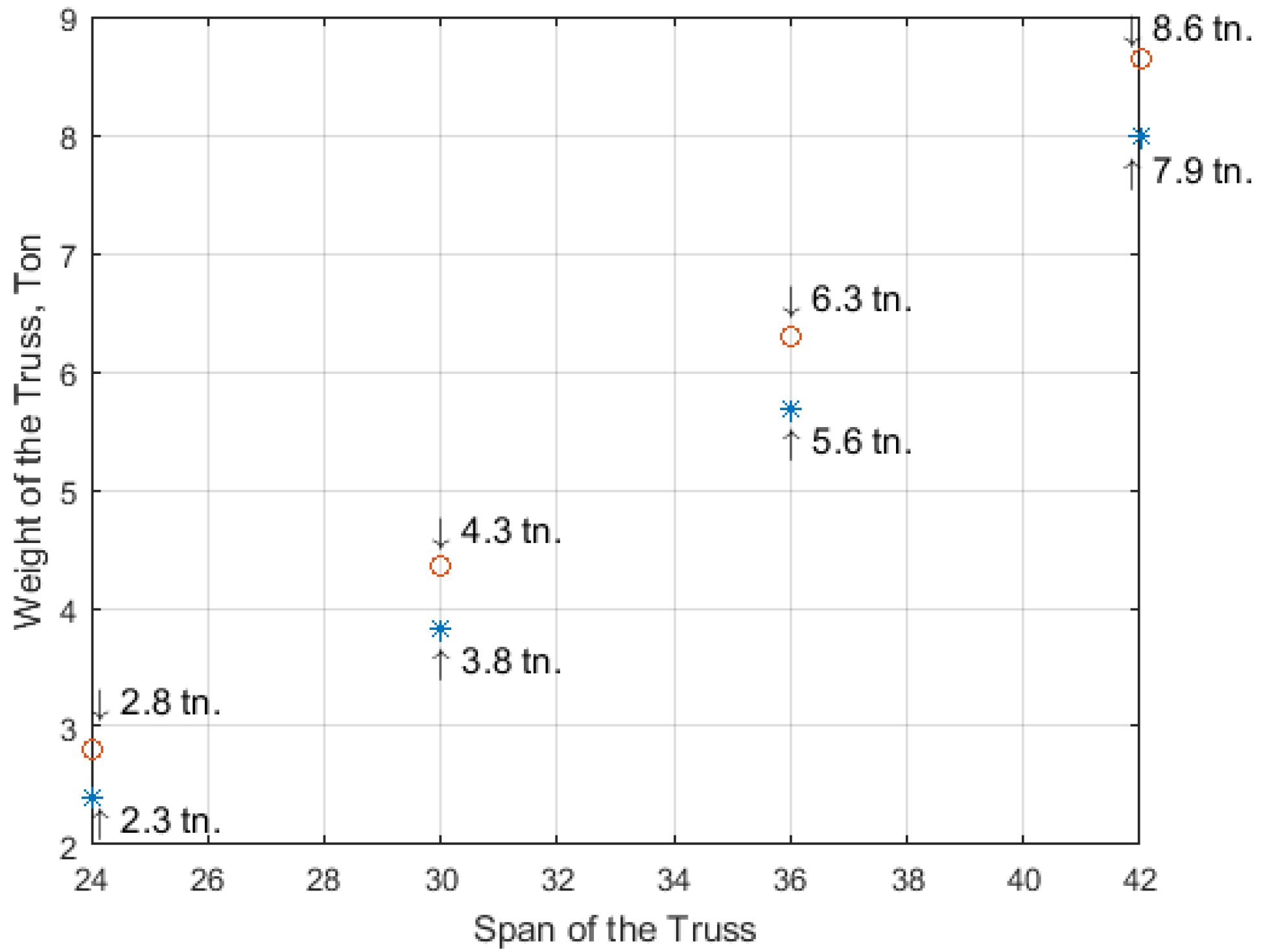
- By the new approaches offered by the authors, the weight of the truss was reduced, and the load capacity, rigidity, reliability, and fatigue resistance of the new truss were increased (see Figure 9);
- (6)
- The rate of prestressing force was increased (the asterisks are below the rings in Figure 9), as a result the elastic region of the working material was extended.
5. Conclusions
- It is recommended to use this new type of prestressed arched truss with a tie member as an innovative long-span roof system optimized and designed by the authors;
- It is recommended to adopt the innovative technique proposed in the process of designing the geometric form of a new type of prestressed arched truss. Thus, the tie member of the truss should be moved from the strut node towards the support node (Figure 2 and Figure 5), to eliminate unloaded elements in the truss structure and to develop a high rate of prestressing force in the primary structure of the truss;
- This research recommends using the performed approach in calculating prestressed arched trusses, where the highest values of the prestressing force are determined by the metaheuristic optimization and matrix stiffness methods;
- The research in this paper recommends the new approaches to obtain a truss with the lowest gravity, as the location of points of minimal weight of the prestressed arched truss by metaheuristic optimization were established and presented in Figure 8a,b;
- The optimization of the prestressed arched truss reduces the self-weight and increases the load capacity of the truss by 8–17%, depending on the span (see Figure 9);
- The new approach to increasing the rate of prestressing force of the truss achieves elastic region of working material expansion by almost 12–14%;
- It is recommended to use the new approaches, instead of several approaches for defining values of truss parameters (prestressing force in the cables, cross-sections in the truss elements), as far as it is possible to define them with a particular single approach;
- Reducing the weight of the new truss consequently reduces CO2 emissions.
- To obtain the prestressed arched truss with minimum weight is necessary to conduct future research not only to optimize the cross-sectional area, but also the truss topology (shape formation). In particular, it will be very relevant to optimize the shape of the chords, the boom lift, the type of lattice, and the number of panels of prestressed trusses.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gosaye, J.; Gardner, L.; Wadee, M.; Ellen, M. Compressive behaviour and design of prestressed steel elements. Structures 2016, 5, 76–87. [Google Scholar] [CrossRef]
- Chen, Y.; Dong, J.; Xu, T. Composite box girder with corrugated steel webs and trusses—A new type of bridge structure. Eng. Struct. 2018, 166, 354–362. [Google Scholar] [CrossRef]
- Partskhaladze, G.; Mshvenieradze, I.; Medzmariashvili, E.; Chavleshvili, G.; Yepes, V.; Alcala, J. Buckling Analysis and Stability of Compressed Low-Carbon Steel Rods in the Elastoplastic Region of Materials. Adv. Civ. Eng. 2019, 2019, 7601260. [Google Scholar] [CrossRef]
- Wang, Z.; Song, W.; Wang, Y.; Wei, H. Numerical Analytical Model for Seismic Behavior of Prestressing Concrete Bridge Column Systems. In Proceedings of the Twelfth East Asia-Pacific Conference on Structural Engineering and Construction, Hong Kong, China, 26–28 January 2011; Elsevier Ltd.: Amsterdam, The Netherlands, 2011; pp. 2333–2340. [Google Scholar] [CrossRef]
- Belletti, B.; Gasperi, A. Behavior of Prestressed Steel Beams. J. Structural. 2010, 9, 1131–1139. [Google Scholar] [CrossRef]
- Afshan, S.; Theofanous, M.; Wang, J.; Gkantou, L. Testing, numerical simulation and design of prestressed high strength steel arched trusses. Eng. Struct. 2019, 15, 510–522. [Google Scholar] [CrossRef]
- Huang, W.; Lai, Z.; Chen, B.; Yao, P. Experimental behavior and analysis of prestressed concrete-filled steel tube (CFT) truss girders. Eng. Struct. 2017, 152, 607–618. [Google Scholar] [CrossRef]
- Chen, Y.; Dong, J.; Xu, T.; Xiao, Y.; Jiang, R.; Nie, X. The shear-lag effect of composite box girder bridges with corrugated steel webs and trusses. Eng. Struct. 2019, 181, 617–628. [Google Scholar] [CrossRef]
- Gesualdo, F.R.; Cunha, T.A.; Rezende, R.B. Numerical and experimental evaluation of a double inverted trussed beam reinforced with steel cable. Constr. Build. Mater. 2014, 50, 736–743. [Google Scholar] [CrossRef]
- Piyasena, R.; Thambiratnam, D.; Chan, T.; Perera, N. Comparative analysis of blast response of cable truss and cable net façades. Eng. Fail. Anal. 2019, 104, 740–757. [Google Scholar] [CrossRef]
- Gao, W.; Lu, X. Modelling unbonded prestressing tendons in self-centering connections through improved sliding cable elements. Eng. Struct. 2019, 180, 809–828. [Google Scholar] [CrossRef]
- Hadjipantelis, N.; Gardner, L.; Wadee, M. Prestressed cold-formed steel beams: Concept and mechanical behaviour. Eng. Struct. 2018, 172, 1057–1072. [Google Scholar] [CrossRef]
- Zhang, P.; Feng, J. Initial prestress design and optimization of tensegrity systems based on symmetry and stiffness. Int. J. Solids Struct. 2017, 106, 68–90. [Google Scholar] [CrossRef]
- Bernardo, L.; Teixeira, M. Modified softened truss-model for prestressed concrete beams under torsion. J. Build. Eng. 2018, 19, 49–61. [Google Scholar] [CrossRef]
- Yang, J.; Haghani, R.; Al-Emrani, M. Innovative prestressing method for externally bonded CFRP laminates without mechanical anchorage. Eng. Struct. 2019, 197, 1–9. [Google Scholar] [CrossRef]
- Yu, J.; Wadee, A. Optimal prestressing of triple-bay prestressed stayed columns. Structures 2017, 12, 132–144. [Google Scholar] [CrossRef]
- Wang, J.; Afshan, S.; Gardner, L. Axial behaviour of prestressed high strength steel tubular members. J. Constr. Steel Res. 2017, 133, 547–563. [Google Scholar] [CrossRef]
- Li, P.; Liu, X.; Zhang, C. Interactive buckling of cable-stiffened steel columns with pin-connected crossarms. J. Constr. Steel Res. 2018, 146, 97–108. [Google Scholar] [CrossRef]
- Sutarja, I.; Widiarsa, I. Partial prestressed concrete slabs as an alternative for vehicle decks of steel truss bridges. In Proceedings of the 5th International Conference of Euro Asia Civil Engineering Forum (EACEF-5), Surabaya, Indonesia, 15–18 September 2015; Elsevier: Amsterdam, The Netherlands, 2015; Volume 125, pp. 974–978. [Google Scholar] [CrossRef]
- Segal, E.; Rhode-Barbarigos, L.; Adriaenssens, S.; Filomeno Coelho, R. Multi-objective optimization of polyester-rope and steel-rope suspended footbridges. Eng. Struct. 2015, 99, 559–567. [Google Scholar] [CrossRef]
- Yepes, V.; Medina, J. Economic heuristic optimization for heterogeneous fleet VRPHESTW. J. Transp. Eng. 2006, 132, 303–311. [Google Scholar] [CrossRef]
- Molina-Moreno, F.; García-Segura, T.; Martí, J.; Yepes, V. Optimization of buttressed earth-retaining walls using hybrid harmony search algorithms. Eng. Struct. 2017, 134, 205–216. [Google Scholar] [CrossRef]
- Carbonell, A.; González-Vidosa, F.; Yepes, V. Design of reinforced concrete road vaults by heuristic optimization. Adv. Eng. Softw. 2011, 42, 151–159. [Google Scholar] [CrossRef]
- Ma, Q.; Ohsaki, M.; Chen, Z.; Yan, X. Multi-objective optimization for prestress design of cable-strut structures. Int. J. Solids Struct. 2019, 165, 137–147. [Google Scholar] [CrossRef]
- Jung, K.H.; Yi, J.W.; Kim, J.H.J. Structural safety and serviceability evaluations of prestressed concrete hybrid bridge girders with corrugated or steel truss web members. Eng. Struct. 2010, 32, 3866–3878. [Google Scholar] [CrossRef]
- Paya-Zaforteza, I.; Yepes, V.; Gonzalez-Vidosa, F.; Hospitaler, A. On the Weibull cost estimation of building frames designed by simulated annealing. Meccanica 2010, 45, 693–704. [Google Scholar] [CrossRef]
- Jang, J.; Hwang, K.; Lee, H.; Kim, B. An assessment of the prestress force on the bonded tendon by SI and impact signal analysis techniques. Nucl. Eng. Des. 2013, 255, 9–15. [Google Scholar] [CrossRef]
- Khalafalla, O.; Pour-Ghaz, M.; ElSaft, A. Durability of CFRP strands used for prestressing of concrete structural members. Constr. Build. Mater. 2019, 2228, 1–11. [Google Scholar] [CrossRef]
- Teixeira, A.; Pfeil, M.; Battista, R. Structural evaluation of a GFRP truss girder for a deployable bridge. Compos. Struct. 2014, 110, 29–38. [Google Scholar] [CrossRef]
- Bačinskas, D.; Rimkus, A.; Rumšys, D.; Meškėnas, A.; Bielinis, S.; Sokolov, A.; Merkevičius, T. Structural analysis of GFRP truss bridge model. In Proceedings of the 12th International Conference Modern Building Materials, Structures and Techniques (MBMST 2016), Vilnius, Lithuania, 26–27 May 2016; Volume 172, pp. 68–74. [Google Scholar] [CrossRef]
- Burgoyne, C.; Mitchell, O. Prestressing in Coventry Cathedral. Structures 2017, 11, 62–83. [Google Scholar] [CrossRef]
- Qin, Y.; Shu, G.P.; Zhou, G.G.; Han, J.-H.; Zhou, X.L. Truss spacing on innovative composite walls under compression. J. Constr. Steel Res. 2019, 160, 1–15. [Google Scholar] [CrossRef]
- Tian, Z.; Liu, Y.; Jiang, L.; Zhu, W.; Ma, Y. A review on application of composite truss bridges composed of hollow structural section members. J. Traffic Transp. Eng. (Engl. Ed.) 2019, 1, 94–108. [Google Scholar] [CrossRef]
- Medzmariashvili, E.; Partskhaladze, G.; Tkeshelashvili, R.; Khazaradze, G. Complex Constructions for Extreme Condition. Bull. Georgian Natl. Acad. Sci. 2018, 1, 76–81. [Google Scholar]
- Machacek, J.; Cudejko, M. Composite steel and concrete bridge trusses. Eng. Struct. 2011, 33, 3136–3142. [Google Scholar] [CrossRef]
- Gaynor, A.; Guest, J.; Moen, C. Reinforced Concrete Force Visualization and Design Using Bilinear Truss-Continuum Topology Optimization. J. Struct. Eng. 2013, 4, 607–618. [Google Scholar] [CrossRef]
- Martí-Vargas, J.R.; Ferri, F.J.; Yepes, V. Prediction of the transfer length of prestressing strands with neu-ral networks. Comput. Concr. 2013, 12, 187–209. [Google Scholar] [CrossRef]
- Yepes-Bellver, L.; Brun-Izquierdo, A.; Alcalá, J.; Yepes, V. CO2-Optimization of Post-Tensioned Concrete Slab-Bridge Decks Using Surrogate Modeling. Materials 2022, 15, 4776. [Google Scholar] [CrossRef]
- Bernardo, L.F.A.; Filho, B.M.V.C.; Horowitz, B. Efficient softened truss model for prestressed steel fiber concrete membrane elements. J. Build. Eng. 2021, 3, 20. [Google Scholar] [CrossRef]
- Huang, Y.; Tao, Y.; Yi, W.; Zhou, Y.; Deng, L. Numerical investigation on compressive arch action of prestressed concrete beam-column assemblies against progressive collapse. J. Build. Eng. 2021, 44, 102991. [Google Scholar] [CrossRef]
- Sun, G.; Xiao, S.; Wu, J. Study on mechanical properties of truss cable structure under low cyclic loading. J. Build. Eng. 2022, 58, 105051. [Google Scholar] [CrossRef]
- Kambal, M.E.M.; Jia, Y. Theoretical and experimental study on flexural behavior of prestressed steel plate girders. J. Constr. Steel Res. 2018, 142, 5–16. [Google Scholar] [CrossRef]
- Zhu, R.; Li, F.; Shao, F.; Zhang, D. Static and dynamic behaviour of a hybrid PFRP-aluminium space truss girder: Experimental and numerical study. Compos. Struct. 2020, 243, 112226. [Google Scholar] [CrossRef]
- Siwowski, T. Fatigue assessment of existing riveted truss bridges: Case study. Bul. Pol. Acad. Sci. 2015, 1, 125–133. [Google Scholar] [CrossRef]
- Liu, Y.; Xin, H.; He, J.; Xue, D.; Ma, B. Experimental and analytical study on fatigue behavior of composite truss joints. J. Constr. Steel Res. 2013, 83, 21–26. [Google Scholar] [CrossRef]
- Bazant, Z.; Yu, Q. Relaxation of Prestressing Steel at Varying Strain and Temperature: Viscoplastic Constitutive Relation. J. Eng. Mech. 2013, 7, 814–823. [Google Scholar] [CrossRef]
- Xie, B.; Hou, J.; Xu, Z.; Dan, M. Component-based model of fin plate connections exposed to fire-part I: Plate in bearing component. J. Constr. Steel Res. 2018, 149, 1–13. [Google Scholar] [CrossRef]
- Wang, H.; Li, P.; Wu, M. Crossarm length optimization and post-buckling analysis of prestressed stayed steel columns. Thin-Walled Struct. 2019, 144, 106371. [Google Scholar] [CrossRef]

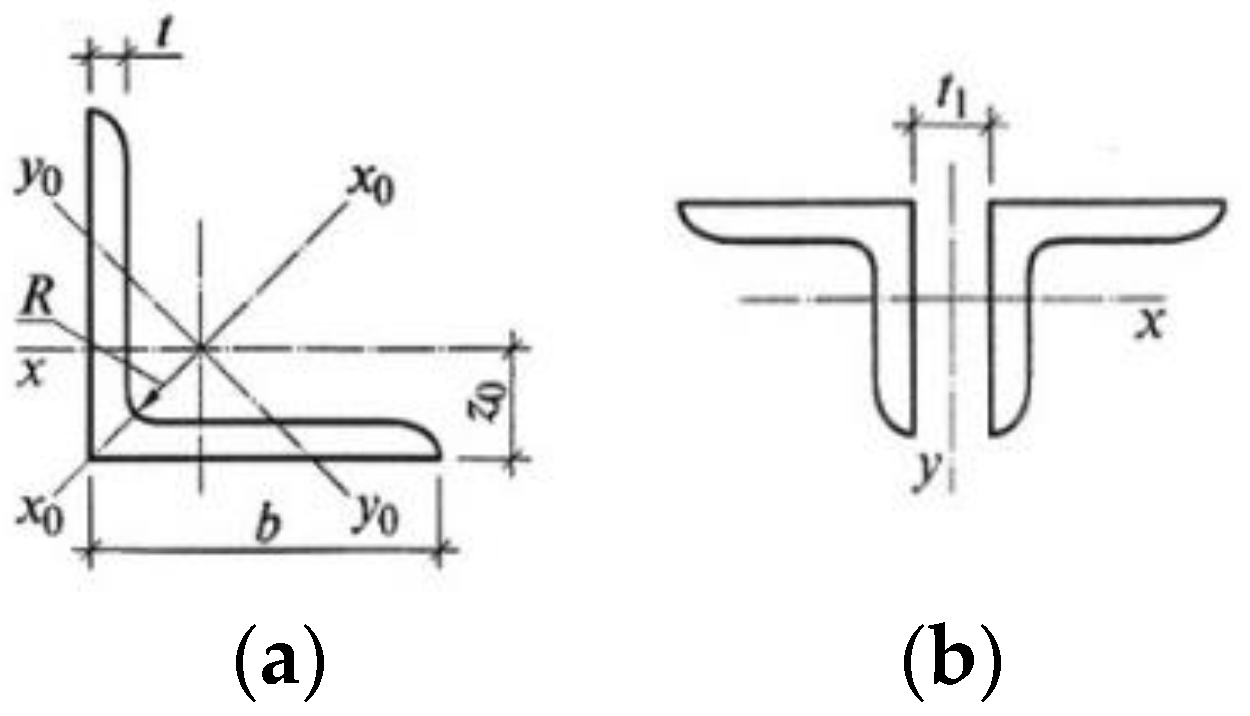
| , Width of a Cross-Section, mm | , Thickness, mm | , Area of a Cross-Section, cm2 | , Radius of Gyration, cm | , Radius of Gyration, cm | , Mass per Meter, kg/m |
|---|---|---|---|---|---|
| 50 | 5 | 4.88 | 1.53 | 2.45 | 3.77 |
| 63 | 5 | 6.13 | 1.94 | 2.96 | 4.81 |
| 70 | 5 | 6.86 | 2.16 | 3.22 | 3.38 |
| 75 | 6 | 8.78 | 2.30 | 3.44 | 6.89 |
| 80 | 6 | 9.38 | 2.47 | 3.65 | 7.36 |
| 90 | 6 | 10.6 | 2.78 | 4.03 | 8.33 |
| 90 | 7 | 12.3 | 2.77 | 4.06 | 9.64 |
| 100 | 7 | 13.8 | 3.08 | 4.44 | 10.8 |
| 100 | 8 | 15.6 | 3.07 | 4.47 | 12.2 |
| 110 | 8 | 17.2 | 3.39 | 4.87 | 13.5 |
| 125 | 8 | 19.7 | 3.87 | 5.46 | 15.5 |
| 125 | 9 | 22.0 | 3.86 | 5.48 | 17.3 |
| 140 | 9 | 24.7 | 4.34 | 6.09 | 19.4 |
| 140 | 10 | 27.3 | 4.33 | 6.11 | 21.5 |
| 160 | 10 | 31.4 | 4.96 | 6.91 | 24.7 |
| 160 | 11 | 34.4 | 4.95 | 6.93 | 27.0 |
| 160 | 16 | 49.1 | 4.89 | 7.03 | 38.5 |
| 180 | 11 | 38.8 | 5.60 | 7.74 | 30.5 |
| 180 | 12 | 42.2 | 5.59 | 7.76 | 33.1 |
| 200 | 12 | 47.1 | 6.22 | 8.55 | 37.0 |
| 200 | 14 | 54.6 | 6.20 | 8.60 | 42.8 |
| 200 | 16 | 62.0 | 6.17 | 8.64 | 48.7 |
| 220 | 16 | 68.6 | 6.81 | 9.42 | 53.8 |
| 250 | 16 | 78.4 | 7.76 | 10.6 | 61.5 |
| 250 | 20 | 97.0 | 7.71 | 10.7 | 76.1 |
| Diameter of the Cable, cm | Cross-Section Area, cm2 | Mass of the Cable (1 m), kg | Breaking Force of the Cable, kN |
|---|---|---|---|
| 3.8 | 6.61 | 5.86 | 907.5 |
| 4.2 | 8.15 | 7.24 | 1120 |
| 4.6 | 9.87 | 8.75 | 1350 |
| 5.1 | 11.74 | 10.45 | 1610 |
| 5.5 | 13.81 | 12.25 | 1895 |
| 5.9 | 16.01 | 14.20 | 2200 |
| 6.3 | 18.37 | 16.30 | 2525 |
| 6.8 | 20.90 | 18.55 | 2825 |
| Joints | X | Y | Joints | X | Y |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 9 | 15 | 1.5 |
| 2 | 3 | 2.1 | 10 | 18 | 3.9 |
| 3 | 6 | 2.7 | 11 | 21 | 3.3 |
| 4 | 9 | 3.3 | 12 | 24 | 2.7 |
| 5 | 12 | 3.9 | 13 | 27 | 2.1 |
| 6 | 15 | 4.5 | 14 | 30 | 0 |
| 7 | 3 | −0.9 | 15 | 21 | 0.3 |
| 8 | 9 | 0.3 | 16 | 27 | −0.9 |
| Bars | Joint (i) | Joint (j) | Bars | Joint (i) | Joint (j) |
|---|---|---|---|---|---|
| 1 | 1 | 2 | 16 | 6 | 10 |
| 2 | 2 | 3 | 17 | 10 | 11 |
| 3 | 3 | 4 | 18 | 11 | 12 |
| 4 | 4 | 5 | 19 | 12 | 13 |
| 5 | 5 | 6 | 20 | 13 | 14 |
| 6 | 1 | 7 | 21 | 9 | 15 |
| 7 | 7 | 8 | 22 | 15 | 16 |
| 8 | 8 | 9 | 23 | 16 | 14 |
| 9 | 7 | 2 | 24 | 15 | 11 |
| 10 | 8 | 4 | 25 | 16 | 13 |
| 11 | 9 | 6 | 26 | 9 | 10 |
| 12 | 7 | 3 | 27 | 10 | 15 |
| 13 | 3 | 8 | 28 | 15 | 12 |
| 14 | 8 | 5 | 29 | 12 | 16 |
| 15 | 5 | 9 | 30 | 1 | 14 |
| Span—24 m | Span—27 m | Span—30 m | Span—33 m | |||||||||
| Itr. | Weight | P0 | Time | Weight | P0 | Time | Weight | P0 | Time | Weight | P0 | Time |
| 1 | 2.3903 | 200 | 118.553 | 2.3903 | 200 | 118.553 | 2.3903 | 200 | 118.553 | 2.3903 | 200 | 118.553 |
| 2 | 2.3903 | 200 | 220.806 | 2.3903 | 200 | 220.806 | 2.3903 | 200 | 220.806 | 2.3903 | 200 | 220.806 |
| 3 | 2.3903 | 200 | 108.674 | 2.3903 | 200 | 108.674 | 2.3903 | 200 | 108.674 | 2.3903 | 200 | 108.674 |
| 4 | 3.0042 | 890 | 117.505 | 3.0042 | 890 | 117.505 | 3.0042 | 890 | 117.505 | 3.0042 | 890 | 117.505 |
| 5 | 2.3903 | 200 | 167.809 | 2.3903 | 200 | 167.809 | 2.3903 | 200 | 167.809 | 2.3903 | 200 | 167.809 |
| 6 | 2.7126 | 570 | 241.135 | 2.7126 | 570 | 241.135 | 2.7126 | 570 | 241.135 | 2.7126 | 570 | 241.135 |
| 7 | 2.3903 | 200 | 220.899 | 2.3903 | 200 | 220.899 | 2.3903 | 200 | 220.899 | 2.3903 | 200 | 220.899 |
| 8 | 2.3903 | 200 | 206.569 | 2.3903 | 200 | 206.569 | 2.3903 | 200 | 206.569 | 2.3903 | 200 | 206.569 |
| 9 | 2.5488 | 380 | 146.296 | 2.5488 | 380 | 146.296 | 2.5488 | 380 | 146.296 | 2.5488 | 380 | 146.296 |
| Span—36 m | Span—39 m | Span—42 m | Span—45 m | |||||||||
| Itr. | Weight | P0 | Time | Weight | P0 | Time | Weight | P0 | Time | Weight | P0 | Time |
| 1 | 2.3903 | 200 | 118.553 | 2.3903 | 200 | 118.553 | 2.3903 | 200 | 118.553 | - | - | - |
| 2 | 2.3903 | 200 | 220.806 | 2.3903 | 200 | 220.806 | 2.3903 | 200 | 220.806 | - | - | - |
| 3 | 2.3903 | 200 | 108.674 | 2.3903 | 200 | 108.674 | 2.3903 | 200 | 108.674 | - | - | - |
| 4 | 3.0042 | 890 | 117.505 | 3.0042 | 890 | 117.505 | 3.0042 | 890 | 117.505 | - | - | - |
| 5 | 2.3903 | 200 | 167.809 | 2.3903 | 200 | 167.809 | 2.3903 | 200 | 167.809 | - | - | - |
| 6 | 2.7126 | 570 | 241.135 | 2.7126 | 570 | 241.135 | 2.7126 | 570 | 241.135 | - | - | - |
| 7 | 2.3903 | 200 | 220.899 | 2.3903 | 200 | 220.899 | 2.3903 | 200 | 220.899 | - | - | - |
| 8 | 2.3903 | 200 | 206.569 | 2.3903 | 200 | 206.569 | 2.3903 | 200 | 206.569 | - | - | - |
| 9 | 2.5488 | 380 | 146.296 | 2.5488 | 380 | 146.296 | 2.5488 | 380 | 146.296 | - | - | - |
| Nodal Force—15 kN | Nodal Force—20 kN | Nodal Force—25 kN | Nodal Force—30 kN | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Itr. | Weight | P0 | Time | Weight | P0 | Time | Weight | P0 | Time | Weight | P0 | Time |
| 1 | 4.4736 | 280 | 238.436 | 5.1709 | 440 | 118.123 | 5.8186 | 650 | 113 | 6.4201 | 660 | - |
| 2 | 4.4832 | 270 | 187.765 | 5.1351 | 380 | 198.251 | 5.8907 | 440 | - | 6.4864 | 650 | - |
| 3 | 4.4928 | 280 | 270.759 | 5.1231 | 400 | 184.268 | 5.8917 | 430 | - | 6.6117 | 870 | - |
| 4 | 4.4892 | 280 | 247.101 | 5.1231 | 400 | 167.945 | 5.8186 | 630 | - | 6.4793 | 630 | - |
| 5 | 4.8831 | 640 | 196.089 | 5.1542 | 430 | 152.751 | 5.8186 | 630 | 124 | 6.6192 | 870 | - |
| 6 | 4.4736 | 270 | 174.967 | 5.1231 | 400 | 224.255 | 5.9131 | 370 | 164 | 6.4121 | 660 | - |
| 7 | 4.4867 | 280 | 238.909 | 5.1231 | 400 | 204.561 | 5.8158 | 620 | 116 | 6.6117 | 870 | - |
| 8 | 4.4747 | 280 | 190.498 | 5.1446 | 370 | 125.209 | 5.8248 | 640 | 115 | 6.4756 | 610 | - |
| 9 | 4.5094 | 320 | 163.796 | 5.1231 | 400 | 198.452 | 5.8214 | 630 | 132 | 6.4675 | 610 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Partskhaladze, G.; Alcala, J.; Medzmariashvili, E.; Chavleshvili, G.; Surguladze, B.; Yepes, V. Heuristic Optimization of a New Type of Prestressed Arched Truss. Materials 2022, 15, 8144. https://doi.org/10.3390/ma15228144
Partskhaladze G, Alcala J, Medzmariashvili E, Chavleshvili G, Surguladze B, Yepes V. Heuristic Optimization of a New Type of Prestressed Arched Truss. Materials. 2022; 15(22):8144. https://doi.org/10.3390/ma15228144
Chicago/Turabian StylePartskhaladze, Gaioz, Julian Alcala, Elguja Medzmariashvili, Gocha Chavleshvili, Bichiko Surguladze, and Víctor Yepes. 2022. "Heuristic Optimization of a New Type of Prestressed Arched Truss" Materials 15, no. 22: 8144. https://doi.org/10.3390/ma15228144
APA StylePartskhaladze, G., Alcala, J., Medzmariashvili, E., Chavleshvili, G., Surguladze, B., & Yepes, V. (2022). Heuristic Optimization of a New Type of Prestressed Arched Truss. Materials, 15(22), 8144. https://doi.org/10.3390/ma15228144








