Supportless Lattice Structure for Additive Manufacturing of Functional Products and the Evaluation of Its Mechanical Property at Variable Strain Rates
Abstract
1. Introduction
2. Materials and Methods
2.1. Design of Supportless Lattice Structure
2.2. Materials
2.3. Support-Free Additive Manufacturing of Lattice Structure
2.4. Compression Test
3. Results and Discussion
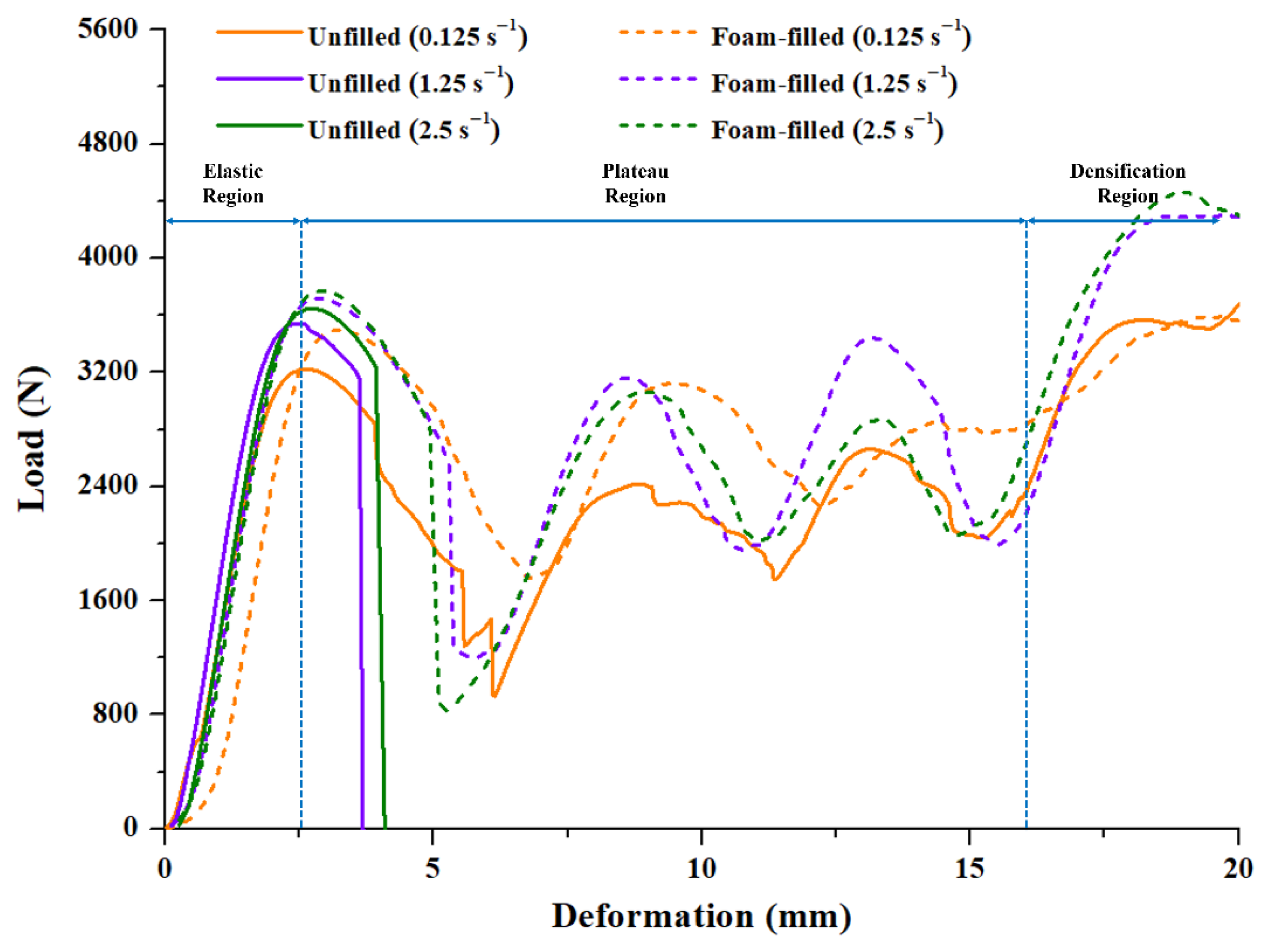
3.1. Variable Strain Rate Compression Testing
3.2. Case Study
4. Conclusions
- Variable strain rate analysis showed that failure of unfilled lattice structures changes from elastic–plastic to brittle with an increase in strain rate. The addition of PU foam improves the resilience of the lattice structure and provides the necessary toughness at higher strain rates.
- At the strain rate of 0.125 s−1 EA increases from 42.15 J to 54.42 J with the addition of foam, whereas at higher strain rates of 1.25 s−1 and 2.5 s−1, EA increases from 9.015 J to 55.85 J and 9.851 J to 57.12 J, respectively.
- Consequently, CFE at 0.125 s−1 increases from 65.41% to 77.85% with foam-filling, whereas at higher strain rates of 1.25 s−1 and 2.5 s−1, CFE increases from 12.72% to 75.1% and 13.5% to 75.7%, respectively.
- Visual inspection showed that all the bottles successfully fit in the designed universal puck without any wobble or dropping of the bottles.
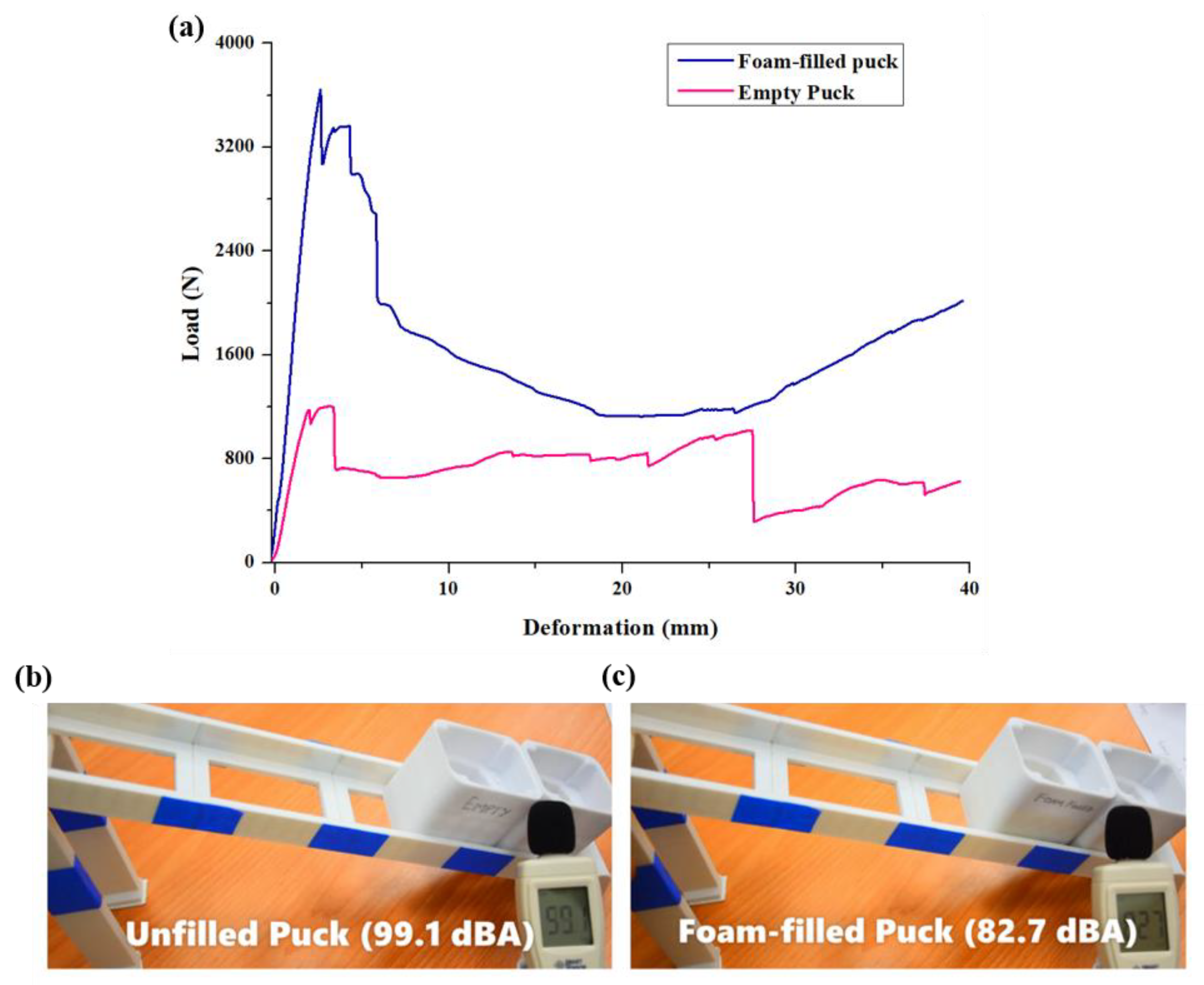
- Mechanical and noise absorption testing of the universal pucks showed that foam-filled pucks have a 133% increase in stiffness, 126% increase in energy absorption and 16.5% noise reduction than unfilled pucks.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Scherer, F.M. Economics of Innovation and Technological Change. In International Encyclopedia of the Social & Behavioral Sciences; Pergamon: Oxford, UK, 2001; pp. 7530–7536. [Google Scholar]
- Ittner, C.D.; Larcker, D.F. Product Development Cycle Time and Organizational Performance. J. Mark. Res. 1997, 34, 13–23. [Google Scholar] [CrossRef]
- Wohlers, T.; Gornet, T. Wohlers Report 2014. History of Additive Manufacturing. 2017, pp. 1–24. Available online: wohlersassociates.com (accessed on 4 October 2022).
- du Plessis, A.; Broeckhoven, C.; Yadroitsava, I.; Yadroitsev, I.; Hands, C.H.; Kunju, R.; Bhate, D. Beautiful and Functional: A Review of Biomimetic Design in Additive Manufacturing. Addit. Manuf. 2019, 27, 408–427. [Google Scholar] [CrossRef]
- Orme, M.E.; Gschweitl, M.; Ferrari, M.; Madera, I.; Mouriaux, F. Designing for Additive Manufacturing: Lightweighting through Topology Optimization Enables Lunar Spacecraft. J. Mech. Des. 2017, 139, 100905. [Google Scholar] [CrossRef]
- Veiga, F.; Suárez, A.; Aldalur, E.; Goenaga, I.; Amondarain, J. Wire Arc Additive Manufacturing Process for Topologically Optimized Aeronautical Fixtures. 3D Print. Addit. Manuf. 2021. [Google Scholar] [CrossRef]
- Veiga, F.; Bhujangrao, T.; Suárez, A.; Aldalur, E.; Goenaga, I.; Gil-Hernandez, D. Validation of the Mechanical Behavior of an Aeronautical Fixing Turret Produced by a Design for Additive Manufacturing (DfAM). Polymers 2022, 14, 2177. [Google Scholar] [CrossRef]
- Abe, T.; Sasahara, H. Layer Geometry Control for the Fabrication of Lattice Structures by Wire and Arc Additive Manufacturing. Addit. Manuf. 2019, 28, 639–648. [Google Scholar] [CrossRef]
- Lin, K.; Yuan, L.; Gu, D. Influence of Laser Parameters and Complex Structural Features on the Bio-Inspired Complex Thin-Wall Structures Fabricated by Selective Laser Melting. J. Mater. Process. Technol. 2019, 267, 34–43. [Google Scholar] [CrossRef]
- Kladovasilakis, N.; Tsongas, K.; Karalekas, D.; Tzetzis, D. Architected Materials for Additive Manufacturing: A Comprehensive Review. Materials 2022, 15, 5919. [Google Scholar] [CrossRef] [PubMed]
- Helou, M.; Kara, S. Design, Analysis and Manufacturing of Lattice Structures: An Overview. Int. J. Comput. Integr. Manuf. 2018, 31, 243–261. [Google Scholar] [CrossRef]
- Nazir, A.; Abate, K.M.; Kumar, A.; Jeng, J.Y. A State-of-the-Art Review on Types, Design, Optimization, and Additive Manufacturing of Cellular Structures. Int. J. Adv. Manuf. Technol. 2019, 104, 3489–3510. [Google Scholar] [CrossRef]
- An, X.; Lai, C.; He, W.; Fan, H. Three-Dimensional Meta-Truss Lattice Composite Structures with Vibration Isolation Performance. Extrem. Mech. Lett. 2019, 33, 100577. [Google Scholar] [CrossRef]
- An, X.; Lai, C.; He, W.; Fan, H. Three-Dimensional Chiral Meta-Plate Lattice Structures for Broad Band Vibration Suppression and Sound Absorption. Compos. Part B Eng. 2021, 224, 109232. [Google Scholar] [CrossRef]
- Wang, S.; Wang, J.; Xu, Y.; Zhang, W.; Zhu, J. Compressive Behavior and Energy Absorption of Polymeric Lattice Structures Made by Additive Manufacturing. Front. Mech. Eng. 2020, 15, 319–327. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, D.; Liu, F.; Li, Z.; Ma, Z.; Ren, Z. Mechanical and Energy Absorption Characteristics of Additively Manufactured Functionally Graded Sheet Lattice Structures with Minimal Surfaces. Int. J. Mech. Sci. 2020, 167, 105262. [Google Scholar] [CrossRef]
- Sur, A.; Narkhede, S.; Darvekar, S. Applications, Manufacturing and Thermal Characteristics of Micro-Lattice Structures: Current State of the Art. Eng. J. 2019, 23, 419–431. [Google Scholar] [CrossRef]
- Sajjad, U.; Rehman, T.; Ali, M.; Park, C.W.; Yan, W.-M. Manufacturing and Potential Applications of Lattice Structures in Thermal Systems: A Comprehensive Review of Recent Advances. Int. J. Heat Mass Transf. 2022, 198, 123352. [Google Scholar] [CrossRef]
- Solomon, I.J.; Sevvel, P.; Gunasekaran, J. A Review on the Various Processing Parameters in FDM. Mater. Today Proc. 2021, 37, 509–514. [Google Scholar] [CrossRef]
- Jiang, J.; Xu, X.; Stringer, J. Support Structures for Additive Manufacturing: A Review. J. Manuf. Mater. Process. 2018, 2, 64. [Google Scholar] [CrossRef]
- Boyard, N.; Christmann, O.; Rivette, M.; Kerbrat, O.; Richir, S. Support Optimization for Additive Manufacturing: Application to FDM. Rapid Prototyp. J. 2018, 24, 69–79. [Google Scholar] [CrossRef]
- Kumar, A.; Verma, S.; Jeng, J.Y. Supportless Lattice Structures for Energy Absorption Fabricated by Fused Deposition Modeling. 3D Print. Addit. Manuf. 2020, 7, 85–96. [Google Scholar] [CrossRef]
- Coupek, D.; Friedrich, J.; Battran, D.; Riedel, O. Reduction of Support Structures and Building Time by Optimized Path Planning Algorithms in Multi-Axis Additive Manufacturing. Procedia CIRP 2018, 67, 221–226. [Google Scholar] [CrossRef]
- Wulle, F.; Coupek, D.; Schäffner, F.; Verl, A.; Oberhofer, F.; Maier, T. Workpiece and Machine Design in Additive Manufacturing for Multi-Axis Fused Deposition Modeling. Procedia CIRP 2017, 60, 229–234. [Google Scholar] [CrossRef]
- Verma, S.; Kumar, A.; Lin, S.C.; Jeng, J.Y. A Bio-Inspired Design Strategy for Easy Powder Removal in Powder-Bed Based Additive Manufactured Lattice Structure. Virtual Phys. Prototyp. 2022, 17, 468–488. [Google Scholar] [CrossRef]
- Prajapati, M.J.; Kumar, A.; Lin, S.C.; Jeng, J.Y. Multi-Material Additive Manufacturing with Lightweight Closed-Cell Foam-Filled Lattice Structures for Enhanced Mechanical and Functional Properties. Addit. Manuf. 2022, 54, 102766. [Google Scholar] [CrossRef]
- Kumar, A.; Collini, L.; Daurel, A.; Jeng, J.Y. Design and Additive Manufacturing of Closed Cells from Supportless Lattice Structure. Addit. Manuf. 2020, 33, 101168. [Google Scholar] [CrossRef]
- Papacharalampopoulos, A.; Karapiperi, A.; Stavropoulos, P. Humanitarian Engineering Design Methodology for AM Metallic Products: A Smart Mobility Platform Case. Procedia CIRP 2020, 97, 59–65. [Google Scholar] [CrossRef]
- Parhofer, C.A.W.; Pancheri, F.; Lueth, T.C. Passive Instrument Holder for Collaborative Robotic Nursing Applications—Automatically Designed and 3D-Printed. In Proceedings of the 2021 IEEE International Conference on Robotics and Biomimetics, ROBIO 2021, Sanya, China, 27–31 December 2021; pp. 1240–1245. [Google Scholar]
- Scaccabarozzi, D.; Saggin, B.; Magni, M.; Valnegri, P.; Corti, M.G.; Palomba, E.; Longobardo, A.; Dirri, F.; Zampetti, E. Design of 3D Printed Holder for Quartz Crystal Microbalances. In Proceedings of the 2021 IEEE 8th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Naples, Italy, 23–25 June 2021; pp. 715–719. [Google Scholar] [CrossRef]
- Kumar, A.; Collini, L.; Ursini, C.; Jeng, J.-Y. Energy Absorption and Stiffness of Thin and Thick-Walled Closed-Cell 3D-Printed Structures Fabricated from a Hyperelastic Soft Polymer. Materials 2022, 15, 2441. [Google Scholar] [CrossRef] [PubMed]
- Diegel, O.; Nordin, A.; Damien, M. A Practical Guide to Design for Additive Manufacturing; Springer Series in Advanced Manufacturing; Springer: Singapore, 2019; ISBN 978-981-13-8281-9. [Google Scholar]
- Alafaghani, A.; Qattawi, A.; Ablat, M.A. Design Consideration for Additive Manufacturing: Fused Deposition Modelling. Open J. Appl. Sci. 2017, 7, 291–318. [Google Scholar] [CrossRef]
- Bikas, H.; Lianos, A.K.; Stavropoulos, P. A Design Framework for Additive Manufacturing. Int. J. Adv. Manuf. Technol. 2019, 103, 3769–3783. [Google Scholar] [CrossRef]
- Bhat, C.; Kumar, A.; Jeng, J.-Y. Effect of Atomic Tessellations on Structural and Functional Properties of Additive Manufactured Lattice Structures. Addit. Manuf. 2021, 47, 102326. [Google Scholar] [CrossRef]
- Bhat, C.; Kumar, A.; Lin, S.C.; Jeng, J.Y. A Novel Bioinspired Architectured Materials with Interlocking Designs Based on Tessellation. Addit. Manuf. 2022, 58, 103052. [Google Scholar] [CrossRef]
- ASTM D638-14; Standard Test Method for Tensile Properties of Plastics. ASTM International: West Conshohocken, PA, USA, 2015.
- ISO 3386-1; Polymeric Materials, Cellular Flexible—Determination of Stress-Strain Characteristics in Compression—Part 1: Low-Density Materials. ISO: Geneva, Switzerland, 1986.
- Abedi, M.M.; Jafari Nedoushan, R.; Sheikhzadeh, M.; Yu, W.R. The Crashworthiness Performance of Thin-Walled Ultralight Braided Lattice Composite Columns: Experimental and Finite Element Study. Compos. Part B Eng. 2020, 202, 108413. [Google Scholar] [CrossRef]
- Wang, H.; Tan, D.; Liu, Z.; Yin, H.; Wen, G. On Crashworthiness of Novel Porous Structure Based on Composite TPMS Structures. Eng. Struct. 2022, 252, 113640. [Google Scholar] [CrossRef]
- Baykasoğlu, A.; Baykasoğlu, C.; Cetin, E. Multi-Objective Crashworthiness Optimization of Lattice Structure Filled Thin-Walled Tubes. Thin-Walled Struct. 2020, 149, 106630. [Google Scholar] [CrossRef]
- Sawyer, M. The Economics of Industries and Firms; Routledge: London, UK, 1985. [Google Scholar] [CrossRef]
- Gharechahi, J.; Asadzadeh, N.; Shahabian, F.; Gharechahi, M. Dimensional Changes of Acrylic Resin Denture Bases: Conventional versus Injection-Molding Technique. J. Dent. 2014, 11, 398–405. [Google Scholar]
- Seow, L.W.; Lam, Y.C. Optimizing Flow in Plastic Injection Molding. J. Mater. Process. Technol. 1997, 72, 333–341. [Google Scholar] [CrossRef]
- Lin, J.H.; Lin, C.M.; Huang, C.C.; Lin, C.C.; Hsieh, C.T.; Liao, Y.C. Evaluation of the Manufacture of Sound Absorbent Sandwich Plank Made of PET/TPU Honeycomb Grid/PU Foam. J. Compos. Mater. 2011, 45, 1355–1362. [Google Scholar] [CrossRef]
- Eleftheriou, P.C. Industrial Noise and Its Effects on Human Hearing. Appl. Acoust. 2002, 63, 35–42. [Google Scholar] [CrossRef]

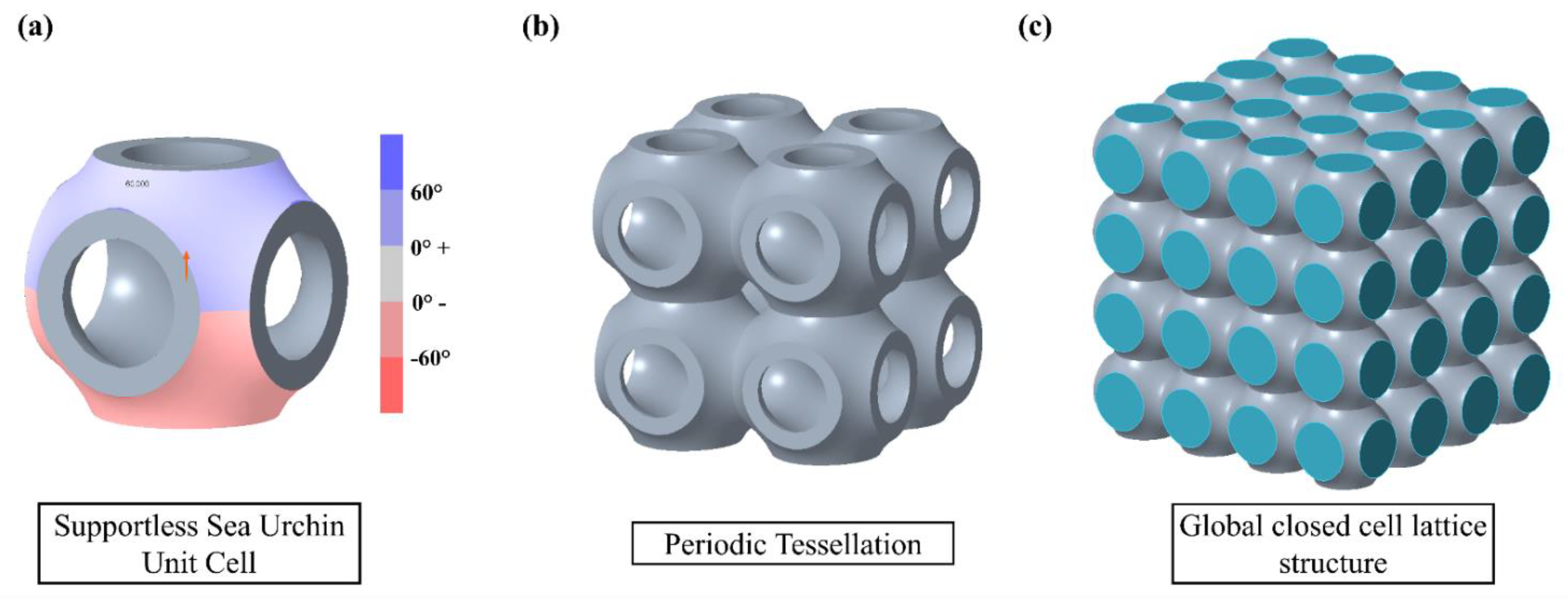


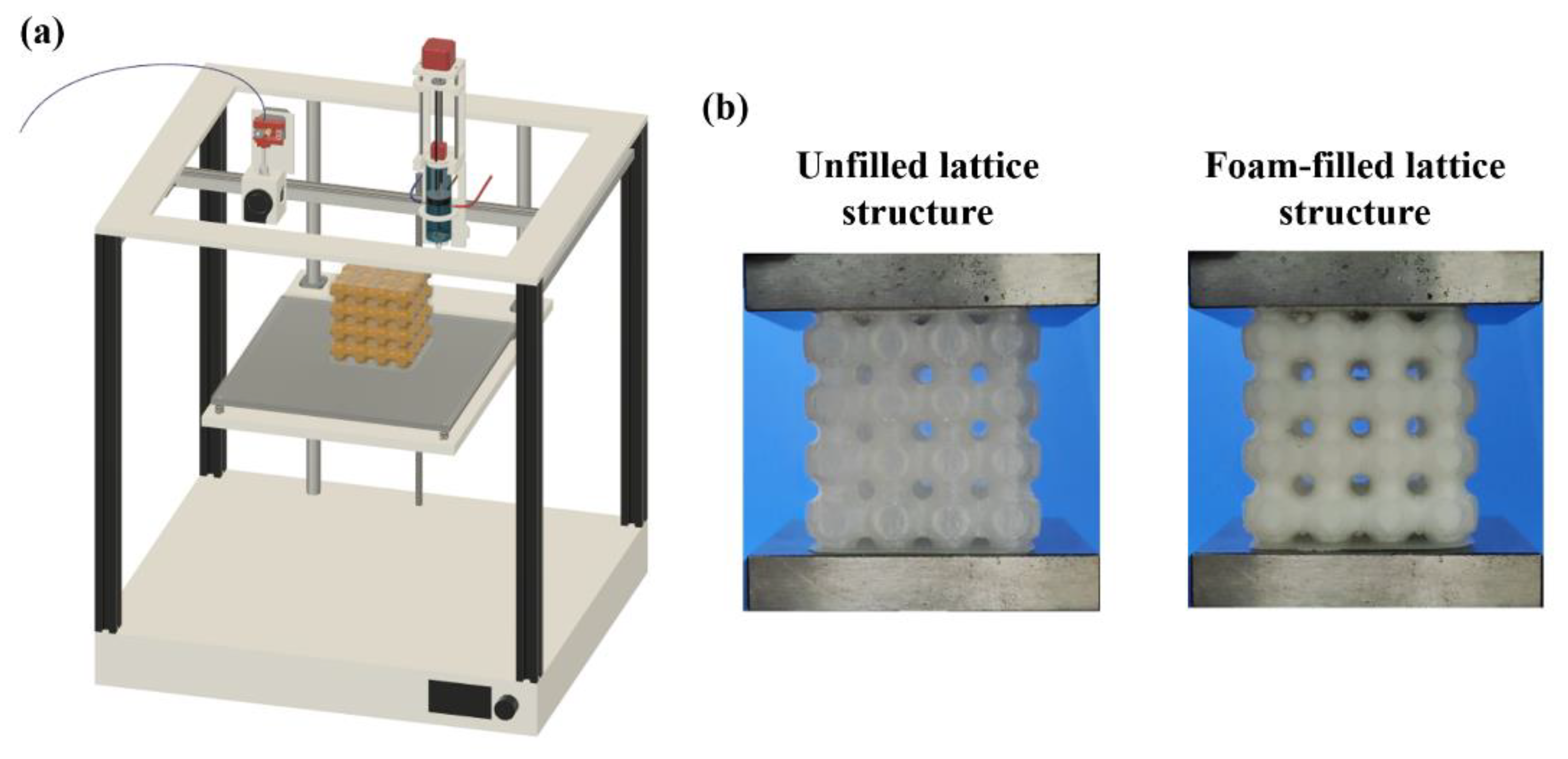

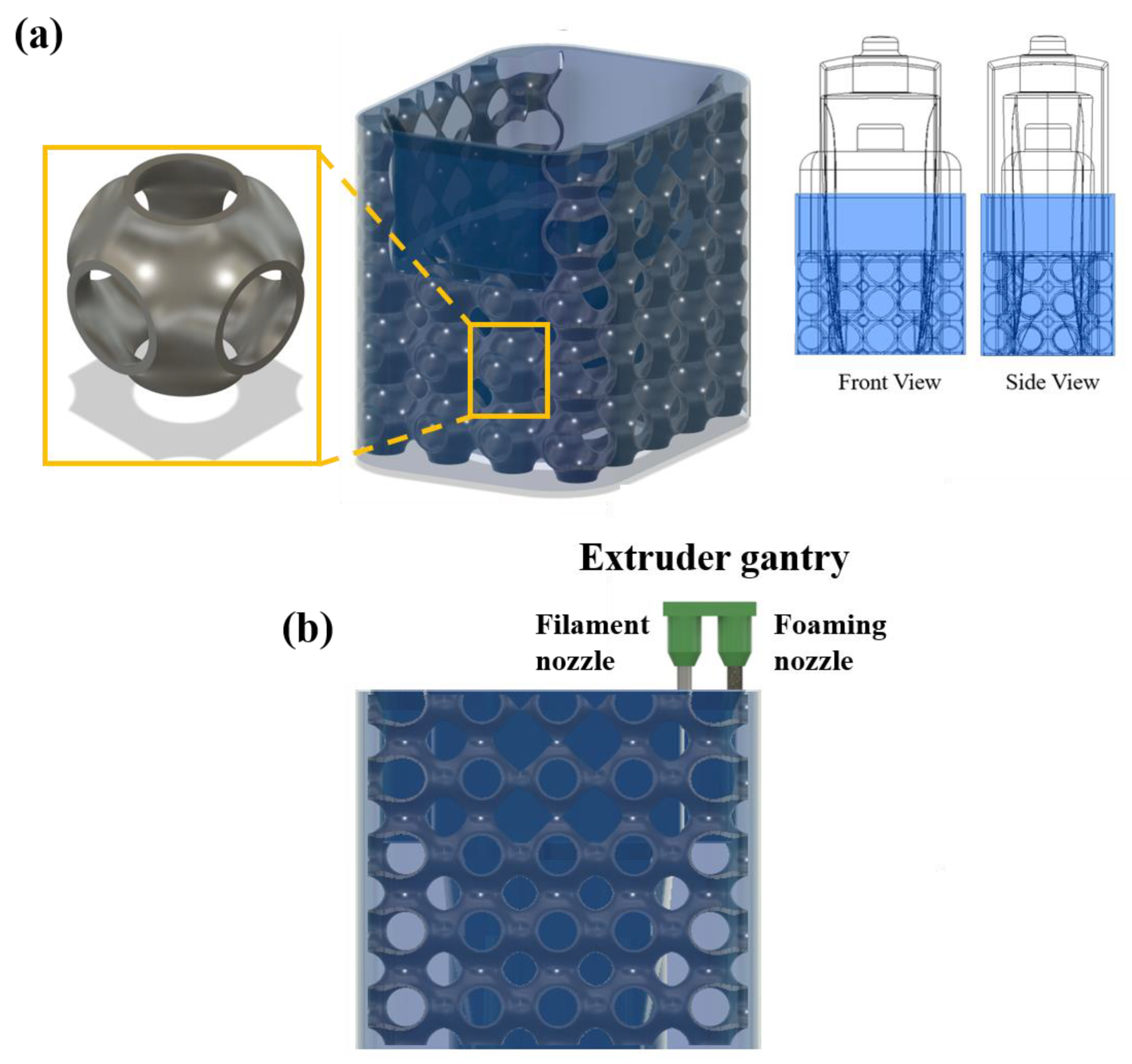


| Primary Cell Structure | Primary Material | Relative Density (RD) | Shell Thickness ‘Ts’ = (r1 − r2) (mm) | Membrane Thickness ‘Mt’ (mm) | Secondary Filled Material |
|---|---|---|---|---|---|
| Global closed sea urchin lattice structure | PETG | 19% | 0.5 | 0.5 | PU Foam |
| Nozzle Diameter (mm) | Printing Temperature (°C) | Bed Temperature (°C) | Layer Height (mm) | Print Infill (%) | Printing Speed (mm/s) |
|---|---|---|---|---|---|
| 0.4 | 220 | 60 | 0.2 | 100 | 90 |
| Strain Rate (s−1) | Energy Absorption (J) | Specific Energy Absorption (J/g) | Peak Force (kN) | Mean Force (kN) | Crash Force Efficiency | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Unfilled | Foam-Filled | Unfilled | Foam-Filled | Unfilled | Foam-Filled | Unfilled | Foam-Filled | Unfilled | Foam-Filled | |
| 0.125 | 42.15 | 54.42 | 2.4 | 2.62 | 3.22 | 3.49 | 2.11 | 2.72 | 65.41 | 77.85 |
| 1.25 | 9.015 | 55.85 | 0.52 | 2.68 | 3.54 | 3.72 | 0.45 | 2.8 | 12.72 | 75.1 |
| 2.5 | 9.851 | 57.12 | 0.56 | 2.75 | 3.65 | 3.77 | 0.49 | 2.86 | 13.5 | 75.7 |
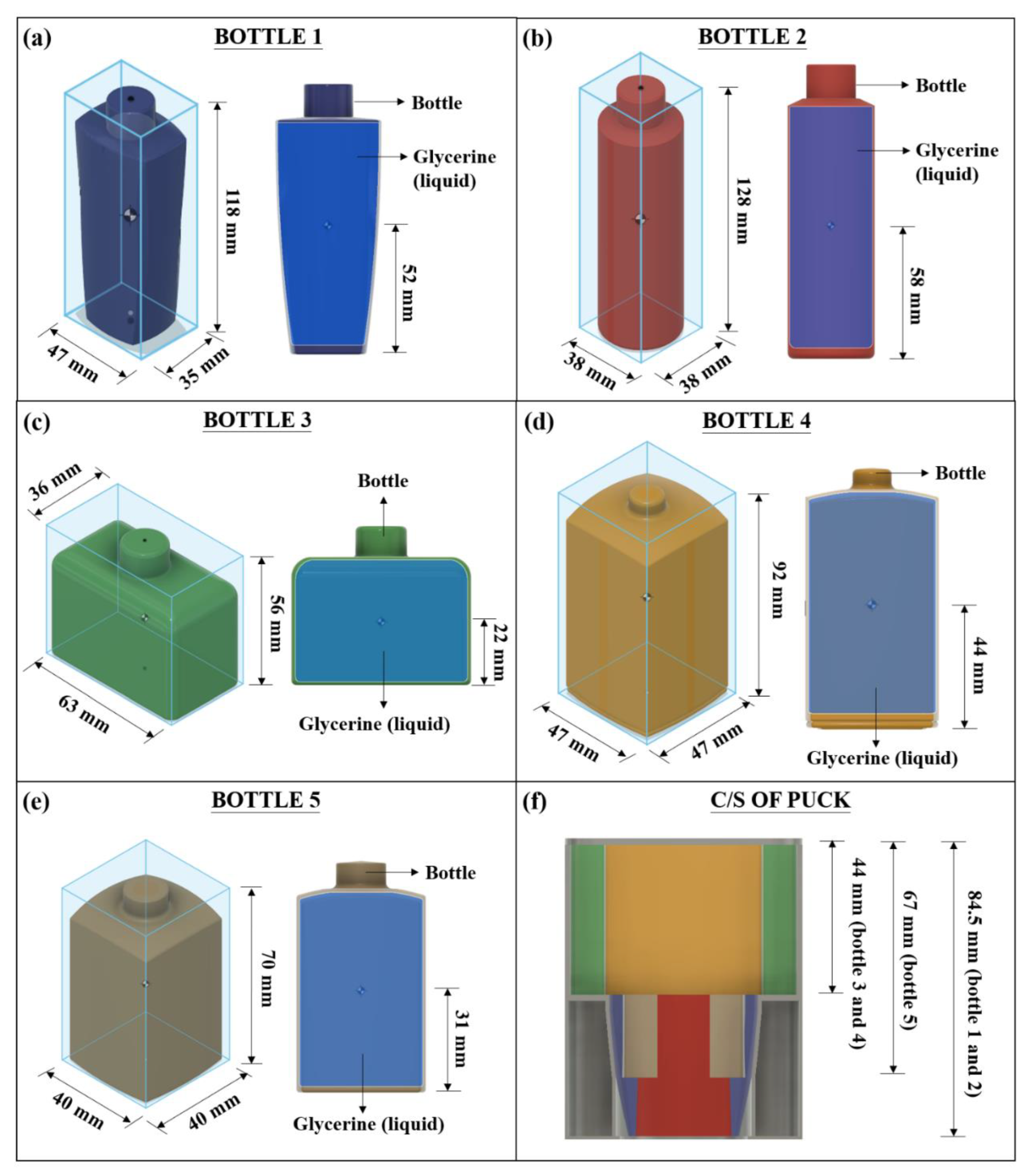
| Bottle Number | Center of Mass (mm) | Accommodating Height in Puck (mm) | Difference (mm) |
|---|---|---|---|
| 1 | 52 | 84.5 | 32.5 |
| 2 | 58 | 84.5 | 26.5 |
| 3 | 22 | 44 | 22 |
| 4 | 44 | 44 | 0 |
| 5 | 31 | 67 | 36 |
| Universal Puck | Printing + Post-Processing Time (min) | Initial Stiffness (N/mm) | Peak Load (N) | Energy Absorption (J) | Collision Noise (dBA) |
|---|---|---|---|---|---|
| Empty puck | 353 | 700 | 1197 | 28.56 | 99.1 |
| Foam filled | 362 | 1631 | 3439 | 64.76 | 82.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prajapati, M.J.; Bhat, C.; Kumar, A.; Verma, S.; Lin, S.-C.; Jeng, J.-Y. Supportless Lattice Structure for Additive Manufacturing of Functional Products and the Evaluation of Its Mechanical Property at Variable Strain Rates. Materials 2022, 15, 7954. https://doi.org/10.3390/ma15227954
Prajapati MJ, Bhat C, Kumar A, Verma S, Lin S-C, Jeng J-Y. Supportless Lattice Structure for Additive Manufacturing of Functional Products and the Evaluation of Its Mechanical Property at Variable Strain Rates. Materials. 2022; 15(22):7954. https://doi.org/10.3390/ma15227954
Chicago/Turabian StylePrajapati, Mayur Jiyalal, Chinmai Bhat, Ajeet Kumar, Saurav Verma, Shang-Chih Lin, and Jeng-Ywan Jeng. 2022. "Supportless Lattice Structure for Additive Manufacturing of Functional Products and the Evaluation of Its Mechanical Property at Variable Strain Rates" Materials 15, no. 22: 7954. https://doi.org/10.3390/ma15227954
APA StylePrajapati, M. J., Bhat, C., Kumar, A., Verma, S., Lin, S.-C., & Jeng, J.-Y. (2022). Supportless Lattice Structure for Additive Manufacturing of Functional Products and the Evaluation of Its Mechanical Property at Variable Strain Rates. Materials, 15(22), 7954. https://doi.org/10.3390/ma15227954