A Gaussian to Vector Vortex Beam Generator with a Programmable State of Polarization
Abstract
1. Introduction
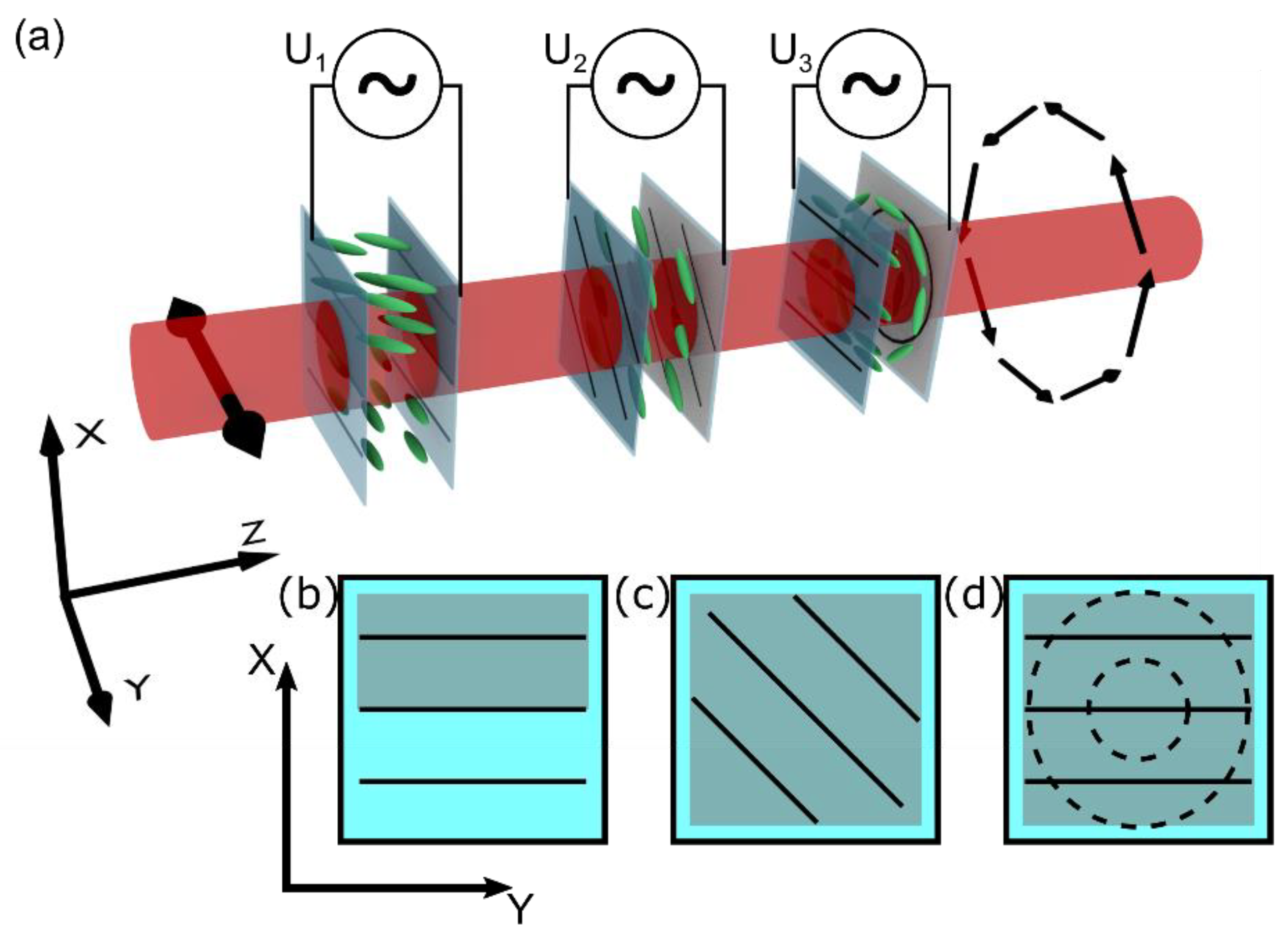
2. Materials and Methods
3. Results
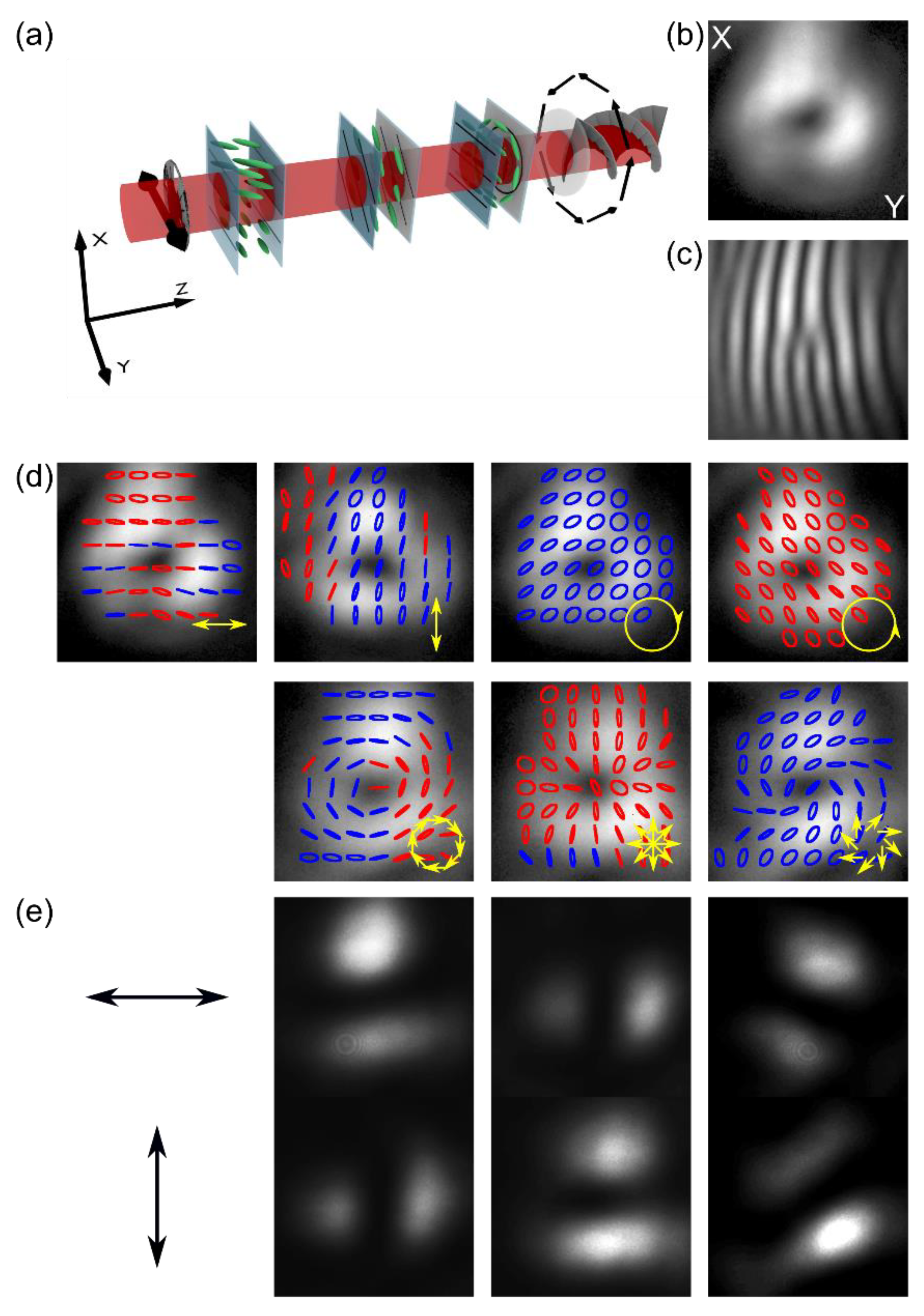
3.1. NLC Polarization Converter
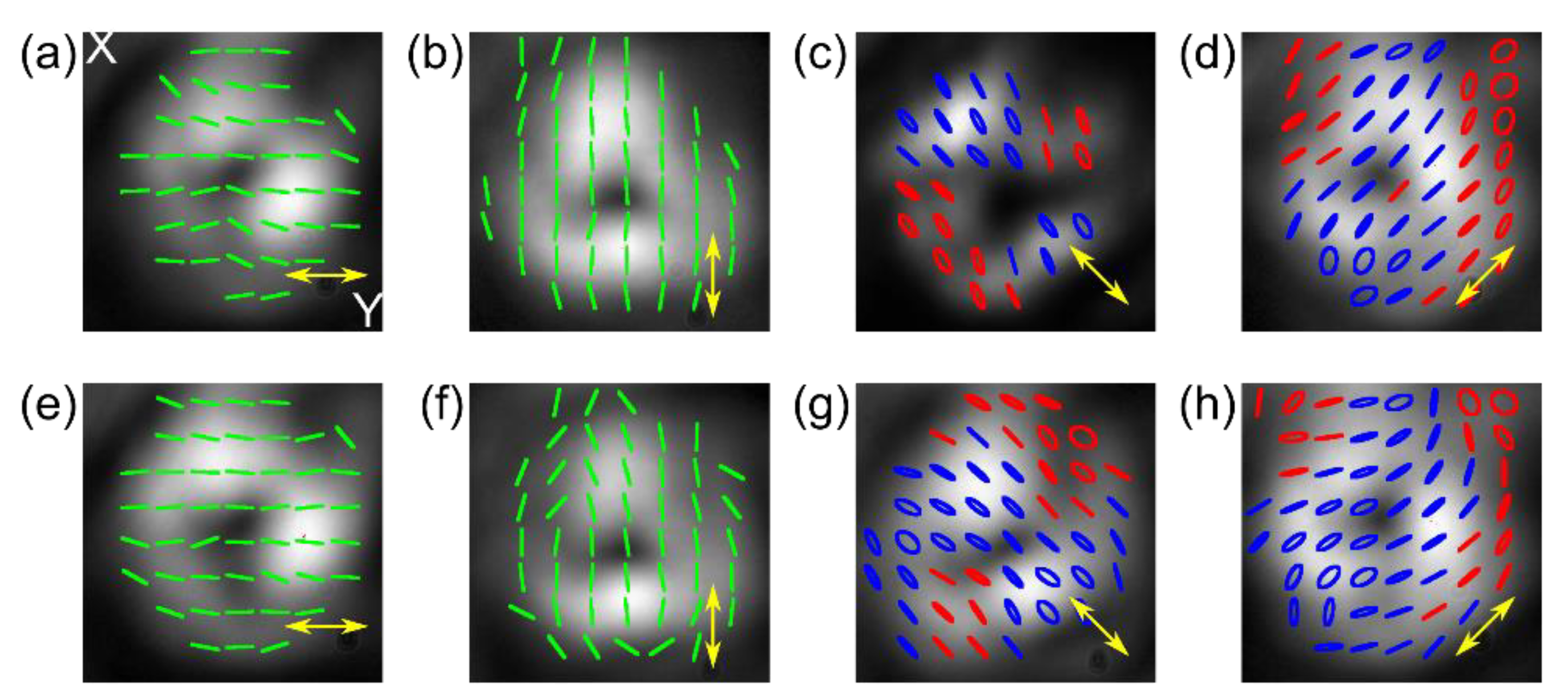
3.2. Polarization and Phase Conversion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T.; et al. Roadmap on Structured Light. J. Opt. 2017, 19, 013001. [Google Scholar] [CrossRef]
- Yao, A.M.; Padgett, M.J. Orbital Angular Momentum: Origins, Behavior and Applications. Adv. Opt. Photon. AOP 2011, 3, 161–204. [Google Scholar] [CrossRef]
- Soskin, M.; Vasnetsov, M. Chapter 4—Singular Optics. Prog. Opt. 2001, 42, 219–276. [Google Scholar] [CrossRef]
- Zhan, Q. Cylindrical Vector Beams: From Mathematical Concepts to Applications. Adv. Opt. Photon. AOP 2009, 1, 1–57. [Google Scholar] [CrossRef]
- Brown, T.G. Unconventional polarization states: Beam propagation, focusing, and imaging. In Progress in Optics; Elsevier: Amsterdam, The Netherlands, 2011; Volume 56, pp. 81–129. [Google Scholar] [CrossRef]
- Quabis, S.; Dorn, R.; Eberler, M.; Glöckl, O.; Leuchs, G. Focusing Light to a Tighter Spot. Opt. Commun. 2000, 179, 1–7. [Google Scholar] [CrossRef]
- Hell, S.W. Far-Field Optical Nanoscopy. Science 2007, 316, 1153–1158. [Google Scholar] [CrossRef]
- Wang, H.; Shi, L.; Lukyanchuk, B.; Sheppard, C.; Chong, C.T. Creation of a Needle of Longitudinally Polarized Light in Vacuum Using Binary Optics. Nat. Photon 2008, 2, 501–505. [Google Scholar] [CrossRef]
- Kitamura, K.; Nishimoto, M.; Sakai, K.; Noda, S. Needle-like Focus Generation by Radially Polarized Halo Beams Emitted by Photonic-Crystal Ring-Cavity Laser. Appl. Phys. Lett. 2012, 101, 221103. [Google Scholar] [CrossRef]
- Chen, P.; Wei, B.-Y.; Ji, W.; Ge, S.-J.; Hu, W.; Xu, F.; Chigrinov, V.; Lu, Y.-Q. Arbitrary and Reconfigurable Optical Vortex Generation: A High-Efficiency Technique Using Director-Varying Liquid Crystal Fork Gratings. Photon. Res. 2015, 3, 133. [Google Scholar] [CrossRef]
- Chen, P.; Lu, Y.-Q.; Hu, W. Beam Shaping via Photopatterned Liquid Crystals. Liq. Cryst. 2016, 43, 2051–2061. [Google Scholar] [CrossRef]
- Preda, L. Generation of Optical Vortices by Fractional Derivative. Opt. Lasers Eng. 2014, 54, 42–48. [Google Scholar] [CrossRef]
- Wei, B.; Hu, W.; Ming, Y.; Xu, F.; Rubin, S.; Wang, J.; Chigrinov, V.; Lu, Y. Generating Switchable and Reconfigurable Optical Vortices via Photopatterning of Liquid Crystals. Adv. Mater. 2014, 26, 1590–1595. [Google Scholar] [CrossRef] [PubMed]
- Beijersbergen, M.W.; Coerwinkel, R.P.C.; Kristensen, M.; Woerdman, J.P. Helical-Wavefront Laser Beams Produced with a Spiral Phaseplate. Opt. Commun. 1994, 112, 321–327. [Google Scholar] [CrossRef]
- Hu, X.-B.; Rosales-Guzmán, C. Generation and Characterization of Complex Vector Modes with Digital Micromirror Devices: A Tutorial. J. Opt. 2022, 24, 034001. [Google Scholar] [CrossRef]
- Igasaki, Y.; Li, F.; Yoshida, N.; Toyoda, H.; Inoue, T.; Mukohzaka, N.; Kobayashi, Y.; Hara, T. High Efficiency Electrically-Addressable Phase-Only Spatial Light Modulator. Opt. Rev. 1999, 6, 339–344. [Google Scholar] [CrossRef]
- Yamaguchi, R.; Nose, T.; Sato, S. Liquid Crystal Polarizers with Axially Symmetrical Properties. Jpn. J. Appl. Phys. 1989, 28, 1730. [Google Scholar] [CrossRef]
- Stalder, M.; Schadt, M. Linearly Polarized Light with Axial Symmetry Generated by Liquid-Crystal Polarization Converters. Opt. Lett. OL 1996, 21, 1948–1950. [Google Scholar] [CrossRef]
- Tzeng, Y.-Y.; Ke, S.-W.; Ting, C.-L.; Fuh, A.Y.-G.; Lin, T.-H. Axially Symmetric Polarization Converters Based on Photo-Aligned Liquid Crystal Films. Opt. Express OE 2008, 16, 3768–3775. [Google Scholar] [CrossRef]
- Ren, H.; Lin, Y.-H.; Wu, S.-T. Linear to Axial or Radial Polarization Conversion Using a Liquid Crystal Gel. Appl. Phys. Lett. 2006, 89, 051114. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Almazov, A.A.; Khonina, S.N.; Soifer, V.A.; Elfstrom, H.; Turunen, J. Generation of Phase Singularity through Diffracting a Plane or Gaussian Beam by a Spiral Phase Plate. J. Opt. Soc. Am. A JOSAA 2005, 22, 849–861. [Google Scholar] [CrossRef] [PubMed]
- Ko, S.-W.; Ting, C.-L.; Fuh, A.Y.-G.; Lin, T.-H. Polarization Converters Based on Axially Symmetric Twisted Nematic Liquid Crystal. Opt. Express OE 2010, 18, 3601–3607. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Xu, M.; Ren, H.; Wang, Q. A Polarization Converter Array Using a Twisted-Azimuthal Liquid Crystal in Cylindrical Polymer Cavities. Opt. Express OE 2013, 21, 16222–16230. [Google Scholar] [CrossRef]
- Karunarathne, M.; Lee, C.-M.; Kwak, K.; Lee, H.; Song, J.-K. Tunable Optical Vortex Arrays Using Spontaneous Periodic Pattern Formation in Nematic Liquid Crystal Cells. Curr. Appl. Phys. 2018, 18, 819–823. [Google Scholar] [CrossRef]
- Maurer, C.; Jesacher, A.; Fürhapter, S.; Bernet, S.; Ritsch-Marte, M. Tailoring of Arbitrary Optical Vector Beams. New J. Phys. 2007, 9, 78. [Google Scholar] [CrossRef]
- Fu, S.; Wang, T.; Gao, C. Generating Perfect Polarization Vortices through Encoding Liquid-Crystal Display Devices. Appl. Opt. 2016, 55, 6501–6505. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, X.; Cai, Y.; Zhang, Y.; Yan, S.; Zhou, M.; Li, M.; Yao, B. Compact Optical Module to Generate Arbitrary Vector Vortex Beams. Appl. Opt. 2020, 59, 8932. [Google Scholar] [CrossRef]
- Liang, Y.; Yun, X.; He, M.; Wang, Z.; Wang, S.; Lei, M. Zero-Order-Free Complex Beam Shaping. Opt. Lasers Eng. 2022, 155, 107048. [Google Scholar] [CrossRef]
- Machavariani, G.; Lumer, Y.; Moshe, I.; Meir, A.; Jackel, S. Spatially-Variable Retardation Plate for Efficient Generation of Radially- and Azimuthally-Polarized Beams. Opt. Commun. 2008, 281, 732–738. [Google Scholar] [CrossRef]
- Chen, P.; Ji, W.; Wei, B.-Y.; Hu, W.; Chigrinov, V.; Lu, Y.-Q. Generation of Arbitrary Vector Beams with Liquid Crystal Polarization Converters and Vector-Photoaligned q-Plates. Appl. Phys. Lett. 2015, 107, 241102. [Google Scholar] [CrossRef]
- Ji, Z.; Ji, Z.; Zhang, X.; Zhang, X.; Zhang, Y.; Zhang, Y.; Wang, Z.; Drevensek-Olenik, I.; Rupp, R.; Li, W.; et al. Electrically Tunable Generation of Vectorial Vortex Beams with Micro-Patterned Liquid Crystal Structures. Chin. Opt. Lett. COL 2017, 15, 070501. [Google Scholar]
- Beresna, M.; Gecevičius, M.; Kazansky, P.G.; Gertus, T. Radially Polarized Optical Vortex Converter Created by Femtosecond Laser Nanostructuring of Glass. Appl. Phys. Lett. 2011, 98, 201101. [Google Scholar] [CrossRef]
- Switkowski, K.; Anuszkiewicz, A.; Filipkowski, A.; Pysz, D.; Stepien, R.; Krolikowski, W.; Buczynski, R. Formation of Optical Vortices with All-Glass Nanostructured Gradient Index Masks. Opt. Express OE 2017, 25, 31443–31450. [Google Scholar] [CrossRef] [PubMed]
- Veysi, M.; Guclu, C.; Capolino, F.; Rahmat-Samii, Y. Revisiting Orbital Angular Momentum Beams: Fundamentals, Reflectarray Generation, and Novel Antenna Applications. IEEE Antennas Propag. Mag. 2018, 60, 68–81. [Google Scholar] [CrossRef]
- Huang, H.-F.; Li, S.-N. High-Efficiency Planar Reflectarray with Small-Size for OAM Generation at Microwave Range. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 432–436. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Switkowski, K.; Filipkowski, A.; Kasztelanic, R.; Pysz, D.; van Le, H.; van Chu, B.; Stepien, R.; Krolikowski, W.; Buczynski, R. All-Fiber Nanostructured Gradient Optics Vortex Beam Converter. Opt. Lasers Eng. 2022, 150, 106841. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, J.C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Nowosielski, J.M. Nanostructured Birefringent and Gradient-Index Micro-Optical Elements. Ph.D. Thesis, Heriot-Watt University, Edinburgh, UK, 2014. [Google Scholar]
- Sihvola, A. Electromagnetic Mixing Formulas and Applications; The Institution of Electrical Engineers: London, UK, 1999; ISBN 978-0-85296-772-0. [Google Scholar]
- Ko, S.-W.; Huang, S.-H.; Fuh, A.; Lin, T.-H. Fabrications of Liquid-Crystal Polarization Converters and Their Applications. Proc. SPIE 2009, 7414, 126–131. [Google Scholar] [CrossRef]
- Jones, J.A.; D’Addario, A.J.; Rojec, B.L.; Milione, G.; Galvez, E.J. The Poincaré-Sphere Approach to Polarization: Formalism and New Labs with Poincaré Beams. Am. J. Phys. 2016, 84, 822–835. [Google Scholar] [CrossRef]
- Yeh, P.; Gu, C. Optics of Liquid Crystal Displays; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 67, ISBN 978-0-470-18176-8. [Google Scholar]
- Dabrowski, R.; Dziaduszek, J.; Szczuciński, T. Mesomorphic Characteristics of Some New Homologous Series with the Isothiocyanato Terminal Group. Mol. Cryst. Liq. Cryst. 1985, 124, 241–257. [Google Scholar] [CrossRef]
- Kwasny, M.; Laudyn, U.A. Electrical Control of Optical Liquid-Crystal-Guided Microstructures. Crystals 2022, 12, 325. [Google Scholar] [CrossRef]
- Vanmol, K.; Baghdasaryan, T.; Vermeulen, N.; Saurav, K.; Watté, J.; Thienpont, H.; van Erps, J. 3D Direct Laser Writing of Microstructured Optical Fiber Tapers on Single-Mode Fibers for Mode-Field Conversion. Opt. Express 2020, 28, 36147. [Google Scholar] [CrossRef] [PubMed]
- Asadollahbaik, A.; Thiele, S.; Weber, K.; Kumar, A.; Drozella, J.; Sterl, F.; Herkommer, A.M.; Giessen, H.; Fick, J. Highly Efficient Dual-Fiber Optical Trapping with 3D Printed Diffractive Fresnel Lenses. ACS Photonics 2020, 7, 88–97. [Google Scholar] [CrossRef]
- Kulbacka, J.; Kasztelanic, R.; Kotulska, M.; Pysz, D.; Stępniewski, G.; Stępień, R.; Saczko, J.; Miklavčič, D.; Buczyński, R. Ultrathin Glass Fiber Microprobe for Electroporation of Arbitrary Selected Cell Groups. Bioelectrochemistry 2020, 135, 107545. [Google Scholar] [CrossRef] [PubMed]


| Cell |  |  |  | 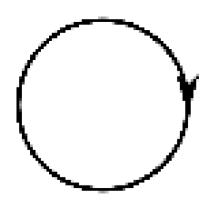 | 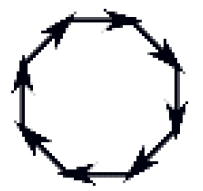 | 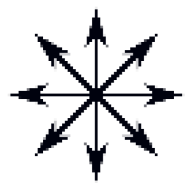 | 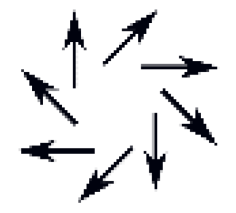 |  |
|---|---|---|---|---|---|---|---|---|
| Phase retarder—U1 [V] | 0 | 0 | 0 | 0 | 2.3 | 2.3 | 2.3 | 2.3 |
| Waveplate—U2 [V] | 1.3 | 2.2 | 1.6 | 3.3 | 1.3 | 2.2 | 1.6 | 3.3 |
| θ-plate—U3 [V] | 5.0 | 5.0 | 5.0 | 5.0 | 0 | 0 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piłka, J.; Kwaśny, M.; Filipkowski, A.; Buczyński, R.; Karpierz, M.A.; Laudyn, U.A. A Gaussian to Vector Vortex Beam Generator with a Programmable State of Polarization. Materials 2022, 15, 7794. https://doi.org/10.3390/ma15217794
Piłka J, Kwaśny M, Filipkowski A, Buczyński R, Karpierz MA, Laudyn UA. A Gaussian to Vector Vortex Beam Generator with a Programmable State of Polarization. Materials. 2022; 15(21):7794. https://doi.org/10.3390/ma15217794
Chicago/Turabian StylePiłka, Jacek, Michał Kwaśny, Adam Filipkowski, Ryszard Buczyński, Mirosław A. Karpierz, and Urszula A. Laudyn. 2022. "A Gaussian to Vector Vortex Beam Generator with a Programmable State of Polarization" Materials 15, no. 21: 7794. https://doi.org/10.3390/ma15217794
APA StylePiłka, J., Kwaśny, M., Filipkowski, A., Buczyński, R., Karpierz, M. A., & Laudyn, U. A. (2022). A Gaussian to Vector Vortex Beam Generator with a Programmable State of Polarization. Materials, 15(21), 7794. https://doi.org/10.3390/ma15217794






