Synthesis of Biocompatible and Biodegradable Polyamidoamines Microgels via a Simple and Reliable Statistical Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. General Polymerization Procedure
2.2. Size Exclusion Chromatography (SEC)
2.3. Dynamic Light Scattering (DLS) Analysis
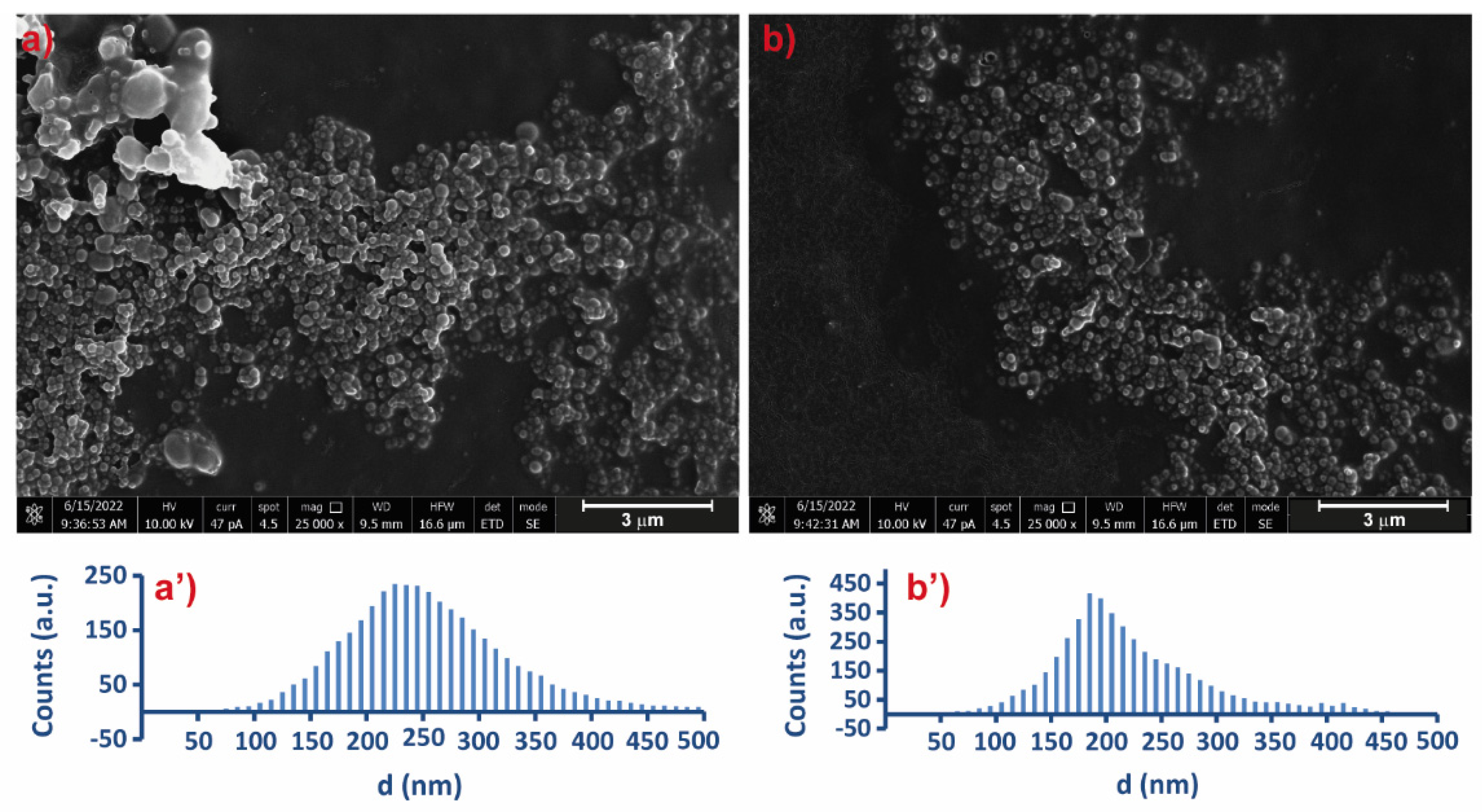
2.4. Scanning Electron Microscopy (SEM)
2.5. Cell Culture and Cell Viability Assay
3. Results and Discussion
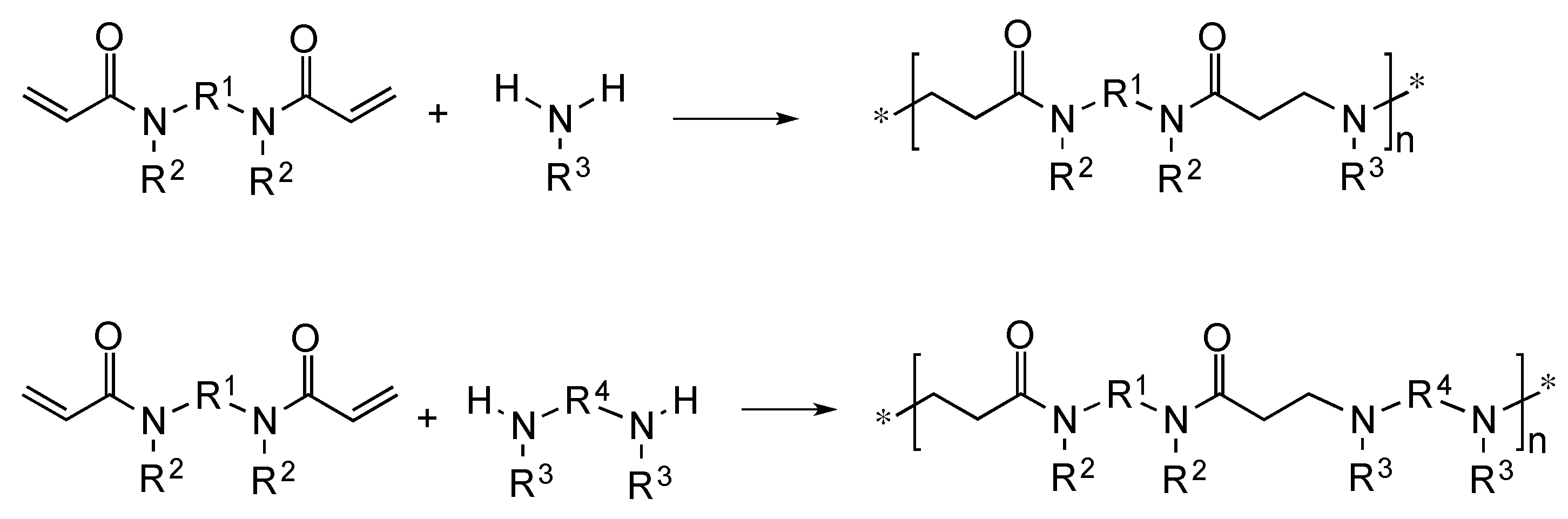
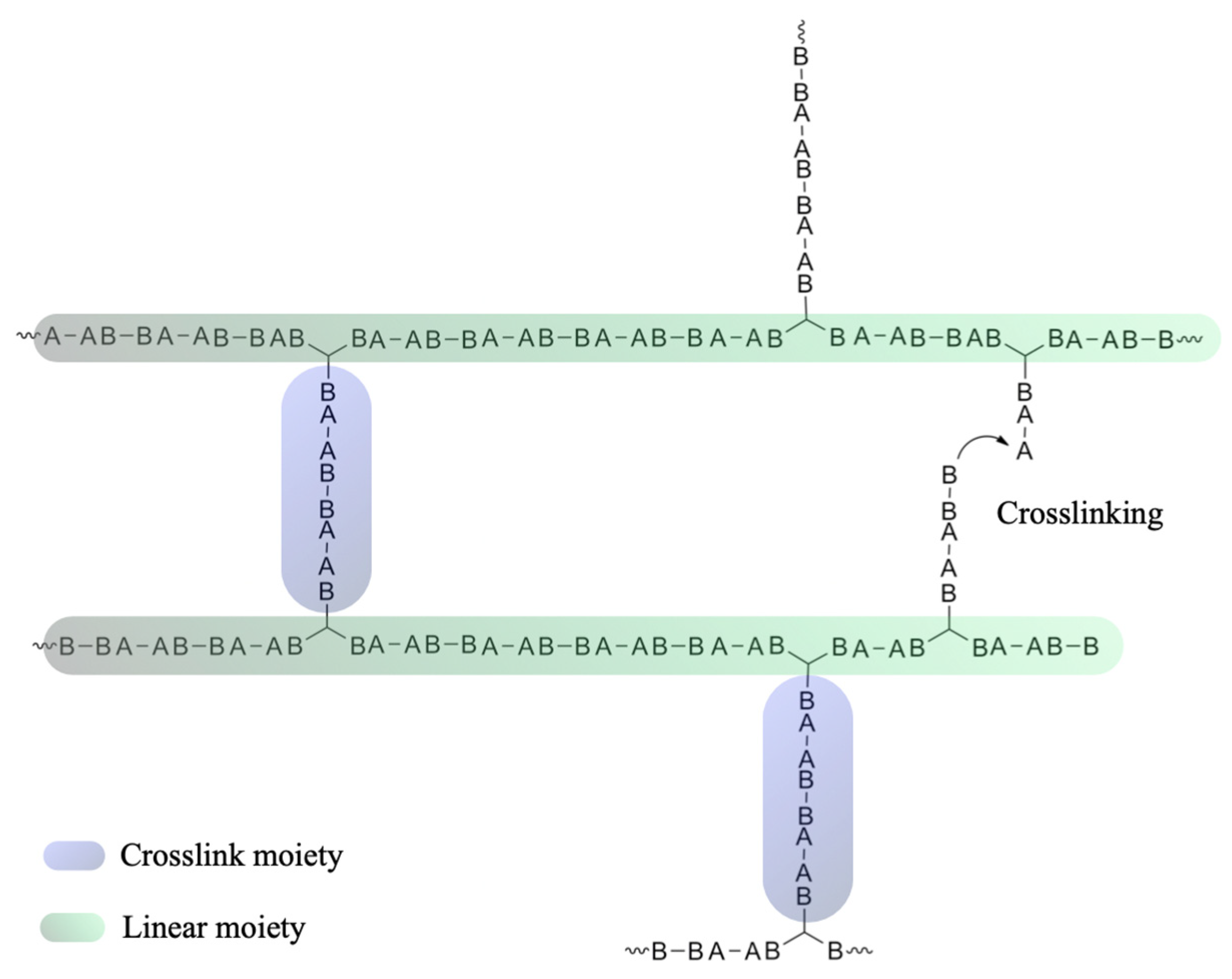
3.1. Theoretical Considerations
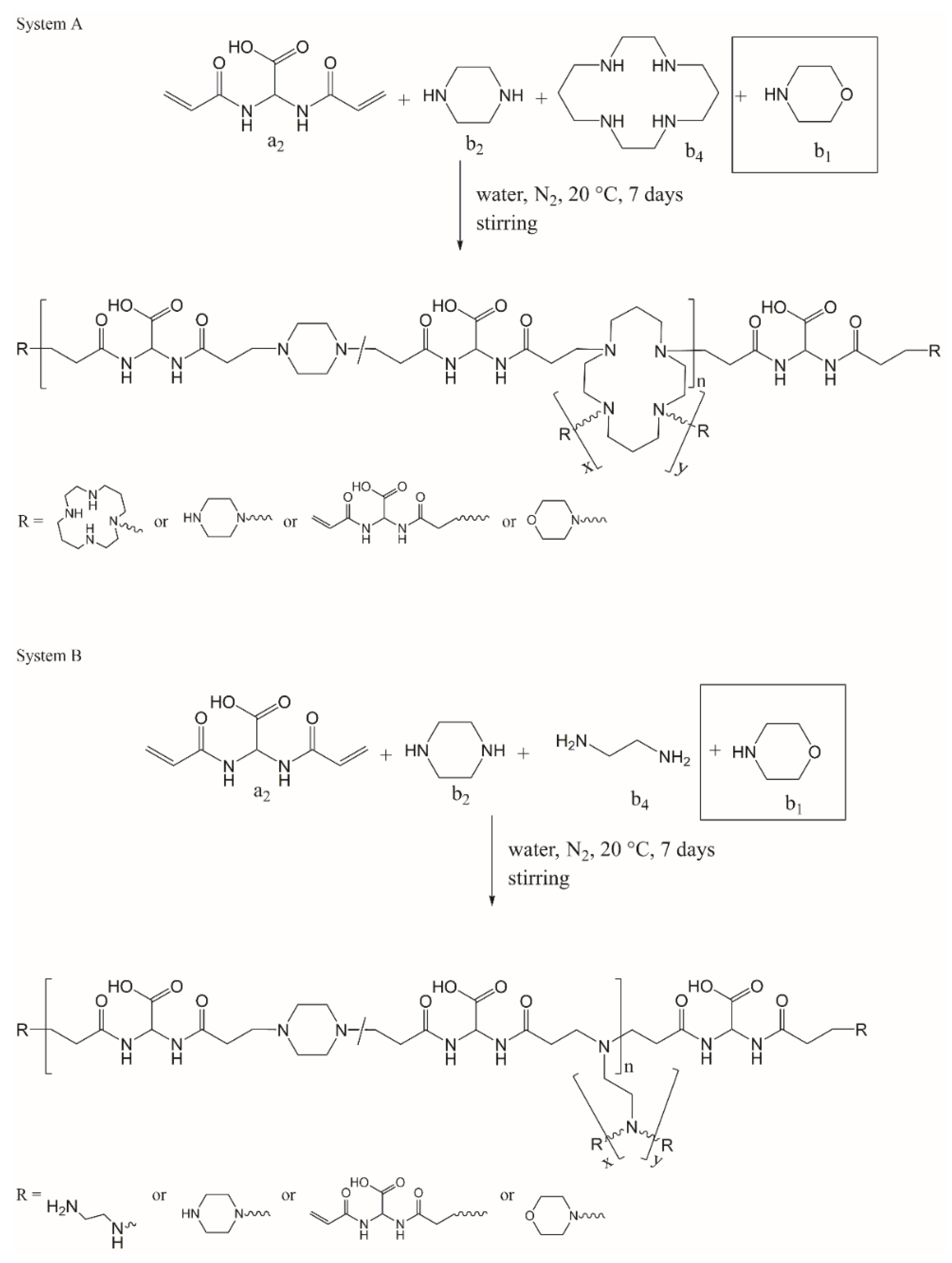
3.2. Systems Adopted and Rationale of the Approach
3.3. Compliance with the Flory–Stockmayer Model
3.4. Physicochemical Characterization of Selected Microgels
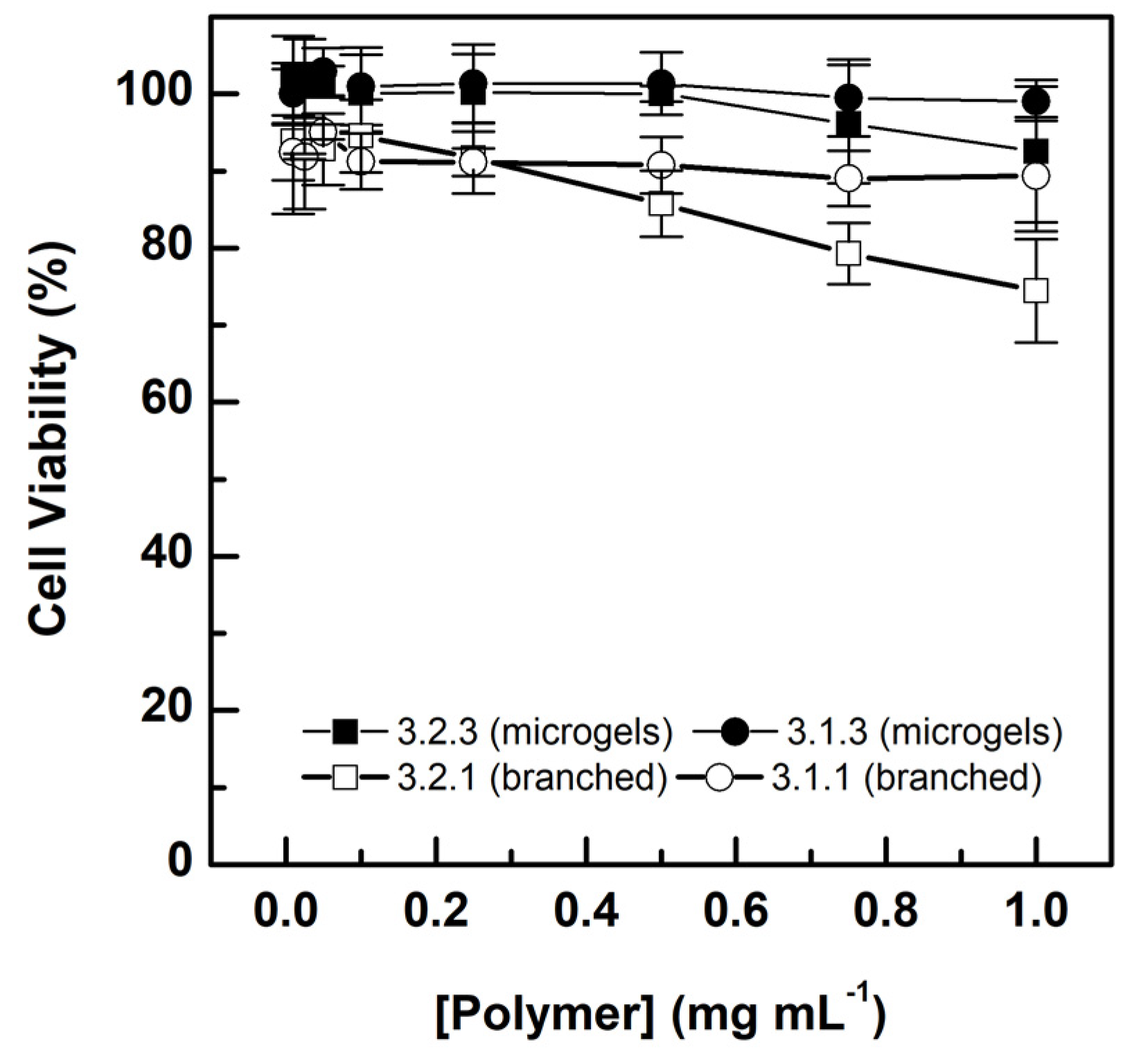
3.5. Cytocompatibility of the Selected Microgels
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ferruti, P. Poly(amidoamine)s: Past, present, and perspectives. J. Polym. Sci. Part A Polym. Chem. 2013, 51, 2319–2353. [Google Scholar] [CrossRef]
- Ferruti, P.; Mauro, N.; Manfredi, A.; Ranucci, E. Hetero-difunctional dimers as building blocks for the synthesis of poly(amidoamine)s with hetero-difunctional chain terminals and their derivatives. J. Polym. Sci. Part A Polym. Chem. 2012, 50, 4947–4957. [Google Scholar] [CrossRef]
- Ferruti, P.; Marchisio, M.A.; Duncan, R. Poly(amido-amine)s: Biomedical Applications. Macromol. Rapid Commun. 2002, 23, 332–355. [Google Scholar] [CrossRef]
- Mauro, N.; Chiellini, F.; Bartoli, C.; Gazzarri, M.; Laus, M.; Antonioli, D.; Griffiths, P.; Manfredi, A.; Ranucci, E.; Ferruti, P. RGD-mimic polyamidoamine-montmorillonite composites with tunable stiffness as scaffolds for bone tissue-engineering applications. J. Tissue Eng. Regen. Med. 2016, 11, 2164–2175. [Google Scholar] [CrossRef] [PubMed]
- Gualandi, C.; Bloise, N.; Mauro, N.; Ferruti, P.; Manfredi, A.; Sampaolesi, M.; Liguori, A.; Laurita, R.; Gherardi, M.; Colombo, V.; et al. Poly-l-Lactic Acid Nanofiber-Polyamidoamine Hydrogel Composites: Preparation, Properties, and Preliminary Evaluation as Scaffolds for Human Pluripotent Stem Cell Culturing. Macromol. Biosci. 2016, 16, 1533–1544. [Google Scholar] [CrossRef] [PubMed]
- Ferruti, P.; Mauro, N.; Falciola, L.; Pifferi, V.; Bartoli, C.; Gazzarri, M.; Chiellini, F.; Ranucci, E. Amphoteric, Prevailingly Cationic L-Arginine Polymers of Poly(Amidoamino Acid) Structure: Synthesis, Acid/Base Properties and Preliminary Cytocompatibility and Cell-Permeating Characterizations. Macromol. Biosci. 2014, 14, 390–400. [Google Scholar] [CrossRef]
- van Dongen, M.A.; Vaidyanathan, S.; Holl, M.M.B. PAMAM dendrimers as quantized building blocks for novel nanostructures. Soft Matter 2013, 9, 11188–11196. [Google Scholar] [CrossRef] [PubMed]
- Gurnani, P.; Blakney, A.K.; Yeow, J.; Bouton, C.R.; Shattock, R.J.; Stevens, M.M.; Alexander, C. An improved synthesis of poly(amidoamine)s for complexation with self-amplifying RNA and effective transfection. Polym. Chem. 2020, 11, 5861–5869. [Google Scholar] [CrossRef]
- Pettit, M.W.; Griffiths, P.; Ferruti, P.; Richardson, S.C. Poly(amidoamine) polymers: Soluble linear amphiphilic drug-delivery systems for genes, proteins and oligonucleotides. Ther. Deliv. 2011, 2, 907–917. [Google Scholar] [CrossRef]
- Ranucci, E.; Suardi, M.A.; Annunziata, R.; Ferruti, P.; Chiellini, F.; Bartoli, C. Poly(amidoamine) Conjugates with Disulfide-Linked Cholesterol Pendants Self-Assembling into Redox-Sensitive Nanoparticles. Biomacromolecules 2008, 9, 2693–2704. [Google Scholar] [CrossRef] [PubMed]
- Mauro, N.; Manfredi, A.; Ranucci, E.; Procacci, P.; Laus, M.; Antonioli, D.; Mantovani, C.; Magnaghi, V.; Ferruti, P. Degradable Poly(amidoamine) Hydrogels as Scaffolds for In Vitro Culturing of Peripheral Nervous System Cells. Macromol. Biosci. 2012, 13, 332–347. [Google Scholar] [CrossRef] [PubMed]
- Ferruti, P.; Ranucci, E.; Manfredi, A.; Mauro, N.; Ferrari, E.; Bruni, R.; Colombo, F.; Mussini, P.; Rossi, M. L-lysine and EDTA polymer mimics as resins for the quantitative and reversible removal of heavy metal ion water pollutants. J. Polym. Sci. Part A Polym. Chem. 2012, 50, 5000–5010. [Google Scholar] [CrossRef]
- Ekkelenkamp, A.E.; Jansman, M.M.; Roelofs, K.; Engbersen, J.F.; Paulusse, J.M. Surfactant-free preparation of highly stable zwitterionic poly(amido amine) nanogels with minimal cytotoxicity. Acta Biomater. 2016, 30, 126–134. [Google Scholar] [CrossRef]
- Stockmayer, W.H. Theory of Molecular Size Distribution and Gel Formation in Branched Polymers II. General Cross Linking. J. Chem. Phys. 1944, 12, 125–131. [Google Scholar] [CrossRef]
- Flory, P.J. Molecular Size Distribution in Three Dimensional Polymers. I. Gelation. J. Am. Chem. Soc. 1941, 63, 3083–3090. [Google Scholar] [CrossRef]
- Flory, P.J. Kinetics of Polyesterification: A Study of the Effects of Molecular Weight and Viscosity on Reaction Rate. J. Am. Chem. Soc. 1939, 61, 3334–3340. [Google Scholar] [CrossRef]
- Ferruti, P.; Ranucci, E.; Trotta, F.; Gianasi, E.; Evagorou, E.G.; Wasil, M.; Wilson, G.; Duncan, R. Synthesis, characterisation and antitumour activity of platinum(II) complexes of novel functionalised poly(amido amine)s. Macromol Chem. Phys. 1999, 200, 1644–1654. [Google Scholar] [CrossRef]
- Durand, D.; Bruneau, C.-M. Average functionalities of macromolecules in stepwise polyfunctional polymerization. Polymer 1982, 23, 69–72. [Google Scholar] [CrossRef]
- Durand, D.; Bruneau, C.M. Statistics of random macromolecular networks. Stepwise polymerization of polyfunctional monomers bearing A and B coreactive groups. Makromol. Chem. 1982, 183, 1021–1035. [Google Scholar] [CrossRef]
- Odian, G. Principles of Polymerization, 4th ed.; Wiley: Hoboken, NJ, USA, 2004; Available online: https://www.wiley.com/en-us/Principles+of+Polymerization,+4th+Edition-p-9780471274001 (accessed on 2 September 2022).
- Mather, B.D.; Viswanathan, K.; Miller, K.M.; Long, T.E. Michael addition reactions in macromolecular design for emerging technologies. Prog. Polym. Sci. 2006, 31, 487–531. [Google Scholar] [CrossRef]
- Licciardi, M.; Paolino, D.; Mauro, N.; Cosco, D.; Giammona, G.; Fresta, M.; Cavallaro, G.; Celia, C. Cationic Supramolecular Vesicular Aggregates for Pulmonary Tissue Selective Delivery in Anticancer Therapy. ChemMedChem 2016, 11, 1734–1744. [Google Scholar] [CrossRef] [PubMed]
- Porsio, B.; Craparo, E.F.; Mauro, N.; Giammona, G.; Cavallaro, G. Mucus and Cell-Penetrating Nanoparticles Embedded in Nano-into-Micro Formulations for Pulmonary Delivery of Ivacaftor in Patients with Cystic Fibrosis. ACS Appl. Mater. Interfaces 2017, 10, 165–181. [Google Scholar] [CrossRef] [PubMed]
- Bhanderi, M.; Shah, J.; Gorain, B.; Nair, A.B.; Jacob, S.; Asdaq, S.M.B.; Fattepur, S.; Alamri, A.S.; Alsanie, W.F.; Alhomrani, M.; et al. Optimized Rivastigmine Nanoparticles Coated with Eudragit for Intranasal Application to Brain Delivery: Evaluation and Nasal Ciliotoxicity Studies. Materials 2021, 14, 6291. [Google Scholar] [CrossRef] [PubMed]
- Riley, M.K.; Vermerris, W. Delivery of DNA into Human Cells by Functionalized Lignin Nanoparticles. Materials 2022, 15, 303. [Google Scholar] [CrossRef] [PubMed]
- Documents Download Module. Available online: https://ec.europa.eu/research/participants/documents/downloadPublic?documentIds=080166e5b3658b32&appId=PPGMS (accessed on 6 September 2022).
- Zhu, J.; Usov, P.M.; Xu, W.; Celis-Salazar, P.J.; Lin, S.; Kessinger, M.C.; Landaverde-Alvarado, C.; Cai, M.; May, A.M.; Slebodnick, C.; et al. A New Class of Metal-Cyclam-Based Zirconium Metal–Organic Frameworks for CO2 Adsorption and Chemical Fixation. J. Am. Chem. Soc. 2018, 140, 993–1003. [Google Scholar] [CrossRef]
| N° | BAC (mmol) | Cy (mmol) | P (mmol) | M (mmol) | Excess Reactive Function (a) | rc(b) | r(c) | r-rc | (10−3) | (10−3) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1.1 | 2.6250 | 0.3750 | 3.0000 | - | N-H | 0.714 | 0.700 | −0.014 | 4.7 | 6.1 |
| 1.2 | 2.4975 | 0.3750 | 3.0000 | - | N-H | 0.714 | 0.667 | −0.047 | 3.9 | 5.7 |
| 1.3 | 3.1875 | 0.3750 | 3.0000 | - | N-H | 0.714 | 0.850 | +0.136 | (d) | (d) |
| 1.4 | 1.5630 | 0.1250 | 1.0000 | - | = | 0.714 | 0.800 | +0.086 | (d) | (d) |
| 1.5 | 1.0004 | 0.1250 | 1.0000 | - | N-H | 0.714 | 0.800 | +0.086 | (d) | (d) |
| 1.6 | 1.7863 | 0.1250 | 1.0000 | - | = | 0.714 | 0.709 | −0.005 | 3.7 | 9.1 |
| 1.7 | 3.9280 | 0.4550 | 3.0000 | 2.0000 | N-H | 0.857 (e) | 0.800 | −0.057 | 3.4 | 4.6 |
| N° | BAC (mmol) | EDA (mmol) | P (mmol) | M (mmol) | Excess Function (a) | rc (b) | r (c) | r-rc | (10−3) | (10−3) |
|---|---|---|---|---|---|---|---|---|---|---|
| 2.1 | 2.6250 | 0.3750 | 3.0000 | - | N-H | 0.714 | 0.700 | −0.014 | 4.7 | 6.1 |
| 2.2 | 2.4975 | 0.3750 | 3.0000 | - | N-H | 0.714 | 0.667 | −0.047 | 3.9 | 5.7 |
| 2.3 | 3.1875 | 0.3750 | 3.0000 | - | N-H | 0.714 | 0.850 | +0.136 | - (d) | - (d) |
| 2.4 | 1.6665 | 0.3750 | 3.0000 | - | N-H | 0.714 | 0.667 | −0.047 | 2.8 | 4.3 |
| 2.5 | 4.9342 | 0.3750 | 3.0000 | - | = | 0.714 | 0.760 | +0.046 | - (d) | - (c) |
| 2.6 | 5.1370 | 0.3750 | 3.0000 | - | = | 0.714 | 0.730 | +0.016 | - (d) | - (d) |
| 2.7 | 5.6222 | 0.3750 | 3.0000 | - | = | 0.714 | 0.667 | −0.047 | 2.2 | 3.5 |
| 2.8 | 3.9280 | 0.4550 | 3.0000 | 2.0000 | N-H | 0.857 (e) | 0.800 | −0.057 | 3.4 | 4.6 |
| 2.9 | 3.5000 | 1.3333 | 3.0000 | - | N-H | 0.515 | 0.618 | +0.103 | 3.4 | 5.3 |
| 2.10 | 3.3333 | 1.3333 | 3.0000 | - | N-H | 0.515 | 0.588 | +0.073 | 2.9 | 4.7 |
| 2.11 | 4.2500 | 1.3333 | 3.0000 | - | N-H | 0.515 | 0.750 | +0.235 | - (d) | - (d) |
| 2.12 | 5.0000 | 0.8889 | 3.0000 | - | = | 0.515 | 0.756 | +0.241 | - (d) | - (d) |
| 2.13 | 4.8000 | 1.3333 | 3.0000 | 2.0000 | N-H | 0.606 (e) | 0.720 | +0.114 | 3.1 | 4.2 |
| N° | BAC (mmol) | EDA (mmol) | P (mmol) | M (mmol) | Excess Function (a) | rc(b) | r (c) | r-rc | (10−3) | (10−3) |
|---|---|---|---|---|---|---|---|---|---|---|
| 3.1 | 2.6250 | 0.3750 | 3.0000 | - | N-H | 0.864 | 0.737 | −0.127 | 4.7 | 6.1 |
| 3.2 | 2.4975 | 0.3750 | 3.0000 | - | N-H | 0.864 | 0.701 | −0.163 | 3.9 | 5.7 |
| 3.3 | 3.1875 | 0.3750 | 3.0000 | - | N-H | 0.864 | 0.895 | +0.031 | - (d) | - (d) |
| 3.4 | 1.6665 | 0.3750 | 3.0000 | - | N-H | 0.864 | 0.701 | −0.163 | 2.8 | 4.3 |
| 3.5 | 4.9342 | 0.3750 | 3.0000 | - | = | 0.864 | 0.736 | −0.128 | - (d) | - (d) |
| 3.6 | 5.1370 | 0.3750 | 3.0000 | - | = | 0.864 | 0.693 | −0.161 | - (d) | - (d) |
| 3.7 | 5.6222 | 0.3750 | 3.0000 | - | = | 0.864 | 0.634 | −0.230 | 2.2 | 3.5 |
| 3.8 | 3.9280 | 0.4550 | 3.0000 | 2.0000 | N-H | 1.000 (e) | 0.839 | −0.161 | 3.4 | 4.6 |
| 3.9 | 3.5000 | 1.3333 | 3.0000 | - | N-H | 0.714 | 0.700 | −0.014 | 3.4 | 5.3 |
| 3.10 | 3.3333 | 1.3333 | 3.0000 | - | N-H | 0.714 | 0.667 | −0.047 | 2.9 | 4.7 |
| 3.11 | 4.2500 | 1.3333 | 3.0000 | - | N-H | 0.714 | 0.850 | +0.136 | - (d) | - (d) |
| 3.12 | 5.0000 | 0.8889 | 3.0000 | - | = | 0.714 | 0.667 | −0.048 | -(d) | - (d) |
| 3.13 | 4.8000 | 1.3333 | 3.0000 | 2.0000 | N-H | 0.857 (e) | 0.800 | −0.057 | 3.1 | 4.2 |
| N° | Z-Average (nm) | PD | ζ (mV) |
|---|---|---|---|
| 2.3 | 481 | 0.288 | +21.1 ± 2.4 |
| 2.5 | 427 | 0.215 | +28.0 ± 3.1 |
| 2.6 | 398 | 0.187 | +18.2 ± 1.3 |
| 2.11 | 473 | 0.238 | +15.9 ± 3.6 |
| 2.12 | 528 | 0.270 | +24.3 ± 1.3 |
| 1.3 | 356 | 0.211 | +21.8 ± 4.9 |
| 1.4 | 294 | 0.239 | +25.1 ± 4.4 |
| 1.5 | 311 | 0.225 | +27.5 ± 3.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mauro, N.; Giammona, G.; Ranucci, E.; Ferruti, P. Synthesis of Biocompatible and Biodegradable Polyamidoamines Microgels via a Simple and Reliable Statistical Approach. Materials 2022, 15, 7280. https://doi.org/10.3390/ma15207280
Mauro N, Giammona G, Ranucci E, Ferruti P. Synthesis of Biocompatible and Biodegradable Polyamidoamines Microgels via a Simple and Reliable Statistical Approach. Materials. 2022; 15(20):7280. https://doi.org/10.3390/ma15207280
Chicago/Turabian StyleMauro, Nicolò, Gaetano Giammona, Elisabetta Ranucci, and Paolo Ferruti. 2022. "Synthesis of Biocompatible and Biodegradable Polyamidoamines Microgels via a Simple and Reliable Statistical Approach" Materials 15, no. 20: 7280. https://doi.org/10.3390/ma15207280
APA StyleMauro, N., Giammona, G., Ranucci, E., & Ferruti, P. (2022). Synthesis of Biocompatible and Biodegradable Polyamidoamines Microgels via a Simple and Reliable Statistical Approach. Materials, 15(20), 7280. https://doi.org/10.3390/ma15207280









