Strength Matching Method of Face Gear Pair Considering Service Space Limitation to Improve Strength Performance
Abstract
:1. Introduction
2. Design of the Profile Shifted Face Gear Pair
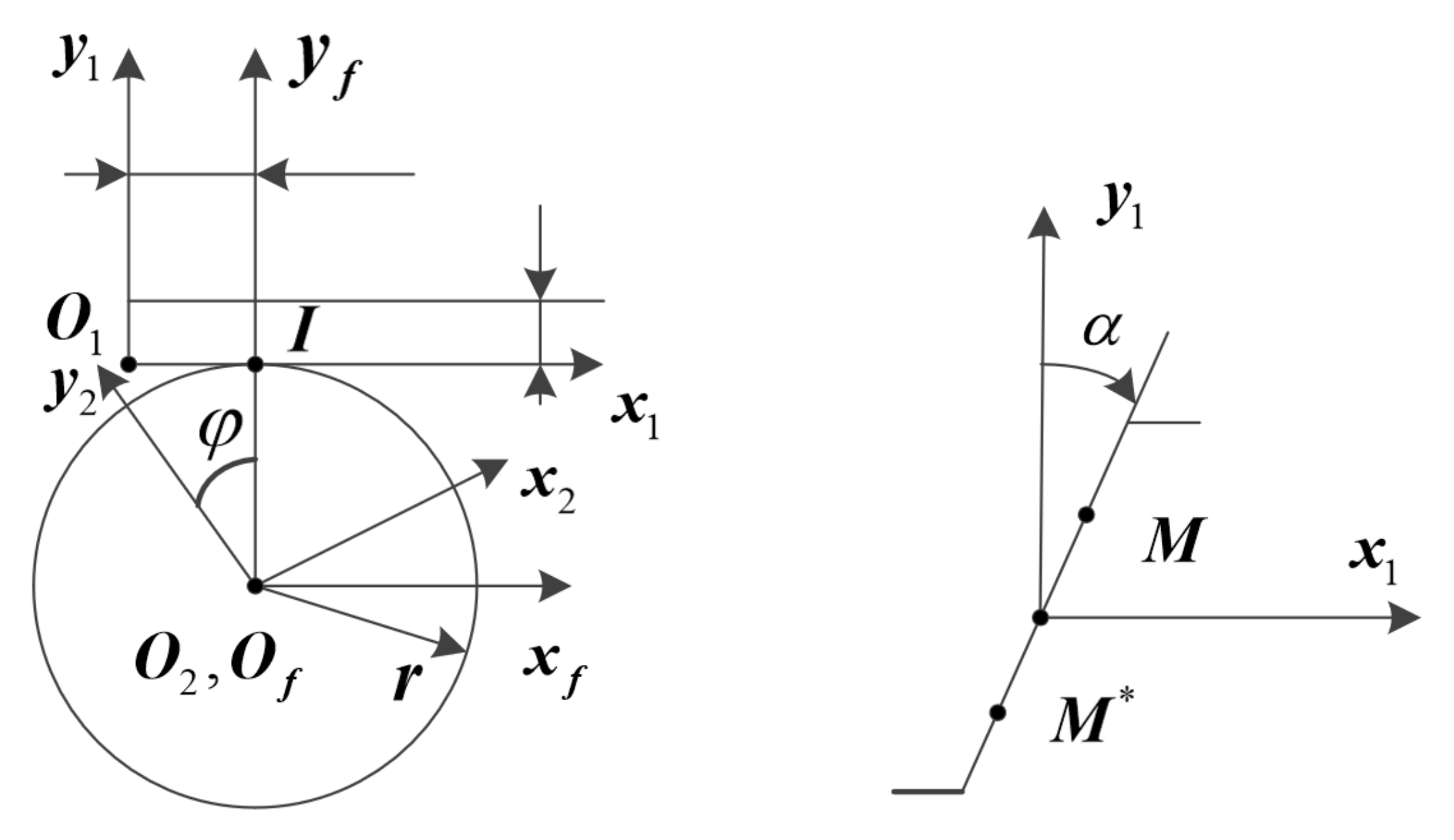
2.1. Rack Cutter Equation
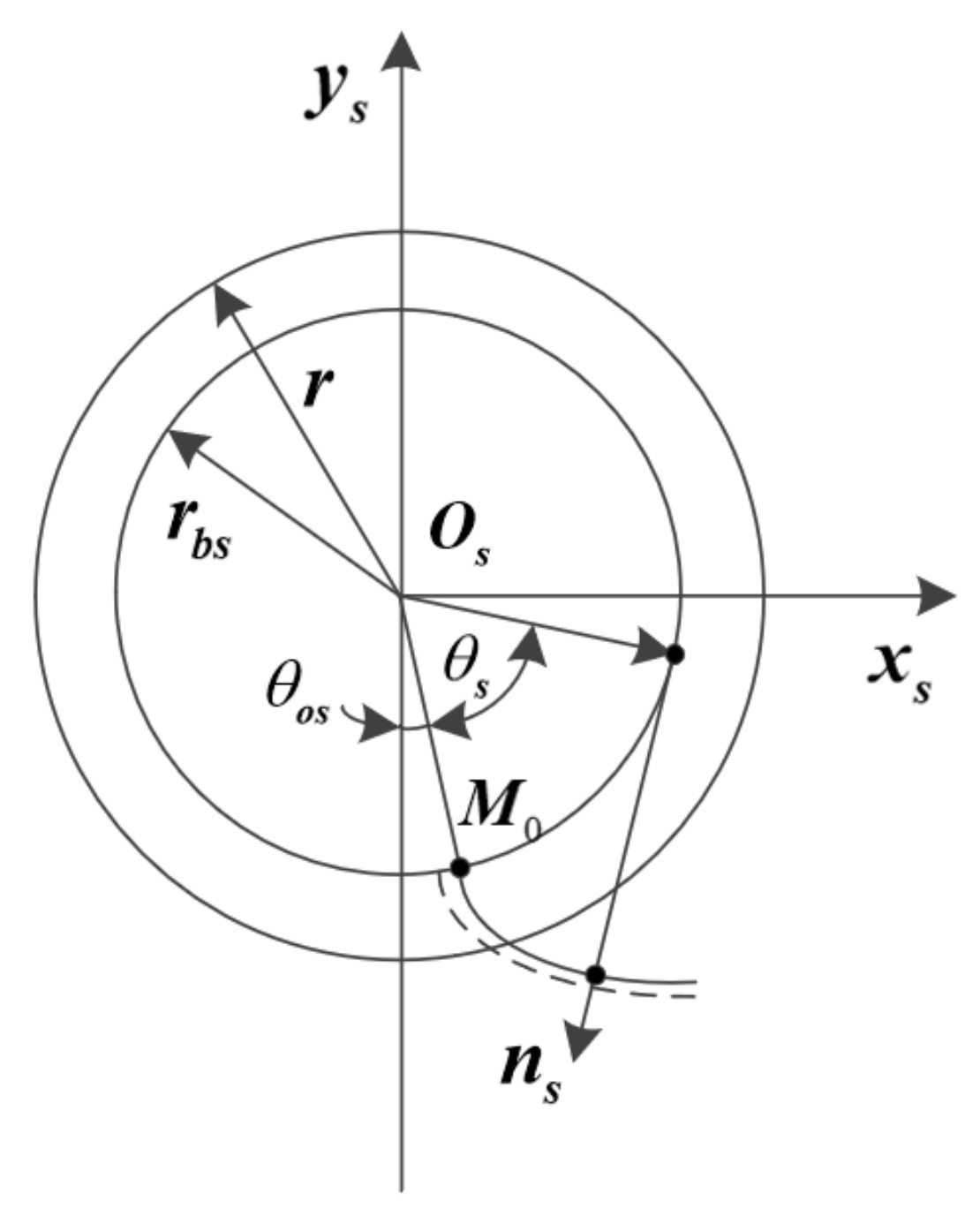
2.2. Tooth Surface Equation of Profile Shifted Pinion and Profile Shifted Shaper
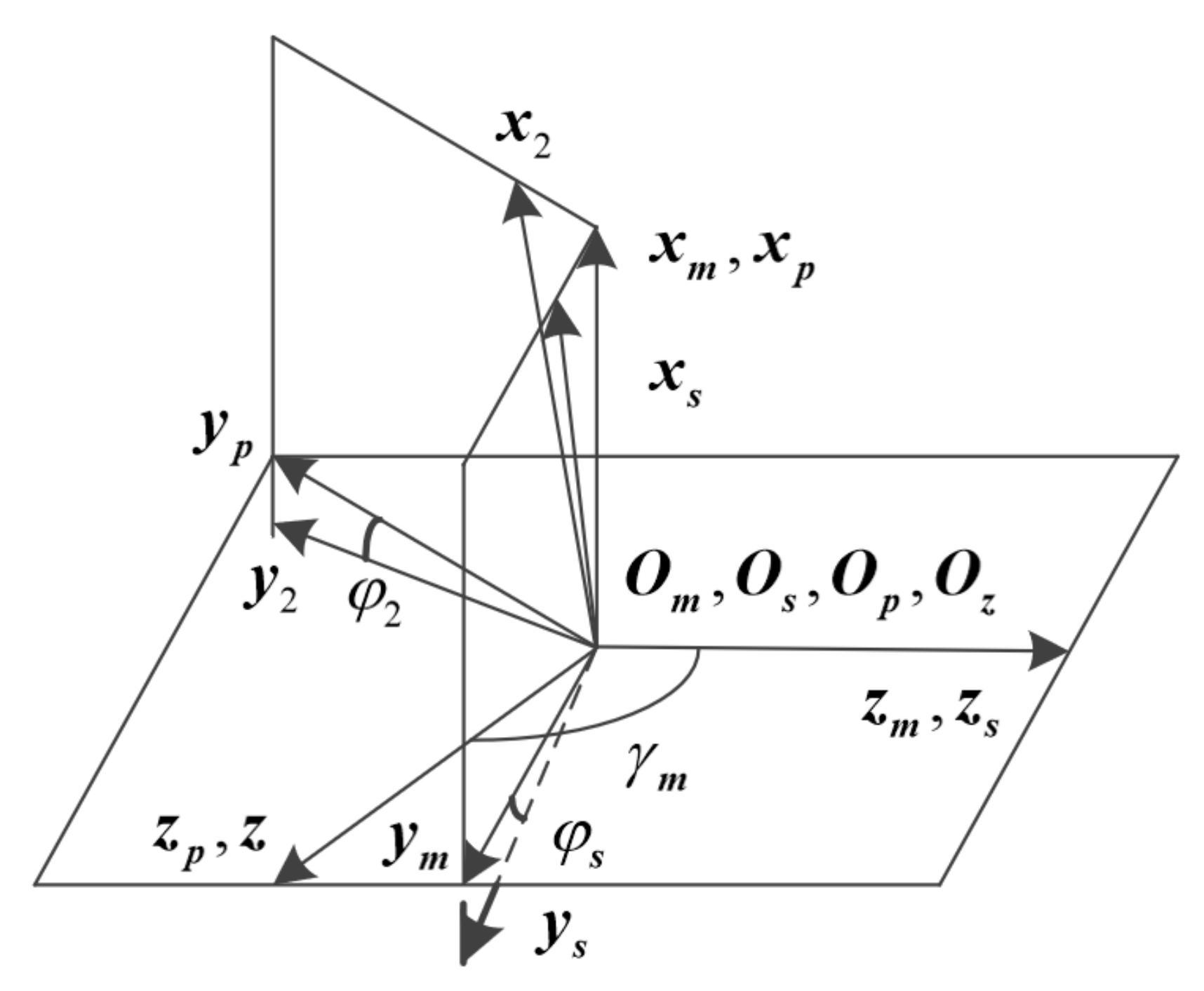
2.3. Tooth Surface Equation of Profile Shifted Face Gear
3. Profile Shifted Face Gear Modification and Strength Analysis
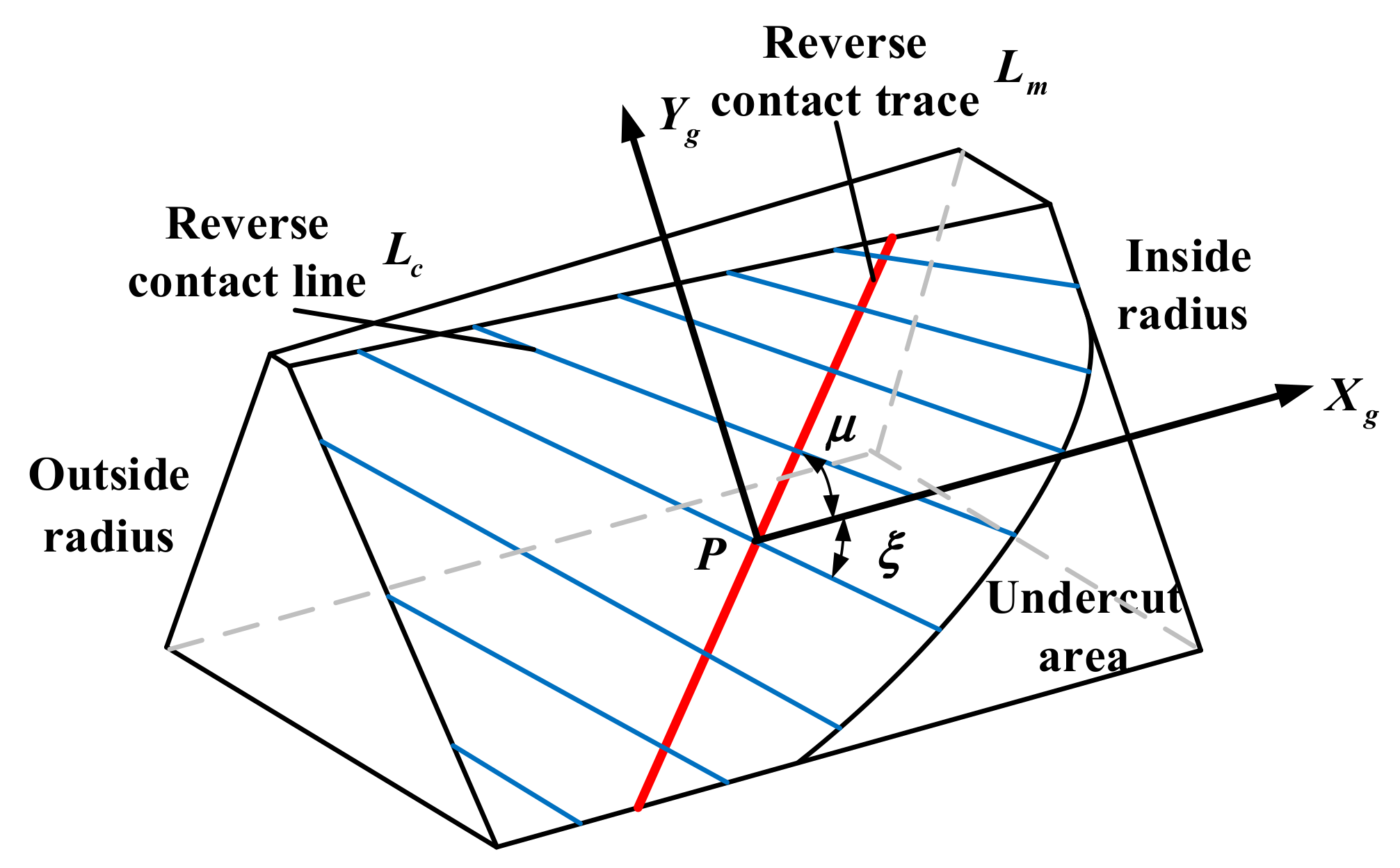
3.1. Bidirectional Modification Design of Profile Shifted Face Gear
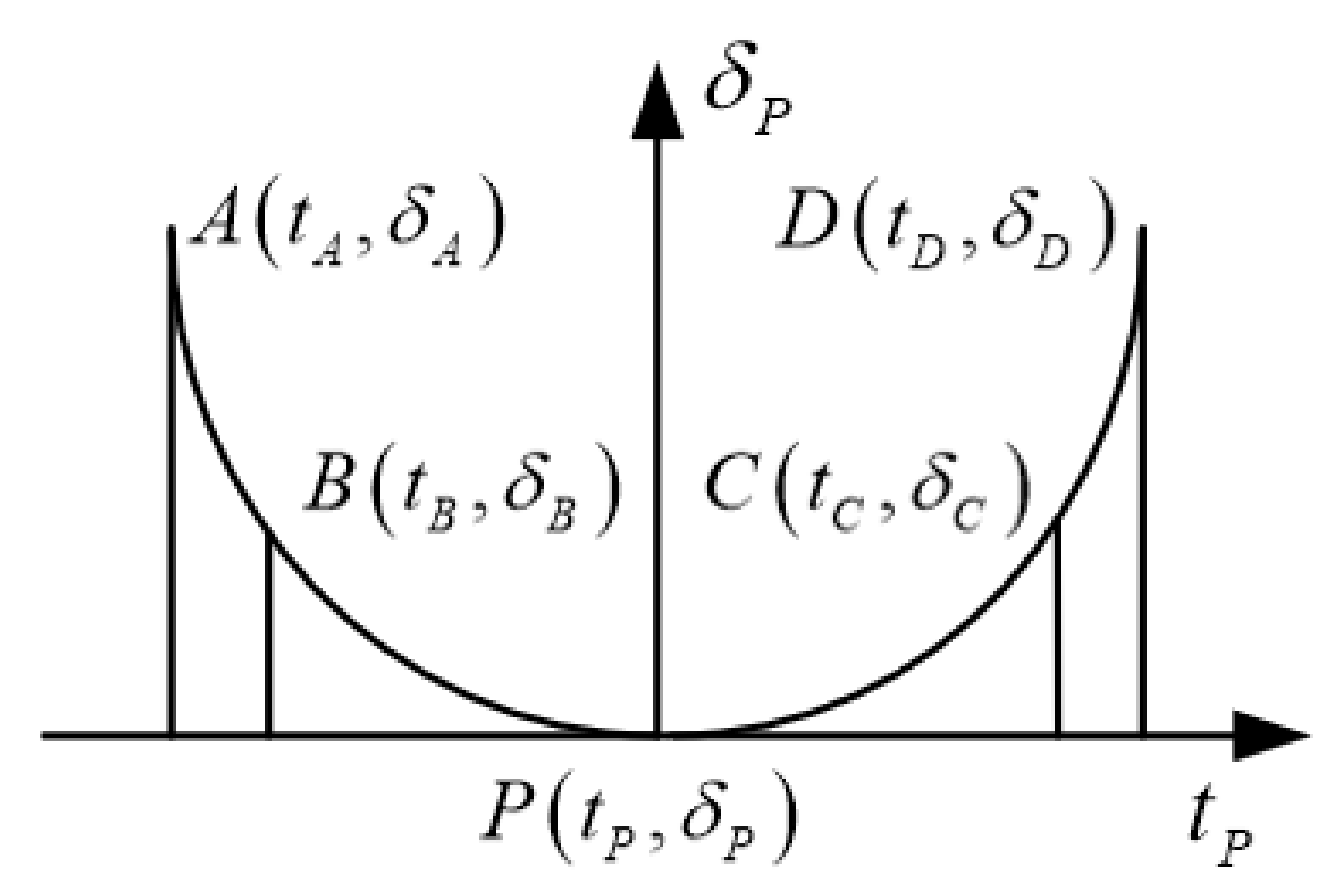
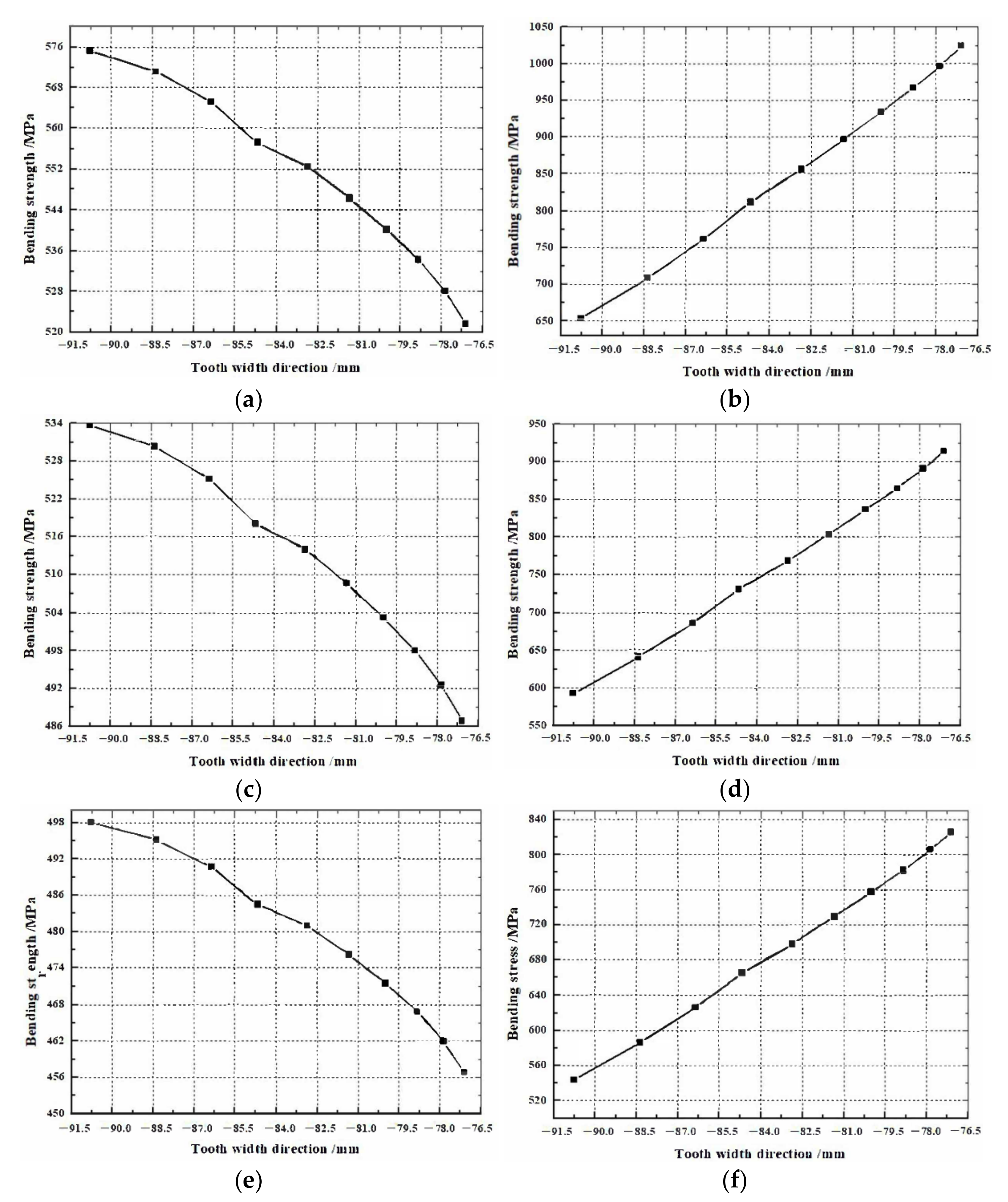
3.2. Strength Analysis of Face Gear Pair before and after Shifting
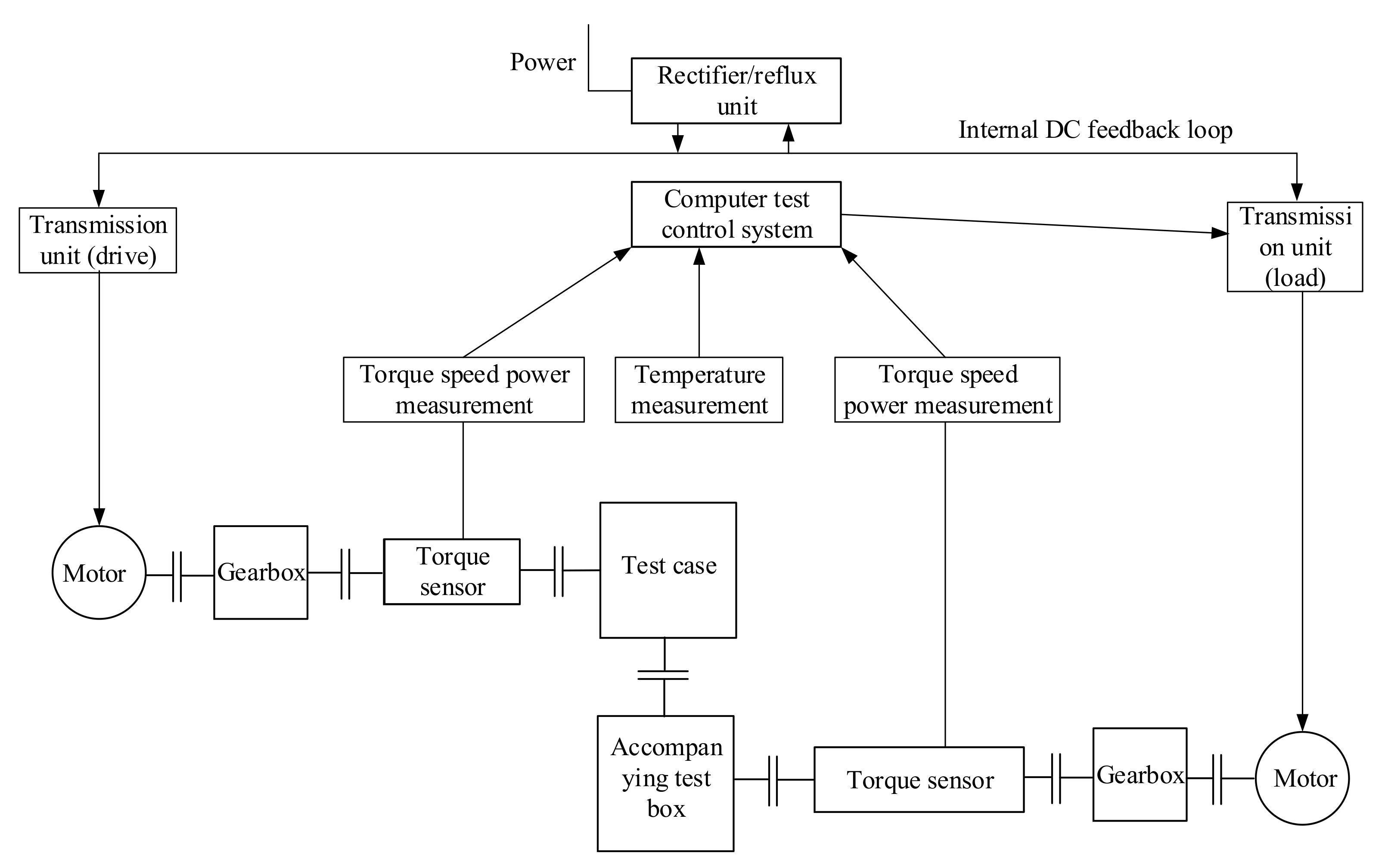
4. Electrochemical Machining and Transmission Performance Test
4.1. Electrochemical Machining Test of Profile Shifted Face Gear
4.2. Electrochemical Machining Test of Profile Shifted Face Gear
5. Conclusions
- (1)
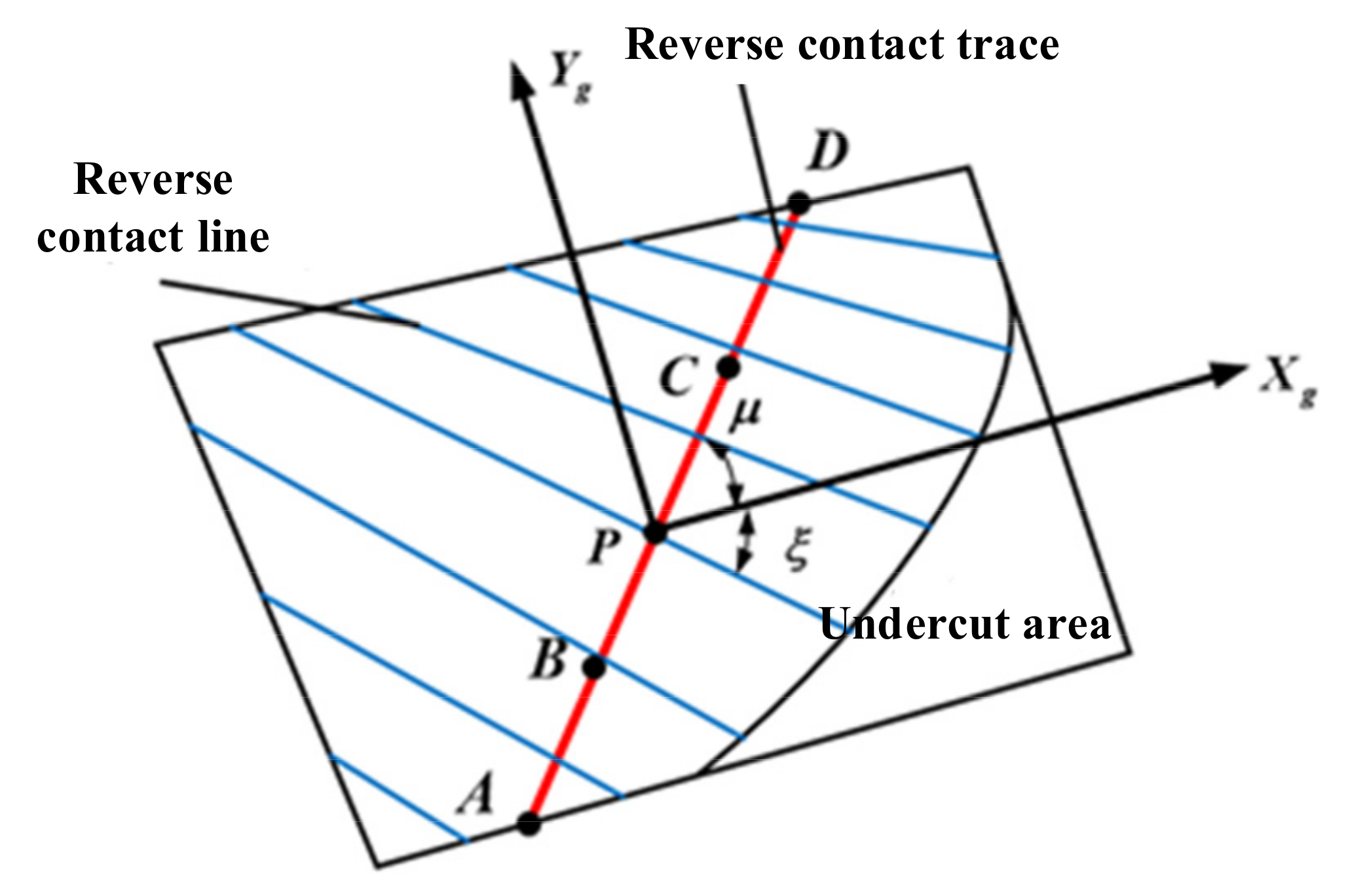
- According to the meshing principle of face gear, a contact trace reverse modification method was proposed to improve the strength performance of the face gear pair.
- (2)
- By analyzing the strength performance of the face gear pair under different parameters, the optimization parameters of the face gear pair based on strength matching were obtained.
- (3)
- According to the characteristics of materials, the machining of face gear by electrochemical machining was carried out, and the precision and consistency of the tooth surface were better than that of grinding.
- (4)
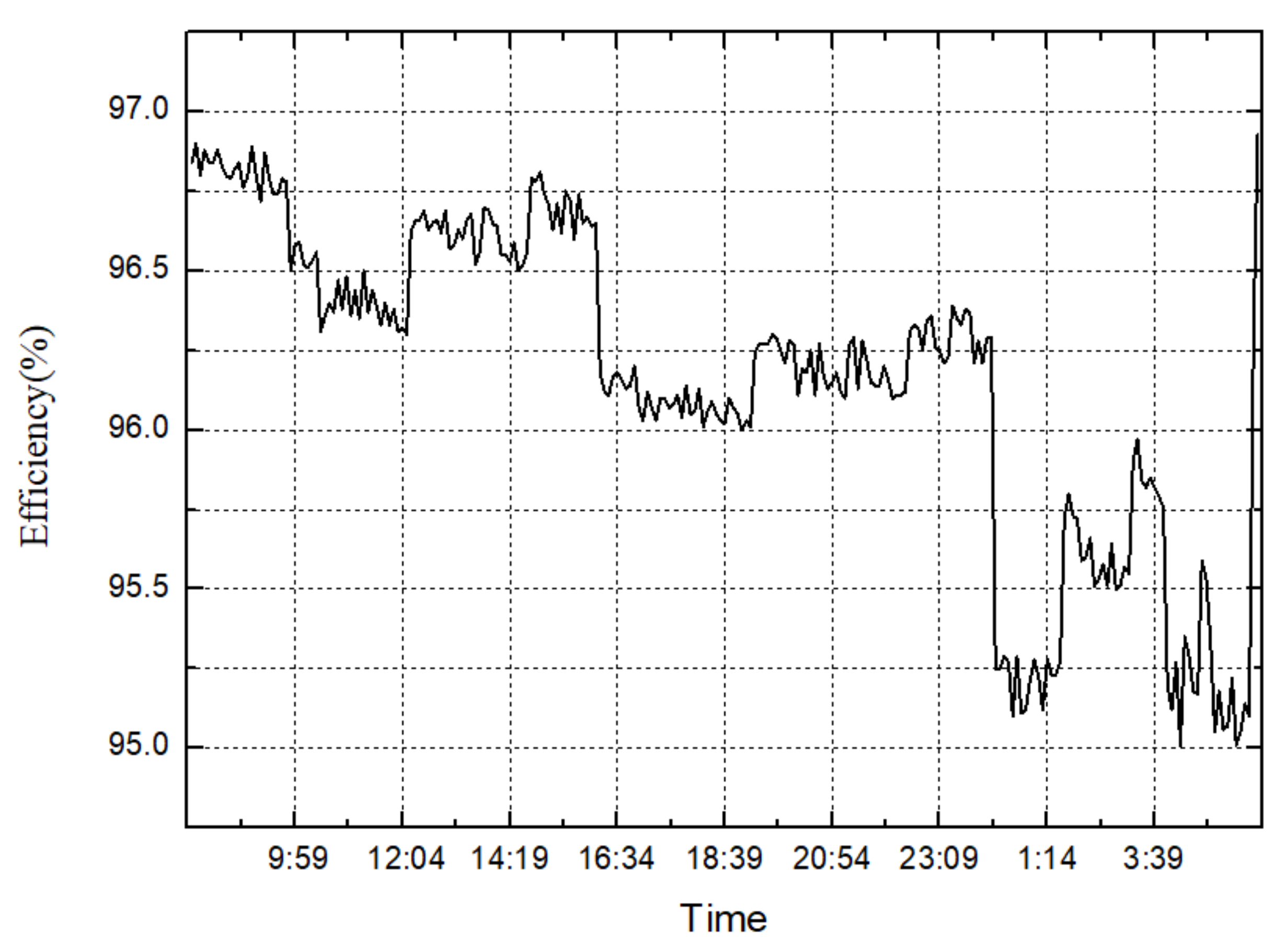
- The experimental results of face gear pair transmission showed that the transmission performance was stable and the strength performance was effectively improved after strength matching, and there were no abnormal phenomenon, such as tooth surface wear, before.
- (5)
- The method presented in this paper could be applied to the engineering popularization of other new transmission systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Pressure angle | |
| Variable parameter | |
| Rack tooth surface equation | |
| Displacement gear tooth surface equation | |
| Coordinate transformation matrix of to | |
| Meshing equation | |
| Relative speed | |
| Base circle radius of the shaper | |
| Tooth surface parameter marked in the direction | |
| Involute parameter | |
| Parameter used to determine the width of the tooth groove of the shaper on the base circle | |
| Reference radius of the shaper | |
| Number of shaper teeth | |
| Relative speed | |
| Conversion matrix | |
| Angle between the reverse contact trace and the projected coordinate axis | |
| Angle between the tooth contact line and the projected coordinate axis | |
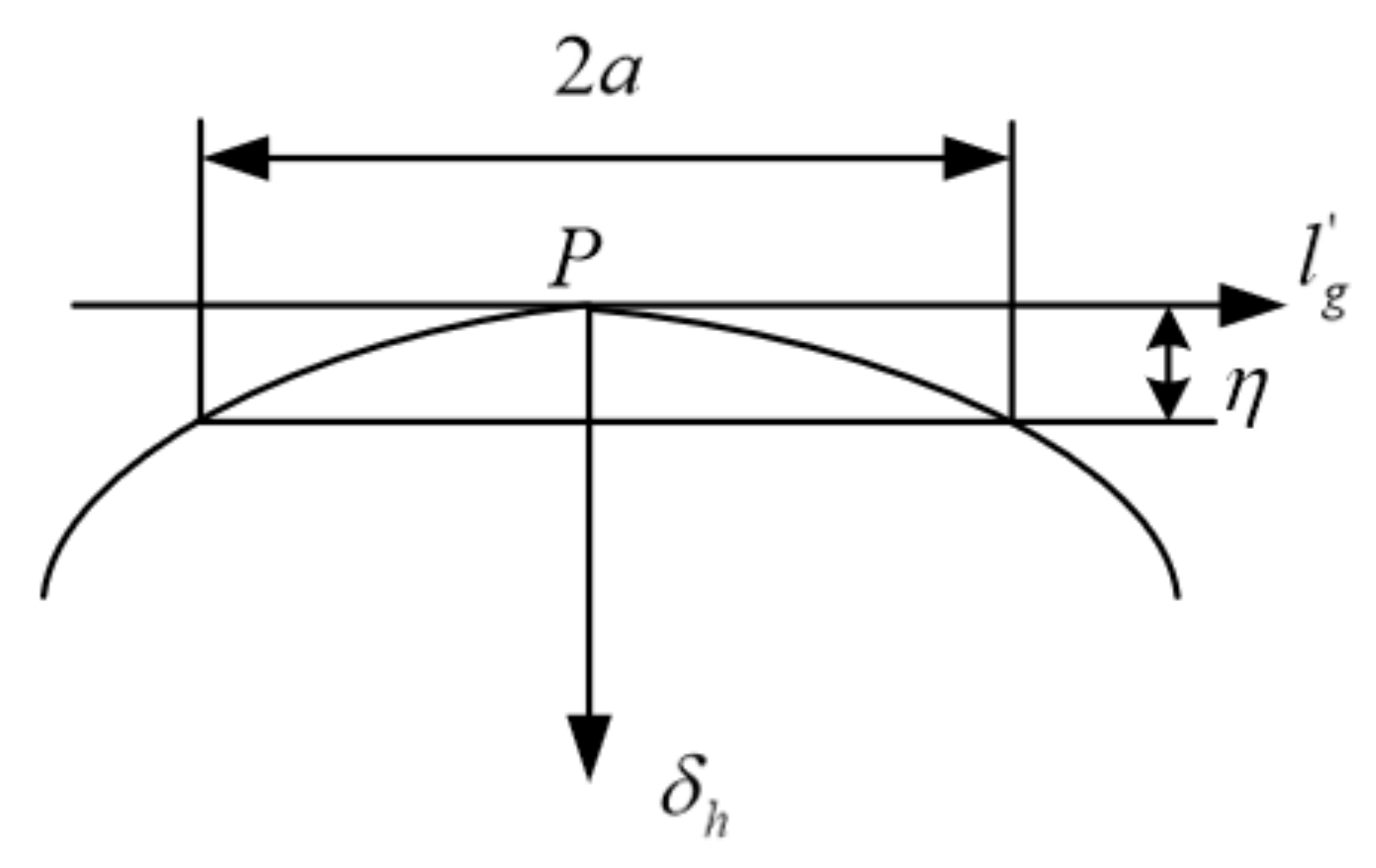
| Amount of variation | |
| Amount of modification along the contact line of the tooth surface |
References
- Litvin, F.L.; Gonzalez-Perez, I.; Fuentes, A.; Vecchiato, D.; Hansen, B.D.; Binneyet, D. Design, generation and stress analysis of face-gear drive with helical pinion. Comput. Methods Appl. Mech. Eng. 2005, 94, 3870–3901. [Google Scholar] [CrossRef]
- Zanzi, C.; Pedrero, J.I. Application of modified geometry of face gear drive. Comput. Methods Appl. Mech. Eng. 2005, 194, 3047–3066. [Google Scholar] [CrossRef]
- Li, Z.; Fan, J.H.; Zhu, R.P. Construction of Tooth Modeling Solutions of Face Gear Drives with an Involute Pinion. Iran. J. Sci. Technol. Trans. Mech. Eng. 2017, 42, 35–39. [Google Scholar] [CrossRef]
- Huang, X.D.; Zhang, X.M.; Ding, H. A novel relaxation-free analytical method for prediction of residual stress induced by mechanical load during orthogonal machining. Int. J. Mech. Sci. 2016, 115, 299–309. [Google Scholar] [CrossRef]
- Lin, C.; Wei, W.J.; Wang, S.; Xia, X.G.; Xin, Q.K. Bending stress analysis of eccentric straight and helical curve-face gear pair. Int. J. Mech. Mater. Des. 2020, 16, 401–414. [Google Scholar] [CrossRef]
- Zschippang, H.A.; Weikert, S.; Küük, K.A.; Wegener, K. Face-gear drive: Geometry generation and tooth contact analysis. Mech. Mach. Theory 2019, 142, 103576. [Google Scholar] [CrossRef]
- Wang, S.H.; Zhou, Y.S.; Tang, J.Y.; Tang, K.; Li, Z. Digital tooth contact analysis of face gear drives with an accurate measurement model of face gear tooth surface inspected by CMMs. Mech. Mach. Theory 2022, 167, 104498. [Google Scholar] [CrossRef]
- Tang, Z.W.; Zhou, Y.S.; Wang, S.H.; Zhu, J.; Tang, J.Y. An innovative geometric error compensation of the multi-axis CNC machine tools with non-rotary cutters to the accurate worm grinding of spur face gears. Mech. Mach. Theory 2022, 169, 104664. [Google Scholar] [CrossRef]
- Zhou, Y.S.; Tang, Z.W.; Shi, X.L.; Tang, J.Y.; Li, Z.M.Q. Efficient and accurate worm grinding of spur face gears according to an advanced geometrical analysis and a closed-loop manufacturing process. J. Cent. South Univ. 2022, 29, 1–13. [Google Scholar] [CrossRef]
- Ma, Y.; Feng, P.F.; Zhang, J.F.; Wu, Z.J.; Yu, D.W. Prediction of surface residual stress after end milling based on cutting force and temperature. J. Mater. Process. Technol. 2016, 235, 41–48. [Google Scholar] [CrossRef]
- Mo, S.; Zhang, T.; Jin, G.-G.; Cao, X.-L.; Gao, H.-J. Analytical Investigation on Load Sharing Characteristics of Herringbone Planetary Gear Train with Flexible Support and Floating Sun Gear. Mech. Mach. Theory 2020, 144, 103670. [Google Scholar] [CrossRef]
- Mo, S.; Yue, Z.X.; Feng, Z.Y.; Shi, L.J.; Zou, Z.X.; Dang, H.Y. Analytical investigation on load-sharing characteristics for multi-power face gear split flow system. J. Mech. Eng. Sci. 2020, 234, 676–692. [Google Scholar] [CrossRef]
- Ming, X.Z.; Gao, Q.; Yan, H.Z.; Liu, J.H.; Liao, C.J. Mathematical modeling and machining parameter optimization for the surface roughness of face gear grinding. Int. J. Adv. Manuf. Technol. 2017, 90, 2453–2460. [Google Scholar] [CrossRef]
- Dong, J.X.; Hu, Z.H.; Tang, J.Y.; Wang, Z.W.; Chen, S.Y. Investigation of the Vibration Features and Dynamic Load Sharing Characteristics of Concentric Face Gear Torque Split Transmission. J. Comput. Nonlinear Dyn. 2021, 16, 071003. [Google Scholar] [CrossRef]
- Lin, C.; Wei, Y.Q.; Cai, Z.Q. Study on the compound transmission mechanism of the curve-face gear based on screw theory. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 3115–3124. [Google Scholar] [CrossRef]
- Pathak, S.; Jain, N.K.; Palani, I.A. Effect of honing gear hardness on microgeometry and surface quality improvement of straight bevel gears in PECH process. Int. J. Adv. Manuf. Technol. 2016, 85, 2197–2205. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Chen, Y.Y.; Zhou, G.M.; Lv, Q.J.; Zhang, Z.Z.; Tang, W.; Liu, Y. Roughness model for tooth surfaces of spiral bevel gears under grinding. Mech. Mach. Theory 2016, 104, 17–30. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Chu, X.M.; Huang, Y.Z.; Su, G.Y.; Liu, D.W. Surface residual stress distribution for face gear under grinding with a long-radius disk wheel. Int. J. Mech. Sci. 2019, 159, 260–266. [Google Scholar] [CrossRef]
- Chu, X.M.; Wang, Y.Z.; Du, S.F.; Huang, Y.Z.; Su, G.Y.; Liu, D.W.; Zang, L. An efficient generation grinding method for spur face gear along contact trace using disk CBN wheel. Int. J. Adv. Manuf. Technol. 2020, 110, 27–29. [Google Scholar] [CrossRef]




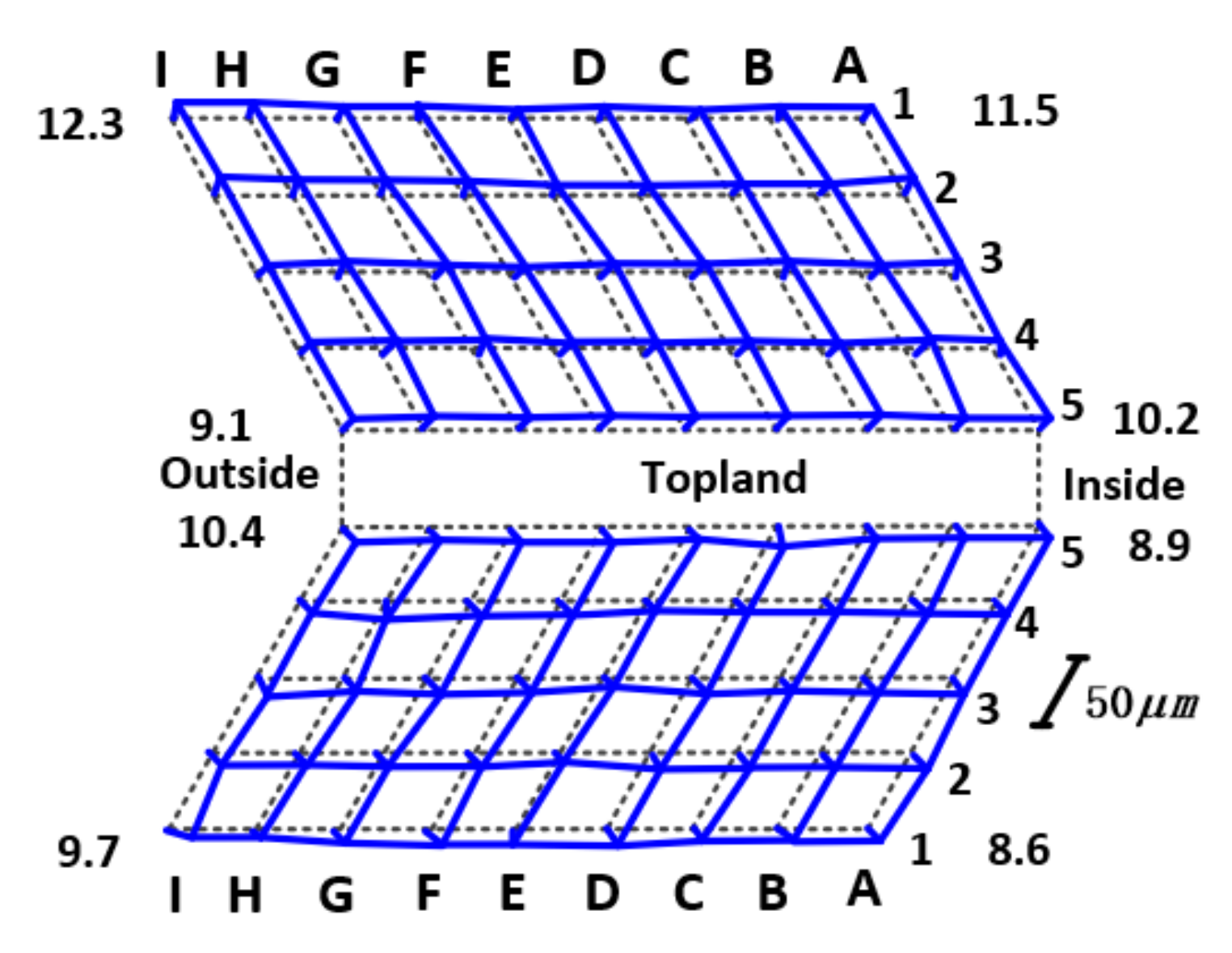


| Parameters | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 |
|---|---|---|---|---|---|---|
| Module | 9 | 9 | 9 | 9 | 9 | 9 |
| Pressure angle | 25° | 25° | 25° | 30° | 30° | 30° |
| Tooth number of the face gear | 17 | 17 | 17 | 17 | 17 | 17 |
| Tooth number of the pinion | 12 | 12 | 12 | 12 | 12 | 12 |
| Modification coefficient | 0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 |
| Tooth width | 20 mm | 20 mm | 20 mm | 30 mm | 30 mm | 30 mm |
| Equivalent input torque | 3000 N∙m | |||||
| Rotation rate | 183 r/min | |||||
| C | Mn | Si | S | P | Cr | Ni |
|---|---|---|---|---|---|---|
| 0.15~0.20 | 0.30~0.60 | 0.35 | 0.010 | 0.015 | 0.80~1.10 | 3.75~4.25 |
| Parameters | Value |
|---|---|
| Electrochemical volume equivalent | 2.22 mm3/(A ∙ min) |
| Processing temperature | (30 ± 2) °C |
| Electrolyte formula | 25% NaNO3 + 75% NaCl |
| Electrolyte concentration | 7.5% |
| Conductivity of electrolyte | 0.0095 (Ω ∙ mm)−1 |
| Processing voltage | 8 V |
| Feed rate | 0.5 mm/min |
| Current efficiency of electrolyte | 70% |
| Feed depth | 1 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, X.; Zeng, H.; Wang, Y.; Huang, Y. Strength Matching Method of Face Gear Pair Considering Service Space Limitation to Improve Strength Performance. Materials 2022, 15, 7081. https://doi.org/10.3390/ma15207081
Chu X, Zeng H, Wang Y, Huang Y. Strength Matching Method of Face Gear Pair Considering Service Space Limitation to Improve Strength Performance. Materials. 2022; 15(20):7081. https://doi.org/10.3390/ma15207081
Chicago/Turabian StyleChu, Xiaomeng, Hong Zeng, Yanzhong Wang, and Yizhan Huang. 2022. "Strength Matching Method of Face Gear Pair Considering Service Space Limitation to Improve Strength Performance" Materials 15, no. 20: 7081. https://doi.org/10.3390/ma15207081
APA StyleChu, X., Zeng, H., Wang, Y., & Huang, Y. (2022). Strength Matching Method of Face Gear Pair Considering Service Space Limitation to Improve Strength Performance. Materials, 15(20), 7081. https://doi.org/10.3390/ma15207081









