A Soft Computing-Based Analysis of Cutting Rate and Recast Layer Thickness for AZ31 Alloy on WEDM Using RSM-MOPSO
Abstract
:1. Introduction
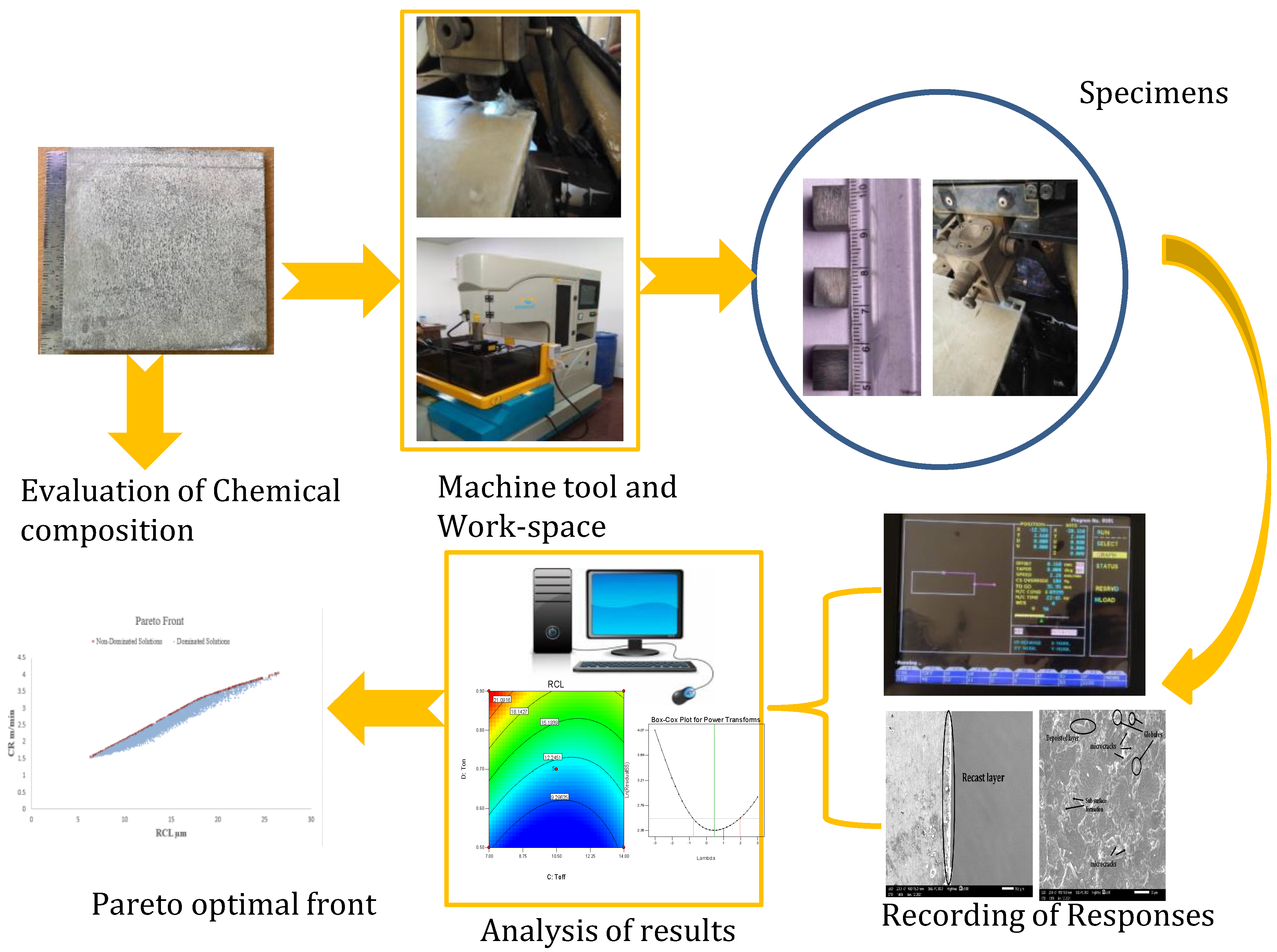
2. Materials and Methods
- I.
- The SF, SV, Ton, and Toff are input machining variables planned per the RSM-based BBD to develop one experimental array.
- II.
- The response characteristics (i.e., CR and RCL) are measured corresponding to the experimental array.
- III.
- The analysis is to be carried out for each response, and the mathematical models are to be developed for the response characteristics.
- IV.
- Hybrid optimization is to be processed by the MOPSO on the mathematical models developed by RSM.
- V.
- Validation experiments are to be performed on the random predicted solution suggested by the optimal Pareto front.
- VI.
- The surface morphology of the machined part (machined at the optimal setting suggested by the hybrid approach) is also studied for its features.
2.1. Experimental Setup
2.2. Experimental Array
3. Methodologies
3.1. Response Surface Methodology (RSM)
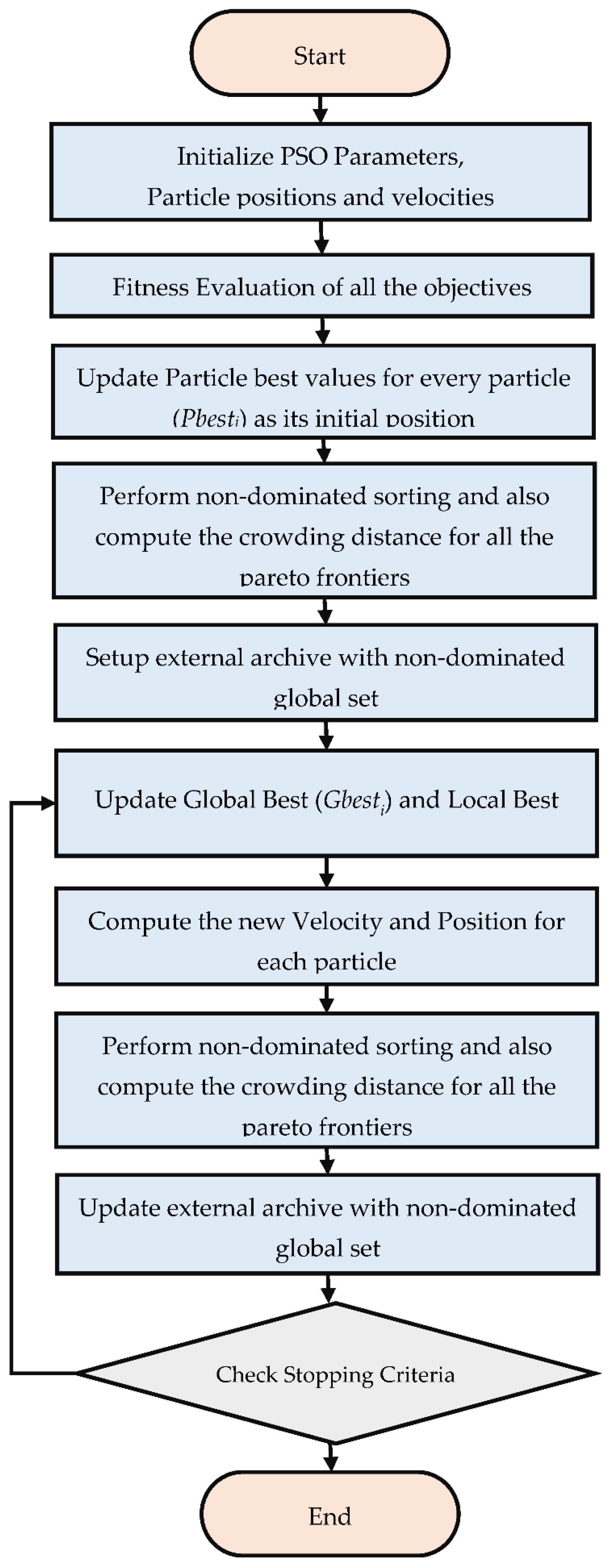
3.2. Implementing Multi-Objective Particle Swarm Optimization (MOPSO)
3.2.1. Multiple Objective Optimization (MOO)
- In all the objectives, solution X1 should not be worse than X2.
- In at least one of the objectives, the solution X1should be better than X2.
3.2.2. Particle Swarm Optimization (PSO)
3.2.3. Multi-Objective Particle Swarm Optimization (MOPSO)
4. Results and Discussion
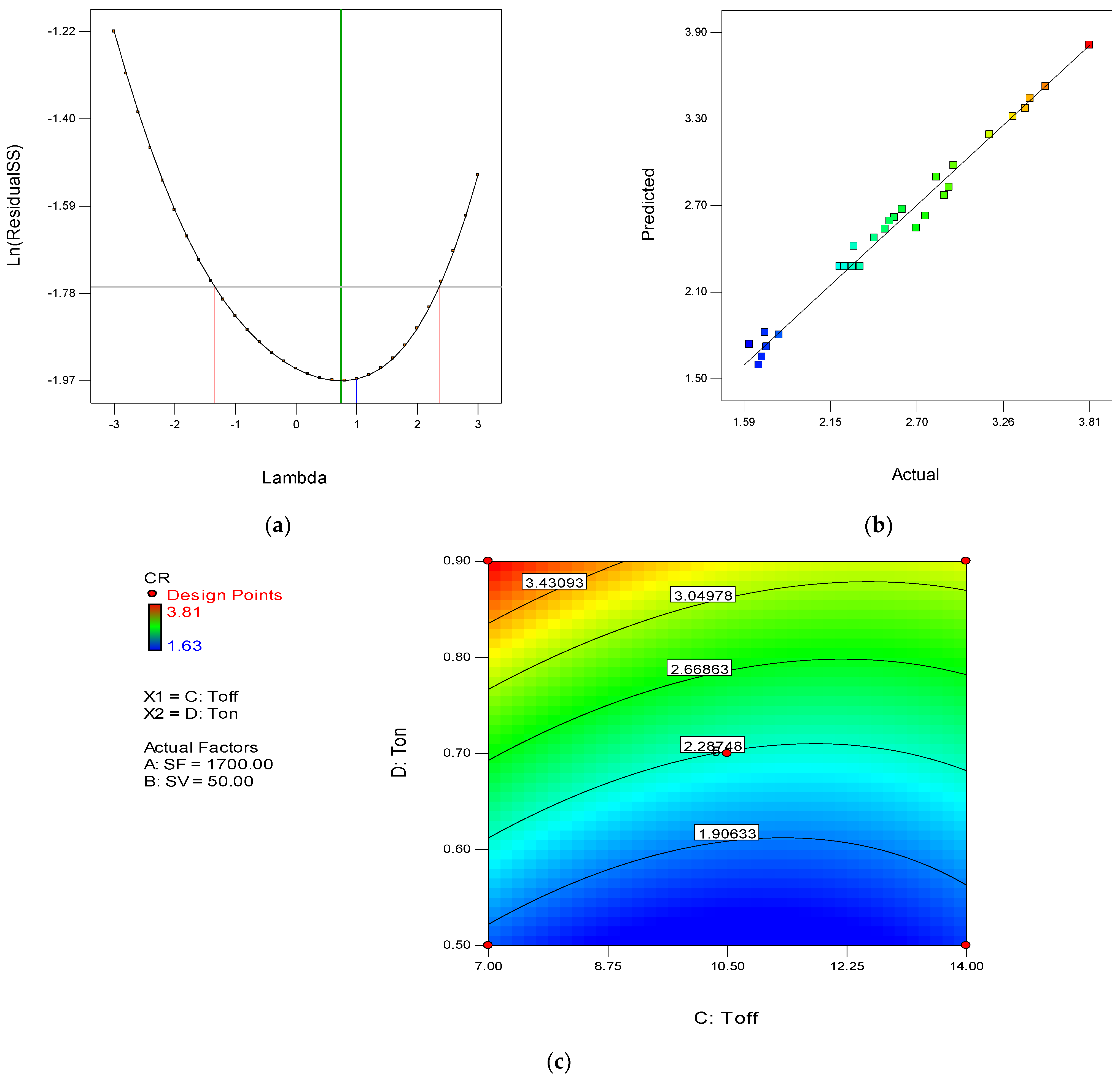
4.1. Analysis of Cutting Rate (CR)
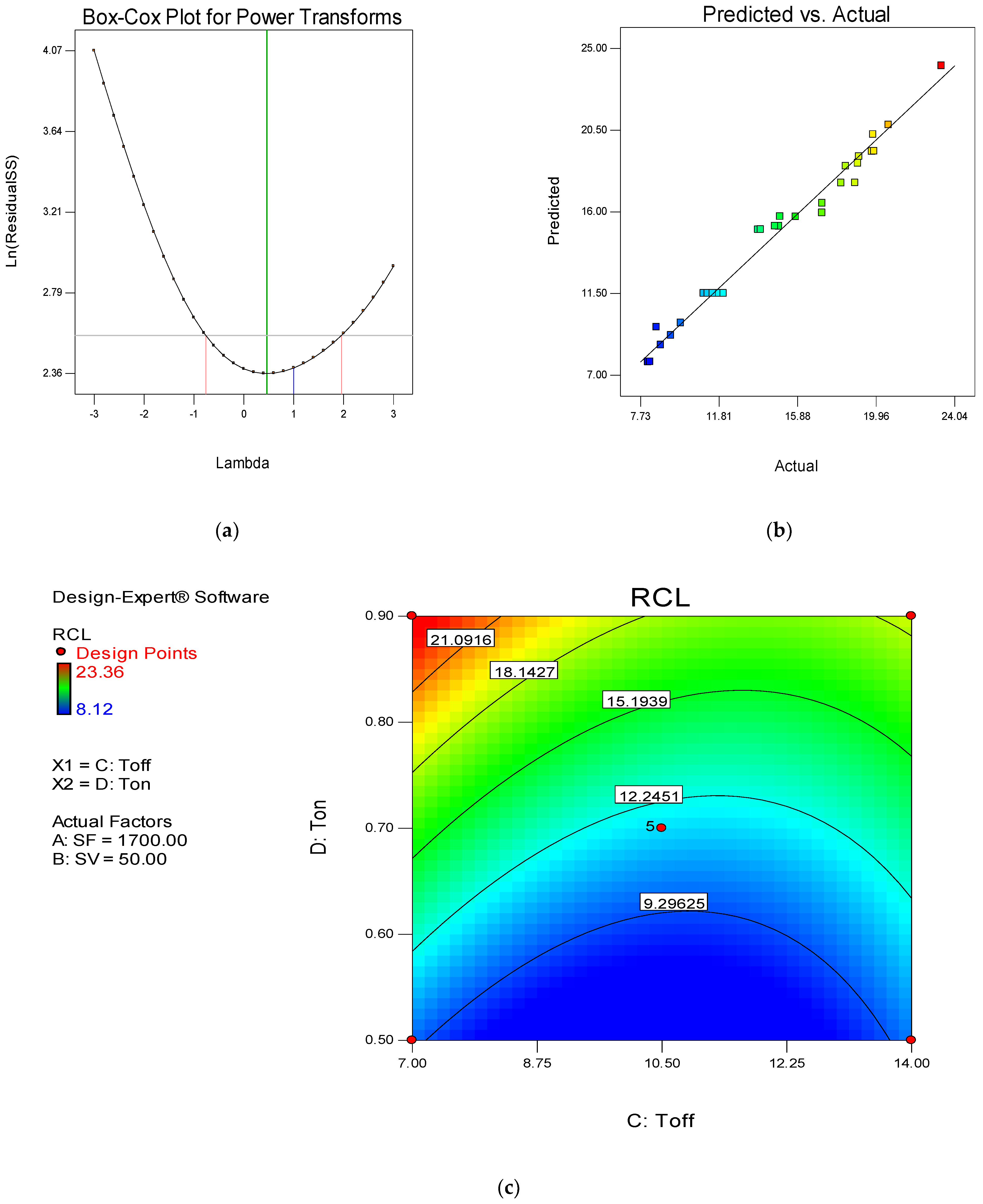
4.2. Analysis of Recast Layer Thickness (RCL)
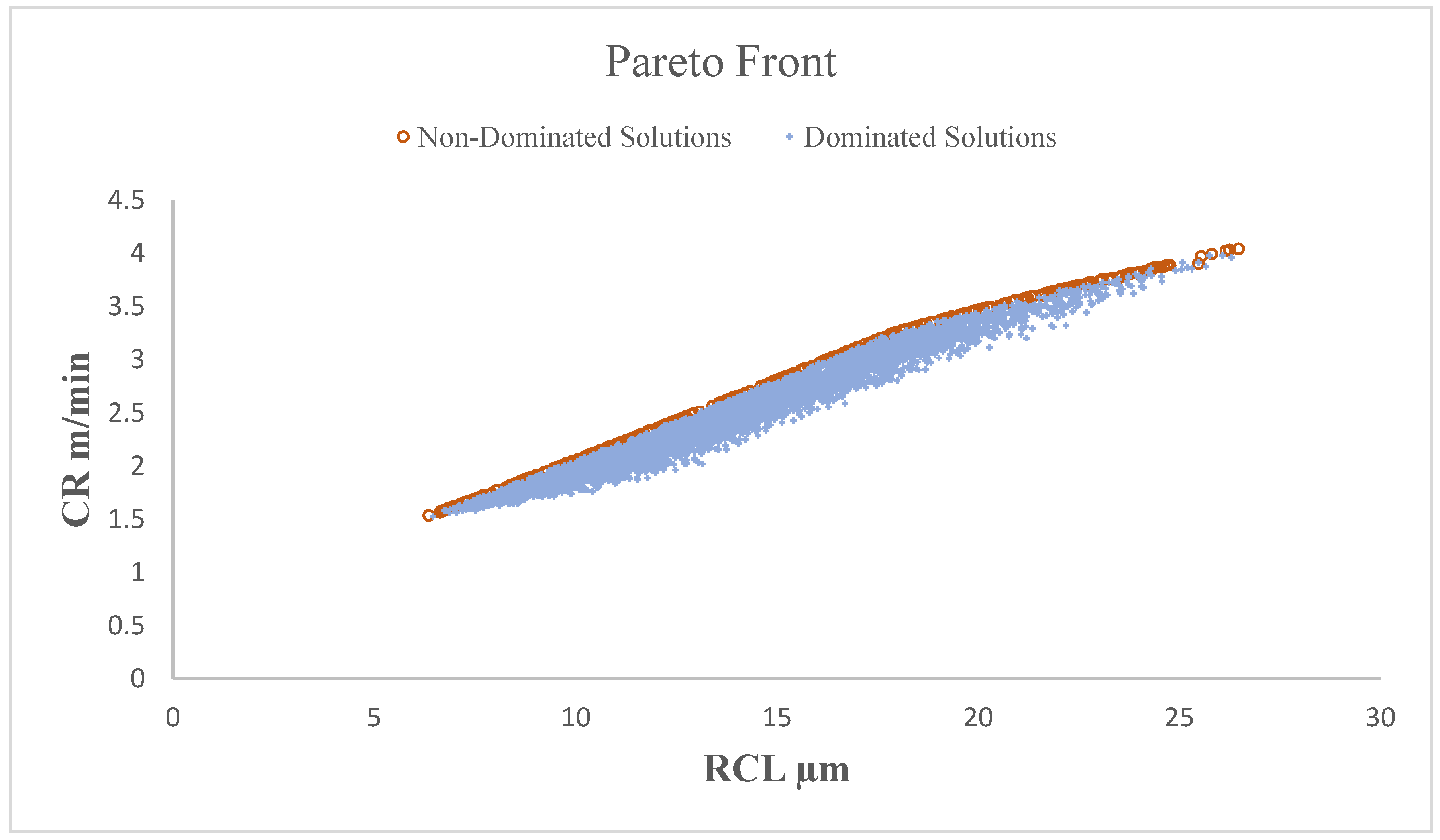
4.3. Multiple Performance Measure Optimization by MOPSO
- Swarm size = 100;
- Number of iterations = 150;
- Size of external repository = 200;
- Acceleration coefficients C1 = 1 and C2 = 1; and
- The minimum and maximum values of inertia are 0.1 and 0.4, respectively.
4.4. Confirmation Experiments
5. Morphological Analysis of Machined Surface
6. Conclusions
- The proposed hybrid approach of optimization is a reliable method to predict the WEDM responses. ANOVA results show that the Ton is the most significant process variable for CR and RCL. Furthermore, an improvement in the response characteristics value is obtained after the confirmation test.
- The hybrid approach suggested different solutions for various response characteristics selection. Based on that, SF: 1830; SV: 42 V; Toff: 7 µs; Ton: 0.9 µs are suggested for maximum CR (3.18 m/min), and SF: 1720; SV: 51 V; Toff:10.5 µs; Ton: 0.5 µs are suggested for minimum RCL (6.37 µm).
- The proposed approach can help the decision-maker select process variables depending upon their requirement of response characteristics during the machining of AZ31 alloy.
- The SEM micrograph shows the debris, deposited lumps, and micro-cracks at the optimized process variables.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Analysis of variance—ANOVA | Pulse on-time—Ton |
| Box–Behnken design—BBD | Recast layer—RCL |
| Cutting rate—CR | Response surface methodology—RSM |
| Multi-Objective Optimization—MOO | Servo feed—SF |
| Multi-Objective Particle Swarm Optimization—MOPSO | Servo voltage—SV |
| ϵ0, ϵk, ϵkk, and ϵkn—Regression coefficients | m—Number of process variables |
| A—Process variables | k—Level of process variables |
| Gbest—Global Best | Pbest—Particle best |
| x—Position of particle | v—Velocity of particle |
| c1 and c2—Coefficients | w—Inertia weight |
| Pulse off-time—Toff | Wire-cut Electric Discharge Machining—WEDM |
References
- Kavimani, V.; Prakash, K.S.; Thankachan, T. Influence of machining parameters on wire electrical discharge machining performance of reduced graphene oxide/magnesium composite and its surface integrity characteristics. Compos. Part B Eng. 2019, 167, 621–630. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Abraham, G.J.; Mishra, A.; Kain, V.; Dey, G.K. Corrosion Behavior of Wire Electrical Discharge Machined Surfaces of P91 Steel. J. Mater. Eng. Perform. 2018, 27, 4561–4570. [Google Scholar] [CrossRef]
- Escobar, A.M.; de Lange, D.F.; Medellín Castillo, H.I. Simplified plasma channel formation model for the electrical discharge machining process. Int. J. Adv. Manuf. Technol. 2020, 106, 143–153. [Google Scholar] [CrossRef]
- Razeghiyadaki, A.; Molardi, C.; Talamona, D.; Perveen, A. Modeling of Material Removal Rate and Surface Roughness Generated during Electro-Discharge Machining. Machines 2019, 7, 47. [Google Scholar] [CrossRef] [Green Version]
- Khullar, V.R.; Sharma, N.; Kishore, S.; Sharma, R. RSM-and NSGA-II-based multiple performance characteristics optimization of EDM parameters for AISI 5160. Arab. J. Sci. Eng. Eng. 2017, 42, 1917–1928. [Google Scholar] [CrossRef]
- Aggarwal, V.; Pruncu, C.I.; Singh, J.; Sharma, S.; Pimenov, D.Y. Empirical Investigations during WEDM of Ni-27Cu-3.15Al-2Fe-1.5Mn Based Superalloy for High Temperature Corrosion Resistance Applications. Materials 2020, 13, 3470. [Google Scholar] [CrossRef] [PubMed]
- Sen, B.; Hussain, S.A.; Gupta, A.D.; Gupta, M.K.; Pimenov, D.Y.; Mikołajczyk, T. Application of Type-2 Fuzzy AHP-ARAS for Selecting Optimal WEDM Parameters. Metals 2021, 11, 42. [Google Scholar] [CrossRef]
- Lenin, N.; Sivakumar, M.; Selvakumar, G.; Rajamani, D.; Sivalingam, V.; Gupta, M.K.; Mikolajczyk, T.; Pimenov, D.Y. Optimization of Process Control Parameters for WEDM of Al-LM25/Fly Ash/B4C Hybrid Composites Using Evolutionary Algorithms: A Comparative Study. Metals 2021, 11, 1105. [Google Scholar] [CrossRef]
- Sharma, N.; Raj, T.; Jangra, K.K. Parameter optimization and experimental study on wire electrical discharge machining of porous Ni40Ti60 alloy. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 231, 956–970. [Google Scholar] [CrossRef]
- Poinern, G.E.J.; Brundavanam, S.; Fawcett, D. Biomedical magnesium alloys: A review of material properties, surface modifications and potential as a biodegradable orthopaedic implant. Am. J. Biomed. Eng. 2012, 2, 218–240. [Google Scholar] [CrossRef] [Green Version]
- Zeng, R.; Dietzel, W.; Witte, F.; Hort, N.; Blawert, C. Progress and Challenge for Magnesium Alloys as Biomaterials. Adv. Eng. Mater. 2008, 10, B3–B14. [Google Scholar] [CrossRef]
- Kannan, M.B.; Raman, R.K.S. In vitro degradation and mechanical integrity of calcium-containing magnesium alloys in modified-simulated body fluid. Biomaterials 2008, 29, 2306–2314. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.-J.; Lin, X.-Z.; Liu, C.-H.; Yang, R.-S.; Zheng, X.-W.; Gong, M. Fabrication and corrosion resistance of a hydrophobic micro-arc oxidation coating on AZ31 Mg alloy. Corros. Sci. 2015, 90, 402–412. [Google Scholar] [CrossRef]
- Lu, D.; Huang, Y.; Jiang, Q.; Zheng, M.; Duan, J.; Hou, B. An approach to fabricating protective coatings on a magnesium alloy utilising alumina. Surf. Coat. Technol. 2019, 367, 336–340. [Google Scholar] [CrossRef]
- Kumar, K.; Gill, R.S.; Batra, U. Challenges and opportunities for biodegradable magnesium alloy implants. Mater. Technol. 2018, 33, 153–172. [Google Scholar] [CrossRef]
- Choudhary, L.; Singh Raman, R.K. Mechanical integrity of magnesium alloys in a physiological environment: Slow strain rate testing based study. Eng. Fract. Mech. 2013, 103, 94–102. [Google Scholar] [CrossRef]
- Cho, D.H.; Lee, B.W.; Park, J.Y.; Cho, K.M.; Park, I.M. Effect of Mn addition on corrosion properties of biodegradable Mg-4Zn-0.5 Ca-xMn alloys. J. Alloy. Compd. 2017, 695, 1166–1174. [Google Scholar] [CrossRef]
- Xu, J.; Xia, K.; Lian, Z.; Zhang, L.; Yu, H.; Yu, Z.; Weng, Z.; Wang, Z. Surface properties on magnesium alloy and corrosion behaviour based high-speed wire electrical discharge machine power tubes. Micro Nano Lett. 2016, 11, 15–19. [Google Scholar] [CrossRef]
- Shufa, S.; Shichun, D.; Pengxiang, L.; Dongbo, W.; Jie, Y.; Yu-peng, G. Microstructure and Properties of Metamor-Phic Layer Formed on Mg-RE Alloy in Micro-EDM Process. Acta Metall. Sin. 2013, 49, 251–256. [Google Scholar]
- Klocke, F.; Schwade, M.; Klink, A.; Veselovac, D.; Kopp, A. Influence of electro discharge machining of biodegradable magnesium on the biocompatibility. Procedia CIRP 2013, 5, 88–93. [Google Scholar] [CrossRef] [Green Version]
- Yoo, B.; Shin, K.R.; Hwang, D.Y.; Lee, D.H.; Shin, D.H. Effect of surface roughness on leakage current and corrosion resistance of oxide layer on AZ91 Mg alloy prepared by plasma electrolytic oxidation. Appl. Surf. Sci. 2010, 256, 6667–6672. [Google Scholar] [CrossRef]
- Walter, R.; Kannan, M.B.; He, Y.; Sandham, A. Effect of surface roughness on the in vitro degradation behaviour of a biodegradable magnesium-based alloy. Appl. Surf. Sci. 2013, 279, 343–348. [Google Scholar] [CrossRef]
- Song, G.-L.; Xu, Z. The surface, microstructure and corrosion of magnesium alloy AZ31 sheet. Electrochim. Acta 2010, 55, 4148–4161. [Google Scholar] [CrossRef]
- Yue, T.M.; Yan, L.J.; Man, H.C. The Effect of Machined Surface Condition on the Corrosion Behavior of Magnesium ZM51/SiC Composite. Mater. Manuf. Process. 2004, 19, 123–138. [Google Scholar] [CrossRef]
- Siddiqui, T.U.; Ramkumar, J. Micro-wire electric discharge machining of Mg alloy used in biodegradable orthopaedic implants. Mater. Today Proc. 2017, 4, 10273–10277. [Google Scholar] [CrossRef]
- Qiu, Y.; Chen, L.; Yang, J.; Zeng, D.; Liu, H.; Han, J.; Li, Q.; Li, J.; Tu, X.; Li, W. Mechanistic Understanding of the Corrosion Behaviors of AZ31 Finished by Wire Electric Discharge Machining. J. Electrochem. Soc. 2021, 168, 071507. [Google Scholar] [CrossRef]
- Jangra, K.; Grover, S.; Aggarwal, A. Simultaneous optimization of material removal rate and surface roughness for WEDM of WC-Co composite using grey relational analysis along with Taguchi method. Int. J. Ind. Eng. Comput. 2011, 2, 479–490. [Google Scholar] [CrossRef]
- Goswami, A.; Kumar, J. Optimization in wire-cut EDM of Nimonic-80A using Taguchi’s approach and utility concept. Eng. Sci. Technol. Int. J. 2014, 17, 236–246. [Google Scholar] [CrossRef] [Green Version]
- Sharma, N.; Khanna, R.; Gupta, R.D.; Sharma, R. Modeling and multiresponse optimization on WEDM for HSLA by RSM. Int. J. Adv. Manuf. Technol. 2013, 67, 2269–2281. [Google Scholar] [CrossRef]
- Goyal, A.; Gautam, N.; Pathak, V.K. An adaptive neuro-fuzzy and NSGA-II-based hybrid approach for modelling and multi-objective optimization of WEDM quality characteristics during machining titanium alloy. Neural Comput. Appl. 2021, 33, 16659–16674. [Google Scholar] [CrossRef]
- Klostermeier, A.D.D.M.A. Magnesium AZ31B Alloy (UNS M11311). November ed.; AZo Materials: 2012. Available online: https://www.azom.com/article.aspx?ArticleID=6707 (accessed on 10 October 2019).
- Kumar, R.; Bilga, P.S.; Singh, S. An Investigation of Energy Efficiency in Finish Turning of EN 353 Alloy Steel. Procedia CIRP 2021, 98, 654–659. [Google Scholar] [CrossRef]
- Sidhu, A.S.; Singh, S.; Kumar, R.; Pimenov, D.Y.; Giasin, K. Prioritizing Energy-Intensive Machining Operations and Gauging the Influence of Electric Parameters: An Industrial Case Study. Energies 2021, 14, 4761. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, S.; Sidhu, A.S.; Pruncu, C.I. Bibliometric Analysis of Specific Energy Consumption (SEC) in Machining Operations: A Sustainable Response. Sustainability 2021, 13, 5617. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, S.; Bilga, P.S.; Jatin; Singh, J.; Singh, S.; Scutaru, M.L.; Pruncu, C.I. Revealing the benefits of entropy weights method for multi-objective optimization in machining operations: A critical review. J. Mater. Res. Technol. 2021, 10, 1471–1492. [Google Scholar] [CrossRef]
- Kumar, R.; Bilga, P.S.; Singh, S. Multi objective optimization using different methods of assigning weights to energy consumption responses, surface roughness and material removal rate during rough turning operation. J. Clean. Prod. 2017, 164, 45–57. [Google Scholar] [CrossRef]
- Bilga, P.S.; Singh, S.; Kumar, R. Optimization of energy consumption response parameters for turning operation using Taguchi method. J. Clean. Prod. 2016, 137, 1406–1417. [Google Scholar] [CrossRef]
- Gallagher, R.H. Optimization: Theory and applications, S. S. Rao, Wiley Eastern Ltd. No. of pages: 711. Int. J. Numer. Methods Eng. 1979, 14, 1734. [Google Scholar] [CrossRef]
- Fonseca, C.M.; Fleming, P.J. Genetic Algorithms for Multi-objective Optimization: Formulation Discussion and Generalization. In Proceedings of the 5th International Conference on Genetic Algorithms, San Francisco, CA, USA, 1 June 1993; pp. 416–423. [Google Scholar]
- Moore, H.L. Cours d’Économie Politique. By VILFREDO PARETO, Professeur à l’Université de Lausanne. Vol. I. Pp. 430. I896. Vol. II. Pp. 426. I897. Lausanne: F. Rouge. ANNALS Am. Acad. Political Soc. Sci. 1897, 9, 128–131. [Google Scholar] [CrossRef]
- Deb, K. Multi-objective optimisation using evolutionary algorithms: An introduction. In Multi-Objective Evolutionary Optimisation for Product Design and Manufacturing; Springer: Berlin/Heidelberg, Germany, 2011; pp. 3–34. Available online: https://www.egr.msu.edu/~kdeb/papers/k2011003.pdf (accessed on 10 October 2021).
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Shi, Y.; Eberhart, R.C. Parameter selection in particle swarm optimization. In Evolutionary Programming VII; Springer: Berlin/Heidelberg, Germany, 1998; pp. 591–600. [Google Scholar]
- Eberhart; Yuhui, S. Particle swarm optimization: Developments, applications and resources. In Proceedings of the 2001 Congress on Evolutionary Computation (IEEE Cat. No.01TH8546), Seoul, Korea, 27–30 May 2001; Volume 81, pp. 81–86. [Google Scholar]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, IEEE World Congress on Computational Intelligence (Cat. No.98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Coello, C.A.C.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation, CEC’02 (Cat. No.02TH8600), Honolulu, HI, USA, 12–17 May 2002; Volume 1052, pp. 1051–1056. [Google Scholar]
- Coello, C.A.; Pulido, G.T. Multi-objective optimization using a micro-genetic algorithm. In Proceedings of the 3rd Annual Conference on Genetic and Evolutionary Computation, San Francisco, CA, USA, 7 July 2001; pp. 274–282. [Google Scholar]
- Knowles, J.D.; Corne, D.W. Approximating the Nondominated Front Using the Pareto Archived Evolution Strategy. Evol. Comput. 2000, 8, 149–172. [Google Scholar] [CrossRef] [PubMed]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Rawat, P.; Chauhan, S. Particle swarm optimization-based energy efficient clustering protocol in wireless sensor network. Neural Comput. Appl. 2021, 33, 14147–14165. [Google Scholar] [CrossRef]
- Nshimirimana, R.; Abraham, A.; Nothnagel, G. A multi-objective particle swarm for constraint and unconstrained problems. Neural Comput. Appl. 2021, 33, 11355–11385. [Google Scholar] [CrossRef]
- Roy, R.K. Design of Experiments Using the Taguchi Approach: 16 Steps to Product and Process Improvement; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Box, G.E.; Wilson, K.B. On the experimental attainment of optimum conditions. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; pp. 270–310. [Google Scholar]
- Gupta, N.K.; Somani, N.; Prakash, C.; Singh, R.; Walia, A.S.; Singh, S.; Pruncu, C.I. Revealing the WEDM Process Parameters for the Machining of Pure and Heat-Treated Titanium (Ti-6Al-4V) Alloy. Materials 2021, 14, 2292. [Google Scholar] [CrossRef] [PubMed]
- Sharma, N.; Khanna, R.; Sharma, Y.K.; Gupta, R.D. Multi-quality characteristics optimisation on WEDM for Ti-6Al-4V using Taguchi-grey relational theory. Int. J. Mach. Mach. Mater. 2019, 21, 66–81. [Google Scholar]
- Manjaiah, M.; Laubscher, R.F.; Kumar, A.; Basavarajappa, S.J.I.J.o.M. Parametric optimization of MRR and surface roughness in wire electro discharge machining (WEDM) of D2 steel using Taguchi-based utility approach. Int. J. Mech. Mater. Eng. 2016, 11, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Shandilya, P.; Bisaria, H.; Jain, P. Parametric study on the recast layer during EDWC of a Ni-rich NiTi shape memory alloy. J. Micromanufacturing 2018, 1, 134–141. [Google Scholar] [CrossRef]
- Sharma, P.; Chakradhar, D.; Narendranath, S. Evaluation of WEDM performance characteristics of Inconel 706 for turbine disk application. Mater. Des. 2015, 88, 558–566. [Google Scholar] [CrossRef]
- Kunieda, M.; Lauwers, B.; Rajurkar, K.P.; Schumacher, B.M. Advancing EDM through Fundamental Insight into the Process. CIRP Ann. 2005, 54, 64–87. [Google Scholar] [CrossRef]
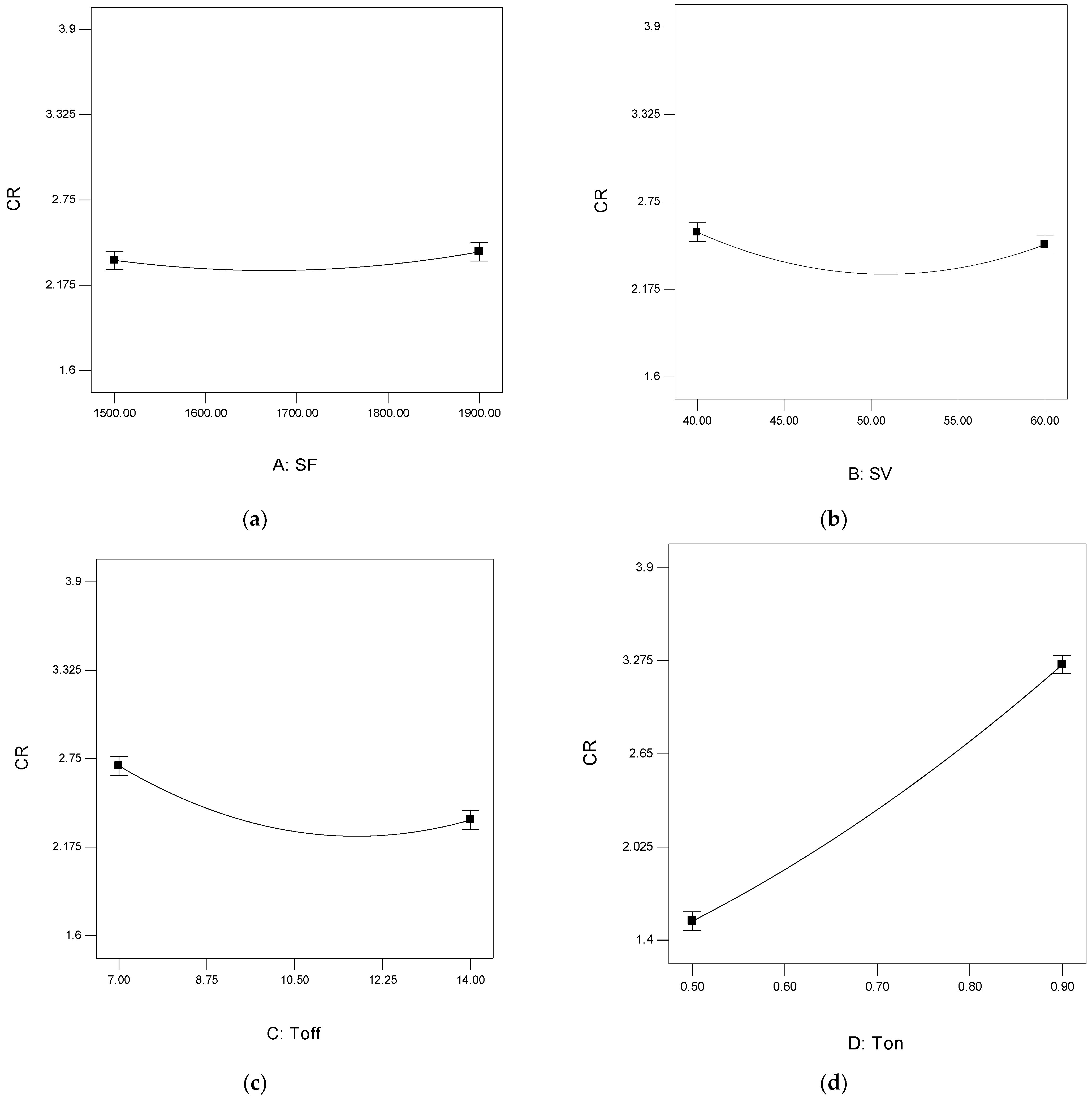
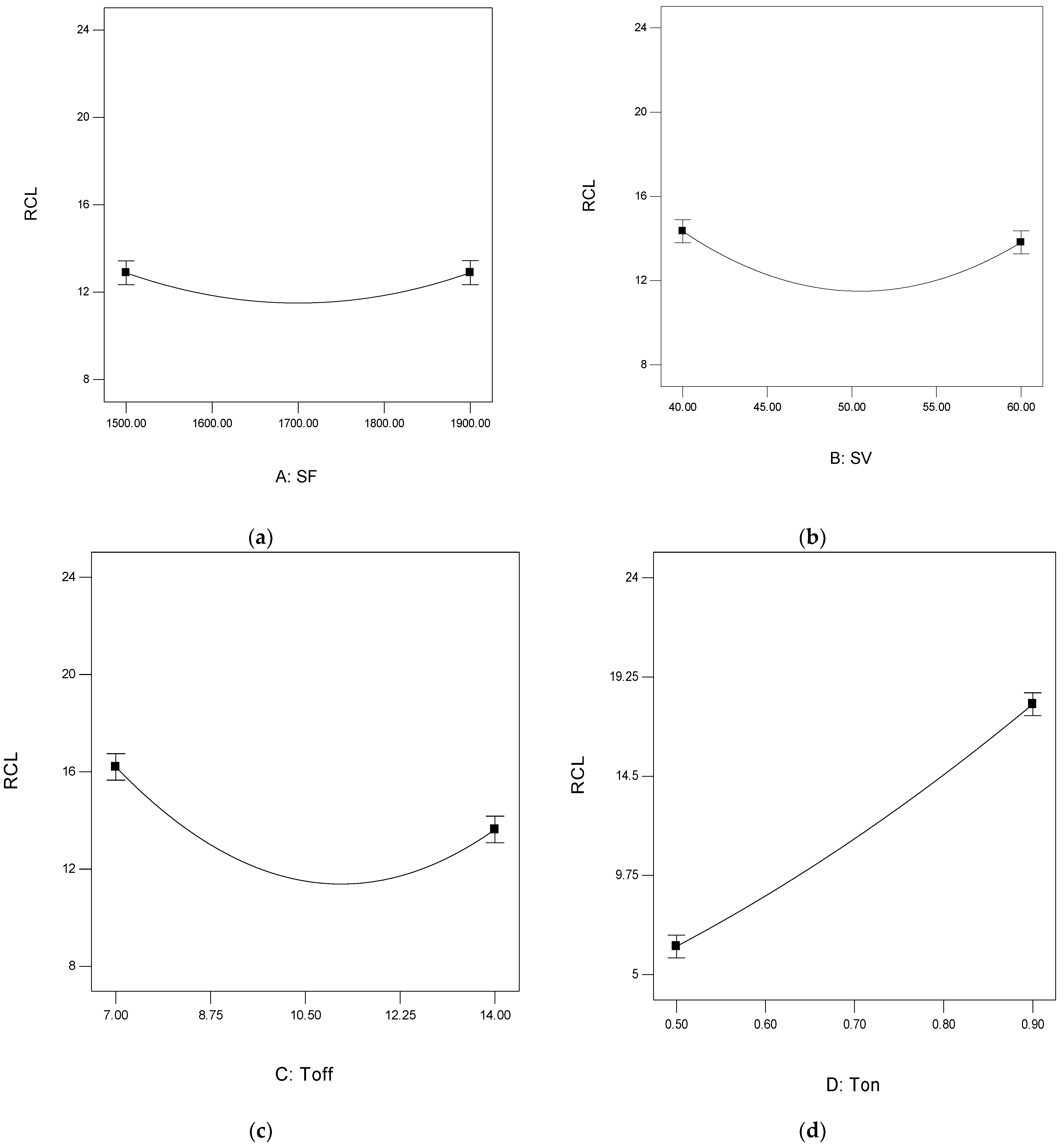


| Characteristics | Value |
|---|---|
| Density (g/cm3) | 1.77 |
| Thermal conductivity (W/mK) | 96 |
| Elastic modulus (GPa) | 45 |
| Co-efficient of thermal expansion (µm/m°C) | 26 |
| Tensile strength (MPa) | 260 |
| Poisson’s ratio | 0.35 |
| Hardness (HRB) | 49 |
| Element | Al | Zn | Mn | Cu | Si | Fe | Ca | Ni | Mg |
|---|---|---|---|---|---|---|---|---|---|
| Percentage | 3.4 | 1.2 | 0.20 | 0.05 | 0.1 | 0.005 | 0.04 | 0.005 | Balance |
| Sr. No. | Process Variable (Notation) | Units | Range of Parameters | Levels | |||
|---|---|---|---|---|---|---|---|
| Lower Limit | Upper Limit | 1 | 2 | 3 | |||
| 1 | Servo feed (SF) | - | 1500 | 1900 | 1500 | 1700 | 1900 |
| 2 | Servo voltage (SV) | V | 40 | 60 | 40 | 50 | 60 |
| 3 | Pulse off-time (Toff) | µs | 7 | 14 | 10.5 | 7 | 14 |
| 4 | Pulse on-time (Ton) | µs | 0.5 | 0.9 | 0.5 | 0.7 | 0.9 |
| Std Order | Run Order | SF | SV | Toff | Ton | RCL (µm) | CR (m/min) |
|---|---|---|---|---|---|---|---|
| 1 | 24 | 1500 | 40 | 10.5 | 0.7 | 15.79 | 1.56 |
| 2 | 5 | 1900 | 40 | 10.5 | 0.7 | 14.98 | 1.61 |
| 3 | 26 | 1500 | 60 | 10.5 | 0.7 | 14.92 | 1.5 |
| 4 | 17 | 1900 | 60 | 10.5 | 0.7 | 14.71 | 1.53 |
| 5 | 19 | 1700 | 50 | 7 | 0.5 | 8.56 | 0.73 |
| 6 | 11 | 1700 | 50 | 14 | 0.5 | 9.82 | 0.63 |
| 7 | 29 | 1700 | 50 | 7 | 0.9 | 23.36 | 2.81 |
| 8 | 23 | 1700 | 50 | 14 | 0.9 | 19.02 | 2.17 |
| 9 | 28 | 1500 | 50 | 10.5 | 0.5 | 8.12 | 0.69 |
| 10 | 16 | 1900 | 50 | 10.5 | 0.5 | 8.23 | 0.71 |
| 11 | 15 | 1500 | 50 | 10.5 | 0.9 | 19.75 | 2.32 |
| 12 | 6 | 1900 | 50 | 10.5 | 0.9 | 19.86 | 2.4 |
| 13 | 22 | 1700 | 40 | 7 | 0.7 | 19.08 | 1.94 |
| 14 | 2 | 1700 | 60 | 7 | 0.7 | 18.39 | 1.83 |
| 15 | 27 | 1700 | 40 | 14 | 0.7 | 17.17 | 1.76 |
| 16 | 25 | 1700 | 60 | 14 | 0.7 | 17.16 | 1.7 |
| 17 | 7 | 1500 | 50 | 7 | 0.7 | 18.15 | 1.88 |
| 18 | 8 | 1900 | 50 | 7 | 0.7 | 18.87 | 1.91 |
| 19 | 20 | 1500 | 50 | 14 | 0.7 | 13.84 | 1.3 |
| 20 | 21 | 1900 | 50 | 14 | 0.7 | 13.97 | 1.43 |
| 21 | 14 | 1700 | 40 | 10.5 | 0.5 | 9.31 | 0.82 |
| 22 | 1 | 1700 | 60 | 10.5 | 0.5 | 8.79 | 0.74 |
| 23 | 3 | 1700 | 40 | 10.5 | 0.9 | 20.61 | 2.53 |
| 24 | 13 | 1700 | 60 | 10.5 | 0.9 | 19.81 | 2.43 |
| 25 | 9 | 1700 | 50 | 10.5 | 0.7 | 11.01 | 1.3 |
| 26 | 18 | 1700 | 50 | 10.5 | 0.7 | 11.22 | 1.34 |
| 27 | 12 | 1700 | 50 | 10.5 | 0.7 | 11.77 | 1.29 |
| 28 | 10 | 1700 | 50 | 10.5 | 0.7 | 11.48 | 1.21 |
| 29 | 4 | 1700 | 50 | 10.5 | 0.7 | 12.04 | 1.24 |
| Source | SS * | Df * | MS * | F-Value | p-Value * | |
|---|---|---|---|---|---|---|
| Model | 10.04 | 9 | 1.12 | 150.82 | <0.0001 | significant |
| SF | 9.63 × 10−3 | 1 | 9.63 × 10−3 | 1.3 | 0.2678 | |
| SV | 0.02 | 1 | 0.02 | 2.71 | 0.1164 | |
| Toff | 0.37 | 1 | 0.37 | 50.18 | <0.0001 | |
| Ton | 8.91 | 1 | 8.91 | 1205.12 | <0.0001 | |
| Toff × Ton | 0.073 | 1 | 0.073 | 9.86 | 0.0054 | |
| SF2 | 0.058 | 1 | 0.058 | 7.9 | 0.0111 | |
| SV2 | 0.35 | 1 | 0.35 | 47.9 | <0.0001 | |
| Toff2 | 0.41 | 1 | 0.41 | 55.35 | <0.0001 | |
| Ton2 | 0.082 | 1 | 0.082 | 11.09 | 0.0035 | |
| Residual | 0.14 | 19 | 7.39 × 10−3 | |||
| Lack of Fit | 0.13 | 15 | 8.66 × 10−3 | 3.29 | 0.129 | not significant |
| Pure Error | 0.011 | 4 | 2.63 × 10−3 | |||
| Cor Total | 10.18 | 28 |
| Source | SS | df | MS | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 534.76 | 9 | 59.42 | 103.76 | <0.0001 | significant |
| SF | 2.08 × 10−4 | 1 | 2.08 × 10−4 | 3.64 × 10−4 | 0.985 | |
| SV | 0.83 | 1 | 0.83 | 1.45 | 0.2428 | |
| Toff | 19.84 | 1 | 19.84 | 34.65 | <0.0001 | |
| Ton | 403.45 | 1 | 403.45 | 704.5 | <0.0001 | |
| Toff × Ton | 7.84 | 1 | 7.84 | 13.69 | 0.0015 | |
| SF2 | 12.45 | 1 | 12.45 | 21.74 | 0.0002 | |
| SV2 | 43.07 | 1 | 43.07 | 75.21 | <0.0001 | |
| Toff2 | 75.45 | 1 | 75.45 | 131.75 | <0.0001 | |
| Ton2 | 2.67 | 1 | 2.67 | 4.66 | 0.0438 | |
| Residual | 10.88 | 19 | 0.57 | |||
| Lack of Fit | 10.2 | 15 | 0.68 | 3.98 | 0.0956 | not significant |
| Pure Error | 0.68 | 4 | 0.17 | |||
| Cor Total | 545.65 | 28 |
| Sr. No. | SF | SV | Toff | Ton | CR (m/min) | RCL (µm) |
|---|---|---|---|---|---|---|
| 1 | 1833.07 | 42.163 | 7.349 | 0.896 | 3.950 | 25.389 |
| 2 | 1675.35 | 57.909 | 7 | 0.896 | 3.905 | 25.329 |
| 3 | 1687.75 | 57.298 | 7.015 | 0.9 | 3.901 | 25.175 |
| 4 | 1869.28 | 58.411 | 7.562 | 0.897 | 3.896 | 25.092 |
| 5 | 1669.8 | 56.698 | 7 | 0.9 | 3.887 | 25.044 |
| 6 | 1709.22 | 56.313 | 7 | 0.9 | 3.880 | 24.897 |
| 7 | 1680.79 | 57.691 | 7.215 | 0.9 | 3.867 | 24.794 |
| 8 | 1825.64 | 42.057 | 7.436 | 0.886 | 3.866 | 24.710 |
| 9 | 1712.67 | 55.944 | 7.067 | 0.9 | 3.857 | 24.612 |
| 10 | 1695.54 | 57.587 | 7.246 | 0.897 | 3.843 | 24.556 |
| 11 | 1720.82 | 51.415 | 10.497 | 0.5 | 1.529 | 6.370 |
| 12 | 1741.25 | 51.724 | 10.491 | 0.503 | 1.546 | 6.502 |
| 13 | 1716.89 | 51.625 | 10.875 | 0.510 | 1.561 | 6.664 |
| 14 | 1699.84 | 52.306 | 10.692 | 0.512 | 1.568 | 6.714 |
| 15 | 1728.42 | 52.182 | 9.860 | 0.510 | 1.584 | 6.768 |
| 16 | 1725.1 | 50.518 | 10.791 | 0.522 | 1.601 | 6.897 |
| 17 | 1725.51 | 50.968 | 10.259 | 0.525 | 1.619 | 6.980 |
| 18 | 1742.24 | 50.201 | 10.034 | 0.525 | 1.631 | 7.056 |
| 19 | 1729.07 | 49.213 | 10.739 | 0.533 | 1.642 | 7.178 |
| 20 | 1734.12 | 48.986 | 10.729 | 0.537 | 1.662 | 7.318 |
| 21 | 1696.5 | 48.736 | 10.457 | 0.815 | 2.820 | 15.148 |
| 22 | 1701.08 | 49.841 | 10.813 | 0.824 | 2.837 | 15.209 |
| 23 | 1728.06 | 51.389 | 10.704 | 0.823 | 2.841 | 15.252 |
| 24 | 1740.52 | 49.286 | 11.286 | 0.831 | 2.859 | 15.360 |
| 25 | 1704.67 | 49.741 | 11.024 | 0.833 | 2.869 | 15.408 |
| 26 | 1734.02 | 49.703 | 10.731 | 0.833 | 2.895 | 15.587 |
| 27 | 1750.68 | 53.258 | 9.2744 | 0.9 | 3.414 | 19.573 |
| 28 | 1716.78 | 51.684 | 9.0931 | 0.9 | 3.418 | 19.606 |
| 29 | 1741.18 | 49.572 | 10.446 | 0.681 | 2.210 | 11.054 |
| 30 | 1736.91 | 50.399 | 10.530 | 0.686 | 2.223 | 11.137 |
| Sr. No. | SF | SV | Toff | Ton | Predicted Solution | Experimental Results | ||
|---|---|---|---|---|---|---|---|---|
| CR (m/min) | RCL (µm) | CR (m/min) | RCL (µm) | |||||
| 1 | 1833.07 | 42.163 | 7.349 | 0.896 | 3.950 | 25.389 | 3.92 | 24.67 |
| 11 | 1720.82 | 51.415 | 10.497 | 0.5 | 1.529 | 6.370 | 1.61 | 6.45 |
| 18 | 1742.24 | 50.201 | 10.034 | 0.525 | 1.631 | 7.056 | 1.68 | 7.18 |
| 23 | 1728.06 | 51.389 | 10.704 | 0.823 | 2.841 | 15.252 | 2.92 | 15.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goyal, K.K.; Sharma, N.; Dev Gupta, R.; Singh, G.; Rani, D.; Banga, H.K.; Kumar, R.; Pimenov, D.Y.; Giasin, K. A Soft Computing-Based Analysis of Cutting Rate and Recast Layer Thickness for AZ31 Alloy on WEDM Using RSM-MOPSO. Materials 2022, 15, 635. https://doi.org/10.3390/ma15020635
Goyal KK, Sharma N, Dev Gupta R, Singh G, Rani D, Banga HK, Kumar R, Pimenov DY, Giasin K. A Soft Computing-Based Analysis of Cutting Rate and Recast Layer Thickness for AZ31 Alloy on WEDM Using RSM-MOPSO. Materials. 2022; 15(2):635. https://doi.org/10.3390/ma15020635
Chicago/Turabian StyleGoyal, Kapil K., Neeraj Sharma, Rahul Dev Gupta, Gurpreet Singh, Deepika Rani, Harish Kumar Banga, Raman Kumar, Danil Yurievich Pimenov, and Khaled Giasin. 2022. "A Soft Computing-Based Analysis of Cutting Rate and Recast Layer Thickness for AZ31 Alloy on WEDM Using RSM-MOPSO" Materials 15, no. 2: 635. https://doi.org/10.3390/ma15020635
APA StyleGoyal, K. K., Sharma, N., Dev Gupta, R., Singh, G., Rani, D., Banga, H. K., Kumar, R., Pimenov, D. Y., & Giasin, K. (2022). A Soft Computing-Based Analysis of Cutting Rate and Recast Layer Thickness for AZ31 Alloy on WEDM Using RSM-MOPSO. Materials, 15(2), 635. https://doi.org/10.3390/ma15020635









