Inelastic Deformation of Coronary Stents: Two-Level Model
Abstract
1. Introduction
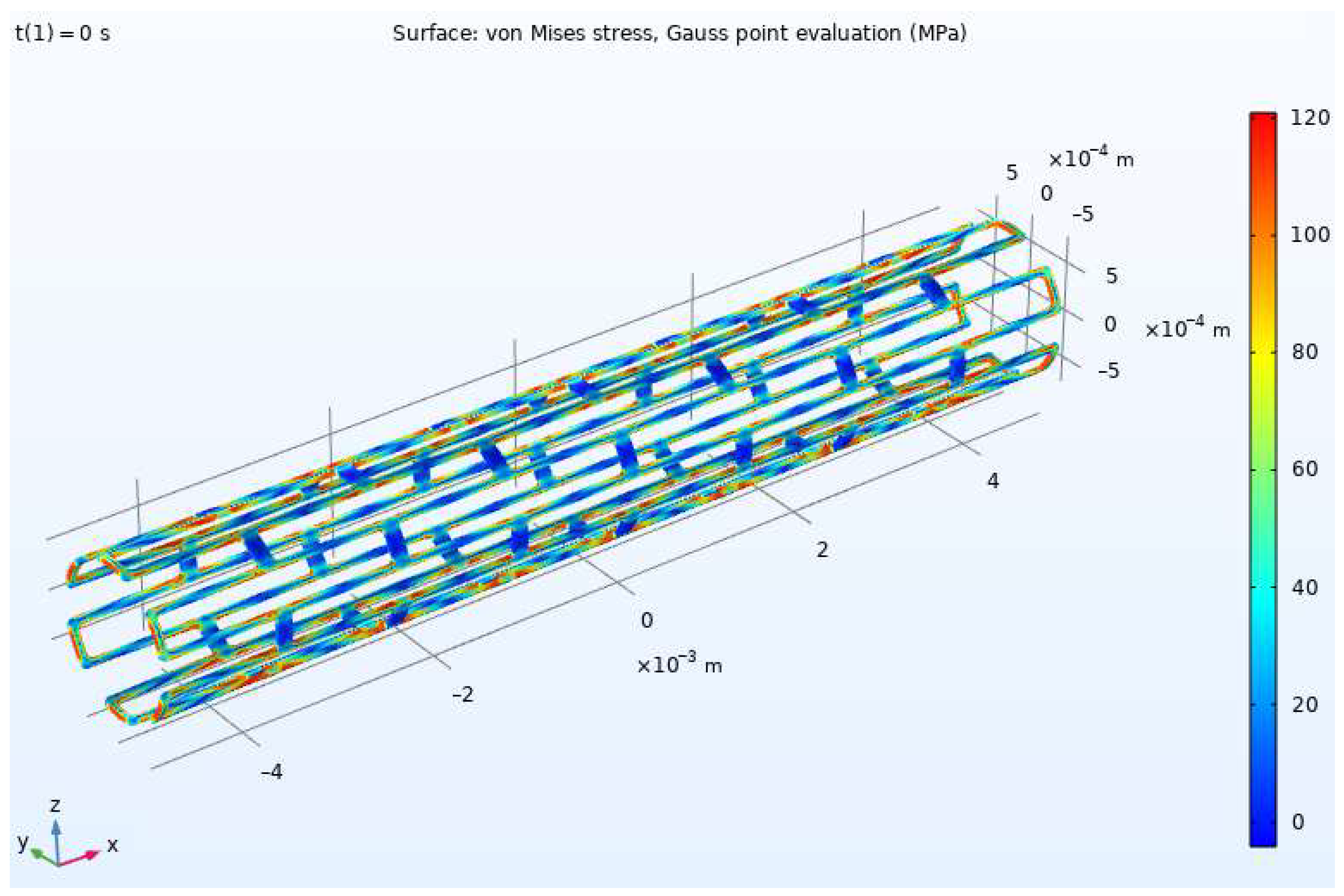
2. Materials and Methods
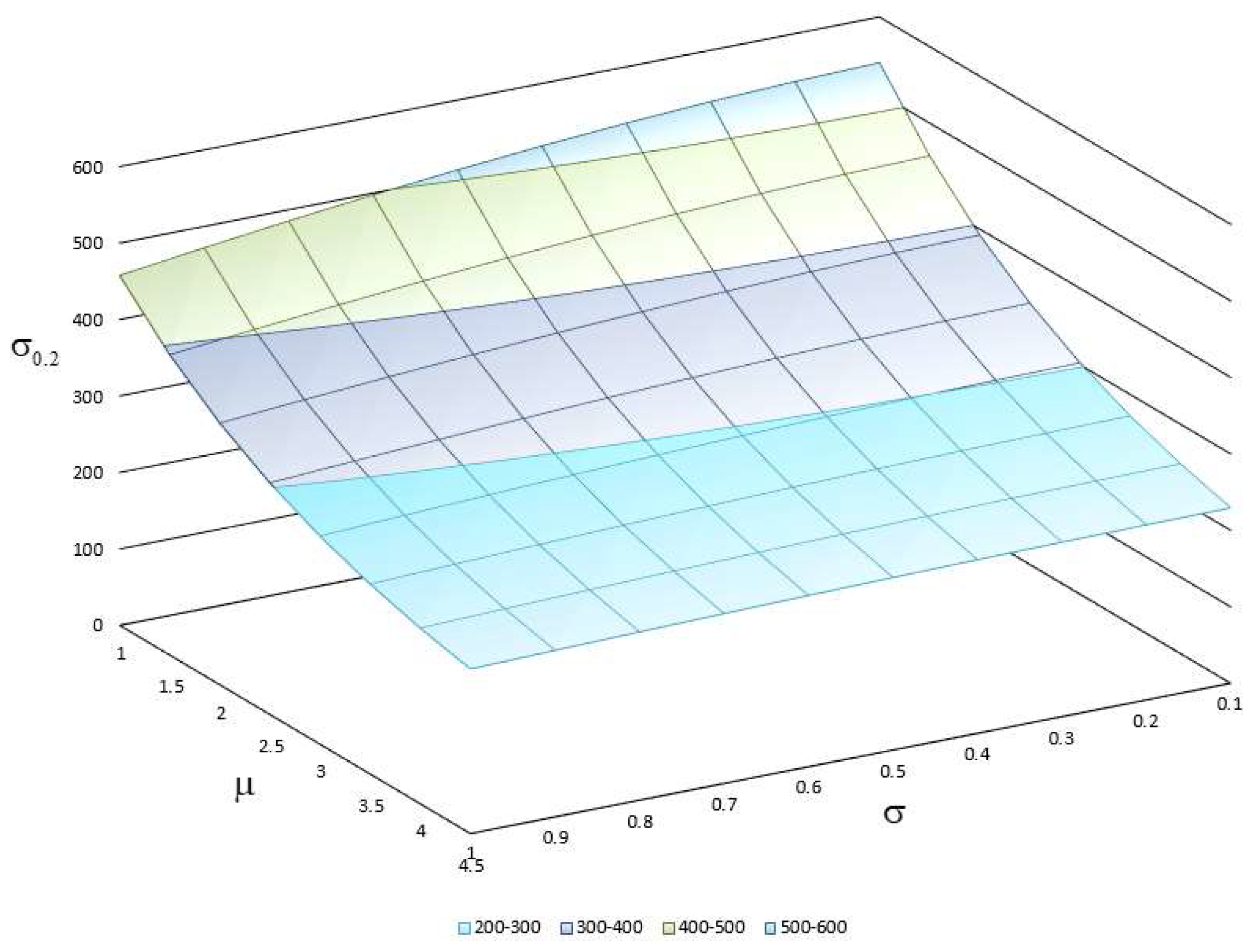
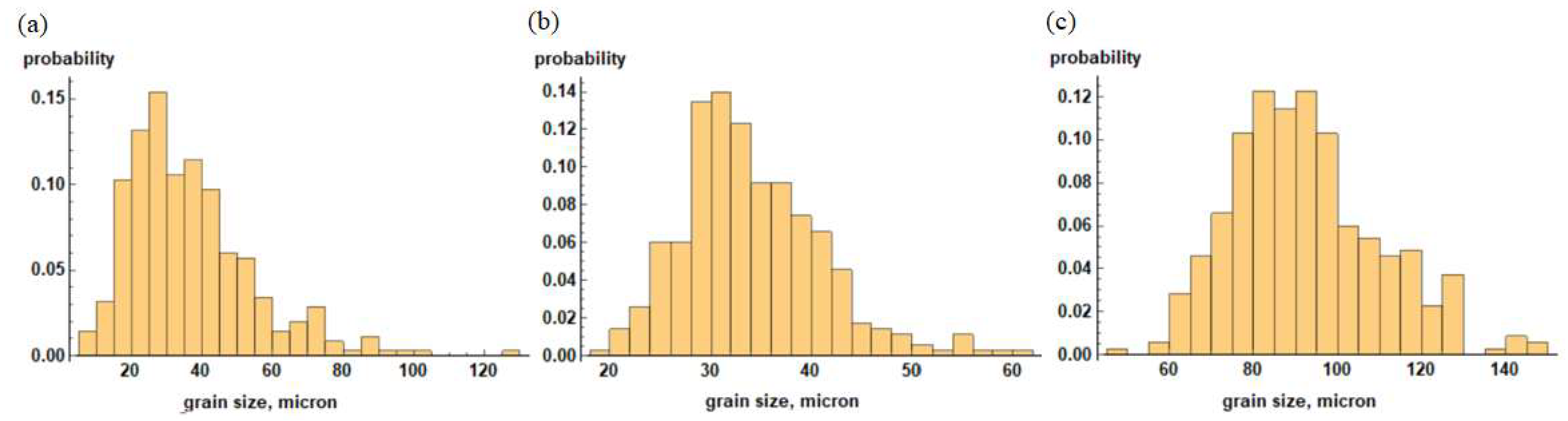
3. Results and Discussion
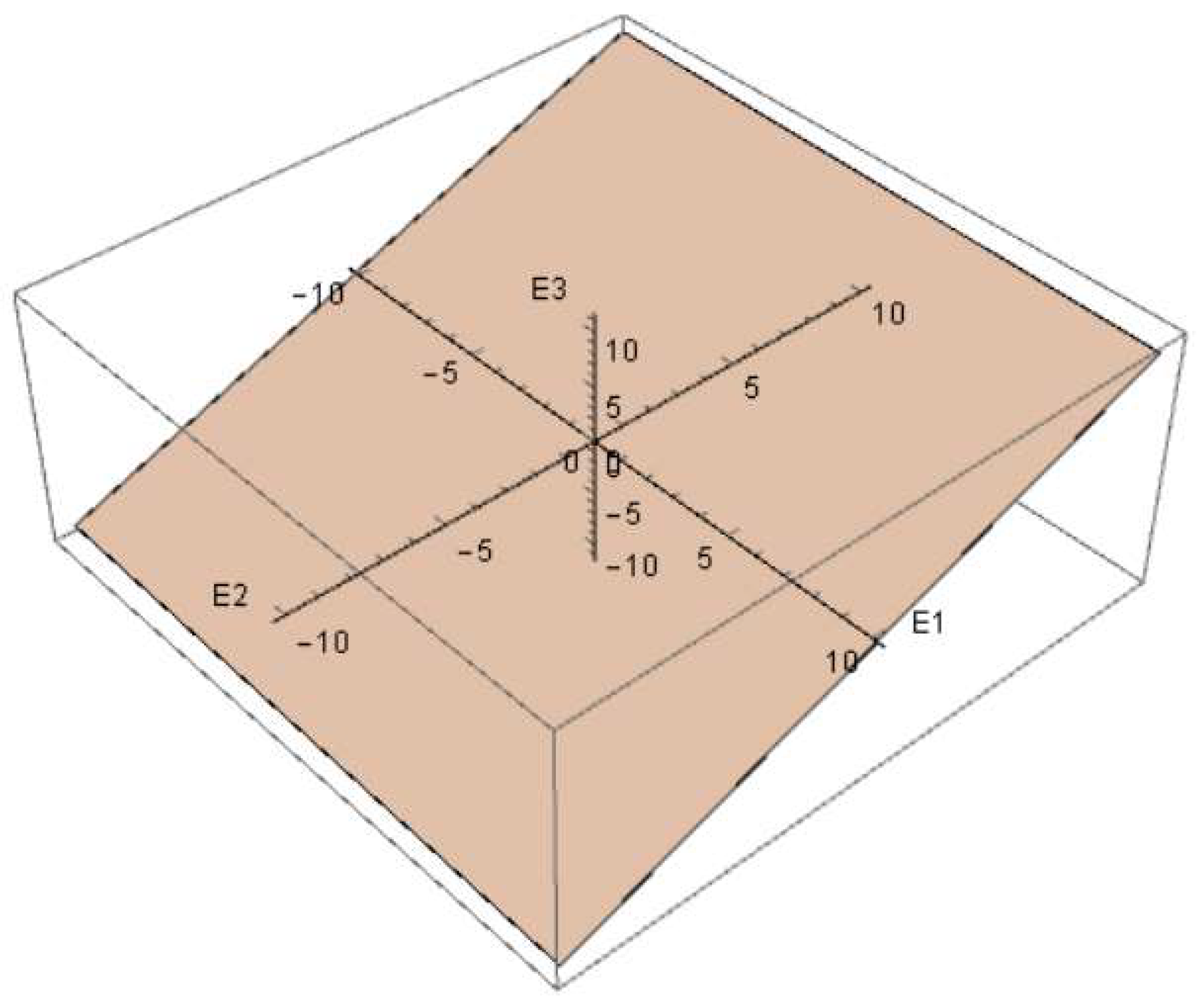
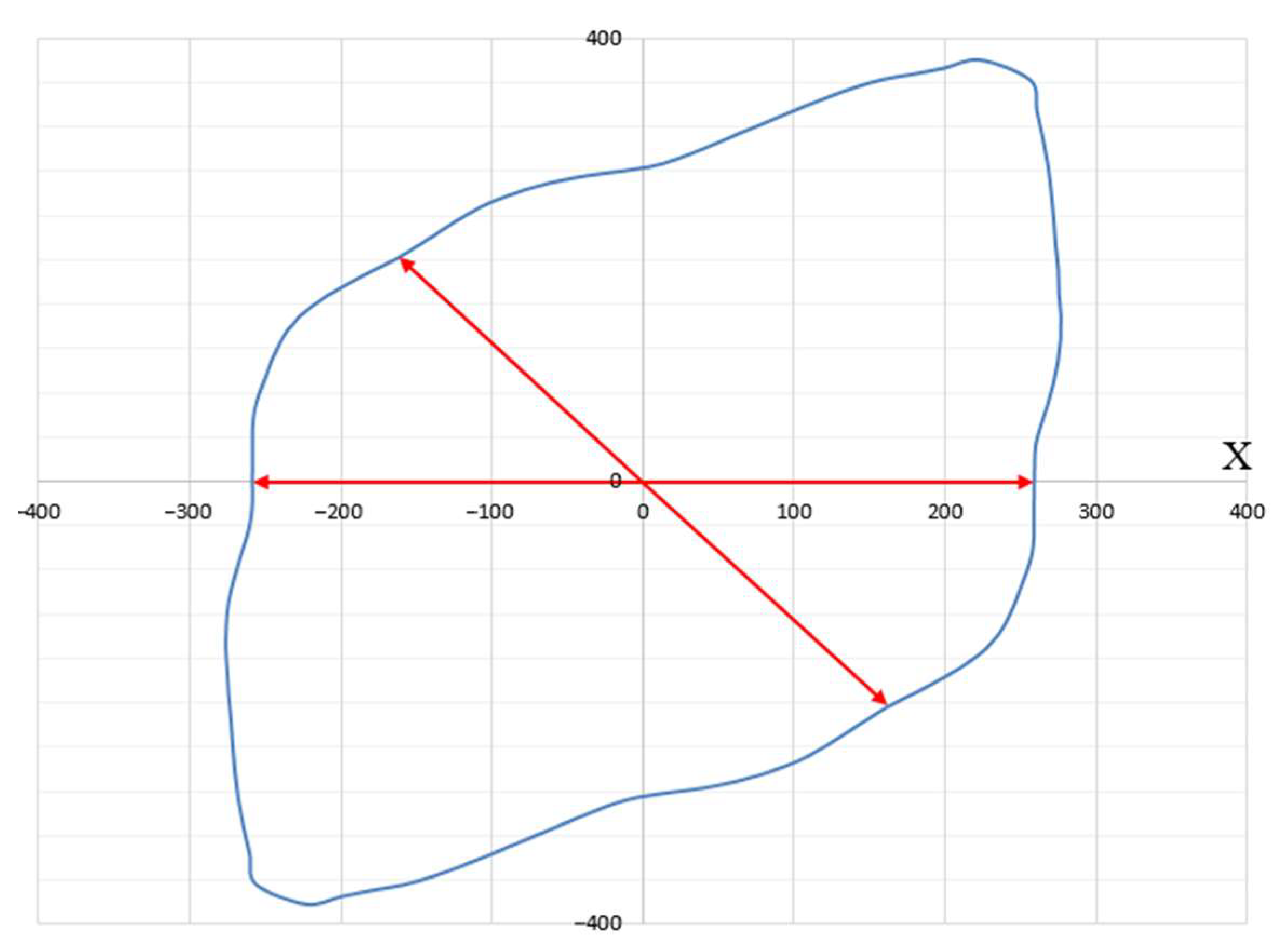
- Angle φ between the deformation direction and the projection of the X-axis of principal deformation E1 on a given plane;
- The radius vector drawn from the origin to the considered point, which is equal to the yield strength of the material.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Schiavone, A.; Zhao, L.G. Modelling of stent deployment and deformation in diseased arteries by considering vessel anisotropy. In Proceedings of the XLIII International Summer School Conference APM 2015, St. Petersburg, Russia, 22 June 2015–27 July 2015. [Google Scholar]
- Ardatov, K.V.; Nushtaev, D.V. Deformation characteristics of coronary stents of the matrix and continuous sinusoidal types in free expansion: Computer simulation. Mod. Technol. Med. 2018, 10, 31–36. [Google Scholar] [CrossRef]
- He, R.; Zhao, L.; Silberschmidt, V.V.; Willcock, H.; Vogt, F. Pioneering personalised design of femoropopliteal nitinol stents. J. Mater. Sci. Eng. C 2021, 130, 112462. [Google Scholar] [CrossRef]
- He, R.; Zhao, L.G.; Silberschmidt, V.V.; Willcock, H. A computational study of fatigue resistance of nitinol stents subjected to walk-induced femoropopliteal artery motion. J. Biomech. 2021, 118, 1–11. [Google Scholar] [CrossRef] [PubMed]
- He, R.; Zhao, L.; Silberschmidt, V.V. Mechanical performance of self-expandable nitinol stent with lesion-specific design. Procedia Struct. Integr. 2019, 15, 24–27. [Google Scholar] [CrossRef]
- Kuo, W.-C.; Wu, T.-C.; Wu, C.-F.; Wang, W.-C. Bioperformance analysis of parylene C coating for implanted nickel titanium alloy. Mater. Today Commun. 2021, 27, 102306. [Google Scholar] [CrossRef]
- Vishnu, J.; Calin, M.; Pilz, S.; Gebert, A.; Kaczmarek, B.; Michalska-Sionkowska, M.; Hoffmann, V.; Manivasagam, G. Superhydrophilic nanostructured surfaces of beta Ti–29Nb alloy for cardiovascular stent applications. J. Surf. Coat. Technol. 2020, 396, 125965. [Google Scholar] [CrossRef]
- Plaine, A.; Silva, M.R.; Bolfarini, C. Microstructure and elastic deformation behavior of β-type Ti-29Nb-13Ta-4.6Zr with promising mechanical properties for stent applications. J. Mater. Res. Technol. 2019, 8, 3852–3858. [Google Scholar] [CrossRef]
- Tian, Y.; Yu, Z.; Ong, C.Y.A.; Kent, D.; Wang, G. Microstructure, elastic deformation behavior and mechanical properties of biomedical β-type titanium alloy thin-tube used for stents. J. Mech. Behav. Biomed. Mater. 2015, 45, 132–141. [Google Scholar] [CrossRef] [PubMed]
- Grogan, J.A.; Leen, S.B.; McHugh, P.E. Influence of statistical size effects on the plastic deformation of coronary stents. J. Mech. Behav. Biomed. Mater. 2013, 2, 61–76. [Google Scholar] [CrossRef]
- Yamanaka, K.; Mori, M.; Koizumi, Y.; Chiba, A. Local strain evolution due to athermal γ→ε martensitic transformation in biomedical Co-Cr-Mo alloys. J. Mech. Behav. Biomed. Mater. 2014, 32, 52–61. [Google Scholar] [CrossRef]
- Yamanaka, K.; Mori, M.; Koizumia, Y.; Chiba, A. Development of new Co–Cr–W-based biomedical alloys: Effects of microalloying and thermomechanical processing on microstructures and mechanical properties. Mater. Des. 2014, 55, 987–998. [Google Scholar] [CrossRef]
- Narushima, T.; Mineta, S.; Kurihara, Y.; Ueda, K. Precipitates in Biomedical Co-Cr Alloys. JOM 2013, 65, 489–504. [Google Scholar] [CrossRef]
- Zahora, J.; Bezrouk, A.; Hanus, J. Models of stents—Comparison and applications. J. Physiol. Res. 2007, 56, 115–121. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.; Lu, W. Optimizing the deformation behavior of stent with nonuniform Poisson’s ratio distribution for curved artery. J. Mech. Behav. Biomed. Mater. 2018, 88, 442–452. [Google Scholar] [CrossRef]
- Gordin, D.M.; Sun, F.; Laille, D.; Prima, F.; Gloriant, T. How a new strain transformable titanium-based biomedical alloy can be designed for balloon expendable stents. Materialia 2020, 10, 100638. [Google Scholar] [CrossRef]
- Langi, E.; Bisht, A.; Silberschmidt, V.V.; Ruiz, P.D.; Vogt, F.; Mailto, L.; Masseling, L.; Zhao, L. Characterisation of additively manufactured metallic stents. Procedia Struct. Integr. 2019, 15, 41–45. [Google Scholar] [CrossRef]
- Fu, J.; Su, Y.; Qin, Y.-X.; Zheng, Y.; Wang, Y.; Zhu, D. Evolution of metallic cardiovascular stent materials: A comparative study among stainless steel, magnesium and zinc. J. Biomater. 2020, 230, 119641. [Google Scholar] [CrossRef] [PubMed]
- Heublein, B.; Rohde, R.; Kaese, V.; Niemeyer, M.; Hartung, W.; Haverich, A. Biocorrosion of magnesium alloys: A new principle in cardiovascular implant technology? Heart 2003, 89, 651–656. [Google Scholar] [CrossRef]
- Ahuja, R.; Kumari, N.; Srivastava, A.; Bhati, P.; Vashisth, P.; Yadav, P.K.; Jacob, T.; Narang, R.; Bhathagar, N. Biocompatibility analysis of PLA based candidate materials for cardiovascular stents in a rat subcutaneous implant model. Acta Histochem. 2020, 122, 151615. [Google Scholar] [CrossRef]
- Carneiro, V.H.; Puga, H. Deformation behavior of self-expanding magnesium stents based on auxetic chiral lattices. Cienc. Technol. Dos Mater. 2016, 28, 14–18. [Google Scholar] [CrossRef]
- Mani, G.; Feldman, M.D.; Patel, D.; Agrawal, C.M. Coronary stents: A materials perspective. Biomaterials 2007, 28, 1689–1710. [Google Scholar] [CrossRef] [PubMed]
- Sangiorgi, G.; Melzi, G.; Agostoni, P.; Cola, C.; Clementi, F.; Romitelli, P.; Virmani, R.; Colombo, A. Engineering aspects of stents design and their translation into clinical practice. Ann. Dell’istituto Super. Di Sanita 2007, 43, 89–100. [Google Scholar]
- Watson, T.; Webster, M.W.; Ormiston, J.A.; Ruygrok, P.N.; Stewart, J.T. Long and short of optimal stent design. Open Heart 2017, 4, e000680. [Google Scholar] [CrossRef] [PubMed]
- Hanratty, C.G.; Walsh, S.J. Longitudinal compression: A “new” complication with modern coronary stent platforms—Time to think beyond deliverability? EuroIntervention 2011, 7, 872–877. [Google Scholar] [CrossRef] [PubMed]
- Pitney, M.; Pitney, K.; Jepson, N.; Friedman, D.; Nguyen-Dang, T.; Matthews, J.; Giles, R.; Taylor, D. Major stent deformation/pseudofracture of 7 Crown Endeavor/Micro Driver stent platform: Incidence and causative factors. EuroIntervention 2011, 7, 256–262. [Google Scholar] [CrossRef]
- Ulyanina, I.; Skakova, T. Structure of materials. Part 1. Atomic-Cristalline Structure of Materials, 2nd ed.; MGIU: Moscow, Russia, 2006; p. 56. [Google Scholar]
- Hirth, J.; Lothe, J. Theory of Dislocations, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1982; p. 857. [Google Scholar]
- Trusov, P.; Shveikin, A. Theory of Plasticity; PNRPU: Perm, Russia, 2011; p. 425. [Google Scholar]
- Trusov, P.V.; Volegov, P.S.; Yants, A.Y. Description of intragrain and grain boundary hardening of mono-and polycrystals. Sci. Tech. Bull. StPSTU: Phys. Math. Sci. 2010, 98, 110–119. [Google Scholar]
- Kaibyshev, O.; Valiev, R. Grain Boundaries and the Properties of Metals; Metallurgia: Moscow, Russia, 1987; p. 214. [Google Scholar]
- Poluhin, P.; Gorelik, S.; Vorontsov, V. Physical Basis of Plastic Deformation; Metallurgia: Moscow, Russia, 1982; p. 584. [Google Scholar]
- Bache, M.R.; Evans, W.J. Dwell sensitive fatigue response of titanium alloys for power plant applications. In Proceedings of the ASME Turbo Expo 2001: Power for Land, Sea, and Air, New Orleans, LA, USA, 4 June 2001–7 June 2001. [Google Scholar]
- Bache, M.R. A review of dwell sensitive fatigue in titanium alloys: The role of microstructure, texture and operating conditions. Int. J. Fatigue 2003, 25, 1079–1087. [Google Scholar] [CrossRef]
- Ozturk, D.; Pilchak, A.L.; Ghosh, S. Experimentally validated dwell and cyclic fatigue crack nucleation model for α–titanium alloys. Scr. Mater. 2017, 127, 15–18. [Google Scholar] [CrossRef]
- Selukov, D.G.; Volegov, P.S. Investigation of the grain size influence on hardening in polycrystals using the two-level model based on crystal plasticity. Bull. Tambov University. Ser. Nat. Tech. Sci. 2016, 21, 1305–1307. [Google Scholar] [CrossRef]
- Mulyukov, R.R.; Nazarov, A.A.; Imaev, R.M. Deformation methods, multiscale structure and properties of nanostructured materials. Matters Mater. Sci. 2008, 2, 20–32. [Google Scholar]
- Trusov, P.V.; Ashikhmin, V.N.; Volegov, P.S.; Shveikin, A.I. Mathematical modelling of the evolution of polycrystalline materials structure under elastoplastic deformation. Sci. Notes Kazan University. Ser. Phys. Math. Sci. 2010, 152, 225–237. [Google Scholar]
- Ozernykh, V.S.; Volegov, P.S. Description of hardening mechanisms in polycrystalline inelastic deformation. Bull. Tambov University. Ser. Nat. Tech. Sci. 2016, 21, 1203–1206. [Google Scholar] [CrossRef]
- Volegov, P.S.; Nikityuk, A.S.; Yants, A.Y. Yield surface geometry and hardening laws in physical theories of plasticity. Bull. PSTU. Mech. 2009, 17, 25–33. [Google Scholar]
- Kotelnikova, N.V.; Volegov, P.S. Description of hardening during inelastic deformation of single crystals taking into account Lomer-Cottrell barriers. Bull. Tambov University. Ser. Nat. Tech. Sci. 2016, 21, 1070–1073. [Google Scholar] [CrossRef]
- Tokarev, A.A.; Yants, A.Y.; Shveykin, A.; Kondratiev, N. Multi-level direct crystal plasticity model of polycrystalline specimen: Grains generation. AIP Conf. Proc. 2021, 2371, 020015. [Google Scholar] [CrossRef]
- Chen, R.C.; Hong, C.; Li, J.J.; Zheng, Z.Z.; Li, P.C. Austenite grain growth and grain size distribution in isothermal heat-treatment of 300M steel. Procedia Eng. 2017, 207, 663–668. [Google Scholar] [CrossRef]
- Tao, W.; Takashi, N.; Takashi, W.; Masatoshi, F.; Hironari, O.; Toshinobu, S. Effects of grain size on ultrasonic attenuation in type 316L stainless steel. Materials 2017, 753, 753. [Google Scholar] [CrossRef]
- Zhang, C.; Enomoto, M.; Suzuki, A.; Ishimaru, T. Characterization of three-dimensional grain structure in polycrystalline Iron by serial sectioning. Metall. Mater. Trans. A 2004, 35, 1927–1933. [Google Scholar] [CrossRef]
- Quey, R.; Renversade, L. Optimal polyhedral description of 3D polycrystals: Method and application to statistical and synchrotron X-ray diffraction data. Comput. Methods Appl. Mech. Eng. 2018, 330, 308–333. [Google Scholar] [CrossRef]
- Simonovski, I.; Cizelj, L. Small crack in a simulated columnar polycrystalline aggregate with random 2D and 3D lattice orientations. In Engineering against Fracture: Proceedings of the 1st Conference; Pantelakis, S., Rodopoulos, C., >University of Patras, Eds.; Springer Science + Business Media: Berlin, Germany, 2009; Volume 4, pp. 235–247. [Google Scholar] [CrossRef]
- Wang, M.; Bu, Y.; Dai, Z.; Zeng, S. Characterization of grain size in 316L stainless steel using the attenuation of Rayleigh wave measured by air-coupled transducer. Materials 2021, 14, 1901. [Google Scholar] [CrossRef]
- McGarry, J.P.; O’Donnell, B.P.; McHugh, P.E.; McGarry, J.G. Analysis of the mechanical performance of a cardiovascular stent design based on micromechanical modelling. Comput. Mater. Sci. 2004, 31, 421–438. [Google Scholar] [CrossRef]
- Sweeney, C.A.; McHugh, P.E.; McGarry, J.P.; Leen, S.B. Micromechanical methodology for fatigue in cardiovascular stents. Int. J. Fatigue 2012, 44, 202–216. [Google Scholar] [CrossRef]
- Ino, Y.; Toyoda, Y.; Tanaka, A.; Ishii, S.; Kusuyama, Y.; Kubo, T.; Takarada, S.; Kitabata, H.; Tanimoto, T.; Mizukoshi, M.; et al. Predictors and prognosis of stent fracture after sirolimus-eluting stent implantation. Circ. J. 2009, 73, 2036–2041. [Google Scholar] [CrossRef] [PubMed]
- Shaikh, F.; Maddikunta, R.; Djelmami-Hani, M.; Solis, J.; Allaqaband, S.; Bajwa, T. Stent fracture. an incidental finding or a significant marker of clinical in-stent restenosis? Catheter. Cardiovasc. Interv. 2008, 71, 614–618. [Google Scholar] [CrossRef] [PubMed]
- Trusov, P.; Volegov, P.; Kondratiev, N. Physical Theories of Plasticity; PNRPU: Perm, Russia, 2013; p. 244. [Google Scholar]
- Trusov, P.V.; Shveykin, A.I.; Nechaeva, E.S.; Volegov, P.S. Multilevel models of inelastic deformation of materials and their application for description of internal structure evolution. Phys. Mesomech. 2012, 15, 33–56. [Google Scholar] [CrossRef]
- Trusov, P.V.; Nechaeva, E.S.; Shveykin, A.I. Asymmetric stress-strain measures in construction of multilevel constitutive models of materials. Phys. Mesomech. 2013, 16, 15–31. [Google Scholar]
- Trusov, P.; Keller, I. Theory of Constitutive Relations. Part 1. General Theory; PSTU: Perm, Russia, 1997; p. 98. [Google Scholar]
- Anand, L. Single-crystal elasto-viscoplasticity: Application to texture evolution in polycrystalline natels at large strains. Comput. Methods Appl. Mech. Eng. 2004, 93, 5359–5383. [Google Scholar] [CrossRef]
- Bronkhorst, C.A.; Kalidindi, S.R.; Anand, L. Polycrystalline plasticity and the evolution of crystallographic texture in FCC metals. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1992, 341, 443–477. [Google Scholar] [CrossRef]
- Keerthana, S.; Visalakshi, C. Finire element analysis of Palmaz-Schatz stent and express stent using three dimensional models. In Proceedings of the 3rd International Conference of Biosignals, Images and Instrumentation (ICBSII), Chennai, India, 16 March 2017–18 March 2017. [Google Scholar]
- Singh, K.K. Strain hardening behaviour of 316L austenitic stainless steel. Mater. Sci. Technol. 2004, 20, 1134–1142. [Google Scholar] [CrossRef]
- Singh, K.K.; Sangal, S.; Murty, G.S. Hall-Petch behaviour of 316L austenitic stainless steel at room temperature. Mater. Sci. Technol. 2002, 18, 165–172. [Google Scholar] [CrossRef]



| Material Parameters | Notation | Value |
|---|---|---|
| Poisson’s ratio | 0.27 | |
| Young’s modulus | 197 GPa | |
| Density | 7000 kg m−3 | |
| Initial shear stresses | 101 MPa |
| Material Parameters | Notation | Value |
|---|---|---|
| Grain count | N | 350 |
| Elastic constant | 163 GPa | |
| Elastic constant | 110 GPa | |
| Elastic constant | 101 GPa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volegov, P.S.; Knyazev, N.A.; Gerasimov, R.M.; Silberschmidt, V.V. Inelastic Deformation of Coronary Stents: Two-Level Model. Materials 2022, 15, 6948. https://doi.org/10.3390/ma15196948
Volegov PS, Knyazev NA, Gerasimov RM, Silberschmidt VV. Inelastic Deformation of Coronary Stents: Two-Level Model. Materials. 2022; 15(19):6948. https://doi.org/10.3390/ma15196948
Chicago/Turabian StyleVolegov, Pavel S., Nikita A. Knyazev, Roman M. Gerasimov, and Vadim V. Silberschmidt. 2022. "Inelastic Deformation of Coronary Stents: Two-Level Model" Materials 15, no. 19: 6948. https://doi.org/10.3390/ma15196948
APA StyleVolegov, P. S., Knyazev, N. A., Gerasimov, R. M., & Silberschmidt, V. V. (2022). Inelastic Deformation of Coronary Stents: Two-Level Model. Materials, 15(19), 6948. https://doi.org/10.3390/ma15196948









