On the Electronic Structure of 2H-MoS2: Correlating DFT Calculations and In-Situ Mechanical Bending on TEM
Abstract
:1. Introduction
2. Methods
2.1. Computational Methods
2.2. Experimental TEM
3. Results and Discussion
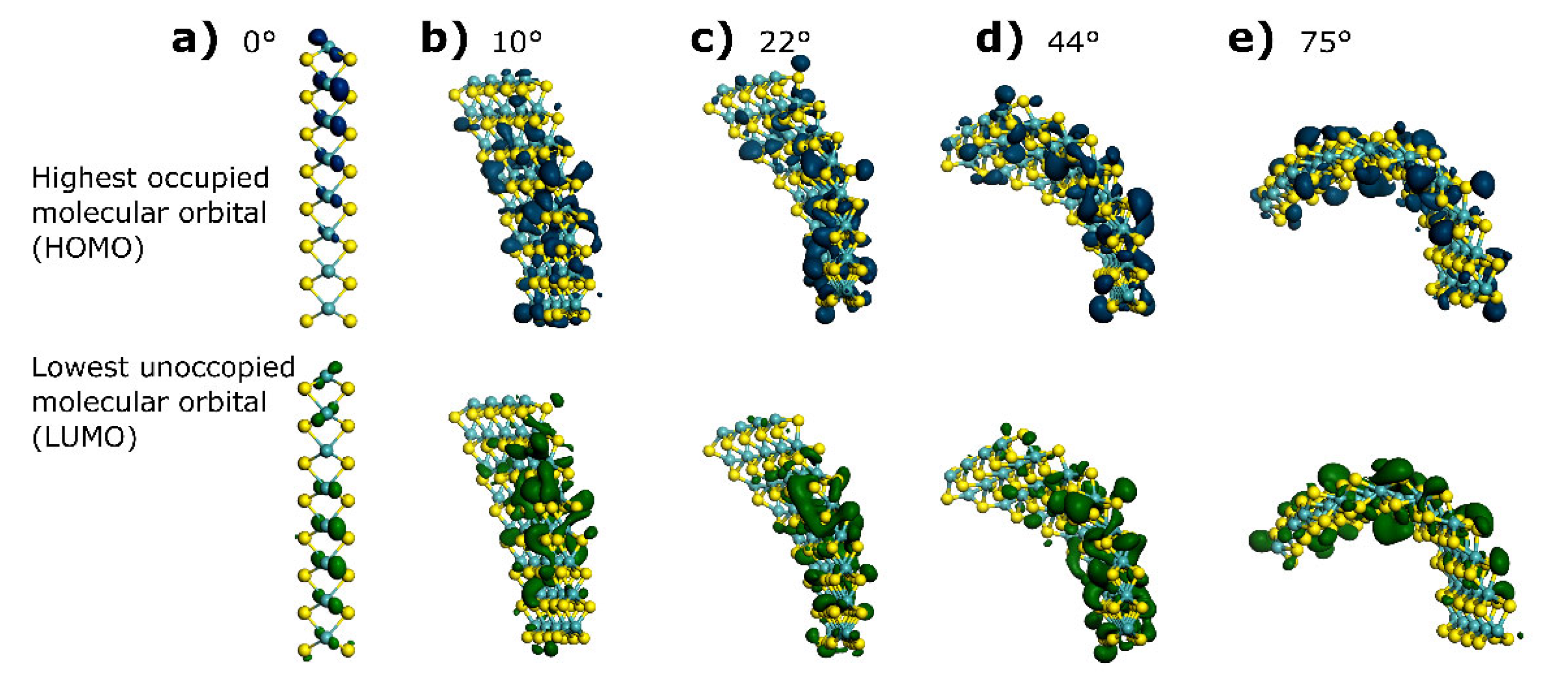
3.1. HOMO and LUMO at Bending Angles
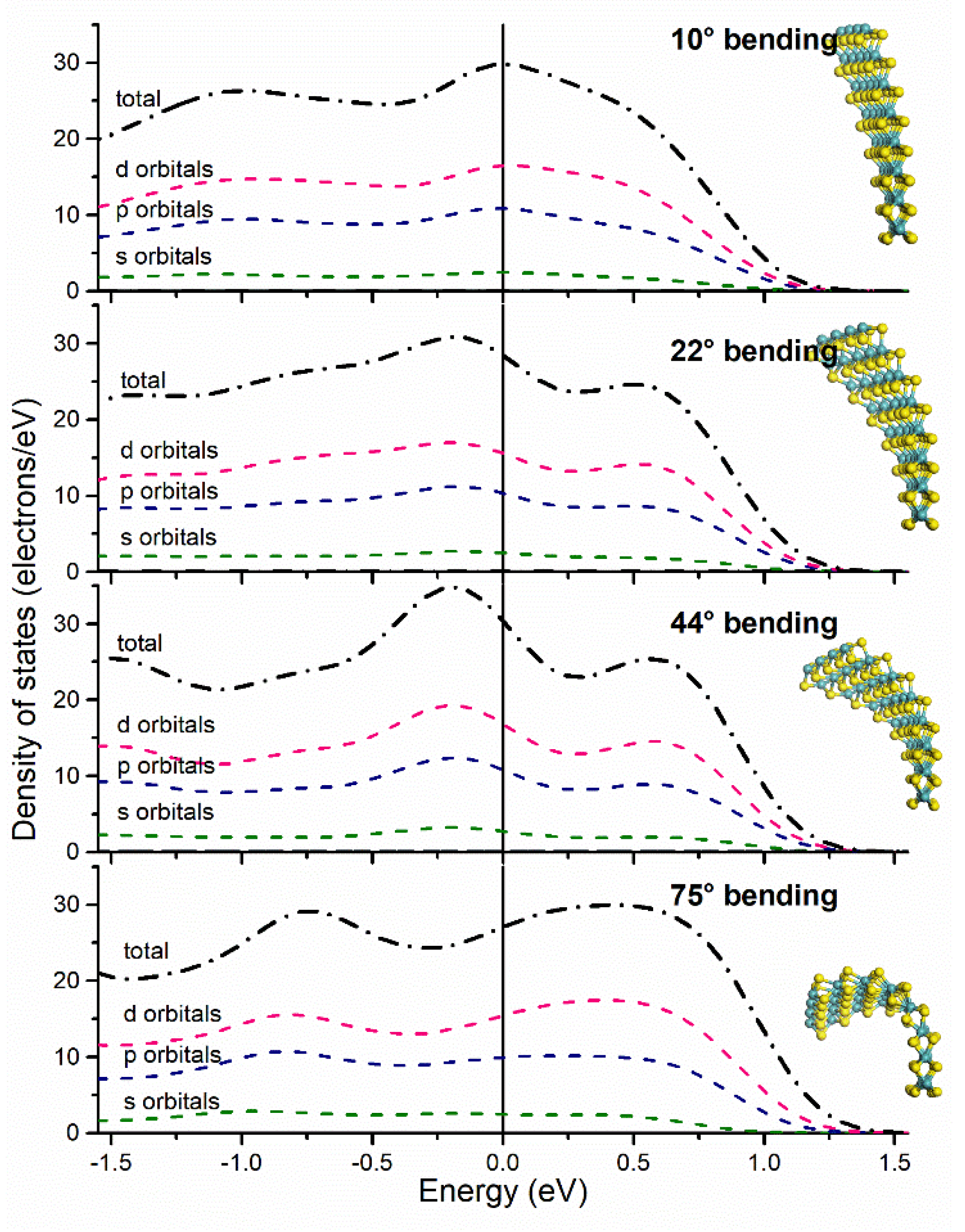
3.2. Electronic Structure by Partial Density of States
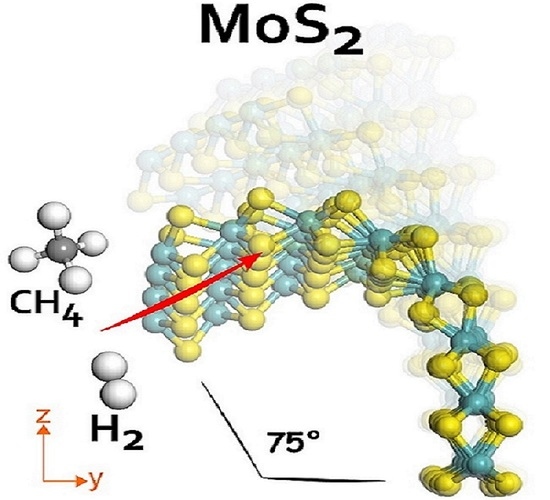
3.3. Catalytic Reactivity in 2H-MoS2 Curved Layers
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chhowalla, M.; Amaratunga, G.A.J. Thin films of fullerene-like MoS2 nanoparticles with ultra-low friction and wear. Nature 2000, 407, 164–167. [Google Scholar] [CrossRef]
- Camacho-Bragado, G.; Elechiguerra, J.; Olivas, A.; Fuentes, S.; Galvan, D.; Yacaman, M. Structure and catalytic properties of nanostructured molybdenum sulfides. J. Catal. 2005, 234, 182–190. [Google Scholar] [CrossRef]
- Ramos, M.; Ferrer, D.; Martinez-Soto, E.; Lopez-Lippmann, H.; Torres, B.; Berhault, G.; Chianelli, R.R. In-situ HRTEM study of the reactive carbide phase of Co/MoS2 catalyst. Ultramicroscopy 2013, 127, 64–69. [Google Scholar] [CrossRef]
- Radisavljevic, B.; Radenovic, A.; Brivio, J.; Giacometti, V.; Kis, A. Single-layer MoS2 transistors. Nat. Nanotechnol. 2011, 6, 147–150. [Google Scholar] [CrossRef]
- Kim, S.; Konar, A.; Hwang, W.S.; Lee, J.H.; Lee, J.; Yang, J.; Jung, C.; Kim, H.; Yoo, J.B.; Choi, J.Y.; et al. High-mobility and low-power thin-film transistors based on multilayer MoS2 crystals. Nat. Commun. 2012, 3, 1011. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.H.; Kalantar-Zadeh, K.; Kis, A.; Coleman, J.N.; Strano, M.S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699–712. [Google Scholar] [CrossRef]
- Splendiani, A.; Sun, L.; Zhang, Y.; Li, T.; Kim, J.; Chim, C.Y.; Galli, G.; Wang, F. Emerging Photoluminescence in Monolayer MoS2. Nano Lett. 2010, 10, 1271–1275. [Google Scholar] [CrossRef]
- Kobayashi, K.; Yamauchi, J. Electronic structure and scanning-tunneling-microscopy image of molybdenum dichalcogenide surfaces. Phys. Rev. B 1995, 51, 17085–17095. [Google Scholar] [CrossRef]
- Lauritsen, J.V.; Kibsgaard, J.; Helveg, S.; Topsøe, H.; Clausen, B.S.; Lægsgaard, E.; Besenbache, F. Size-dependent structure of MoS2 nanocrystals. Nat. Nanotechnol. 2007, 2, 53–58. [Google Scholar] [CrossRef]
- Camacho-Bragado, G.A.; Elechiguerra, J.L.; Yacaman, M.J. Characterization of low dimensional molybdenum sulfide nanostructures. Mater. Charact. 2008, 59, 204–212. [Google Scholar] [CrossRef]
- Ramos, M.; Berhault, G.; Ferrer, D.A.; Torres, B.; Chianelli, R.R. HRTEM and molecular modeling of the MoS2–Co9S8 interface: Understanding the promotion effect in bulk HDS catalysts. Catal. Sci. Technol. 2012, 2, 164–178. [Google Scholar] [CrossRef]
- Liu, X.; Cao, D.; Yang, T.; Li, H.; Ge, H.; Ramos, M.; Peng, Q.; Dearden, A.K.; Cao, Z.; Yang, Y.; et al. Insight into the structure and energy of Mo27SxOy clusters. RSC Adv. 2017, 7, 9513–9520. [Google Scholar] [CrossRef]
- Wang, C.-X.; Zhang, C.; Jiang, J.-W.; Rabczuk, T. A coarse-grained simulation for the folding of molybdenum disulphide. J. Phys. D Appl. Phys. 2016, 49, 025302. [Google Scholar] [CrossRef]
- Ghorbani-Asl, M.; Borini, S.; Kuc, A.; Heine, T. Strain-dependent modulation of conductivity in single-layer transition-metal dichalcogenides. Phys. Rev. B 2013, 87, 235434. [Google Scholar] [CrossRef]
- Sharma, M.; Kumar, A.; Ahluwalia, P.K.; Pandey, R. Strain and electric field induced electronic properties of two-dimensional hybrid bilayers of transition-metal dichalcogenides. J. Appl. Phys. 2014, 116, 063711. [Google Scholar] [CrossRef]
- Terrones, H.; López-Urías, F.; Terrones, M. Novel hetero-layered materials with tunable direct band gaps by sandwiching different metal disulfides and diselenides. Sci. Rep. 2013, 3, 1549. [Google Scholar] [CrossRef] [PubMed]
- Ramos, M.A.; Chianelli, R.; Enriquez-Carrejo, J.L.; Gonzalez, G.A.; Berhault, G. Metallic states by angular dependence in 2H-MoS2 slabs. Comput. Mater. Sci. 2014, 84, 18–22. [Google Scholar] [CrossRef]
- Sun, J.; Xu, F.; Sun, L. In situ investigation of the mechanical properties of nanomaterials by transmission electron microscopy. Acta Mech. Sin. 2012, 28, 1513–1527. [Google Scholar] [CrossRef]
- Colas, G.; Serles, P.; Saulot, A.; Filleter, T. Strength measurement and rupture mechanisms of a micron thick nanocrystalline MoS2 coating using AFM based micro-bending tests. J. Mech. Phys. Solids 2019, 128, 151–161. [Google Scholar] [CrossRef]
- Ramos, M.; Nogan, J.; Ortíz-Díaz, M.; Enriquez-Carrejo, J.L.; Rodriguez-González, C.A.; Mireles-Jr-Garcia, J.; Ornelas, C.; Hurtado-Macias, A. Mechanical properties of RF-sputtering MoS2 thin films. Surf. Topogr. Metrol. 2017, 5, 025003. [Google Scholar] [CrossRef]
- Lahouij, I.; Dassenoy, F.; Vacher, B.; Martin, J.-M. Real Time TEM Imaging of Compression and Shear of Single Fullerene-Like MoS2 Nanoparticle. Tribol. Lett. 2012, 45, 131–141. [Google Scholar] [CrossRef]
- Casillas, G.; Santiago, U.; Barrón, H.; Alducin, D.; Ponce, A.; José-Yacamán, M. Elasticity of MoS2 Sheets by mechanical deformation observed by in situ electron microscopy. J. Phys. Chem. C 2015, 119, 710–715. [Google Scholar] [CrossRef]
- Available online: https://avogadro.cc/ (accessed on 25 January 2021).
- Bhattacharyya, S.; Pandey, T.; Singh, A.K. Effect of strain on electronic and thermoelectric properties of few layers to bulk MoS2. Nanotechnology 2014, 25, 465701. [Google Scholar] [CrossRef]
- Ding, S.; Jiang, S.; Zhou, Y.; Wei, Q.; Zhou, W. Catalytic characteristics of active corner sites in CoMoS nanostructure hydrodesulfurization–A mechanism study based on DFT calculations. J. Catal. 2017, 345, 24–38. [Google Scholar] [CrossRef]
- Yazyev, O.V.; Kis, A. MoS2 and semiconductors in the flatland. Mater. Today 2015, 18, 20–30. [Google Scholar] [CrossRef]
- Peña-Álvarez, M.; del Corro, E.; Morales-García, Á.; Kavan, L.; Kalbac, M.; Frank, O. Single Layer Molybdenum Disulfide under Direct Out-of-Plane Compression: Low-Stress Band-Gap Engineering. Nano Lett. 2015, 15, 3139–3146. [Google Scholar] [CrossRef]
- Espejo, C.; Rangel, T.; Romero, A.H.; Gonze, X.; Rignanese, G.-M. Band structure tunability in MoS2 under interlayer compression: A DFT and GW study. Phys. Rev. B 2013, 87, 245114. [Google Scholar] [CrossRef]
- Nogueira, A.; Znaiguia, R.; Uzio, D.; Afanasiev, P.; Berhault, G. Curved nanostructures of unsupported and Al2O3-supported MoS2 catalysts: Synthesis and HDS catalytic properties. Appl. Catal. A Gen. 2012, 429–430, 92–105. [Google Scholar] [CrossRef]
- Jiang, J.; Qi, Z.; Park, H.S.; Rabczuk, T. Elastic bending modulus of single-layer molybdenum disulfide (MoS2): Finite thickness effect. Nanotechnology 2013, 24, 435705. [Google Scholar] [CrossRef]
- López-Galán, O.A.; Ramos, M.; Berhault, G.; Torres, B.; Chianelli, R.R. Electronic states and metallic character of carbide Co/MoS2 catalytic interface. Electron. Struct. 2021, 3, 025002. [Google Scholar] [CrossRef]
- Ge, H.; Wen, X.D.; Ramos, M.A.; Chianelli, R.R.; Wang, S.; Wang, J.; Qin, Z.; Lyu, Z.; Li, X. Carbonization of Ethylenediamine Coimpregnated CoMo/Al2O3 Catalysts Sulfided by Organic Sulfiding Agent. ACS Catal. 2014, 4, 2556–2565. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, K.; Wang, H.; Lin, H.; Zheng, Y. In-plane defect engineering on MoS2 through a novel two-phase hydrothermal synthesis. Catalysis Today 2022, in press. [Google Scholar] [CrossRef]
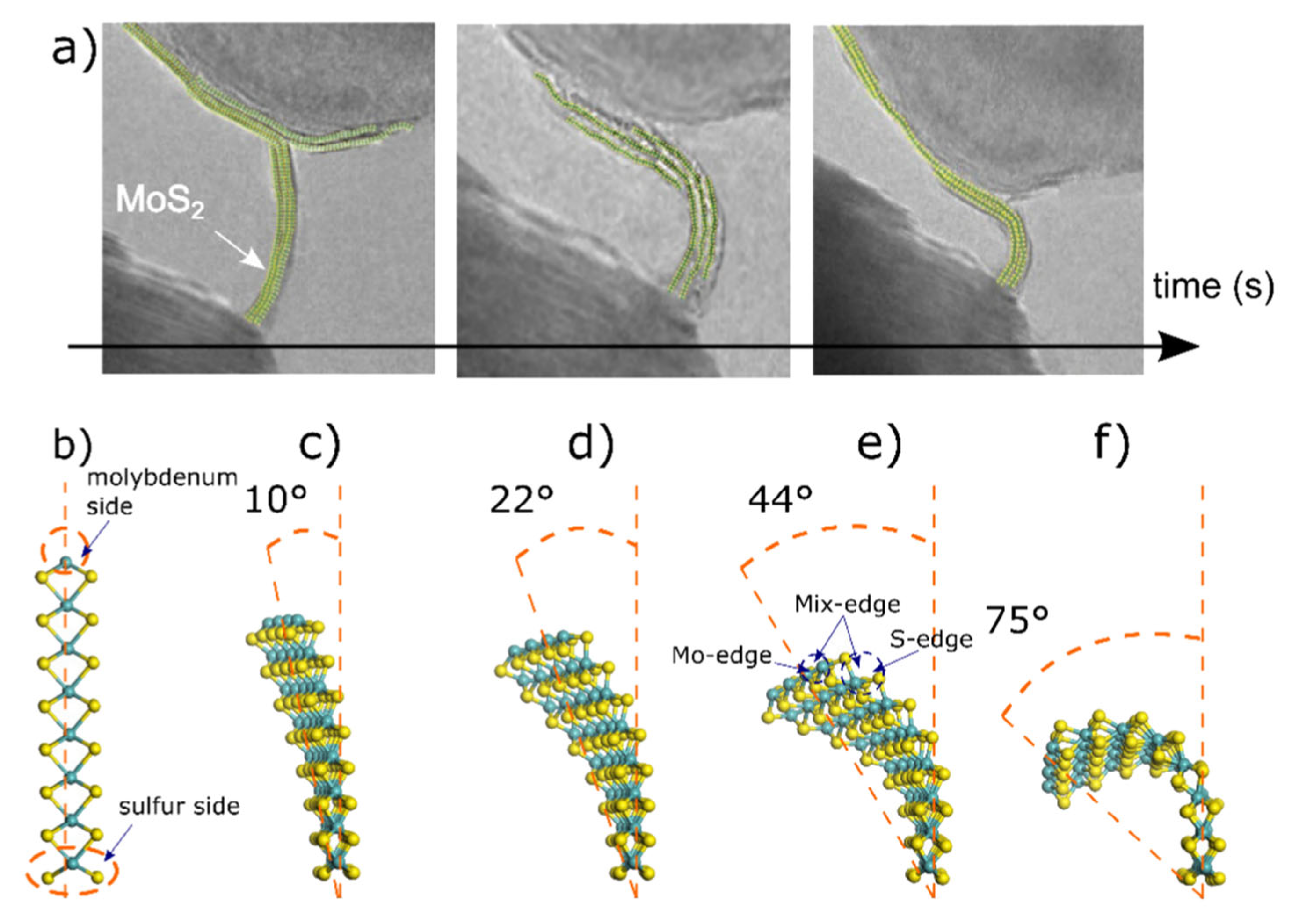
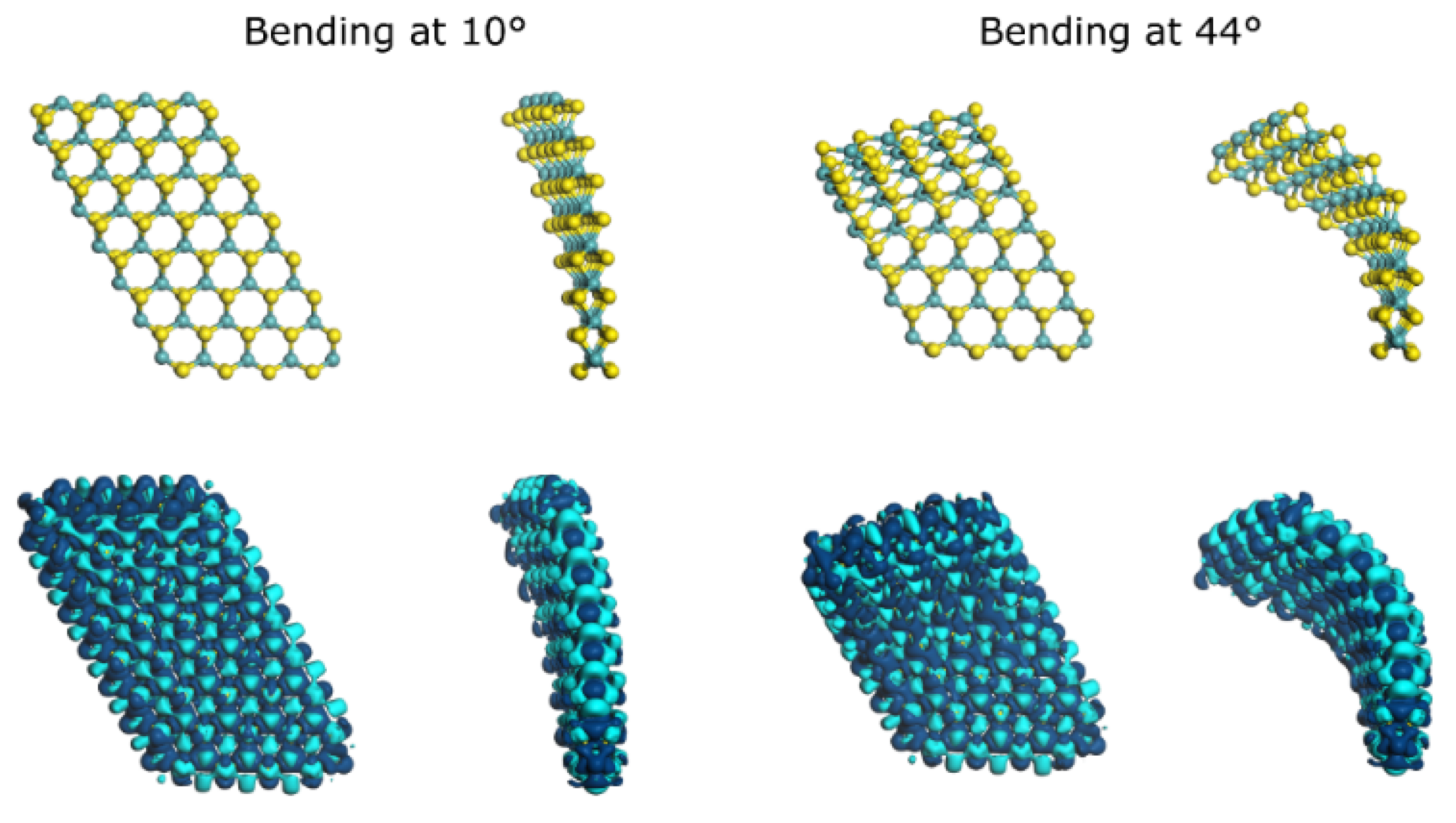
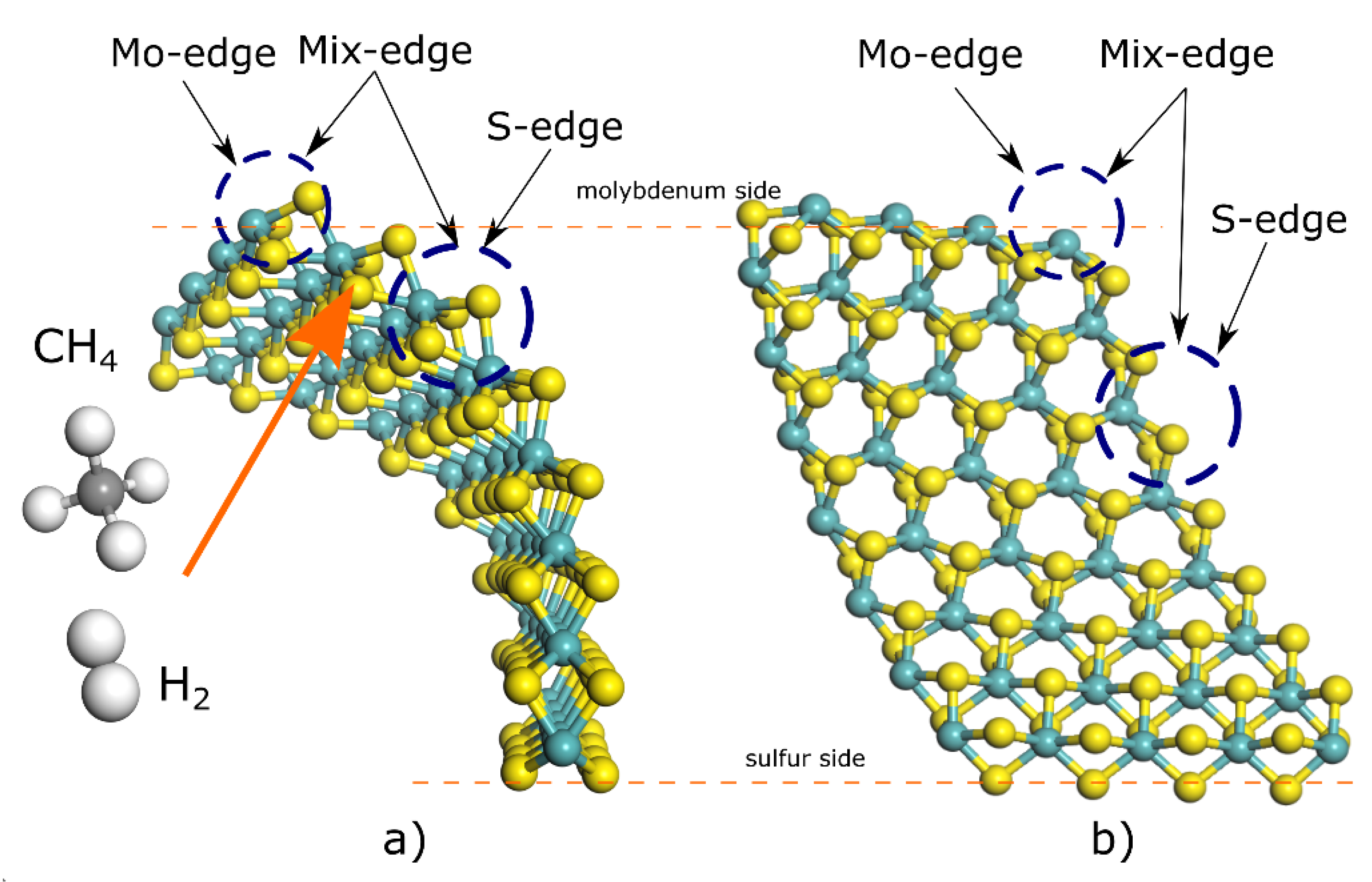
| Bending Angle | Bending Angle (Radians) | Cord Length (Å) | Radius (Å) | Arc Length (Å) |
|---|---|---|---|---|
| 10° | 0.174532925 | 12.25 | 70.27 | 12.26 |
| 22° | 0.383972435 | 11.97 | 31.36 | 12.04 |
| 44° | 0.767944871 | 11.32 | 15.10 | 11.60 |
| 75° | 1.308996939 | 10.27 | 8.43 | 11.04 |
| Bending Angle | HOMO (eV) | LUMO (eV) | ΔE (eV) | DOS Integration (e−) | Fermi Level Crossing Point (e−/eV) |
|---|---|---|---|---|---|
| 0° | −4.833 | −4.633 | 0.2 | 30 | 32 |
| 10° | −3.67173 | −3.61125 | 0.060480 | 26.8 | 29 |
| 22° | −3.77025 | −3.70124 | 0.069012 | 27.1 | 28 |
| 44° | −3.85106 | −3.77579 | 0.075276 | 28.7 | 30 |
| 75° | −3.69625 | −3.64605 | 0.050193 | 27.2 | 27 |
| Absorption Energy on 44° (Eads/kcal mol−1) | Absorption Energy on 10° (Eads/kcal mol−1) | Absorption Energy on 0° (Eads/kcal mol−1) | |
|---|---|---|---|
| H2 (@S-edge) | 22.95 | 43.75 | No convergence found |
| H2 (@Mo-edge) | 100.00 | 185.34 | 847.5 |
| H2 (@Mix-edge) | 93.91 | 169.07 | 5085.9 |
| C (@S-edge) | −1.82 × 103 | −1.99 × 103 | 5.17 × 103 |
| C (@S-edge) (2) | −1.97 × 103 | −2.22 × 104 | 5.18 × 103 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos, M.; López-Galán, O.A.; Polanco, J.; José-Yacamán, M. On the Electronic Structure of 2H-MoS2: Correlating DFT Calculations and In-Situ Mechanical Bending on TEM. Materials 2022, 15, 6732. https://doi.org/10.3390/ma15196732
Ramos M, López-Galán OA, Polanco J, José-Yacamán M. On the Electronic Structure of 2H-MoS2: Correlating DFT Calculations and In-Situ Mechanical Bending on TEM. Materials. 2022; 15(19):6732. https://doi.org/10.3390/ma15196732
Chicago/Turabian StyleRamos, Manuel, Oscar A. López-Galán, Javier Polanco, and Miguel José-Yacamán. 2022. "On the Electronic Structure of 2H-MoS2: Correlating DFT Calculations and In-Situ Mechanical Bending on TEM" Materials 15, no. 19: 6732. https://doi.org/10.3390/ma15196732
APA StyleRamos, M., López-Galán, O. A., Polanco, J., & José-Yacamán, M. (2022). On the Electronic Structure of 2H-MoS2: Correlating DFT Calculations and In-Situ Mechanical Bending on TEM. Materials, 15(19), 6732. https://doi.org/10.3390/ma15196732