Identification of Relatively Weak Areas of Planar Structures Based on Modal Strain Energy Decomposition Method
Abstract
:1. Introduction
2. Modal Strain Energy Decomposition of a Planar Square Element
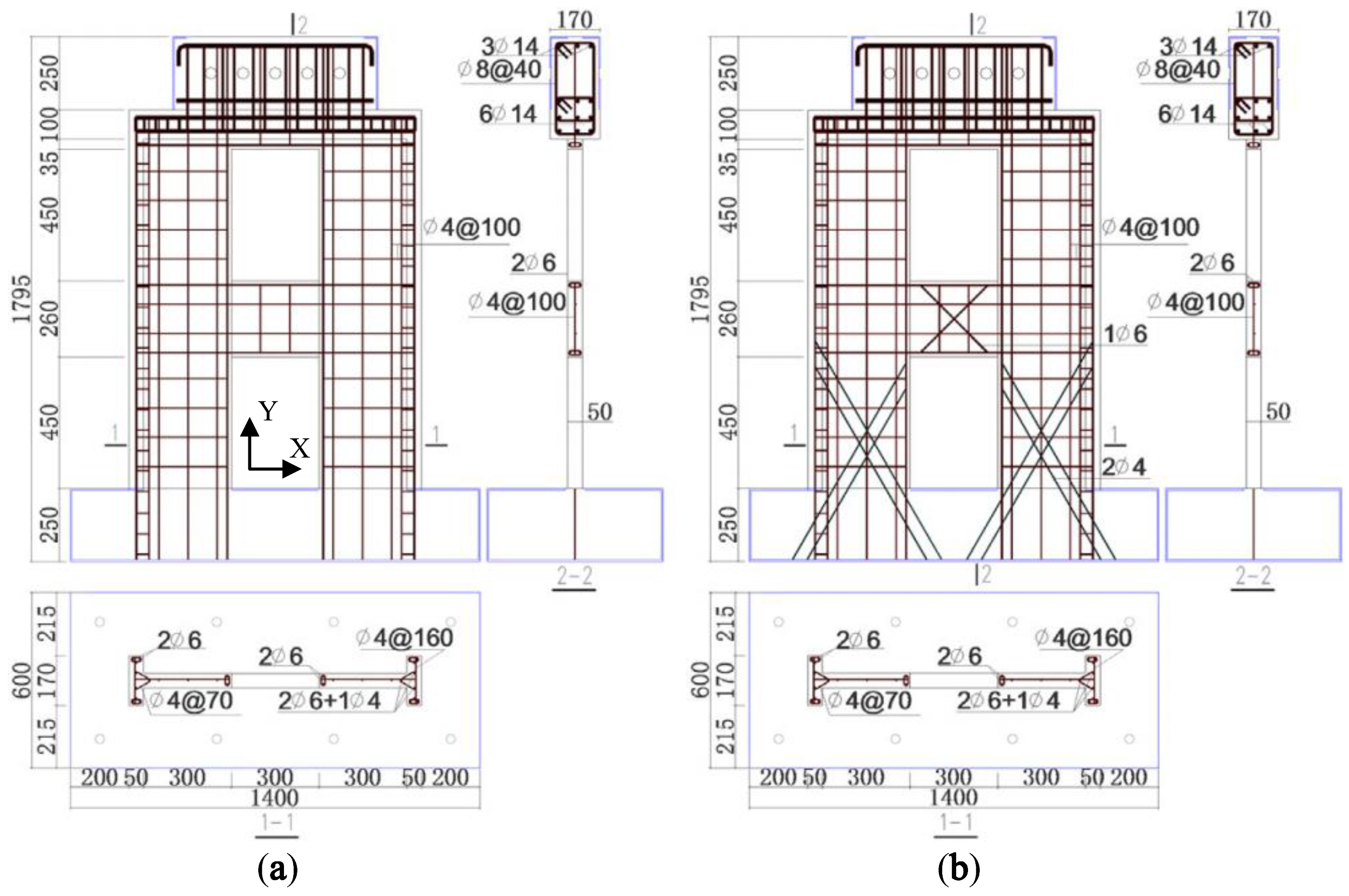
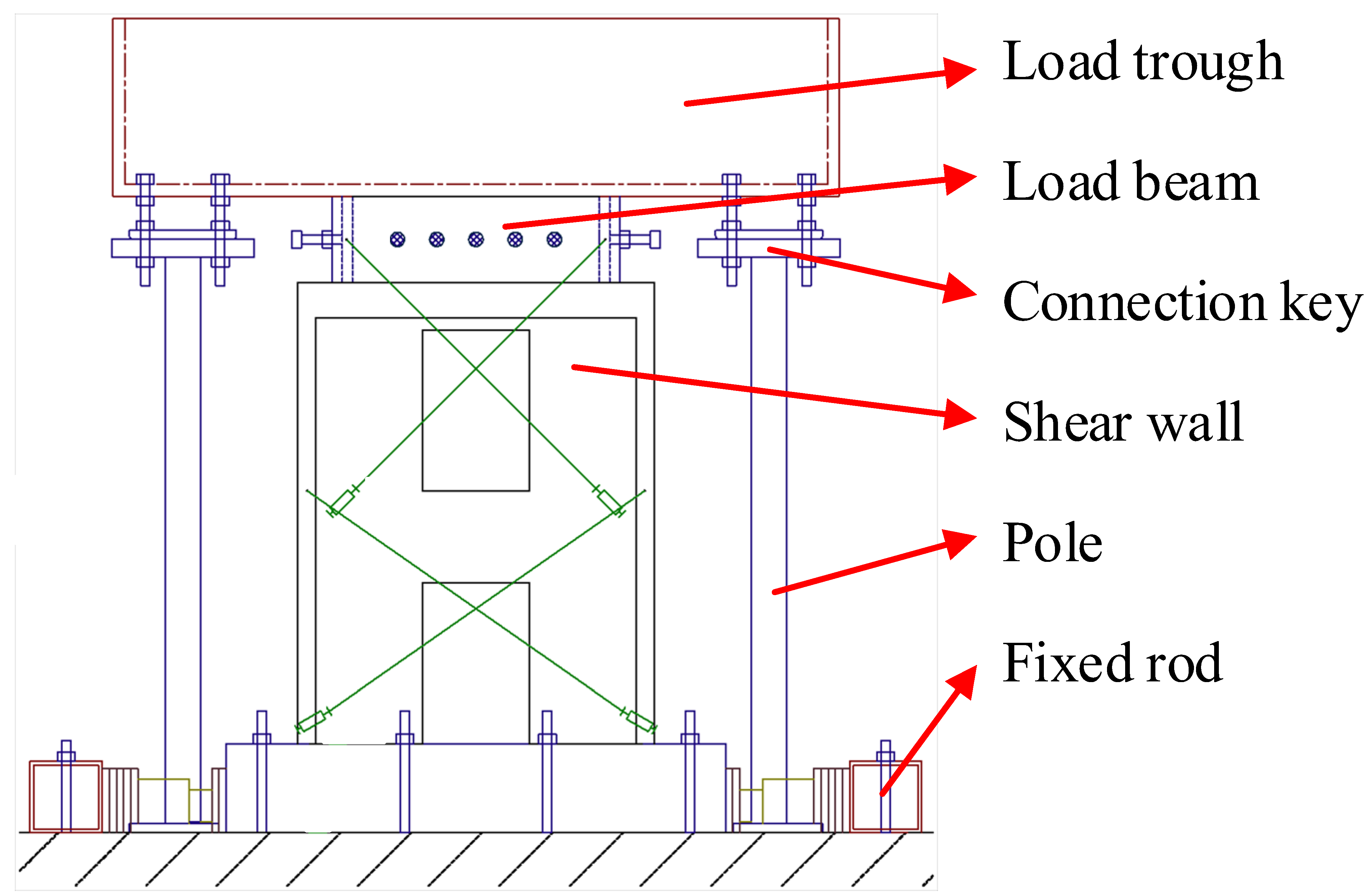
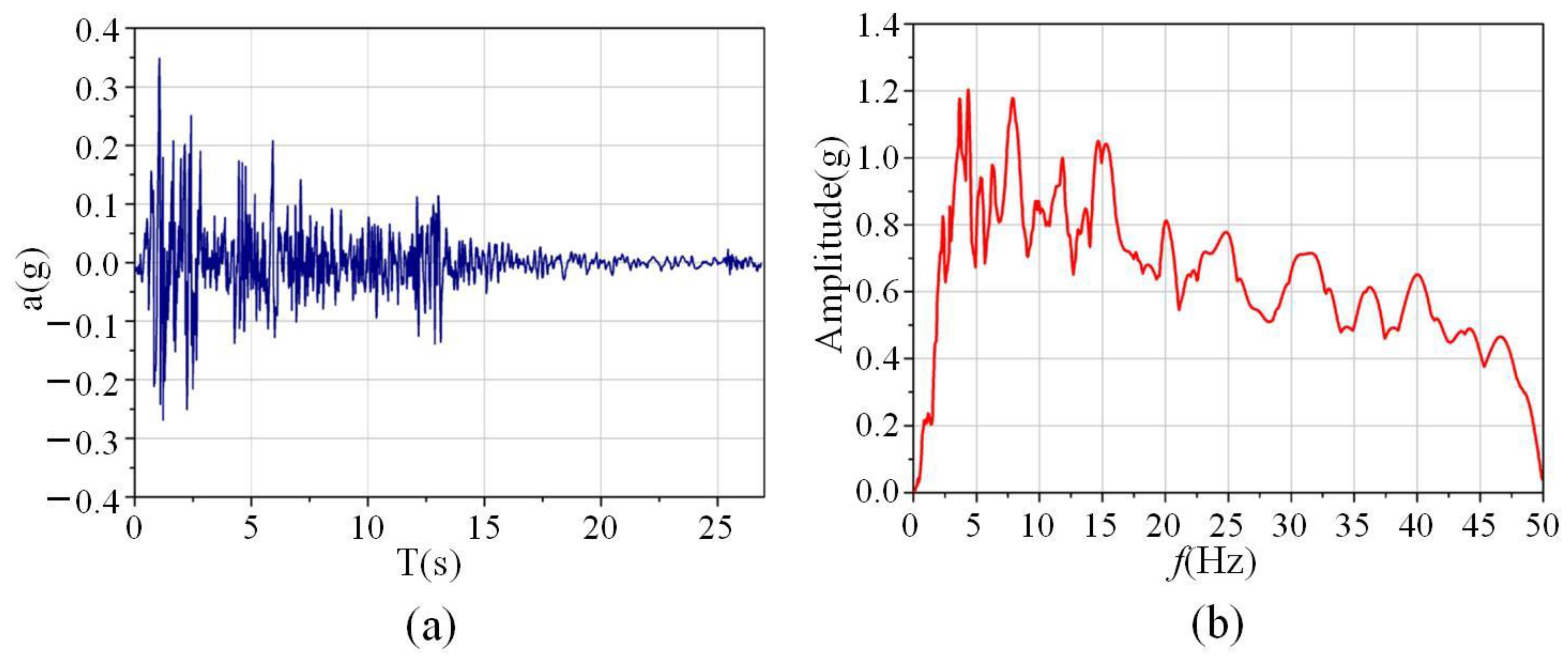
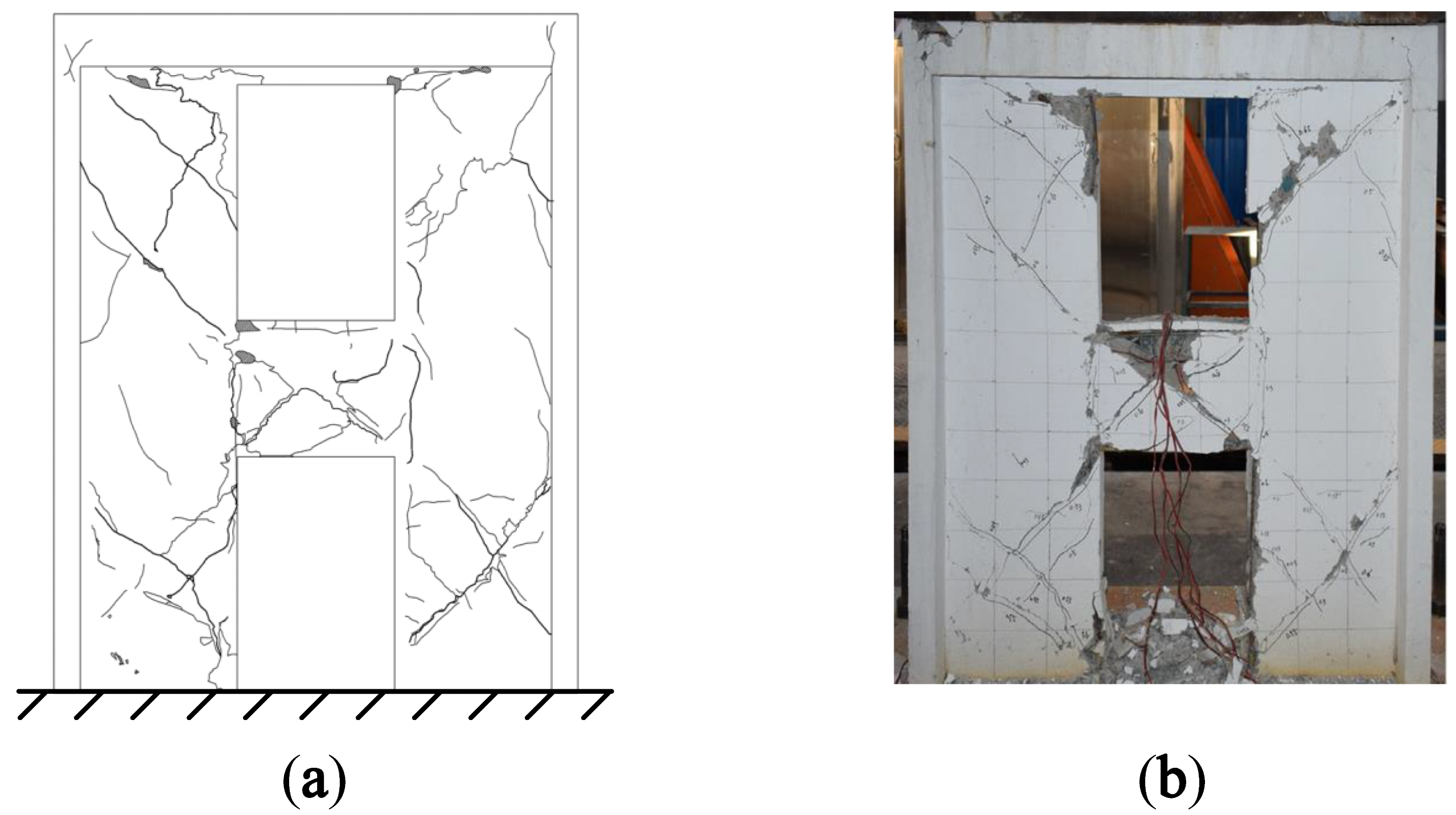
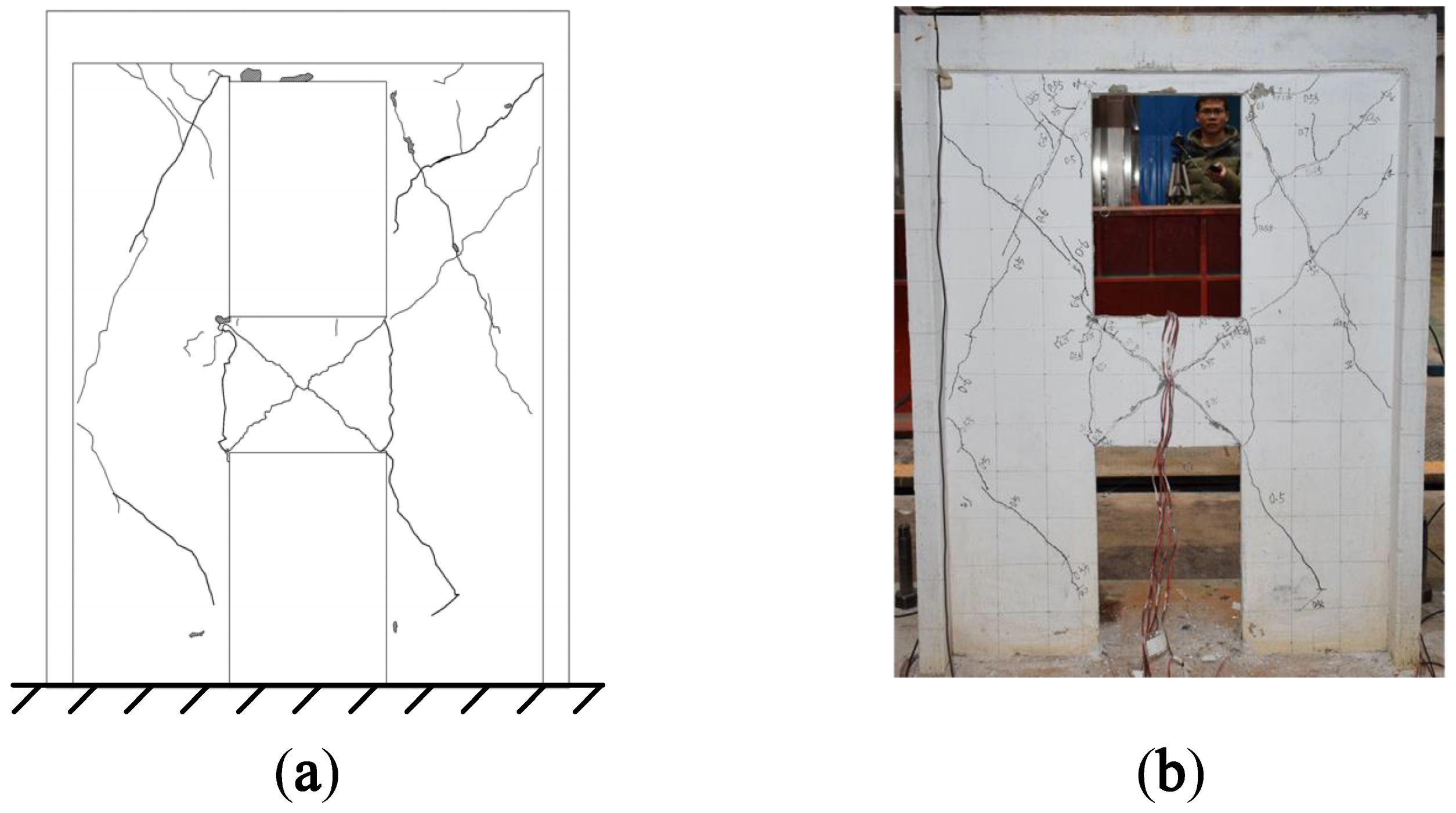
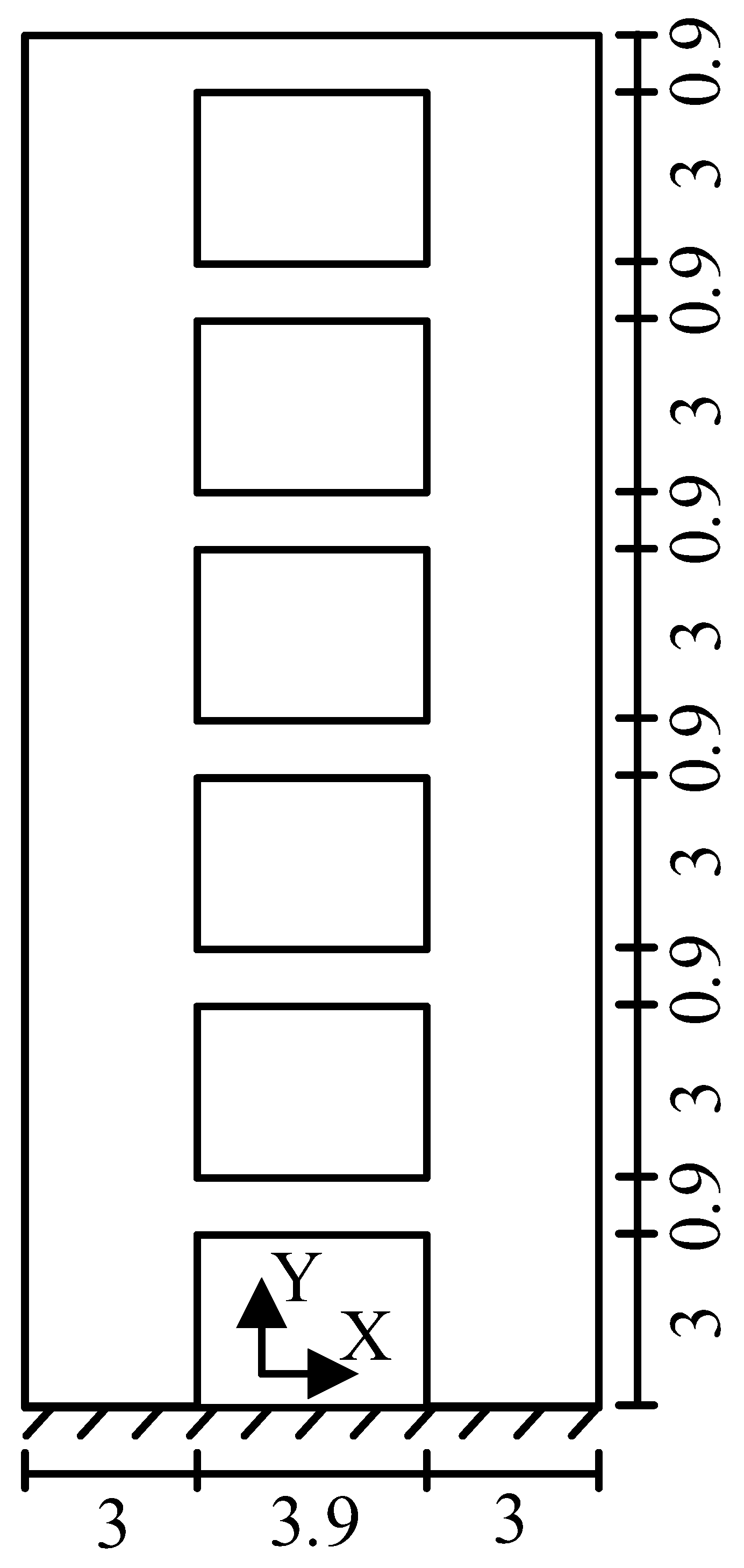
3. Experimental Verification
4. Identification of Relatively Weak Areas of a Structure Based on Different Order Vibration Modes
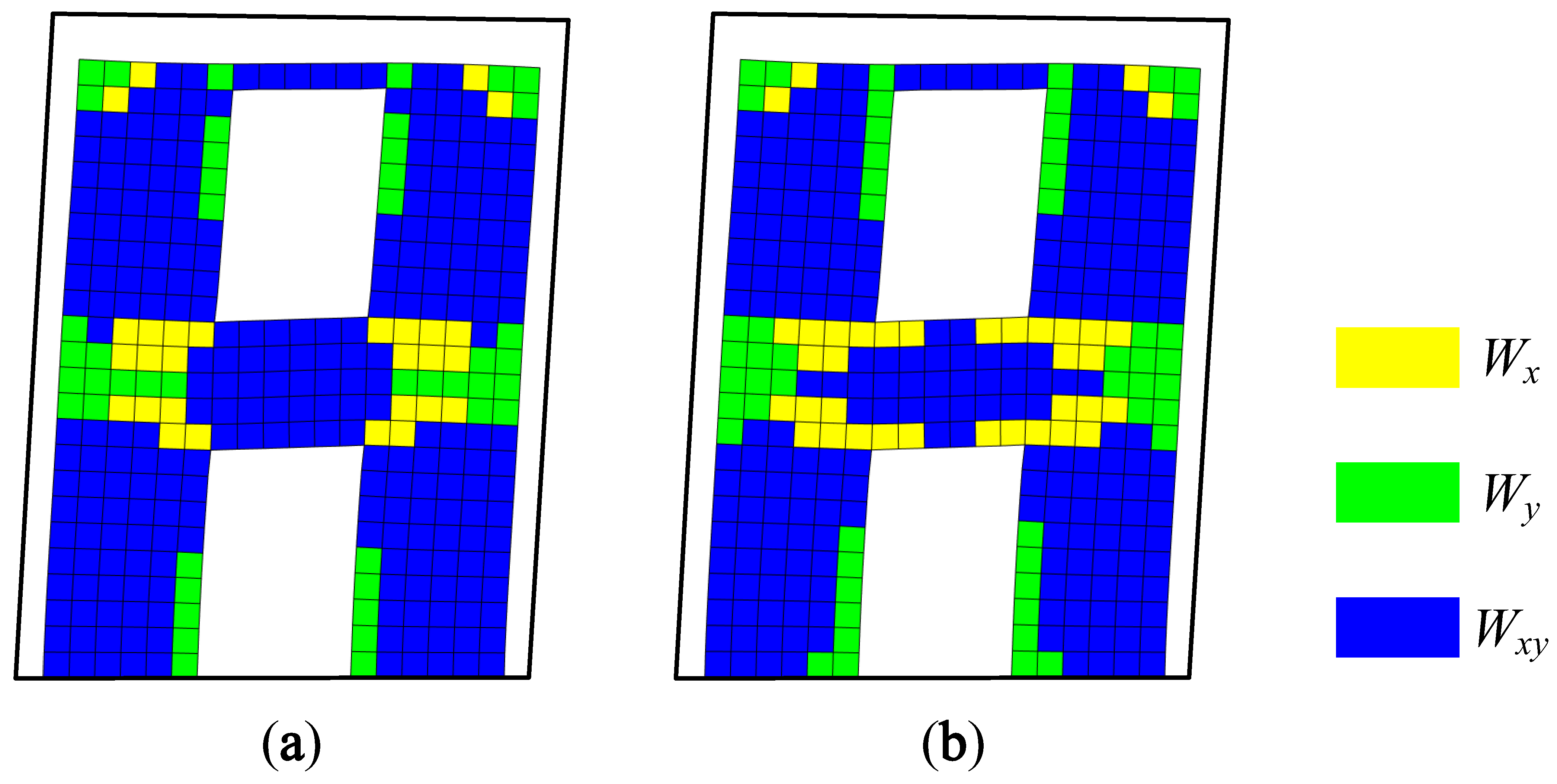
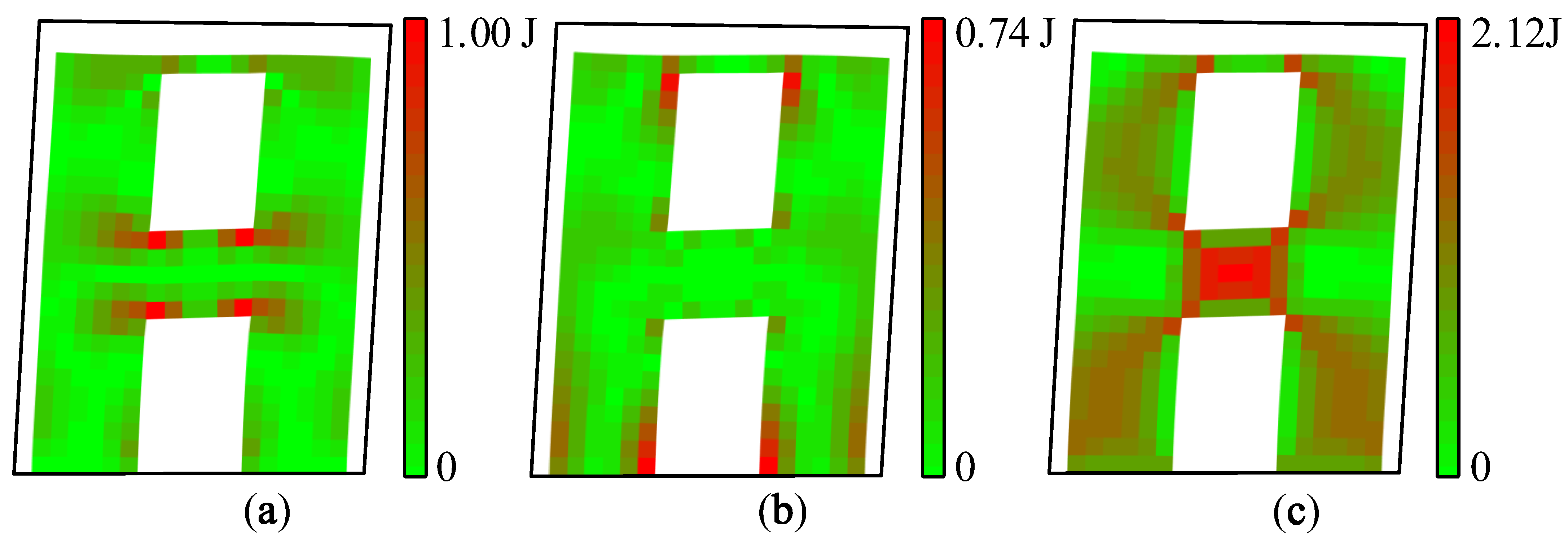
4.1. Identification Result Based on First-Order Vibration Mode
4.2. Identification Results Based on Second-Order Vibration Mode
5. Conclusions
- By decomposing the comprehensive modal strain energy of the planar structure into X- and Y-direction modal normal strain energy and modal shear strain energy, the quantitative visual analysis of the vibration mode can be realized.
- The modal strain energy decomposition diagram can visualize the areas dominated by different modal strain energies, and the cracking mode of a structure can be predicted. The modal strain energy cloud diagram can quantify the concentration degree of different modal strain energies, thereby predicting which areas are prone to cracking and evaluating the cracking type.
- The modal strain energy decomposition method does involve load condition information and can effectively identify the relatively weak areas of a structure and guide the implementation of targeted reinforcement.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Seyedkhoei, A.; Akbari, R.; Maalek, S. Earthquake-Induced Domino-Type Progressive Collapse in Regular, Semiregular, and Irregular Bridges. Shock Vib. 2019, 2019, 8348596. [Google Scholar] [CrossRef]
- Göçer, C. Structural Evaluation of Masonry Building Damages during the April 24, 2014 Gökçeada Earthquake in the Aegean Sea. Bull. Earthq. Eng. 2020, 18, 3459–3483. [Google Scholar] [CrossRef]
- Nale, M.; Minghini, F.; Chiozzi, A.; Tralli, A. Fragility Functions for Local Failure Mechanisms in Unreinforced Masonry Buildings. Bull. Earthq. Eng. 2021, 2021, 6049–6079. [Google Scholar] [CrossRef]
- Cimmino, M.; Magliulo, G.; Manfredi, G. Seismic Collapse Assessment of New European Single-Story Rc Precast Buildings with Weak Connections. Bull. Earthq. Eng. 2020, 18, 6661–6686. [Google Scholar] [CrossRef]
- Gong, M.S.; Zuo, Z.X.; Wang, X.M.; Lu, X.T.; Xie, L.L. Comparing Seismic Performances of Pilotis and Bare Rc Frame Structures by Shaking Table Tests. Eng. Struct. 2019, 199, 109442. [Google Scholar] [CrossRef]
- Li, S.; Tian, J.B.; Liu, Y.H. Performance-Based Seismic Design of Eccentrically Braced Steel Frames Using Target Drift and Failure Mode. Earthq. Struct. 2017, 13, 443–454. [Google Scholar]
- Guo, T.N.; Meng, L.J.; Zhou, C.; Hua, X. Research on the Dynamic Hammering Method for Identifying Weak Parts in Cantilever Structures. Sci. Prog. 2021, 104, 1–22. [Google Scholar] [CrossRef]
- Zhang, A.L.; Xie, Z.Q.; Zhang, Y.X.; Lin, H.P. Shaking Table Test of a Prefabricated Steel Frame Structure with All-Bolted Connections. Eng. Struct. 2021, 248, 113273. [Google Scholar] [CrossRef]
- Sheng, E.F.; Ji, Y.H. Statics-Based Model-Free Damage Detection Under Uncertainties Using Modal Interval Analysis. Materials 2020, 13, 1567. [Google Scholar]
- Deng, T.F.; Huang, J.W.; Cao, M.S.; Li, D.Y.; Bayat, M. Seismic Damage Identification Method for Curved Beam Bridges Based on Wavelet Packet Norm Entropy. Sensors 2022, 22, 239. [Google Scholar] [CrossRef]
- Mccrory, J.P.; Pearson, M.R.; Pullin, R.; Holford, K.M. Optimisation of Acoustic Emission Wavestreaming for Structural Health Monitoring. Struct. Health Monit. 2020, 19, 1475–9217. [Google Scholar] [CrossRef]
- Cao, P.Y.; Niu, K.M.; Sun, J.H.; Zhao, S.L.; Liu, Y.P. Reordering of Vertical Vibration Modes in an Axially Compressed Beam on a Winkler Foundation. J. Sound Vib. 2022, 526, 116841. [Google Scholar] [CrossRef]
- Cong, P.H.; Van Thom, D.; Duc, D.H. Phase Field Model for Fracture Based on Modified Couple Stress. Eng. Fract. Mech. 2022, 269, 108534. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Shi, Y.Z.; You, X.; Jiang, R.J.; Gai, W.M. Dynamic Behaviour of Bridge Girders with Trapezoidal Profiled Webs Subjected to Moving Loads. Materials 2021, 14, 38. [Google Scholar] [CrossRef]
- Treyssède, F. Finite Element Modeling of Temperature Load Effects on the Vibration of Local Modes in Multi-Cable Structures. J. Sound Vib. 2018, 413, 191–204. [Google Scholar] [CrossRef]
- Guan, X.M.; Yang, N.; Zhang, W.J.; Li, M.G.; Liu, Z.L.; Wang, X.H.; Zhang, S.L. Vibration Response and Failure Modes Analysis of the Temporary Support Structure Under Blasting Excavation of Tunnels. Eng. Fail. Anal. 2022, 136, 106188. [Google Scholar] [CrossRef]
- Mazanoglu, K.; Kandemir-Mazanoglu, E.C. A New Simplified Method for Anti-Symmetric Mode in-Plane Vibrations of Frame Structures with Column Cracks. J. Vib. Control 2018, 24, 5794–5810. [Google Scholar] [CrossRef]
- Ibrahimbegovic, A.; Wilson, E.L. Automated Truncation of Ritz Vector Basis in Modal Transformation. J. Eng. Mech. 1990, 116, 2506–2520. [Google Scholar] [CrossRef]
- Zhang, J.W.; Zheng, W.B.; Yu, C.; Cao, W.L. Shaking Table Test of Reinforced Concrete Coupled Shear Walls with Single Layer of Web Reinforcement and Inclined Steel Bars. Adv. Struct. Eng. 2018, 21, 2282–2298. [Google Scholar] [CrossRef]
- Zhang, J.W.; Cao, W.L.; Yin, W.S. Study on Seismic Performance of Mid-Rise RC Shear Wall with Single Row of Steel Bars and Simplified Boundary Elements. Chin. Civ. Eng. J. 2009, 42, 99–104. (In Chinese) [Google Scholar]
- Tho, N.C.; Ta, N.T.; Thom, D.V. New Numerical Results from Simulations of Beams and Space Frame Systems with a Tuned Mass Damper. Materials 2019, 12, 1329. [Google Scholar] [CrossRef] [Green Version]

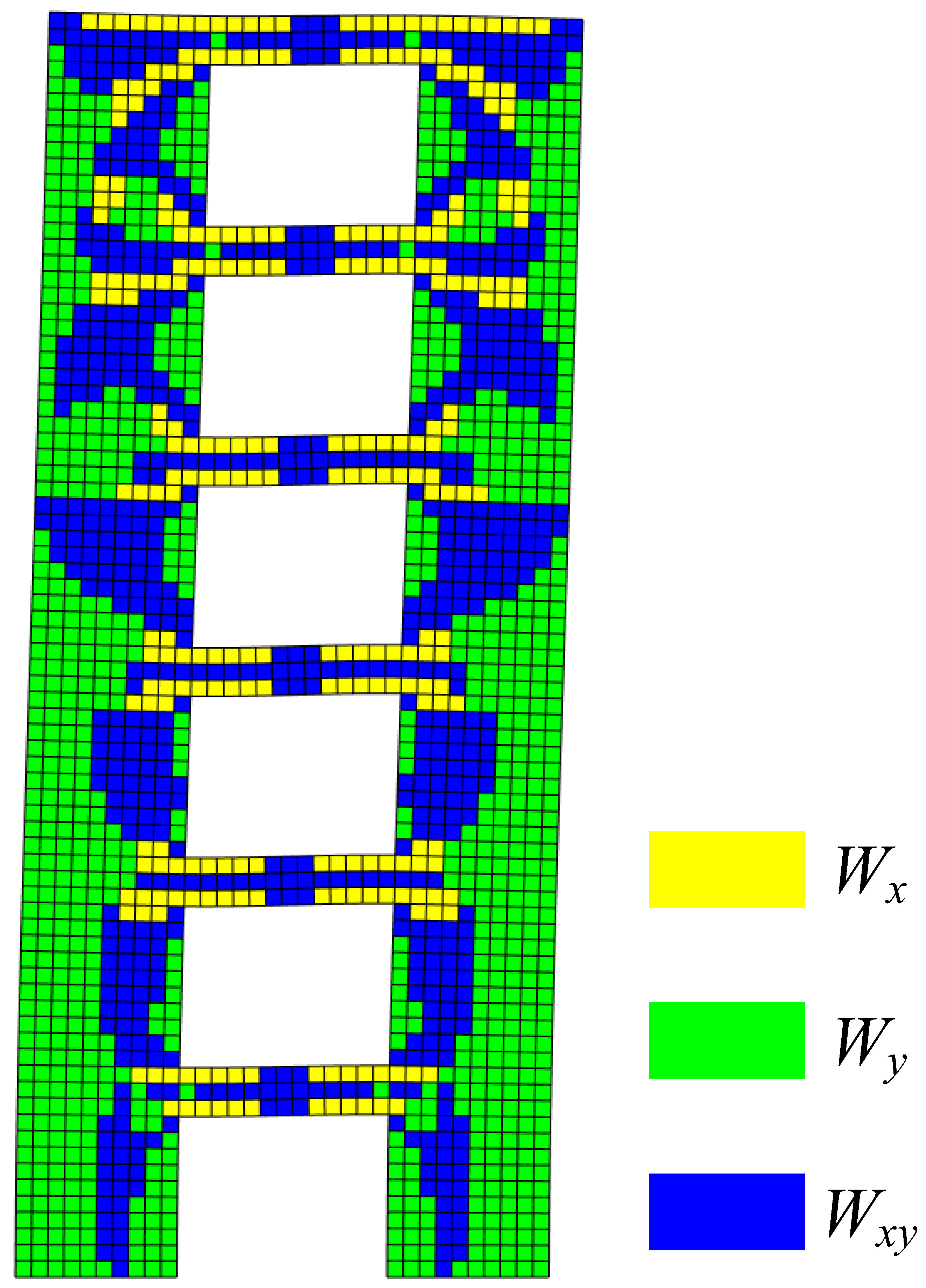

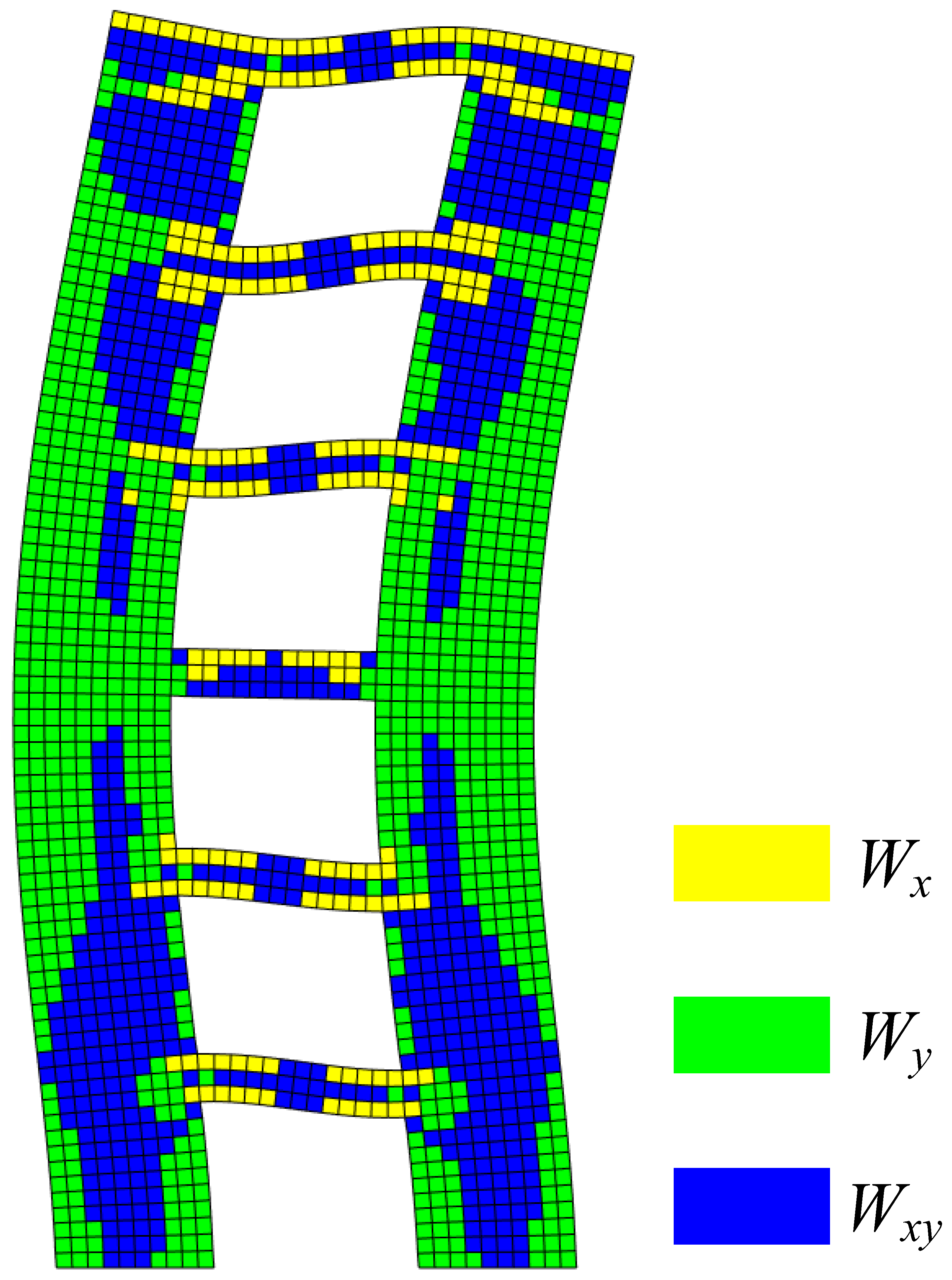

| X-Direction Modal Normal Strain Energy | Y-Direction Modal Normal Strain Energy | Modal Shear Strain Energy |
|---|---|---|
 |  |  |
| Steel Reinforcement Diameter (mm) | Yield Strength (MPa) | Ultimate Strength (MPa) | Elastic Modulus (GPa) |
|---|---|---|---|
| Ø4 | 730.3 | 903.0 | 190.6 |
| Ø6 | 394.5 | 578.3 | 220.7 |
| Shear Walls | PGA (g) | ||||||
|---|---|---|---|---|---|---|---|
| T-1 | T-2 | T-3 | T-4 | T-5 | T-6 | T-7 | |
| A1 | 0.189 | 0.388 | 0.524 | 0.615 | 0.815 | 1.155 | 1.219 |
| A2 | 0.191 | 0.330 | 0.492 | 0.650 | 0.782 | 0.875 | 1.126 |
| Order | Tension and Compression | Shear | |
|---|---|---|---|
| X-Direction | Y-Direction | ||
| 1st | joint areas between coupling beam and wall limbs of the 2nd–4th stories | bottom of the wall limbs | coupling beams of the 2nd–4th stories, and the wall limbs of the 1st–3rd stories |
| 2nd | joint areas between coupling beam and wall limbs of the 5th story | bottom of the wall limbs, and outer side of the 3rd–4th stories | coupling beams of the 5th story, and the wall limbs of the 1st–2nd stories |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Liang, K.; Sun, P. Identification of Relatively Weak Areas of Planar Structures Based on Modal Strain Energy Decomposition Method. Materials 2022, 15, 6391. https://doi.org/10.3390/ma15186391
Wang D, Liang K, Sun P. Identification of Relatively Weak Areas of Planar Structures Based on Modal Strain Energy Decomposition Method. Materials. 2022; 15(18):6391. https://doi.org/10.3390/ma15186391
Chicago/Turabian StyleWang, Dongwei, Kaixuan Liang, and Panxu Sun. 2022. "Identification of Relatively Weak Areas of Planar Structures Based on Modal Strain Energy Decomposition Method" Materials 15, no. 18: 6391. https://doi.org/10.3390/ma15186391
APA StyleWang, D., Liang, K., & Sun, P. (2022). Identification of Relatively Weak Areas of Planar Structures Based on Modal Strain Energy Decomposition Method. Materials, 15(18), 6391. https://doi.org/10.3390/ma15186391








