Mechanical Properties of Robocast Glass Scaffolds Assessed through Micro-CT-Based Finite Element Models
Abstract
:1. Introduction
2. Materials and Methods
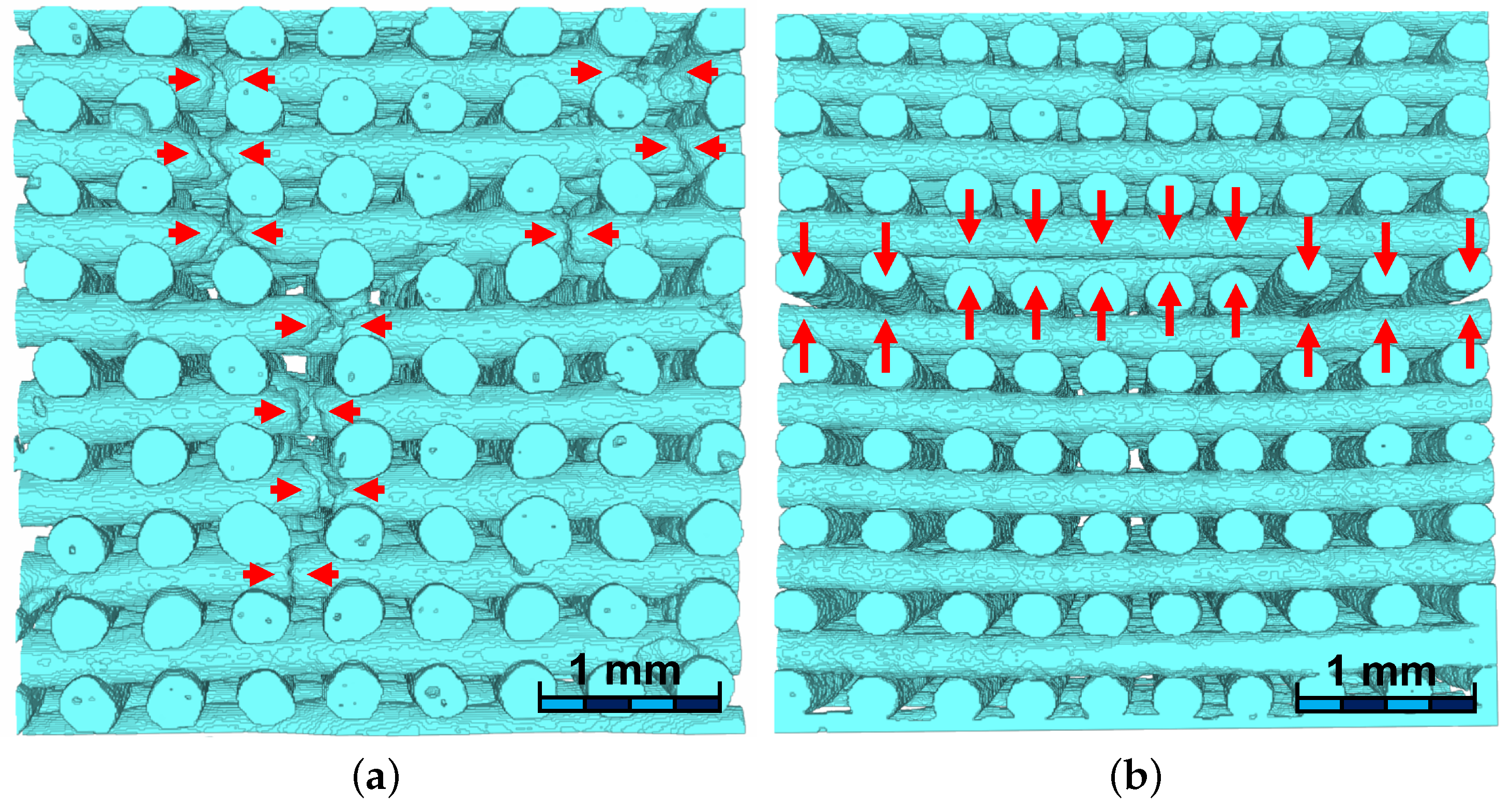
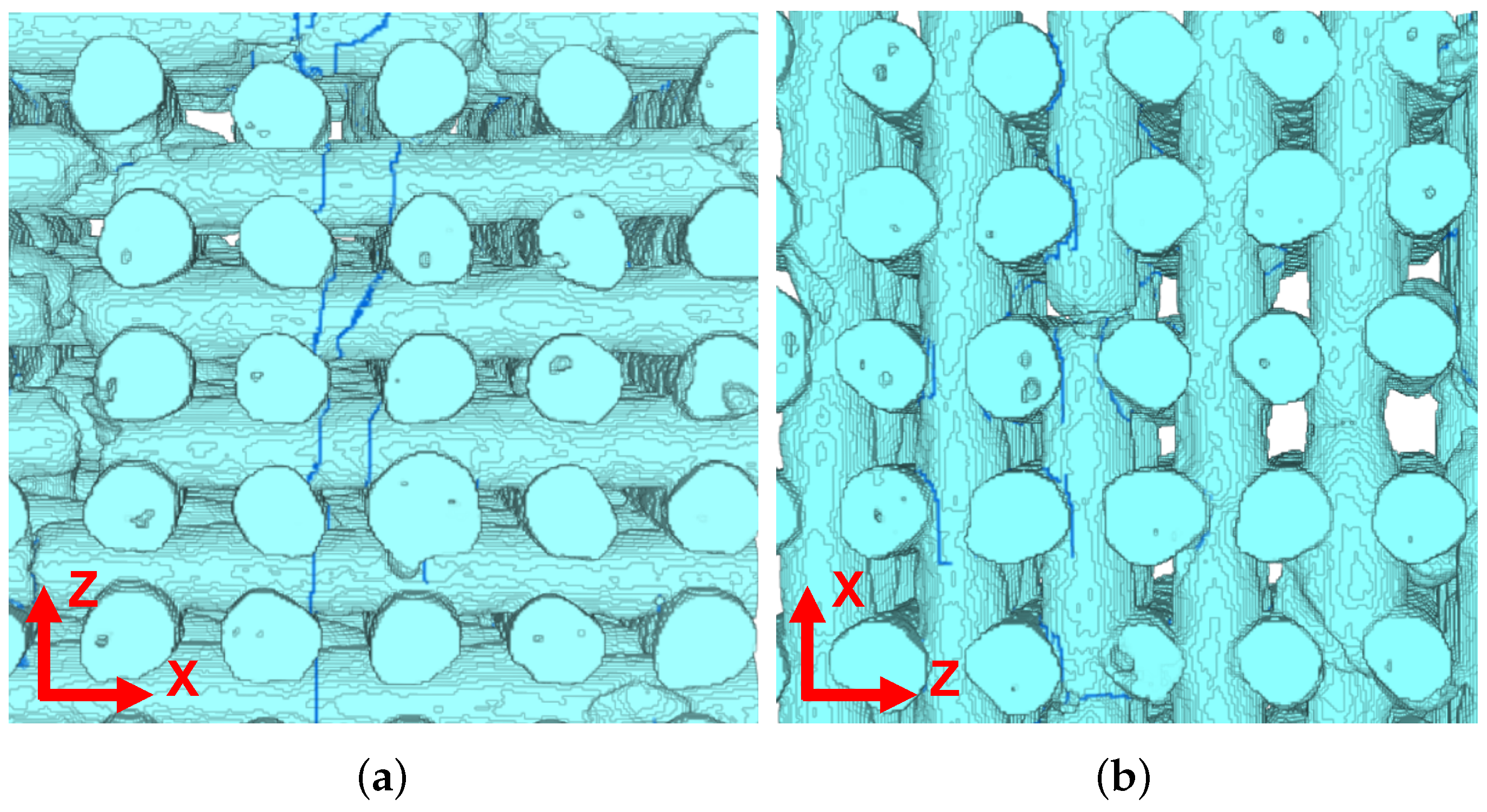
2.1. Scaffold Manufacturing, Micro-CT Scans and Defect Identification
2.2. Micro-CT Based Finite Element Modeling
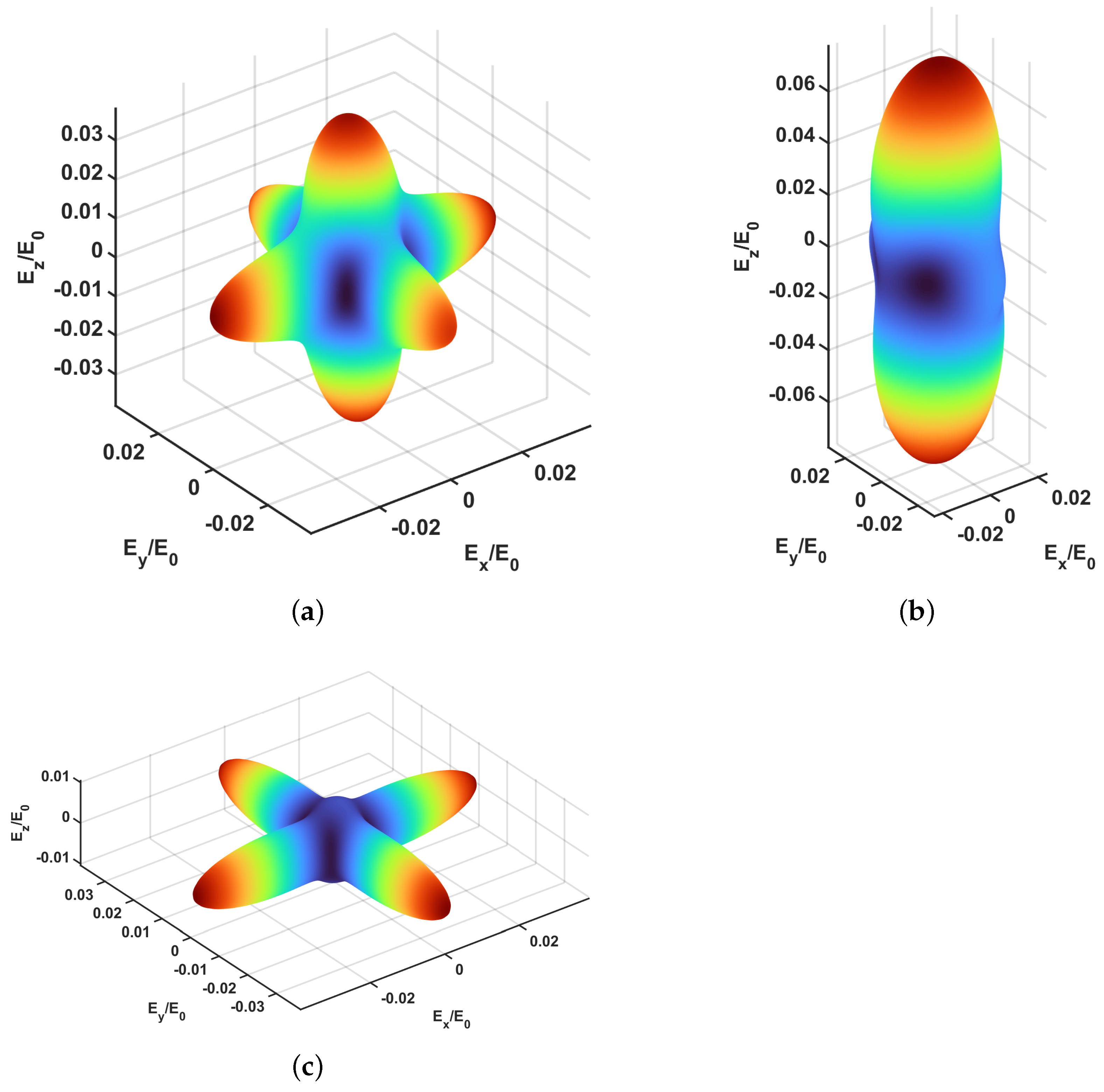
2.2.1. Elastic Analyses
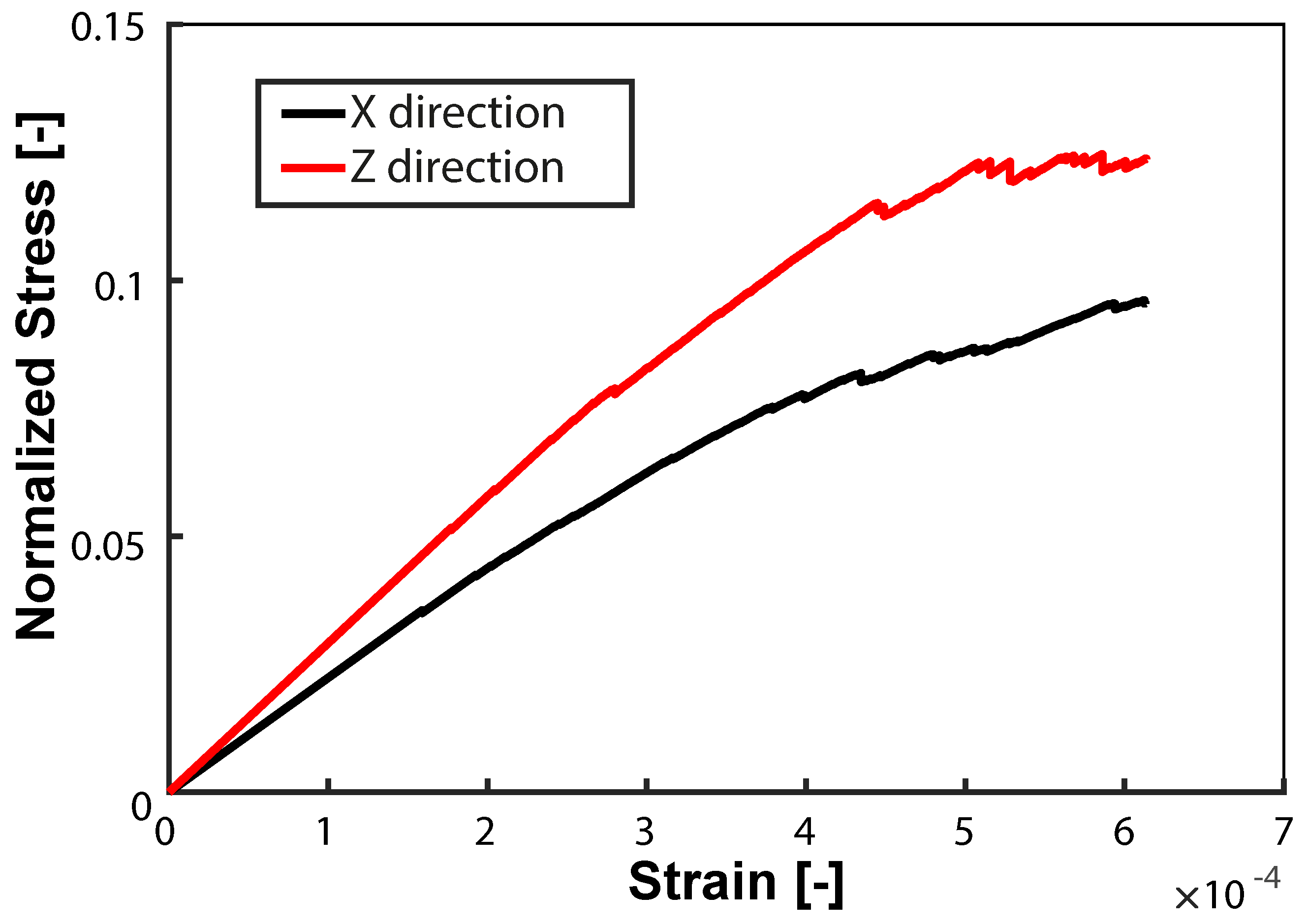
2.2.2. Assessment of Strength
3. Results
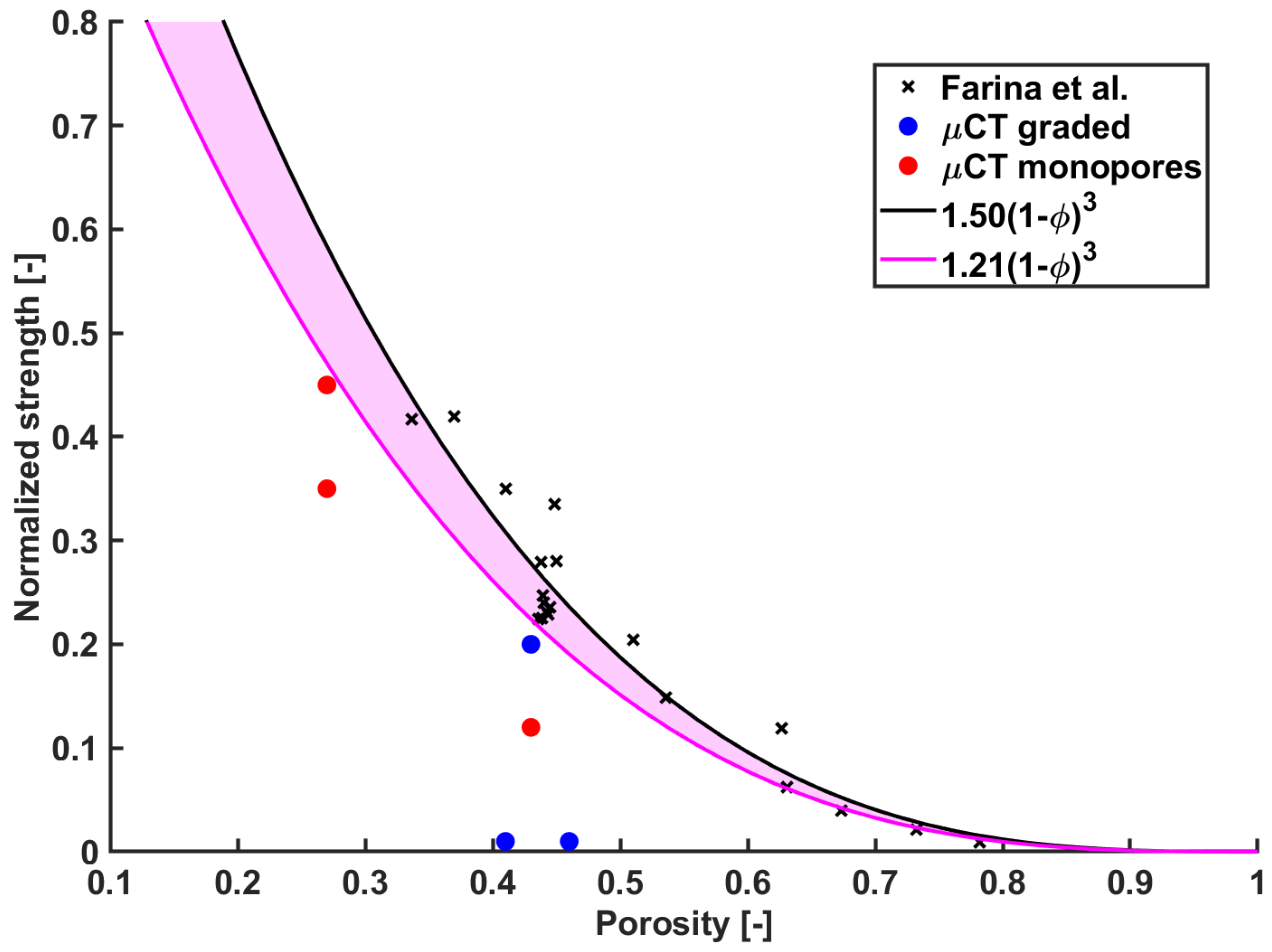
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Roseti, L.; Parisi, V.; Petretta, M.; Cavallo, C.; Desando, G.; Bartolotti, I.; Grigolo, B. Scaffolds for bone tissue engineering: State of the art and new perspectives. Mater. Sci. Eng. C 2017, 78, 1246–1262. [Google Scholar] [CrossRef] [PubMed]
- Fu, Q.; Saiz, E.; Rahaman, M.; Tomsia, A. Bioactive glass scaffolds for bone tissue engineering: State of the art and future perspectives. Mater. Sci. Eng. C 2011, 31, 1245–1256. [Google Scholar] [CrossRef] [PubMed]
- Baino, F.; Fiume, E.; Barberi, J.; Kargozar, S.; Marchi, J.; Massera, J.; Verné, E. Processing methods for making porous bioactive glass-based scaffolds—A state-of-the-art review. Int. J. Appl. Ceram. Technol. 2019, 16, 1762–1796. [Google Scholar] [CrossRef]
- Baino, F.; Caddeo, S.; Novajra, G.; Vitale-Brovarone, C. Using porous bioceramic scaffolds to model healthy and osteoporotic bone. J. Eur. Ceram. Soc. 2016, 36, 2175–2182. [Google Scholar] [CrossRef]
- El-Rashidy, A.A.; Roether, J.A.; Harhaus, L.; Kneser, U.; Boccaccini, A.R. Regenerating bone with bioactive glass scaffolds: A review of in vivo studies in bone defect models. Acta Biomater. 2017, 62, 1–28. [Google Scholar] [CrossRef] [PubMed]
- Hench, L. Bioceramics—From Concept to Clinic. J. Am. Ceram. Soc. 1991, 74, 1487–1510. [Google Scholar] [CrossRef]
- Shahgholi, M.; Oliviero, S.; Baino, F.; Vitale-Brovarone, C.; Gastaldi, D.; Vena, P. Mechanical characterization of glass-ceramic scaffolds at multiple characteristic lengths through nanoindentation. J. Eur. Ceram. Soc. 2016, 36, 2403–2409. [Google Scholar] [CrossRef]
- Ghorbani, F.; Li, D.; Ni, S.; Zhou, Y.; Yu, B. 3D printing of acellular scaffolds for bone defect regeneration: A review. Mater. Today Commun. 2020, 22, 100979. [Google Scholar] [CrossRef]
- Eqtesadi, S.; Motealleh, A.; Miranda, P.; Pajares, A.; Lemos, A.; Ferreira, J.M. Robocasting of 45S5 bioactive glass scaffolds for bone tissue engineering. J. Eur. Ceram. Soc. 2014, 34, 107–118. [Google Scholar] [CrossRef]
- Hollister, S.; Maddox, R.; Taboas, J. Optimal design and fabrication of scaffolds to mimic tissue properties and satisfy biological constraints. Biomaterials 2002, 23, 4095–4103. [Google Scholar] [CrossRef]
- Zhang, S.; Vijayavenkataraman, S.; Lu, W.F.; Fuh, J.Y.H. A review on the use of computational methods to characterize, design, and optimize tissue engineering scaffolds, with a potential in 3D printing fabrication. J. Biomed. Mater. Res. Part B Appl. Biomater. 2019, 107, 1329–1351. [Google Scholar] [CrossRef] [PubMed]
- Asadi-Eydivand, M.; Solati-Hashjin, M.; Fathi, A.; Padashi, M.; Abu Osman, N.A. Optimal design of a 3D-printed scaffold using intelligent evolutionary algorithms. Appl. Soft Comput. 2016, 39, 36–47. [Google Scholar] [CrossRef]
- Barba, D.; Alabort, E.; Reed, R. Synthetic bone: Design by additive manufacturing. Acta Biomater. 2019, 97, 637–656. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S.; Sinibaldi, R.; Pichler, B.; Komlev, V.; Renghini, C.; Vitale-Brovarone, C.; Rustichelli, F.; Hellmich, C. Micromechanics of bone tissue-engineering scaffolds, based on resolution error-cleared computer tomography. Biomaterials 2009, 30, 2411–2419. [Google Scholar] [CrossRef] [PubMed]
- Miranda, P.; Pajares, A.; Guiberteau, F. Finite element modeling as a tool for predicting the fracture behavior of robocast scaffolds. Acta Biomater. 2008, 4, 1715–1724. [Google Scholar] [CrossRef] [PubMed]
- Entezari, A.; Roohani-Esfahani, S.I.; Zhang, Z.; Zreiqat, H.; Dunstan, C.R.; Li, Q. Fracture behaviors of ceramic tissue scaffolds for load bearing applications. Sci. Rep. 2016, 6, 28816. [Google Scholar] [CrossRef]
- Genet, M.; Houmard, M.; Eslava, S.; Saiz, E.; Tomsia, A.P. A two-scale Weibull approach to the failure of porous ceramic structures made by robocasting: Possibilities and limits. J. Eur. Ceram. Soc. 2013, 33, 679–688. [Google Scholar] [CrossRef]
- Farina, E.; Gastaldi, D.; Baino, F.; Vernè, E.; Massera, J.; Orlygsson, G.; Vena, P. Micro computed tomography based finite element models for elastic and strength properties of 3D printed glass scaffolds. Acta Mech. Sin. 2021, 37, 292–306. [Google Scholar] [CrossRef]
- Baino, F.; Barberi, J.; Fiume, E.; Orlygsson, G.; Massera, J.; Verné, E. Robocasting of Bioactive SiO2-P2O5-CaO-MgO-Na2O-K2O Glass Scaffolds. J. Healthc. Eng. 2019, 2019, 5153136. [Google Scholar] [CrossRef]
- Barberi, J.; Baino, F.; Fiume, E.; Orlygsson, G.; Nommeots-Nomm, A.; Massera, J.; Verné, E. Robocasting of SiO2-based bioactive glass scaffolds with porosity gradient for bone regeneration and potential load-bearing applications. Materials 2019, 12, 2691. [Google Scholar] [CrossRef] [Green Version]
- Tulyaganov, D.U.; Fiume, E.; Akbarov, A.; Ziyadullaeva, N.; Murtazaev, S.; Rahdar, A.; Massera, J.; Verné, E.; Baino, F. In Vivo Evaluation of 3D-Printed Silica-Based Bioactive Glass Scaffolds for Bone Regeneration. J. Funct. Biomater. 2022, 13, 74. [Google Scholar] [CrossRef] [PubMed]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Barberi, J.; Nommeots-Nomm, A.; Fiume, E.; Verné, E.; Massera, J.; Baino, F. Mechanical characterization of pore-graded bioactive glass scaffolds produced by robocasting. Biomed. Glasses 2019, 5, 140–147. [Google Scholar] [CrossRef]
- Flaig, C. A Highly Scalable Memory Efficient Multigrid Solver for μ-Finiteelement Analyses. Ph.D. Thesis, ETH, Zürich, Switzerland, 2012. [Google Scholar]
- Tagliabue, S.; Rossi, E.; Baino, F.; Vitale-Brovarone, C.; Gastaldi, D.; Vena, P. Micro-CT based finite element models for elastic properties of glass-ceramic scaffolds. J. Mech. Behav. Biomed. Mater. 2017, 65, 248–255. [Google Scholar] [CrossRef] [PubMed]
- Munz, D.; Fett, T. Ceramics, Mechanical Properties, Failure Behaviour, Materials Selection; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Miranda, P.; Pajares, A.; Saiz, E.; Tomsia, A.P.; Guiberteau, F. Fracture modes under uniaxial compression in hydroxyapatite scaffolds fabricated by robocasting. J. Biomed. Mater. Res. Part A 2007, 83A, 646–655. [Google Scholar] [CrossRef]
- Petit, C.; Meille, S.; Maire, E.; Gremillard, L.; Adrien, J.; Lau, G.Y.; Tomsia, A.P. Fracture behavior of robocast HA/β-TCP scaffolds studied by X-ray tomography and finite element modeling. J. Eur. Ceram. Soc. 2017, 37, 1735–1745. [Google Scholar] [CrossRef]
- Hollister, S.J.; Kikuchi, N. Homogenization Theory and Digital Imaging—A Basis for Studying the Mechanics and Design Principles of Bone Tissue. Biotechnol. Bioeng. 1994, 43, 586–596. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Sigmund, O. Material interpolation schemes in topology optimization. Arch. Appl. Mech. 1999, 69, 635–654. [Google Scholar] [CrossRef]
- Hamdia, K.M.; Ghasemi, H.; Zhuang, X.; Rabczuk, T. Multilevel Monte Carlo method for topology optimization of flexoelectric composites with uncertain material properties. Eng. Anal. Bound. Elem. 2022, 134, 412–418. [Google Scholar] [CrossRef]
- Stipsitz, M.; Zysset, P.K.; Pahr, D.H. Efficient materially nonlinear μFE solver for simulations of trabecular bone failure. Biomech. Model. Mechanobiol. 2020, 19, 861–874. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Baino, F.; Spriano, S.; Pugno, N.; Vitale-Brovarone, C. Modelling of the strength-porosity relationship in glass-ceramic foam scaffolds for bone repair. J. Eur. Ceram. Soc. 2014, 34, 2663–2673. [Google Scholar] [CrossRef] [Green Version]

| graded | 0.28 ± 0.02 | 0.27 ± 0.03 | 0.15 ± 0.08 | 0.03 ± 0.01 | 0.06 ± 0.01 | 0.06 ± 0.02 |
| monoporous | 0.19 ± 0.02 | 0.17 ± 0.04 | 0.44 ± 0.14 | 0.07 ± 0.02 | 0.11 ± 0.03 | 0.11 ± 0.03 |
| graded | 0.24 ± 0.05 | 0.08 ± 0.09 |
| monoporous | 0.08 ± 0.02 | 0.31 ± 0.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Andrea, L.; Gastaldi, D.; Verné, E.; Baino, F.; Massera, J.; Örlygsson, G.; Vena, P. Mechanical Properties of Robocast Glass Scaffolds Assessed through Micro-CT-Based Finite Element Models. Materials 2022, 15, 6344. https://doi.org/10.3390/ma15186344
D’Andrea L, Gastaldi D, Verné E, Baino F, Massera J, Örlygsson G, Vena P. Mechanical Properties of Robocast Glass Scaffolds Assessed through Micro-CT-Based Finite Element Models. Materials. 2022; 15(18):6344. https://doi.org/10.3390/ma15186344
Chicago/Turabian StyleD’Andrea, Luca, Dario Gastaldi, Enrica Verné, Francesco Baino, Jonathan Massera, Gissur Örlygsson, and Pasquale Vena. 2022. "Mechanical Properties of Robocast Glass Scaffolds Assessed through Micro-CT-Based Finite Element Models" Materials 15, no. 18: 6344. https://doi.org/10.3390/ma15186344
APA StyleD’Andrea, L., Gastaldi, D., Verné, E., Baino, F., Massera, J., Örlygsson, G., & Vena, P. (2022). Mechanical Properties of Robocast Glass Scaffolds Assessed through Micro-CT-Based Finite Element Models. Materials, 15(18), 6344. https://doi.org/10.3390/ma15186344









