Magneto-Thermoelastic Response in an Infinite Medium with a Spherical Hole in the Context of High Order Time-Derivatives and Triple-Phase-Lag Model
Abstract
:1. Introduction
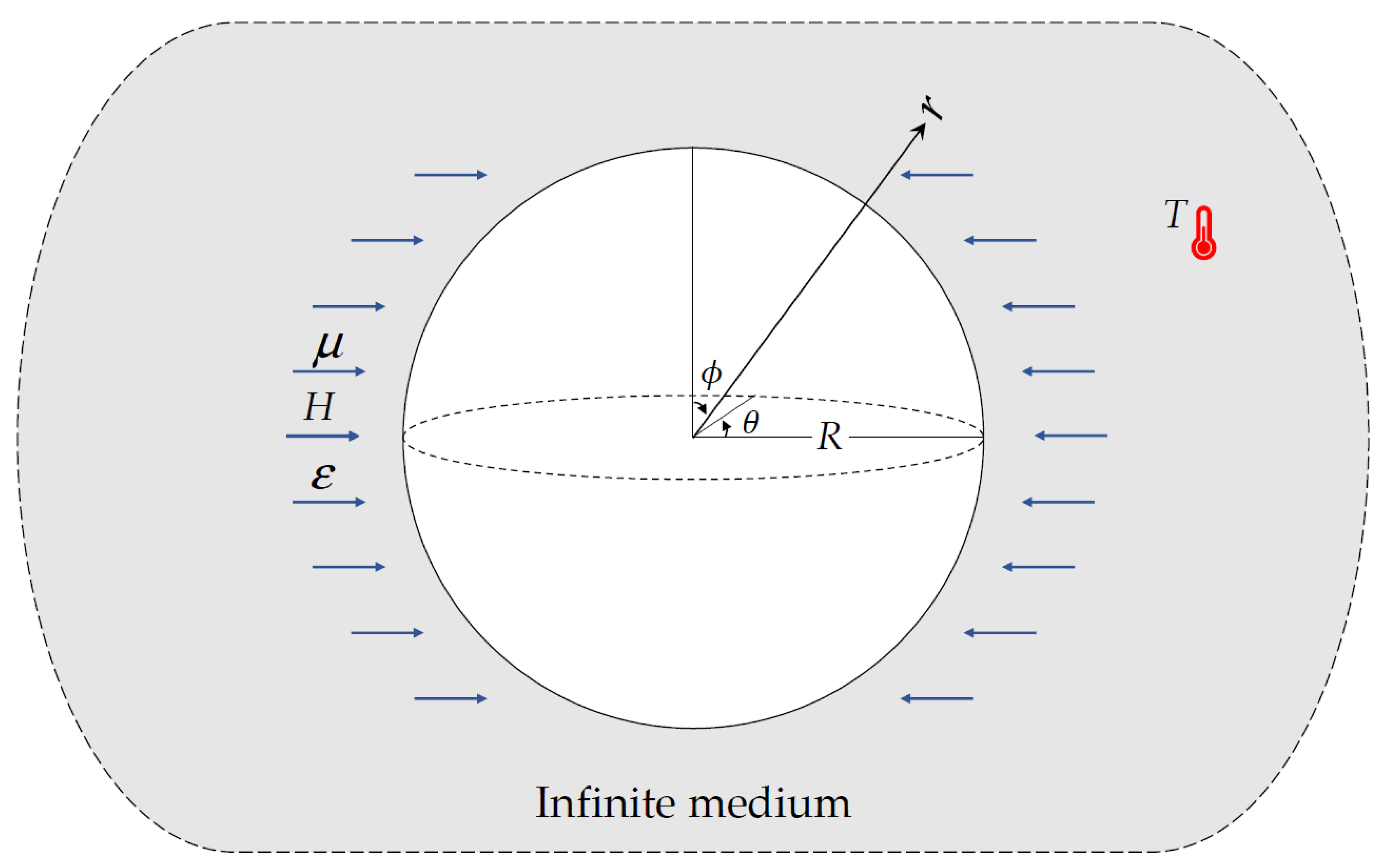
2. Formulation of the Problem
- The equation of motion
- The heat conduction equation
- (i)
- Coupled thermoelasticity (CTE) model [1]: , , and ,
- (ii)
- Lord and Shulman (L–S) model [2]: , , , , and ,
- (iii)
- (iv)
- Simple generalized thermoelasticity theory with triple-phase-lag (Simple TPL-GN theory): , , and ,
- (v)
- Refined generalized thermoelasticity theory with triple-phase-lag (Refined TPL-GN theory): , , and
3. Closed-Form Solution
- Continuous heat is applied to the spherical hole’s outer surface
- Due to the lack of traction on the hole’s surface, the mechanical boundary condition is met
4. Validation
4.1. First Justification
- The RTPL models were developed with equal to 3, 4, and 5. Nevertheless, the STPL model was essentially provided when .
- Using the RTPL model, incredibly accurate results were generated.
- The RTPL model yielded closed outcomes. All variables may be insensitive to larger values of , particularly when exceeds 5.
- The magnetic field variables, which are the electric permittivity and magnetic field intensity , were taken into account to show their effects via all thermoelasticity theorems with various values and in different positions.
4.2. Second Justification
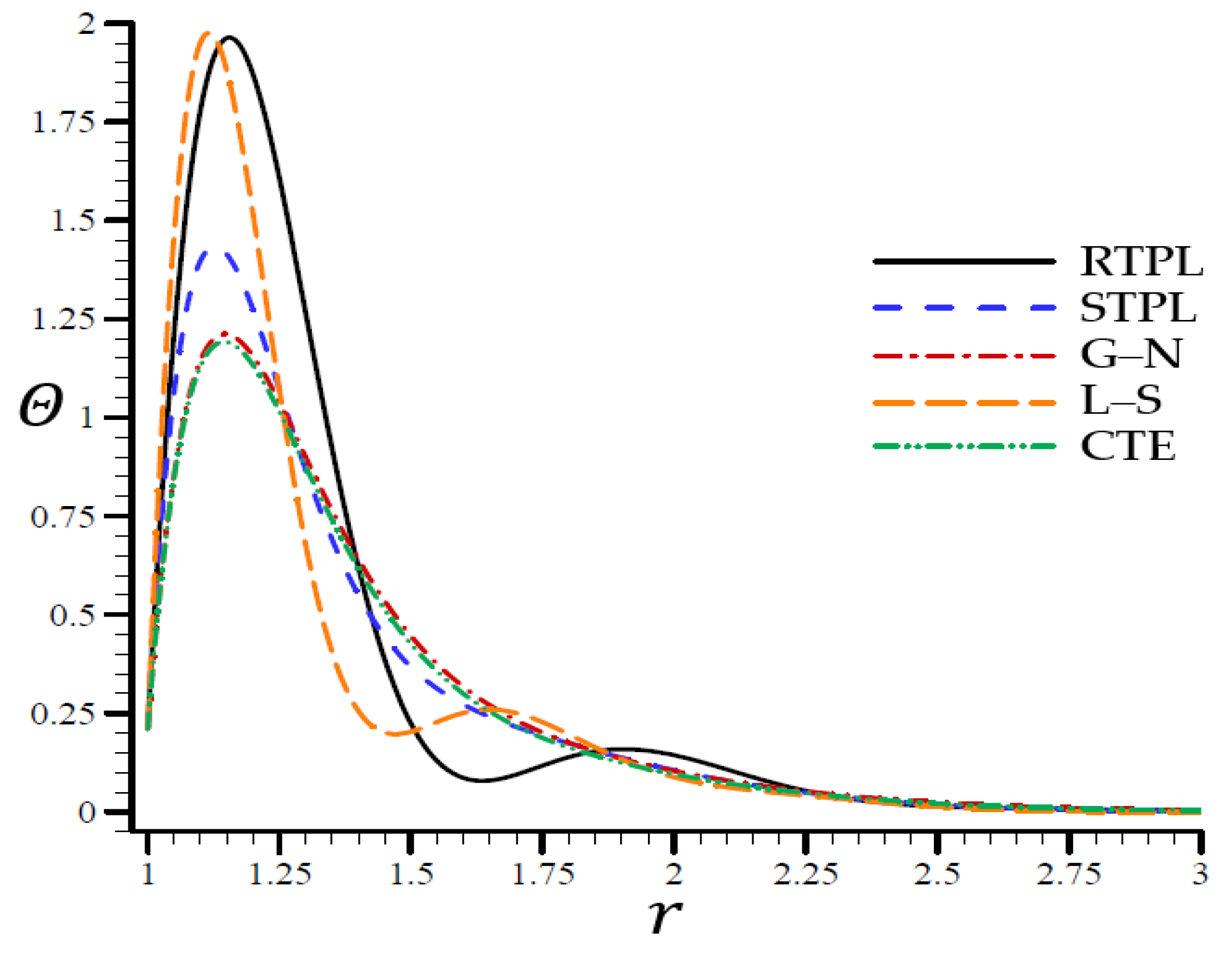
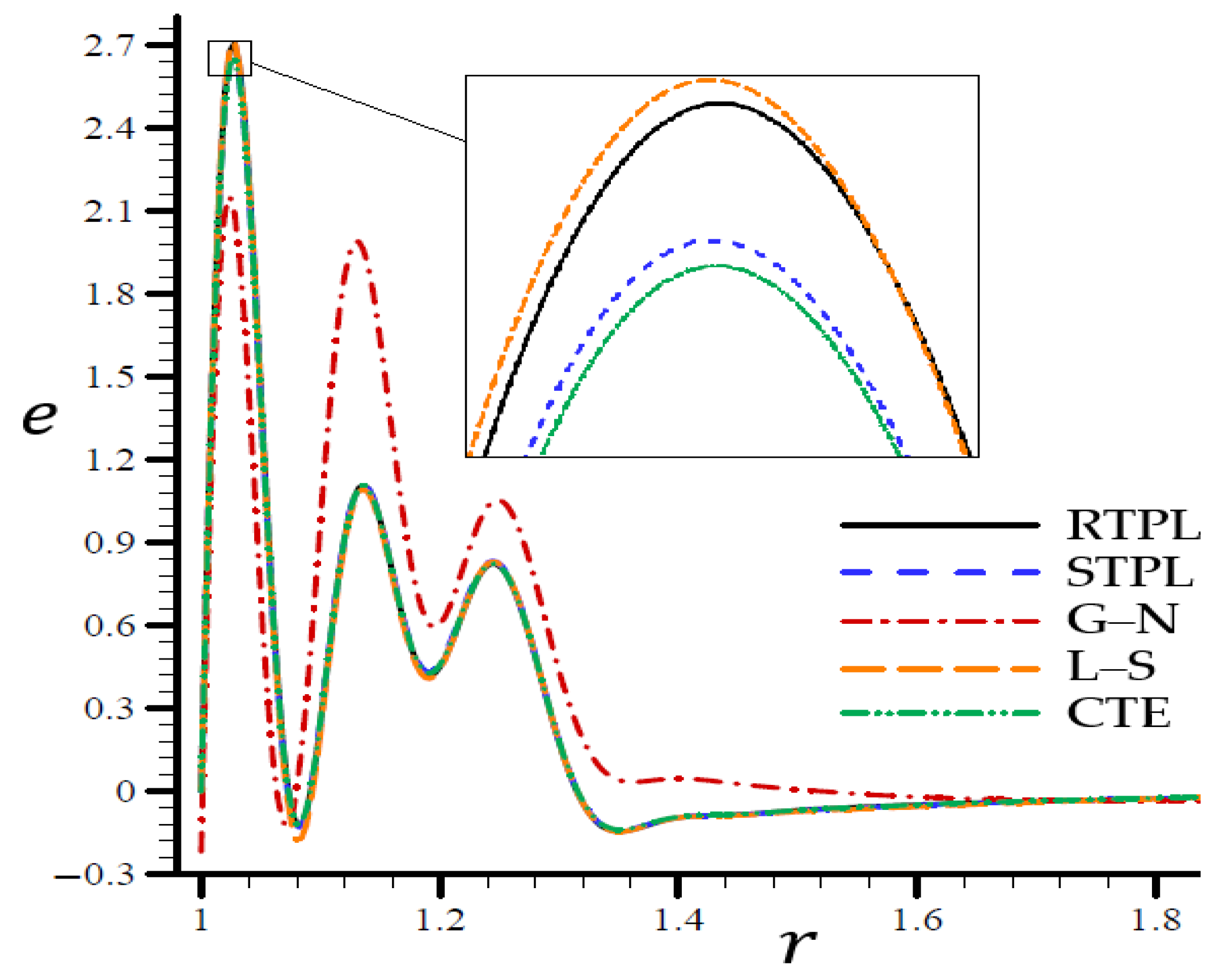
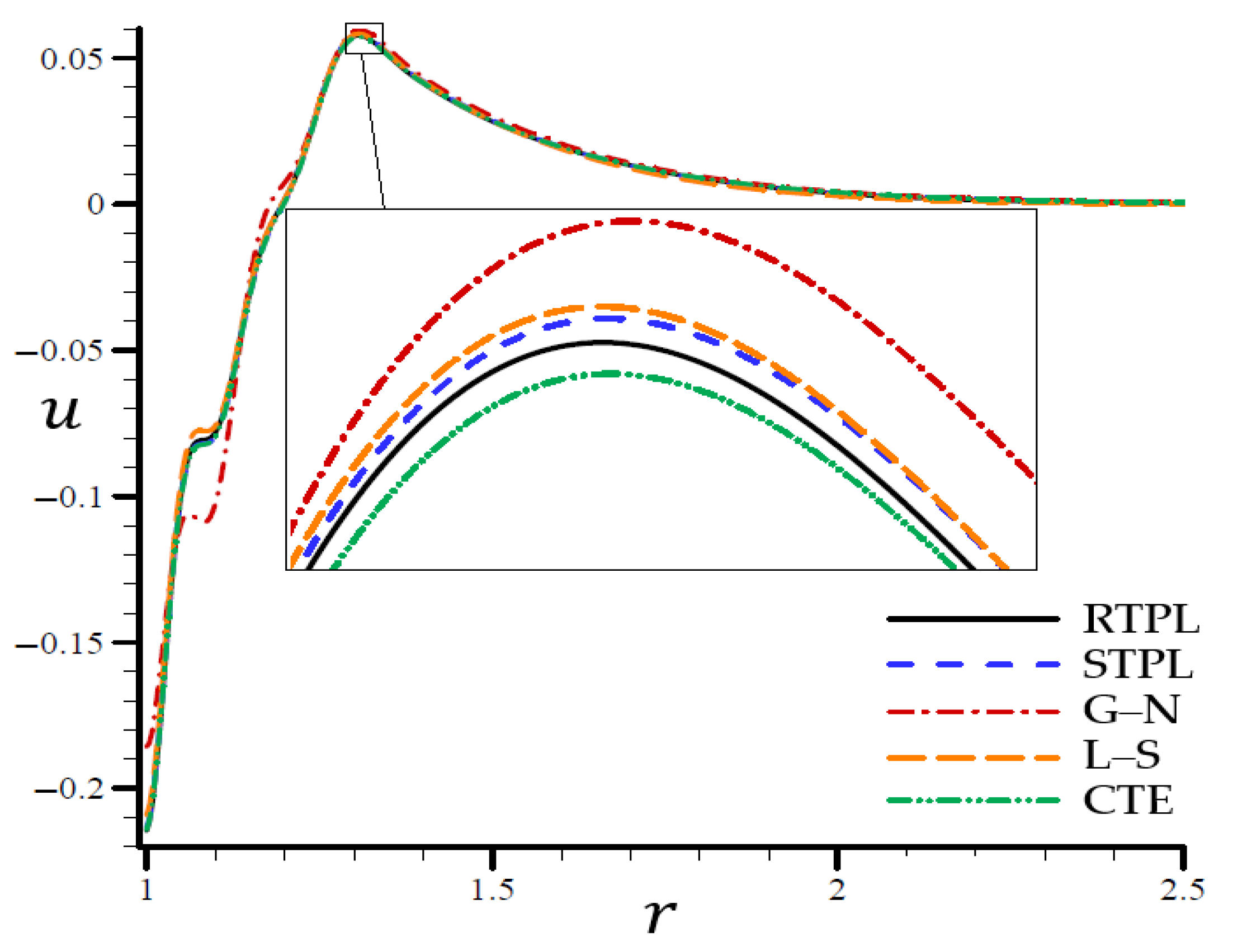
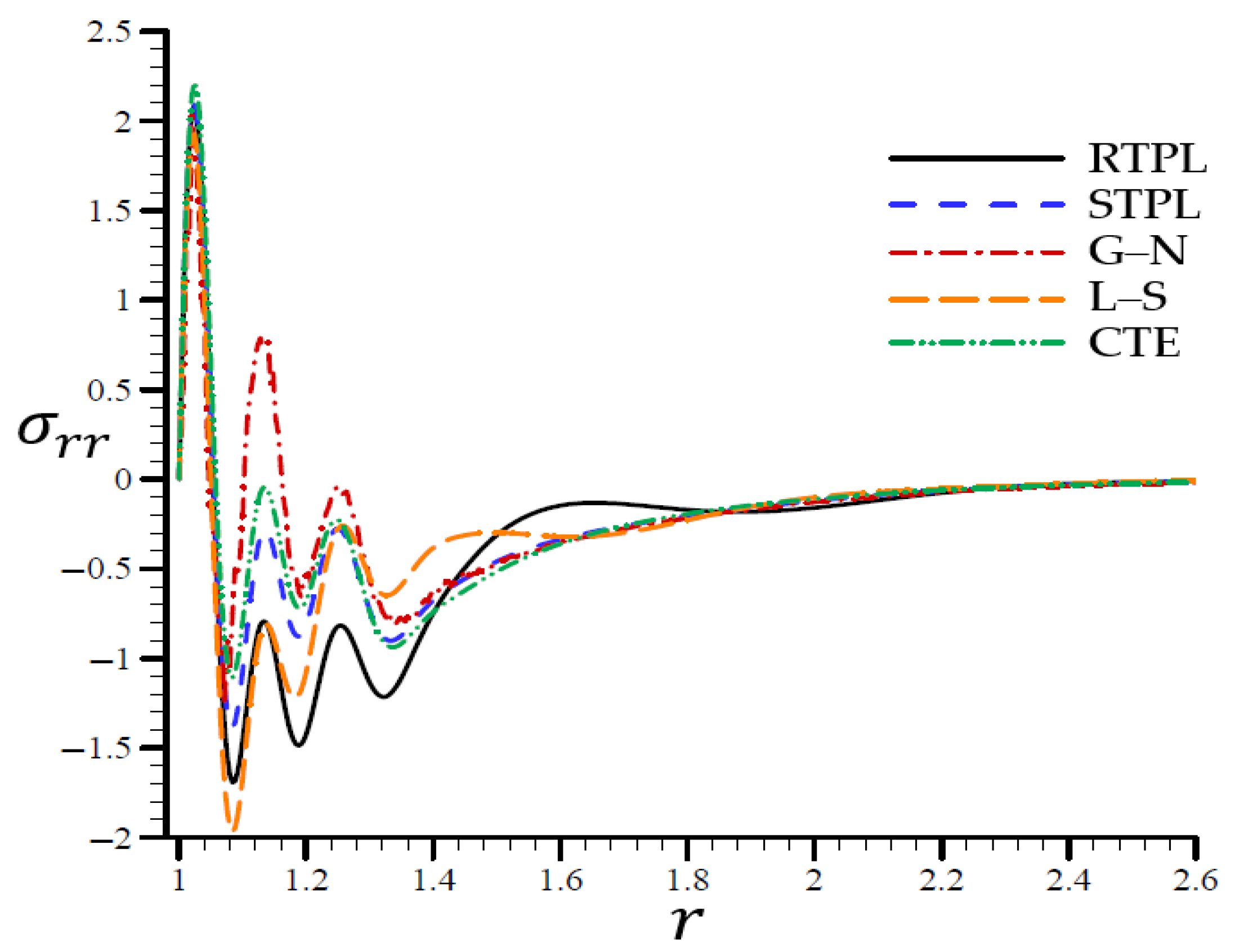
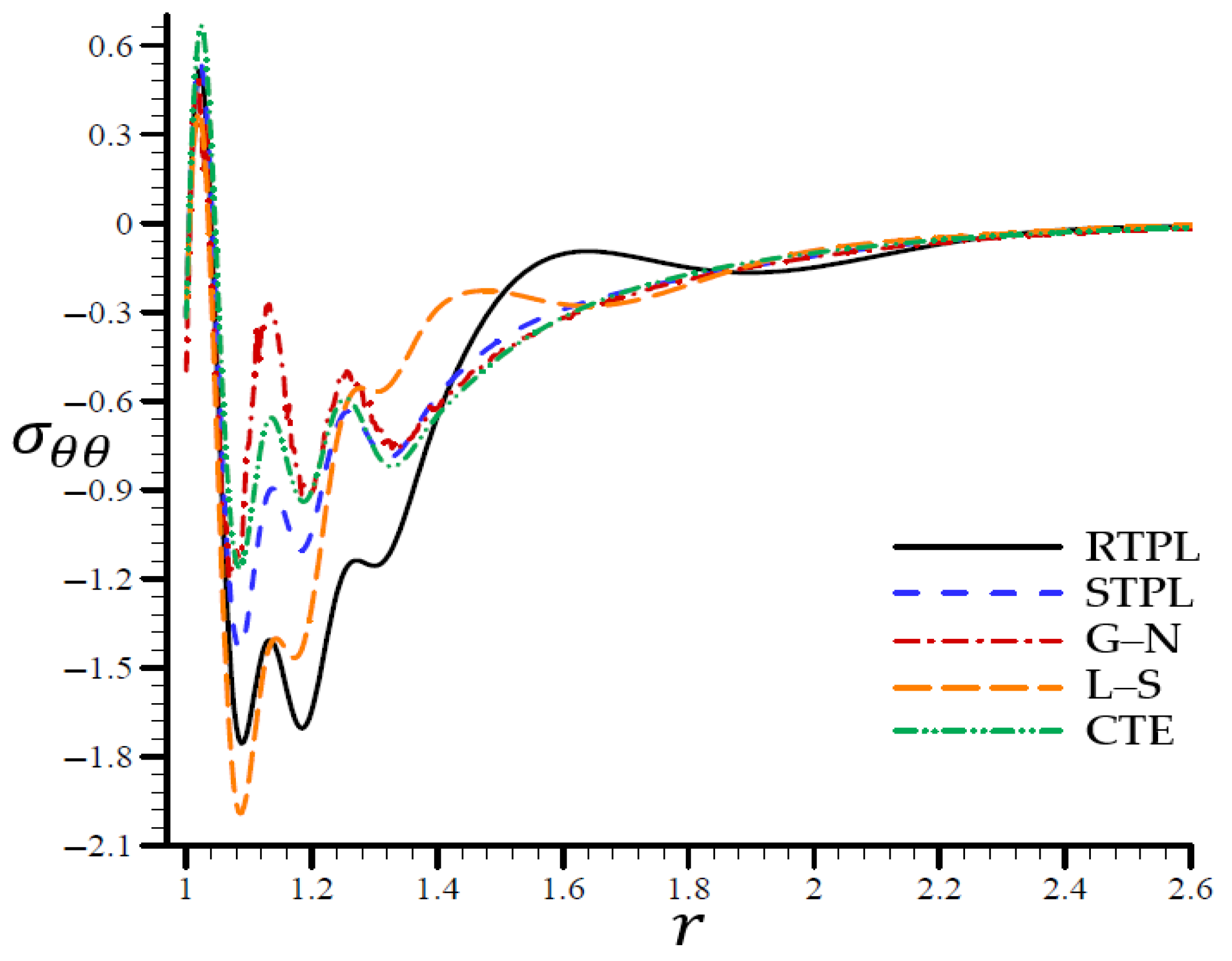
4.3. The Influence of Dimensionless Time
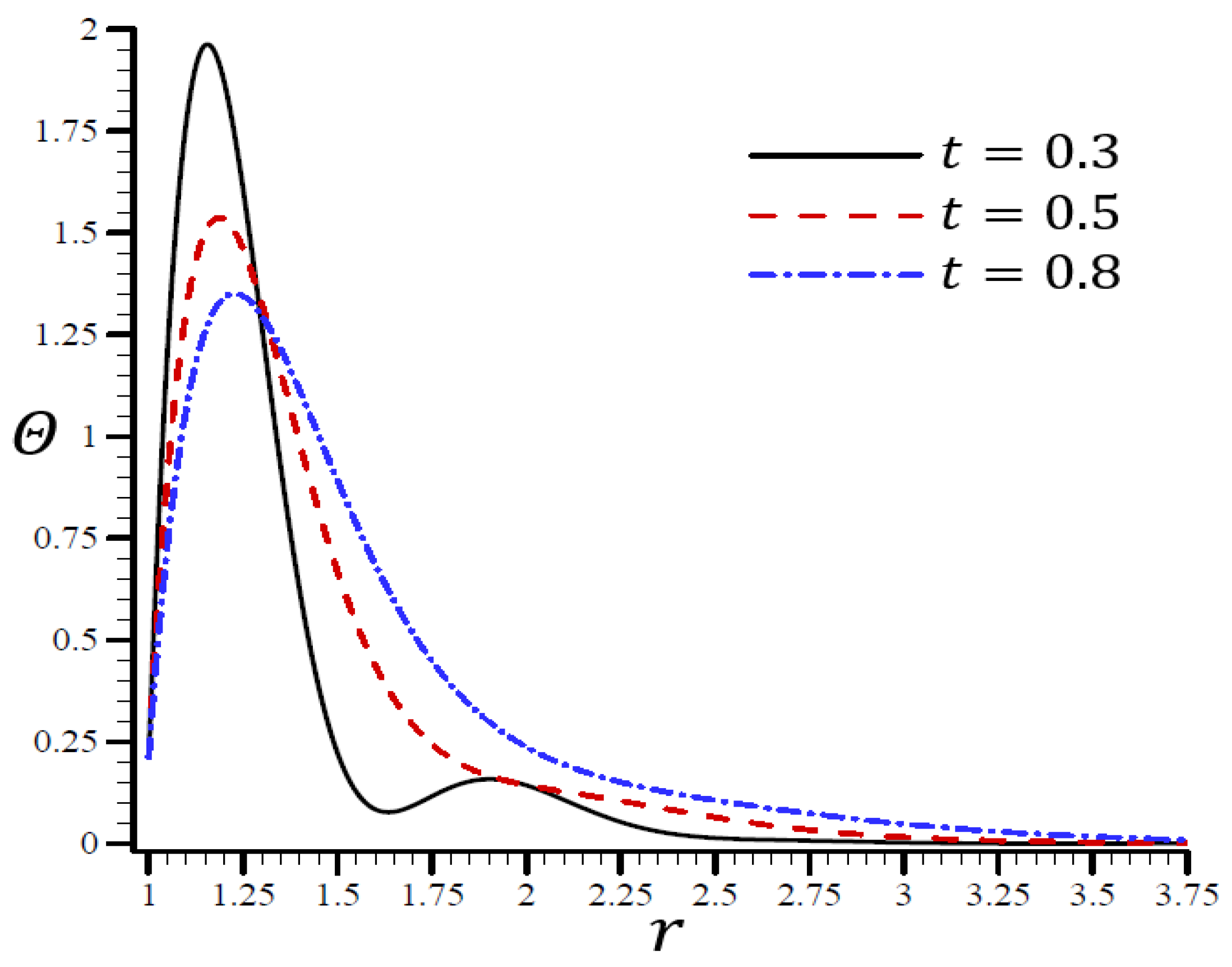
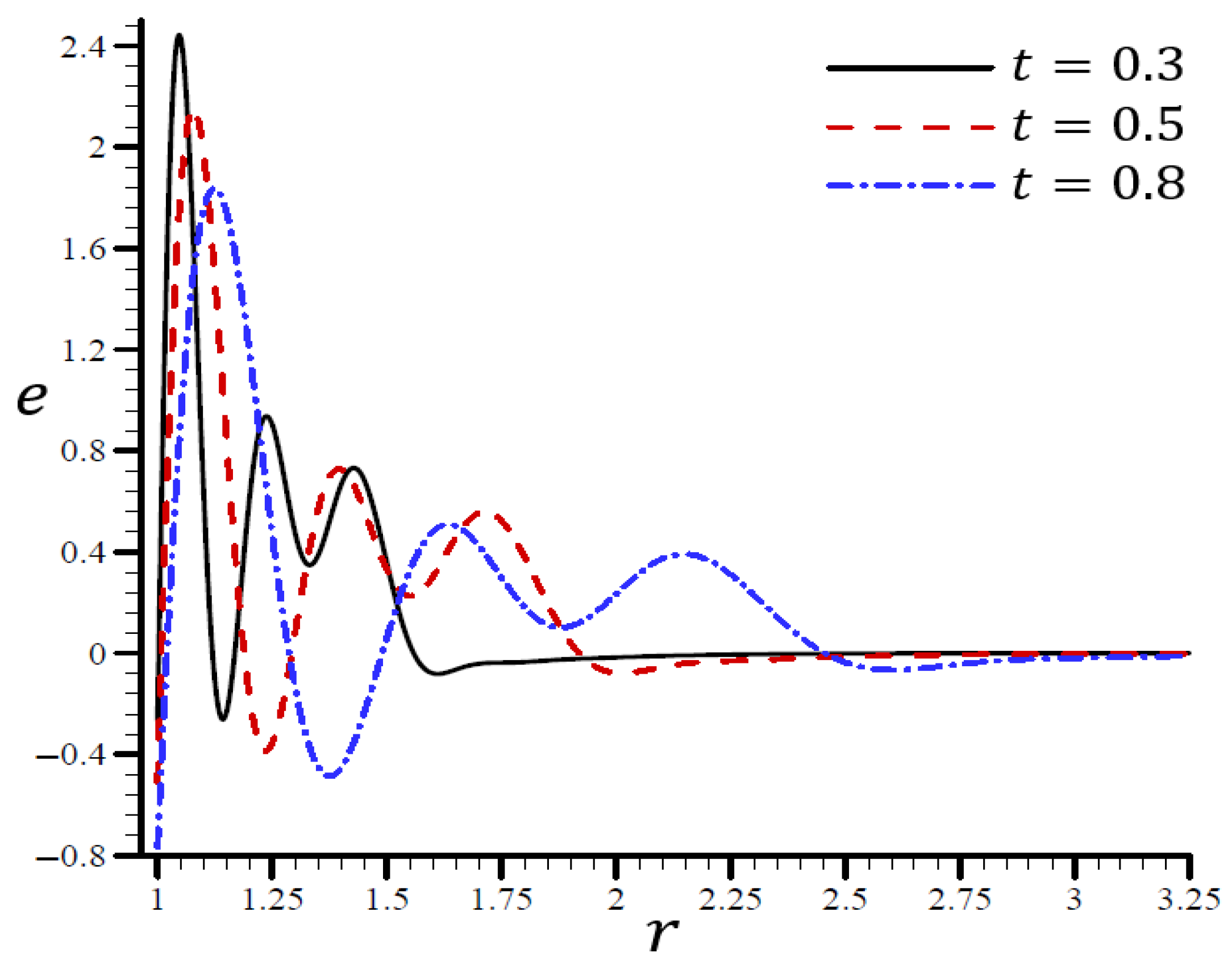
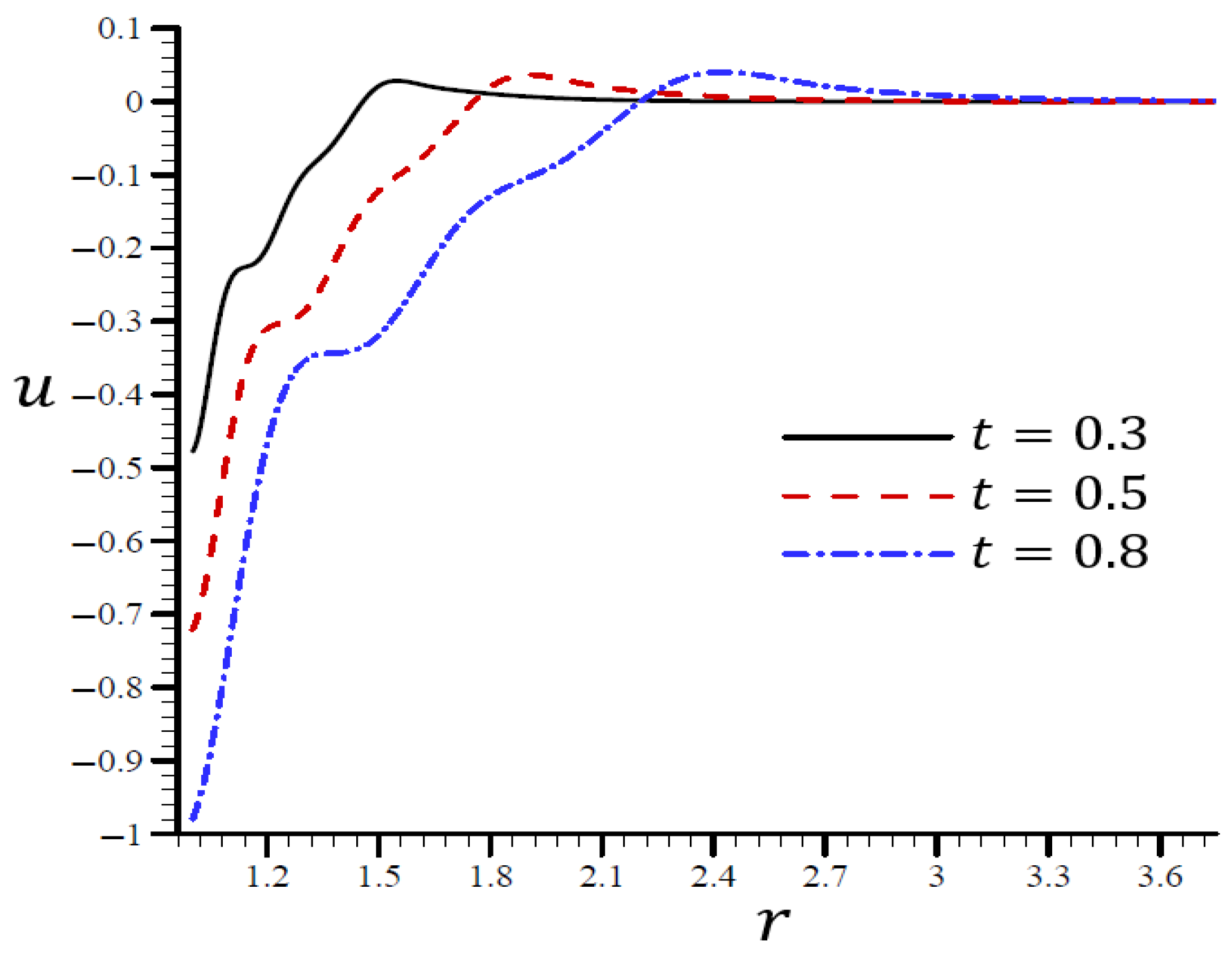
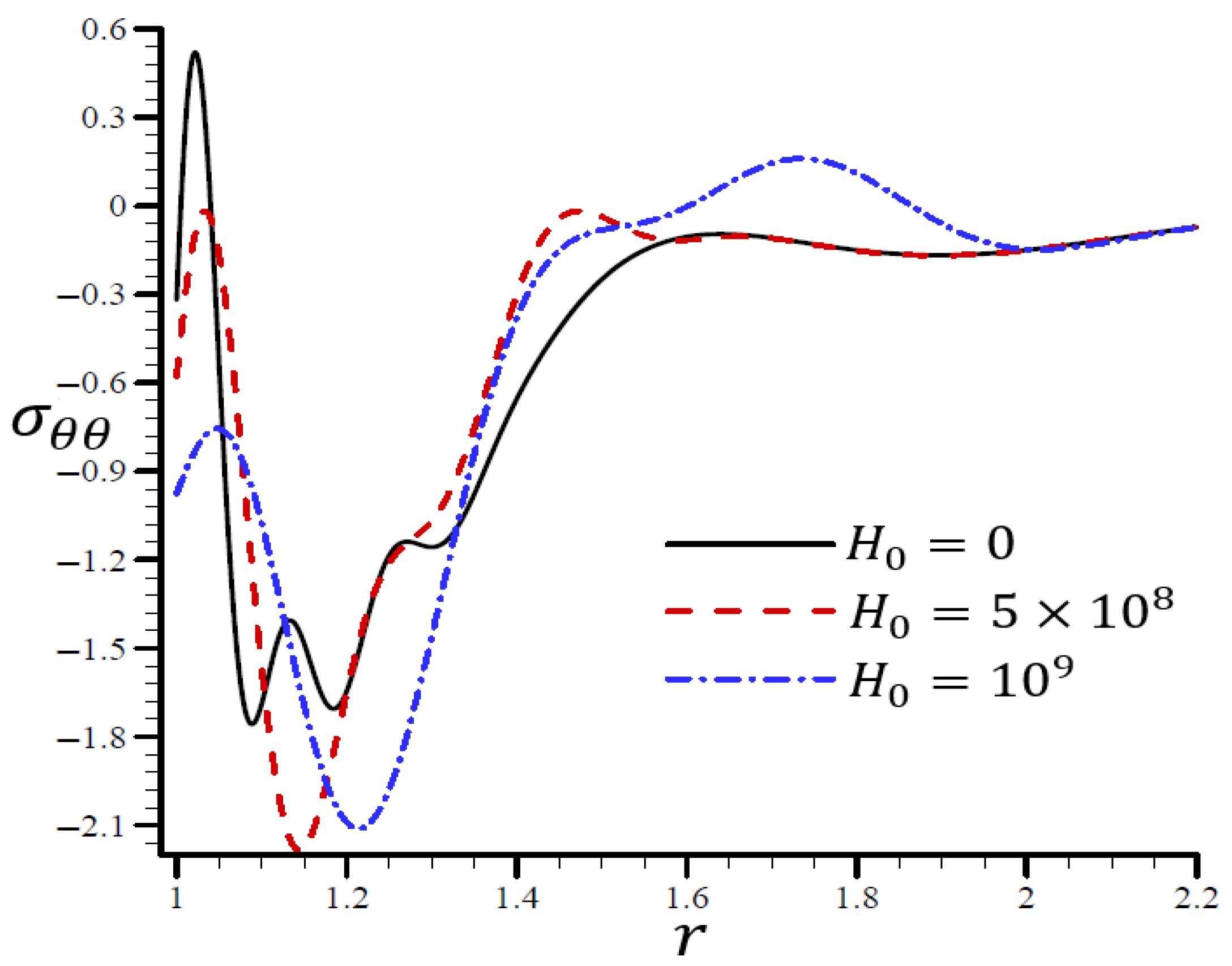
4.4. The Influence of Dimensionless Magnetic Field Intensity
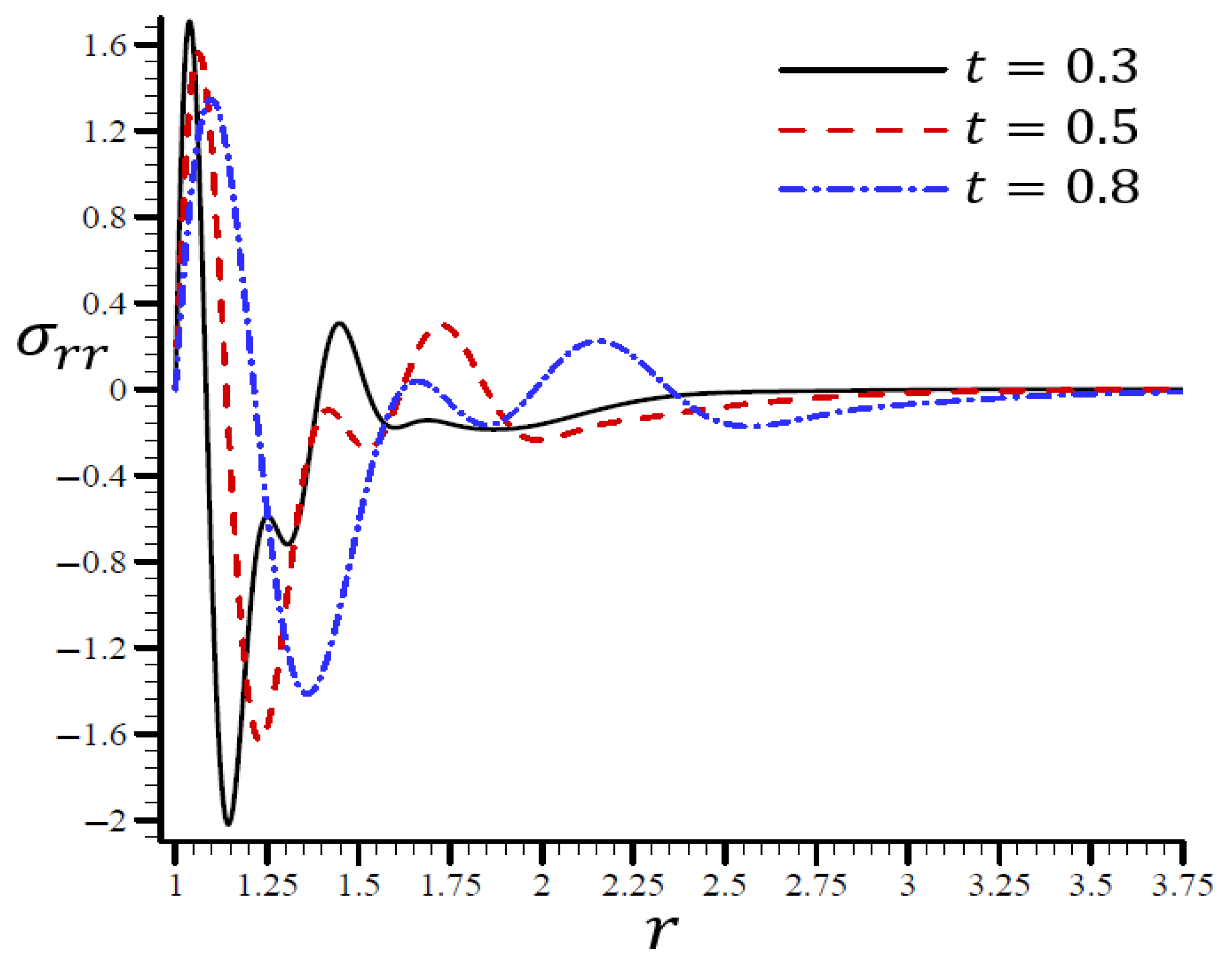
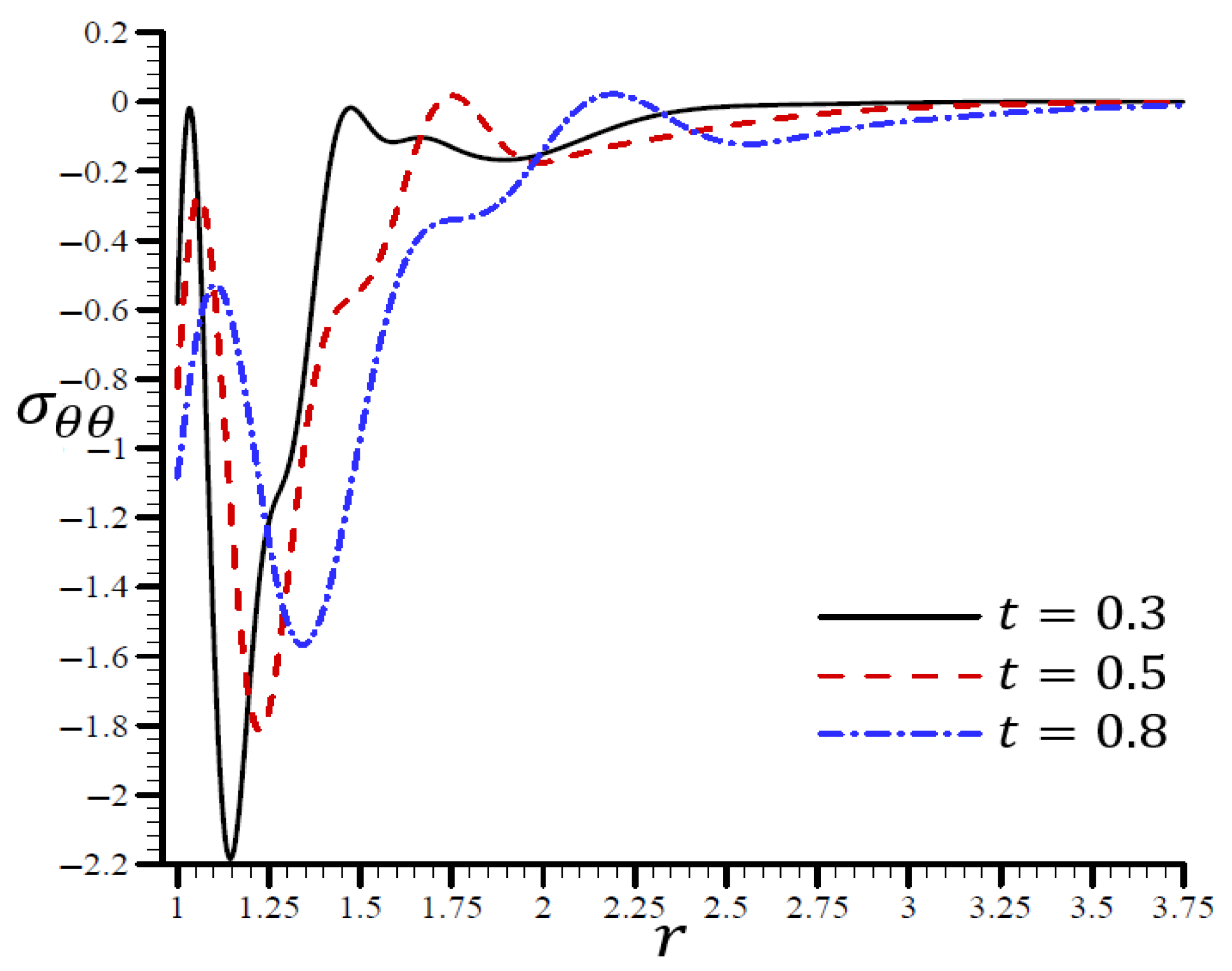
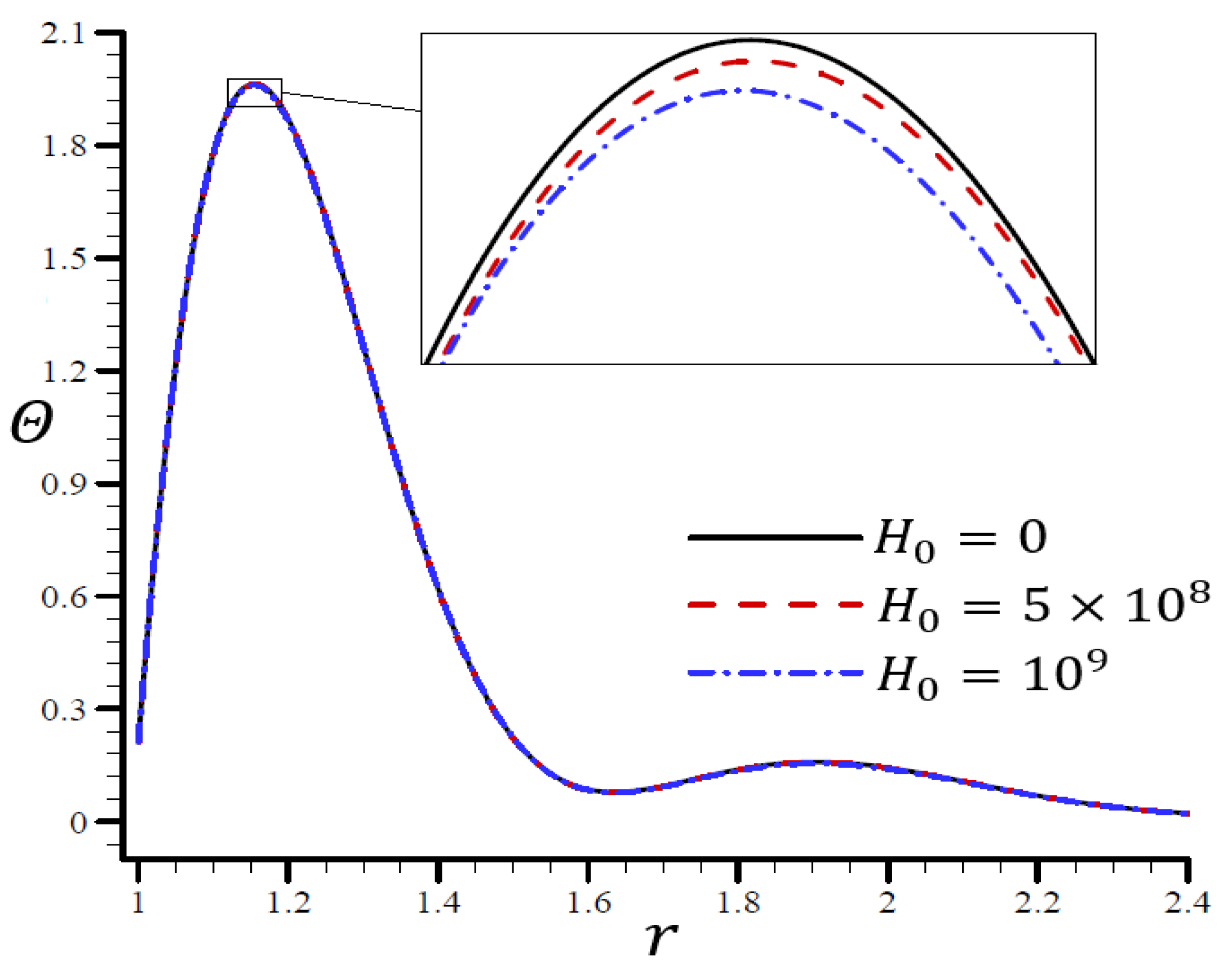
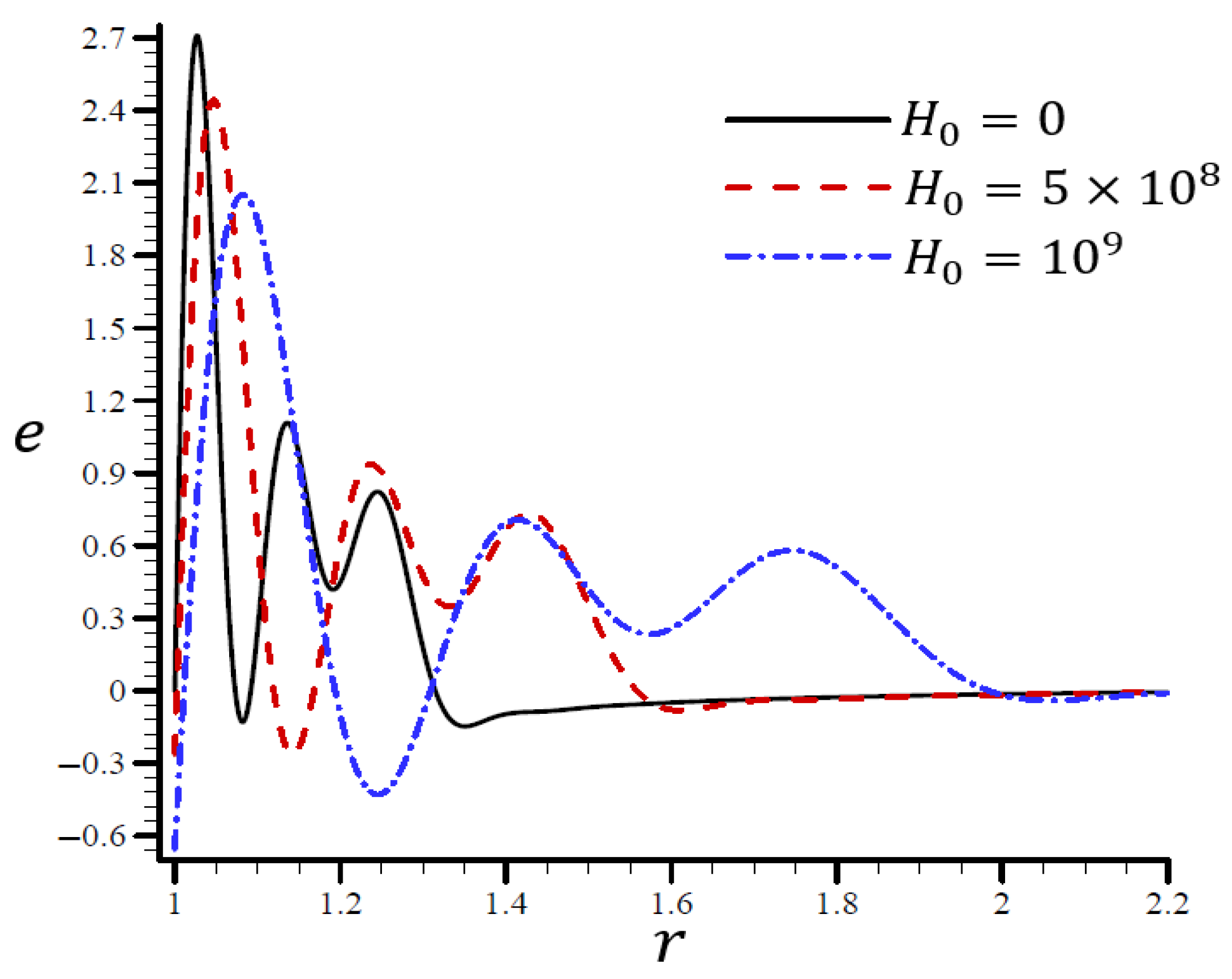
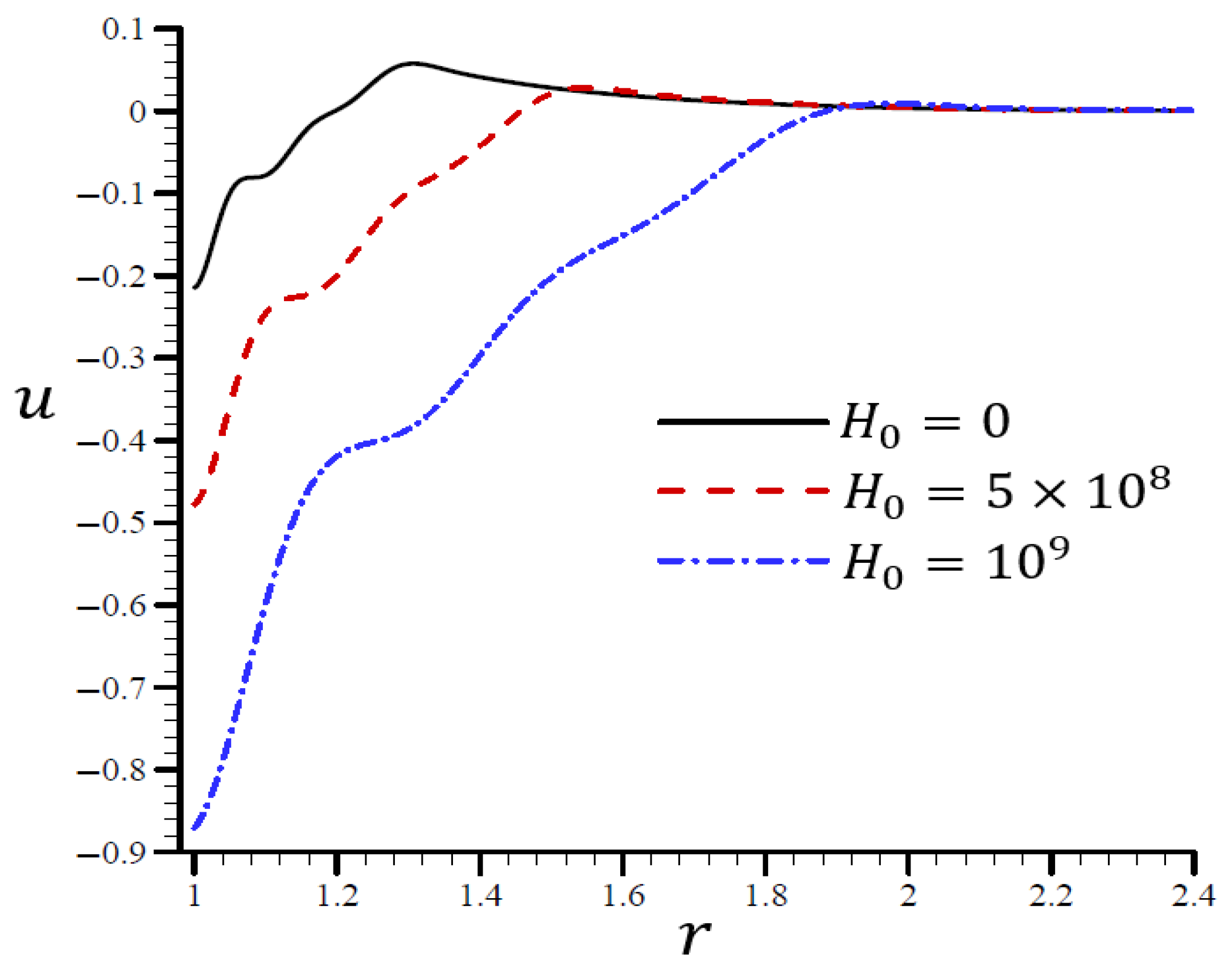
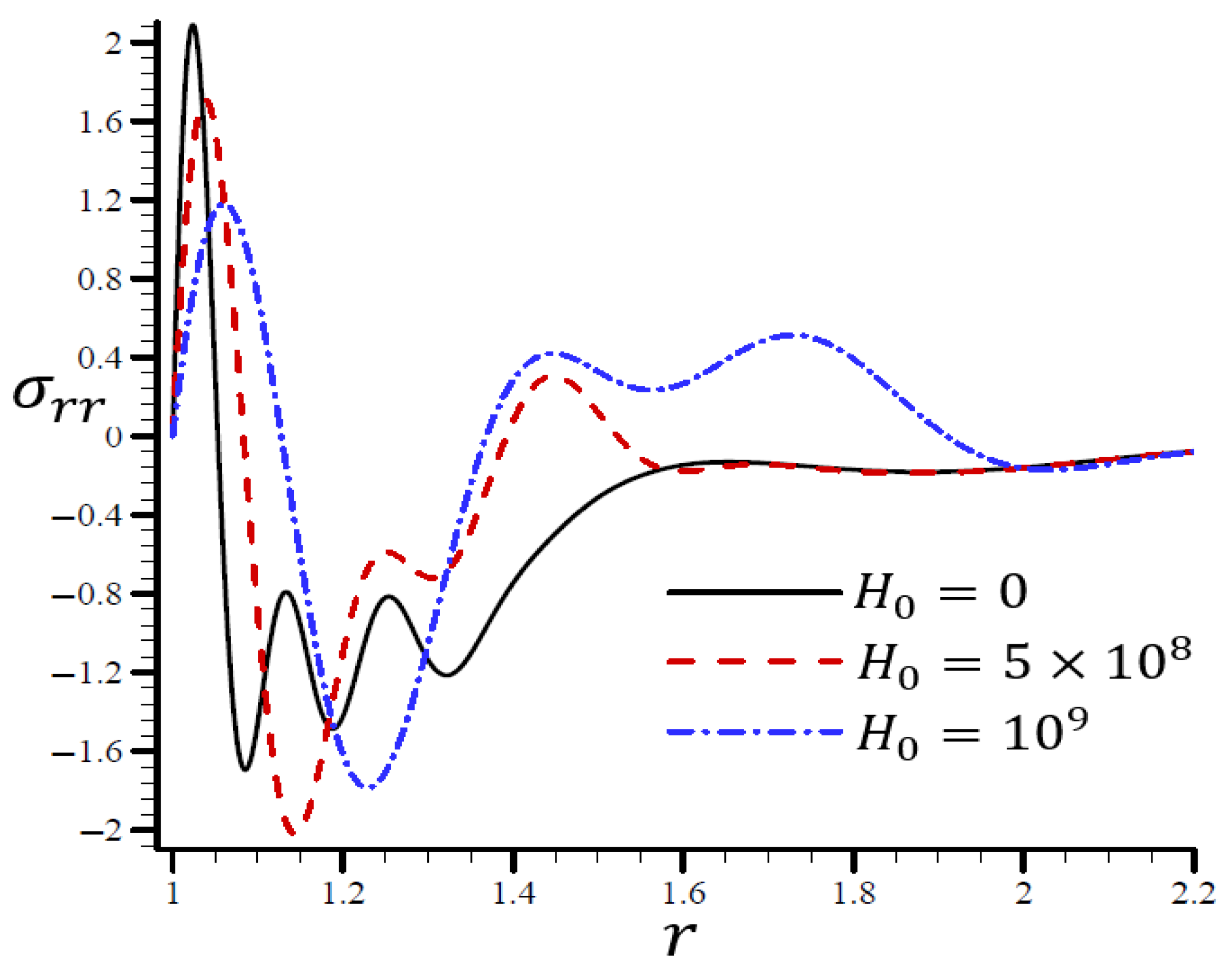
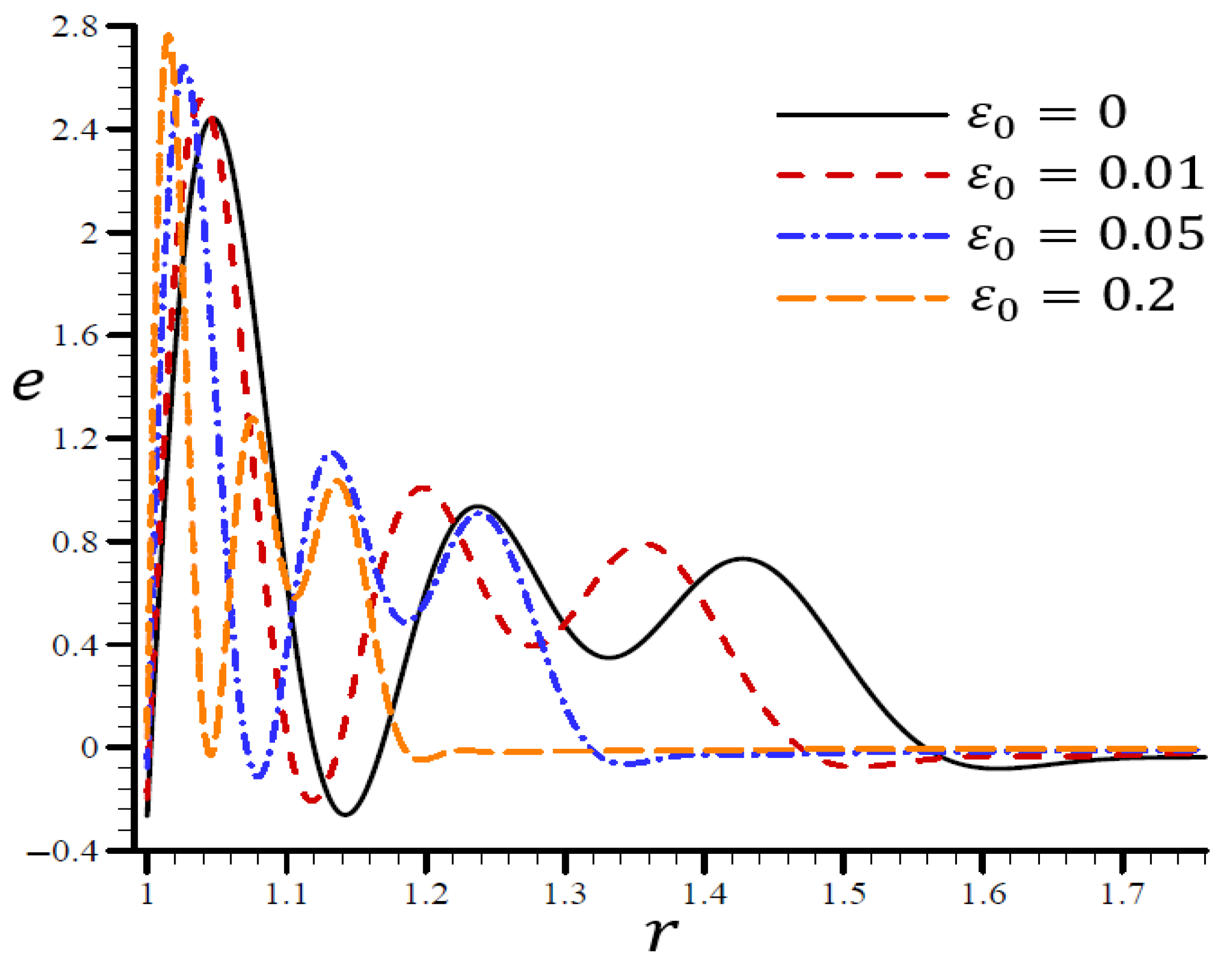
4.5. The Influence of Dimensionless Electric Permittivity

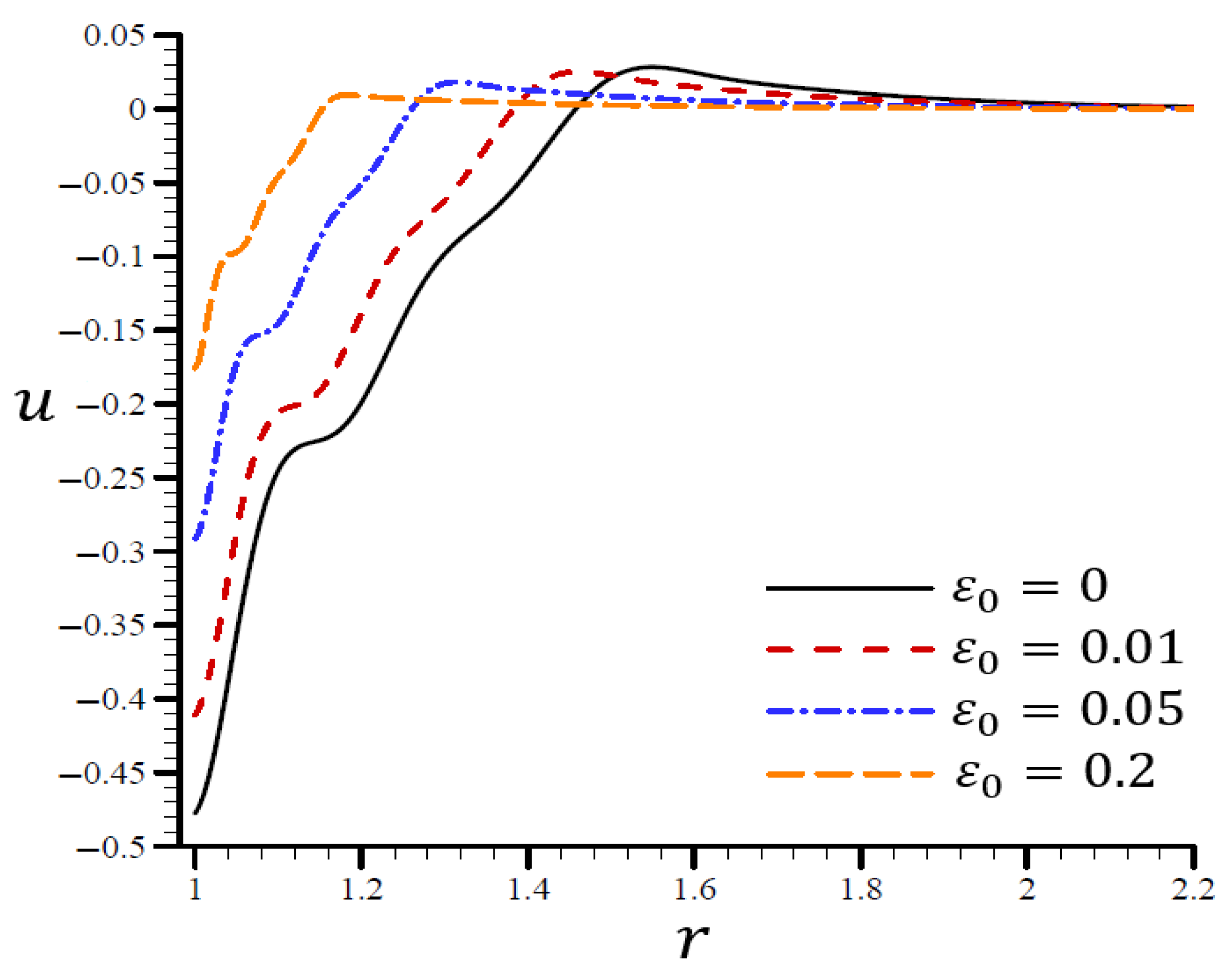
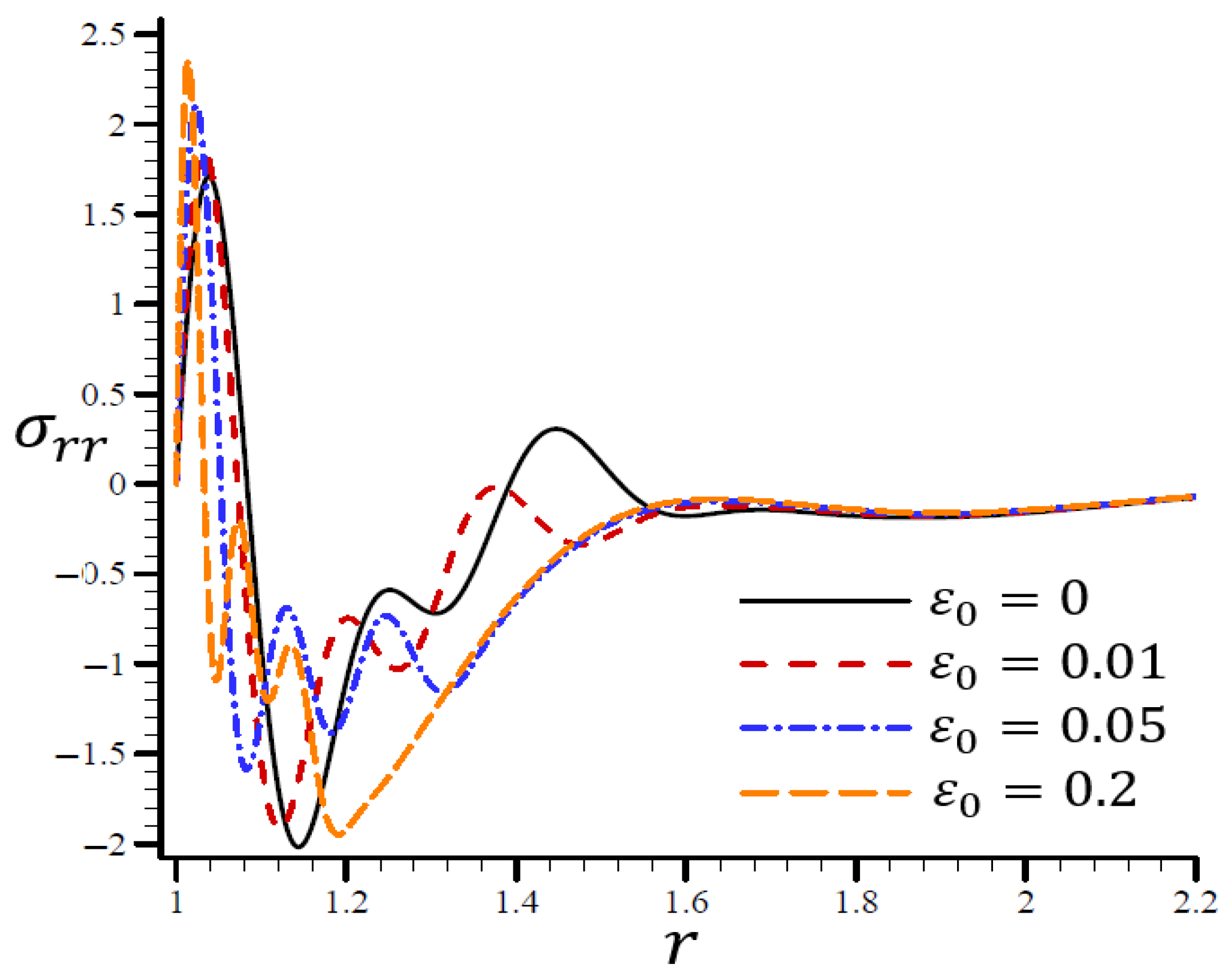

5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Biot, M.A. Thermoelasticity and Irreversible Thermodynamics. J. Appl. Phys. 1956, 27, 240–253. [Google Scholar] [CrossRef]
- Lord, H.; Shulman, Y. A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Green, A.E.; Lindsay, K.A. Thermoelasticity. J. Elast. 1972, 2, 1–7. [Google Scholar] [CrossRef]
- Green, A.E.; Naghdi, P.M. A re-examination of the basic postulates of thermomechanics. Proc. Roy. Soc. Lond. A 1991, 432, 171–194. [Google Scholar] [CrossRef]
- Green, A.E.; Naghdi, P.M. On undamped heat waves in an elastic solid. J. Therm. Stress. 1992, 15, 253–264. [Google Scholar] [CrossRef]
- Green, A.E.; Naghdi, P.M. Thermoelasticity without energy dissipation. J. Elast. 1993, 31, 189–208. [Google Scholar] [CrossRef]
- Hetnarski, R.B.; Ignaczak, J. Generalized thermoelasticity. J. Therm. Stress. 1999, 22, 451–476. [Google Scholar]
- Tzou, D.Y. A Unified Field Approach for Heat Conduction From Macro- to Micro-Scales. J. Heat Transf. 1995, 117, 8–16. [Google Scholar] [CrossRef]
- Chandrasekharaiah, D.S. Thermoelasticity with Second Sound: A Review. Appl. Mech. Rev. 1986, 39, 355–376. [Google Scholar] [CrossRef]
- Chandrasekharaiah, D.S. Hyperbolic Thermoelasticity: A Review of Recent Literature. Appl. Mech. Rev. 1998, 51, 705–729. [Google Scholar] [CrossRef]
- Choudhuri, S.K.R. On A Thermoelastic Three-Phase-Lag Model. J. Therm. Stress. 2007, 30, 231–238. [Google Scholar] [CrossRef]
- Quintanilla, R.; Racke, R. A note on stability in three-phase-lag heat conduction. Int. J. Heat Mass Transf. 2008, 51, 24–29. [Google Scholar] [CrossRef]
- Quintanilla, R. A Well-Posed Problem for the Three-Dual-Phase-Lag Heat Conduction. J. Therm. Stress. 2009, 32, 1270–1278. [Google Scholar] [CrossRef]
- El-Karamany, A.S.; Ezzat, M.A. On the phase-lag Green–Naghdi thermoelasticity theories. Appl. Math. Model. 2016, 40, 5643–5659. [Google Scholar] [CrossRef]
- Zenkour, A.M. Refined two-temperature multi-phase-lags theory for thermomechanical response of microbeams using the modified couple stress analysis. Acta Mech. 2018, 229, 3671–3692. [Google Scholar] [CrossRef]
- Zenkour, A.M. Refined microtemperatures multi-phase-lags theory for plane wave propagation in thermoelastic medium. Results Phys. 2018, 11, 929–937. [Google Scholar] [CrossRef]
- Zenkour, A.M. Refined multi-phase-lags theory for photothermal waves of a gravitated semiconducting half-space. Compos. Struct. 2019, 212, 346–364. [Google Scholar] [CrossRef]
- Zenkour, A.M. Effect of thermal activation and diffusion on a photothermal semiconducting half-space. J. Phys. Chem. Solids 2019, 132, 56–67. [Google Scholar] [CrossRef]
- Zenkour, A.M. Wave propagation of a gravitated piezo-thermoelastic half-space via a refined multi-phase-lags theory. Mech. Adv. Mater. Struct. 2020, 27, 1923–1934. [Google Scholar] [CrossRef]
- Zenkour, A.M. Magneto-thermal shock for a fiber-reinforced anisotropic half-space studied with a refined multi-dual-phase-lag model. J. Phys. Chem. Solids 2020, 137, 109213. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Kothari, S.; Kumar, R. On the representation of solutions for the theory of generalized thermoelasticity with three phase lags. Acta Mech. 2010, 214, 305–314. [Google Scholar] [CrossRef]
- Kumar, R.; Mukhopadhyay, S. Effects of Three Phase Lags on Generalized Thermoelasticity for an Infinite Medium with a Cylindrical Cavity. J. Therm. Stress. 2009, 32, 1149–1165. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Kumar, R. Analysis of phase-lag effects on wave propagation in a thick plate under axisymmetric temperature distribution. Acta Mech. 2010, 210, 331–344. [Google Scholar] [CrossRef]
- Knopoff, L. The interaction between elastic wave motions and a magnetic field in electrical conductors. J. Geophys. Res. Earth Surf. 1955, 60, 441–456. [Google Scholar] [CrossRef]
- Chadwick, P. Elastic wave propagation in a magnetic field. In Proceedings of the 9th International Congress of Applied Mechanics, Brussels, Belgium, 5–13 September 1957; Volume 7, pp. 143–153. [Google Scholar]
- Kaliski, S.; Petykiewicz, J. Equation of motion coupled with the field of temperature in a magnetic field involving mechanical and electrical relaxation for anisotropic bodies. Proc. Vibr. Probl. 1959, 4, 17–28. [Google Scholar]
- Chiriţă, S. High-order approximations of three-phase-lag heat conduction model: Some qualitative results. J. Therm. Stress. 2018, 41, 608–626. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ghasemi, A. Solidification heat transfer of nanofluid in existence of thermal radiation by means of FEM. Int. J. Heat Mass Transf. 2018, 123, 418–431. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Jafaryar, M.; Li, Z. Nanofluid turbulent convective flow in a circular duct with helical turbulators considering CuO nanoparticles. Int. J. Heat Mass Transf. 2018, 124, 980–989. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Haq, R.-U.; Shafee, A.; Li, Z. Heat transfer behavior of nanoparticle enhanced PCM solidification through an enclosure with V shaped fins. Int. J. Heat Mass Transf. 2019, 130, 1322–1342. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Haq, R.-U.; Shafee, A.; Li, Z.; Elaraki, Y.G.; Tlili, I. Heat transfer simulation of heat storage unit with nanoparticles and fins through a heat exchanger. Int. J. Heat Mass Transf. 2019, 135, 470–478. [Google Scholar] [CrossRef]
- Prasad, R.; Kumar, R.; Mukhopadhyay, S. Effects of phase lags on wave propagation in an infinite solid due to a continuous line heat source. Acta Mech. 2011, 217, 243–256. [Google Scholar] [CrossRef]
- Zenkour, A.; El-Mekawy, H. On a multi-phase-lag model of coupled thermoelasticity. Int. Commun. Heat Mass Transf. 2020, 116, 104722. [Google Scholar] [CrossRef]
- Biswas, S.; Mukhopadhyay, B.; Shaw, S. Effect of rotation in magne-to-thermoelastic transversely isotropic hollow cylinder with three-phase-lag model. Mech. Bas. Design Struct. Mach. 2019, 47, 234–254. [Google Scholar] [CrossRef]
- Honig, G.; Hirdes, U. A method for the numerical inversion of Laplace transforms. J. Comput. Appl. Math. 1984, 10, 113–132. [Google Scholar] [CrossRef]
- Zenkour, A.M. On Generalized Three-Phase-Lag Models in Photo-Thermoelasticity. Int. J. Appl. Mech. 2022, 14, 2250005. [Google Scholar] [CrossRef]
- Mondal, S.; Sur, A. Photo-thermo-elastic wave propagation in an orthotropic semiconductor with a spherical cavity and memory responses. Waves Random Complex Media 2021, 31, 1835–1858. [Google Scholar] [CrossRef]
| r | t | CTE | G–N | L–S | STPL | RTPL | ||
|---|---|---|---|---|---|---|---|---|
| N = 1 | N = 3 | N = 4 | N = 5 | |||||
| 1.001 | 0.3 | −0.1600507 | −0.1103681 | −0.1550835 | −0.1590269 | −0.1588199 | −0.1596750 | −0.1596267 |
| 0.5 | −0.4421455 | −0.4275114 | −0.4390305 | −0.4434662 | −0.4443045 | −0.4443921 | −0.4443562 | |
| 0.8 | −0.7204259 | −0.7270958 | −0.7191311 | −0.7256527 | −0.7265913 | −0.7265860 | −0.7265783 | |
| 1.0108 | 0.3 | 0.7907324 | 0.9283637 | 0.8158773 | 0.7976376 | 0.8076523 | 0.8034979 | 0.8027793 |
| 0.5 | 0.1513132 | 0.1735829 | 0.1667559 | 0.1553263 | 0.1569277 | 0.1563401 | 0.1563651 | |
| 0.8 | −0.3411962 | −0.3475165 | −0.3323632 | −0.3422239 | −0.3425316 | −0.3425963 | −0.3425864 | |
| 1.035 | 0.3 | 2.2338375 | 2.8512535 | 2.2802879 | 2.2427386 | 2.2771291 | 2.2703739 | 2.2670290 |
| 0.5 | 1.3241083 | 1.4192143 | 1.3607036 | 1.3359762 | 1.3456487 | 1.3440881 | 1.3439886 | |
| 0.8 | 0.4858891 | 0.4793232 | 0.5099324 | 0.4931183 | 0.4951689 | 0.4949403 | 0.4949480 | |
| r | t | CTE | G–N | L–S | STPL | RTPL | ||
|---|---|---|---|---|---|---|---|---|
| N = 1 | N = 3 | N = 4 | N = 5 | |||||
| 1.02 | 0.3 | −0.4446010 | −0.4587127 | −0.4416027 | −0.4442389 | −0.4446845 | −0.4452007 | −0.4451150 |
| 0.5 | −0.6879661 | −0.6641208 | −0.6859852 | −0.6897589 | −0.6907317 | −0.6907757 | −0.6907412 | |
| 0.8 | −0.94270823 | −0.9609906 | −0.9420769 | −0.9482101 | −0.9491696 | −0.9491588 | −0.9491515 | |
| 1.2 | 0.3 | −0.1990386 | −0.1923100 | −0.1999577 | −0.1995811 | −0.1997097 | −0.1990796 | −0.1991871 |
| 0.5 | −0.3095016 | −0.3218320 | −0.3080032 | −0.3111561 | −0.3096710 | −0.3097699 | −0.3098091 | |
| 0.8 | −0.4649046 | −0.4700720 | −0.4608963 | −0.4675405 | −0.4668571 | −0.4669065 | −0.4669071 | |
| 1.4 | 0.3 | −0.0421606 | −0.0347817 | −0.0412343 | −0.0414258 | −0.0426042 | −0.0424287 | −0.0422553 |
| 0.5 | −0.1976639 | −0.1892863 | −0.1990575 | −0.1983774 | −0.1989738 | −0.1988528 | −0.1988503 | |
| 0.8 | −0.3399756 | −0.3397367 | −0.3428069 | −0.3434390 | −0.3428693 | −0.3428636 | −0.3428703 | |
| r | t | CTE | G–N | L–S | STPL | RTPL | ||
|---|---|---|---|---|---|---|---|---|
| N = 1 | N = 3 | N = 4 | N = 5 | |||||
| 1.02 | 0.3 | 0.5197161 | 0.5231952 | 0.8158523 | 0.6321797 | 0.7257061 | 0.6687072 | 0.6619560 |
| 0.5 | 0.4551331 | 0.4591944 | 0.6034615 | 0.5250257 | 0.5347617 | 0.5288343 | 0.5292230 | |
| 0.8 | 0.4065923 | 0.4113274 | 0.4823044 | 0.4480926 | 0.4475421 | 0.4469535 | 0.4470211 | |
| 1.2 | 0.3 | 1.1328376 | 1.1551850 | 1.5158575 | 1.2732250 | 1.8693517 | 1.8697841 | 1.7797076 |
| 0.5 | 1.1441023 | 1.1762359 | 1.6486669 | 1.3572497 | 1.5595642 | 1.5331112 | 1.5294970 | |
| 0.8 | 1.0991674 | 1.1409540 | 1.4633732 | 1.2932336 | 1.3452712 | 1.3412060 | 1.3411794 | |
| 1.4 | 0.3 | 0.6166223 | 0.6403425 | 0.2553162 | 0.5498148 | 0.4213529 | 0.6197291 | 0.6189961 |
| 0.5 | 0.7944132 | 0.8302729 | 0.7959542 | 0.8370789 | 0.9866523 | 0.9826821 | 0.9777945 | |
| 0.8 | 0.9145463 | 0.9654823 | 1.1009292 | 1.0413519 | 1.1155064 | 1.112294 | 1.1119570 | |
| r | t | CTE | G–N | L–S | STPL | RTPL | ||
|---|---|---|---|---|---|---|---|---|
| N = 1 | N = 3 | N = 4 | N = 5 | |||||
| 1.02 | 0.3 | 1.4250082 | 1.7169427 | 1.1644764 | 1.3218307 | 1.2488604 | 1.3002398 | 1.3052216 |
| 0.5 | 0.8697574 | 0.8919956 | 0.7447060 | 0.8095222 | 0.8052005 | 0.8101600 | 0.8097287 | |
| 0.8 | 0.5084246 | 0.5016690 | 0.4473304 | 0.4747826 | 0.4767497 | 0.4771983 | 0.4771340 | |
| 1.2 | 0.3 | −0.3476186 | −0.2060406 | −0.7381048 | −0.4810923 | −1.1013084 | −1.0979774 | −1.0048155 |
| 0.5 | −1.0358693 | −0.4342299 | −1.5929489 | −1.2634836 | −1.4691980 | −1.4406952 | −1.4372923 | |
| 0.8 | 0.4730670 | 0.4169757 | 0.0996810 | 0.2792902 | 0.2373867 | 0.2412938 | 0.2412457 | |
| 1.4 | 0.3 | 0.0720812 | −0.0097442 | 0.4509219 | 0.1469006 | 0.2787176 | 0.0756354 | 0.0768349 |
| 0.5 | 0.0635672 | 0.0801358 | 0.0794198 | 0.0336441 | −0.1175433 | −0.1139438 | −0.1088892 | |
| 0.8 | −1.1153279 | −1.1761286 | −1.3292837 | −1.2426448 | −1.3245219 | −1.3209060 | −1.3205495 | |
| r | t | CTE | G–N | L–S | STPL | RTPL | ||
|---|---|---|---|---|---|---|---|---|
| N = 1 | N = 3 | N = 4 | N = 5 | |||||
| 1.02 | 0.3 | 0.0198399 | 0.1669378 | −0.2555124 | −0.0876141 | −0.1712722 | −0.1175958 | −0.1116476 |
| 0.5 | −0.4645790 | −0.4416541 | −0.5992993 | −0.5313858 | −0.5393601 | −0.5339610 | −0.5343373 | |
| 0.8 | −0.8709283 | −0.8892813 | −0.9386944 | −0.9138763 | −0.9135551 | −0.9130260 | −0.9130849 | |
| 1.2 | 0.3 | −0.9048642 | −0.8304659 | −1.2923918 | −1.0422374 | −1.6505469 | −1.6485684 | −1.5570346 |
| 0.5 | −1.3474299 | −1.0602676 | −1.8770728 | −1.5692064 | −1.7719893 | −1.7445910 | −1.7411154 | |
| 0.8 | −0.6979375 | −0.7436193 | −1.0634094 | −0.8940525 | −0.9404411 | −0.9364963 | −0.9365076 | |
| 1.4 | 0.3 | −0.3014565 | −0.3536854 | 0.0693004 | −0.2301085 | −0.1008053 | −0.3014154 | −0.3003248 |
| 0.5 | −0.5053201 | −0.5032281 | −0.4991360 | −0.5421070 | −0.6929150 | −0.6890443 | −0.6840712 | |
| 0.8 | −1.2577217 | −1.3109739 | −1.4599464 | −1.3872542 | −1.4648736 | −1.4614548 | −1.4611128 | |
| r | H0 | CTE | G–N | L–S | STPL | RTPL | ||
|---|---|---|---|---|---|---|---|---|
| N = 1 | N = 3 | N = 4 | N = 5 | |||||
| 1.001 | 0 | 0.1782137 | 0.5045876 | 0.1876537 | 0.1803101 | 0.1815128 | 0.1801641 | 0.1801591 |
| −0.1600507 | −0.1260185 | −0.1550835 | −0.1590269 | −0.1588199 | −0.1596750 | −0.1596267 | ||
| −0.5963013 | −0.5838559 | −0.5942398 | −0.5959014 | −0.5961448 | −0.5966622 | −0.5965978 | ||
| 1.0108 | 0 | 1.6863479 | 3.1787268 | 1.7322308 | 1.6976456 | 1.7199434 | 1.7128199 | 1.7110496 |
| 0.7907324 | 0.9125334 | 0.8158773 | 0.7976376 | 0.8076523 | 0.8034979 | 0.8027793 | ||
| −0.0216654 | −0.0121308 | −0.0097624 | −0.0180902 | −0.0141696 | −0.0163392 | −0.0165856 | ||
| 1.035 | 0 | 2.4534254 | 7.7106569 | 2.4972843 | 2.4545775 | 2.5100973 | 2.5053423 | 2.4991835 |
| 2.2338375 | 2.8364917 | 2.2802879 | 2.2427386 | 2.2771291 | 2.2703739 | 2.2670290 | ||
| 1.1346513 | 1.1417442 | 1.1625329 | 1.1418607 | 1.1575618 | 1.1530407 | 1.1516357 | ||
| CTE | G–N | L–S | STPL | RTPL | ||||
|---|---|---|---|---|---|---|---|---|
| 1.02 | 0 | −0.1767007 | −0.2365661 | −0.1712572 | −0.1759073 | −0.1761001 | −0.1767683 | −0.1766927 |
| −0.4446010 | −0.4556610 | −0.4416027 | −0.4442389 | −0.4446845 | −0.4452007 | −0.4451150 | ||
| −0.8377249 | −0.8346584 | −0.8365695 | −0.8376432 | −0.8381650 | −0.8385221 | −0.8384422 | ||
| 1.2 | 0 | 0.0006626 | 0.0211928 | 0.0018281 | 0.0009625 | 0.0010703 | 0.0015785 | 0.0014699 |
| −0.1990386 | −0.1927053 | −0.1999577 | −0.1995811 | −0.1997097 | −0.1990796 | −0.1991871 | ||
| −0.4200627 | −0.4180902 | −0.4204997 | −0.4207381 | −0.4193394 | −0.4190292 | −0.4192868 | ||
| 1.4 | 0 | 0.0415410 | 0.0465105 | 0.0418797 | 0.0420817 | 0.0412667 | 0.0413940 | 0.0415588 |
| −0.0421606 | −0.0352435 | −0.0412343 | −0.0414258 | −0.0426042 | −0.0424287 | −0.0422553 | ||
| −0.2954475 | −0.2962609 | −0.2956049 | −0.2953487 | −0.2970595 | −0.2968102 | −0.2965584 | ||
| CTE | G–N | L–S | STPL | RTPL | ||||
|---|---|---|---|---|---|---|---|---|
| 1.02 | 0 | 0.5195277 | 0.5231952 | 0.8149122 | 0.6317500 | 0.7249938 | 0.6681243 | 0.6613913 |
| 0.5197161 | 0.5231952 | 0.8158523 | 0.6321797 | 0.7257061 | 0.6687072 | 0.6619559 | ||
| 0.5202053 | 0.5231952 | 0.8171815 | 0.6329834 | 0.7267366 | 0.6695850 | 0.6628219 | ||
| 1.2 | 0 | 1.1328485 | 1.1551850 | 1.5160141 | 1.2730366 | 1.8699681 | 1.8702848 | 1.7801007 |
| 1.1328376 | 1.1551850 | 1.5158575 | 1.2732250 | 1.8693517 | 1.8697841 | 1.7797076 | ||
| 1.1302030 | 1.1551850 | 1.5072709 | 1.2688359 | 1.8634498 | 1.8652445 | 1.7751423 | ||
| 1.4 | 0 | 0.6178070 | 0.6403425 | 0.2557158 | 0.5506273 | 0.4221051 | 0.6206186 | 0.6198641 |
| 0.6166223 | 0.6403425 | 0.2553162 | 0.5498148 | 0.4213529 | 0.6197291 | 0.6189961 | ||
| 0.6177501 | 0.6403425 | 0.2597756 | 0.5516250 | 0.4242953 | 0.6217558 | 0.6210694 | ||
| CTE | G–N | L–S | STPL | RTPL | ||||
|---|---|---|---|---|---|---|---|---|
| 1.02 | 0 | 2.1413094 | 5.0084304 | 1.9012246 | 2.0400614 | 1.9882193 | 2.0368781 | 2.0397306 |
| 1.4250082 | 1.7098567 | 1.1644764 | 1.3218307 | 1.2488604 | 1.3002398 | 1.3052216 | ||
| 0.7663735 | 0.7619035 | 0.4877997 | 0.6591606 | 0.5742749 | 0.6284021 | 0.6344444 | ||
| 1.2 | 0 | −0.6773446 | 0.6615173 | −1.0776863 | −0.8119883 | −1.4290790 | −1.4239547 | −1.3317608 |
| −0.3476186 | −0.2009060 | −0.7381048 | −0.4810923 | −1.1013084 | −1.0979774 | −1.0048155 | ||
| −0.8607713 | −0.8969050 | −1.2863322 | −1.0105215 | −1.6267403 | −1.6169840 | −1.5257144 | ||
| 1.4 | 0 | −0.7407481 | −0.7747852 | −0.3827128 | −0.6759330 | −0.5439698 | −0.7468172 | −0.7458980 |
| 0.0720812 | −0.0016496 | 0.4509219 | 0.1469006 | 0.2787176 | 0.0756354 | 0.0768349 | ||
| 0.2771069 | 0.2558551 | 0.6657660 | 0.3510599 | 0.4892780 | 0.2833072 | 0.2842716 | ||
| CTE | G–N | L–S | STPL | RTPL | ||||
|---|---|---|---|---|---|---|---|---|
| 1.02 | 0 | 0.6413170 | 1.9878850 | 0.3789836 | 0.5353730 | 0.4626946 | 0.5147940 | 0.5196557 |
| 0.0198399 | 0.1372332 | −0.2555124 | −0.0876141 | −0.1712722 | −0.1175958 | −0.1116476 | ||
| −0.6954887 | −0.6792086 | −0.9821086 | −0.8053970 | −0.8952159 | −0.8399301 | −0.8334501 | ||
| 1.2 | 0 | −0.9039566 | −0.2244379 | −1.2947625 | −1.0411157 | −1.6480632 | −1.6452294 | −1.5541281 |
| −0.9048642 | −0.8273155 | −1.2923918 | −1.0422374 | −1.6505469 | −1.6485684 | −1.5570346 | ||
| −1.3447378 | −1.3652770 | −1.7464786 | −1.4895059 | −2.0937861 | −2.0895322 | −1.9990591 | ||
| 1.4 | 0 | −0.6498027 | −0.6794221 | −0.2895031 | −0.5834226 | −0.4537569 | −0.6543521 | −0.6533975 |
| −0.3014565 | −0.3479797 | 0.0693004 | −0.2301085 | −0.1008053 | −0.3014154 | −0.3003248 | ||
| −0.3799260 | −0.4038305 | −0.0066819 | −0.3098064 | −0.1782388 | −0.3797877 | −0.3787822 | ||
| CTE | G–N | L–S | STPL | RTPL | ||||
|---|---|---|---|---|---|---|---|---|
| 1.001 | 0.00 | −0.1600507 | −0.1817118 | −0.1550835 | −0.1590269 | −0.1588199 | −0.1596750 | −0.1596267 |
| 0.01 | −0.0728988 | −0.2495945 | −0.0685479 | −0.0719793 | −0.0716577 | −0.0723496 | −0.0723247 | |
| 0.05 | 0.1069584 | 0.5070073 | 0.1099905 | 0.1076340 | 0.1080314 | 0.1076008 | 0.1075979 | |
| 0.20 | 0.3598124 | −0.1230445 | 0.3614521 | 0.3602013 | 0.3605292 | 0.3603088 | 0.3602955 | |
| 1.0108 | 0.00 | 0.7907324 | 0.7422693 | 0.8158773 | 0.7976376 | 0.8076523 | 0.8034979 | 0.8027793 |
| 0.01 | 1.0444167 | 1.1310202 | 1.0660570 | 1.0501743 | 1.0593502 | 1.0558573 | 1.0551759 | |
| 0.05 | 1.6586577 | 2.2876971 | 1.6733614 | 1.6622524 | 1.6694769 | 1.6672005 | 1.6666240 | |
| 0.20 | 2.5373701 | −0.1390619 | 2.5446030 | 2.5388002 | 2.5434033 | 2.5423482 | 2.5419391 | |
| 1.035 | 0.00 | 2.2338375 | 2.0604843 | 2.2802879 | 2.2427386 | 2.2771291 | 2.2703739 | 2.2670290 |
| 0.01 | 2.4541706 | 3.6055484 | 2.4889375 | 2.4596437 | 2.4888941 | 2.4840987 | 2.4811503 | |
| 0.05 | 2.3896894 | 3.7194494 | 2.4028985 | 2.3898009 | 2.4073189 | 2.4059421 | 2.4039812 | |
| 0.20 | 0.5555053 | −3.5966438 | 0.5537322 | 0.5538753 | 0.5579398 | 0.5586249 | 0.5580035 | |
| CTE | G–N | L–S | STPL | RTPL | ||||
|---|---|---|---|---|---|---|---|---|
| 1.02 | 0.00 | −0.4446010 | −0.4702098 | −0.4416027 | −0.4442389 | −0.4446845 | −0.4452007 | −0.4451150 |
| 0.01 | −0.3761698 | −0.3938417 | −0.3735556 | −0.3758274 | −0.3760925 | −0.3764870 | −0.3764284 | |
| 0.05 | −0.2514169 | −0.2002410 | −0.2496761 | −0.2511617 | −0.2512163 | −0.2514271 | −0.2514038 | |
| 0.20 | −0.1285389 | −0.1350768 | −0.1277263 | −0.1284124 | −0.1283882 | −0.1284682 | −0.1284637 | |
| 1.2 | 0.00 | −0.1990386 | −0.1982898 | −0.1999577 | −0.1995811 | −0.1997097 | −0.1990796 | −0.1991871 |
| 0.01 | −0.1388393 | −0.1242475 | −0.1387854 | −0.1389520 | −0.1390226 | −0.1386521 | −0.1387124 | |
| 0.05 | −0.0514207 | −0.0617681 | −0.0510383 | −0.0513124 | −0.0512864 | −0.0511259 | −0.0511593 | |
| 0.20 | 0.0085746 | 0.0088881 | 0.0087642 | 0.0086495 | 0.0086748 | 0.0087255 | 0.0087156 | |
| 1.4 | 0.00 | −0.0421606 | −0.0399129 | −0.0412343 | −0.0414258 | −0.0426042 | −0.0424287 | −0.0422553 |
| 0.01 | 0.0104176 | 0.0181003 | 0.0115143 | 0.0111229 | 0.0104788 | 0.0105647 | 0.0106848 | |
| 0.05 | 0.0128624 | 0.0116589 | 0.0129452 | 0.0130233 | 0.0127674 | 0.0128069 | 0.0128582 | |
| 0.20 | 0.0039736 | 0.0026442 | 0.0039234 | 0.0039991 | 0.0039099 | 0.0039224 | 0.0039389 | |
| CTE | G–N | L–S | STPL | RTPL | ||||
|---|---|---|---|---|---|---|---|---|
| 1.02 | 0.00 | 0.5197161 | 0.5231952 | 0.8158523 | 0.6321797 | 0.7257061 | 0.6687072 | 0.6619559 |
| 0.01 | 0.5196226 | 0.5231952 | 0.8155291 | 0.6320045 | 0.7254572 | 0.6684988 | 0.6617520 | |
| 0.05 | 0.5195045 | 0.5231952 | 0.8149457 | 0.6317351 | 0.7250108 | 0.6681320 | 0.6613971 | |
| 0.20 | 0.5194992 | 0.5231952 | 0.8144369 | 0.6315960 | 0.7246144 | 0.6678177 | 0.6611030 | |
| 1.2 | 0.00 | 1.1328376 | 1.1551850 | 1.5158575 | 1.2732250 | 1.8693517 | 1.8697841 | 1.7797076 |
| 0.01 | 1.1325365 | 1.1551850 | 1.5158537 | 1.2728365 | 1.8696724 | 1.8700076 | 1.7798489 | |
| 0.05 | 1.1326225 | 1.1551850 | 1.5155747 | 1.2727896 | 1.8697239 | 1.8700990 | 1.7799023 | |
| 0.20 | 1.1330736 | 1.1551850 | 1.5160089 | 1.2731337 | 1.8702705 | 1.8706068 | 1.7803877 | |
| 1.4 | 0.00 | 0.6166223 | 0.6403425 | 0.2553162 | 0.5498148 | 0.4213529 | 0.6197291 | 0.6189961 |
| 0.01 | 0.6163464 | 0.6403425 | 0.2546471 | 0.5492825 | 0.4209161 | 0.6193444 | 0.6186026 | |
| 0.05 | 0.6175008 | 0.6403425 | 0.2554513 | 0.5503468 | 0.4216919 | 0.6202147 | 0.6194853 | |
| 0.20 | 0.6182038 | 0.6403425 | 0.2561957 | 0.5510730 | 0.4223512 | 0.6209149 | 0.6201905 | |
| CTE | G–N | L–S | STPL | RTPL | ||||
|---|---|---|---|---|---|---|---|---|
| 1.02 | 0.00 | 1.4250082 | 1.4417132 | 1.1644764 | 1.3218307 | 1.2488604 | 1.3002398 | 1.3052216 |
| 0.01 | 1.6799725 | 2.3462039 | 1.4135395 | 1.5747718 | 1.4996322 | 1.5520136 | 1.5571447 | |
| 0.05 | 2.1955956 | 2.8931530 | 1.9176461 | 2.0867605 | 2.0068048 | 2.0610981 | 2.0665780 | |
| 0.20 | 2.1293602 | −1.9570943 | 1.8395231 | 2.0174381 | 1.9310497 | 1.9872334 | 1.9932340 | |
| 1.2 | 0.00 | −0.3476186 | −0.7002070 | −0.7381048 | −0.4810923 | −1.1013084 | −1.0979774 | −1.0048155 |
| 0.01 | −0.0084140 | 0.7900171 | −0.3912182 | −0.1439469 | −0.7489823 | −0.7479519 | −0.6564771 | |
| 0.05 | −0.5214154 | 0.2873304 | −0.9091673 | −0.6595318 | −1.2628424 | −1.2615757 | −1.1707216 | |
| 0.20 | −1.1843148 | −3.7578587 | −1.5710519 | −1.3248846 | −1.9236769 | −1.9235961 | −1.8331840 | |
| 1.4 | 0.00 | 0.0720812 | −0.0630823 | 0.4509219 | 0.1469006 | 0.2787176 | 0.0756354 | 0.0768349 |
| 0.01 | −0.0733074 | −0.1260033 | 0.2946380 | −0.0050862 | 0.1296550 | −0.0721929 | −0.0714200 | |
| 0.05 | −0.6513165 | −0.4203154 | −0.2904336 | −0.5848771 | −0.4551246 | −0.6549940 | −0.6542153 | |
| 0.20 | −0.6302124 | −1.3114760 | −0.2682290 | −0.5632011 | −0.4341115 | −0.6331041 | −0.6323633 | |
| CTE | G–N | L–S | STPL | RTPL | ||||
|---|---|---|---|---|---|---|---|---|
| 1.02 | 0.00 | 0.0198399 | −0.1007279 | −0.2555124 | −0.0876141 | −0.1712722 | −0.1707365 | −0.1706840 |
| 0.01 | 0.2147006 | 0.3924400 | −0.0638714 | 0.1062539 | 0.0217218 | 0.0222527 | 0.0223048 | |
| 0.05 | 0.5953855 | 1.0740053 | 0.3104173 | 0.4851070 | 0.3984551 | 0.3989805 | 0.3990321 | |
| 0.20 | 0.6824975 | −1.5054263 | 0.3909123 | 0.5706121 | 0.4809410 | 0.4814663 | 0.4815179 | |
| 1.2 | 0.00 | −0.9048642 | −1.1056940 | −1.2923918 | −1.0422374 | −1.6505469 | −1.6485537 | −1.6483581 |
| 0.01 | −0.6845724 | −0.3075093 | −1.0675876 | −0.8225765 | −1.4235815 | −1.4215722 | −1.4213750 | |
| 0.05 | −0.8690243 | −0.4528431 | −1.2540643 | −1.0080733 | −1.6081824 | −1.6061455 | −1.6059456 | |
| 0.20 | −1.1516241 | −2.2032886 | −1.5363075 | −1.2918775 | −1.8898230 | −1.8877660 | −1.8875641 | |
| 1.4 | 0.00 | −0.3014565 | −0.3782174 | 0.0693004 | −0.2301085 | −0.1008053 | −0.0993506 | −0.0992079 |
| 0.01 | −0.3366938 | −0.3633738 | 0.0289190 | −0.2685467 | −0.1374440 | −0.1359819 | −0.1358384 | |
| 0.05 | −0.6252768 | −0.5124963 | −0.2637530 | −0.5583662 | −0.4293436 | −0.4278723 | −0.4277280 | |
| 0.20 | −0.6213890 | −0.9706441 | −0.2594291 | −0.5542999 | −0.4254574 | −0.4239819 | −0.4238371 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allehaibi, A.M.; Zenkour, A.M. Magneto-Thermoelastic Response in an Infinite Medium with a Spherical Hole in the Context of High Order Time-Derivatives and Triple-Phase-Lag Model. Materials 2022, 15, 6256. https://doi.org/10.3390/ma15186256
Allehaibi AM, Zenkour AM. Magneto-Thermoelastic Response in an Infinite Medium with a Spherical Hole in the Context of High Order Time-Derivatives and Triple-Phase-Lag Model. Materials. 2022; 15(18):6256. https://doi.org/10.3390/ma15186256
Chicago/Turabian StyleAllehaibi, Ashraf M., and Ashraf M. Zenkour. 2022. "Magneto-Thermoelastic Response in an Infinite Medium with a Spherical Hole in the Context of High Order Time-Derivatives and Triple-Phase-Lag Model" Materials 15, no. 18: 6256. https://doi.org/10.3390/ma15186256
APA StyleAllehaibi, A. M., & Zenkour, A. M. (2022). Magneto-Thermoelastic Response in an Infinite Medium with a Spherical Hole in the Context of High Order Time-Derivatives and Triple-Phase-Lag Model. Materials, 15(18), 6256. https://doi.org/10.3390/ma15186256






