Strength of Partially Encased Steel-Concrete Composite Column for Modular Building Structures
Abstract
:1. Introduction
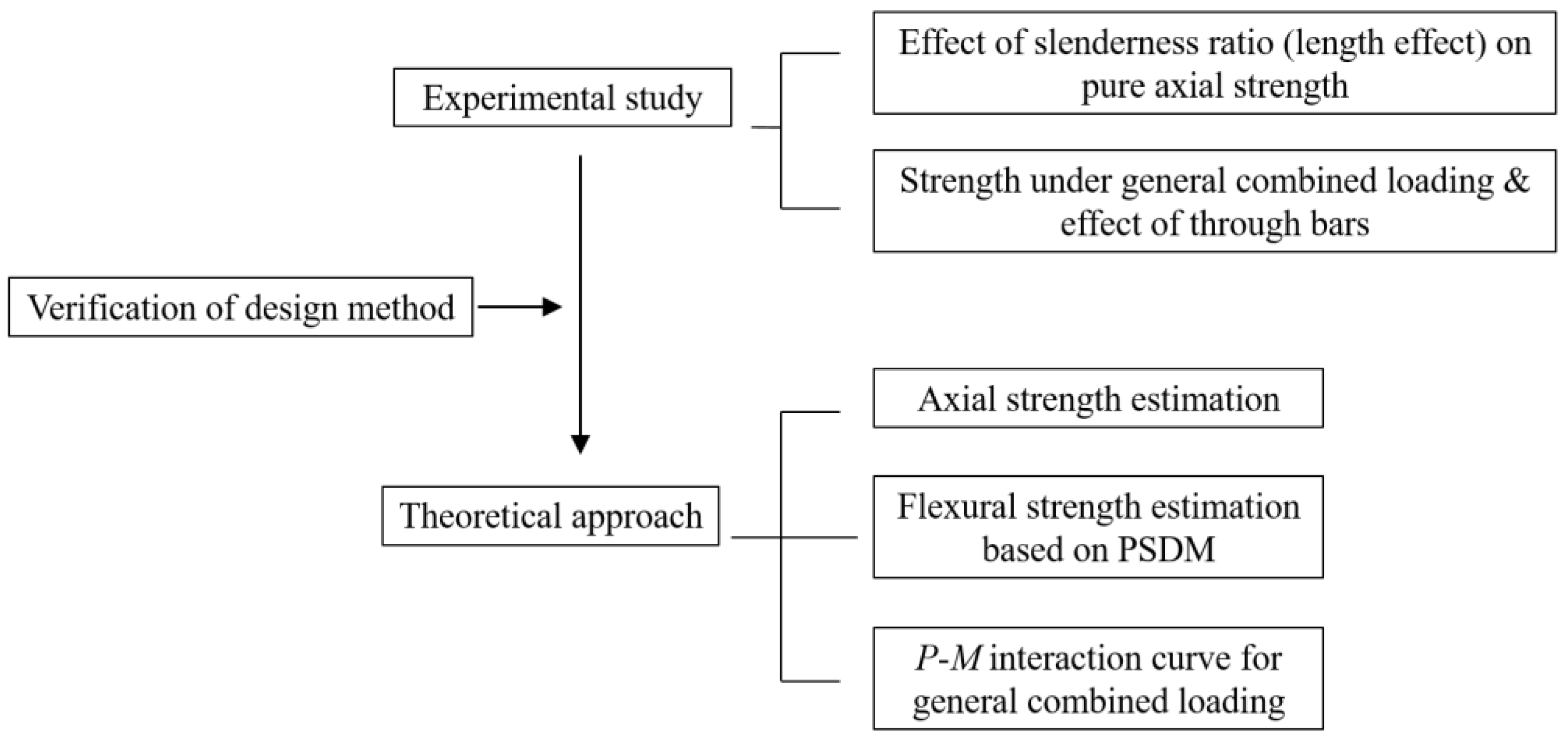
2. Experimental Study
2.1. Description of Test Specimen and Setup
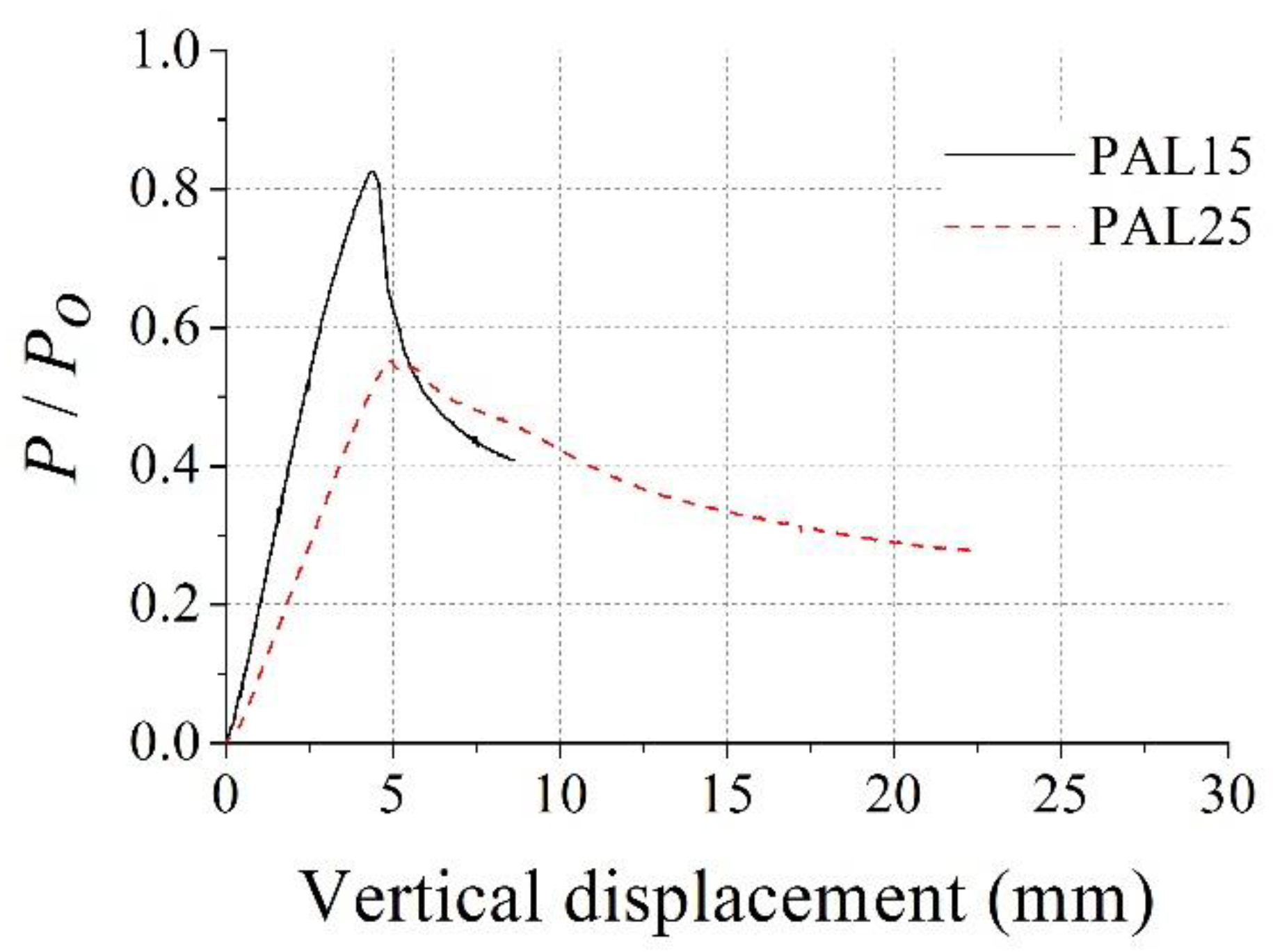
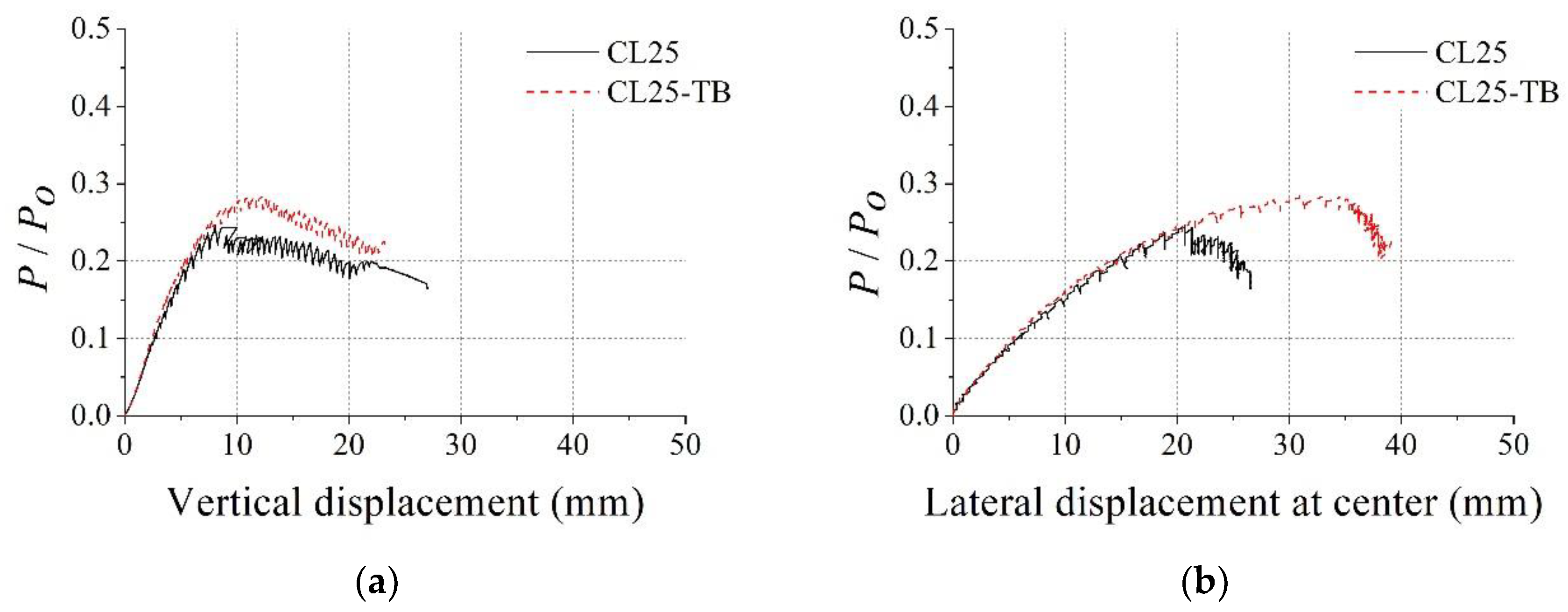
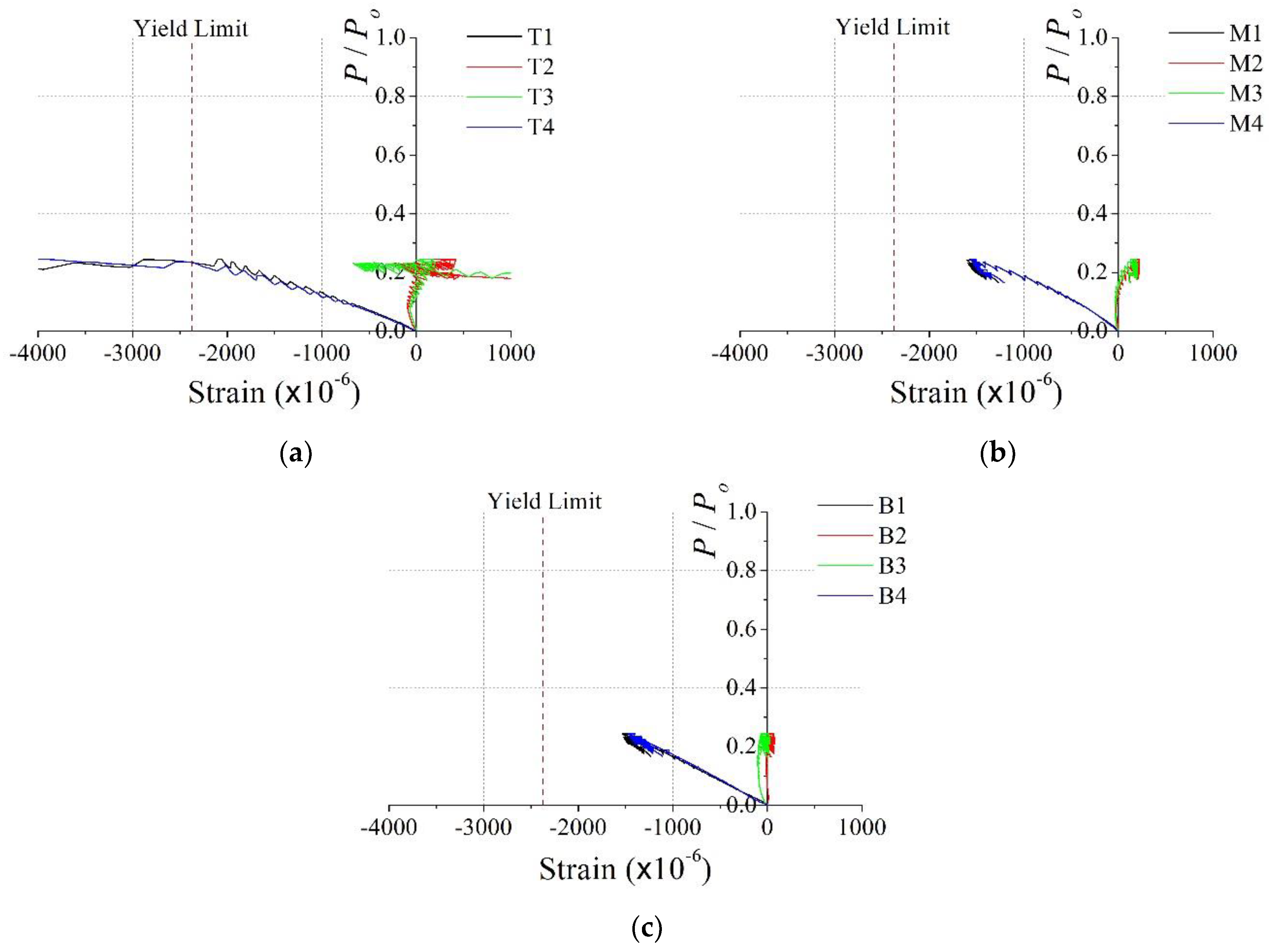
2.2. Test Results
3. Design Equations
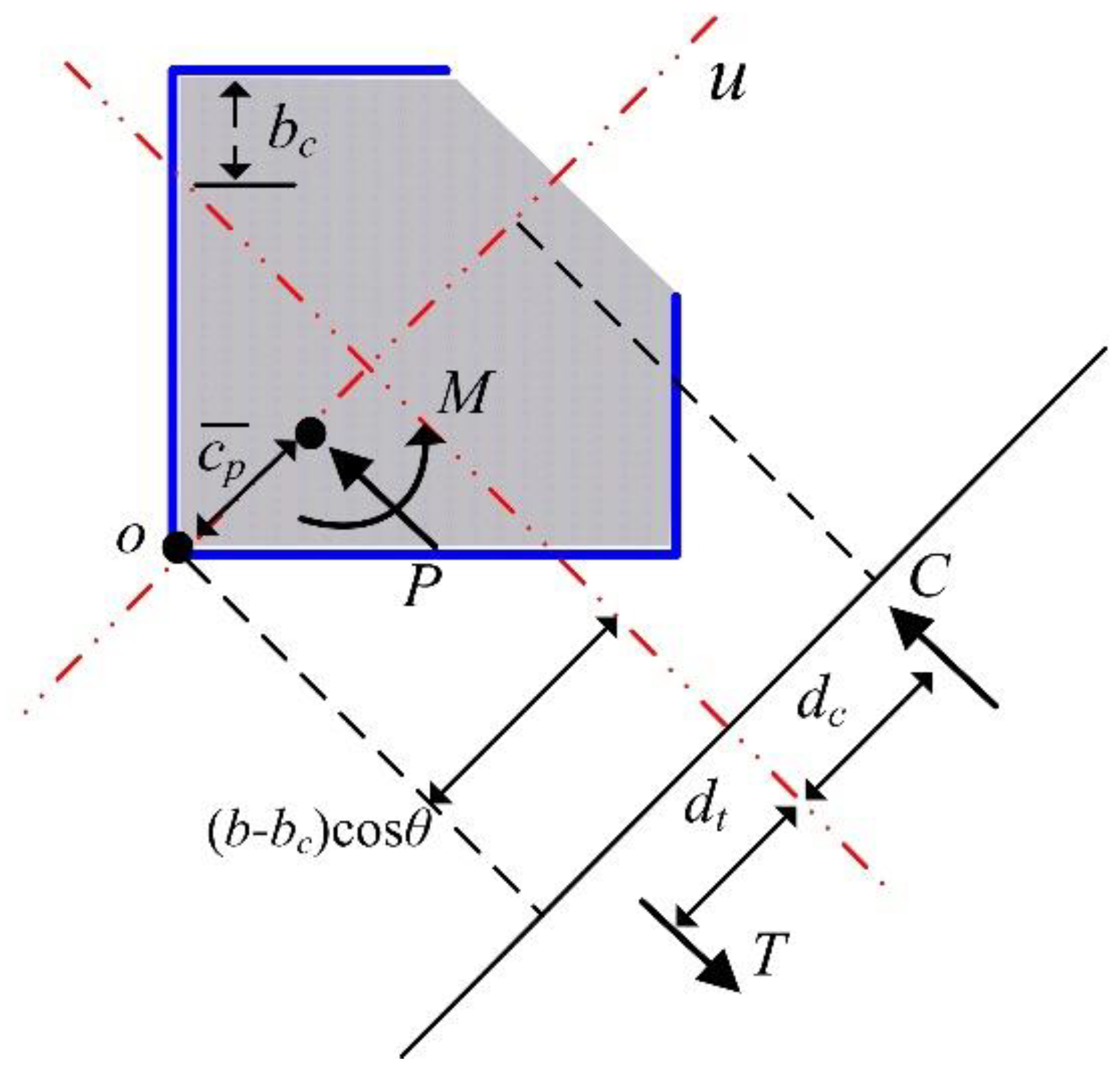
3.1. Axial Strength
3.2. Flexural Strength
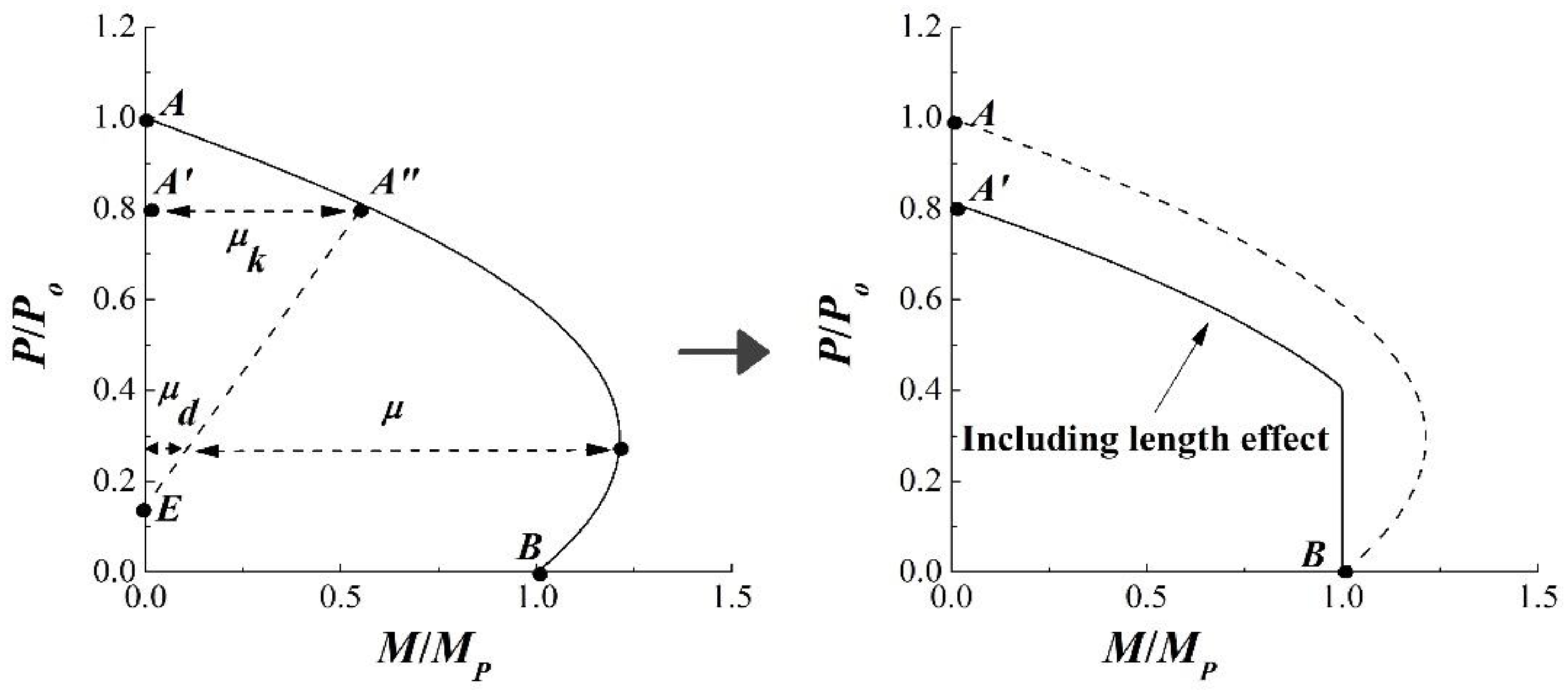
3.3. Strength under General Combined Loading
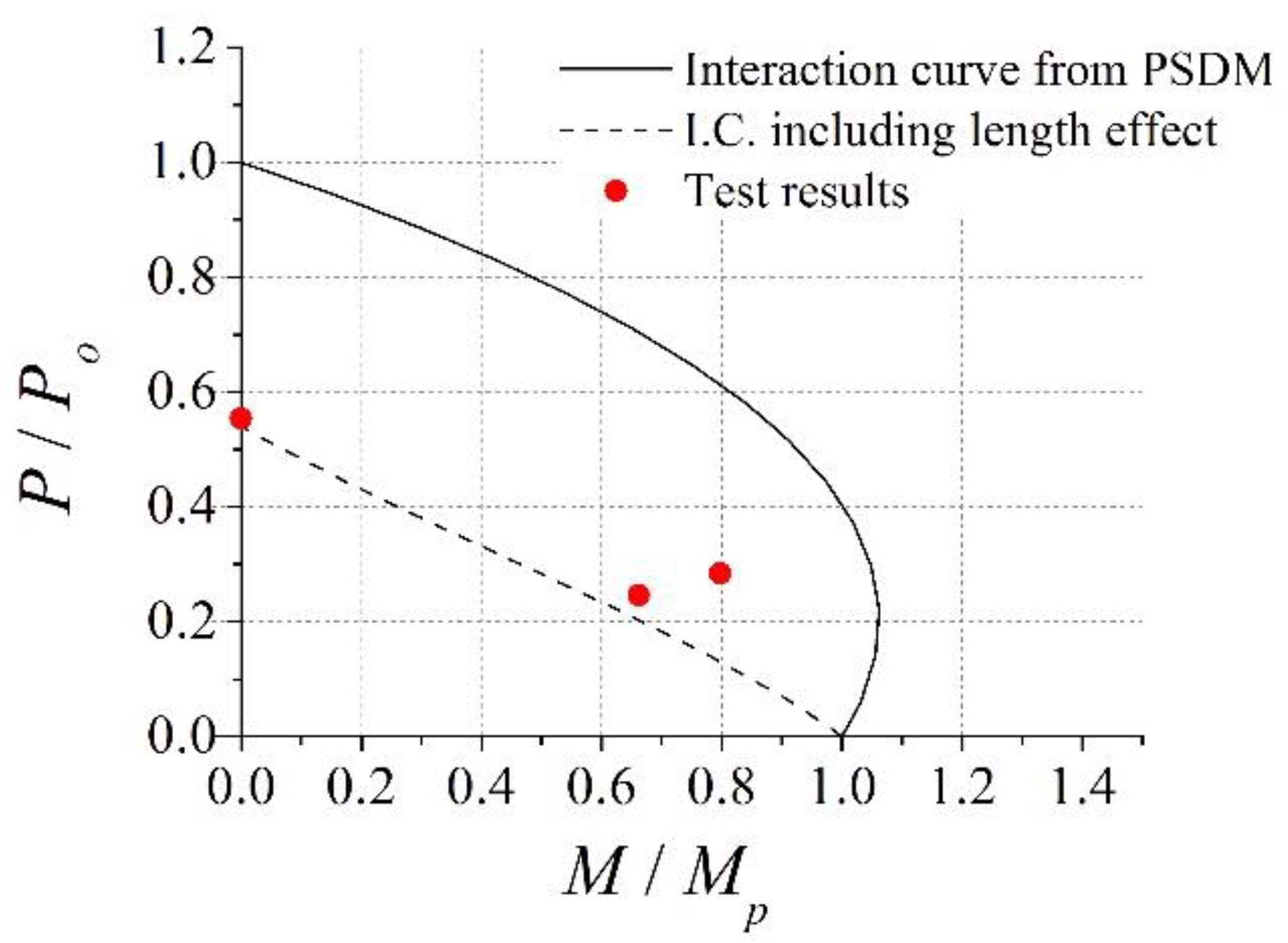
4. Comparison of Proposed Design Equations with Test Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Park, K.-S.; Moon, J.; Lee, S.-S.; Bae, K.-Y.; Roeder, C.W. Embedded steel column-to-foundation connection for a modular structural system. Eng. Struct. 2016, 110, 244–257. [Google Scholar] [CrossRef]
- Annan, C.D.; Youssef, M.A.; Naggar, M.H. Experimental evaluation of the seismic performance of modular steel-braced frames. Eng. Struct. 2009, 31, 1435–1446. [Google Scholar] [CrossRef]
- Lawson, R.M.; Ogden, R.G.; Bergin, R. Application of modular construction in high-rise buildings. J. Arch. Eng. ASCE 2012, 18, 148–154. [Google Scholar] [CrossRef]
- Lawson, R.M.; Richards, J. Modular design for highrise buildings. Proc. Inst. Civ. Eng. Struct. Build. 2010, 163, 151–164. [Google Scholar] [CrossRef]
- Annan, C.D.; Youssef, M.A.; El-Naggar, M.H. Seismic overstrength in braced frames of modular steel buildings. J. Earthq. Engrg. 2009, 13, 1–21. [Google Scholar] [CrossRef]
- Hong, S.-G.; Cho, B.-H.; Chung, K.-S.; Moon, J.-H. Behavior of framed modular building system with double skin steel panels. J. Constr. Steel Res. 2011, 67, 936–946. [Google Scholar] [CrossRef]
- Liew, J.Y.R.; Chua, Y.S.; Dai, Z. Steel concrete composite systems for modular construction of high-rise buildings. Structures 2019, 21, 135–149. [Google Scholar] [CrossRef]
- Sheehan, T.; Dai, X.; Yang, J.; Zhou, K.; Lam, D. Flexural behaviour of composite slim floor beams. Structures 2019, 21, 22–32. [Google Scholar] [CrossRef]
- John, K.; Rahman, S.; Kafle, B.; Weiss, M.; Hansen, K.; Elchalakani, M.; Udawatta, N.; Hosseini, M.R.; Al-Ameri, R. Structural Performance Assessment of Innovative Hollow Cellular Panels for Modular Flooring System. Buildings 2022, 12, 57. [Google Scholar] [CrossRef]
- Zhao, B.; Wu, D.; Zhu, H. New modular precast composite shear wall structural system and experimental study on its seismic performance. Eng. Struct. 2022, 264, 114381. [Google Scholar] [CrossRef]
- Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. New interlocking inter-module connection for modular steel buildings: Experimental and numerical studies. Eng. Struct. 2019, 198, 109465. [Google Scholar] [CrossRef]
- Lacey, A.W.; Chen, W.; Hao, H. Experimental methods for inter-module joints in modular building structures—A state-of-the-art review. J. Build. Eng. 2022, 46, 103792. [Google Scholar] [CrossRef]
- Zhai, S.-Y.; Lyu, Y.-F.; Cao, K.; Li, G.-Q.; Wang, W.-Y.; Chen, C. Experimental study on bolted-cover plate corner connections for column-supported modular steel buildings. J. Constr. Steel Res. 2022, 189, 107060. [Google Scholar] [CrossRef]
- Lyu, Y.-F.; Li, G.-Q.; Cao, K.; Zhai, S.-Y.; Wang, Y.-B.; Mao, L.; Ran, M.-M. Bending behavior of splice connection for corner-supported steel modular buildings. Eng. Struct. 2022, 250, 113460. [Google Scholar] [CrossRef]
- Deng, E.-F.; Lian, J.-Y.; Liu, Z.; Zhang, G.-C.; Wang, S.-B.; Cao, D.-B. Compressive behavior of a fully prefabricated liftable connection for modular steel construction. Buildings 2022, 12, 649. [Google Scholar] [CrossRef]
- Hernández-Figueirido, D.; Piquer, A. Protected steel columns vs partially encased columns: Fire resistance and economic considerations. J. Constr. Steel Res. 2014, 124, 47–56. [Google Scholar]
- Debski, H.; Teter, A.; Kubiak, T.; Samborski, S. Local buckling and collapse of thin-walled channel section composite columns subjected to quasi-static compression. Compos. Struct. 2016, 136, 593–601. [Google Scholar] [CrossRef]
- Yadav, A.; Panda, S.K.; Dey, T. Non-linear dynamic instability analysis of mono-symmetric thin walled columns with various boundary conditions. Int. J. Mech. Sci. 2017, 126, 242–254. [Google Scholar] [CrossRef]
- Young, B.; Chen, J. Column tests of cold-formed steel non-symmetric lipped angle sections. J. Constr. Steel Res. 2008, 64, 808–815. [Google Scholar] [CrossRef]
- Taras, A.; Kugler, P.; Unterweger, H. On the behavior and eurocode design of T-section columns, beams and beam-columns with slender webs. J. Constr. Steel Res. 2017, 129, 250–262. [Google Scholar] [CrossRef]
- CEN. Eurocode 4—Design of Composite Steel and Concrete Structures; CEN: Brussels, Belgium, 2002. [Google Scholar]
- Heins, C.P. Bending and Torsional Design in Structural Member; DC Heath and Company: Lexington, MA, USA, 1975. [Google Scholar]
- CEN. Eurocode 3—Design of Steel Structures; CEN: Brussels, Belgium, 2003. [Google Scholar]
- ACI. Building Code Requirements for Structural Concrete ACI 318-11; ACI: Farmington Hills, MI, USA, 2011.
- AISC. Specifications for Structural Steel Buildings; AISC: Chicago, IL, USA, 2010. [Google Scholar]
- Moon, J.; Lehman, D.E.; Roeder, C.W.; Lee, H.-E. Strength of circular concrete-filled tubes (CFT) with and without internal reinforcement under combined loading. J. Struct. Eng. ASCE 2013, 139, 04013012. [Google Scholar] [CrossRef] [Green Version]














| Name | E (mm) | b (mm) | b1 (mm) | t (mm) | L (mm) | Remark |
|---|---|---|---|---|---|---|
| PAL15 | 0 | 150 | 75 | 4.5 | 1500 | - |
| PAL25 | 2500 | - | ||||
| CL25 | 75 | 2500 | - | |||
| CL25-TB | 2500 | Through bars were installed |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, K.-S.; Lee, S.-S.; Bae, K.-W.; Moon, J. Strength of Partially Encased Steel-Concrete Composite Column for Modular Building Structures. Materials 2022, 15, 6045. https://doi.org/10.3390/ma15176045
Park K-S, Lee S-S, Bae K-W, Moon J. Strength of Partially Encased Steel-Concrete Composite Column for Modular Building Structures. Materials. 2022; 15(17):6045. https://doi.org/10.3390/ma15176045
Chicago/Turabian StylePark, Keum-Sung, Sang-Sup Lee, Kyu-Woong Bae, and Jiho Moon. 2022. "Strength of Partially Encased Steel-Concrete Composite Column for Modular Building Structures" Materials 15, no. 17: 6045. https://doi.org/10.3390/ma15176045
APA StylePark, K.-S., Lee, S.-S., Bae, K.-W., & Moon, J. (2022). Strength of Partially Encased Steel-Concrete Composite Column for Modular Building Structures. Materials, 15(17), 6045. https://doi.org/10.3390/ma15176045






