Ball Bearing Fault Diagnosis Using Recurrence Analysis
Abstract
:1. Introduction
1.1. Fault Bearing Diagnosis
1.2. Motivation and Aim
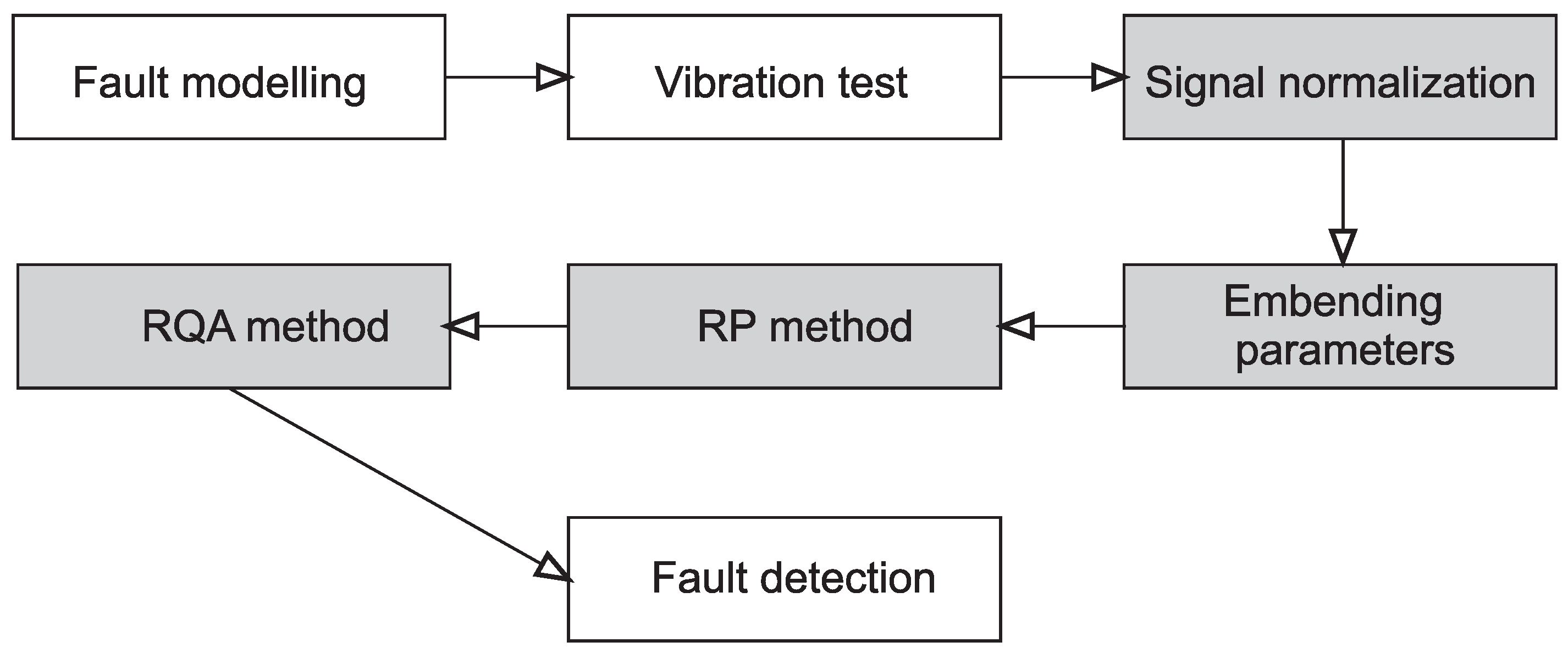
2. Materials and Methods
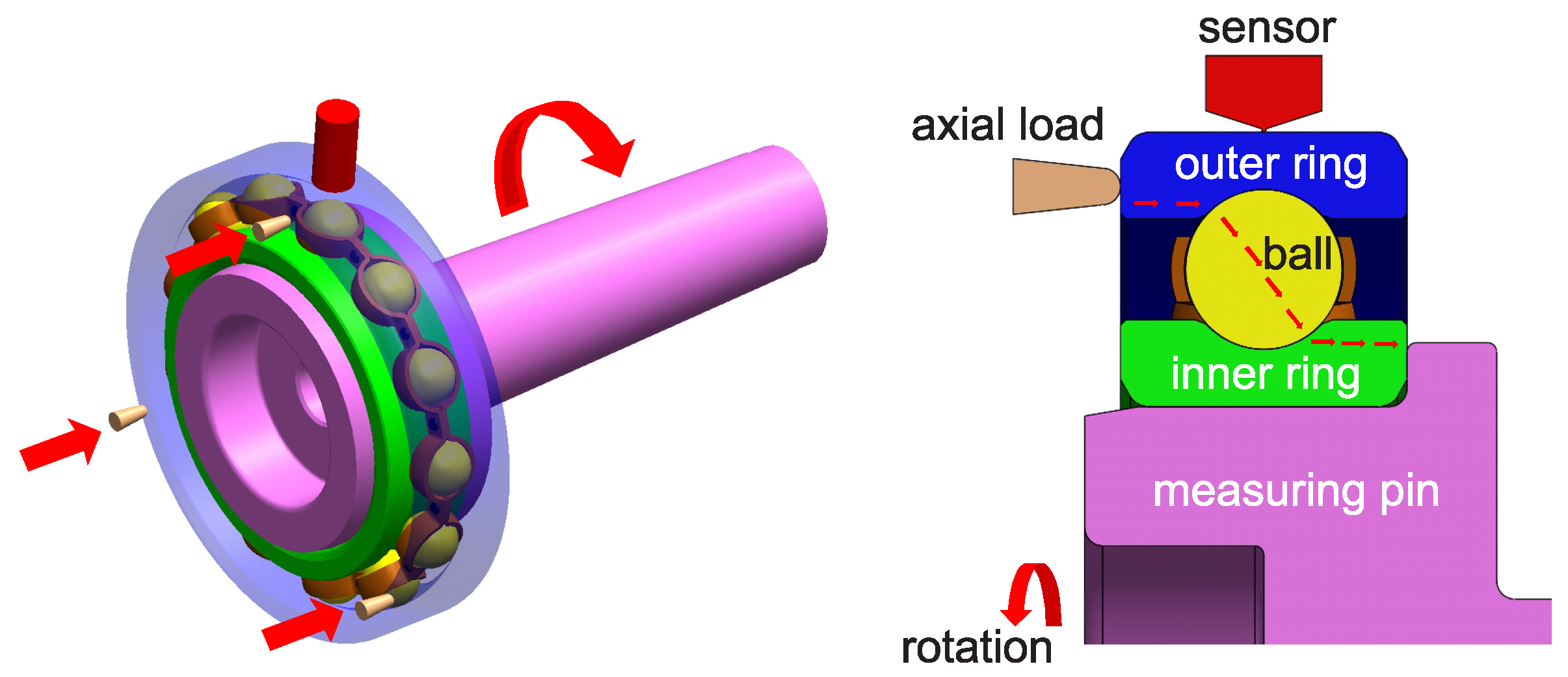
2.1. Experimental Setup
2.2. Recurrence Method
2.3. Fault Modeling
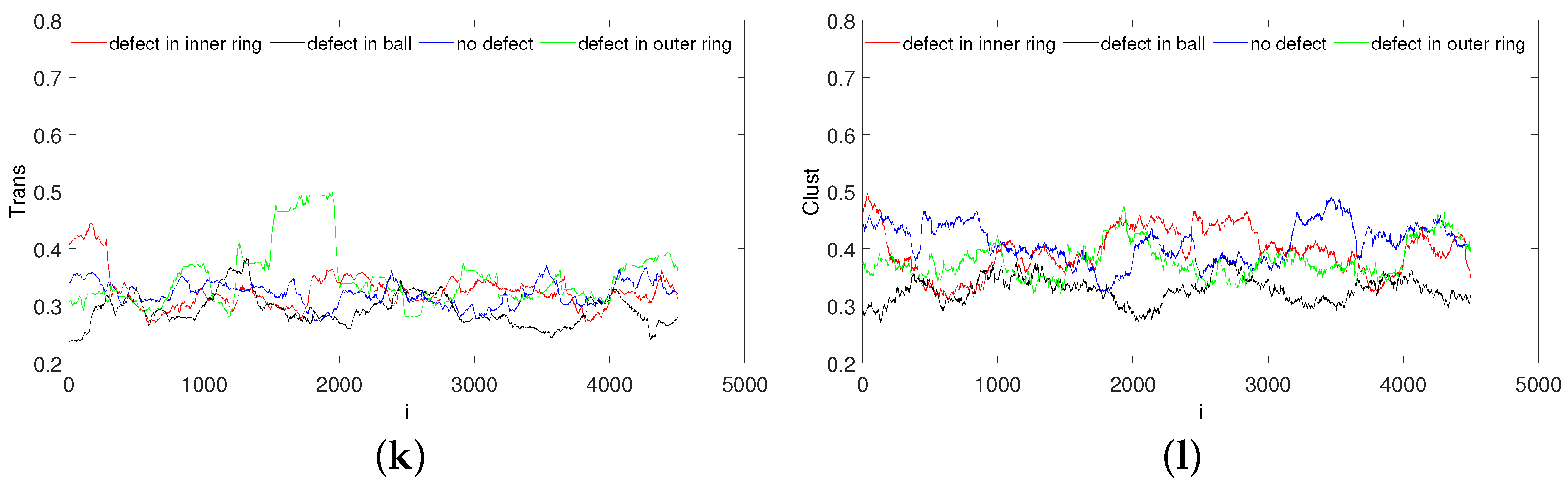
3. Results and Discussion
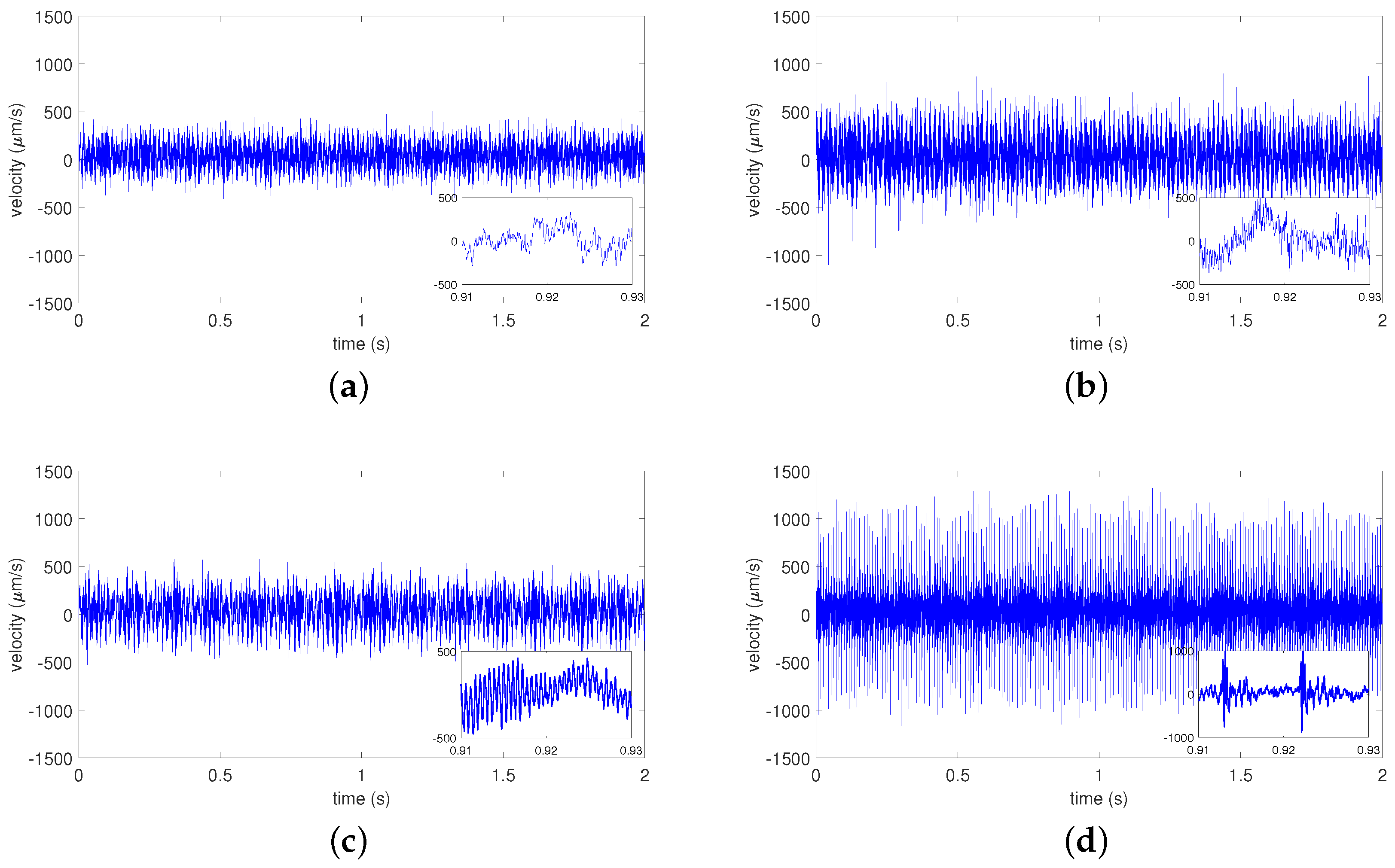
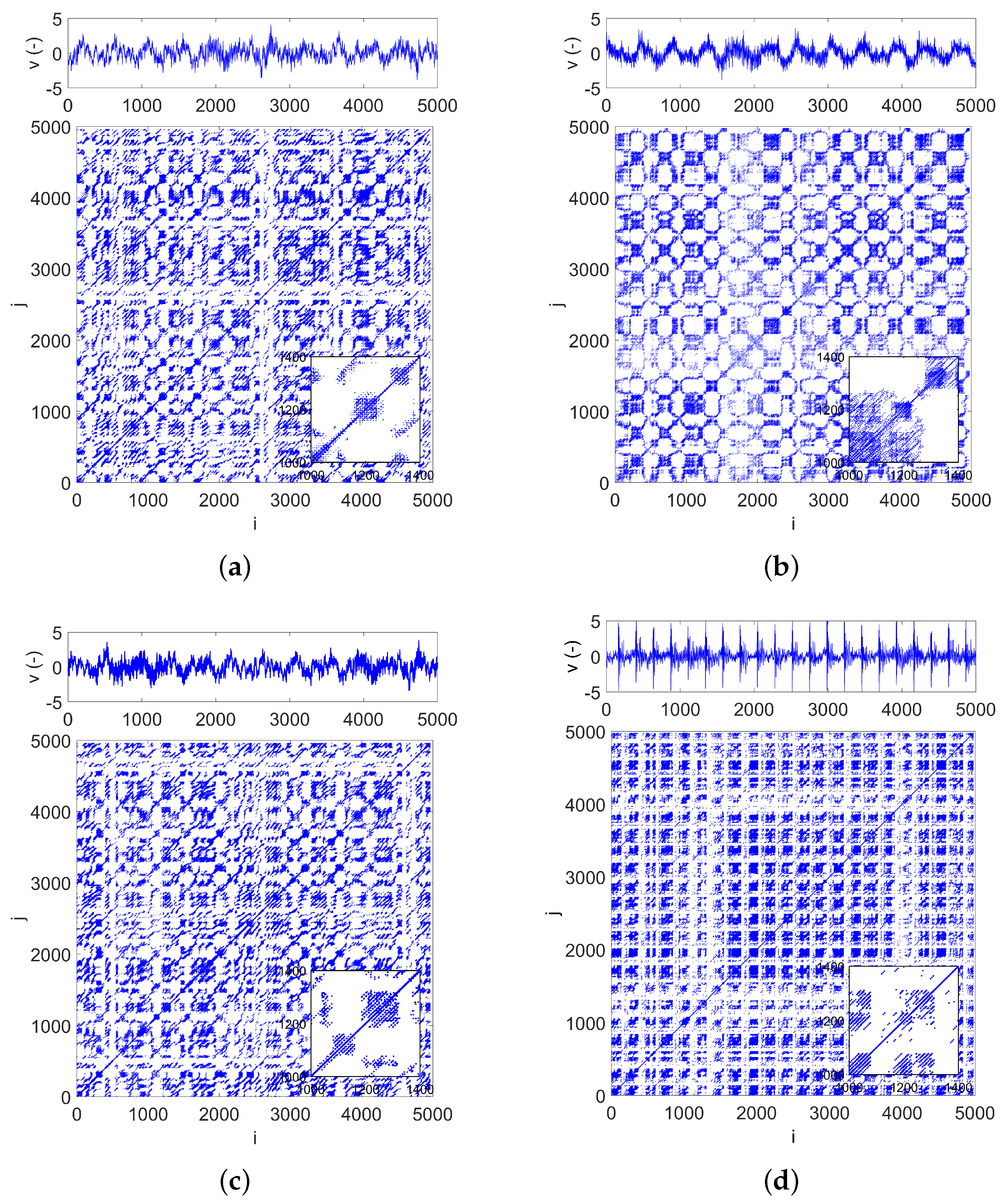
3.1. Measured Time Series
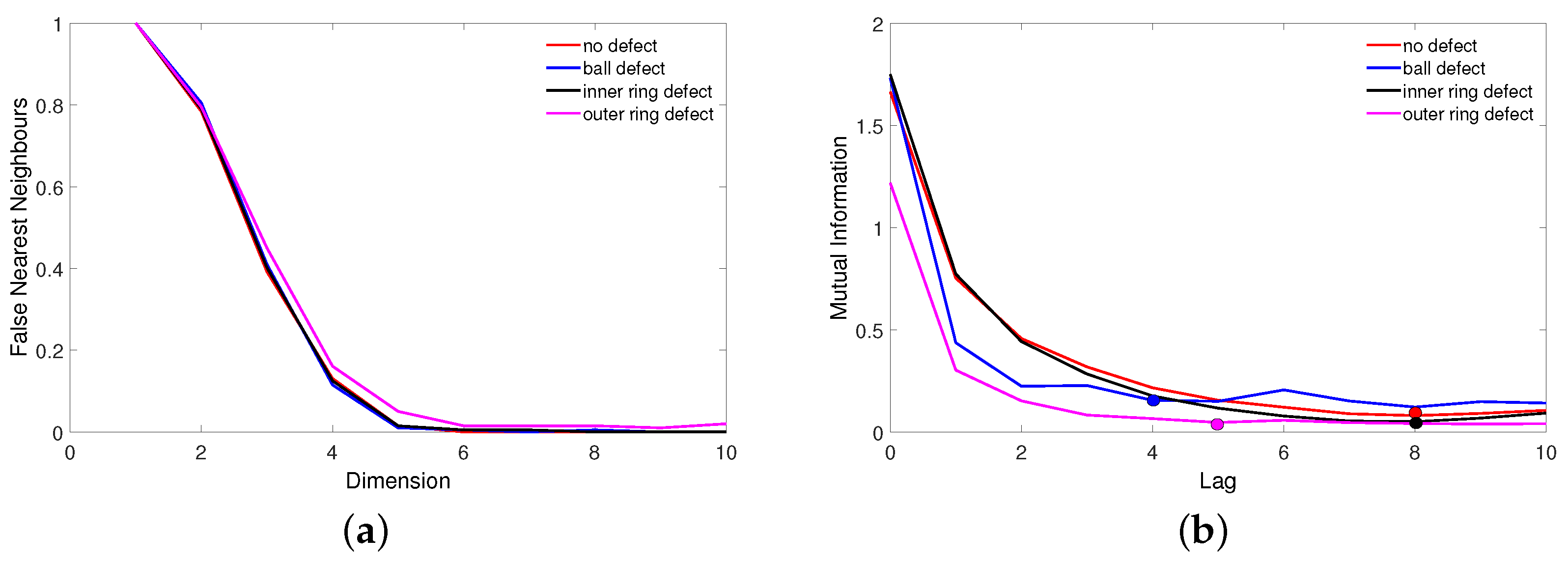
3.2. Recurrence Plot Analysis
- The recurrence plot is covered by a small overlap window of size w that slides with steps s,
- The time signal is divided into overlapping segments, from which the RP diagrams and RQA indicators are calculated.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, Q.; Guo, Y. Dynamic model of faulty rolling element bearing on double impact phenomenon. In Proceedings of the 2015 IEEE International Conference on Information and Automation, Lijiang, China, 8–10 August 2015; pp. 2017–2021. [Google Scholar] [CrossRef]
- Patil, M.; Mathew, J.; Rajendrakumar, P.; Desai, S. A theoretical model to predict the effect of localized defect on vibrations associated with ball bearing. Int. J. Mech. Sci. 2010, 52, 1193–1201. [Google Scholar] [CrossRef]
- Petersen, D.; Howard, C.; Sawalhi, N.; Moazen Ahmadi, A.; Singh, S. Analysis of bearing stiffness variations, contact forces and vibrations in radially loaded double row rolling element bearings with raceway defects. Mech. Syst. Signal Process. 2015, 50–51, 139–160. [Google Scholar] [CrossRef]
- Saucedo-Dorantes, J.J.; Zamudio-Ramirez, I.; Cureno-Osornio, J.; Osornio-Rios, R.A.; Antonino-Daviu, J.A. Condition Monitoring Method for the Detection of Fault Graduality in Outer Race Bearing Based on Vibration-Current Fusion, Statistical Features and Neural Network. Appl. Sci. 2021, 11, 8033. [Google Scholar] [CrossRef]
- Moazen Ahmadi, A.; Petersen, D.; Howard, C. A nonlinear dynamic vibration model of defective bearings—The importance of modelling the finite size of rolling elements. Mech. Syst. Signal Process. 2015, 52–53, 309–326. [Google Scholar] [CrossRef]
- Moazen-Ahmadi, A.; Howard, C.Q. A defect size estimation method based on operational speed and path of rolling elements in defective bearings. J. Sound Vib. 2016, 385, 138–148. [Google Scholar] [CrossRef]
- Minervini, M.; Mognaschi, M.E.; Di Barba, P.; Frosini, L. Convolutional Neural Networks for Automated Rolling Bearing Diagnostics in Induction Motors Based on Electromagnetic Signals. Appl. Sci. 2021, 11, 7878. [Google Scholar] [CrossRef]
- Cheng, L.; Lu, J.; Li, S.; Ding, R.; Xu, K.; Li, X. Fusion Method and Application of Several Source Vibration Fault Signal Spatio-Temporal Multi-Correlation. Appl. Sci. 2021, 11, 4318. [Google Scholar] [CrossRef]
- Shalalfeh, L.; AlShalalfeh, A. Early Warning Signals for Bearing Failure Using Detrended Fluctuation Analysis. Appl. Sci. 2020, 10, 8489. [Google Scholar] [CrossRef]
- Tandon, N.; Choudhury, A. A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings. Tribol. Int. 1999, 32, 469–480. [Google Scholar] [CrossRef]
- Ferrando Chacon, J.L.; Kappatos, V.; Balachandran, W.; Gan, T.H. A novel approach for incipient defect detection in rolling bearings using acoustic emission technique. Appl. Acoust. 2015, 89, 88–100. [Google Scholar] [CrossRef]
- Singh, S.; Howard, C.Q.; Hansen, C.H. An extensive review of vibration modelling of rolling element bearings with localised and extended defects. J. Sound Vib. 2015, 357, 300–330. [Google Scholar] [CrossRef]
- McFadden, P.; Smith, J. Model for the vibration produced by a single point defect in a rolling element bearing. J. Sound Vib. 1984, 96, 69–82. [Google Scholar] [CrossRef]
- Eftekharnejad, B.; Carrasco, M.; Charnley, B.; Mba, D. The application of spectral kurtosis on Acoustic Emission and vibrations from a defective bearing. Mech. Syst. Signal Process. 2011, 25, 266–284. [Google Scholar] [CrossRef]
- Bastami, A.R.; Vahid, S. A comprehensive evaluation of the effect of defect size in rolling element bearings on the statistical features of the vibration signal. Mech. Syst. Signal Process. 2021, 151, 107334. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, M. An adaptive SK technique and its application for fault detection of rolling element bearings. Mech. Syst. Signal Process. 2011, 25, 1750–1764. [Google Scholar] [CrossRef]
- Junsheng, C.; Dejie, Y.; Yu, Y. A fault diagnosis approach for roller bearings based on EMD method and AR model. Mech. Syst. Signal Process. 2006, 20, 350–362. [Google Scholar] [CrossRef]
- Jiang, F.; Zhu, Z.; Li, W. An Improved VMD with Empirical Mode Decomposition and its application in incipient fault detection of rolling bearing. IEEE Access 2018, 6, 44483–44493. [Google Scholar] [CrossRef]
- Abbasion, S.; Rafsanjani, A.; Farshidianfar, A.; Irani, N. Rolling element bearings multi-fault classification based on the wavelet denoising and support vector machine. Mech. Syst. Signal Process. 2007, 21, 2933–2945. [Google Scholar] [CrossRef]
- Nikolaou, N.; Antoniadis, I. Rolling element bearing fault diagnosis using wavelet packets. NDT E Int. 2002, 35, 197–205. [Google Scholar] [CrossRef]
- Butler, D. The Shock-pulse method for the detection of damaged rolling bearings. Non-Destr. Test. 1973, 6, 92–95. [Google Scholar] [CrossRef]
- Zhen, L.; Zhengjia, H.; Yanyang, Z.; Xuefeng, C. Bearing condition monitoring based on shock pulse method and improved redundant lifting scheme. Math. Comput. Simul. 2008, 79, 318–338. [Google Scholar] [CrossRef]
- Long, J.; Qin, Y.; Yang, Z.; Huang, Y.; Li, C. Discriminative feature learning using a multiscale convolutional capsule network from attitude data for fault diagnosis of industrial robots. Mech. Syst. Signal Process. 2023, 182, 109569. [Google Scholar] [CrossRef]
- Long, J.; Zhang, R.; Yang, Z.; Huang, Y.; Liu, Y.; Li, C. Self-Adaptation Graph Attention Network via Meta-Learning for Machinery Fault Diagnosis with Few Labeled Data. IEEE Trans. Instrum. Meas. 2022, 71, 1–11. [Google Scholar] [CrossRef]
- Wu, Y.; Jiang, B.; Wang, Y. Incipient winding fault detection and diagnosis for squirrel-cage induction motors equipped on CRH trains. ISA Trans. 2020, 99, 488–495. [Google Scholar] [CrossRef]
- Bo, L.; Liu, X.; Xu, G. Intelligent Diagnostics for Bearing Faults Based on Integrated Interaction of Nonlinear Features. IEEE Trans. Ind. Inform. 2020, 16, 1111–1119. [Google Scholar] [CrossRef]
- Qian, Y.; Yan, R.; Hu, S. Bearing degradation evaluation using Recurrence Quantification Analysis and Kalman Filter. IEEE Trans. Instrum. Meas. 2014, 63, 2599–2610. [Google Scholar] [CrossRef]
- Ciecieląg, K.; Skoczylas, A.; Matuszak, J.; Zaleski, K.; Kecik, K. Defect detection and localization in polymer composites based on drilling force signal by recurrence analysis. Measurement 2021, 186, 110126. [Google Scholar] [CrossRef]
- Kecik, K.; Ciecieląg, K.; Zaleski, K. Damage detection by recurrence and entropy methods on the basis of time series measured during composite milling. Int. J. Adv. Manuf. Technol. 2020, 111, 1433–3015. [Google Scholar] [CrossRef]
- Zbilut, J.P.; Webber, C.L. Embeddings and delays as derived from quantification of recurrence plots. Phys. Lett. A 1992, 171, 199–203. [Google Scholar] [CrossRef]
- Marwan, N.; Carmen Romano, M.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Marwan, N.; Kurths, J.; Foerster, S. Analysing spatially extended high-dimensional dynamics by recurrence plots. Phys. Lett. A 2015, 379, 894–900. [Google Scholar] [CrossRef]
- Gao, J.; Cai, H. On the structures and quantification of recurrence plots. Phys. Lett. A 2000, 270, 75–87. [Google Scholar] [CrossRef]
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134–1140. [Google Scholar] [CrossRef] [PubMed]
- Marwan, N. Command Line Recurrence Plot. 2006. Available online: http://tocsy.pik-potsdam.de/commandline-rp.php (accessed on 10 April 2022).
- Webber, C.L.; Marwan, J. Recurrence Quantification Analysis: Theory and Best Practices; Springer: Cham, Switzerland, 2015; Volume XIV, p. 421. [Google Scholar]
- Marwan, J. Cross Recurrence Plot Toolbox for Matlab, Reference Manual. 2021. Version 5.22, Release 33. Available online: http://tocsy.pik-potsdam.de/crp.php (accessed on 10 April 2022).


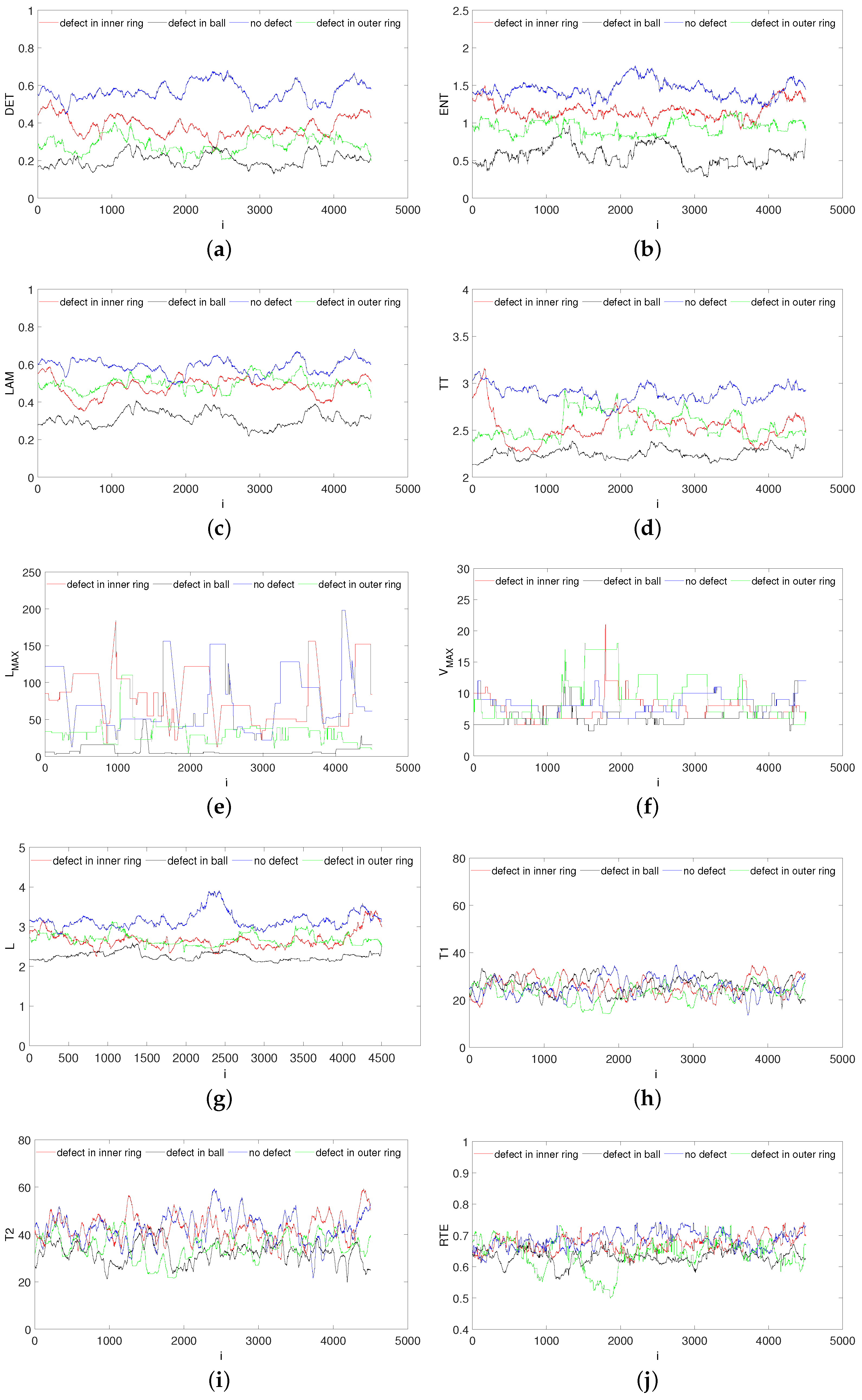
| Quantification | Equation | Description |
|---|---|---|
| Recurrence Rate | Recurrence point density. | |
| Determinism | Portion of recurrence points forming diagonal lines. | |
| Entropy | Entropy of the frequency distribution of the diagonal lines. | |
| Laminarity | Amount of recurrence points that form vertical lines. | |
| Trapping Time | Average length of vertical lines. | |
| Longest diagonal line | Maximal line length in the diagonal direction. | |
| Longest vertical line | Maximal length of the vertical structures. | |
| Averaged diagonal line L | Average diagonal line length. | |
| Recurrences time | Recurrence time of the 1st Poincare recurrence. | |
| Recurrences time | Recurrence time of the 2nd Poincare recurrence. | |
| Recurrence time entropy | Shannon entropy of the recurrence times. | |
| Transitivity | Local recurrence rate. | |
| Clustering coefficient | The probability that two recurrence states are neighbors. |
| Location of Defect | Embedding Dimension, m | Lag, d | Recurrence Rate, RR | Threshold, |
|---|---|---|---|---|
| No defect | 6 | 8 | 0.02 | 0.88 |
| Ball | 6 | 4 | 0.02 | 0.80 |
| Outer ring | 6 | 5 | 0.02 | 0.61 |
| Inner ring | 6 | 8 | 0.02 | 0.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kecik, K.; Smagala, A.; Lyubitska, K. Ball Bearing Fault Diagnosis Using Recurrence Analysis. Materials 2022, 15, 5940. https://doi.org/10.3390/ma15175940
Kecik K, Smagala A, Lyubitska K. Ball Bearing Fault Diagnosis Using Recurrence Analysis. Materials. 2022; 15(17):5940. https://doi.org/10.3390/ma15175940
Chicago/Turabian StyleKecik, Krzysztof, Arkadiusz Smagala, and Kateryna Lyubitska. 2022. "Ball Bearing Fault Diagnosis Using Recurrence Analysis" Materials 15, no. 17: 5940. https://doi.org/10.3390/ma15175940
APA StyleKecik, K., Smagala, A., & Lyubitska, K. (2022). Ball Bearing Fault Diagnosis Using Recurrence Analysis. Materials, 15(17), 5940. https://doi.org/10.3390/ma15175940









