Hybrid Density Functional Investigation of Cu Doping Impact on the Electronic Structures and Optical Characteristics of TiO2 for Improved Visible Light Absorption
Abstract
:1. Introduction
2. Materials and Methods
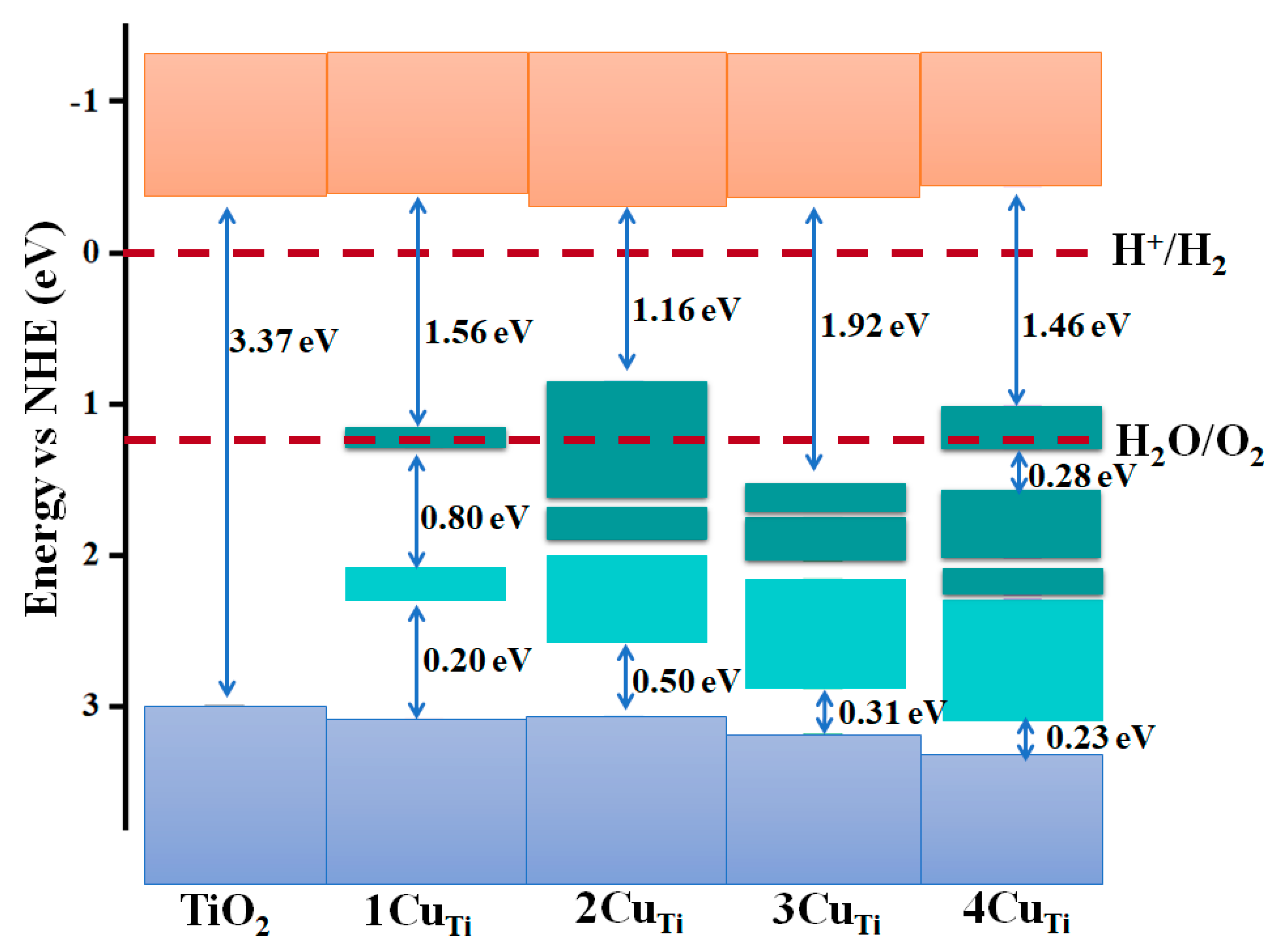
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Li, K.; Peng, B.; Peng, T. Recent Advances in Heterogeneous Photocatalytic CO2 Conversion to Solar Fuels. ACS Catal. 2016, 6, 7485–7527. [Google Scholar] [CrossRef]
- Byrne, C.; Subramanian, G.; Pillai, S.C. Recent Advances in Photocatalysis for Environmental Applications. J. Environ. Chem. Eng. 2018, 6, 3531–3555. [Google Scholar] [CrossRef]
- Jafar, T.; Moharreri, E.; Amin, A.S.; Miao, R.; Song, W.; Suib, S.L. Photocatalytic Water Splitting—The Untamed Dream: A Review of Recent Advances. Molecules 2016, 21, 900. [Google Scholar] [CrossRef] [PubMed]
- Jia, J.; Seitz, L.C.; Benck, J.D.; Huo, Y.; Chen, Y.; Ng, J.W.D.; Bilir, T.; Harris, J.S.; Jaramillo, T.F. Solar water splitting by photovoltaic-electrolysis with a solar-to-hydrogen efficiency over 30%. Nat. Commun. 2016, 7, 13237. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Domen, K. Particulate Photocatalysts for Light-Driven Water Splitting: Mechanisms, Challenges, and Design Strategies. Chem. Rev. 2020, 120, 919–985. [Google Scholar] [CrossRef]
- Etacheri, V.; Di Valentin, C.; Schneider, J.; Bahnemann, D.; Pillai, S.C. Visible-light activation of TiO2 photocatalysts: Advances in theory and experiments. J. Photochem. Photobiol. C Photochem. Rev. 2015, 25, 1–29. [Google Scholar] [CrossRef]
- Xu, H.; Ouyang, S.; Liu, L.; Reunchan, P.; Umezawa, N.; Ye, J. Recent advances in TiO2-based photocatalysis. J. Mater. Chem. A 2014, 2, 12642–12661. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Kudo, A. Visible light responsive photocatalysts developed by substitution with metal cations aiming at artificial photosynthesis Front. Energy 2021, 15, 568–576. [Google Scholar]
- Valero-Romero, M.J.; Santaclara, J.G.; Oar-Arteta, L.; van Koppen, L.; Osadchii, D.Y.; Gascon, J.; Kapteijn, F. Photocatalytic properties of TiO2 and Fe-doped TiO2 prepared by metal organic framework-mediated synthesis. Chem. Eng. J. 2019, 360, 75–88. [Google Scholar] [CrossRef]
- Dozzi, M.V.; Selli, E. Doping TiO2 with p-block elements: Effects on photocatalytic activity. J. Photochem. Photobiol. C 2013, 14, 13–28. [Google Scholar] [CrossRef]
- Piskunov, S.; Lisovski, O.; Begens, J.; Bocharov, D.; Zhukovskii, Y.F.; Wessel, M.; Spohr, E. C-, N-, S-, and Fe-Doped TiO2 and SrTiO3 Nanotubes for Visible-Light-Driven Photocatalytic Water Splitting: Prediction from First Principles. J. Phys. Chem. C 2015, 119, 18686. [Google Scholar] [CrossRef]
- Boningari, T.; Inturi, S.N.R.; Suidan, M.; Smirniotis, P.G. Novel one-step synthesis of nitrogen-doped TiO2 by flame aerosol technique for visible-light photocatalysis: Effect of synthesis parameters and secondary nitrogen (N) source. Chem. Eng. J. 2018, 350, 324–334. [Google Scholar] [CrossRef]
- Prabakaran, E.; Pillay, K. Synthesis of N-doped ZnO nanoparticles with cabbage morphology as a catalyst for the efficient photocatalytic degradation of methylene blue under UV and visible light. RSC Adv. 2019, 9, 7509–7535. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Tade, M.O.; Shao, Z.P. Nitrogen-doped simple and complex oxides for photocatalysis: A review. Prog. Mater. Sci. 2018, 92, 33–63. [Google Scholar] [CrossRef]
- Bensouici, F.; Bououdina, M.; Dakhel, A.A.; Tala-Ighil, R.; Tounane, M.; Iratni, A.; Cai, W. Optical, structural and photocatalysis properties of Cu-doped TiO2 thin films. Appl. Surf. Sci. 2017, 395, 110. [Google Scholar] [CrossRef]
- Wang, Y.; Duan, W.; Liu, B.; Chen, X.; Yang, F.; Guo, J. The Effects of Doping Copper and Mesoporous Structure on Photocatalytic Properties of TiO2. J. Nanomater. 2014, 178152. [Google Scholar] [CrossRef]
- Mathew, S.; Ganguly, P.; Rhatigan, S.; Kumaravel, V.; Byrne, C.; Hinder, S.J.; Pillai, S.C. Cu-Doped TiO2: Visible Light Assisted Photocatalytic Antimicrobial Activity. Appl. Sci. 2018, 8, 2067. [Google Scholar] [CrossRef]
- Momeni, M.M.; Ghayeb, Y.; Ghonchegi, Z. Fabrication and characterization of copper doped TiO2 nanotube arrays by in situ electrochemical method as efficient visible-light photocatalyst. Ceram. Int. 2015, 41, 8735. [Google Scholar] [CrossRef]
- Turkten, N.; Cinar, Z.; Tomruk, A.; Bekbolet, M. Copper-doped TiO2 photocatalysts: Application to drinking water by humic matter degradation, Environ. Sci. Pollut. Res. 2019, 26, 36096. [Google Scholar] [CrossRef]
- Yoong, L.; Chong, F.K.; Dutta, B.K. Development of copper-doped TiO2 photocatalyst for hydrogen production under visible light. Energy 2009, 34, 1652–1661. [Google Scholar] [CrossRef]
- Xu, S.; Du, A.J.; Liu, J.; Ng, J.; Sun, D.D. Highly efficient CuO incorporated TiO2 nanotube photocatalyst for hydrogen production from water. Int. J. Hydrogen Energy 2011, 36, 6560–6568. [Google Scholar] [CrossRef]
- Yuzer, B.; Aydın, M.I.; Con, A.H.; Inan, H.; Can, S.; Selcuk, H.; Kadmi, Y. Photocatalytic, self-cleaning and antibacterial properties of Cu(II) doped TiO2. J. Environ. Manag. 2022, 302, 114023. [Google Scholar] [CrossRef] [PubMed]
- Nur, A.S.M.; Sultana, M.; Mondal, A.; Islam, S. A review on the development of elemental and codoped TiO2 photocatalysts for enhanced dye degradation under UV–vis irradiation. J. Water Process. Eng. 2022, 47, 102728. [Google Scholar] [CrossRef]
- Bhattacharyya, K.; Mane, G.P.; Rane, V.; Tripathi, A.K.; Tyagi, A.K. Selective CO2 Photoreduction with Cu-Doped TiO2 Photocatalyst: Delineating the Crucial Role of Cu-Oxidation State and Oxygen Vacancies. J. Phys. Chem. C 2021, 125, 1793–1810. [Google Scholar] [CrossRef]
- Dashora, A.; Patel, N.; Kothari, D.C.; Ahuja, B.L.; Miotello, A. Formation of an intermediate band in the energy gap of TiO2 by Cu–N-codoping: First principles study and experimental evidence. Sol. Energy Mater Sol. Cells 2014, 125, 120–126. [Google Scholar] [CrossRef]
- Liu, J.; Weng, M.; Li, S.; Chen, X.; Cen, J.; Jie, J.; Xiao, W.; Zheng, J.; Pan, F. High-Throughput HSE Study on the Doping Effect in Anatase TiO2. Phys. Chem. Chem. Phys. 2020, 22, 39–53. [Google Scholar] [CrossRef]
- Khan, M.; Zeng, Y. Improving the photo-response of TiO2 by tri-doping: A DFT based atomistic study, Mater. Res. Express 2019, 6, 115510. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, R.; Li, J.; Li, L.; Lin, S. First-principles study on transition metal-doped anatase TiO2. Nanoscale Res. Lett. 2014, 9, 46. [Google Scholar] [CrossRef]
- Guo, M.; Du, J. First-principles study of electronic structures and optical properties of Cu, Ag, and Au-doped anatase TiO2. Physica. B 2012, 407, 1003–1007. [Google Scholar] [CrossRef]
- Navas, J.; Sanchez-Coronilla, A.; Aguilar, T.; Hernandez, N.C.; de los Santos, D.M.; Sanchez-Marquez, J.; Zorrilla, D.; Fernandez-Lorenzo, C.; Alcantaraa, R.; Martın-Callejaa, J. Experimental and theoretical study of the electronic properties of Cu-doped anatase TiO2. Phys. Chem. Chem. Phys. 2014, 16, 3835. [Google Scholar] [CrossRef]
- Zhang, H.; Yu, X.; McLeod, J.A.; Sun, X. First-principles study of Cu-doping and oxygen vacancy effects on TiO2 for water splitting. Chem. Phy.s Lett. 2014, 612, 106–110. [Google Scholar] [CrossRef]
- Khlyustova, A.; Sirotkin, N.; Kusova, T.; Kraev, A.; Titov, V.; Agafonov, A. Doped TiO2: The effect of doping elements on photocatalytic activity. Mater. Adv. 2020, 1, 1193. [Google Scholar] [CrossRef]
- Smidstrup, S.; Markussen, T.; Vancraeyveld, P.; Wellendorff, J.; Schneider, J.; Gunst, T.; Verstichel, B.; Stradi, D.; Khomyakov, P.A.; Vej-Hansen, U.G.; et al. QuantumATK: An integrated platform of electronic and atomic-scale modelling tools. J. Phys. Condens. Matter 2020, 32, 015901. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Van Setten, M.; Giantomassi, M.; Bousquet, E.; Verstraete, M.; Hamann, D.; Gonze, X.; Rignanese, G.-M. The PseudoDojo: Training and grading a 85 element optimized norm-conserving pseudopotential table. Comput. Phys. Commun. 2018, 226, 39–54. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Kanoun, M.-B.; Goumri-Said, S.; Schwingenschlögl, U.; Manchon, A. Magnetism in Sc-doped ZnO with zinc vacancies: A hybrid density functional and GGA+U approaches. Chem. Phys. Lett. 2012, 532, 96–99. [Google Scholar] [CrossRef]
- Ikram, M.; Abid, N.; Haider, A.; Ul-Hamid, A.; Haider, J.; Shahzadi, J.; Nabgan, W.; Goumri-Said, S.; Butt, A.R.; Kanoun, M.B. Toward efficient dye degradation and the bactericidal behavior of Mo-doped La2O3 nanostructures. Nanoscale Adv. 2022, 4, 926–942. [Google Scholar] [CrossRef]
- Wooten, F. Optical Properties of Solids; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Kanoun, M.B.; Goumri-Said, S. Tailoring optoelectronic properties of monolayer transition metal dichalcogenide through alloying. Materialia 2020, 12, 100708. [Google Scholar] [CrossRef]
- Horn, M.; Schwerdtfeger, C.F.; Meagher, E.P. Refinement of the structure of anatase at several temperatures. Z. Kristallogr. 1972, 136, 273–281. [Google Scholar] [CrossRef]
- Shahzad, N.; Hussain, A.; Mustaf, N.; Ali, N.; Kanoun, M.B.; Goumri-Said, S. First principles study of the adsorption and dissociation mechanisms of H2S on a TiO2 anatase (001) surface. RSC Adv. 2016, 6, 7941. [Google Scholar] [CrossRef]
- Ahmed, F.; Kanoun, M.B.; Awada, C.; Jonin, C.; Brevet, P.-F. An Experimental and Theoretical Study on the Effect of Silver Nanoparticles Concentration on the Structural, Morphological, Optical, and Electronic Properties of TiO2 Nanocrystals. Crystals 2021, 11, 1488. [Google Scholar] [CrossRef]
- Janotti, A.; Van de Walle, C.G. Native point defects in ZnO. Phys. Rev. B 2007, 76, 165202. [Google Scholar] [CrossRef]
- Kanoun, M.B. Vacancy defects- and strain-tunable electronic structures and magnetism in two-dimensional MoTe2: Insight from first-principles calculations. Surf. Interfaces 2021, 27, 101442. [Google Scholar] [CrossRef]
- Xu, Y.; Schoonen, M.A.A. The absolute energy positions of conduction and valence bands of selected semiconducting minerals. Am. Mineral. 2000, 85, 543–556. [Google Scholar]
- Wang, J.; Huang, J.; Meng, J.; Li, Q.; Yang, J. Enhanced photoelectrochemical performance of anatase TiO2 for water splitting via surface codping. RSC Adv. 2017, 7, 39877. [Google Scholar] [CrossRef]
- Chen, S.; Takata, T.; Domen, K. Particulate photocatalysts for overall water splitting. Nat. Rev. Mater. 2017, 2, 17050. [Google Scholar] [CrossRef]
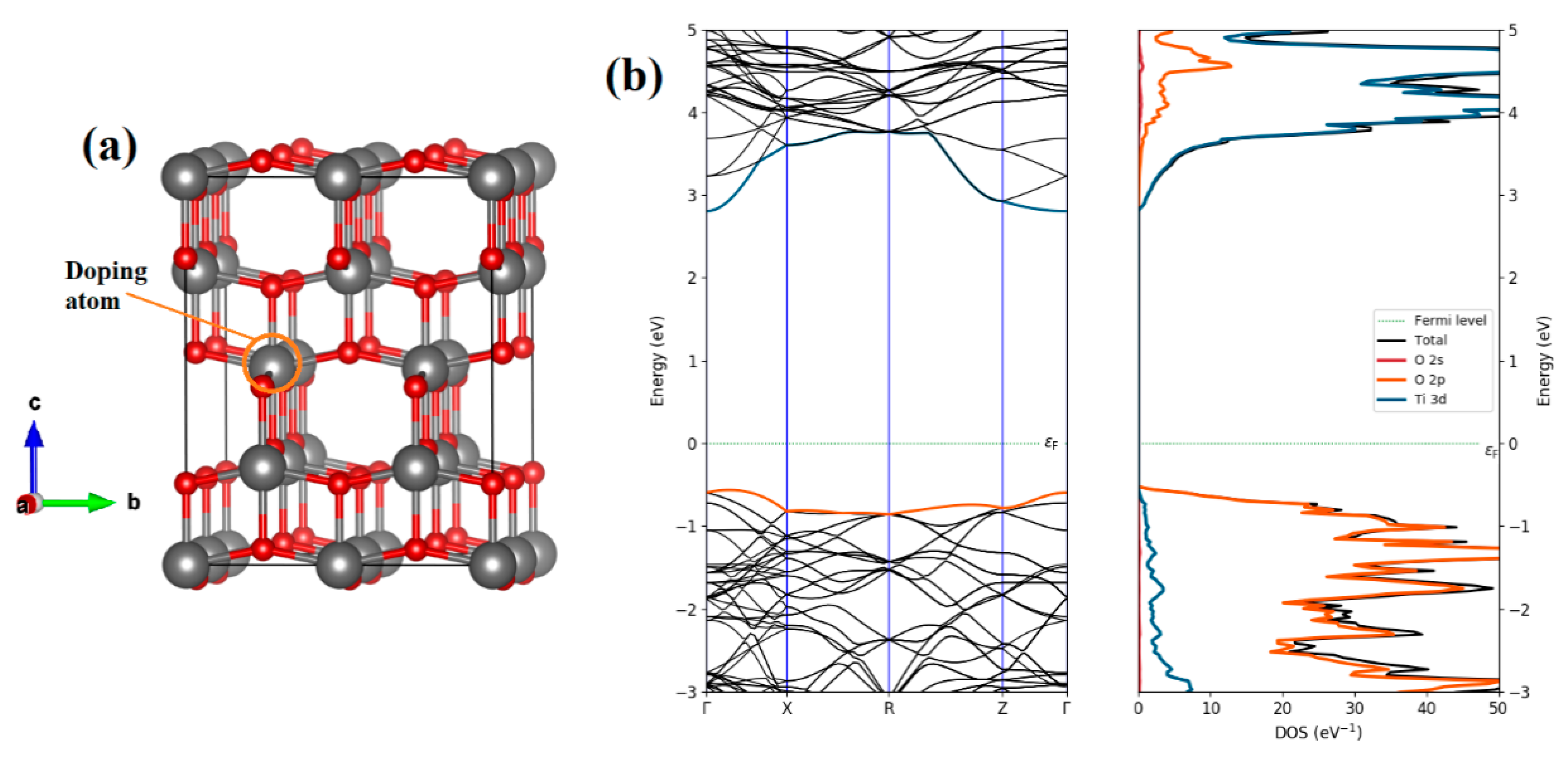
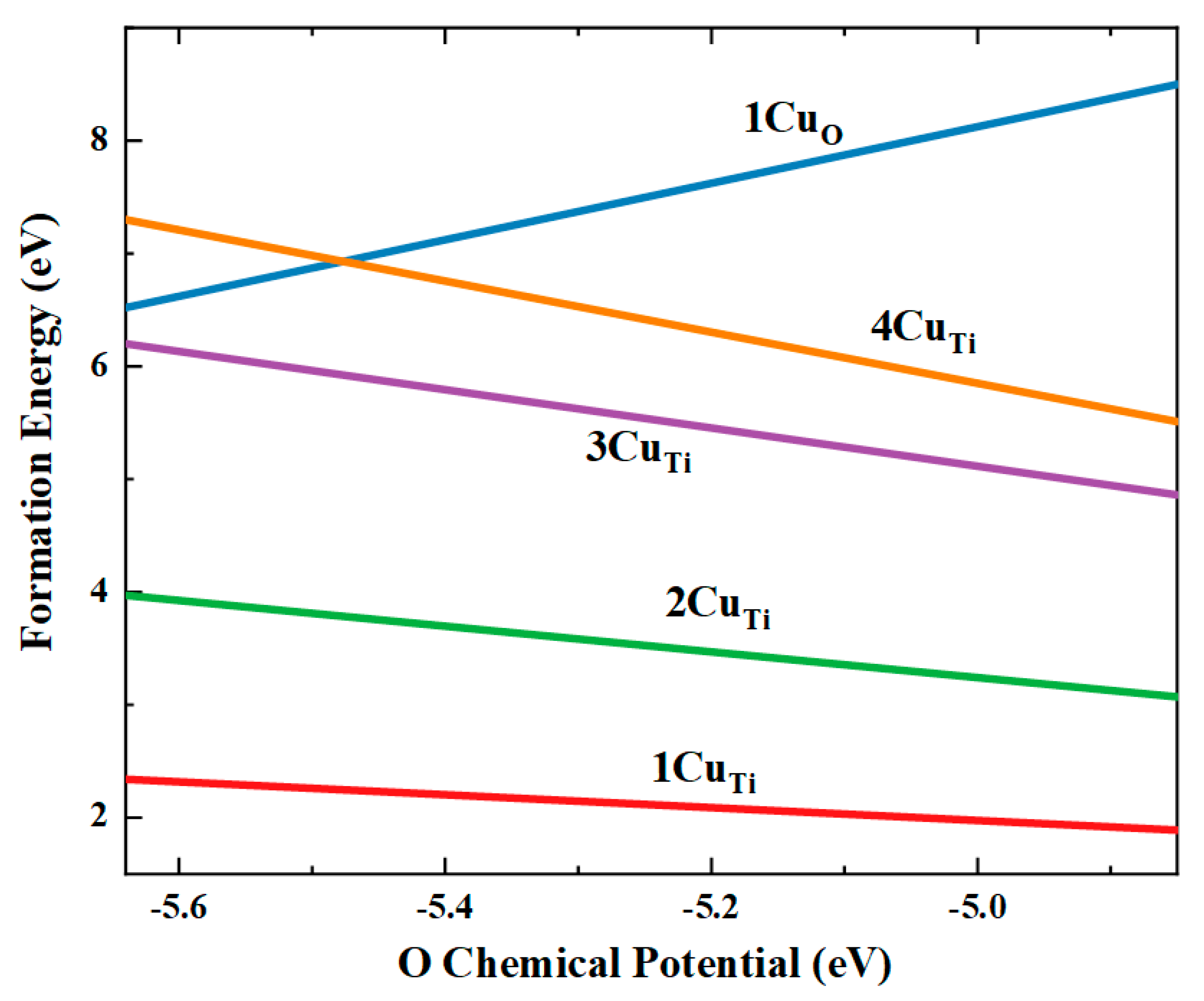
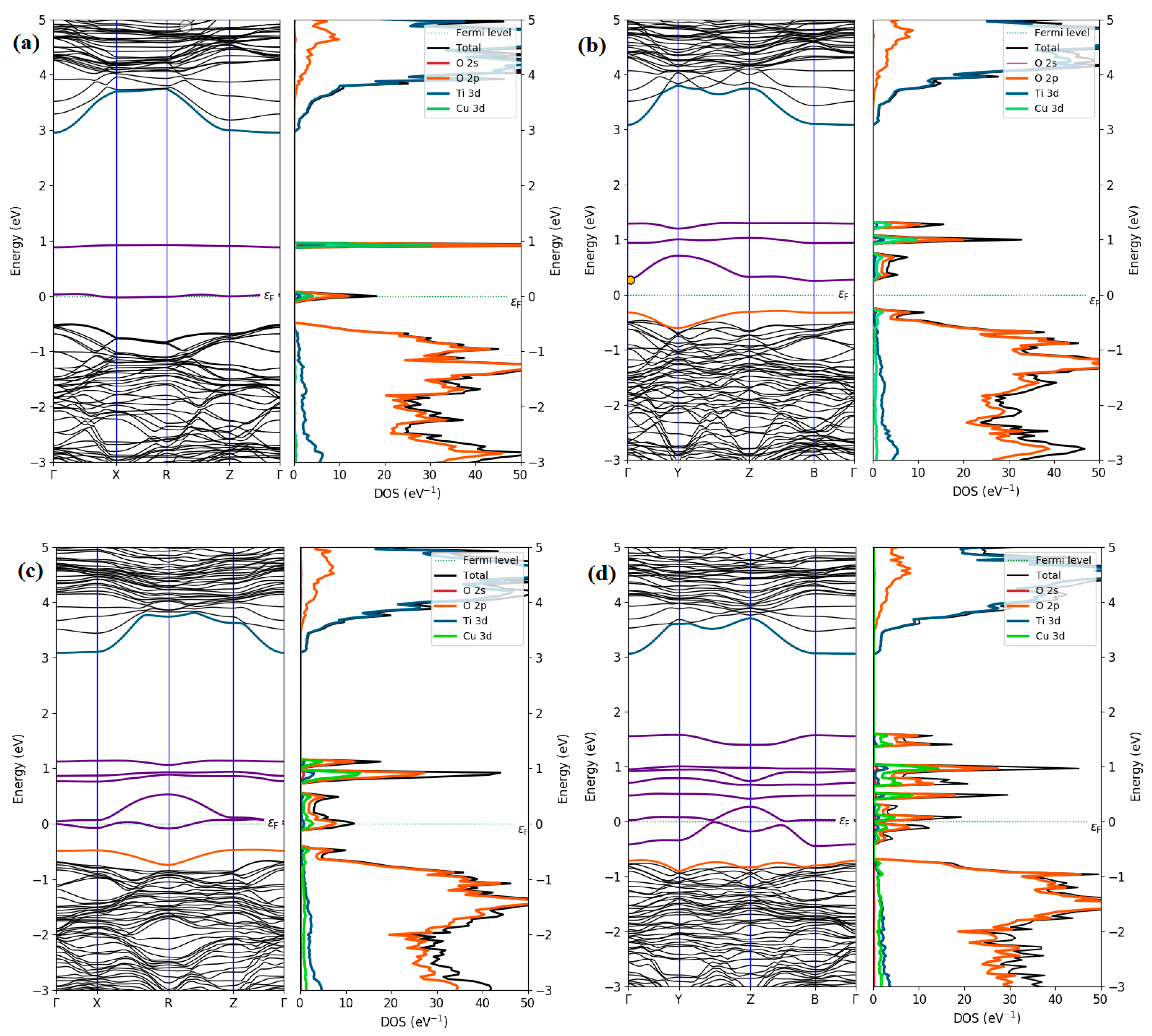
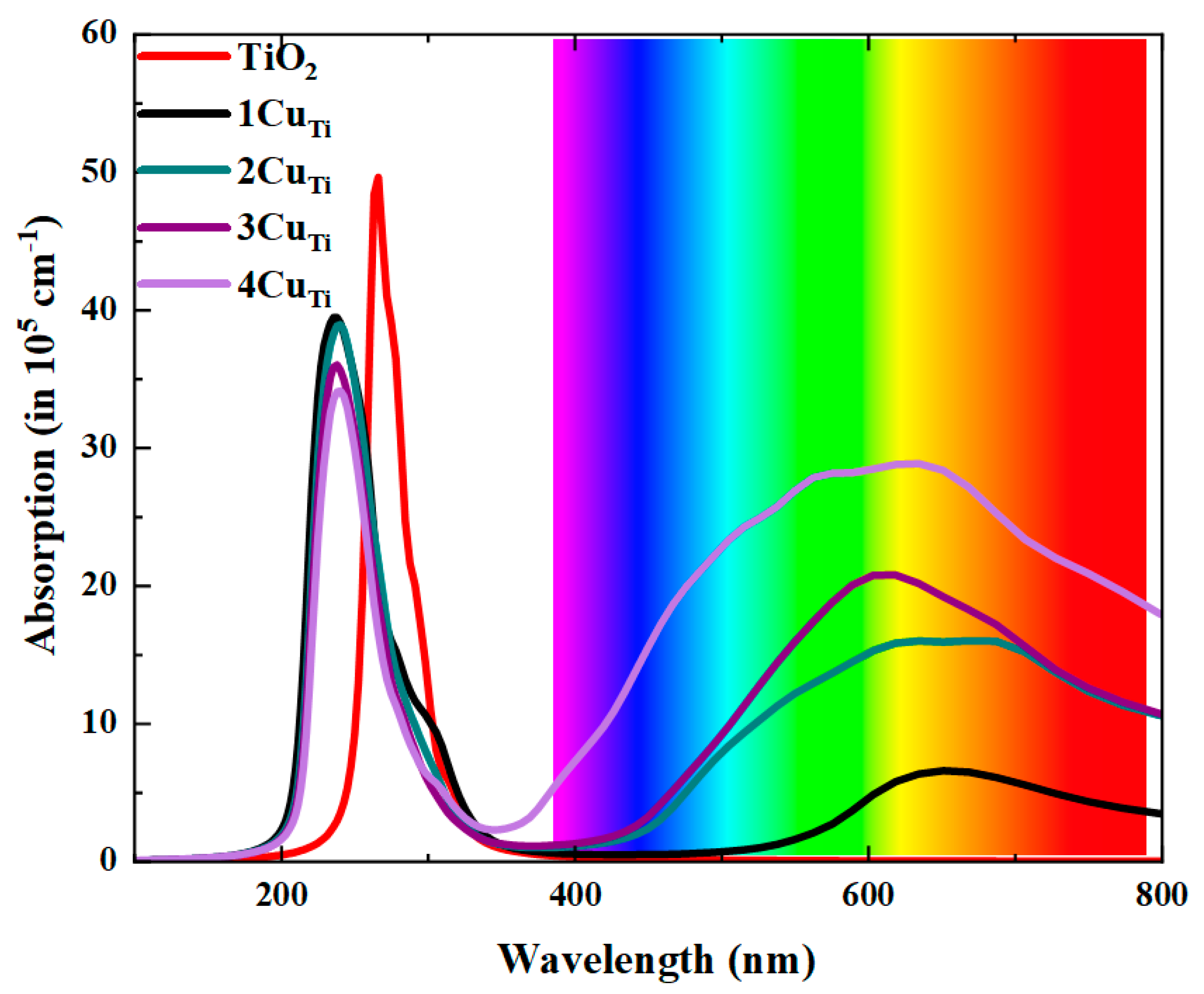
| a (Å) | c (Å) | V (Å3) | Ef (eV) | ||
|---|---|---|---|---|---|
| Ti-rich | O-rich | ||||
| 1CuTi | 3.785 | 9.456 | 541.95 | 2.34 | 1.89 |
| 1CuO | 3.812 | 9.430 | 548.17 | 6.52 | 8.50 |
| 2CuTi | 3.782 | 9.471 | 541.86 | 3.97 | 3.07 |
| 3CuTi | 3.782 | 9.428 | 540.05 | 6.20 | 4.86 |
| 4CuTi | 3.761 | 9.430 | 539.23 | 7.30 | 5.51 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanoun, M.B.; Alshoaibi, A.; Goumri-Said, S. Hybrid Density Functional Investigation of Cu Doping Impact on the Electronic Structures and Optical Characteristics of TiO2 for Improved Visible Light Absorption. Materials 2022, 15, 5645. https://doi.org/10.3390/ma15165645
Kanoun MB, Alshoaibi A, Goumri-Said S. Hybrid Density Functional Investigation of Cu Doping Impact on the Electronic Structures and Optical Characteristics of TiO2 for Improved Visible Light Absorption. Materials. 2022; 15(16):5645. https://doi.org/10.3390/ma15165645
Chicago/Turabian StyleKanoun, Mohammed Benali, Adil Alshoaibi, and Souraya Goumri-Said. 2022. "Hybrid Density Functional Investigation of Cu Doping Impact on the Electronic Structures and Optical Characteristics of TiO2 for Improved Visible Light Absorption" Materials 15, no. 16: 5645. https://doi.org/10.3390/ma15165645
APA StyleKanoun, M. B., Alshoaibi, A., & Goumri-Said, S. (2022). Hybrid Density Functional Investigation of Cu Doping Impact on the Electronic Structures and Optical Characteristics of TiO2 for Improved Visible Light Absorption. Materials, 15(16), 5645. https://doi.org/10.3390/ma15165645







