A New Stored Energy Model Based on Plastic Work of Back Stress during Cyclic Loading in Polycrystalline Metal
Abstract
:1. Introduction
- The stored energy Es is only a small part of the total plastic work Wp: only 1% to 15% for the pure metals [8].
2. Relationship between Stored Energy and Back Stress
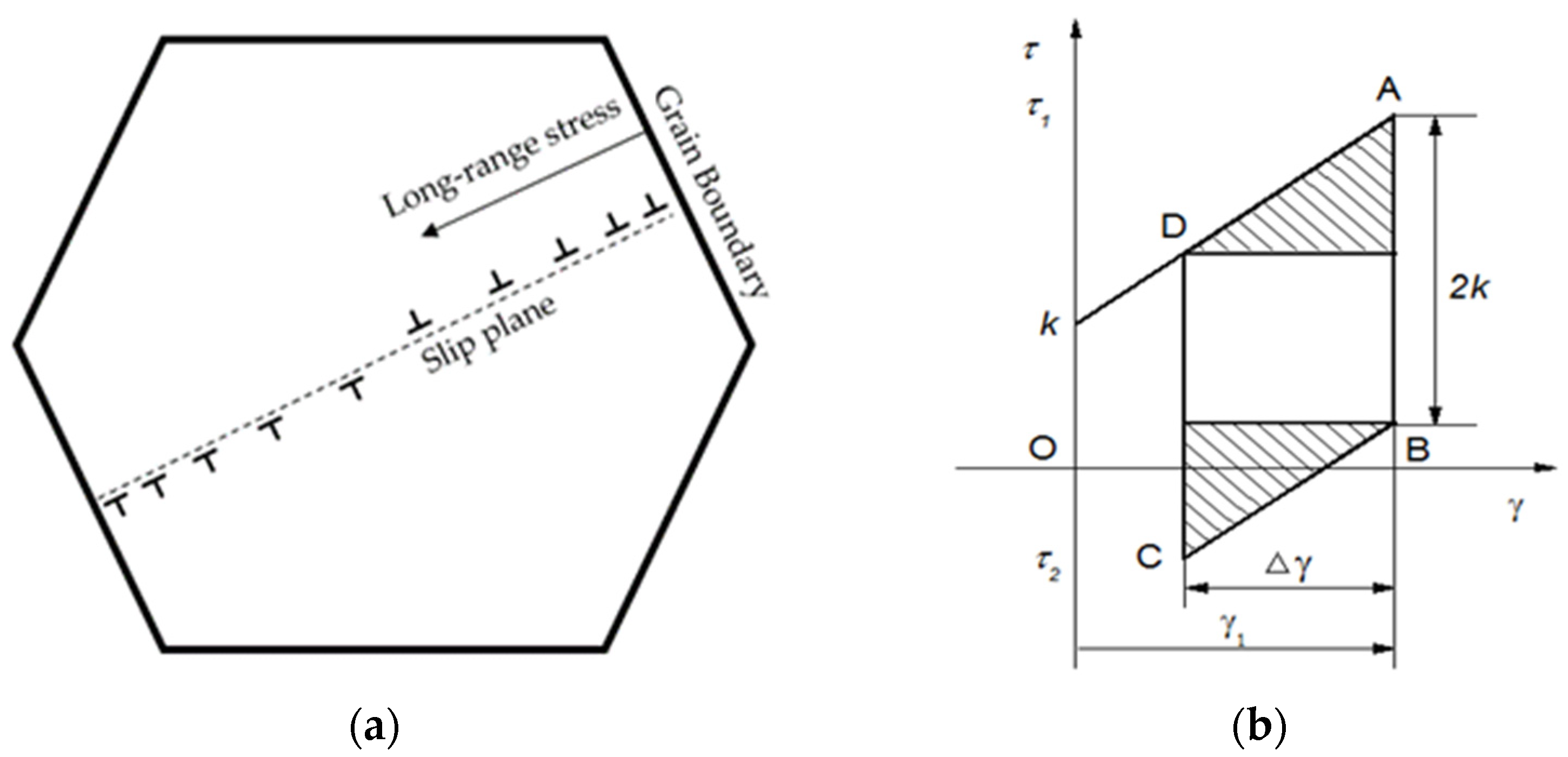
2.1. Relationship between ESR and Xinter
2.2. Relationship between ESD and Xintra
3. Plastic Work of Back Stress during Cyclic Loading
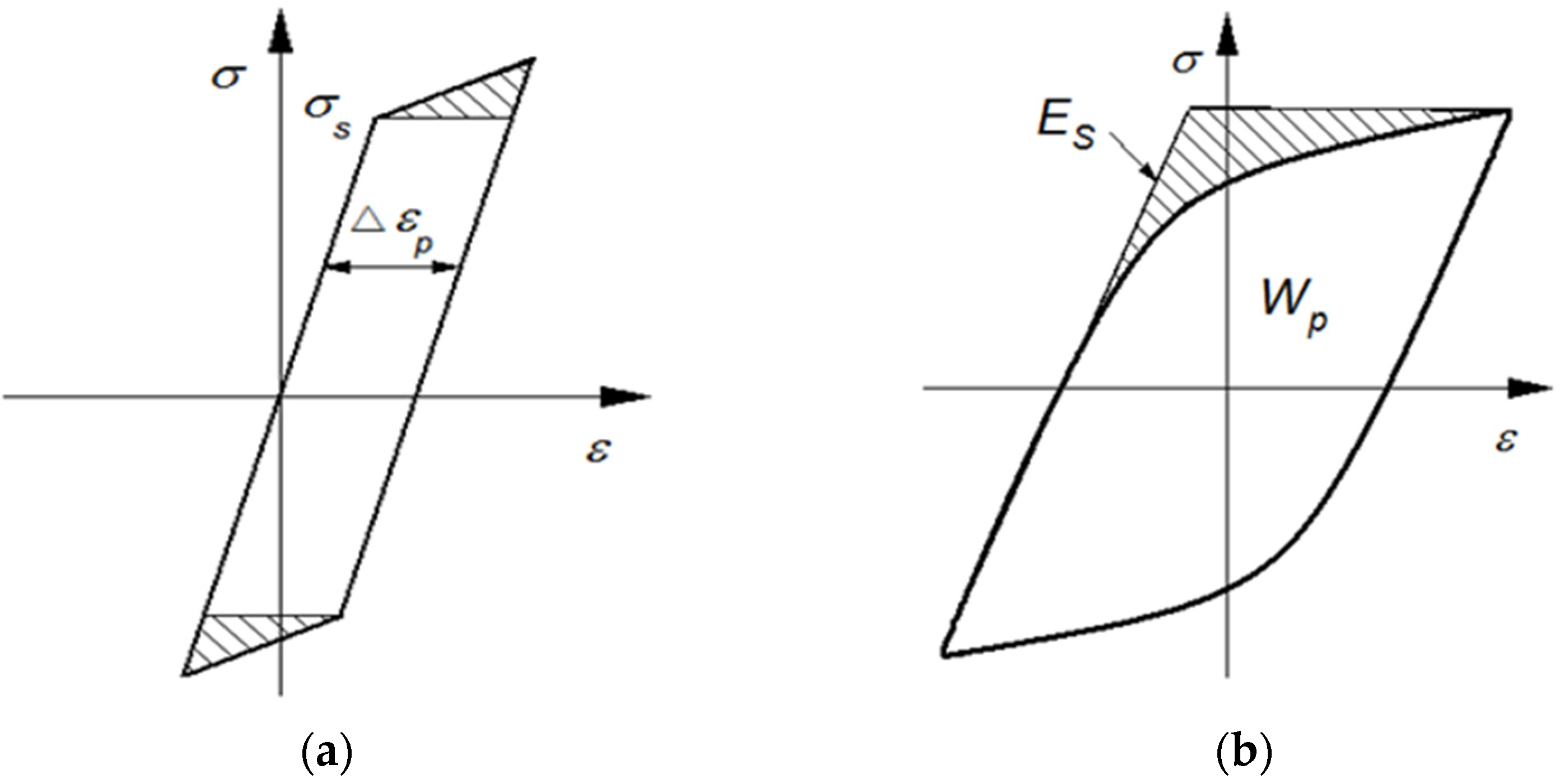
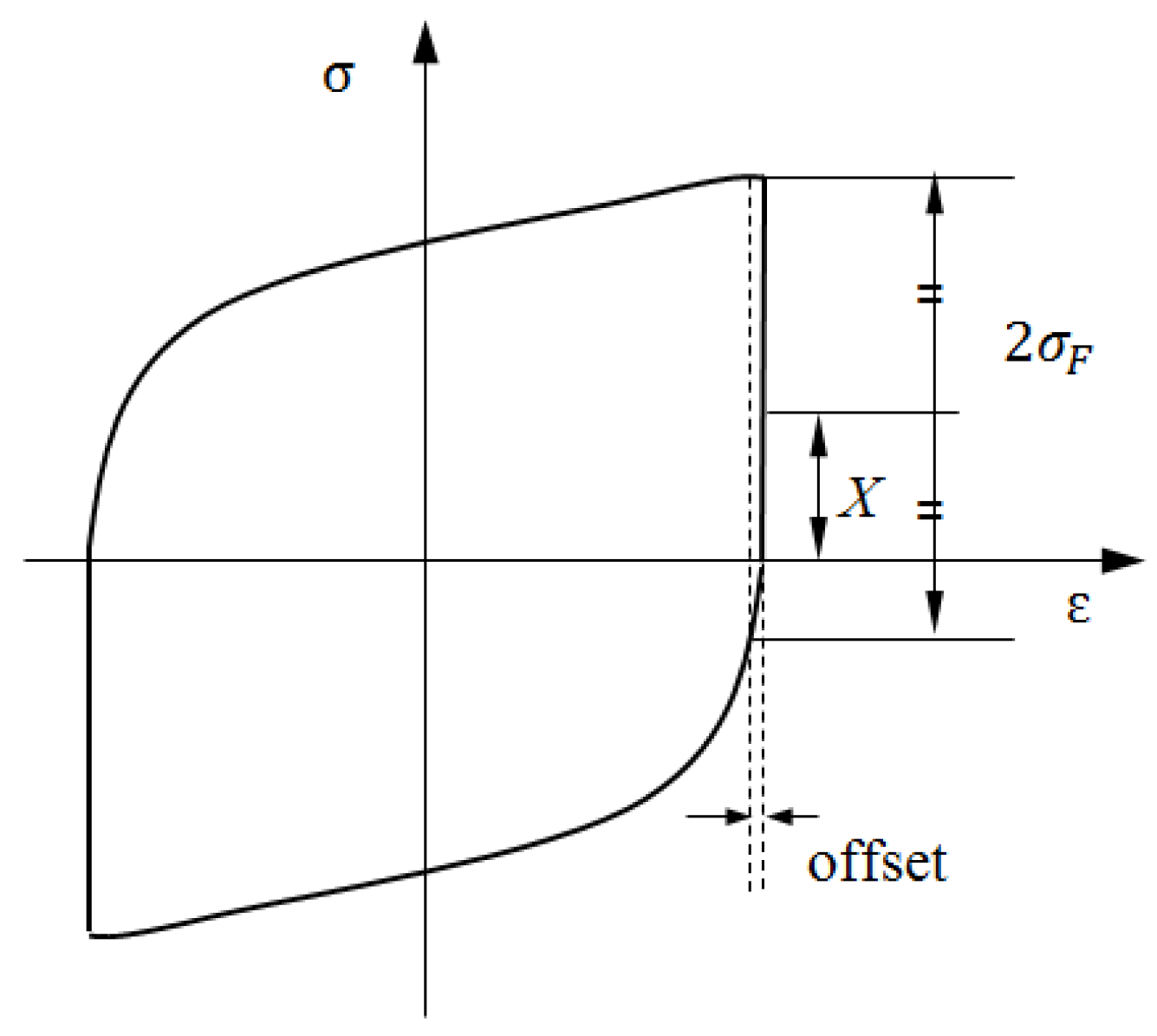
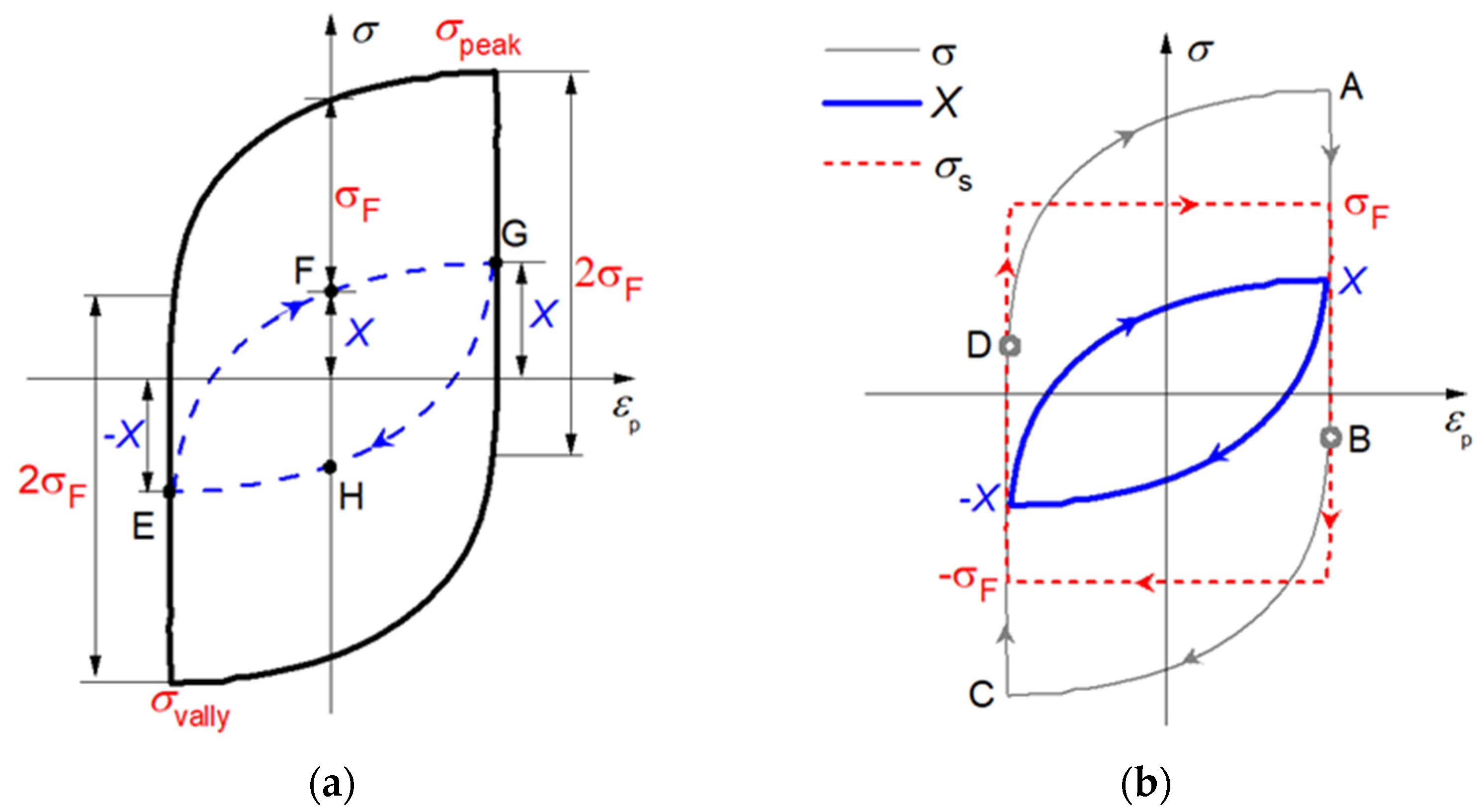
3.1. Hysteresis Loop of Back Stress
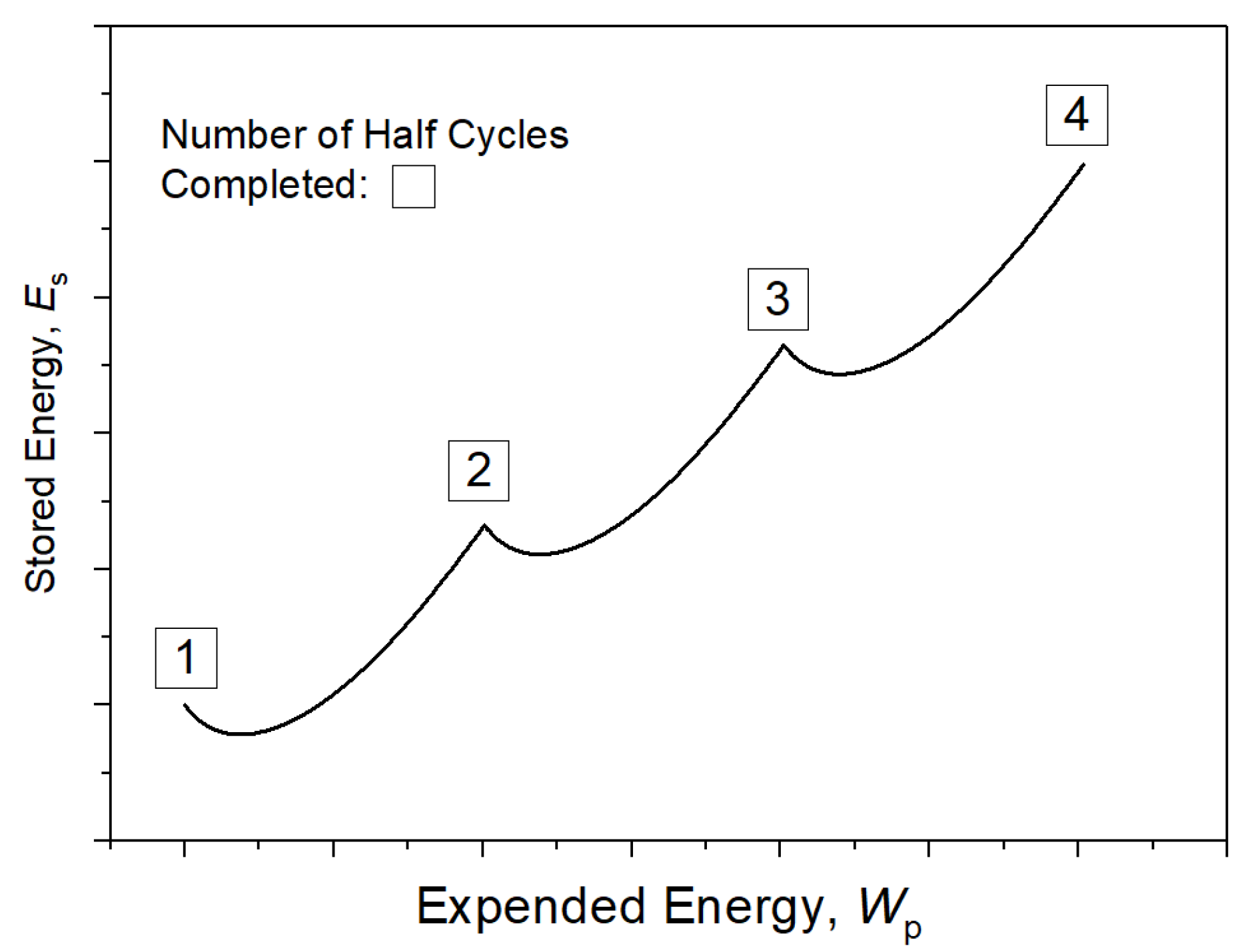
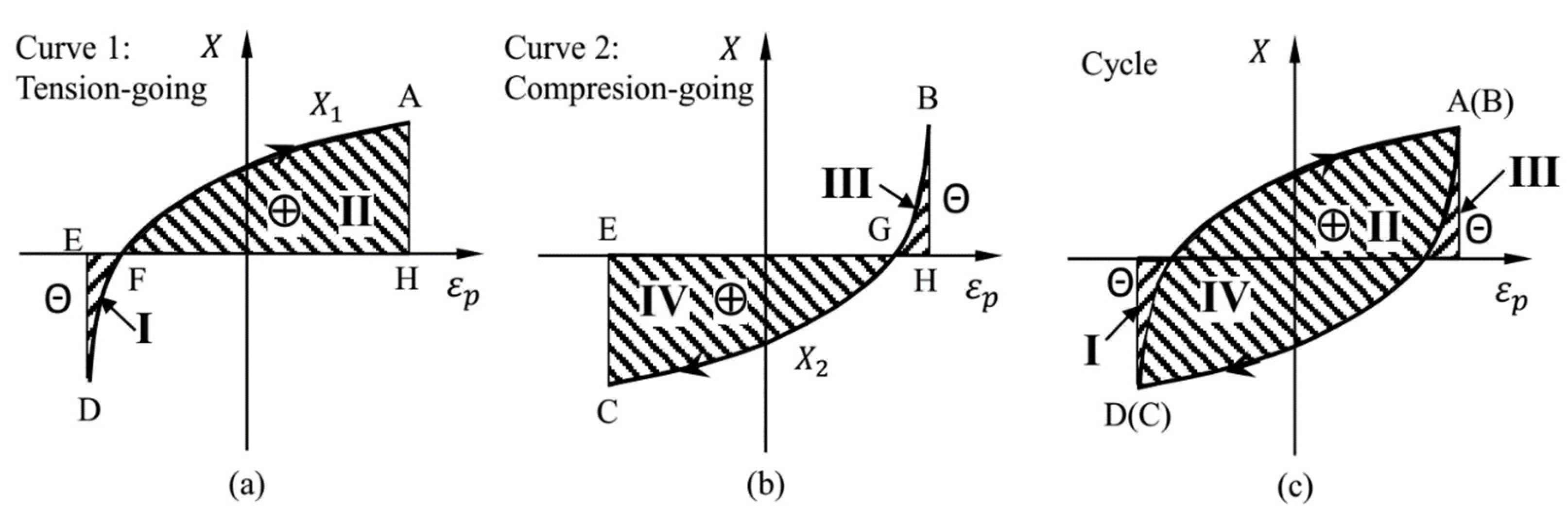
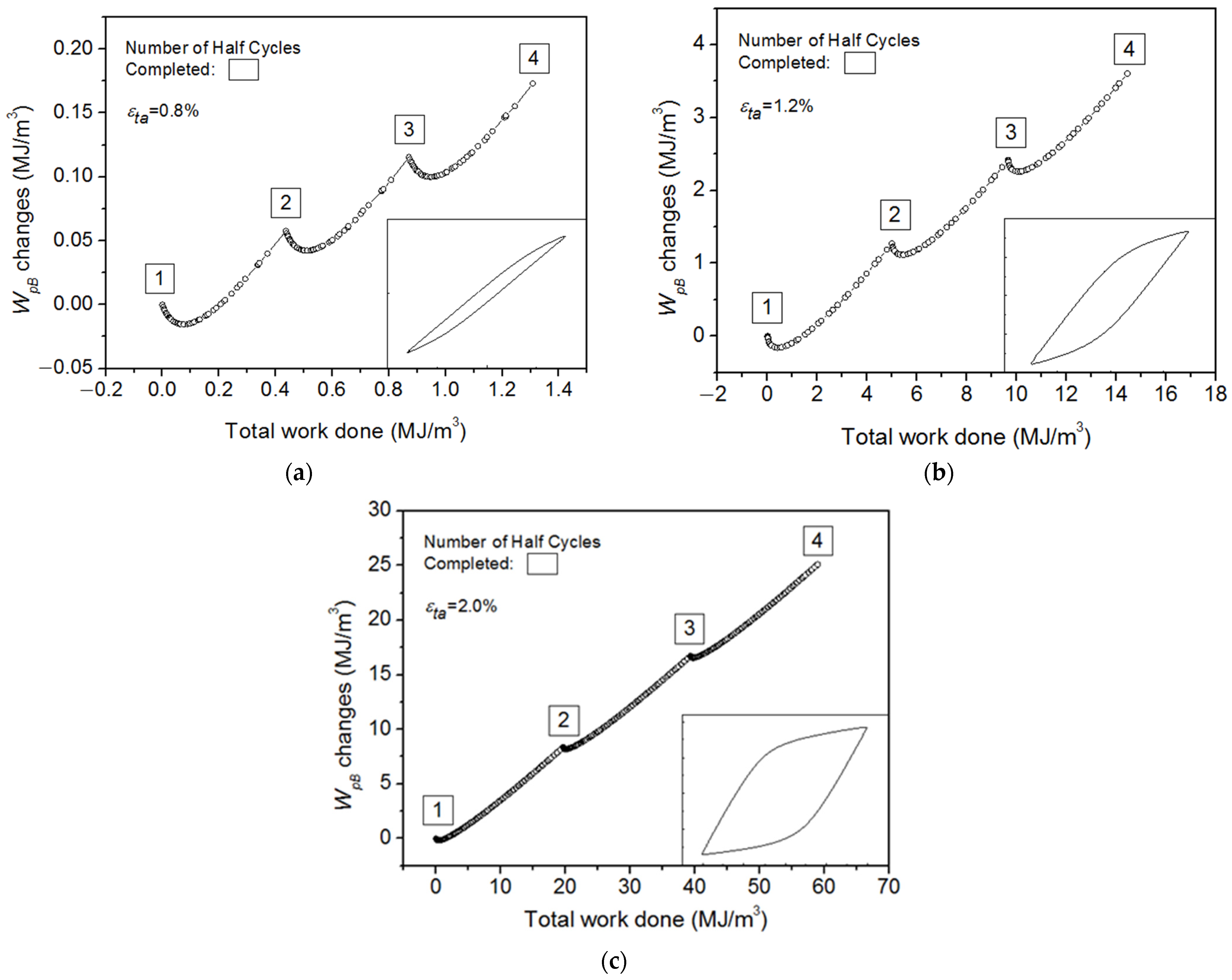
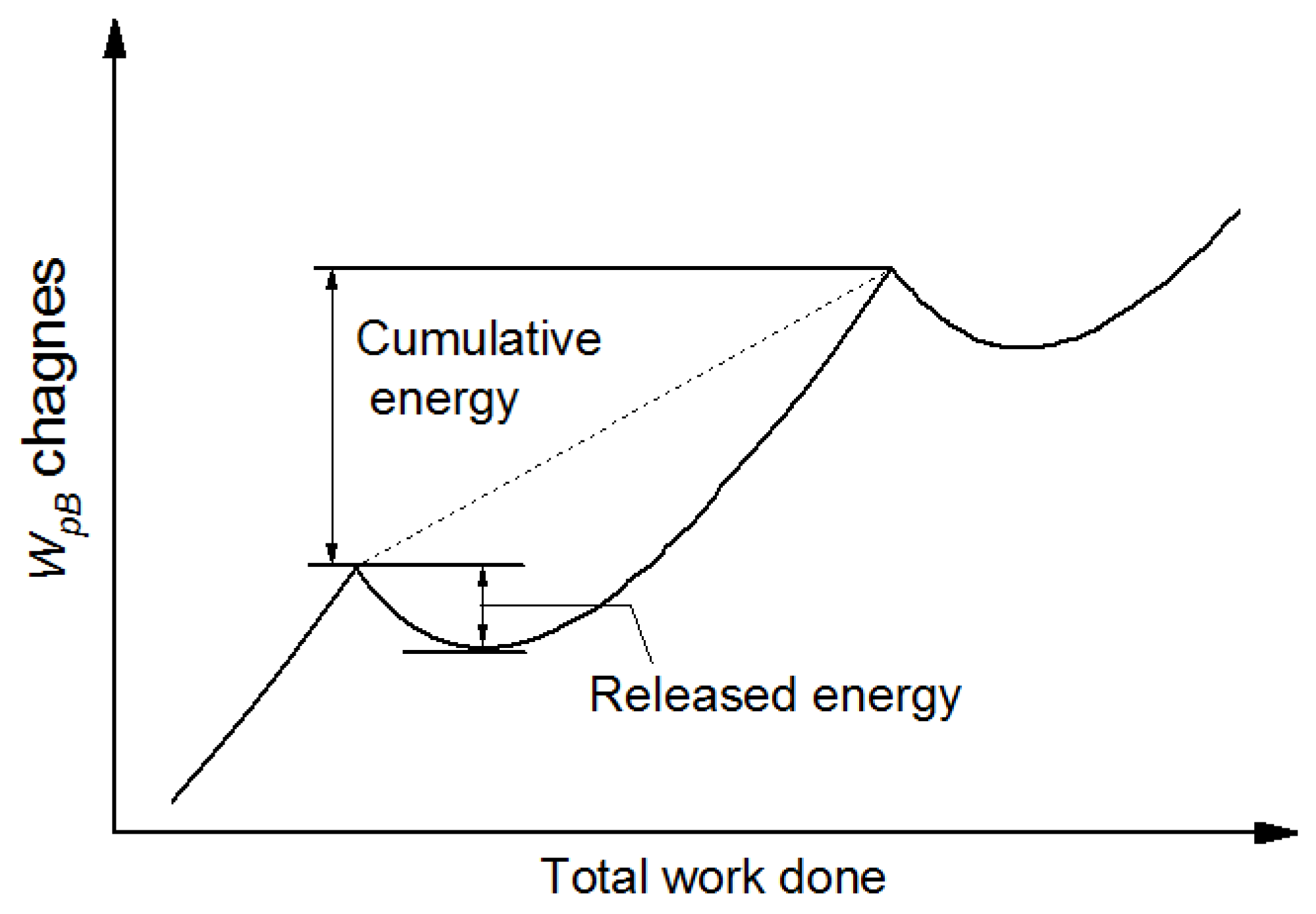
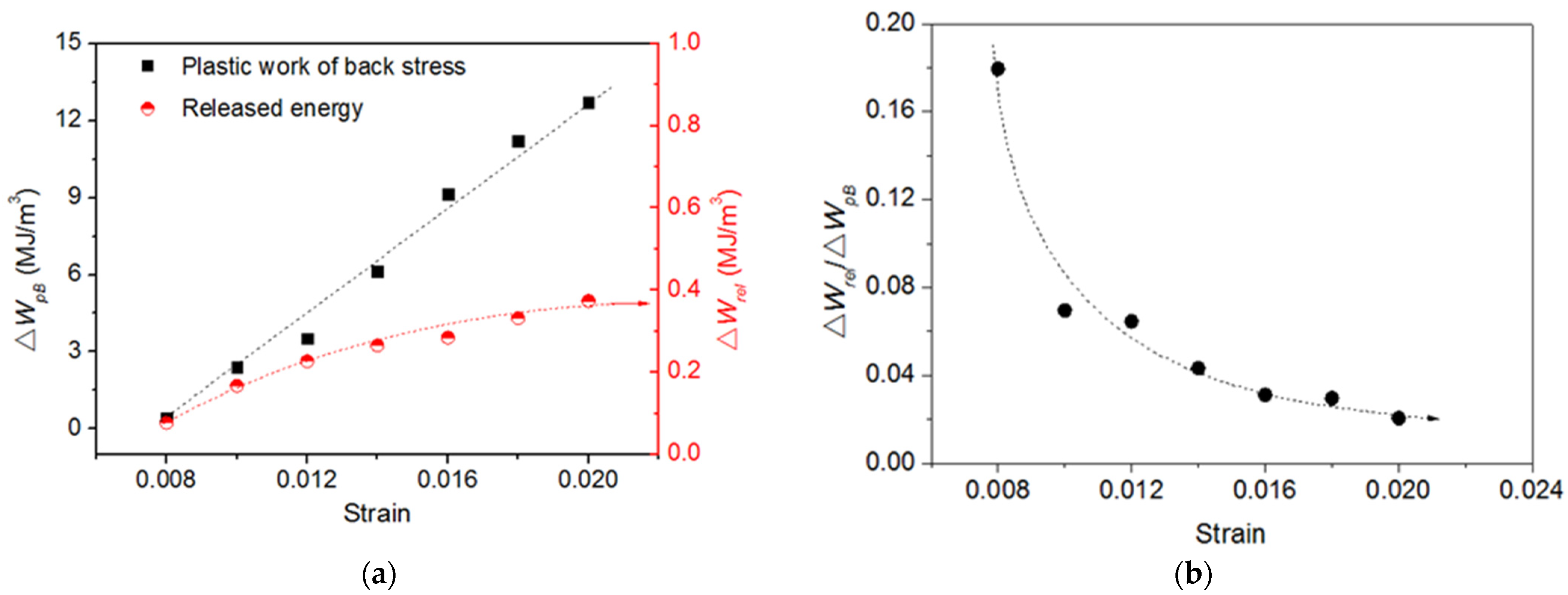
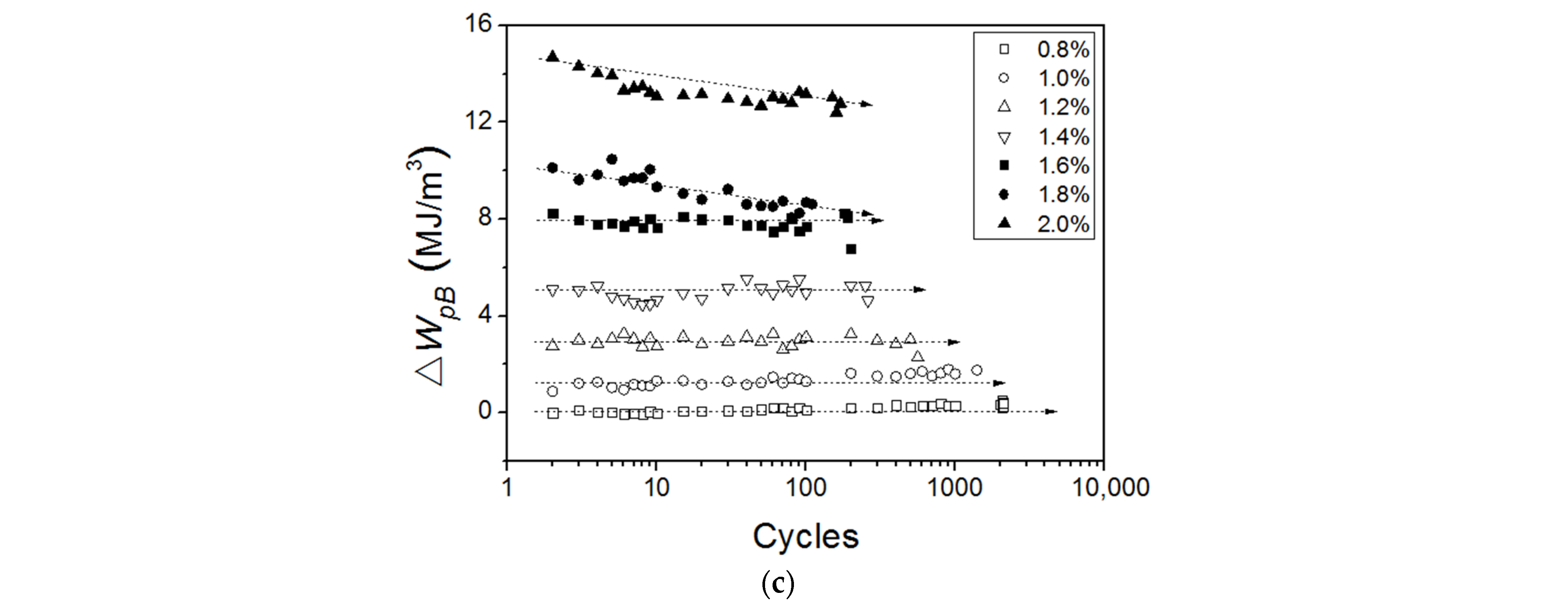
3.2. Accumulation and Dissipation of the Plastic Work of Back Stress
4. Conclusions
- (1)
- Based on the mesomechanics model, our study on the process of cyclic loading reveals that the partial release of stored energy is related to the decrease of residual microstresses remaining in elements resulting from the decrease of the degree of the plastic strain incompatibility between grains. Additionally, the |Xinter| is a macroscopic representation of the residual microstresses.
- (2)
- In Tanaka′s dislocation model, the amount of stored energy of dislocations (ESD) for a single crystal is equal to plastic work done by Xintra.
- (3)
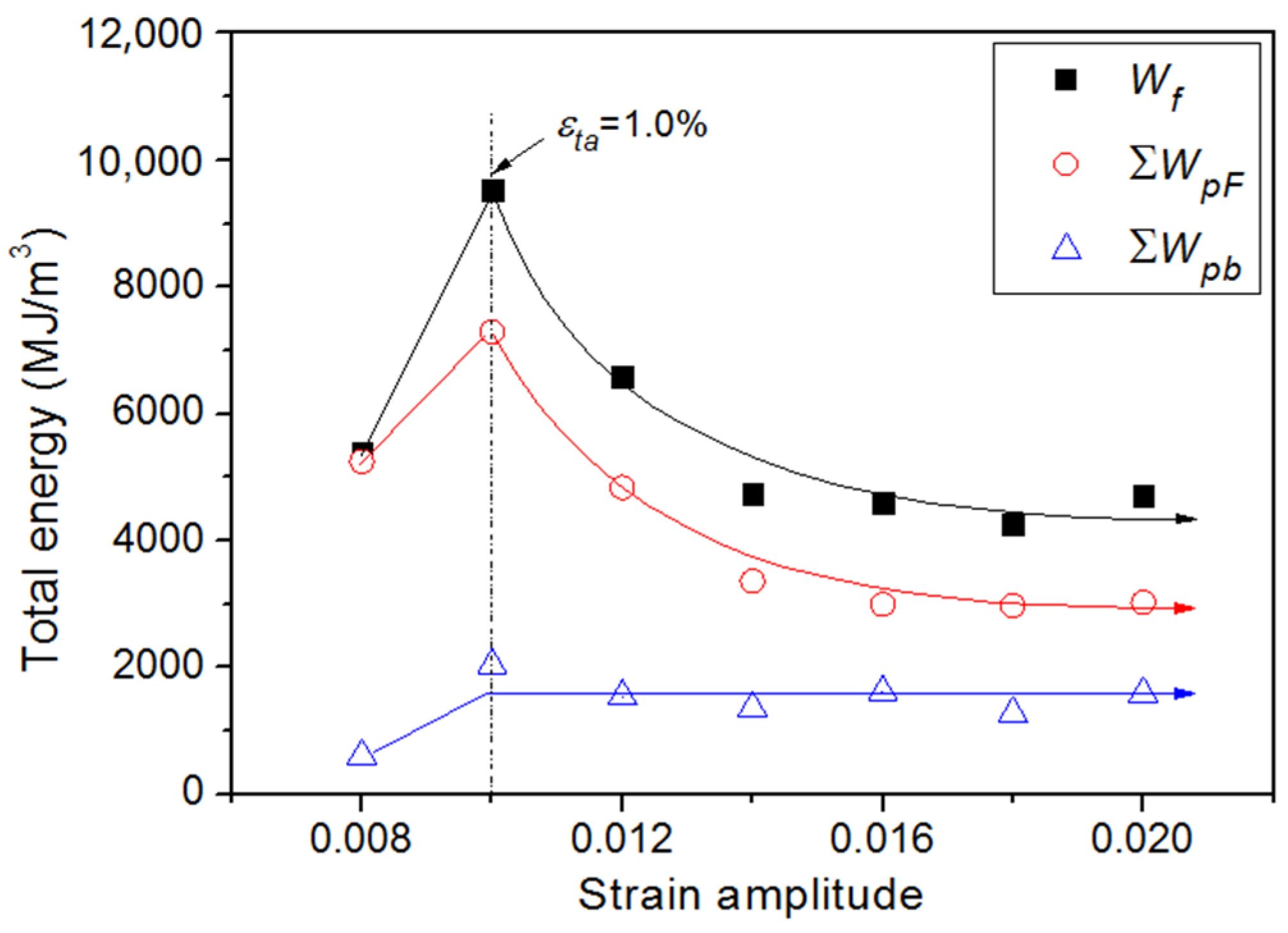
- The plastic work of back stress (WpB) was calculated with the low cycle fatigue experimental data of Ti-6Al-4V. The results show that WpB is partially released at every reverse loading, sufficient to reproduce the evolution of stored energy correctly under cyclic loading. Furthermore, the total plastic work of back stress ∑WpB up to failure is almost constant over the strain range of εta ≥ 1.0%, while the fatigue toughness Wf decrease exponentially with increasing applied strain. Thus, the plastic work of back stress is a more suitable damage criterion.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xiong, Q.L.; Li, Z.; Shimada, T.; Kitamura, T. Energy storage and dissipation of elastic-plastic deformation under shock compression: Simulation and Analysis. Mech. Mater. 2021, 158, 103876. [Google Scholar] [CrossRef]
- Benzerga, A.A.; Bréchet, Y.; Needleman, A.; Van der Giessen, E. The stored energy of cold work: Predictions from discrete dislocation plasticity. Acta Mater. 2005, 53, 4765–4779. [Google Scholar] [CrossRef] [Green Version]
- Aravas, N.; Kim, K.S.; Leckie, F.A. On the calculations of the stored energy of cold work. J. Eng. Mater. Technol. 1990, 112, 465–470. [Google Scholar] [CrossRef] [Green Version]
- Meneghetti, G. Analysis of the fatigue strength of a stainless steel based on the energy dissipation. Int. J. Fatigue 2007, 29, 81–94. [Google Scholar] [CrossRef]
- Xu, Y.; Wan, W.; Dunne, F.P. Microstructural fracture mechanics: Stored energy density at fatigue cracks. J. Mech. Phys. Solids 2021, 146, 104209. [Google Scholar] [CrossRef]
- Farren, W.S.; Taylor, G.I. The heat developed during plastic extension of metals. Proc. R. Soc. Lond. 1925, 107, 422–451. [Google Scholar]
- Taylor, G.I.; Quinney, H. The latent energy remaining in a metal after cold working. Proc. R. Soc. Lond. 1934, 143, 307–326. [Google Scholar]
- Bever, M.B.; Holt, D.L.; Titchener, A.L. The stored energy of cold work. Prog. Mater. Sci. 1973, 17, 5–177. [Google Scholar] [CrossRef]
- Hodowany, J.; Ravichandran, G.; Rosakis, A.J.; Rosakis, P. Partition of plastic work into heat and stored energy in metals. Exp. Mech. 2000, 40, 113–123. [Google Scholar] [CrossRef]
- Oliferuk, W.; Maj, M. Stress–strain curve and stored energy during uniaxial deformation of polycrystals. Eur. J. Mech.-A/Solids 2009, 28, 266–272. [Google Scholar] [CrossRef] [Green Version]
- Oliferuk, W.; Maj, M.; Zembrzycki, K. Determination of the energy storage rate distribution in the area of strain localization using infrared and visible imaging. Exp. Mech. 2015, 55, 753–760. [Google Scholar] [CrossRef] [Green Version]
- Bartels, A.; Bartel, T.; Canadija, M.; Mosler, J. On the thermomechanical coupling in dissipative materials: A variational approach for generalized standard materials. J. Mech. Phys. Solids 2015, 82, 218–234. [Google Scholar] [CrossRef]
- Helm, D. Thermomechanical representation of the stored energy during plastic deformation. Int. J. Mater. Res. 2010, 101, 972–980. [Google Scholar] [CrossRef]
- Halford, G.R. Stored Energy of Cold Work Changes Induced by Cyclic Deformation; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 1966. [Google Scholar]
- Chaboche, J.L. Cyclic viscoplastic constitutive equations, part II: Stored energy—Comparison between models and experiments. J. Appl. Mech. 1993, 60, 822–828. [Google Scholar] [CrossRef]
- Martin, D.E. An energy criterion for low-cycle fatigue. J. Fluids Eng. 1961, 83, 565. [Google Scholar] [CrossRef]
- Tanaka, K.; Mura, T. A dislocation model for fatigue crack initiation. J. Appl. Mech. 1981, 48, 97–103. [Google Scholar] [CrossRef]
- Skelton, R.P. Cyclic stress-strain properties during high strain fatigue. In High Temperature Fatigue; Springer: Dordrecht, The Netherlands, 1987; pp. 27–112. [Google Scholar]
- Skelton, R.P. Bauschinger and yield effects during cyclic loading of high temperature alloys at 550 °C. Mater. Sci. Technol. 1994, 10, 627–639. [Google Scholar] [CrossRef]
- Skelton, R.P. Bauschinger yield in the range 400–1025 C during cyclic deformation of high temperature alloys. Mater. High Temp. 2013, 30, 241–260. [Google Scholar] [CrossRef]
- Szczepiński, W. The stored energy in metals and the concept of residual microstresses in plasticity. Arch. Mech. 2001, 53, 615–629. [Google Scholar]
- Mollica, F.; Rajagopal, K.R.; Srinivasa, A.R. The inelastic behavior of metals subject to loading reversal. Int. J. Plast. 2001, 17, 1119–1146. [Google Scholar] [CrossRef]
- Kamlah, M.; Haupt, P. On the macroscopic description of stored energy and self heating during plastic deformation. Int. J. Plast. 1997, 13, 893–911. [Google Scholar] [CrossRef]
- Cho, H.E.; Hammi, Y.; Bowman, A.L.; Karato, S.I.; Baumgardner, J.R.; Horstemeyer, M.F. A unified static and dynamic recrystallization Internal State Variable (ISV) constitutive model coupled with grain size evolution for metals and mineral aggregates. Int. J. Plast. 2019, 112, 123–157. [Google Scholar] [CrossRef]
- Kim, D.K.; Woo, W.; Park, W.W.; Im, Y.T.; Rollett, A. Mesoscopic coupled modeling of texture formation during recrystallization considering stored energy decomposition. Comput. Mater. Sci. 2017, 129, 55–65. [Google Scholar] [CrossRef] [Green Version]
- Giordana, M.F.; Alvarez-Armas, I.; Armas, A. Microstructural characterization of EUROFER 97 during low-cycle fatigue. J. Nucl. Mater. 2012, 424, 247–251. [Google Scholar] [CrossRef]
- Oliferuk, W.; Świa̧tnicki, W.A.; Grabski, M.W. Effect of the grain size on the rate of energy storage during the tensile deformation of an austenitic steel. Mater. Sci. Eng. A 1995, 197, 49–58. [Google Scholar] [CrossRef]
- Connesson, N.; Maquin, F.; Pierron, F. Dissipative energy: Monitoring microstructural evolutions during mechanical tests. In Thermomechanics and Infra-Red Imaging; Springer: New York, NY, USA, 2011; Volume 7, pp. 59–65. [Google Scholar]
- Maquin, F.; Pierron, F. Heat dissipation measurements in low stress cyclic loading of metallic materials: From internal friction to micro-plasticity. Mech. Mater. 2009, 41, 928–942. [Google Scholar] [CrossRef]
- Caillard, D.; Martin, J.L. (Eds.) Thermally Activated Mechanisms in Crystal Plasticity; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Mughrabi, H. A two-parameter description of heterogeneous dislocation distributions in deformed metal crystals. Mater. Sci. Eng. 1987, 85, 15–31. [Google Scholar] [CrossRef]
- Feaugas, X. On the origin of the tensile flow stress in the stainless steel AISI 316L at 300 K: Back stress and effective stress. Acta Mater. 1999, 47, 3617–3632. [Google Scholar] [CrossRef]
- Kuhlmann-Wilsdorf, D.; Laird, C. Dislocation behavior in fatigue II. Friction stress and back stress as inferred from an analysis of hysteresis loops. Mater. Sci. Eng. 1979, 37, 111–120. [Google Scholar] [CrossRef]
- Fournier, B.; Sauzay, M.; Caës, C.; Noblecourt, M.; Mottot, M. Analysis of the hysteresis loops of a martensitic steel: Part I: Study of the influence of strain amplitude and temperature under pure fatigue loadings using an enhanced stress partitioning method. Mater. Sci. Eng. A 2006, 437, 183–196. [Google Scholar] [CrossRef]
- Moosbrugger, J.C.; Morrison, D.J.; Jia, Y. Nonlinear kinematic hardening rule parameters—relationship to substructure evolution in polycrystalline nickel. Int. J. Plast. 2000, 16, 439–467. [Google Scholar] [CrossRef]
- Lemaitre, J.; Chaboche, J.L. Mechanics of Solid Materials; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Xu, H.; Ye, D.; Mei, L. A study of the back stress and the friction stress behaviors of Ti-6Al-4V alloy during low cycle fatigue at room temperature. Mater. Sci. Eng. A 2017, 700, 530–539. [Google Scholar] [CrossRef]
- Wong, A.K.; Kirby, G.C., III. A hybrid numerical/experimental technique for determining the heat dissipated during low cycle fatigue. Eng. Fract. Mech. 1990, 37, 493–504. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Li, X.; Li, W.; Jiang, P.; Zhao, Y.; Liu, Y. A New Stored Energy Model Based on Plastic Work of Back Stress during Cyclic Loading in Polycrystalline Metal. Materials 2022, 15, 5267. https://doi.org/10.3390/ma15155267
Xu H, Li X, Li W, Jiang P, Zhao Y, Liu Y. A New Stored Energy Model Based on Plastic Work of Back Stress during Cyclic Loading in Polycrystalline Metal. Materials. 2022; 15(15):5267. https://doi.org/10.3390/ma15155267
Chicago/Turabian StyleXu, Haifeng, Xiaopeng Li, Wei Li, Peng Jiang, Yuanbo Zhao, and Yinghonglin Liu. 2022. "A New Stored Energy Model Based on Plastic Work of Back Stress during Cyclic Loading in Polycrystalline Metal" Materials 15, no. 15: 5267. https://doi.org/10.3390/ma15155267





