Deformation Behavior and Constitutive Model of 34CrNi3Mo during Thermo-Mechanical Deformation Process
Abstract
:1. Introduction
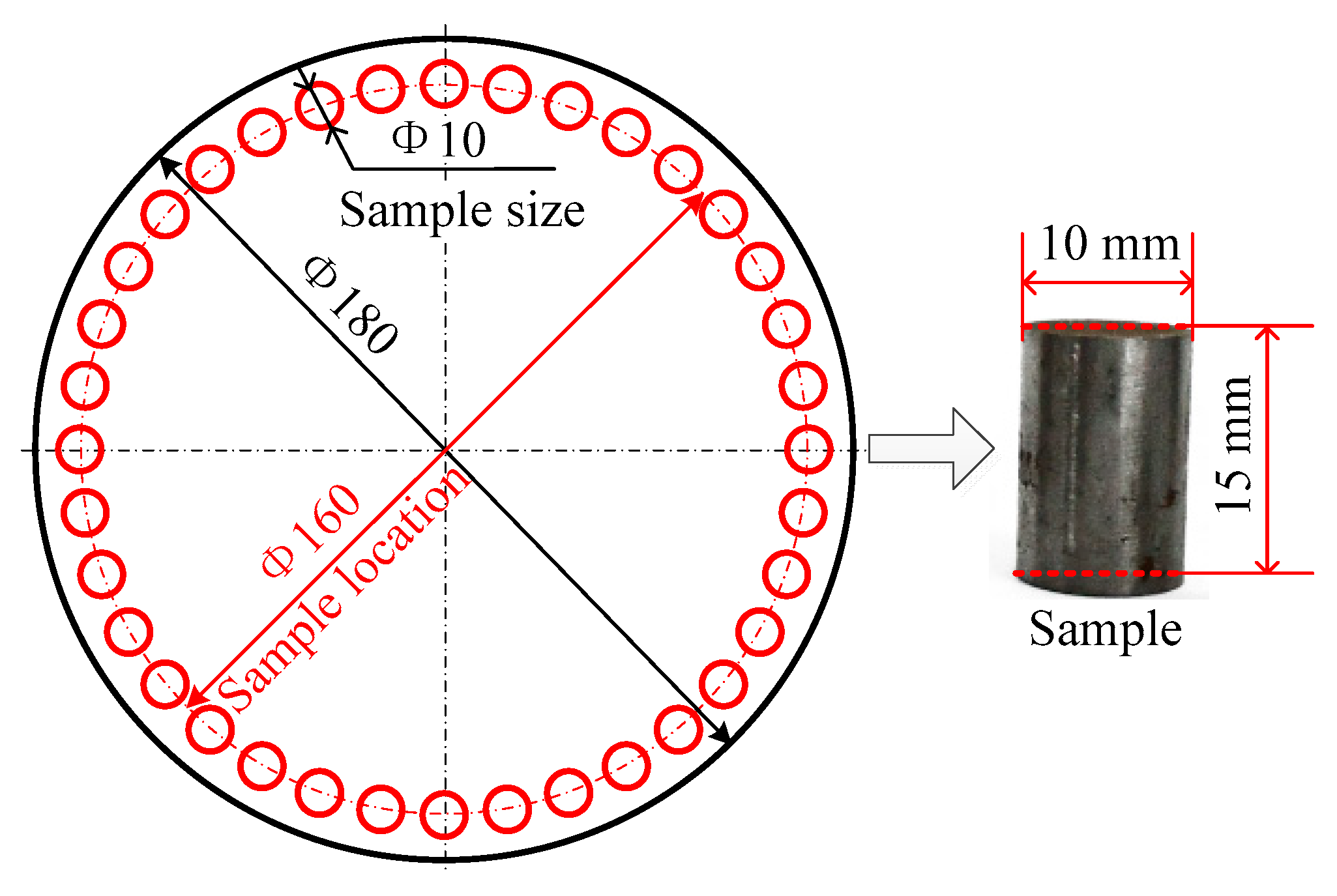
2. Experiment
2.1. Experiment Method
2.2. Results and Analysis
3. Constitutive Model
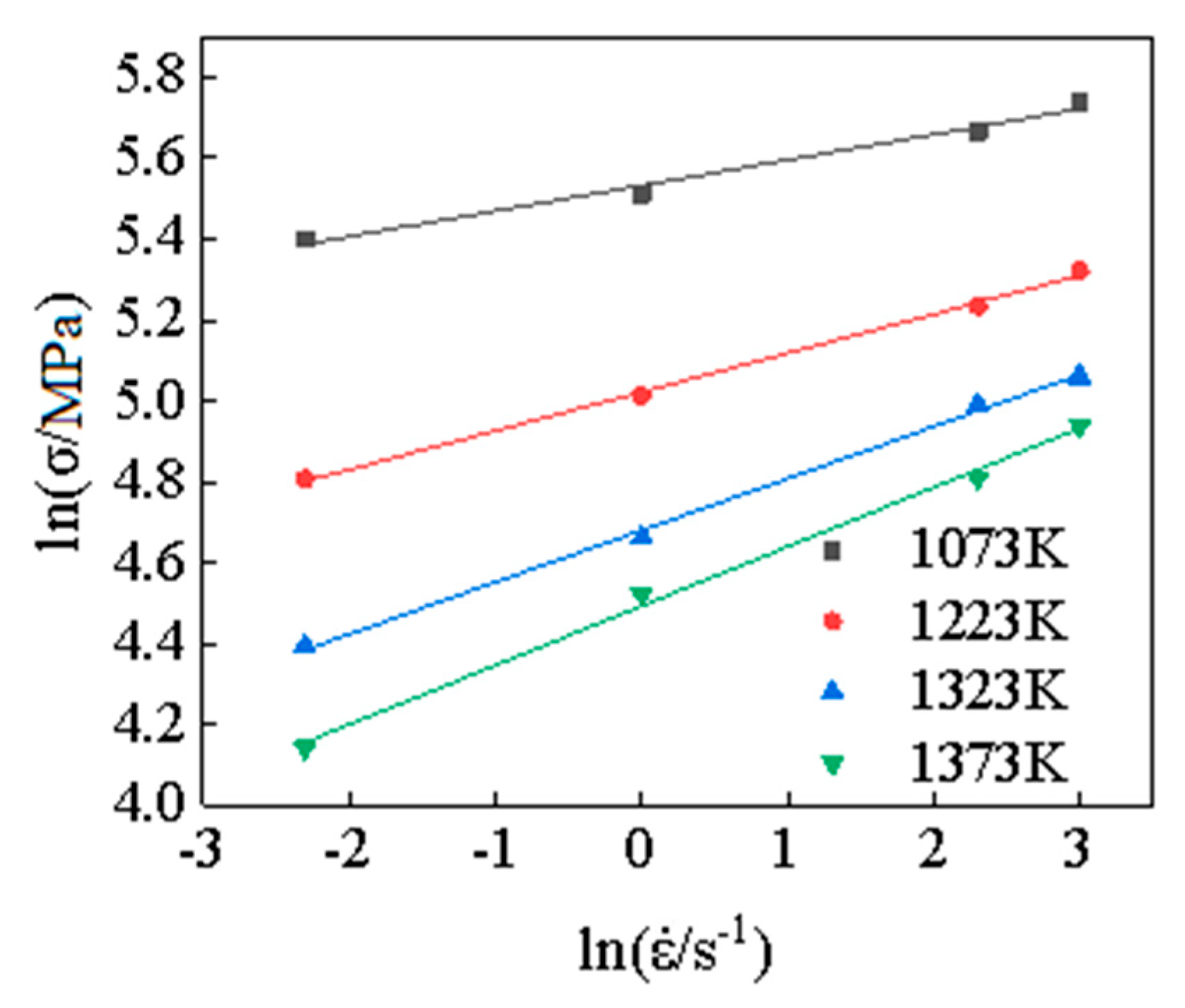
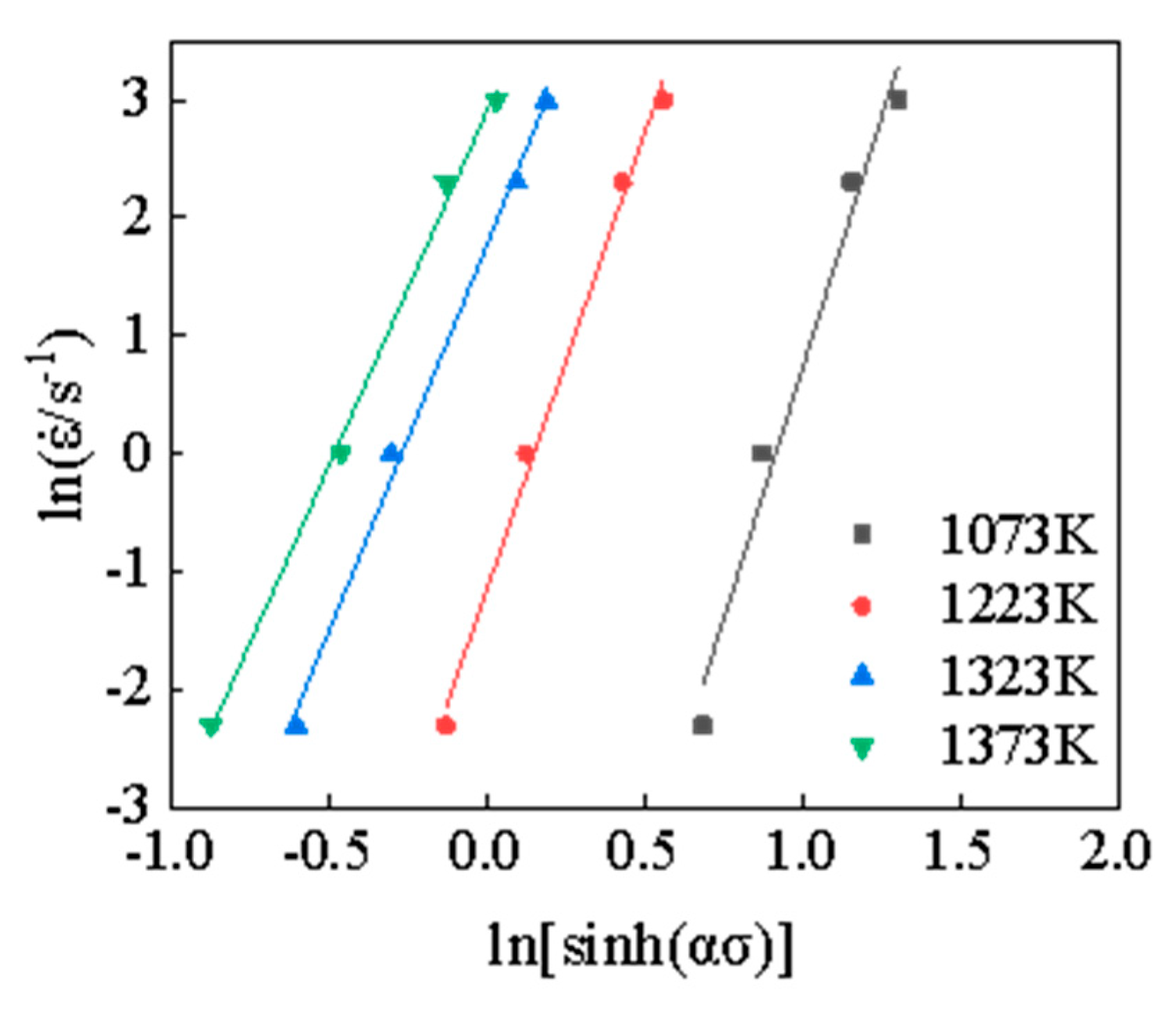
3.1. Arrhenius-Type Constitutive Model
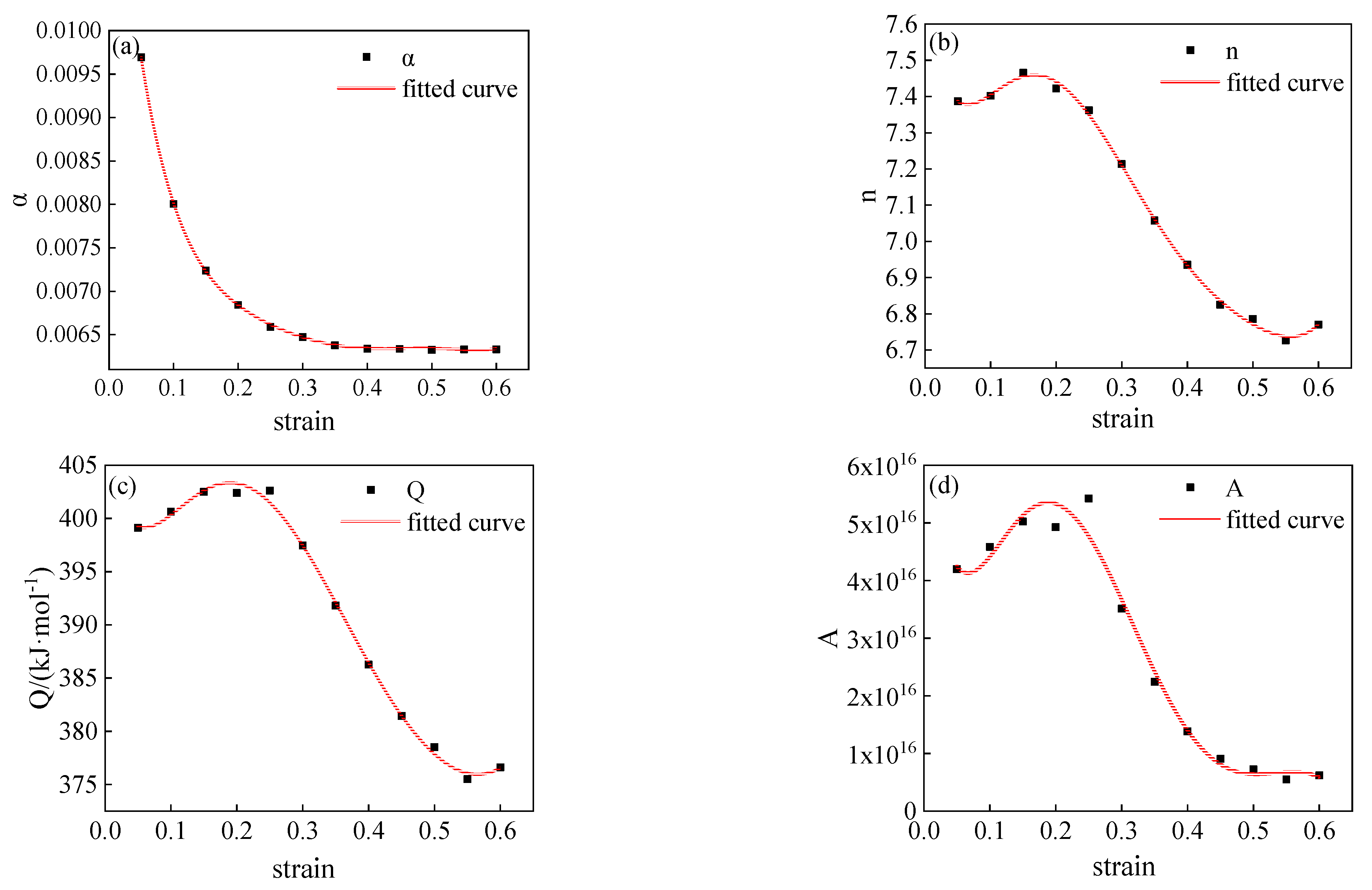
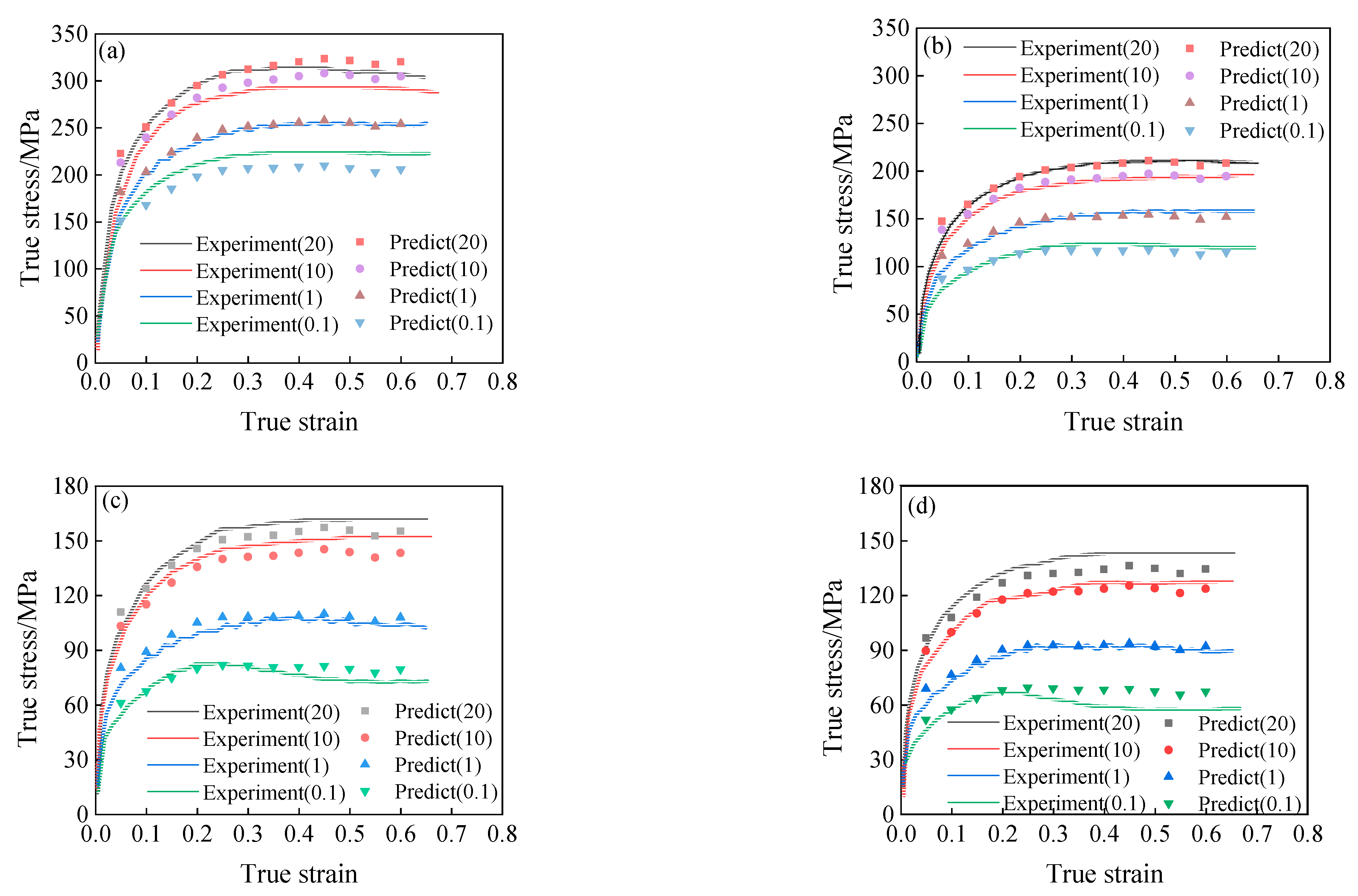
3.2. Modified Arrhenius-Type Constitutive Model
4. Thermal Deformation Behavior
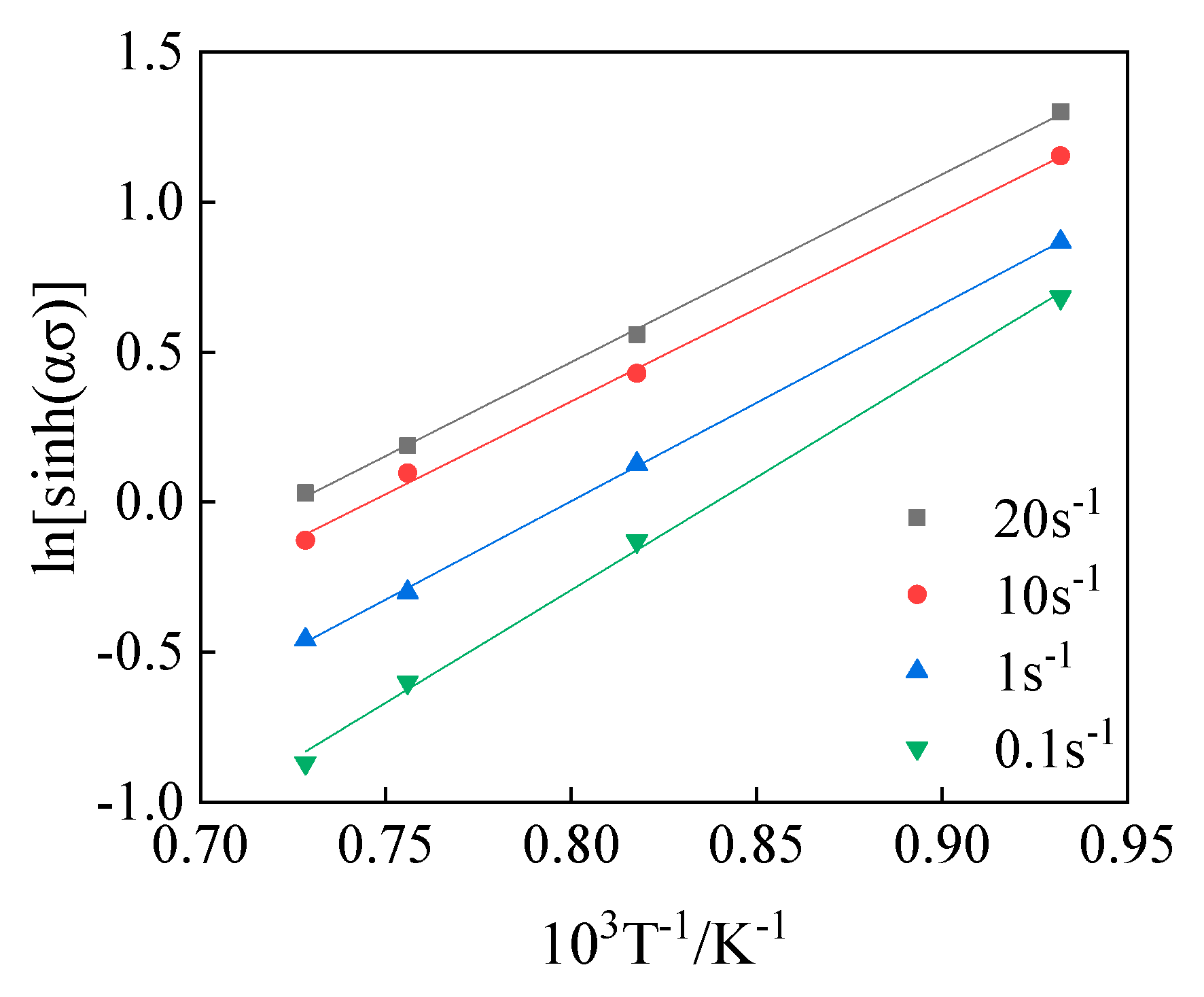
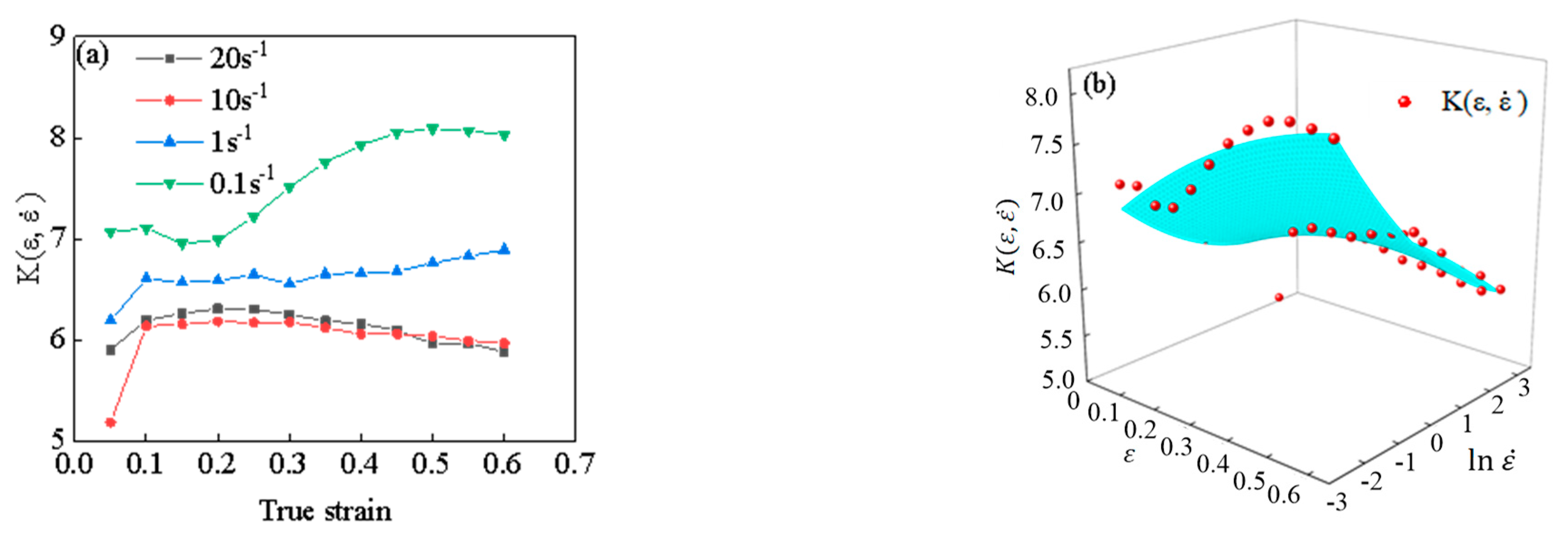
4.1. Evolution of Activation Energy
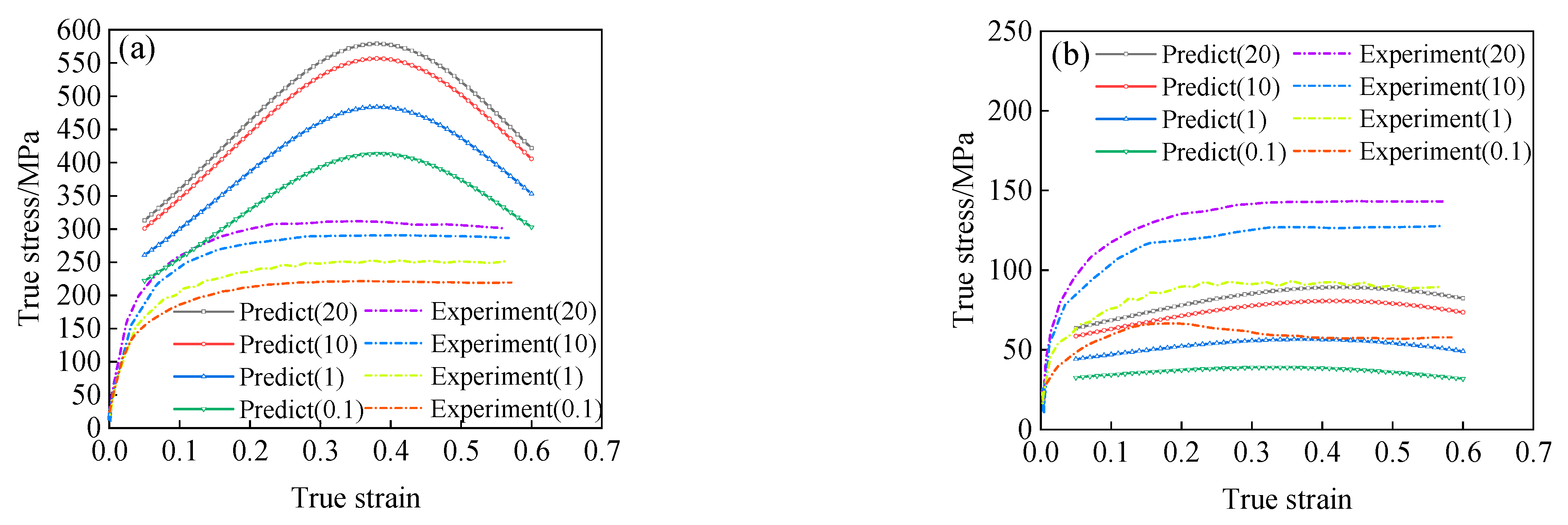
4.2. Processing Map
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Luo, Y.; Guo, H.; Guo, J.; Yang, W. Gleeble-Simulated and Semi-Industrial Studies on the Microstructure Evolution of Fe-Co-Cr-Mo-W-V-C Alloy During Hot Deformation. Materials 2018, 11, 2577. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Li, W.; Ma, J.; Hu, S.; He, Y.; Li, L.; Xiao, B. Thermo-Physical Simulation of the Compression Testing for Constitutive Modeling of GH4169 Superalloy During Linear Friction Welding. J. Alloy. Compd. 2016, 656, 395–407. [Google Scholar] [CrossRef]
- Haghdadi, N.; Martin, D.; Hodgson, P. Physically-based constitutive modelling of hot deformation behavior in a LDX 2101 duplex stainless steel. Mater. Des. 2016, 106, 420–427. [Google Scholar] [CrossRef]
- He, T.; Huo, Y.; Shi, X.; Chen, S. Modeling of Carbide Spheroidization Mechanism of 52100 Bearing Steel Under Warm Forming Conditions. Metall. Mater. Trans. A 2019, 50, 936–946. [Google Scholar] [CrossRef]
- Liu, L.; Wu, Y.X.; Gong, H.; Wang, K. Modification of constitutive model and evolution of activation energy on 2219 aluminum alloy during warm deformation process. Trans. Nonferrous Met. Soc. China 2019, 29, 448–459. [Google Scholar] [CrossRef]
- Wang, M.H.; Yang, Y.C.; Tu, S.L.; Wei, K. A modified constitutive model and hot compression instability behavior of Cu-Ag alloy. Trans. Nonferrous Met. Soc. China 2019, 29, 764–774. [Google Scholar] [CrossRef]
- Xiao, Y.H.; Guo, C.; Guo, X.Y. Constitutive modeling of hot deformation behavior of H62 brass. Mater. Sci. Eng. A 2011, 528, 6510–6518. [Google Scholar] [CrossRef]
- Peng, W.W.; Zeng, W.D.; Wang, Q.J.; Yu, H. Comparative study on constitutive relationship of as-cast Ti60 titanium alloy during hot deformation based on Arrhenius-type-type and artificial neural network models. Mater. Des. 2013, 51, 95–104. [Google Scholar] [CrossRef]
- Wang, L.; Liu, F.; Cheng, J.J.; Zuo, Q.; Chen, C.F. Arrhenius-type-Type Constitutive Model for High Temperature Flow Stress in a Nickel-Based Corrosion-Resistant Alloy. J. Mater. Eng. Perform. 2016, 25, 1394–1406. [Google Scholar] [CrossRef]
- Li, C.S.; He, S.; Ren, J.; Han, Y. The Flow Stress Behavior and Constitutive Model of Cr8Mo2SiV Tool Steel during Hot Deformation. Steel Res. Int. 2021, 92, 200043. [Google Scholar]
- Safari, A.; Imran, M.; Weiss, S. A Comparative Study on Modified Johnson–Cook and Arrhenius-type-Type Constitutive Models to Predict the Hot Deformation Behaviour of Molybdenum-Hafnium-Carbide Alloy. J. Mater. Eng. Perform. 2021, 30, 1945–1956. [Google Scholar] [CrossRef]
- Tao, Z.; Yang, H.; Li, H.; Ma, J.; Gao, P. Constitutive modeling of compression behavior of TC4 tube based on modified Arrhenius-type and artificial neural network models. Rare Met. 2016, 35, 162–171. [Google Scholar] [CrossRef]
- Wang, J.; Yuan, X.; Jin, P.; Ma, H.; Shi, B.; Zheng, H.; Chen, T.; Xia, W. Study on modified Johnson-Cook constitutive material model to predict the dynamic behavior Mg-1Al-4Y alloy. Mater. Res. Express 2020, 7, 026522. [Google Scholar] [CrossRef]
- Mirzadeh, H. Constitutive modeling and prediction of hot deformation flow stress under dynamic recrystallization conditions. Mech. Mater. 2015, 85, 66–79. [Google Scholar] [CrossRef]
- Martins, J.M.P.; Thuillier, S.; Andrade-Campos, A. Calibration of a modified Johnson-Cook model using the Virtual Fields Method and a heterogeneous thermo-mechanical tensile test. Int. J. Mech. Sci. 2021, 202–203, 106511. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Song, Y.; Hong, X.; Wang, Z.-G. A modified Johnson–Cook model for 7N01 aluminum alloy under dynamic condition. J. Cent. South Univ. 2017, 24, 2550–2555. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Yang, H.; Liu, J.; Ji, C. A Modified Johnson-Cook Constitutive Model for Characterizing the Hardening Behavior of Typical Magnesium Alloys under Tension at Different Strain Rates: Experiment and Simulation. J. Mater. Eng. Perform. 2020, 29, 8319–8330. [Google Scholar] [CrossRef]
- Liu, D.; Li, B.; Guo, Z.; Huang, Z. Finite element analysis on electromagnetic forming of DP780 high-strength steel sheets. Int. J. Adv. Manuf. Technol. 2021, 112, 1–13. [Google Scholar] [CrossRef]
- Ding, F.J.; Jia, X.D.; Hong, T.J.; Xu, Y.L. Prediction model on flow stress of 6061 aluminum alloy sheet based on GA-BP and PSO-BP neural networks. Rare Met. Mater. Eng. 2020, 49, 1840–1853. [Google Scholar]
- Wang, M.H.; Wang, G.T.; Wang, R. Flow stress behavior and constitutive modeling of 20MnNiMo low carbon alloy. J. Cent. South Univ. 2016, 8, 45–54. [Google Scholar] [CrossRef]
- Ashtiani, H.R.; Shayanpoor, A.A. Hot Deformation Characterization of Pure Aluminum Using artificial neural network (ANN) and Processing Map Considering Initial Grain Size. Met. Mater. Int. 2021, 27, 5017–5033. [Google Scholar] [CrossRef]
- Quan, G.Z.; Zou, Z.Y.; Tong, W.; Liu, B.; Li, J.-C. Modeling the Hot Deformation Behaviors of As-Extruded 7075 Aluminum Alloy by an Artificial Neural Network with Back-Propagation Algorithm. High Temp. Mater. Process. 2016, 36, 1–13. [Google Scholar] [CrossRef]
- Xi, S.P.; Gao, X.L.; Liu, W.; Lu, Y.-L.; Fu, G.-Q.; Tao, H.-C.; Zang, Y.-C. Hot deformation behavior and processing map of low-alloy offshore steel. J. Iron Steel Res. Int. 2021, 29, 474–483. [Google Scholar] [CrossRef]
- Zhao, H.; Qi, J.; Su, R.; Zhang, H.; Chen, H.; Bai, L.; Wang, C. Hot deformation behaviour of 40CrNi steel and evaluation of different processing map construction methods. J. Mater. Res. Technol. 2020, 9, 2856–2869. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Gegel, H.L.; Doraivelu, S.M.; Malas, J.C.; Morgan, J.T.; Lark, K.A.; Barker, D.R. Modeling of dynamic material behavior in hot deformation: Forging of Ti-6242. Metall. Trans. A 1984, 15, 1883–1892. [Google Scholar] [CrossRef]
- Murty, S.V.S.N.; Rao, B.N. On the development of instability criteria during hotworking with reference to IN 718. Mater. Sci. Eng. A 1998, 254, 76–82. [Google Scholar] [CrossRef]
- Jia, X.D.; Wang, Y.N.; Zhou, Y.; Cao, M.Y. The Study on Forming Property at High Temperature and Processing Map of 2219 Aluminum Alloy. Met.-Open Access Metall. J. 2021, 11, 77. [Google Scholar] [CrossRef]
- Chen, X.; Liao, Q.; Niu, Y.; Jia, Y.; Le, Q.; Ning, S.; Hu, C.; Hu, K.; Yu, F. Comparison study of hot deformation behavior and processing map of AZ80 magnesium alloy casted with and without ultrasonic vibration. J. Alloy. Compd. 2019, 803, 585–596. [Google Scholar] [CrossRef]
- Yuan, C.H.; Liu, B.; Liu, Y.X.; Liu, Y. Processing map and hot deformation behavior of Ta-particle reinforced TiAl composite. Trans. Nonferrous Met. Soc. China 2020, 30, 657–667. [Google Scholar] [CrossRef]
- Gao, P.; Chen, L.; Luo, R.; Peng, C.-T.; Sheng, D.; Liu, T.; Cheng, X. Investigation of Hot Working Performance and Microstructure Evolution of GH1059 Superalloy Based on Processing Map. Trans. Indian Inst. Met. 2021, 74, 2729–2737. [Google Scholar] [CrossRef]
- Chegini, M.; Aboutalebi, M.R.; Seyedein, S.H.; Ebrahimi, G.R.; Jahazi, M. Study on hot deformation behavior of AISI 414 martensitic stainless steel using 3D processing map—ScienceDirect. J. Manuf. Process. 2020, 56, 916–927. [Google Scholar] [CrossRef]







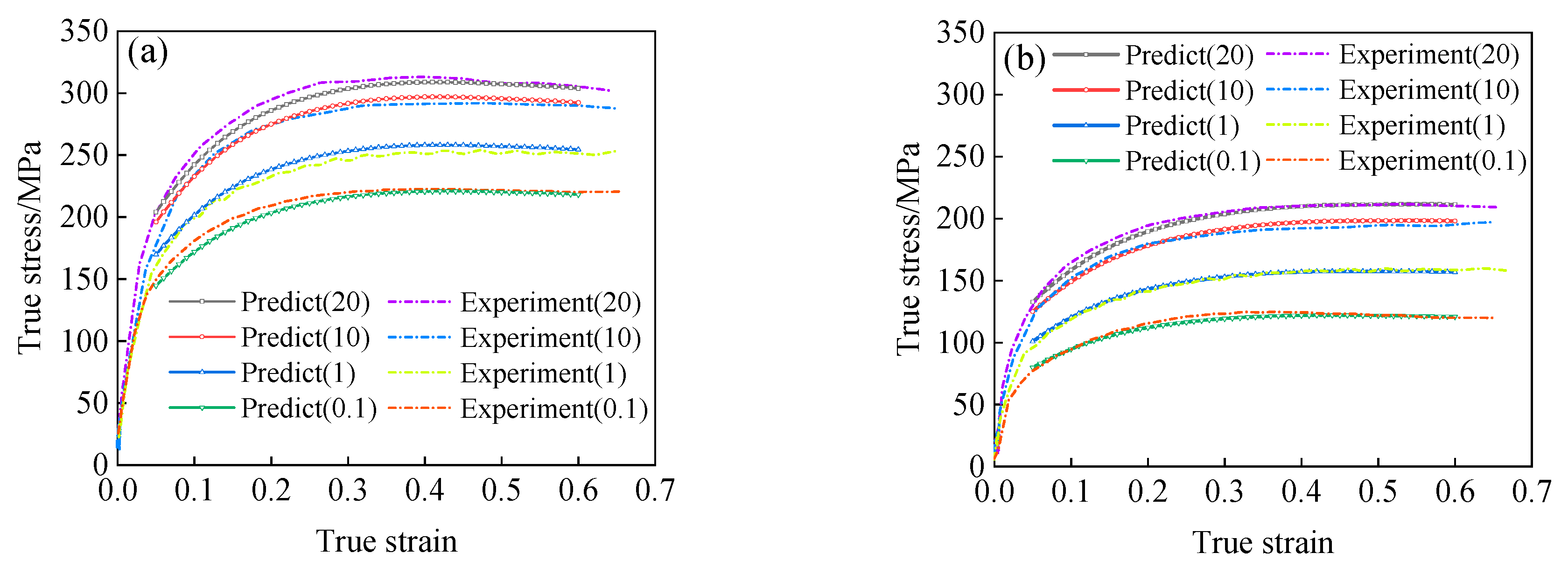
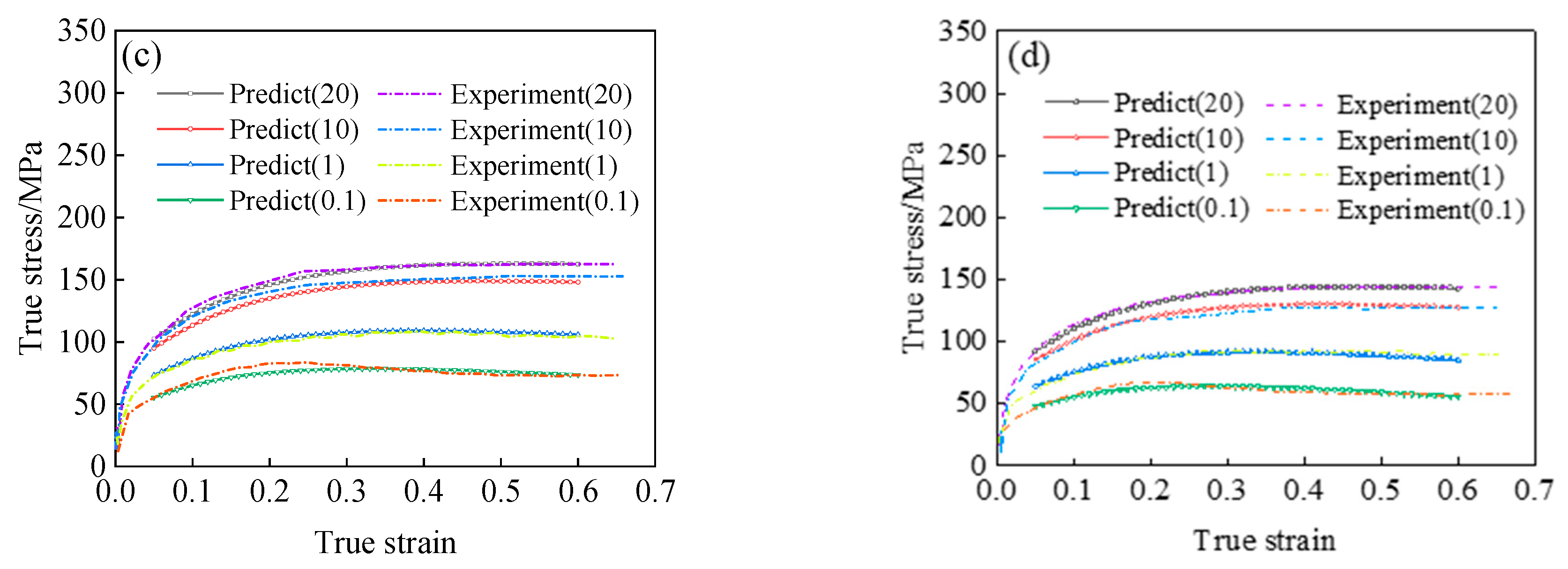


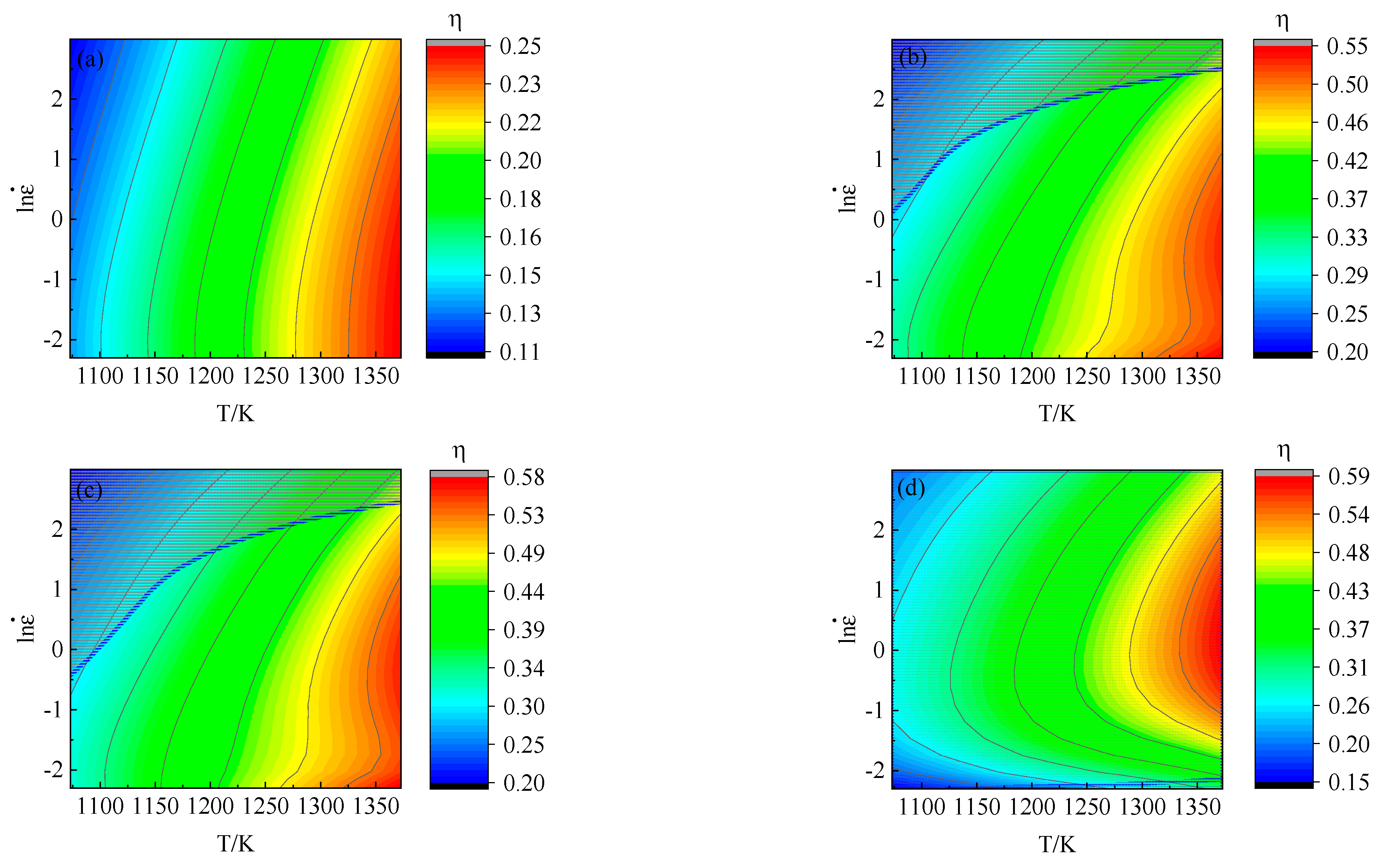
| Temp./K | 1073 | 1223 | 1323 | 1373 | Average |
|---|---|---|---|---|---|
| n1 | 15.873 | 10.425 | 7.7972 | 6.8264 | 10.231 |
| β | 0.0605 | 0.0654 | 0.0676 | 0.0713 | 0.0662 |
| α | 0.0038 | 0.0062 | 0.0087 | 0.0104 | 0.0064 |
| Temp./K | 1073 | 1223 | 1323 | 1373 | Average |
|---|---|---|---|---|---|
| n | 8.51745 | 7.75401 | 6.5601 | 6.0217 | 7.2133 |
| Strain Rate/s−1 | 0.1 | 1 | 10 | 20 | Average |
|---|---|---|---|---|---|
| Q | 443.084 | 398.4061 | 357.6501 | 376.2161 | 397.4488 |
| Strain | Q/MPa | n/MPa | LnA | α |
|---|---|---|---|---|
| 0.05 | 399.1256 | 7.38668 | 38.27542 | 0.00969 |
| 0.1 | 400.6295 | 7.40179 | 38.36398 | 0.008 |
| 0.15 | 402.4933 | 7.46533 | 38.45559 | 0.00724 |
| 0.2 | 402.38308 | 7.42159 | 38.43599 | 0.00684 |
| 0.25 | 402.62062 | 7.36242 | 38.53199 | 0.00659 |
| 0.3 | 397.44876 | 7.2133 | 38.09718 | 0.00647 |
| 0.35 | 391.81027 | 7.05774 | 37.64784 | 0.00638 |
| 0.4 | 386.26765 | 6.93568 | 37.16344 | 0.00634 |
| 0.45 | 381.4456 | 6.82569 | 36.74357 | 0.00634 |
| 0.5 | 378.517 | 6.78605 | 36.51825 | 0.00632 |
| 0.55 | 375.50975 | 6.72715 | 36.24138 | 0.00633 |
| 0.6 | 376.62529 | 6.77065 | 36.36216 | 0.00633 |
| B0 | B1 | B2 | B3 | B4 | B5 | B6 |
| 0.01209 | −0.07008 | 0.40198 | −1.32864 | 2.54498 | −2.59908 | 1.08967 |
| C0 | C1 | C2 | C3 | C4 | C5 | C6 |
| 7.64236 | −10.40617 | 139.43461 | −761.53963 | 1911.63147 | −2288.30462 | 1068.61673 |
| D0 | D1 | D2 | D3 | D4 | D5 | D6 |
| 442.8039 | −1133.84 | 11,184.9 | −50,811.3 | 115,013 | −128,989 | 57,596.7 |
| E0 | E1 | E2 | E3 | E4 | E5 | E6 |
| 1.10 × 1017 | −2.03 × 1018 | 2.21 × 1019 | −1.06 × 1020 | 2.43 × 1020 | −2.67 × 1020 | 1.14 × 1020 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, X.-D.; Zhou, Y.; Wang, Y.-N. Deformation Behavior and Constitutive Model of 34CrNi3Mo during Thermo-Mechanical Deformation Process. Materials 2022, 15, 5220. https://doi.org/10.3390/ma15155220
Jia X-D, Zhou Y, Wang Y-N. Deformation Behavior and Constitutive Model of 34CrNi3Mo during Thermo-Mechanical Deformation Process. Materials. 2022; 15(15):5220. https://doi.org/10.3390/ma15155220
Chicago/Turabian StyleJia, Xiang-Dong, Ying Zhou, and Yi-Ning Wang. 2022. "Deformation Behavior and Constitutive Model of 34CrNi3Mo during Thermo-Mechanical Deformation Process" Materials 15, no. 15: 5220. https://doi.org/10.3390/ma15155220
APA StyleJia, X.-D., Zhou, Y., & Wang, Y.-N. (2022). Deformation Behavior and Constitutive Model of 34CrNi3Mo during Thermo-Mechanical Deformation Process. Materials, 15(15), 5220. https://doi.org/10.3390/ma15155220






