Estimating the Axial Compression Capacity of Concrete-Filled Double-Skin Tubular Columns with Metallic and Non-Metallic Composite Materials
Abstract
:1. Introduction
Pre-Existing Formulae and Design Codes
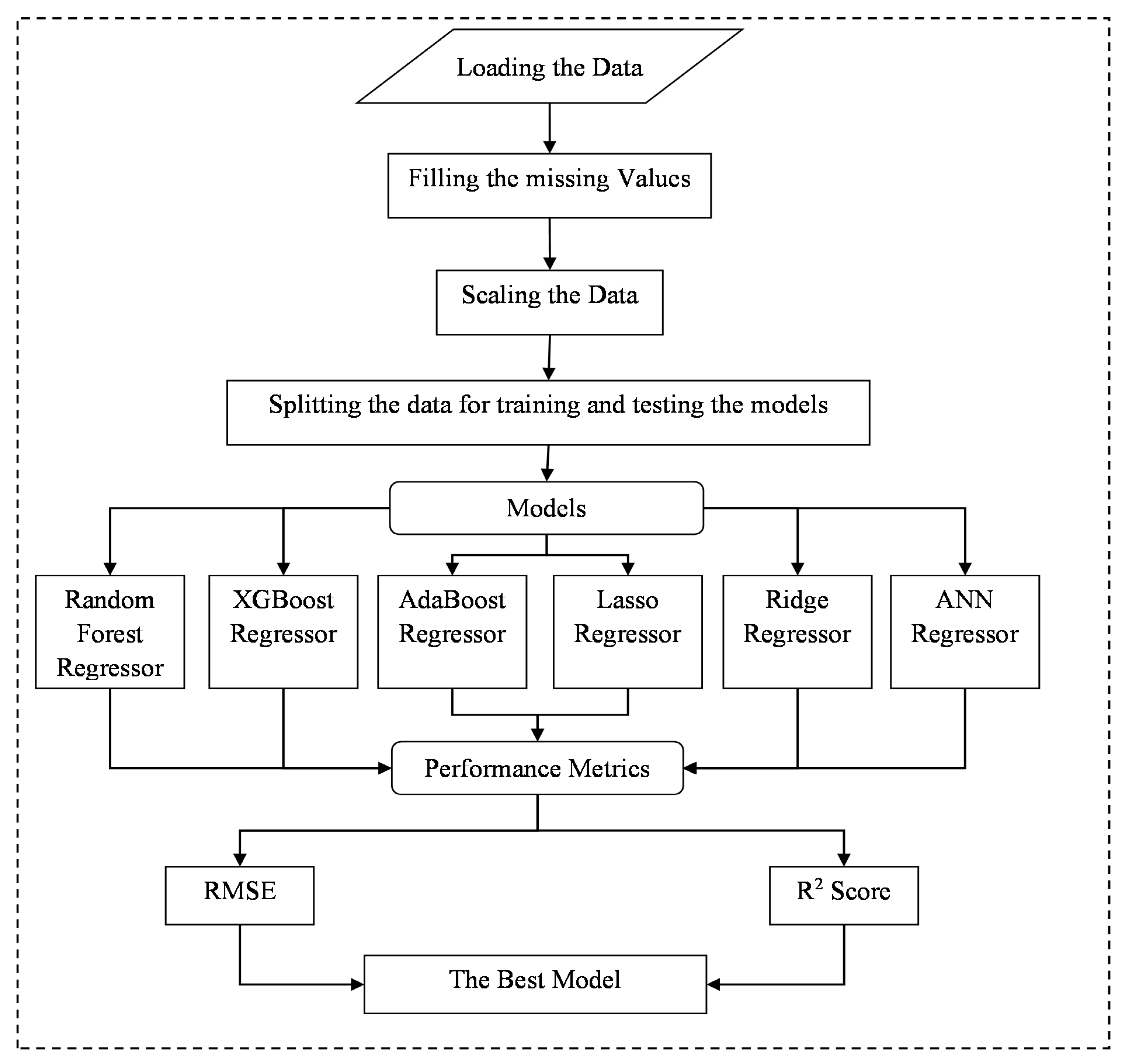
2. Statistical Analysis
- Random Forest Regression (RFR): The RFR method in machine-learning-based algorithms is a process/analysis where regression, classification and other functions that work upon a multitude decision tree during the training phase of datasets that finally offers the outcomes as “classes” aka “classification” or prediction value of average/mean values (regression) that represents the individual trees.
- XGBoost Regression (XGBR): This is an approach that is utilised by researchers for supervised regression-based models that work upon the decision tree approach. In general, the XGBoost is utilised in various ranges of solving problems and applications such as regression, classification, and prediction-based user-defined and ranking problems.
- AdaBoost Regression (ABR): ABR is an estimation process (meta-estimator) where initially it fits the regressor upon the original dataset, and later it additionally fits regressor copies to the same dataset by adjusting the instance weights based on the prediction’s recent error estimation.
- Lasso Regression (LR): LR is a linear regression in ML that utilises shrinkage (i.e., the process of shrinking data values directed to central point/mean value). It generally aims at minimising the prediction error towards quantitative variables, unlike other regression techniques, and makes use of model parameters through constraints which results in “zero” shrink or with a lesser shrink value.
- Ridge Regression (RR): The ridge approach is generally adopted by researchers towards “multicollinearity” problems. This approach/model tunes the data that has suffered from multicollinearity damage/error, where unbiased least-squares and large variance-based predictions are found far away from the original mean values.
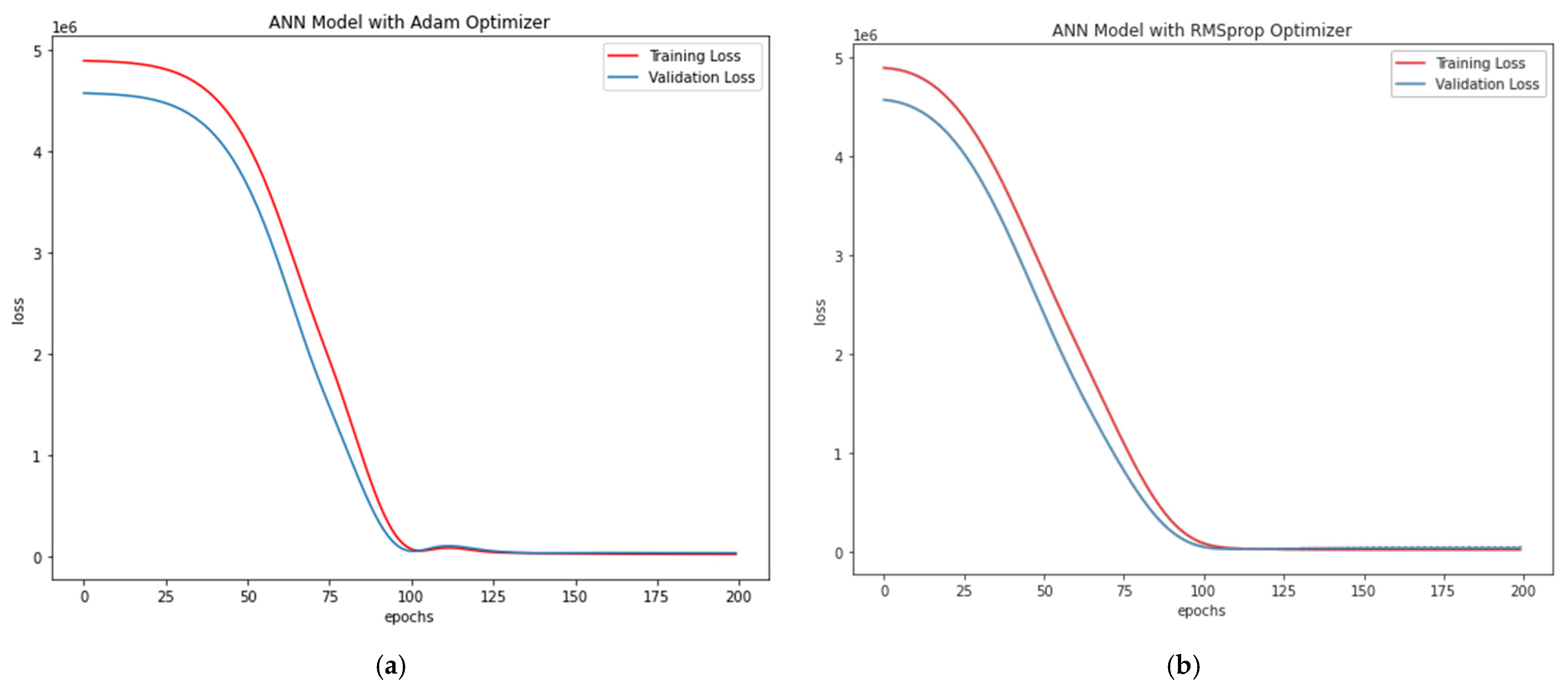
- ANN Regression (ANN-R): In regression, the Artificial Neural Network generally predicts the input functions through the output variable (example: binary) and functions as a classifier (class). To predict and estimate complicated problems in machine language and machine-learning-based algorithms, ANN architecture is widely utilised by researchers along with optimisers (Optimisation: Adaptive Moment as Adam and Gradient Algorithm as RMSprop).
2.1. Random Forest Regression (RFR) through Gini Gain
2.2. XGBoost Regression (XGBR)
2.3. AdaBoost Regression (ABR)
2.4. Lasso Regression (LR)
2.5. Ridge Regression (RR)
2.6. ANN Regression (ANN-R)
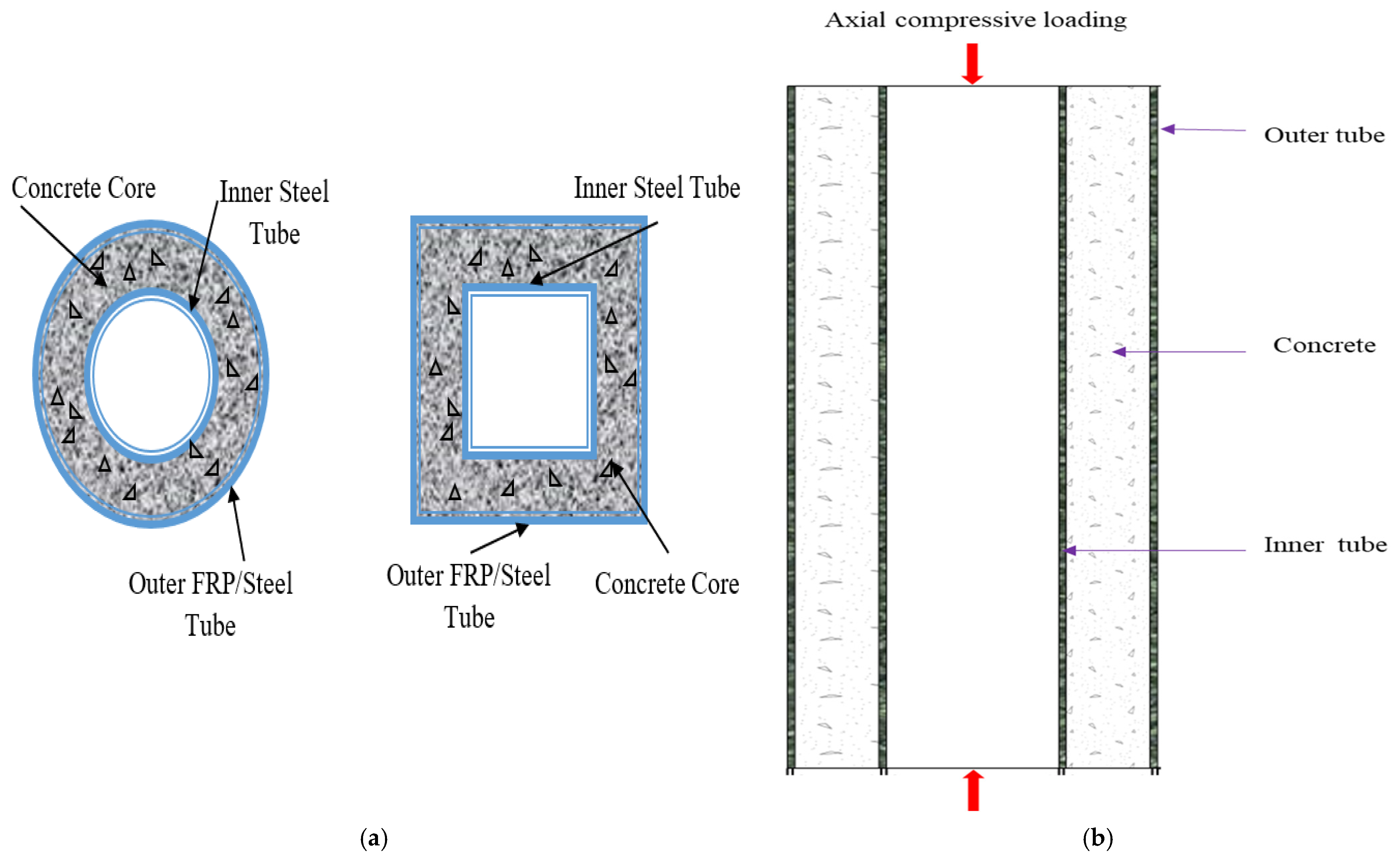
3. Methodology for Analysis of ACC
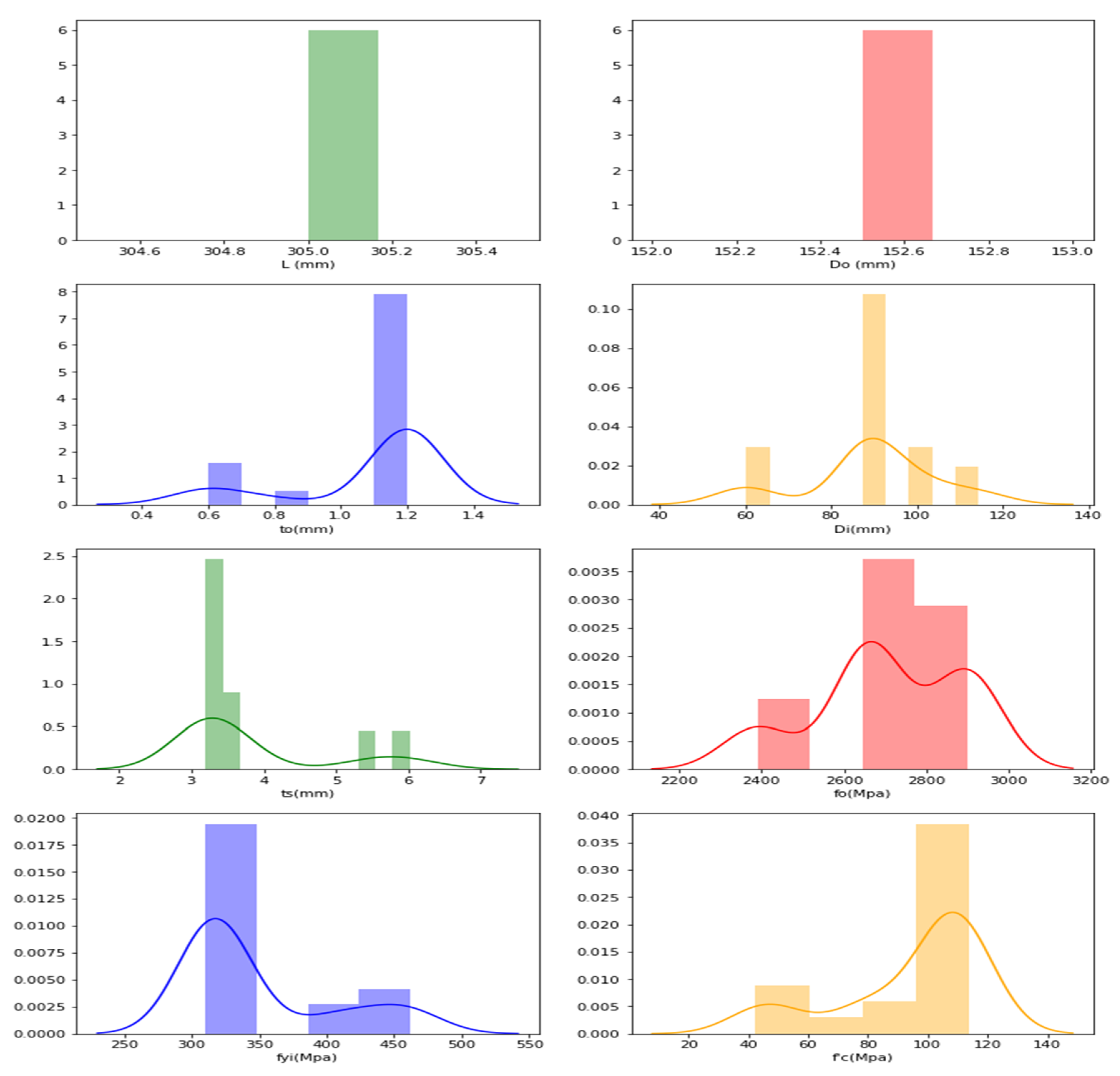
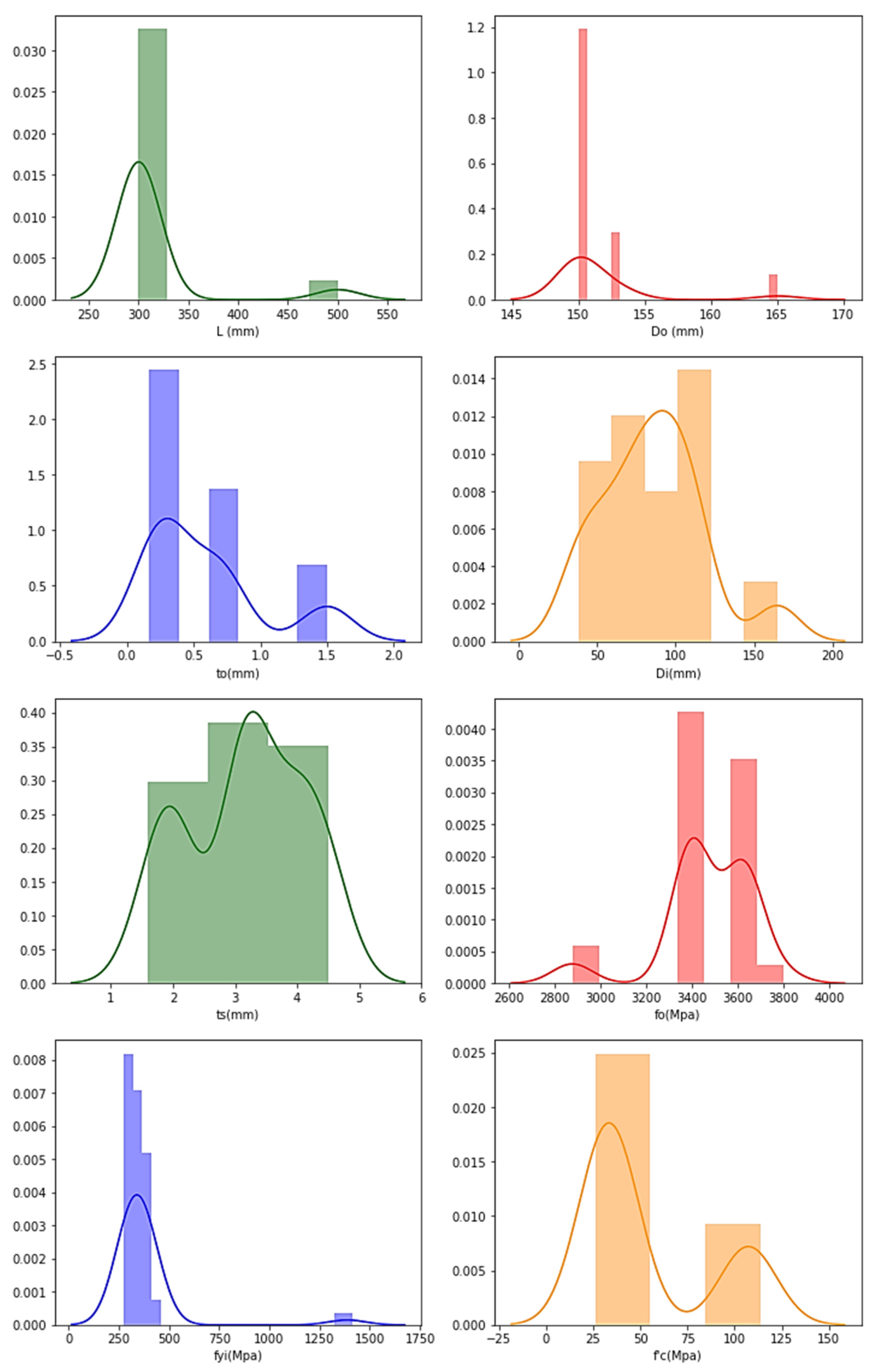
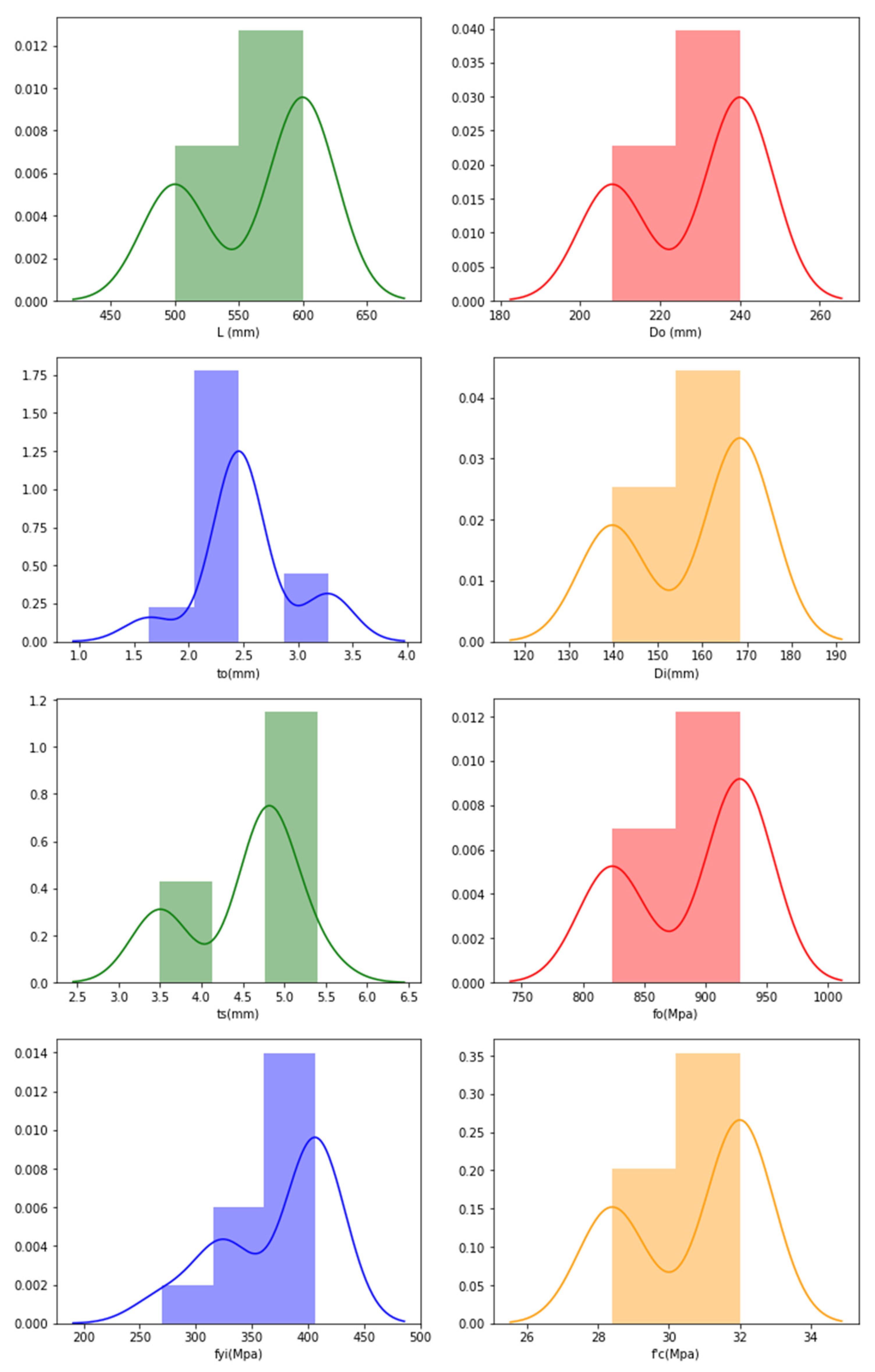
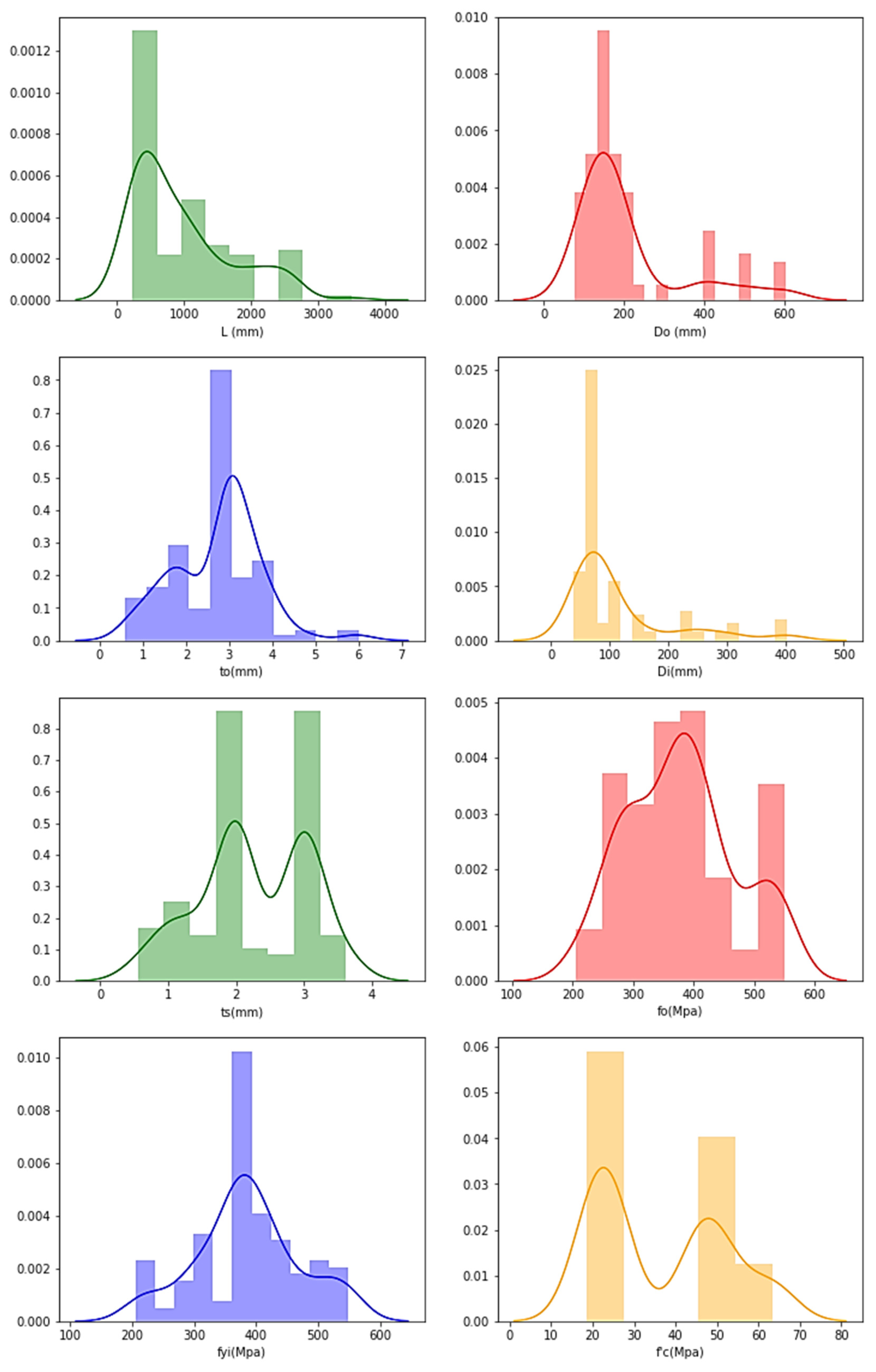
4. Data Collection
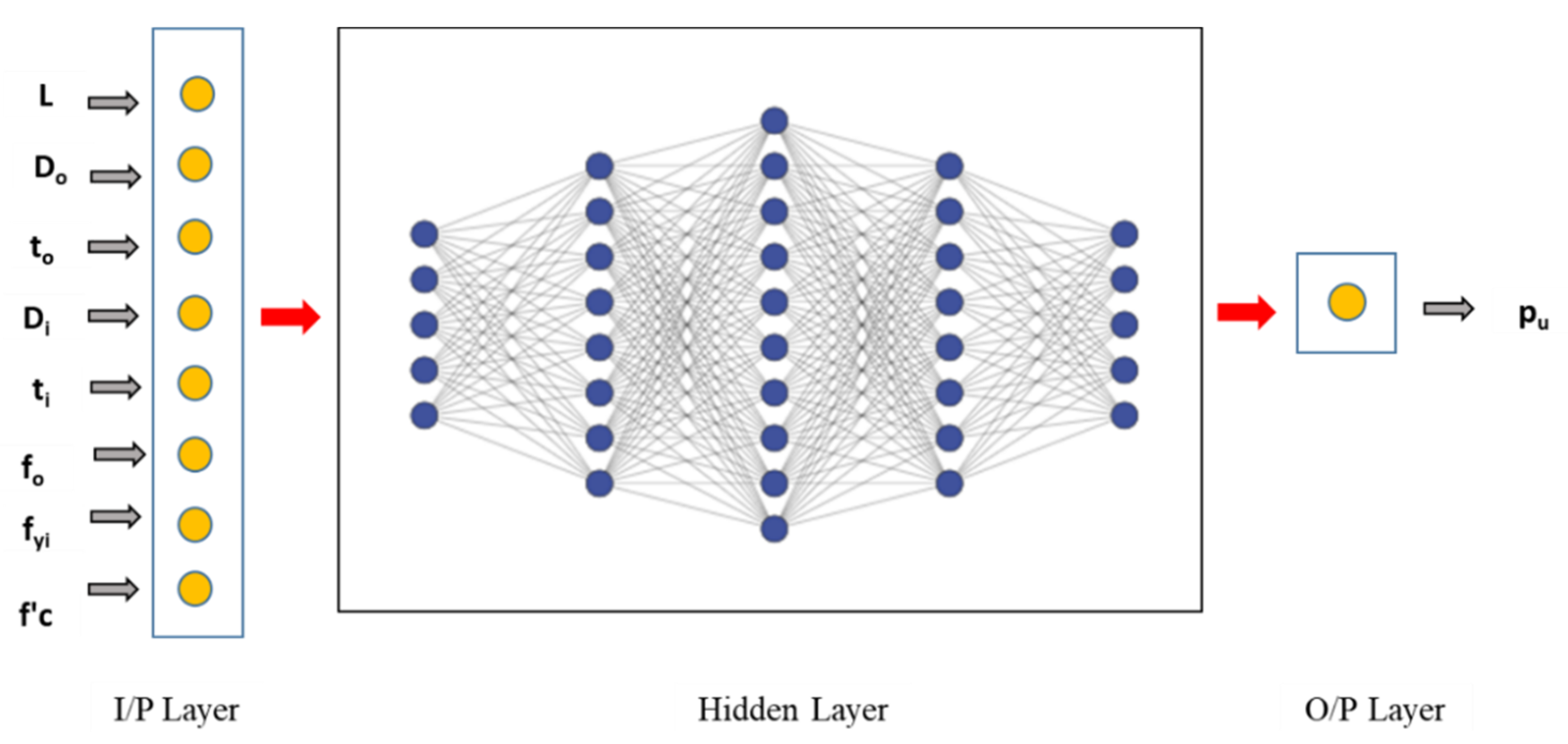
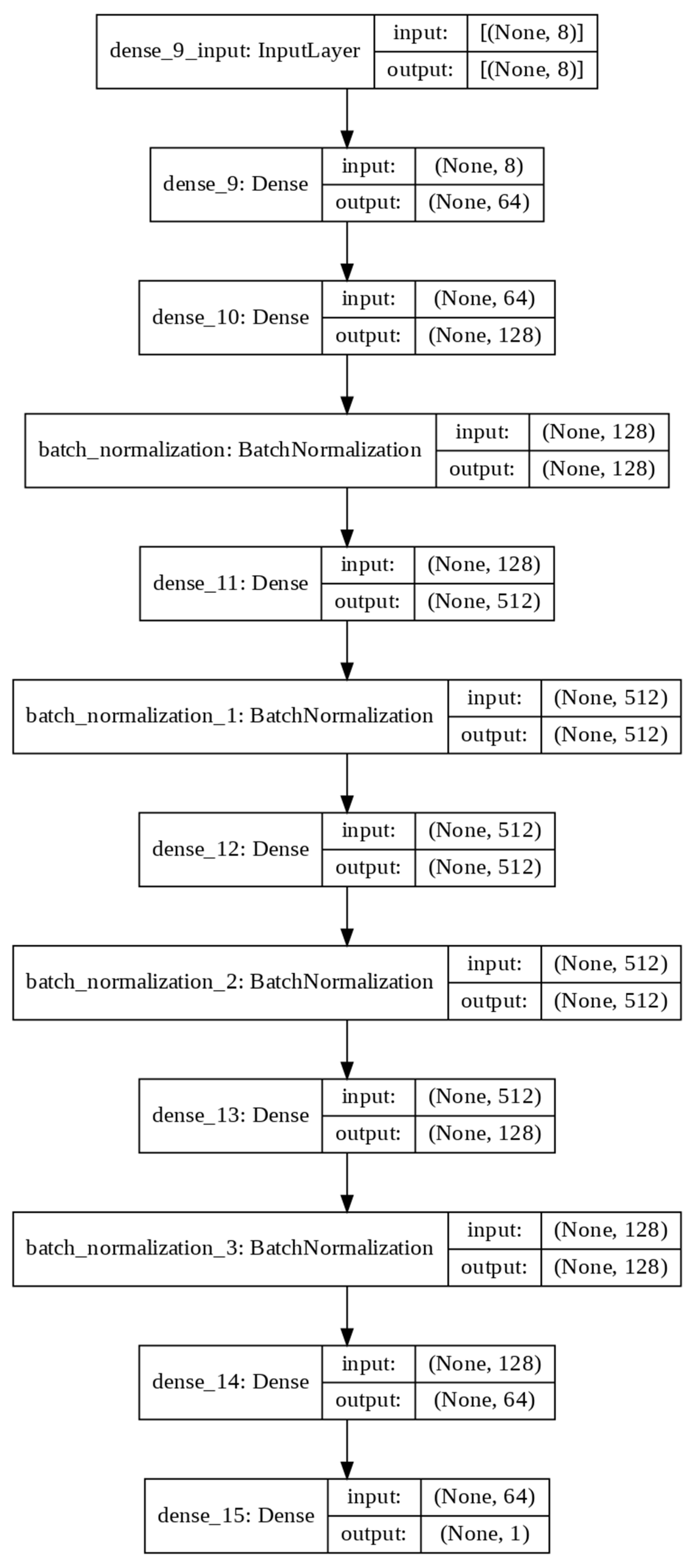
5. ANN Architecture, Parameters and Datasets
5.1. Input Parameters
5.2. Network Architecture:
Auto-Encoder
5.3. Pre-Processing Datasets
6. Results and Findings
6.1. AFRP Dataset
- RFR: The estimated RMSE value is 537.12, where the R2 score is 0.58;
- XGBR: The estimated RMSE is 542.54, where the R2 score is 0.70;
- ABR: The estimated RMSE value is 510.00 where R2 score is 0.62;
- LR: The estimated RMSE value is 660.82, where the R2 score is 0.37;
- RR: The estimated RMSE value is 654.41, where the R2 score is 0.38.
- ANN-R:
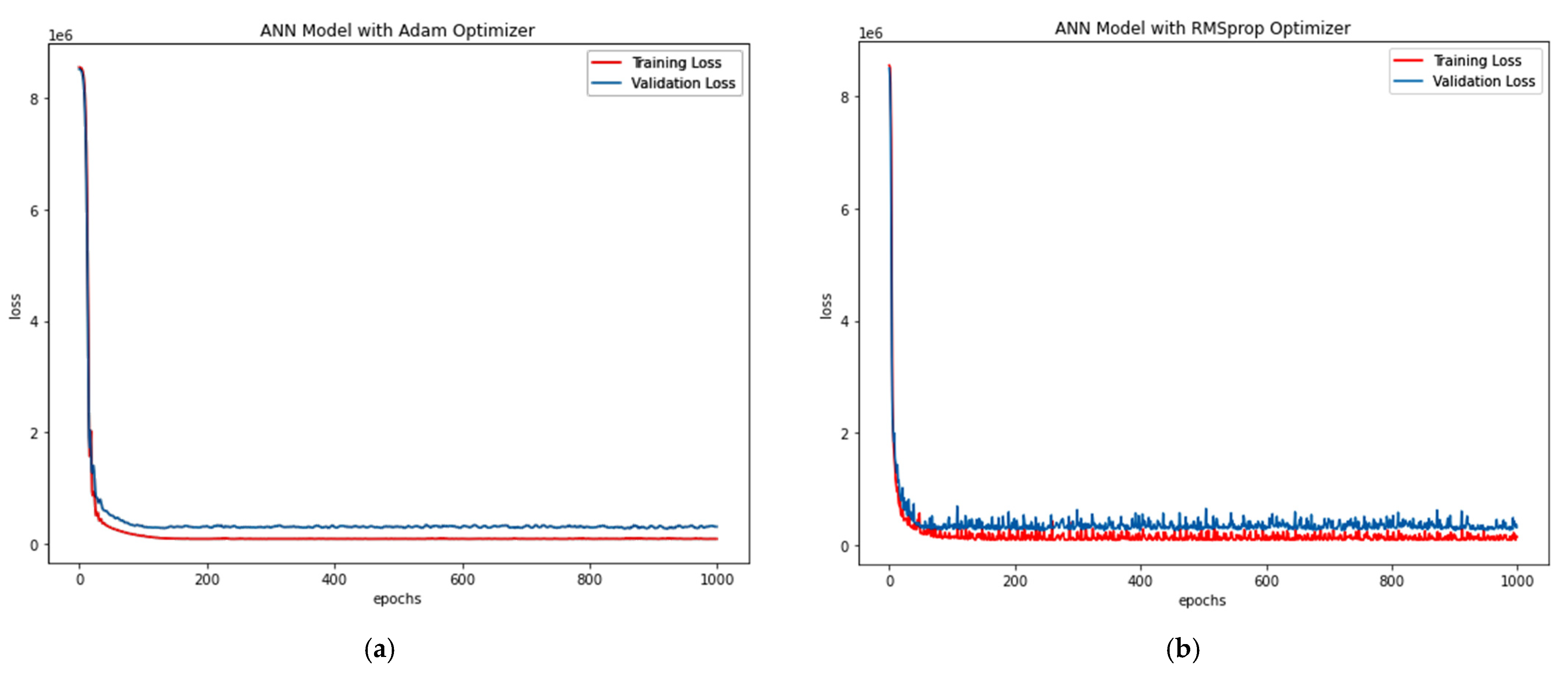
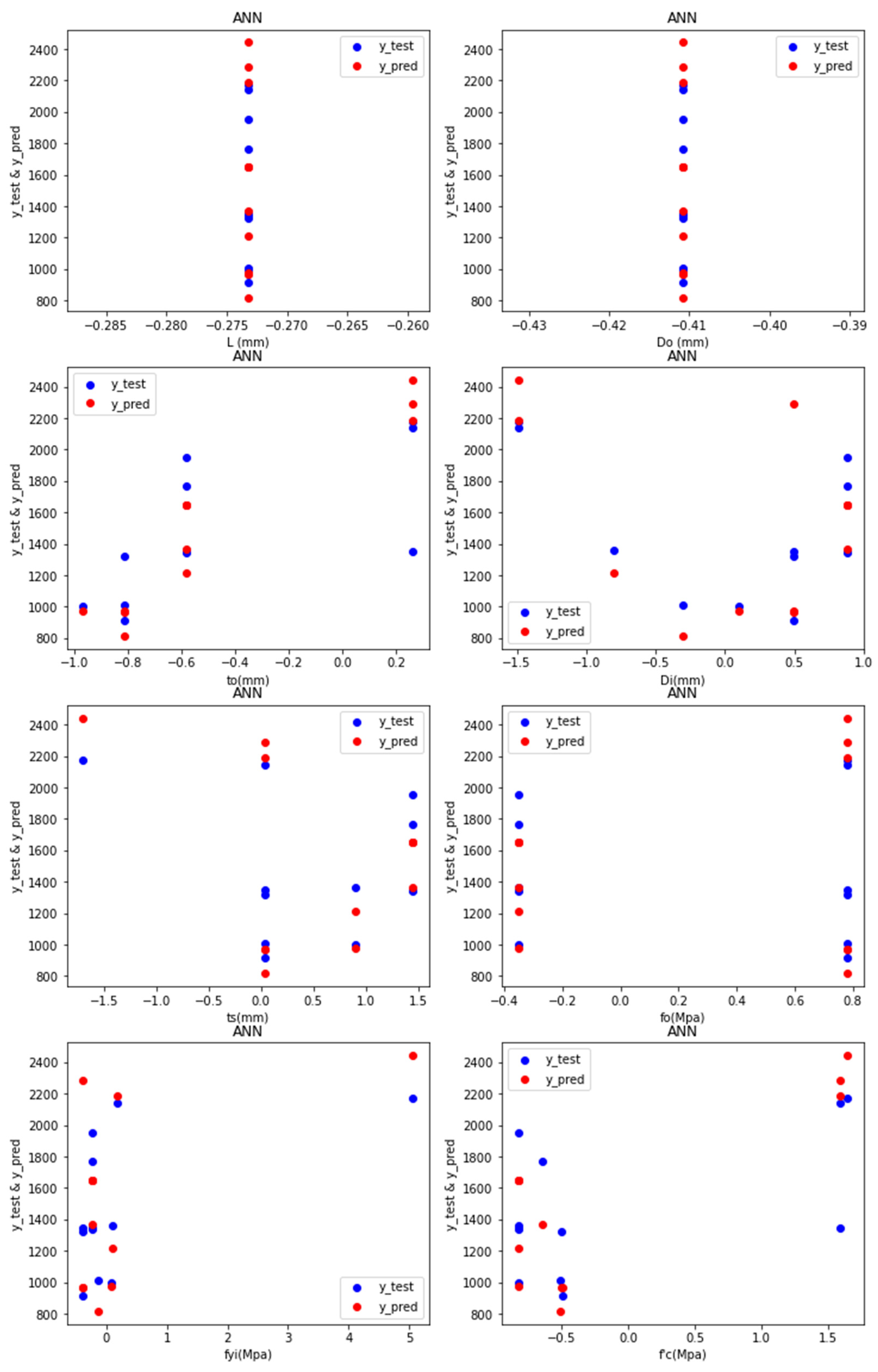
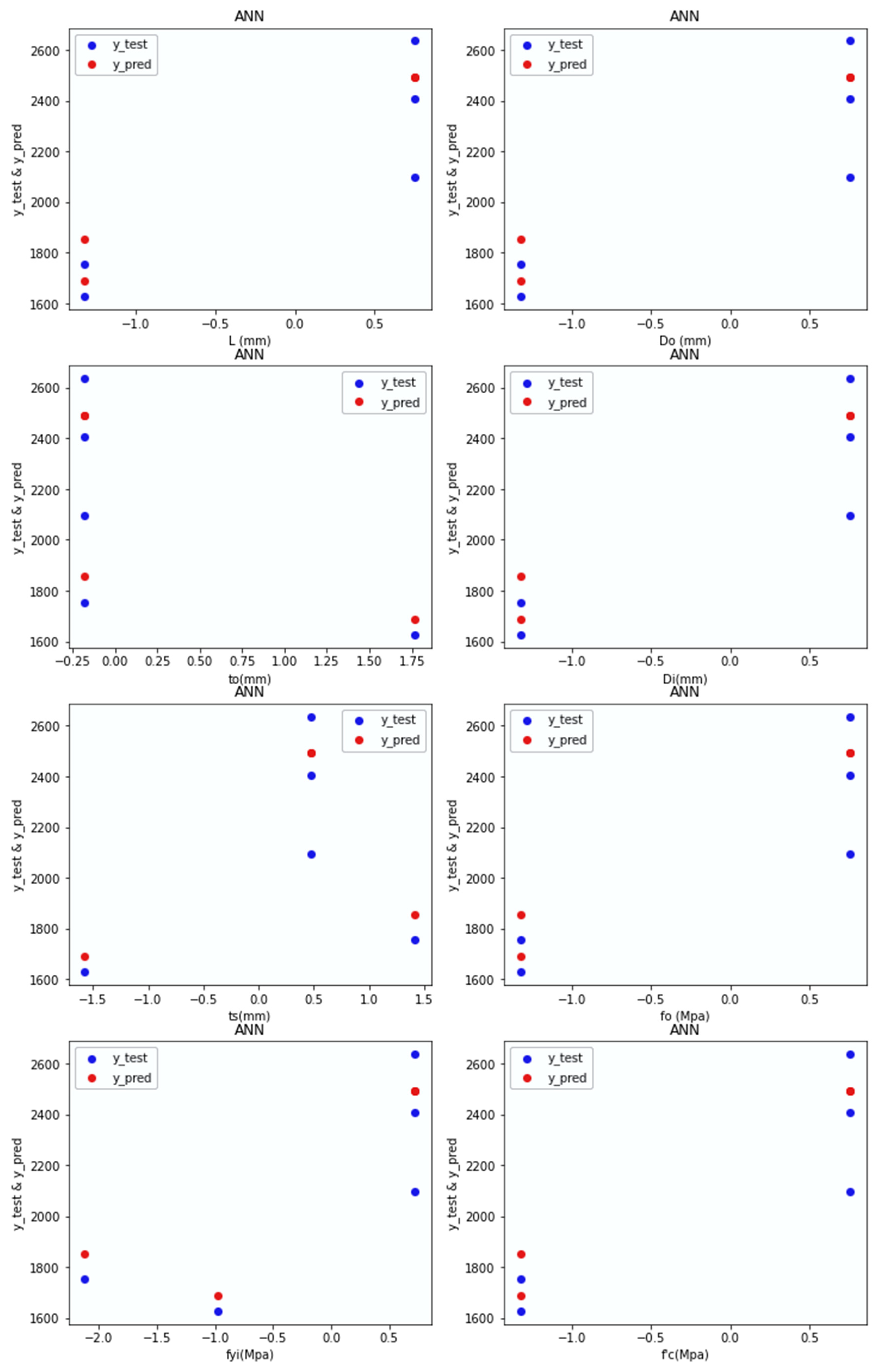
- Adam Optimiser in ANN-R: The estimated RMSE value is 547.77, where the R2 score is 0.57, and the Pu (kN) values of the predicted loss with respect to the values and original values are plotted in Figure 8a.
- RMS prop Optimiser in ANN-R: The estimated RMSE value is 558.12, where the R2 score is 0.55. The Pu (kN) values of the predicted loss with respect to the original values are plotted in Figure 8b.
6.2. CFRP Dataset
- (a)
- RFR: The estimated RMSE value is 355.50, where the R2 score is 0.27;
- (b)
- XGBR: The estimated RMSE is 355.22, where the R2 score is 0.27;
- (c)
- ABR: The estimated RMSE value is 371.04, where the R2 score is 0.20;
- (d)
- LR: The estimated RMSE value is 380.38, where the R2 score is 0.16;
- (e)
- RR: The estimated RMSE value is 380.71, where the R2 score is 0.16.
- (a)
- ANN-R:
- Adam Optimiser in ANN-R: The estimated RMSE value is 380.81, where the R2 score is 0.16, and the Pu (kN) values of the predicted loss with respect to the values and original values are plotted in Figure 11a.
- RMS prop Optimiser in ANN-R: estimated RMSE value is 359.93 where R2 score is 0.25. The Pu (kN) values of the predicted loss with respect to the original values are plotted in Figure 11b.
6.3. GFRP Dataset
- (a)
- RFR: The estimated RMSE value is 670.26, where the R2 score is of 0.25;
- (b)
- XGBR: The estimated RMSE is 569.86, where the R2 score is of 0.45;
- (c)
- ABR: The estimated RMSE value is 549.96, where the R2 score is of 0.49;
- (d)
- LR: The estimated RMSE value is 630.14, where the R2 score is of 0.33;
- (e)
- RR: The estimated RMSE value is 585.16, where the R2 score is of 0.42.
- (f)
- ANN-R:
- Adam Optimiser in ANN-R: estimated RMSE value is 493.80 where R2 score is 0.59, and the Pu (kN) values of the predicted loss with respect to values and original values are plotted in Figure 14a.
- RMS prop Optimiser in ANN-R: estimated RMSE value is 531.77 where R2 score is 0.52. The Pu (kN) values of the predicted loss with respect to and original values are plotted in Figure 14b.
6.4. PETFRP Dataset
- (a)
- RFR: The estimated RMSE value is 204.39, where the R2 score is 0.71;
- (b)
- XGBR: The estimated RMSE is 208.50, where the R2 score is 0.75;
- (c)
- ABR: The estimated RMSE value is 206.84, where the R2 score is 0.70;
- (d)
- LR: The estimated RMSE value is 200.63, where the R2 score is 0.72;
- (e)
- RR: The estimated RMSE value is 200.58, where the R2 score is 0.72.
- (f)
- ANN-R:
- Adam Optimiser in ANN-R: The estimated RMSE value is 202.16, where the R2 score is 0.71, and the pu (kN) values of the predicted loss with respect to values and original values are plotted in Figure 17a.
- RMS prop Optimiser in ANN-R: The estimated RMSE value is 228.49, where the R2 score is 0.63. The pu (kN) values of the predicted loss with respect to and original values are plot-ted in Figure 17b.
6.5. Steel Dataset
- (a)
- RFR: The estimated RMSE value is 195.57, where the R2 score is 0.98;
- (b)
- XGBR: The estimated RMSE is 202.54, where the R2 score is 0.97;
- (c)
- ABR: The estimated RMSE value is 182.86, where the R2 score is 0.98;
- (d)
- LR: The estimated RMSE value is 315.97, where the R2 score is 0.94;
- (e)
- RR: The estimated RMSE value is 317.03, where the R2 score is 0.94.
- (f)
- ANN-R:
- Adam Optimiser in ANN-R: The estimated RMSE value is 172.76, where the R2 score is 0.984, and the pu (kN) values of the predicted loss with respect to values and original values are plotted in Figure 20a.
- RMSprop Optimiser in ANN-R: The estimated RMSE value is 156.10, where the R2 score is 0.987. The pu (kN) values of the predicted loss with respect to and original values are plot-ted in Figure 20b.
7. Development of the Predictive Equations
8. Performance Evaluation and Findings
- The ANN-R with an Adam optimiser is more effective than the RMSprop Optimiser with a RMSE score of 547.77 and R2 score of 0.57. Similarly, it can also be inferred that, among the existing empirical evaluation techniques and formulae aimed at estimating the ACC capacity of CFDST columns in AFRP dataset, the AdaBoost Regressor technique is the most effective, with a lower RMSE score (510.00) and higher R2 score (0.62).
- The ANN-R with a RMSprop Optimiser, more than the Adam optimiser, is effective with a RMSE score of 359.93 and R2 score of 0.25. Likewise, it can also be inferred that the Random Forest Regressor technique is the overall adopted empirical evaluation technique with the most successful formulae aimed at estimating the ACC capacity of CFDST columns in the CFRP dataset. The Random Forest Regressor technique is the most effective, with a lower RMSE score (355.50) and higher R2 score (0.27).
- The ANN-R with an Adam optimiser is more effective than the RMSprop Optimiser, with a RMSE score of 493.80 and R2 score of 0.59. Similarly, it could also be inferred that, among the overall adopted existing empirical evaluation techniques and formulae aimed at estimating the ACC capacity of CFDST columns in the GFRP dataset, the AdaBoost Regressor technique is the most effective, with a lower RMSE score (549.96) and a higher R2 score (0.49).
- The Adam Optimiser-based ANN-R is more effective than the RMSprop Optimiser, with a RMSE score of 202.16 and R2 score of 0.71. Correspondingly, it can also be inferred that the Ridge Regressor technique is the overall adopted empirical evaluation technique with the most successful formulae aimed at estimating the ACC capacity of the CFDST columns in the PETFRP dataset. The Ridge Regressor technique is the most effective, with a lower RMSE score (200.58) and higher R2 score (0.72).
- The ANN-R with a RMSprop Optimiser is more effective than the Adam optimiser, with a RMSE score of 156.10 and R2 score of 0.987. It can also be inferred that, among the overall adopted existing empirical evaluation techniques and formulae towards estimating the ACC capacity of CFDST columns in Steel dataset, the AdaBoost Regressor technique is the most effective, with a lower RMSE score (156.10) and higher R2 score (0.987).
- (a)
- For the Aramid FRP dataset, the ABR is effective, where the RMSE is 510.00, and the R2 is 0.62;
- (b)
- For the Carbon FRP dataset, the RFR is effective, where the RMSE is 355.50, and the R2 is 0.27;
- (c)
- For the Glass FRP dataset the ABR is effective, where the RMSE is 549.96, and the R2 is 0.49;
- (d)
- For the Poly Ethylene Terephthalate FRP dataset the RR is effective, where the RMSE is 200.58, and the R2 is 0.72;
- (e)
- For the Steel dataset the ABR is effective, where the RMSE is 182.26, and the R2 is 0.98.
9. Conclusions
- The main perspective of this study is to indicate the applicability of the ANN technique to derive an effective statistical model for estimating the ultimate axial strength of CFDST composite columns. Moreover, the prediction performances of the design models generated from these techniques are shown statistically.
- The research developed has been used to estimate the axial compression capacity of the concrete-filled double-skin tubular columns with metallic and non-metallic composite materials, which is intended to be used in validating the better formula with statistical analysis. Through the evaluation outcomes, it was found that the ABR along with the RFR techniques in CFDST were reasonably more effective than the other techniques, and thus, it could be concluded that AdaBoost and Random-Forest Regressions are the effective empirical formulae to evaluate the ACC in CFDST columns through the Artificial Neural Network system.
- It can be concluded from the evaluation outcomes that for the outer skin and inner skin with ‘steel’ as the tube’s confinement, capacity would be higher where the R2 score is more than 0.90. Thus, Steel is more effective in the construction of CFDST columns than FRP-based CFDST columns. The developed computational model is valid and reliable, since the outcome yielded had neither a negative value nor a zero value.
- The same techniques and developed architecture could be compared and weighed against other CFDST column-based studies in the future. This research thus provides an effective base for future CFDST-oriented studies. Moreover, it provides the best model to adopt in estimating the ACC of CFDST columns in engineering out of a huge set of existing novel/empirical models. Thus, the study also shows that, given higher R2 scores and lower RMSE scores of the evaluation techniques proves, the adopted empirical formulae is quite effective, where it can be employed in similar research in other fields (medicine, management, etc.) to test the reliability, accuracy and validity of the variables prior to applying the test upon factors to derive outcomes.
- The availability of closed-form equations for accurate predictions of structural responses is beneficial in engineering practice. However, it should be noted that the developed equations are based on an experimental database consisting of 244 samples, and further studies in this area using larger databases are warranted. Furthermore, it should be noted that the results predicted by the developed equations are only valid within the range of the database used. In addition to experimental research, well-calibrated finite-element models could be used to improve the databases. Future study in this area might concentrate on predicting the axial load-carrying capacity under eccentric axial loading in addition to expanding the size of the database utilised in model training.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Specimens | L (mm) | Do (mm) | to (mm) | Di (mm) | ts (mm) | fo (Mpa) | fyi (Mpa) | f′c (Mpa) | Pu (kN) | Author | Year |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CFRP SPECIMENS (outer-CFRP, inner-steel) | |||||||||||
| DSTC-1 | 305 | 152.5 | 0.702 | 88.9 | 3.2 | 3800 | 314.2 | 113.8 | 1624 | Fanggi and Ozbakkaloglu [35] | 2013 |
| DSTC-2 | 305 | 152.5 | 0.702 | 88.9 | 3.2 | 3800 | 314.2 | 113.8 | 1622 | ||
| DSTC-1 | 300 | 150 | 0.234 | 101.6 | 3.2 | 3626 | 302 | 37 | 914 | Ozbakkaloglu and Fanggi [21] | 2014 |
| DSTC-2 | 300 | 150 | 0.234 | 101.6 | 3.2 | 3626 | 302 | 37 | 955 | ||
| DSTC-3 | 300 | 150 | 0.234 | 101.6 | 3.2 | 3626 | 302 | 36.7 | 1145 | ||
| DSTC-4 | 300 | 150 | 0.234 | 101.6 | 3.2 | 3626 | 302 | 36.7 | 1322 | ||
| DSTC-5 | 300 | 150 | 0.234 | 76.1 | 3.2 | 3626 | 358 | 36.9 | 911 | ||
| DSTC-6 | 300 | 150 | 0.234 | 76.1 | 3.2 | 3626 | 358 | 36.9 | 932 | ||
| DSTC-7 | 300 | 150 | 0.234 | 76.1 | 3.2 | 3626 | 351 | 36.4 | 1009 | ||
| DSTC-8 | 300 | 150 | 0.234 | 76.1 | 3.2 | 3626 | 351 | 36.4 | 1048 | ||
| DSTC-9 | 300 | 150 | 0.702 | 101.6 | 3.2 | 3626 | 302 | 37 | 1448 | ||
| DSTC-10 | 300 | 150 | 0.702 | 101.6 | 3.2 | 3626 | 302 | 37 | 1497 | ||
| DSTC-11 | 300 | 150 | 0.702 | 101.6 | 3.2 | 3626 | 302 | 106 | 1513 | ||
| DSTC-12 | 300 | 150 | 0.702 | 101.6 | 3.2 | 3626 | 302 | 106 | 1349 | ||
| DSTC-13 | 300 | 150 | 0.702 | 101.6 | 3.2 | 3626 | 302 | 106 | 2534 | ||
| DSTC-14 | 300 | 150 | 0.702 | 101.6 | 3.2 | 3626 | 302 | 106 | 3185 | ||
| DSTC-15 | 300 | 150 | 0.702 | 76.1 | 3.2 | 3626 | 358 | 106 | 2066 | ||
| DSTC-16 | 300 | 150 | 0.702 | 76.1 | 3.2 | 3626 | 358 | 106 | 1912 | ||
| DSTC-17 | 300 | 150 | 0.702 | 76.1 | 3.2 | 3626 | 351 | 107 | 2627 | ||
| DSTC-18 | 300 | 150 | 0.702 | 76.1 | 3.2 | 3626 | 351 | 107 | 2521 | ||
| DSTC-19 | 300 | 150 | 0.702 | 38.1 | 3.2 | 3626 | 411 | 106 | 2203 | ||
| DSTC-20 | 300 | 150 | 0.702 | 38.1 | 3.2 | 3626 | 411 | 106 | 2142 | ||
| DSTC-21 | 300 | 150 | 0.702 | 38.1 | 1.6 | 3626 | 434 | 106 | 2294 | ||
| DSTC-22 | 300 | 150 | 0.702 | 38.1 | 1.6 | 3626 | 434 | 106 | 2384 | ||
| DSTC-23 | 300 | 150 | 0.702 | 38.1 | 1.6 | 3626 | 1360 | 108 | 2175 | ||
| DSTC-24 | 300 | 150 | 0.702 | 38.1 | 1.6 | 3626 | 1414 | 108 | 2533 | ||
| DN2-60-I | 300 | 150 | 0.334 | 60 | 4 | 3400 | 394 | 32 | 1490 | Qi Cao [35] | 2017 |
| DN2-60-II | 300 | 150 | 0.334 | 60 | 4 | 3400 | 394 | 32 | 1560 | ||
| DE2-60-I | 300 | 150 | 0.334 | 60 | 4 | 3400 | 394 | 26 | 1255 | ||
| DE2-60-II | 300 | 150 | 0.334 | 60 | 4 | 3400 | 394 | 26 | 1362 | ||
| DN1-89-I | 300 | 150 | 0.167 | 89 | 4 | 3400 | 391 | 32 | 1118 | ||
| DN1-89-II | 300 | 150 | 0.167 | 89 | 4 | 3400 | 391 | 32 | 1103 | ||
| DE1-89-I | 300 | 150 | 0.167 | 89 | 4 | 3400 | 391 | 26 | 994 | ||
| DE1-89-II | 300 | 150 | 0.167 | 89 | 4 | 3400 | 391 | 26 | 1001 | ||
| DN2-89-I | 300 | 150 | 0.334 | 89 | 4 | 3400 | 391 | 32 | 1438 | ||
| DN2-89-II | 300 | 150 | 0.334 | 89 | 4 | 3400 | 391 | 32 | 1373 | ||
| DE2-89-I | 300 | 150 | 0.334 | 89 | 4 | 3400 | 391 | 26 | 1341 | ||
| DE2-89-II | 300 | 150 | 0.334 | 89 | 4 | 3400 | 391 | 26 | 1365 | ||
| DN2-114-I | 300 | 150 | 0.334 | 114 | 4.5 | 3400 | 332 | 32 | 1340 | ||
| DN2-114-II | 300 | 150 | 0.334 | 114 | 4.5 | 3400 | 332 | 32 | 1313 | ||
| DE2-114-I | 300 | 150 | 0.334 | 114 | 4.5 | 3400 | 332 | 26 | 1349 | ||
| DE2-114-II | 300 | 150 | 0.334 | 114 | 4.5 | 3400 | 332 | 26 | 1342 | ||
| DN2-114N-I | 300 | 150 | 0.334 | 114 | 4.5 | 3400 | 332 | 32 | 1767 | ||
| DN2-114N-II | 300 | 150 | 0.334 | 114 | 4.5 | 3400 | 332 | 32 | 1724 | ||
| DE2-114N-I | 300 | 150 | 0.334 | 114 | 4.5 | 3400 | 332 | 26 | 1945 | ||
| DE2-114N-II | 300 | 150 | 0.334 | 114 | 4.5 | 3400 | 332 | 26 | 1953 | ||
| DC28(1) | 300 | 153 | 1.5 | 42.2 | 2 | 3400 | 289 | 39.8 | 1133 | Ying Wu Zhou [36] | 2017 |
| DC28(2) | 300 | 153 | 1.5 | 42.2 | 2 | 3400 | 289 | 39.8 | 1118 | ||
| DC28(3) | 300 | 153 | 1.5 | 42.2 | 2 | 3400 | 289 | 39.8 | 1113 | ||
| DC36(1) | 300 | 153 | 1.5 | 54.7 | 2 | 3400 | 366 | 39.8 | 1082 | ||
| DC36(2) | 300 | 153 | 1.5 | 54.7 | 2 | 3400 | 366 | 39.8 | 1078 | ||
| DC36(3) | 300 | 153 | 1.5 | 54.7 | 2 | 3400 | 366 | 39.8 | 1060 | ||
| DC47(1) | 300 | 153 | 1.5 | 70.8 | 2 | 3400 | 288 | 39.8 | 1026 | ||
| DC47(2) | 300 | 153 | 1.5 | 70.8 | 2 | 3400 | 288 | 39.8 | 971 | ||
| DC47(3) | 300 | 153 | 1.5 | 70.8 | 2 | 3400 | 288 | 39.8 | 956 | ||
| CCFST-1 | 500 | 165 | 0.167 | 164.8 | 2 | 2878 | 275 | 31.2 | 1948.8 | Jun Deng [37] | 2017 |
| CCFST-2 | 500 | 165 | 0.167 | 164.8 | 2 | 2878 | 275 | 31.2 | 1948.8 | ||
| CCFST-3 | 500 | 165 | 0.167 | 164.8 | 2 | 2878 | 275 | 31.2 | 1948.8 | ||
| CCFST-4 | 500 | 165 | 0.167 | 164.8 | 2 | 2878 | 275 | 31.2 | 1948.8 | ||
| AFRP SPECIMENS (outer-AFRP, inner-steel) | |||||||||||
| DSTC-3 | 305 | 152.5 | 0.8 | 88.9 | 3.2 | 2900 | 314.2 | 113.8 | 1919 | Fanggi and Ozbakkaloglu [20] | 2013 |
| DSTC-4 | 305 | 152.5 | 0.8 | 88.9 | 3.2 | 2900 | 314.2 | 113.8 | 1965 | ||
| DSTC-5 | 305 | 152.5 | 1.2 | 88.9 | 3.2 | 2900 | 314.2 | 113.8 | 2247 | ||
| DSTC-6 | 305 | 152.5 | 1.2 | 88.9 | 3.2 | 2900 | 314.2 | 113.8 | 2251 | ||
| DSTC-7 | 305 | 152.5 | 0.6 | 88.9 | 3.2 | 2900 | 314.2 | 49.8 | 1664 | ||
| DSTC-8 | 305 | 152.5 | 0.6 | 88.9 | 3.2 | 2900 | 314.2 | 49.8 | 1567 | ||
| DSTC-9 | 305 | 152.5 | 1.2 | 60.3 | 3.6 | 2900 | 459.4 | 113.8 | 2745 | ||
| DSTC-10 | 305 | 152.5 | 1.2 | 60.3 | 3.6 | 2900 | 459.4 | 113.8 | 2783 | ||
| DSTC-11 | 305 | 152.5 | 1.2 | 88.9 | 5.5 | 2900 | 407.7 | 113.8 | 2843 | ||
| DSTC-12 | 305 | 152.5 | 1.2 | 88.9 | 5.5 | 2900 | 407.7 | 113.8 | 2846 | ||
| DSTC-13 | 305 | 152.5 | 1.2 | 114.3 | 6.02 | 2900 | 342.3 | 113.8 | 2331 | ||
| DSTC-14 | 305 | 152.5 | 1.2 | 114.3 | 6.02 | 2900 | 342.3 | 113.8 | 2228 | ||
| DSTC-15 | 305 | 152.5 | 1.2 | 89 | 3.5 | 2900 | 461.8 | 113.8 | 1482 | ||
| DSTC-16 | 305 | 152.5 | 1.2 | 89 | 3.5 | 2900 | 461.8 | 113.8 | 1346 | ||
| DSTC-1 | 305 | 152.5 | 0.6 | 88.9 | 3.2 | 2663 | 320 | 47.3 | 2261 | Togay Ozbakkaloglu [38] | 2015 |
| DSTC-2 | 305 | 152.5 | 0.6 | 88.9 | 3.2 | 2663 | 320 | 47.3 | 2217 | ||
| DSTC-3 | 305 | 152.5 | 1.2 | 88.9 | 3.2 | 2663 | 320 | 75.95 | 3844 | ||
| DSTC-4 | 305 | 152.5 | 1.2 | 88.9 | 3.2 | 2663 | 320 | 75.95 | 3789 | ||
| DSTC-5 | 305 | 152.5 | 1.2 | 88.9 | 3.2 | 2663 | 320 | 104.6 | 3534 | ||
| DSTC-6 | 305 | 152.5 | 1.2 | 88.9 | 3.2 | 2663 | 320 | 104.6 | 3357 | ||
| DSTC-7 | 305 | 152.5 | 1.2 | 88.9 | 5.5 | 2663 | 408 | 104.6 | 3713 | ||
| DSTC-8 | 305 | 152.5 | 1.2 | 88.9 | 5.5 | 2663 | 408 | 104.6 | 4110 | ||
| DSTC-9 | 305 | 152.5 | 1.2 | 60.3 | 3.6 | 2663 | 319 | 104.6 | 3496 | ||
| DSTC-10 | 305 | 152.5 | 1.2 | 60.3 | 3.6 | 2663 | 319 | 104.6 | 3314 | ||
| DSTC-11 | 305 | 152.5 | 1.2 | 101.6 | 3.2 | 2663 | 310 | 104.6 | 3816 | ||
| DSTC-12 | 305 | 152.5 | 1.2 | 101.6 | 3.2 | 2663 | 310 | 104.6 | 3678 | ||
| DSTC-13 | 305 | 152.5 | 1.2 | 114.3 | 6.02 | 2663 | 449 | 104.6 | 4293 | ||
| DSTC-14 | 305 | 152.5 | 1.2 | 114.3 | 6.02 | 2663 | 449 | 104.6 | 3964 | ||
| DSTC-15 | 305 | 152.5 | 1.2 | 101.6 | 3.2 | 2663 | 310 | 104.6 | 2022 | ||
| DSTC-16 | 305 | 152.5 | 1.2 | 101.6 | 3.2 | 2663 | 310 | 104.6 | 2021 | ||
| DSTC-17 | 305 | 152.5 | 1.2 | 101.6 | 3.2 | 2663 | 310 | 104.6 | 2011 | ||
| DSTC-18 | 305 | 152.5 | 1.2 | 101.6 | 3.2 | 2663 | 310 | 104.6 | 1839 | ||
| DSTC-1C | 305 | 152.5 | 0.6 | 88.9 | 3.2 | 2390 | 320 | 42.5 | 2072 | ||
| DSTC-2C | 305 | 152.5 | 0.6 | 88.9 | 3.2 | 2390 | 320 | 42.5 | 1936 | ||
| DSTC-3C | 305 | 152.5 | 1.2 | 88.9 | 3.2 | 2390 | 320 | 82.4 | 3679 | ||
| DSTC-4C | 305 | 152.5 | 1.2 | 88.9 | 3.2 | 2390 | 320 | 82.4 | 3812 | ||
| DSTC-5C | 305 | 152.5 | 1.2 | 60.3 | 3.6 | 2390 | 319 | 82.4 | 3515 | ||
| DSTC-6C | 305 | 152.5 | 1.2 | 60.3 | 3.6 | 2390 | 319 | 82.4 | 3632 | ||
| GFRP SPECIMENS (outer-GFRP, inner-steel) | |||||||||||
| DS1A | 305 | 152.5 | 0.17 | 76.1 | 3.2 | 1825.5 | 352.7 | 39.6 | 793.75 | Teng [18] | 2007 |
| DS2A | 305 | 152.5 | 0.34 | 76.1 | 3.2 | 1825.5 | 352.7 | 39.6 | 1044.2 | ||
| DS3A | 305 | 152.5 | 0.51 | 76.1 | 3.2 | 1825.5 | 352.7 | 39.6 | 1214 | ||
| DS1B | 305 | 152.5 | 0.17 | 76.1 | 3.2 | 1825.5 | 352.7 | 39.6 | 829.27 | ||
| DS2B | 305 | 152.5 | 0.34 | 76.1 | 3.2 | 1825.5 | 352.7 | 39.6 | 1024.8 | ||
| DS3B | 305 | 152.5 | 0.51 | 76.1 | 3.2 | 1825.5 | 352.7 | 39.6 | 1201.9 | ||
| FS-Y0-C30-T4 | 800 | 400 | 4 | 325 | 3.25 | 215 | 235 | 29.9 | 2824 | Zhe Xiong [39] | 2018 |
| FS-Y25-C30-T4 | 800 | 400 | 4 | 325 | 3.25 | 215 | 235 | 32.2 | 2714 | ||
| FS-Y50-C30-T4 | 800 | 400 | 4 | 325 | 3.25 | 215 | 235 | 30.7 | 2884 | ||
| FS-Y75-C30-T4 | 800 | 400 | 4 | 325 | 3.25 | 215 | 235 | 32.2 | 2694 | ||
| FS-Y100-C30-T4 | 800 | 400 | 4 | 325 | 3.25 | 215 | 235 | 33.4 | 2765 | ||
| FS-Y100-C40-T4 | 800 | 400 | 4 | 325 | 3.25 | 215 | 235 | 33.4 | 2860 | ||
| FS-Y100-C30-T4.5 | 800 | 400 | 4.5 | 325 | 3.25 | 215 | 235 | 33.4 | 3314 | ||
| FS-Y100-C30-T5 | 800 | 400 | 5 | 325 | 3.25 | 215 | 235 | 38.9 | 2962 | ||
| D30-A4-F80-M1 | 400 | 200 | 4 | 140 | 5 | 1970 | 365.8 | 29.3 | 2563.7 | Bing Zhang [40] | 2020 |
| D30-A4-F80-M2 | 400 | 200 | 4 | 140 | 5 | 1970 | 365.8 | 29.3 | 2359.4 | ||
| D30-B4-F80-M1 | 400 | 200 | 4 | 120 | 4.5 | 1970 | 358.7 | 29.3 | 2685.5 | ||
| D30-B4-F80-M2 | 400 | 200 | 4 | 120 | 4.5 | 1970 | 358.7 | 29.3 | 2735.5 | ||
| D30-A4-F60-M1 | 400 | 200 | 4 | 140 | 5 | 1970 | 365.8 | 29.3 | 2186.6 | ||
| D30-A4-F60-M2 | 400 | 200 | 4 | 140 | 5 | 1970 | 365.8 | 29.3 | 2185.5 | ||
| D30-B4-F60-M1 | 400 | 200 | 4 | 120 | 4.5 | 1970 | 358.7 | 29.3 | 2156 | ||
| D30-B4-F60-M2 | 400 | 200 | 4 | 120 | 4.5 | 1970 | 358.7 | 29.3 | 2109.2 | ||
| D30-A8-F60-M1 | 400 | 200 | 8 | 140 | 5 | 1970 | 365.8 | 29.3 | 3100.6 | ||
| D30-A8-F60-M2 | 400 | 200 | 8 | 140 | 5 | 1970 | 365.8 | 29.3 | 2975 | ||
| D30-A4-F45-M1 | 400 | 200 | 4 | 140 | 5 | 1970 | 365.8 | 29.3 | 1207.3 | ||
| D30-A4-F45-M2 | 400 | 200 | 4 | 140 | 5 | 1970 | 365.8 | 29.3 | 1232.3 | ||
| D30-B4-F45-M1 | 400 | 200 | 4 | 120 | 4.5 | 1970 | 358.7 | 29.3 | 1284.9 | ||
| D30-B4-F45-M2 | 400 | 200 | 4 | 120 | 4.5 | 1970 | 358.7 | 29.3 | 1176.6 | ||
| D30-A8-F45-M1 | 400 | 200 | 8 | 140 | 5 | 1970 | 365.8 | 29.3 | 1562.7 | ||
| D30-A8-F45-M2 | 400 | 200 | 8 | 140 | 5 | 1970 | 365.8 | 29.3 | 1441.2 | ||
| M1 | 400 | 205.3 | 0.17 | 140.3 | 5.3 | 1752 | 325.5 | 43.9 | 1824 | Yu and Zhang [41] | 2012 |
| M2 | 400 | 205.3 | 0.34 | 140.3 | 5.3 | 1752 | 325.5 | 43.9 | 1799 | ||
| F1 | 400 | 205.3 | 0.17 | 140.3 | 5.3 | 1752 | 325.5 | 43.9 | 1798 | ||
| F2 | 400 | 205.3 | 0.34 | 140.3 | 5.3 | 1752 | 325.5 | 43.9 | 1724 | ||
| PU1 | 400 | 205.3 | 0.17 | 140.3 | 5.3 | 1752 | 325.5 | 43.9 | 1783 | ||
| PU2 | 400 | 205.3 | 0.34 | 140.3 | 5.3 | 1752 | 325.5 | 43.9 | 1794 | ||
| PR1 | 400 | 205.3 | 0.17 | 140.3 | 5.3 | 1752 | 325.5 | 43.9 | 1774 | ||
| PR2 | 400 | 205.3 | 0.34 | 140.3 | 5.3 | 1752 | 325.5 | 43.9 | 1637 | ||
| F4-24-E325 | 2032 | 610 | 9.5 | 356 | 6.4 | 575 | 324 | 35.6 | - | Omar [42] | 2017 |
| F4-24-E344 | 2032 | 610 | 9.5 | 406 | 12.7 | 575 | 324 | 39.8 | - | ||
| F4-24-P124-R | 2032 | 610 | 3.2 | 406 | 6.4 | 575 | 324 | 39.8 | - | ||
| D37-6-0.2 | 1350 | 300 | 6 | 219 | 6 | - | 360.3 | 37.4 | 530.8 | Zhang [43] | 2015 |
| D56-6-0.2 | 1350 | 300 | 6 | 219 | 6 | - | 360.3 | 56 | 668.3 | ||
| D80-6-0.4 | 1350 | 300 | 6 | 219 | 6 | - | 360.3 | 80 | 1546 | ||
| D80-6-0.4-S | 1350 | 300 | 6 | 219 | 6 | - | 360.3 | 80 | 1624 | ||
| D80-10-0.4 | 1350 | 300 | 10 | 219 | 6 | - | 360.3 | 82.7 | 1479 | ||
| D116-6-0.2 | 1350 | 300 | 6 | 219 | 6 | - | 360.3 | 116.4 | 1060 | ||
| D116-6-0.4 | 1350 | 300 | 6 | 219 | 6 | - | 360.3 | 117.3 | 2116 | ||
| D116-10-0.4 | 1350 | 300 | 10 | 219 | 6 | - | 360.3 | 114.8 | 2103 | ||
| D54-2FW-M | 400 | 200 | 2.2 | 159 | 5 | - | 320.4 | 54.1 | 1965 | Zhang [22] | 2017 |
| D54-4FW-M | 400 | 200 | 4.7 | 159 | 5 | - | 320.4 | 54.1 | 2530 | ||
| D84-4FW-M1 | 400 | 200 | 4.7 | 159 | 5 | - | 320.4 | 84.6 | 4461 | ||
| D84-4FW-M2 | 400 | 200 | 4.7 | 159 | 5 | - | 320.4 | 84.6 | 2650 | ||
| D84-4FW-MB | 400 | 200 | 4.7 | 120 | 4.5 | - | 419.5 | 84.6 | 2763 | ||
| D84-9FW-M | 400 | 200 | 9.5 | 159 | 5 | - | 320.4 | 84.6 | 3413 | ||
| D104-4FW-M | 400 | 200 | 4.7 | 159 | 5 | - | 320.4 | 104.6 | 2616 | ||
| D104-9FW-M | 400 | 200 | 9.5 | 159 | 5 | - | 320.4 | 104.6 | 3512 | ||
| D40-6FW-M | 600 | 300 | 6 | 219 | 6 | - | 319.4 | 40.9 | 6002 | ||
| D66-6FW-M | 600 | 300 | 6 | 219 | 6 | - | 319.4 | 66.1 | 5284 | ||
| D85-6FW-M | 600 | 300 | 6 | 219 | 6 | - | 319.4 | 85.8 | 5482 | ||
| D85-10FW-M | 600 | 300 | 10 | 219 | 6 | - | 319.4 | 85.8 | 7089 | ||
| PETFRP SPECIMENS (outer-PETFRP, inner-steel) | |||||||||||
| DSTC-A2-I | 500 | 208 | 1.638 | 139.7 | 3.5 | 823.9 | 325 | 28.4 | 1268 | Tao Yu [44] | 2017 |
| DSTC-A2-II | 500 | 208 | 1.638 | 139.7 | 3.5 | 823.9 | 325 | 28.4 | 1305 | ||
| DSTC-A3-I | 500 | 208 | 2.457 | 139.7 | 3.5 | 823.9 | 325 | 28.4 | 1424 | ||
| DSTC-A3-II | 500 | 208 | 2.457 | 139.7 | 3.5 | 823.9 | 325 | 28.4 | 1581 | ||
| DSTC-A4-I | 500 | 208 | 3.276 | 139.7 | 3.5 | 823.9 | 325 | 28.4 | 1658 | ||
| DSTC-A4-II | 500 | 208 | 3.276 | 139.7 | 3.5 | 823.9 | 325 | 28.4 | 1627 | ||
| DSTC-B3-I | 500 | 208 | 2.457 | 139.7 | 5.4 | 823.9 | 270 | 28.4 | 1755 | ||
| DSTC-B3-II | 500 | 208 | 2.457 | 139.7 | 5.4 | 823.9 | 270 | 28.4 | 1897 | ||
| STEEL SPECIMENS (outer-steel, inner-steel) | |||||||||||
| A2-l | 230 | 75.4 | 1.29 | 62.7 | 1.23 | 486 | 470 | 46.2 | 348 | Wei et al. [45] | 1995 |
| A2-2 | 230 | 75.2 | 1.19 | 62.4 | 1.2 | 486 | 470 | 46.2 | 348 | ||
| A3-l | 230 | 76.3 | 1.78 | 62 | 1 | 486 | 470 | 46.2 | 395 | ||
| A3-2 | 230 | 76.3 | 1.74 | 62 | 0.94 | 512 | 470 | 46.2 | 395 | ||
| B2-1 | 230 | 81.5 | 1.11 | 62.7 | 1.14 | 524 | 470 | 46.2 | 386 | ||
| B2-2 | 230 | 81.5 | 1.14 | 62.2 | 1.13 | 524 | 470 | 46.2 | 395 | ||
| Cl-I | 230 | 87.4 | 0.99 | 61.8 | 0.87 | 428 | 452 | 46.2 | 378 | ||
| Cl-2 | 230 | 87.3 | 0.94 | 61.6 | 0.88 | 428 | 452 | 46.2 | 385 | ||
| D I-I | 230 | 99.7 | 0.59 | 80.3 | 0.55 | 409 | 474 | 46.2 | 283 | ||
| D4-1 | 230 | 99.9 | 0.7 | 74 | 0.62 | 409 | 512 | 46.2 | 380 | ||
| D5-1 | 230 | 99.8 | 0.66 | 61.4 | 0.55 | 409 | 432 | 46.2 | 443 | ||
| D6-1 | 230 | 101.7 | 1.61 | 61.5 | 0.56 | 409 | 432 | 46.2 | 644 | ||
| E2- l | 230 | 101.4 | 1.56 | 63.4 | 1.15 | 255 | 216 | 46.2 | 477 | ||
| E3- I | 230 | 101.5 | 1.65 | 76.1 | 1.19 | 255 | 235 | 46.2 | 417 | ||
| E4-I | 230 | 114.3 | 1.64 | 63.5 | 1.12 | 262 | 216 | 46.2 | 598 | ||
| E5-I | 230 | 114.3 | 1.64 | 76.1 | 1.14 | 262 | 235 | 46.2 | 551 | ||
| E6-I | 230 | 114.3 | 1.64 | 88.9 | 1.56 | 262 | 286 | 46.2 | 524 | ||
| cc2a | 540 | 180 | 3 | 48 | 3 | 275.9 | 396.1 | 47.4 | 1790 | Tao et al. [9] | 2004 |
| cc2b | 540 | 180 | 3 | 48 | 3 | 275.9 | 396.1 | 47.4 | 1791 | ||
| cc3a | 540 | 180 | 3 | 88 | 3 | 275.9 | 370.2 | 47.4 | 1648 | ||
| cc3b | 540 | 180 | 3 | 88 | 3 | 275.9 | 370.2 | 47.4 | 1650 | ||
| cc4a | 540 | 180 | 3 | 140 | 3 | 275.9 | 342 | 47.4 | 1435 | ||
| cc4b | 540 | 180 | 3 | 140 | 3 | 275.9 | 342 | 47.4 | 1358 | ||
| cc5a | 342 | 114 | 3 | 58 | 3 | 294.5 | 374.5 | 47.4 | 904 | ||
| cc5b | 342 | 114 | 3 | 58 | 3 | 294.5 | 374.5 | 47.4 | 898 | ||
| cc6a | 720 | 240 | 3 | 114 | 3 | 275.9 | 294.5 | 47.4 | 2421 | ||
| cc6b | 720 | 240 | 3 | 114 | 3 | 275.9 | 294.5 | 47.4 | 2460 | ||
| cc7a | 900 | 300 | 3 | 165 | 3 | 275.9 | 320.5 | 47.4 | 3331 | ||
| cc7b | 900 | 300 | 3 | 165 | 3 | 275.9 | 320.5 | 47.4 | 3266 | ||
| O1I1 | 400 | 114.3 | 6 | 48.3 | 2.9 | 454 | 425 | 63.4 | 1665 | Zhao et al. [46] | 2010 |
| O2I1 | 400 | 114.3 | 4.8 | 48.3 | 2.9 | 416 | 425 | 63.4 | 1441 | ||
| O3I1 | 400 | 114.3 | 3.6 | 48.3 | 2.9 | 453 | 425 | 63.4 | 1243 | ||
| O4I1 | 400 | 114.3 | 3.2 | 48.3 | 2.9 | 430 | 425 | 63.4 | 1145 | ||
| O5I2 | 400 | 165.1 | 3.5 | 101.6 | 3.3 | 433 | 394 | 63.4 | 1629 | ||
| O6I2 | 500 | 165.1 | 3 | 101.6 | 3.2 | 395 | 394 | 63.4 | 1613 | ||
| O7I2 | 500 | 163.8 | 2.35 | 101.6 | 3.2 | 395 | 394 | 63.4 | 1487 | ||
| O8I2 | 500 | 163 | 1.95 | 101.6 | 3.2 | 395 | 394 | 63.4 | 1328 | ||
| O9I2 | 500 | 162.5 | 1.7 | 101.6 | 3.2 | 395 | 394 | 63.4 | 1236 | ||
| c10-375 | 450 | 158 | 0.9 | 38 | 0.9 | 221 | 221 | 18.7 | 635 | Uenaka et al. [33] | 2010 |
| c10-750 | 450 | 159 | 0.9 | 76 | 0.9 | 221 | 221 | 18.7 | 540 | ||
| c16-375 | 450 | 158 | 1.5 | 39 | 1.5 | 308 | 308 | 18.7 | 851.6 | ||
| c16-750 | 450 | 158 | 1.5 | 77 | 1.5 | 308 | 308 | 18.7 | 728.1 | ||
| c16-1125 | 450 | 158 | 1.5 | 114 | 1.5 | 308 | 308 | 18.7 | 589 | ||
| c23-375 | 450 | 158 | 2.14 | 40 | 2.14 | 286 | 286 | 18.7 | 968.2 | ||
| c23-750 | 450 | 158 | 2.14 | 77 | 2.14 | 286 | 286 | 18.7 | 879.1 | ||
| c23-1125 | 450 | 157 | 2.14 | 115 | 2.14 | 286 | 286 | 18.7 | 703.6 | ||
| DC-1 | 1324 | 120 | 1.96 | 60 | 1.96 | 311 | 380 | 53.45 | 779.1 | Han et al. [47] | 2011 |
| DC-2 | 1324 | 120 | 1.96 | 60 | 1.96 | 311 | 380 | 53.45 | 836.9 | ||
| DCc-1 | 1324 | 120 | 1.96 | 60 | 1.96 | 311 | 380 | 53.45 | 789.9 | ||
| DCc-2 | 1324 | 120 | 1.96 | 60 | 1.96 | 311 | 380 | 53.45 | 715.4 | ||
| 1 | 660 | 220 | 3.62 | 159 | 3.62 | 319.6 | 319.6 | 52.7 | 2537 | Han et al. [48] | 2011 |
| 2 | 660 | 220 | 3.62 | 159 | 3.62 | 319.6 | 319.6 | 52.7 | 2566 | ||
| 3 | 660 | 220 | 3.62 | 106 | 3.62 | 319.6 | 319.6 | 52.7 | 3436 | ||
| 4 | 660 | 220 | 3.62 | 106 | 3.62 | 319.6 | 319.6 | 52.7 | 3506 | ||
| 7 | 660 | 220 | 3.62 | 159 | 3.62 | 319.6 | 319.6 | 52.7 | 2908 | ||
| 8 | 660 | 220 | 3.62 | 159 | 3.62 | 319.6 | 319.6 | 52.7 | 2860 | ||
| DCS500-4-300A | 998 | 500.2 | 4.02 | 301.6 | 3.02 | 366 | 366 | 25.32 | 4206 | Chen et al. [49] | 2015 |
| DCS500-4-300B | 1001 | 500.3 | 4.03 | 302.1 | 3.01 | 366 | 366 | 25.32 | 4606 | ||
| DCS500-4-300C | 1000 | 500.1 | 4.01 | 300.9 | 3 | 366 | 366 | 25.32 | 4789 | ||
| DCS500-3-300A | 1001 | 498.9 | 3.01 | 299.8 | 3 | 366 | 366 | 25.32 | 4162 | ||
| DCS500-3-300B | 1002 | 498.5 | 2.99 | 302.1 | 2.98 | 366 | 366 | 25.32 | 3886.5 | ||
| DCS500-3-300C | 1000 | 499.6 | 3.02 | 301.5 | 2.99 | 366 | 366 | 25.32 | 3882 | ||
| DCS600-4-400A | 1001 | 601.1 | 4.01 | 401.2 | 2.98 | 366 | 366 | 25.32 | 5383.5 | ||
| DCS600-4-400B | 1003 | 602.3 | 4.02 | 402.1 | 2.97 | 366 | 366 | 25.32 | 5370.5 | ||
| DCS600-4-400C | 1001 | 603.4 | 3.98 | 401.5 | 3.02 | 366 | 366 | 25.32 | 4820 | ||
| DCS600-3-400A | 999 | 601.5 | 2.98 | 399.8 | 3.01 | 366 | 366 | 25.32 | 4415 | ||
| DCS600-3-400B | 999 | 601.2 | 3.02 | 400.1 | 3.02 | 366 | 366 | 25.32 | 4084.5 | ||
| CDCS400-3-1000 | 1002 | 400.2 | 3.01 | 241.2 | 3.01 | 366 | 366 | 25.32 | 3423 | ||
| CDCS400-3-2000 | 2003 | 400.6 | 3.02 | 240.5 | 3 | 366 | 366 | 25.32 | 3013 | ||
| CDCS400-3-2500 | 2501 | 398.2 | 3 | 239.8 | 3 | 366 | 366 | 25.32 | 3256.5 | ||
| CDCS400-3-3500 | 3502 | 398.6 | 3 | 239.6 | 3.02 | 366 | 366 | 25.32 | 2923 | ||
| DCS400-4-1000 | 1001 | 401.2 | 4 | 240.2 | 3 | 366 | 366 | 25.32 | 3828 | ||
| DCS400-4-2000B | 2005 | 400.7 | 4.02 | 240.1 | 3.02 | 366 | 366 | 25.32 | 3542 | ||
| DCS400-4-2500 | 2502 | 400.3 | 4.05 | 240 | 3.05 | 366 | 366 | 25.32 | 3790 | ||
| DCS400-3-1000 | 1002 | 401.2 | 3.02 | 240 | 2.99 | 366 | 366 | 25.32 | 2990 | ||
| DCS400-3-2500 | 2498 | 400.1 | 2.98 | 240.2 | 2.98 | 366 | 366 | 25.32 | 3490 | ||
| S139.2-1.0 | 998 | 139.2 | 3 | 76 | 2 | 418 | 418 | 21.81 | 1059.2 | Essopjee and Dundu [50] | 2015 |
| S139.2-1.0 | 1001 | 139.2 | 3 | 76 | 2 | 418 | 418 | 21.81 | 1056.1 | ||
| S139.2-1.5 | 1500 | 139.2 | 3 | 76 | 2 | 418 | 418 | 21.81 | 905.5 | ||
| S139.2-1.5 | 1503 | 139.2 | 3 | 76 | 2 | 418 | 418 | 21.81 | 901.6 | ||
| S139.2-2.0 | 2000 | 139.2 | 3 | 76 | 2 | 418 | 418 | 21.81 | 831.7 | ||
| S139.2-2.0 | 1998 | 139.2 | 3 | 76 | 2 | 418 | 418 | 21.81 | 837.4 | ||
| S139.2-2.5 | 2502 | 139.2 | 3 | 76 | 2 | 418 | 418 | 21.81 | 732.1 | ||
| S139.2-2.5 | 2498 | 139.2 | 3 | 76 | 2 | 418 | 418 | 21.81 | 729 | ||
| S152.4-1.0 | 1003 | 152.4 | 3 | 76 | 2 | 549 | 549 | 21.81 | 1263.5 | ||
| S152.4-1.0 | 1002 | 152.4 | 3 | 76 | 2 | 549 | 549 | 21.81 | 1254.9 | ||
| S152.4-1.5 | 1497 | 152.4 | 3 | 76 | 2 | 549 | 549 | 21.81 | 1195.6 | ||
| S152.4-1.5 | 1503 | 152.4 | 3 | 76 | 2 | 549 | 549 | 21.81 | 1191.2 | ||
| S152.4-2.0 | 1997 | 152.4 | 3 | 76 | 2 | 549 | 549 | 21.81 | 1047.3 | ||
| S152.4-2.0 | 2000 | 152.4 | 3 | 76 | 2 | 549 | 549 | 21.81 | 1041.6 | ||
| S152.4-2.5 | 2498 | 152.4 | 3 | 76 | 2 | 549 | 549 | 21.81 | 941.4 | ||
| S152.4-2.5 | 2500 | 152.4 | 3 | 76 | 2 | 549 | 549 | 21.81 | 949 | ||
| S165.1-1.0 | 998 | 165.1 | 3 | 76 | 2 | 516 | 516 | 21.81 | 1512.3 | ||
| S165.1-1.0 | 999 | 165.1 | 3 | 76 | 2 | 516 | 516 | 21.81 | 1510.6 | ||
| S165.1-1.5 | 1504 | 165.1 | 3 | 76 | 2 | 516 | 516 | 21.81 | 1286.4 | ||
| S165.1-1.5 | 1498 | 165.1 | 3 | 76 | 2 | 516 | 516 | 21.81 | 1275.1 | ||
| S165.1-2.0 | 2003 | 165.1 | 3 | 76 | 2 | 516 | 516 | 21.81 | 1187.2 | ||
| S165.1-2.0 | 1998 | 165.1 | 3 | 76 | 2 | 516 | 516 | 21.81 | 1199.8 | ||
| S165.1-2.5 | 2498 | 165.1 | 3 | 76 | 2 | 516 | 516 | 21.81 | 1028 | ||
| S165.1-2.5 | 2502 | 165.1 | 3 | 76 | 2 | 516 | 516 | 21.81 | 1036.5 | ||
| S193.7-1.0 | 1003 | 193.7 | 3.5 | 76 | 2 | 391 | 391 | 21.81 | 2010 | ||
| S193.7-1.0 | 1000 | 193.7 | 3.5 | 76 | 2 | 391 | 391 | 21.81 | 2030 | ||
| S193.7-1.5 | 1502 | 193.7 | 3.5 | 76 | 2 | 391 | 391 | 21.81 | 1730 | ||
| S193.7-1.5 | 1500 | 193.7 | 3.5 | 76 | 2 | 391 | 391 | 21.81 | 1720 | ||
| S193.7-2.0 | 1998 | 193.7 | 3.5 | 76 | 2 | 391 | 391 | 21.81 | 1581.6 | ||
| S193.7-2.0 | 2003 | 193.7 | 3.5 | 76 | 2 | 391 | 391 | 21.81 | 1584.1 | ||
| S193.7-2.5 | 2503 | 193.7 | 3.5 | 76 | 2 | 391 | 391 | 21.81 | 1451.4 | ||
| S193.7-2.5 | 2497 | 193.7 | 3.5 | 76 | 2 | 391 | 391 | 21.81 | 1458.7 | ||
References
- Naser, M.Z.; Thai, S.; Thai, H.-T. Evaluating structural response of concrete-filled steel tubular columns through machine learning. J. Build. Eng. 2021, 34, 101888. [Google Scholar] [CrossRef]
- Liu, S.; Ding, X.; Li, X.; Liu, Y.; Zhao, S. Behavior of Rectangular-Sectional Steel Tubular. Materials 2019, 12, 2716. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vatulia, G.; Lobiak, A.; Orel, Y. Simulation of performance of circular CFST columns under short-time and long-time load. MATEC Web Conf. 2017, 116, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Zheng, J.; Wang, J. Concrete-Filled Steel Tube Arch Bridges in China. Engineering 2018, 4, 143–155. [Google Scholar] [CrossRef]
- Botchkarev, A. A new typology design of performance metrics to measure errors in machine learning regression algorithms. Interdiscip. J. Inf. Knowl. Manag. 2019, 14, 45–76. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.L.; Grzebieta, R. Strength and ductility of concrete filled double skin (SHS inner and SHS outer) tubes. Thin-Walled Struct. 2002, 40, 199–213. [Google Scholar] [CrossRef]
- Woldemariam, A.M.; Oyawa, W.O.; Nyomboi, T. The Behavior of Concrete-Filled Single and Double-Skin uPVC Tubular Columns Under Axial Com-pression Loads. Open Constr. Build. Technol. J. 2019, 13, 164–177. [Google Scholar] [CrossRef]
- Abramski, M.; Korzeniowski, P.; Klempka, K. Experimental studies of concrete-filled composite tubes under axial short- and long-term loads. Materials 2020, 13, 2080. [Google Scholar] [CrossRef]
- Tao, Z.; Han, L.; Zhao, X. Behaviour of concrete-filled double skin (CHS inner and CHS outer) steel tubular stub columns and beam-columns. J. Constr. Steel Res. 2004, 60, 1129–1158. [Google Scholar] [CrossRef]
- Baghi, H. Shear Strengthening of Reinforced Concrete Beams with SHCC-FRP Panels; Universidade do MinhoEscola de Engenharia: Braga, Portugal, 2015. [Google Scholar]
- Shakir Abbood, I.; aldeen Odaa, S.; Hasan, K.F.; Jasim, M.A. Properties evaluation of fiber reinforced polymers and their constituent materials used in structures—A review. Mater. Today Proc. 2021, 43, 1003–1008. [Google Scholar] [CrossRef]
- Karthika, S.; Ranjitham, M. Study of Strength and Behaviour of Concrete Filled Double Skin Tubular Square Columns under Axial Compressive Loads. Int. J. Eng. Res. 2016, V5, 746–751. [Google Scholar] [CrossRef]
- Skaria, A.; Kuriakose, M. Numerical Study on Axial Behaviour of Concrete Filled Double Skin Steel Tubular (CFDST) Column with Cross Helical FRP Wrappings. IOP Conf. Ser. Mater. Sci. Eng. 2018, 396, 012008. [Google Scholar] [CrossRef]
- Hsiao, P.-C.; Kazuhiro Hayashi, K.; Nishi, R.; Lin, X.-C.; Nakashima, M. Investigation of Concrete-Filled Double-Skin Steel Tubular Columns with Ultrahigh-Strength Steel. J. Struct. Eng. 2015, 141, 04014166. [Google Scholar] [CrossRef]
- Romero, M.L.; Espinos, A.; Portolés, J.M.; Hospitaler, A.; Ibañez, C. Slender double-tube ultra-high strength concrete-filled tubular columns under ambient temperature and fire. Eng. Struct. 2015, 99, 536–545. [Google Scholar] [CrossRef] [Green Version]
- Mohd Zuki, S.S.; Shahidan, S.; Keong, C.K.; Jayaprakash, J.; Ali, N. Concrete-Filled Double Skin Steel Tubular Columns Exposed to ASTM E-119 Fire Curve for 60 and 90 Minutes of Fire. MATEC Web Conf. 2017, 103, 02009. [Google Scholar] [CrossRef] [Green Version]
- Alias, A.; Jacob, S. An overview on Concrete Filled Double Skin Steel Tube (CFDST) column with FRP wrapping. Int. Res. J. Eng. Technol. 2017, 4, 2081–2083. [Google Scholar]
- Teng, J.G.; Yu, T.; Wong, Y.L.; Dong, S.L. Hybrid FRP-concrete-steel tubular columns: Concept and behavior. Constr. Build. Mater. 2007, 21, 846–854. [Google Scholar] [CrossRef]
- Wang, J.; Liu, W.; Zhou, D.; Zhu, L.; Fang, H. Mechanical behaviour of concrete filled double skin steel tubular stub columns confined by FRP un-der axial compression. Steel Compos. Struct. 2014, 17, 431–452. [Google Scholar] [CrossRef]
- Louk Fanggi, B.A.; Ozbakkaloglu, T. Compressive behavior of aramid FRP-HSC-steel double-skin tubular columns. Constr. Build. Mater. 2013, 48, 554–565. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Fanggi, B.L. Axial compressive behavior of FRP-concrete-steel double-skin tubular columns made of normal- and high-strength concrete. J. Compos. Constr. 2014, 18, 04013027. [Google Scholar] [CrossRef]
- Zhang, B.; Teng, J.G.; Yu, T. Compressive Behavior of Double-Skin Tubular Columns with High-Strength Concrete and a Filament-Wound FRP Tube. J. Compos. Constr. 2017, 21, 04017029. [Google Scholar] [CrossRef]
- İpek, S.; Güneyisi, E.M. Ultimate Axial Strength of Concrete-Filled Double Skin Steel Tubular Column Sections. Adv. Civ. Eng. 2019, 2019, 6493037. [Google Scholar] [CrossRef] [Green Version]
- Hossain, K.M.A.; Chu, K. Confinement of six different concretes in CFST columns having different shapes and slenderness. Int. J. Adv. Struct. Eng. 2019, 11, 255–270. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.Y.; Chan, T.M. Experimental investigation on octagonal concrete filled steel stub columns under uniaxial compression. J. Constr. Steel Res. 2018, 147, 457–467. [Google Scholar] [CrossRef]
- Du, Y.; Chen, Z.; Richard Liew, J.Y.; Xiong, M.-X. Rectangular concrete-filled steel tubular beam-columns using high-strength steel: Experiments and design. J. Constr. Steel Res. 2017, 131, 1–18. [Google Scholar] [CrossRef]
- Karim, S.A.; Ipe, B.A. Comparative Study on Cfrp Concrete Filled Double Skin Tube (Cfdst) Columns. Int. J. Innov. Res. Technol. 2016, 3, 148–155. [Google Scholar]
- Le, T.T.; Phan, H.C. Prediction of Ultimate Load of Rectangular CFST Columns Using Interpretable Machine Learning Method. Adv. Civ. Eng. 2020, 2020, 1–16. [Google Scholar] [CrossRef]
- Lee, N.K.; Souri, H.; Lee, H.K. Neural network application overview in prediction of properties of cement-based mortar and concrete. In Proceedings of the 2014 World Congress on Advances in Civil, Environmental, and Materials Research (ACEM14), Busan, Korea, 24–28 August 2014. [Google Scholar]
- Hou, C.; Zhou, X.G. Strength prediction of circular CFST columns through advanced machine learning methods. J. Build. Eng. 2022, 51, 104289. [Google Scholar] [CrossRef]
- Mai, S.H.; Ben Seghier, M.E.A.; Nguyen, P.L.; Jafari-Asl, J.; Thai, D.K. A hybrid model for predicting the axial compression capacity of square concrete-filled steel tubular columns. Eng. Comput. 2022, 38, 1205–1222. [Google Scholar] [CrossRef]
- Cakiroglu, C.; Islam, K.; Bekdaş, G.; Kim, S.; Geem, Z.W. Interpretable Machine Learning Algorithms to Predict the Axial Capacity of FRP-Reinforced Concrete Columns. Materials. 2022, 15, 2742. [Google Scholar] [CrossRef]
- Uenaka, K.; Kitoh, H.; Sonoda, K. Concrete filled double skin circular stub columns under compression. Thin-Walled Struct. 2010, 48, 19–24. [Google Scholar] [CrossRef]
- Liao, J.; Asteris, P.G.; Cavaleri, L.; Mohammed, A.S.; Lemonis, M.E.; Tsoukalas, M.Z.; Skentou, A.D.; Maraveas, C.; Koopialipoor, M.; Armaghani, D.J. Novel fuzzy-based optimization approaches for the prediction of ultimate axial load of circular concrete-filled steel tubes. Buildings 2021, 11, 629. [Google Scholar] [CrossRef]
- Cao, Q.; Asce, A.M.; Tao, J.; Wu, Z.; Ma, Z.J.; Asce, F. Behavior of FRP-Steel Confined Concrete Tubular Columns Made of Expansive Self-Consolidating Concrete under Axial Compression Behavior of FRP-Steel Confined Concrete Tubular Columns Made of Expansive Self-Consolidating Concrete under Axial Compression. J. Compos. Constr. 2017, 21, 04017037. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, X.; Xing, F.; Li, D.; Wang, Y.; Sui, L. Behavior and modeling of FRP-concrete-steel double-skin tubular columns made of full lightweight aggregate concrete. Constr. Build. Mater. 2017, 139, 52–63. [Google Scholar] [CrossRef]
- Deng, J.; Zheng, Y.; Wang, Y.; Liu, T.; Li, H. Study on Axial Compressive Capacity of FRP-Confined Concrete-Filled Steel Tubes and Its Comparisons with Other Composite Structural Systems. Int. J. Polym. Sci. 2017, 2017. [Google Scholar] [CrossRef] [Green Version]
- Ozbakkaloglu, T. Thin-Walled Structures A novel FRP–dual-grade concrete–steel composite column system. Thin Walled Struct. 2015, 96, 295–306. [Google Scholar] [CrossRef]
- Xiong, Z.; Deng, J.; Liu, F.; Li, L.; Feng, W. Experimental investigation on the behavior of GFRP-RAC-steel double-skin tubular columns under axial compression. Thin-Walled Struct. 2018, 132, 350–361. [Google Scholar] [CrossRef]
- Zhang, B.; Hu, X.; Wei, W.; Zhang, Q.; Zhang, N.; Zhang, Y. Effect of Cross-Sectional Aspect Ratio on Rectangular FRP-Concrete-Steel Double-Skin Tubular Columns under Axial Compression. Adv. Polym. Technol. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Yu, T.; Zhang, B.; Cao, Y.B.; Teng, J.G. Thin-Walled Structures Behavior of hybrid FRP-concrete-steel double-skin tubular columns subjected to cyclic axial compression. Thin-Walled Struct. 2012, 61, 196–203. [Google Scholar] [CrossRef]
- Abdelkarim, O.I.; ElGawady, M.A.; Gheni, A.; Anumolu, S.; Abdulazeez, M. Seismic Performance of Innovative Hollow-Core FRP–Concrete–Steel Bridge Columns. J. Bridge Eng. 2017, 22, 1–15. [Google Scholar] [CrossRef]
- Zhang, B.; Teng, J.G.; Yu, T. Experimental behavior of hybrid FRP–concrete–steel double-skin tubular columns under combined axial compression and cyclic lateral loading. Eng. Struct. 2015, 99, 214–231. [Google Scholar] [CrossRef]
- Yu, T.; Zhang, S.; Huang, L.; Chan, C. Compressive behavior of hybrid double-skin tubular columns with a large rupture strain FRP tube. Compos. Struct. 2017, 171, 10–18. [Google Scholar] [CrossRef] [Green Version]
- Wei, S.; Mau, S.T.; Vipulanandan, C.; Mantrala, S.K. Performance of New Sandwich Tube under Axial Loading: Experiment. J. Struct. Eng. 1995, 121, 1806–1814. [Google Scholar] [CrossRef]
- Zhao, X.L.; Tong, L.W.; Wang, X.Y. CFDST stub columns subjected to large deformation axial loading. Eng. Struct. 2010, 32, 692–703. [Google Scholar] [CrossRef]
- Han, L.H.; Li, Y.J.; Liao, F.Y. Concrete-filled double skin steel tubular (CFDST) columns subjected to long-term sustained loading. Thin-Walled Struct. 2011, 49, 1534–1543. [Google Scholar] [CrossRef]
- Han, L.H.; Ren, Q.X.; Li, W. Tests on stub stainless steelconcretecarbon steel double-skin tubular (DST) columns. J. Constr. Steel Res. 2011, 67, 437–452. [Google Scholar] [CrossRef]
- Chen, J.; Ni, Y.Y.; Jin, W.L. Column tests of dodecagonal section double skin concrete-filled steel tubes. Thin-Walled Struct. 2015, 88, 28–40. [Google Scholar] [CrossRef]
- Essopjee, Y.; Dundu, M. Performance of concrete-filled double-skin circular tubes in compression. Compos. Struct. 2015, 133, 1276–1283. [Google Scholar] [CrossRef]


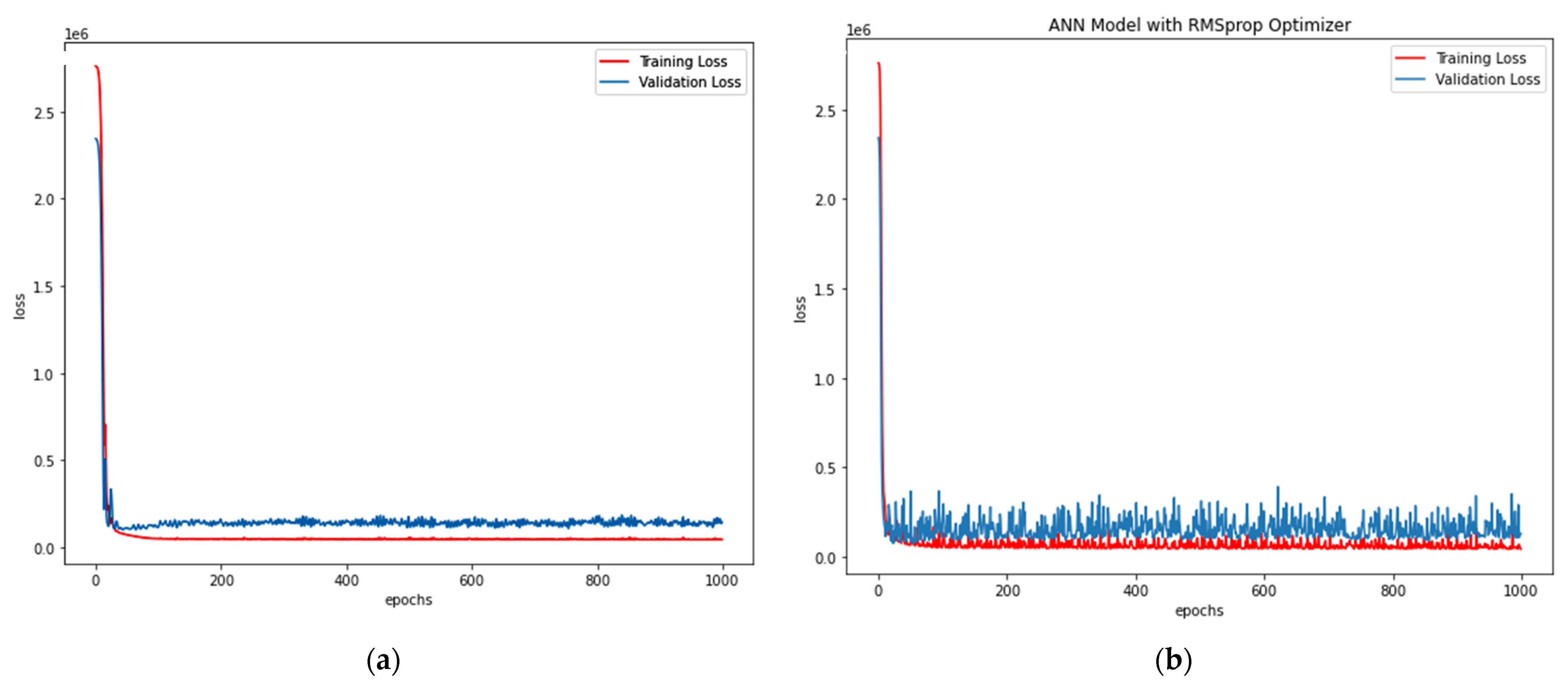
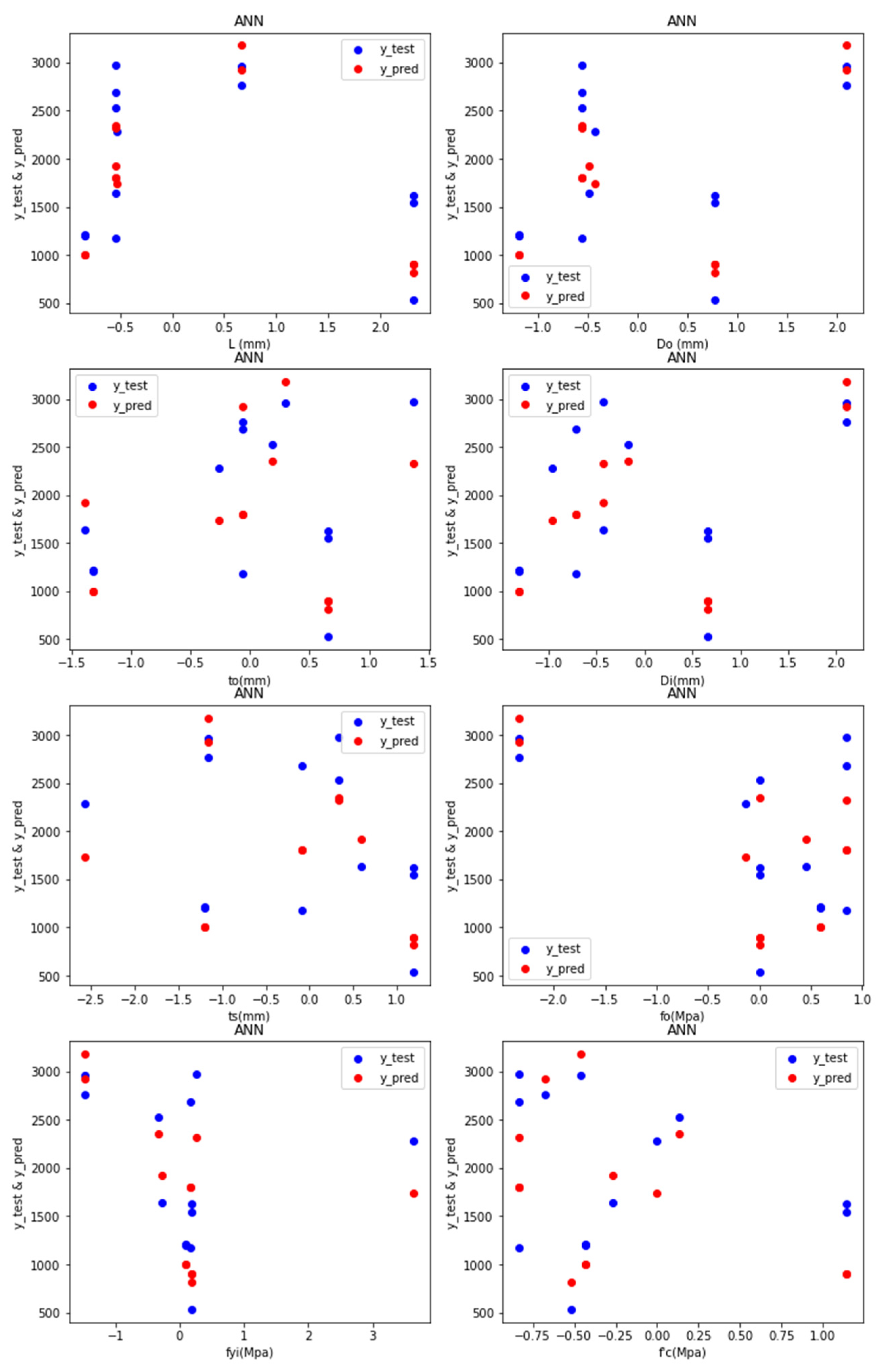
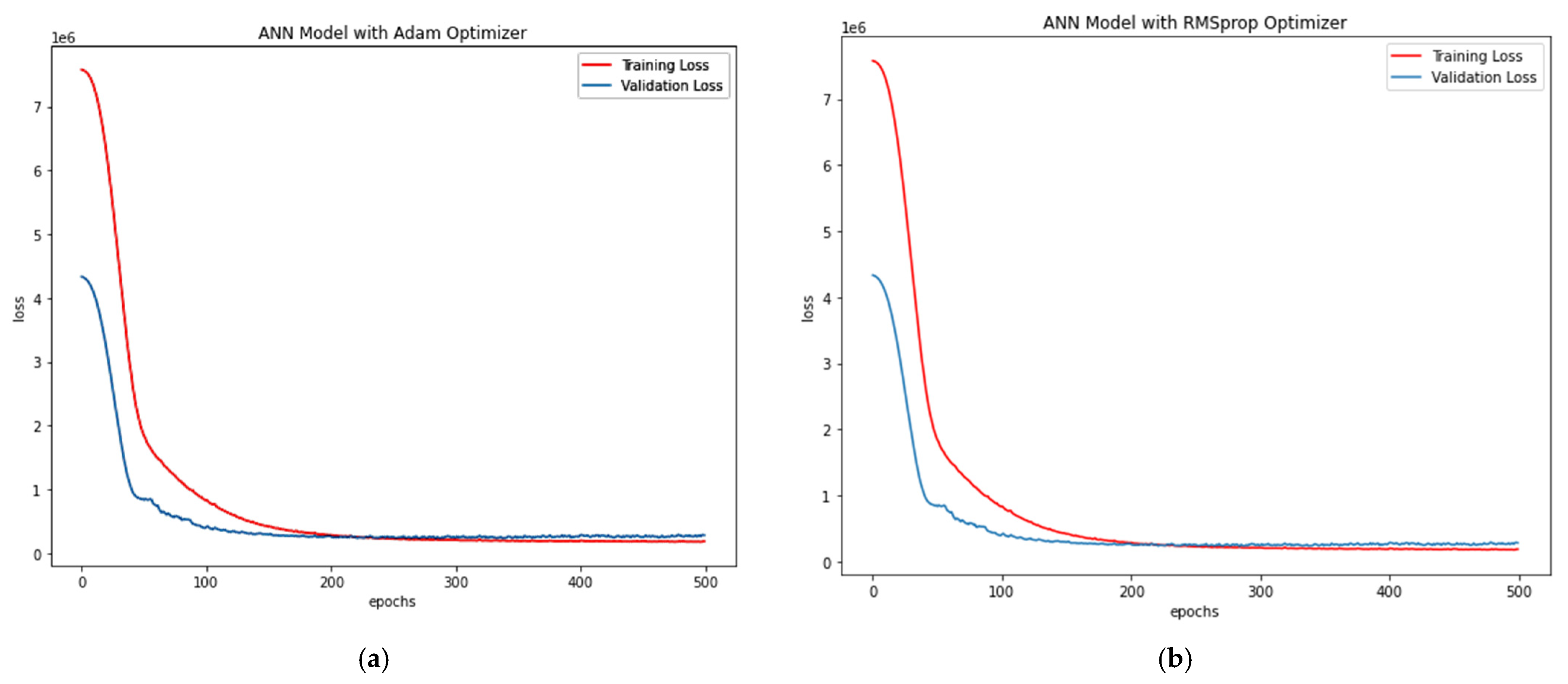


| RFR | XGBR | ABR | LR | RR | ANN R (Adam) | ANN R (RMSprop) | ||
|---|---|---|---|---|---|---|---|---|
| AFRP | RMSE | 537.12 | 542.54 | 510.00 | 660.82 | 654.41 | 547.77 | 558.12 |
| R2 | 0.58 | 0.70 | 0.62 | 0.37 | 0.38 | 0.57 | 0.55 | |
| CFRP | RMSE | 355.50 | 355.22 | 371.04 | 380.38 | 380.71 | 380.81 | 359.93 |
| R2 | 0.27 | 0.27 | 0.20 | 0.16 | 0.16 | 0.16 | 0.25 | |
| GFRP | RMSE | 670.26 | 569.86 | 549.96 | 630.14 | 585.16 | 493.80 | 531.77 |
| R2 | 0.25 | 0.45 | 0.49 | 0.33 | 0.42 | 0.59 | 0.52 | |
| PETFRP | RMSE | 204.39 | 208.50 | 206.84 | 355.50 | 200.58 | 202.16 | 228.49 |
| R2 | 0.71 | 0.70 | 0.70 | 0.27 | 0.72 | 0.71 | 0.63 | |
| STEEL | RMSE | 195.57 | 202.54 | 182.86 | 315.97 | 317.03 | 172.76 | 156.10 |
| R2 | 0.98 | 0.97 | 0.98 | 0.94 | 0.94 | 0.984 | 0.987 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chandramouli, P.; Jayaseelan, R.; Pandulu, G.; Sathish Kumar, V.; Murali, G.; Vatin, N.I. Estimating the Axial Compression Capacity of Concrete-Filled Double-Skin Tubular Columns with Metallic and Non-Metallic Composite Materials. Materials 2022, 15, 3567. https://doi.org/10.3390/ma15103567
Chandramouli P, Jayaseelan R, Pandulu G, Sathish Kumar V, Murali G, Vatin NI. Estimating the Axial Compression Capacity of Concrete-Filled Double-Skin Tubular Columns with Metallic and Non-Metallic Composite Materials. Materials. 2022; 15(10):3567. https://doi.org/10.3390/ma15103567
Chicago/Turabian StyleChandramouli, Pavithra, Revathy Jayaseelan, Gajalakshmi Pandulu, Veerappan Sathish Kumar, Gunasekaran Murali, and Nikolai Ivanovich Vatin. 2022. "Estimating the Axial Compression Capacity of Concrete-Filled Double-Skin Tubular Columns with Metallic and Non-Metallic Composite Materials" Materials 15, no. 10: 3567. https://doi.org/10.3390/ma15103567
APA StyleChandramouli, P., Jayaseelan, R., Pandulu, G., Sathish Kumar, V., Murali, G., & Vatin, N. I. (2022). Estimating the Axial Compression Capacity of Concrete-Filled Double-Skin Tubular Columns with Metallic and Non-Metallic Composite Materials. Materials, 15(10), 3567. https://doi.org/10.3390/ma15103567










